Ottimizzazione degli analizzatori ottici nel dominio del tempo Brillouin basati sull'ingegneria dello spettro del guadagno

Riepilogo

Viene presentato un protocollo per gli analizzatori ottici nel dominio del tempo Brillouin basato sull'ingegneria dello spettro di guadagno. Si ottengono miglioramenti nelle prestazioni di rilevamento, tra cui la distanza di rilevamento e la risoluzione del misurando, e si studia l'eccesso di rumore di intensità di Brillouin. Il protocollo introduce un nuovo modo per migliorare le prestazioni di rilevamento distribuito di Brillouin.

Abstract

È stato dimostrato un metodo unico per il miglioramento delle prestazioni di rilevamento negli analizzatori ottici nel dominio del tempo (BOTDA) Brillouin. Uno spettro di guadagno di Brillouin (BGS) è sovrapposto a due spettri di perdita di Brillouin simmetrici (BLS). Ciò porta a una forma dello spettro ingegnerizzata complessa che è più resistente al rumore del sistema di rilevamento. Invece di una sola interazione tra pompa e sonda come nella configurazione BOTDA convenzionale, vengono sfruttate tre onde ottiche della sonda, con una sonda situata nel BGS e le altre due simmetricamente nel BLS. Grazie alla resistenza e all'insensibilità della forma dello spettro ingegnerizzata al rumore, le prestazioni di rilevamento sono migliorate del 60% e la risoluzione del misuratore è raddoppiata.

Introduzione

Il rilevamento distribuito delle fibre (DFS) è un meccanismo unico che impiega un'intera fibra come mezzo di rilevamento. Ha suscitato molto interesse a causa della bassa perdita di fibra; di piccole dimensioni; e la capacità di essere facilmente incorporato in varie strutture, come dighe, ponti ed edifici, per eseguire la sorveglianza ambientale come un sistema nervoso artificiale. Rispetto all'applicazione di numerosi sensori puntiformi tradizionali, come i reticoli in fibra di Bragg (FBG), fornisce una soluzione più efficiente ed economica in un'ampia gamma di attività di rilevamento su larga scala, come il monitoraggio delle infrastrutture e della salute strutturale¹.

I sensori distribuiti in corrente sfruttano diversi meccanismi di scattering all'interno della fibra per misurare la temperatura e la distribuzione della deformazione. Tra questi, il DFS basato sullo scattering di Brillouin è il più interessante a causa dei notevoli vantaggi dello scattering di Brillouin stimolato (SBS), come l'elevato rapporto segnale/rumore (SNR), la bassa soglia e la sensibilità sia alla temperatura² che alla deformazione³. La SBS può essere classicamente descritta come un'interazione tra le onde ottiche continue incidenti (CW), cioè la pompa, e l'onda della sonda CW contropropagante tramite un'onda acustica. In base alla conservazione dell'energia e della quantità di moto, l'onda della sonda viene spostata in frequenza verso la pompa. Questo spostamento è chiamato spostamento di frequenza di Brillouin (BFS). Considerando la durata finita di un'onda acustica di 10 ns, esiste una distribuzione spettrale finita dell'onda rifratta, chiamata anche spettro di guadagno di Brillouin (BGS), in cui il BFS è la differenza di frequenza tra l'onda di pompa e la frequenza centrale di picco. L'interazione tra le onde porta a una regione di guadagno con spostamento verso il basso della frequenza e a una regione di perdita con spostamento verso l'alto della frequenza in cui l'onda della sonda viene amplificata e attenuata, rispettivamente. Per una fibra monomodale standard (SSMF) in banda C, il BFS è di circa 11 GHz e il BGS ha una forma lorentziana con una larghezza intera ultra-stretta a metà massimo (FWHM) di 10-30 MHz, che può essere ulteriormente ridotta a 3,4 MHz con tecniche specifiche 4,5,6,7. Sulla base di queste caratteristiche, SBS può essere applicato anche nei filtri fotonici a microonde ^8,9,10, nei filtri ottici¹¹, nella luce lenta e veloce 12,13,14 e nella spettroscopia ottica ad alta risoluzione ^7,15.

Una delle applicazioni SBS più promettenti è il rilevamento distribuito di Brillouin. Questi sensori sfruttano la dipendenza BFS dalla temperatura e dalla deformazione. Il primo ad essere dimostrato è stato l'analizzatore ottico nel dominio del tempo Brillouin (BOTDA)¹⁶, che è la tecnica di rilevamento Brillouin distribuita nel dominio del tempo più consolidata. Si differenzia dall'interazione CW-SBS convenzionale in quanto sfrutta l'interazione SBS tra un'onda di pompa pulsata e una sonda CW in modo che l'informazione ambientale venga interrogata localmente su ogni sezione di fibra. La frequenza della pompa o della sonda è solitamente fissa mentre la frequenza della sonda o della pompa viene scansionata nelle vicinanze del BFS. La potenza della sonda viene registrata per la ricostruzione del BGS e il BFS è idealmente la frequenza di picco del BGS locale in ogni sezione di fibra. Tuttavia, a causa dell'inevitabile rumore del sistema, il picco BGS è solitamente ambiguo e deve essere applicato un algoritmo adatto¹⁷, che porta a un certo errore di stima nella frequenza¹⁸ e influenza la risoluzione del misurando.

Statisticamente, l'errore di stima BFS è inversamente proporzionale al rapporto segnale/rumore (SNR) del sistema. Il modo più semplice per migliorare l'SNR è aumentare la potenza della pompa e della sonda. Tuttavia, questi sono limitati dall'instabilità di modulazione (MI)¹⁹ e dagli effetti non locali (NLE)^{da 20,21} a ~20 dBm e -14 dBm, rispettivamente. Numerose tecniche, come la codifica²² e l'amplificazione in linea basata su Raman²³ sono state proposte per superare questi limiti. Recentemente, è stato riportato che questo errore di frequenza può essere minimizzato scegliendo un algoritmo di adattamento adeguato²⁴. Allo stesso modo, le misure che sfruttano la fase di Brillouin e un algoritmo di fitting lineare hanno anche un errore di frequenza ridotto²⁵, che indica il potenziale di un BGS ben progettato per il miglioramento delle prestazioni di rilevamento. Un'altra opzione per migliorare l'SNR è la riduzione del rumore. Tuttavia, secondo il punto di vista tradizionale, il rumore del sistema di rilevamento proviene principalmente dal rivelatore (cioè il rumore di modo comune, incluso il rumore scuro, il rumore di sparo, ecc.)^26,27 e il miglioramento è meno probabile.

L'idea di base di questo articolo è quella di ingegnerizzare il BGS mediante la sovrapposizione di un BGS convenzionale con due spettri di perdita di Brillouin simmetrici (BLS) (vedi Figura 1). Rispetto a uno spettro BGS convenzionale, che segue una forma lorentziana, lo spettro ingegnerizzato è più nitido e robusto con lo stesso livello di rumore del sistema. Pertanto, il rumore ha meno influenza sulla determinazione della frequenza di picco. Ciò può essere verificato raccogliendo e adattando i dati di misurazione BGS un numero statisticamente significativo di volte. Grazie a questa migliore resistenza al rumore, si ottengono miglioramenti delle prestazioni di rilevamento, tra cui il campo di rilevamento del 60% e la risoluzione del misurando raddoppiata, ovvero un errore di frequenza ridotto del 50%. A causa del coinvolgimento della misura con l'interazione di perdita di Brillouin in una parte del BGS ingegnerizzato, viene effettuato un confronto diretto del rumore di traccia con e senza interazione di Brillouin. A causa dell'elusione dell'eccesso di rumore Brillouin, la traccia con il BGS ingegnerizzato è molto più chiara.

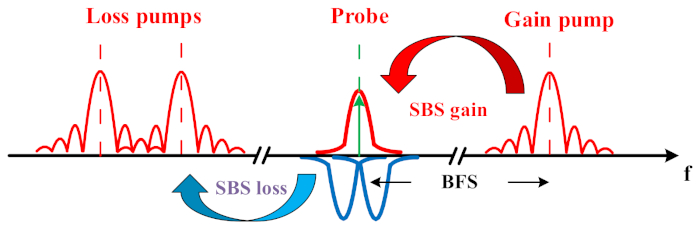
Figura 1: Schema di un BGS ingegnerizzato mediante la sovrapposizione di un guadagno di Brillouin e due spettri di perdita di Brillouin simmetrici. Clicca qui per visualizzare una versione più grande di questa figura.

Access restricted. Please log in or start a trial to view this content.

Protocollo

1. Selezione di parametri ottimizzati per l'ingegneria dello spettro tramite simulazione

1. Modella il BGS g_SBS(ν,z) ingegnerizzato con le equazioni ^28,29
   
   come implementato, ad esempio, dallo script MATLAB supplementare.
   NOTA: Qui, G(ν) è il coefficiente di guadagno complesso, calcolato nello script come G_complex all'interno della funzione SBS_g per il BGS convenzionale o della funzione SBS_gl per il BGS ingegnerizzato; g(ν,z) è il complesso locale guadagno di Brillouin; e g_SBS e φ_SBS sono la parte reale e immaginaria di g(ν,z) e simboleggiano rispettivamente la risposta di fase BGS e SBS nella posizione z dall'estremità di lancio della pompa. Nello script, g_SBS è simboleggiato dalle variabili SBS_g_log e SBS_gl_log rispettivamente per il BGS convenzionale e ingegnerizzato in scala logaritmica. P_p = 20 dBm (P_pump nello script) è la potenza di picco dell'impulso della pompa all'estremità di lancio della fibra; ν_B è il BFS (normalizzato nello script); g₀ = 0,2 ^{W-1 m-1} (g₀ nello script) è il coefficiente di guadagno di Brillouin; Δν_B = 50 MHz (gamma_B nello script) è l'FWHM del BGS; α = 0,2 dB/km è il coefficiente di perdita della fibra ed è rappresentato da alpha_log e alpha_lin come il valore in scala logaritmica e lineare nello script, rispettivamente; ν è la frequenza d'onda della sonda in modo che l'offset di frequenza della pompa e della sonda ν - ν_B venga scansionato da -250 MHz a 250 MHz. L'offset di frequenza della pompa e della sonda è rappresentato nello script come vettore globale f. Il termine g₁ = mg₀ è il fattore di perdita; 2d∙Δν_B è l'offset di frequenza tra le due perdite; e L_eff = 10 m (L_eff nello script) è la lunghezza dell'interazione di Brillouin per un'ampiezza dell'impulso di 100 ns. La forma spettrale ingegnerizzata può essere facilmente regolata regolando due fattori normalizzati, m e d. Il BGS convenzionale può essere modellato semplicemente da m = 0.
2. Aggiungi rumore casuale (cioè rumore gaussiano bianco additivo) con lo stesso livello sia sul BGS convenzionale che su quello ingegnerizzato. La regolazione del noise_level dei parametri nello script può modificare il livello di rumore.
3. Adattare il BGS rumoroso convenzionale con la funzione lorentziana (funzione Lorentz_g_gain_fun nello script) e il BGS rumoroso ingegnerizzato con la funzione lorentziana sovrapposta (funzione Lorentz_gl_gain_fun nello script) (vedere la Figura 2A).
4. Determinare l'offset della frequenza di picco dovuto al rumore per il BGS convenzionale e ingegnerizzato (Figura 2B).
5. Ripetere i passaggi 1.2-1.4 per N = 500 e raccogliere tutti gli offset di frequenza di picco Δf_ci e Δf_pi (rappresentati rispettivamente da delta_g_g e delta_g_gl nello script) per il BGS convenzionale e ingegnerizzato nel processo^i-esimo , rispettivamente.

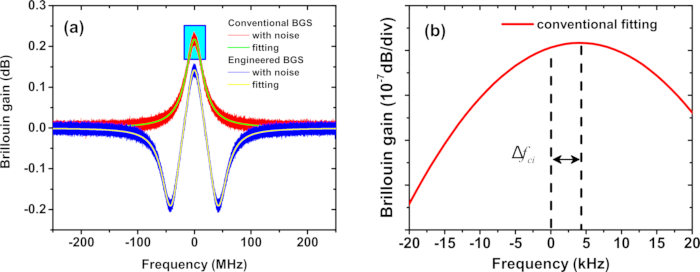
Figura 2: BGS simulato. (A) Dimostrazione dell'adattamento di un tipico BGS lorentziano (rosso) e ingegnerizzato (blu) nella simulazione. (B) Il picco Lorentzian BGS da (A). Δf_ci rappresenta l'errore di stima BFS per il BGS convenzionale nell'i-esima misurazione. Clicca qui per visualizzare una versione più grande di questa figura.

6. Calcolare il rapporto tra la deviazione standard degli errori di stima BFS indotti dal rumore come:
   
7. Tracciare η in funzione di m e d (vedi Figura 3A). Trova il valore minimo η_min e i corrispondenti m e d. Il vantaggio dell'accuratezza della stima sarà mantenuto lungo tutta la fibra²⁸.
8. Regolare il valore di z (cioè la lunghezza della fibra, anche z nello script) nell'equazione (2) da 0 km a 60 km, fare un passo di 50 m e ripetere i passaggi 1.1-1.7 con alcuni valori m e d selezionati. Quindi è possibile acquisire il rapporto tra la deviazione standard in funzione della lunghezza della fibra (vedi Figura 3B).

2. Preparare e testare la configurazione BOTDA convenzionale (blocco evidenziato nella Figura 4B)

1. Accendere il diodo laser (LD) e verificare la funzionalità del LD con l'analizzatore di spettro ottico (OSA). Di solito, viene utilizzata una lunghezza d'onda intorno a 1.550 nm.
2. Collegare il LD con l'accoppiatore ottico 10:90 (OC). Controllare l'alimentazione dall'uscita OC al 10%. Se la potenza è superiore a 13 dBm (la potenza di ingresso massima dello scrambler di polarizzazione [Pol.S.]), ridurre la potenza di uscita LD abbassando la corrente LD.
3. Collegare l'uscita OC al 10% con il Pol.S. Per evitare che la polarizzazione sbiadisca¹, impostare la frequenza di scrambling su 1 kHz.
4. Controllare l'alimentazione dall'uscita del Pol.S. Se la potenza è superiore a -3 dBm (il limite massimo di potenza in ingresso dell'amplificatore ottico a semiconduttore [SOA]), aggiungere attenuatori fino a quando non viene soddisfatto il requisito di alimentazione. Collegare il Pol.S. con la SOA.
5. Applicare il segnale elettrico del treno di impulsi con un'ampiezza dell'impulso di 100 ns e una frequenza di ripetizione di 4 kHz dal generatore di impulsi (PG) sul SOA. Assicurarsi che l'ampiezza del segnale dell'impulso sia superiore alla soglia TTL (transistor-transistor) della SOA (cioè 4 dBm) e che la frequenza di ripetizione soddisfi il requisito di andata e ritorno³⁰.
6. Collegare l'uscita della SOA con l'amplificatore in fibra drogata con erbio (EDFA 1) e far funzionare l'EDFA in modalità di controllo automatico della corrente (ACC). Collegare l'uscita da EDFA 1 alla porta 1 del circolatore (Cir).
7. Controllare il segnale dell'impulso ottico dalla porta 2 di Cir nel digitalizzatore collegandolo al fotodiodo (PD). Per evitare danni al PD, è necessaria un'attenuazione sufficiente.
8. Calcola la potenza di picco dell'impulso ottico in base alla forma d'onda misurata nel digitalizzatore. La potenza di picco ottica P_o è stimata in base a
   
   dove V_E è la tensione di picco dell'impulso elettrico e R _{e R f} sono la reattività e la transresistenza PD. In questo calcolo si tiene conto dell'attenuazione della protezione, in modo da valutare la corretta potenza della pompa in ingresso nella fibra in prova (FUT, 10,6 km).
9. Annotare il valore di corrente EDFA I₂₀ quando la potenza di picco dell'impulso ottico calcolata raggiunge i 20 dBm (soglia MI¹⁹). Il rapporto di estinzione (ER) del treno di impulsi ottici può essere valutato in base alla conservazione dell'energia:
   
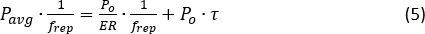
   dove P_avg è la potenza ottica media del treno di impulsi; f_rep è il tasso di ripetizione; e τ è l'ampiezza dell'impulso. L'ER della SOA è solitamente superiore a 30 dBm, evitando efficacemente NLE^31,32.
   NOTA: Spegnere l'EDFA prima di scollegare il PD e continuare a costruire il sistema.
10. Collega la porta 2 del Cir con un'estremità del FUT per completare la configurazione del ramo della pompa. Controlla se il sistema soffrirà di MI controllando lo spettro dall'altra estremità del FUT nell'OSA e impostando l'EDFA su un valore di corrente costante, I₂₀. Se lo spettro rilevato è lo stesso (nella forma, non necessariamente in ampiezza) a quello misurato nel passaggio 2.1, allora il sistema è libero da MI. In caso contrario, quando si osserva un evidente allargamento dello spettro o una suddivisione del picco³³ , ridurre la corrente EDFA 1 per mantenere la forma dello spettro.
11. Collegare l'uscita del 90% dell'OC a un OC 1 50:50 e collegare una delle uscite OC 1 al modulatore Mach-Zehnder (MZM 1) tramite un controller di polarizzazione (PC). Impostare correttamente la polarizzazione, in modo che l'uscita da MZM 1 sia massimizzata (allineamento della polarizzazione).
12. Applica il segnale a radiofrequenza (RF) dal generatore RF (RFG 1) con il BFS della FUT (per SSMF a circa 11 GHz) e l'ampiezza di 16 dBm all'MZM 1. Impostare la tensione di polarizzazione CC dell'MZM 1 in modo che la portante sia soppressa al minimo.
13. Collegare l'uscita dell'MZM 1 con un reticolo in fibra di Bragg (FBG 1). Controllare lo spettro di uscita dall'FBG 1 nell'OSA in modo che l'FBG 1 sia impostato per bloccare la banda laterale della frequenza superiore e la portante.
14. Collegare consecutivamente l'uscita dall'FBG 1 all'EDFA 2, un altro OC 2 50:50 e un isolatore (ISO).
15. Utilizzare EDFA 2 anche in modalità ACC e impostare il valore di corrente su I_g, in modo che la potenza di uscita dall'ISO sia inferiore a -14 dBm, riducendo al minimo NLE²⁰. Spegnere l'EDFA prima di scollegare il misuratore di potenza e continuare la costruzione del sistema. Collega l'uscita ISO all'altra estremità del FUT per completare la configurazione del ramo della sonda del guadagno.
16. Collegare la porta Cir 3 all'EDFA 4 (per la preamplificazione³⁴) e al PD. Impostare l'EDFA in modalità ACC. Il valore di corrente I₄ dovrebbe consentire che la potenza di uscita da EDFA sia 4 inferiore al limite di ingresso del PD. Collegare l'uscita RF PD a un filtro passa-basso RF da 10 MHz^35,36. Collegare l'uscita del filtro al digitalizzatore.
17. Collegare il trigger del digitalizzatore con l'uscita sincronizzata (o inversa) del generatore di impulsi. Impostare i parametri del digitalizzatore come segue: Frequenza di campionamento: 500 MSa/s; media: 4.096 volte; Numero di campioni: 10.000.
18. Impostare il valore corrente di EDFA 1, EDFA 2 e EDFA 4 rispettivamente su I₂₀, I_g e I₄. Eseguire un programma di registrazione delle tracce. Controllare la traccia misurata nel digitalizzatore. Se l'ampiezza della traccia segue il decadimento esponenziale, allora il sistema di rilevamento è privo di MI. In caso contrario, ridurre il valore corrente di EDFA 1.

3. Misurazione con la configurazione BOTDA convenzionale ed elaborazione dei dati

1. Impostare i valori di EDFA 1 e EDFA 2 rispettivamente su I₂₀ e I_g. Scansiona la frequenza di RFG 1 nell'intervallo di BFS ± 90 MHz con incrementi di 1 MHz. Registrare la traccia dal programma di registrazione dopo ogni passaggio di scansione.
2. Calcola il guadagno locale di Brillouin dividendo l'ampiezza della traccia (nel periodo di interazione di Brillouin) per ciascun offset DC (periodo di interazione non di Brillouin).
3. Recuperare il BGS in ogni sezione di fibra adattando il BGS rumoroso misurato con il raccordo lorentziano. Determinare l'FWHM del BGS convenzionale Δν_B0 dal raccordo.
4. Ripetere i passaggi 3.1 e 3.2 per N = 48 volte e raccogliere tutte le distribuzioni di frequenza di picco stimate (BFS) lungo la fibra ν_Bci(z) nell'i-esimo processo (vedere Figura 5A).
5. Calcolare l'errore di stima BFS come deviazione standard del BFS montato in ciascuna sezione di fibra nelle 48 misurazioni (vedere Figura 5B).

4. Preparazione del resto della configurazione

NOTA: In questo caso, sono stati utilizzati m = 1 e d = 1,24, in base ai risultati della simulazione (vedere la sezione 1 e la Figura 3).

1. Collegare l'altra uscita del 50:50 OC 1 nel ramo della sonda con l'EDFA 3 e il 50:50 OC 3.
2. Collegare una delle uscite di 50:50 OC 3 a un PC e MZM 2. Regolare la polarizzazione in modo che l'uscita da MZM 2 sia massimizzata.
3. Applicare il segnale RF da RFG 2 con BFS - d∙Δν_B0 e ampiezza di 16 dBm su MZM 2. Controllare lo spettro di modulazione nell'OSA e regolare la tensione di polarizzazione per ridurre al minimo l'ampiezza della portante.
4. Collegare l'uscita da MZM 2 all'ingresso di un interruttore ottico (OS 1), uno degli ingressi di 50:50 OC 4 e l'FBG 2.
5. Controllare il segnale ottico nell'OSA e regolare la lunghezza d'onda centrale dell'FBG 2 in modo che la portante e la banda laterale di frequenza inferiore siano bloccate (vedere la Figura 4A). L'impostazione del ramo della sonda di perdita 1 sarà quindi completa.
6. Collegare l'altra uscita del 50:50 OC 3 a un PC e all'MZM 3. Regolare la polarizzazione in modo che l'uscita da MZM 3 sia massimizzata.
7. Applicare il segnale RF dall'RFG 3 con BFS + d∙Δν_B0 e l'ampiezza di 16 dBm su MZM 3. Controllare lo spettro di modulazione nell'OSA e regolare la tensione di polarizzazione per ridurre al minimo l'ampiezza della portante.
8. Collegare l'uscita da MZM 3 a un attenuatore ottico variabile (VOA) con funzione di commutazione (OS 2) e l'altro ingresso di 50:50 OC 4. Considerando che l'offset tra le frequenze della sonda di perdita è relativamente piccolo rispetto alla finestra di trasmissione FBG 2 (diversi GHz), anche la portante e la banda laterale di frequenza inferiore di MZM 3 saranno bloccate da FBG 2. L'impostazione del ramo della sonda loss 2 sarà quindi completa.
9. Chiudere OS 1, aprire OS 2 e impostare il valore di corrente EDFA 3 su I_l in modo che la potenza della sonda di perdita 1 sia pari a -14 dBm (m = 1).
10. Aprire OS 1, chiudere OS 2 e regolare l'attenuazione del VOA in modo che anche la potenza della sonda di perdita 2 sia pari a -14 dBm.

5. Misurazione utilizzando la configurazione BOTDA completa proposta ed elaborazione dei dati

1. Chiudere OS 1, chiudere OS 2 e impostare il valore corrente di EDFA 1, EDFA 2, EDFA 3 e EDFA 4 rispettivamente su I₂₀, I_g, I_l e I₄. Scansiona la frequenza dell'RFG 1 nell'intervallo di BFS ± 90 MHz in incrementi di 1 MHz. Le frequenze di RFG 2 e RFG 3 scansionano di conseguenza. Registrare la traccia dal programma dopo ogni passaggio di scansione.
2. Calcolare il guadagno di Brillouin locale come al punto 3.2 e recuperare il BGS ingegnerizzato in ogni sezione di fibra adattando il BGS rumoroso misurato con la funzione lorentziana sovrapposta.
3. Ripetere i passaggi 5.1 e 5.2 per N = 48 volte e raccogliere tutte le distribuzioni di frequenza di picco stimate (BFS) lungo la fibra ν_Bpi(z) nell'i-esimo processo (vedere Figura 5A).
4. Calcolare l'errore di stima BFS come deviazione standard del BFS montato in ciascuna sezione di fibra nelle 48 misurazioni (vedere Figura 5B).

Access restricted. Please log in or start a trial to view this content.

Risultati

La Figura 3 mostra i risultati della simulazione. I punti con η < 1 nella Figura 3A indicano un errore di frequenza minore (risoluzione del misurando più elevata) con il BGS ingegnerizzato. Più basso era il valore, maggiore era il vantaggio. Il rapporto minimo era a m = 1, indicando che è possibile eseguire uno schema multisonda invece di multipompa (vedi Di...

Access restricted. Please log in or start a trial to view this content.

Discussione

Il passaggio più critico durante l'esperimento è l'equalizzazione delle tre potenze della sonda in modo da ottenere m = 1 e la simmetria tra i due spettri di perdita di Brillouin. Oltre al controllo separato della potenza utilizzando il misuratore di potenza alla porta Cir 2, come illustrato nei passaggi 4.9 e 4.10, l'equalizzazione della potenza può essere controllata in modo più preciso nel digitalizzatore. Impostando la frequenza RF 1 a ~11 GHz (la fibra BFS) e disattivan...

Access restricted. Please log in or start a trial to view this content.

Materiali

Name	Company	Catalog Number	Comments
Current controller for laser diode	ILX Lightwave	LDX3220
Digitizer	Acqiris SA	U5309A-1039
Erbium doped fiber amplifier 1	Photop	PTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2	LiComm	OFA-TCH
Erbium doped fiber amplifier 3	Calmar Optcom	AMP-ST30
Erbium doped fiber amplifier 4	Photop	PTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1	Advanced Optics Solutions	T-FBG
Fiber Bragg grating 2	Advanced Optics Solutions	T-FBG
Fiber under test	ofs
Isolator	General Photonics	S-15-NTSS
Laser diode	3SP Group	A1905 LMI
Mach-Zehnder modulator 1	Avanex	IM10
Mach-Zehnder modulator 2	Avanex	IM10
Mach-Zehnder modulator 3	Avanex	IM10
Nanosecond driving board for semiconductor optical amplifier	Highland Technology	T160-9 (28A160-9C)
Optical coupler 10:90	Newport		Benchtop coupler/WDM
Optical coupler 50:50	Newport		Benchtop coupler/WDM
Optical spectrum analyzer	Hewlett Packard	86145A
Optical switch 1	JDSU	SN12-1075NC
Photodiode	Thorlabs	D400FC
Polarization scrambler	General Photonics	PSY-101
Pulase generator	Hewlett Packard	8082A
Radio function generator 1	Anritsu	MG3692C
Radio function generator 2	Agilent Technology	E8257D
Radio function generator 3	HTM	T2100
Semiconductor optical amplifier	Thorlabs	SOA1013SXS
Temperature controller for laser diode	ILX Lightwave	LDT5948
Temperature controller for semiconductor optical amplifier	Tektronix	TED200
Variable optical attenuator	JDSU	mVOA-A1	With optical switch function