Gain Spectrum Engineering을 기반으로 한 Brillouin Optical Time-Domain Analyzer 최적화

요약

이득 스펙트럼 엔지니어링을 기반으로 하는 Brillouin 광학 시간 영역 분석기를 위한 프로토콜이 제시됩니다. 감지 범위 및 측정 분해능을 포함한 감지 성능의 향상이 달성되고 과도한 Brillouin 강도 잡음이 연구됩니다. 이 프로토콜은 분산 브릴루인 감지 성능을 향상시키는 새로운 방법을 도입합니다.

초록

Brillouin 광학 시간 영역 분석기(BOTDA)에서 성능 향상을 감지하는 고유한 방법을 시연했습니다. Brillouin 이득 스펙트럼(BGS)에는 두 개의 대칭 Brillouin 손실 스펙트럼(BLS)이 중첩됩니다. 이로 인해 감지 시스템 잡음에 더 잘 견디는 복잡하게 설계된 스펙트럼 모양이 생성됩니다. 기존 BOTDA 설정에서와 같이 하나의 펌프와 프로브가 상호 작용하는 대신 3개의 광학 프로브 웨이브가 활용되며, 하나의 프로브는 BGS에 있고 다른 두 개는 BLS에 대칭으로 있습니다. 엔지니어링된 스펙트럼 모양의 잡음에 대한 저항과 둔감성으로 인해 감지 성능이 60% 향상되고 측정 분해능이 두 배로 증가합니다.

서문

DFS(Distributed Fiber Sensing)는 전체 광섬유를 감지 매체로 사용하는 고유한 메커니즘입니다. 섬유 손실이 적기 때문에 많은 관심을 끌었습니다. 작은 크기; 댐, 교량, 건물 등 다양한 구조물에 쉽게 매립되어 인공 신경계로 환경 감시를 수행할 수 있는 능력. 광섬유 브래그 격자(FBG)와 같은 수많은 기존 포인트 센서를 적용하는 것과 비교하여 인프라 및 구조 건전성 모니터링¹과 같은 광범위한 대규모 감지 작업에서 보다 효율적이고 비용 효율적인 솔루션을 제공합니다.

전류 분산 센서는 광섬유 내부의 다양한 산란 메커니즘을 활용하여 온도와 변형률 분포를 측정합니다. 그 중 브릴루인 산란을 기반으로 하는 DFS는 높은 신호 대 잡음비(SNR), 낮은 임계값, 온도² 및 변형률³에 대한 민감도와 같은 유도 브릴루인 산란(SBS)의 눈에 띄는 장점으로 인해 가장 매력적입니다. SBS는 고전적으로 입사 광학 연속파(CW), 즉 펌프와 음파를 통한 역전파 CW 프로브파 간의 상호 작용으로 설명할 수 있습니다. 에너지와 운동량의 보존에 따라 프로브 파동은 펌프로 주파수 하향 이동됩니다. 이러한 이동을 브릴루인 주파수 편이(BFS)라고 합니다. 10ns 음파의 유한한 수명을 고려할 때, Brillouin gain spectrum (BGS)라고도하는 굴절파의 유한 스펙트럼 분포가 있으며, 여기서 BFS는 펌프파와 피크 중심 주파수 사이의 주파수 차이입니다. 파동 간의 상호 작용은 프로브 파동이 각각 증폭 및 감쇠되는 주파수 하향 이동 이득 영역과 주파수 상향 이동 손실 영역으로 이어집니다. C-Band의 표준 단일 모드 광섬유(SSMF)의 경우 BFS는 약 11GHz이고 BGS는 10-30MHz의 FWHM(ultra-narrow full-width at half maximum)을 가진 로렌찔 모양이며, 이는 특정 기술 ^4,5,6,7을 사용하여 3.4MHz로 더 줄일 수 있습니다. 이러한 특성을 바탕으로 SBS는 마이크로파 포토닉스 필터 ^8,9,10, 광학 필터¹¹, 저속 및 고속 광 12,13,14 및 고해상도 광학 분광법 ^7,15에도 적용할 수 있습니다.

가장 유망한 SBS 응용 프로그램 중 하나는 분산 Brillouin 감지입니다. 이 센서는 온도 및 변형률에 대한 BFS 의존성을 이용합니다. 가장 먼저 시연된 것은 Brillouin 광학 시간 도메인 분석기(BOTDA)¹⁶으로, 이는 가장 통합된 시간 도메인 분포 Brillouin 감지 기술입니다. 이는 펄스 펌프파와 프로브 CW 사이의 SBS 상호 작용을 활용하여 환경 정보가 모든 광섬유 섹션에서 국부적으로 조사된다는 점에서 기존의 CW-SBS 상호 작용과 다릅니다. 펌프 또는 프로브 주파수는 일반적으로 프로브 또는 펌프 주파수가 BFS 근처에서 스캔되는 동안 고정됩니다. 프로브 전력은 BGS 재구성을 위해 기록되며 BFS는 이상적으로 각 광섬유 섹션에서 로컬 BGS의 피크 주파수입니다. 그러나 불가피한 시스템 노이즈로 인해 BGS 피크는 일반적으로 모호하고 피팅 알고리즘⁽¹⁷)을 적용해야 하며, 이는 주파수⁽¹⁸ )에서 특정 추정 오류를 유발하고 측정 분해능에 영향을 미칩니다.

통계적으로 BFS 추정 오차는 시스템 신호 대 잡음비(SNR)에 반비례합니다. SNR을 향상시키는 가장 간단한 방법은 펌프와 프로브 출력을 높이는 것입니다. 그러나 이는 변조 불안정성(MI)¹⁹ 및 비국소 효과(NLE)^20,21 - ~20 dBm 및 -14 dBm에 의해 제한됩니다. 이러한 한계를 극복하기 위해 코딩⁽²²) 및 라만 기반 인라인 증폭(²³)과 같은 수많은 기술이 제안되었습니다. 최근에, 이러한 주파수 오차는 적절한 피팅 알고리즘⁽²⁴)을 선택함으로써 최소화될 수 있다는 것이 보고되고 있다. 이와 관련하여, Brillouin 위상 및 선형 피팅 알고리즘을 활용하는 측정은 주파수 오류²⁵가 감소하는 것으로 보고되었으며, 이는 감지 성능 향상에 대한 잘 설계된 BGS의 잠재력을 나타냅니다. SNR을 향상시키는 또 다른 옵션은 노이즈 감소입니다. 그러나 전통적인 관점에 따르면 감지 시스템 노이즈는 주로 검출기에서 발생합니다(즉, 암흑 노이즈, 샷 노이즈 등을 포함한 공통 모드 노이즈).^26,27 그리고 개선될 가능성은 적습니다.

이 논문의 기본 아이디어는 기존 BGS를 두 개의 대칭 Brillouin 손실 스펙트럼(BLS)과 중첩하여 BGS를 엔지니어링하는 것입니다( 그림 1 참조). 로렌쯔안 모양을 따르는 기존 BGS 스펙트럼과 비교할 때 엔지니어링 스펙트럼은 동일한 수준의 시스템 잡음으로 더 선명하고 견고합니다. 따라서 잡음은 피크 주파수의 결정에 미치는 영향이 적습니다. 이는 BGS 측정 데이터를 통계적으로 유의미한 횟수만큼 수집하고 피팅하여 확인할 수 있습니다. 이러한 잡음에 대한 저항력이 향상되기 때문에 감지 범위가 60% 증가하고 측정 분해능이 두 배로 증가하여 주파수 오류가 50% 감소하는 등 감지 성능이 향상됩니다. 엔지니어링된 BGS의 일부에서 Brillouin 손실 상호 작용과 측정의 관련으로 인해 Brillouin 상호 작용이 있는 것과 없는 미량 잡음의 직접적인 비교가 이루어집니다. 과도한 Brillouin 노이즈의 우회로 인해 엔지니어링 된 BGS의 추적이 훨씬 명확합니다.

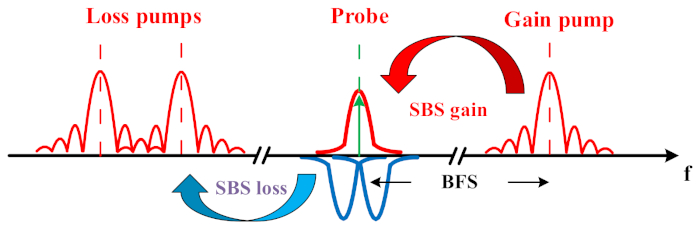
그림 1: 하나의 Brillouin 이득과 두 개의 대칭 Brillouin 손실 스펙트럼의 중첩에 의한 엔지니어링된 BGS의 개략도. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.

프로토콜

1. 시뮬레이션을 통한 스펙트럼 엔지니어링에 최적화된 파라미터 선택

1. 방정식^28,29를 사용하여 엔지니어링된 BGS g_SBS(ν,z)를 모델링합니다.
   
   예를 들어, 추가 MATLAB 스크립트에 의해 구현됩니다.
   참고: 여기서 G(ν)는 기존 BGS의 SBS_g 함수 또는 엔지니어링된 BGS의 SBS_gl 함수 내에서 G_complex 스크립트에서 계산된 복합 이득 계수입니다. g(ν,z)는 국소 복소 브릴루인 이득입니다. g_SBS 및 φ_SBS는 g(ν,z)의 실수 및 허수 부분이며 각각 펌프 발사 끝에서 z 위치에서 BGS 및 SBS 위상 응답을 상징합니다. 스크립트에서 g_SBS는 각각 로그 스케일의 기존 BGS와 엔지니어링 BGS에 대한 변수 SBS_g_log 및 SBS_gl_log로 기호화됩니다. P_p = 20dBm(스크립트에서 P_pump)은 광섬유 발사 끝단의 펌프 펄스 피크 전력입니다. ν_B는 BFS(스크립트에서 정규화됨)입니다. g₀ = 0.2 ^{W-1 m-1} (스크립트에서 g₀)은 Brillouin 이득 계수입니다. Δν_B = 50MHz(스크립트에서 gamma_B)는 BGS의 FWHM입니다. α = 0.2dB/km는 광섬유 손실 계수이며 스크립트에서 각각 alpha_log 및 alpha_lin 값으로 표시됩니다. ν는 펌프 및 프로브 주파수 오프셋 ν - ν_B가 -250MHz에서 250MHz까지 스캔되도록 프로브파 주파수입니다. 펌프 및 프로브 주파수 오프셋은 스크립트에서 전역 벡터 f로 표시됩니다. 항 g₁ = mg₀은 손실 계수입니다. 2d∙Δν_B는 두 손실 사이의 주파수 오프셋입니다. L_eff = 10m(스크립트에서 L_eff)는 100ns 펄스 폭에 대한 Brillouin 상호 작용 길이입니다. 엔지니어링된 스펙트럼 모양은 두 개의 정규화된 요인 m과 d를 조정하여 쉽게 조정할 수 있습니다. 기존 BGS는 m = 0으로 간단하게 모델링할 수 있습니다.
2. 기존 BGS와 엔지니어링 BGS 모두에서 동일한 수준의 랜덤 노이즈 (즉, 가산 백색 가우스 노이즈)를 추가합니다. 스크립트에서 매개 변수 noise_level 조정하면 노이즈 수준이 변경될 수 있습니다.
3. 기존의 노이즈가 있는 BGS에는 로렌츠 함수(스크립트의 Lorentz_g_gain_fun 함수)를 적용하고, 엔지니어링된 노이즈가 있는 BGS에는 중첩된 로렌츠 함수(스크립트의 Lorentz_gl_gain_fun 함수)를 적용합니다( 그림 2A 참조).
4. 기존 BGS와 엔지니어링된 BGS의 노이즈로 인한 피크 주파수 오프셋을 결정합니다(그림 2B).
5. N = 500에 대해 1.2-1.4단계를 반복하고 i^번째 프로세스에서 기존 BGS와 엔지니어링 BGS에 대해 각각 모든 피크 주파수 오프셋 Δf_ci 및 Δf_pi(스크립트에서 각각 delta_g_g 및 delta_g_gl로 표시)를 수집합니다.

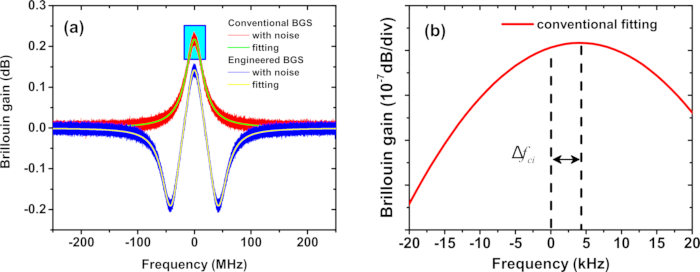
그림 2: 시뮬레이션된 BGS. (A) 시뮬레이션에서 일반적인 Lorentzian (빨간색) 및 엔지니어링 (파란색) BGS의 피팅 시연. (B) (A)의 로렌츠안 BGS 피크. _Δfci는 i^번째 측정에서 종래 BGS에 대한 BFS 추정 오차를 나타낸다. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.

6. 잡음으로 인한 BFS 추정 오차의 표준 편차 비율을 다음과 같이 계산합니다.
   
7. η m과 d의 함수로 플롯합니다(그림 3A 참조). _{최소값 η min}과 해당 m 및 d를 찾습니다. 추정 정확도의 이점은 전체 섬유⁽²⁸)를 따라 유지될 것이다.
8. 방정식 (2)의 z 값(즉, 파이버 길이, 스크립트의 z )을 0km에서 60km까지 조정하고 50m 단계를 수행하고 선택한 m 및 d 값으로 1.1-1.7 단계를 반복합니다. 그런 다음 섬유 길이의 함수로 표준 편차의 비율을 얻을 수 있습니다( 그림 3B 참조).

2. 기존 BOTDA 설정을 준비하고 테스트합니다( 그림 4B에서 강조 표시된 블록).

1. 레이저 다이오드(LD)를 켜고 광 스펙트럼 분석기(OSA)로 LD의 기능을 확인합니다. 일반적으로 약 1,550nm의 파장이 사용됩니다.
2. LD를 10:90 광 커플러(OC)에 연결합니다. 10% OC 출력의 전원을 확인하십시오. 전력이 13dBm(편광 스크램블러의 최대 입력 전력[Pol.S.])보다 높으면 LD 전류를 낮추어 LD 출력 전력을 낮추십시오.
3. 10% OC 출력을 Pol.S에 연결합니다. 편광 페이딩¹을 방지하려면 스크램블링 주파수를 1kHz로 설정하십시오.
4. Pol.S의 출력에서 전원을 확인하십시오. 전력이 -3dBm(반도체 광 증폭기[SOA]의 최대 입력 전력 제한)보다 높으면 전력 요구 사항이 충족될 때까지 감쇠기를 추가합니다. Pol.S를 연결합니다. SOA와 함께.
5. SOA의 펄스 발생기(PG)에서 100ns 펄스 폭과 4kHz 반복률로 전기 펄스 트레인 신호를 적용합니다. 펄스 신호의 진폭이 SOA의 TTL(transistor-transistor logic) 임계값(즉, 4dBm)보다 높고 반복률이 왕복 요구 사항³⁰을 충족하는지 확인합니다.
6. SOA의 출력을 에르븀 도핑 광섬유 증폭기(EDFA 1)와 연결하고 자동 전류 제어(ACC) 모드에서 EDFA를 작동합니다. EDFA 1의 출력을 순환기(Cir)의 포트 1에 연결합니다.
7. 디지타이저에서 Cir의 포트 2에서 옵티컬 펄스 신호를 포토다이오드(PD)와 연결하여 확인합니다. PD의 손상을 방지하려면 충분한 감쇠가 필요합니다.
8. 디지타이저에서 측정된 파형으로 광 펄스 피크 전력을 계산합니다. 광 피크 전력 _PO는 다음에 따라 추정됩니다.
   
   여기서 _Ve는 전기 펄스 피크 전압이고 R 및 _Rf는 PD 응답성 및 반저항입니다. 이 계산에서 보호 감쇠를 고려하여 테스트 중인 파이버(FUT, 10.6km)에 대한 올바른 입력 펌프 전력을 평가합니다.
9. 계산된 광 펄스 피크 전력이 20dBm(MI 임계값¹⁹)에 도달하면 EDFA 전류 값 I₂₀에 유의하십시오. 광 펄스 트레인의 소광비(ER)는 에너지 보존에 따라 평가할 수 있습니다.
   
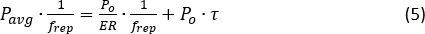
   여기서 P_avg는 펄스 트레인의 광학 평균 전력입니다. f_rep는 반복률입니다. τ는 펄스 폭입니다. SOA의 ER은 일반적으로 30dBm 이상이며 NLE^31,32를 효율적으로 회피합니다.
   알림: PD를 분리하고 시스템 구축을 계속하기 전에 EDFA를 끄십시오.
10. Cir의 포트 2를 FUT의 한쪽 끝에 연결하여 펌프 분기 설정을 완료합니다. OSA에서 FUT의 다른 쪽 끝에서 스펙트럼을 확인하고 EDFA를 정전류 값 I₂₀으로 설정하여 시스템에 MI가 발생하는지 확인합니다. 검출된 스펙트럼이 2.1단계에서 측정된 것과 동일하면(반드시 진폭이 아닌 모양으로) 시스템에 MI가 없는 것입니다. 그렇지 않고 명백한 스펙트럼 확장 또는 피크 분할⁽³³ )이 관찰될 때 EDFA 1 전류를 줄여 스펙트럼 모양을 유지합니다.
11. OC의 90% 출력을 50:50 OC 1에 연결하고 편광 컨트롤러(PC)를 통해 OC 1 출력 중 하나를 Mach-Zehnder 변조기(MZM 1)에 연결합니다. MZM 1의 출력이 최대화되도록 편광을 올바르게 설정합니다(편광 정렬).
12. FUT의 BFS(SSMF의 경우 약 11GHz) 및 16dBm 진폭을 사용하여 RF 발생기(RFG 1)의 RF(Radio Frequency) 신호를 MZM 1에 적용합니다. MZM 1의 DC 바이어스 전압을 설정하여 반송파가 최소로 억제되도록 합니다.
13. MZM 1의 출력을 광섬유 브래그 격자(FBG 1)와 연결합니다. FBG 1이 상위 주파수 측파대와 반송파를 차단하도록 설정되어 있도록 OSA에서 FBG 1의 출력 스펙트럼을 확인하십시오.
14. FBG 1의 출력을 EDFA 2, 다른 50:50 OC 2 및 절연기(ISO)에 연속적으로 연결합니다.
15. ACC 모드에서도 EDFA 2를 작동하고 현재 값을 IG로 설정하여 ISO의 출력 전력이 -14dBm보다 낮도록 하여 NLE²⁰을 최소화합니다. 전력계를 분리하기 전에 EDFA를 끄고 시스템 구축을 계속하십시오. ISO 출력을 FUT의 다른 쪽 끝에 연결하여 게인 프로브 브랜치의 설정 빌드를 완료합니다.
16. Cir 포트 3을 EDFA 4(사전 증폭³⁴) 및 PD에 연결합니다. EDFA를 ACC 모드로 설정합니다. 현재 값 I₄ 는 EDFA의 출력 전력이 PD의 입력 한계보다 4 작아야합니다. PD RF 출력을 10MHz RF 저역 통과 필터^35,36에 연결합니다. 필터 출력을 디지타이저에 연결합니다.
17. 디지타이저의 트리거를 펄스 발생기의 동기화된(또는 역) 출력과 연결합니다. 디지타이저 매개변수를 다음과 같이 설정합니다. 샘플링 속도: 500MSa/s; 평균 : 4,096 회; 샘플 수: 10,000.
18. EDFA 1, EDFA 2 및 EDFA 4의 현재 값을 각각 I₂₀, I_g 및 I₄로 설정합니다. 추적 레코딩 프로그램을 실행합니다. 디지타이저에서 측정된 트레이스를 확인합니다. 트레이스 진폭이 지수 감쇠를 따르는 경우 감지 시스템은 MI가 없습니다. 그렇지 않으면 EDFA 1의 현재 값을 줄이십시오.

3. 기존의 BOTDA 설정 및 데이터 처리를 사용한 측정

1. EDFA 1 및 EDFA 2의 값을 각각 I₂₀ 및 I_g로 설정합니다. BFS ± 90MHz 범위에서 RFG 1의 주파수를 1MHz 단계로 스캔합니다. 각 스캔 단계 후에 레코딩 프로그램의 트레이스를 기록합니다.
2. 트레이스 진폭(Brillouin 상호 작용 기간)을 각 DC 오프셋(비Brillouin 상호 작용 기간)으로 나누어 국소 Brillouin 이득을 계산합니다.
3. 측정된 잡음이 있는 BGS를 Lorentzian 피팅에 피팅하여 각 파이버 섹션에서 BGS를 검색합니다. 피팅에서 기존 BGS Δν_B0 의 FWHM을 결정합니다.
4. N = 48회에 대해 3.1단계와 3.2단계를 반복하고 i^번째 과정에서 섬유 ν_Bci(z)를 따라 추정된 피크(BFS) 주파수 분포를 모두 수집합니다(그림 5A 참조).
5. BFS 추정 오차를 48개 측정의 각 광섬유 섹션에서 피팅된 BFS의 표준 편차로 계산합니다( 그림 5B 참조).

4. 나머지 설정 준비

참고: 이 경우 시뮬레이션 결과에 따라 m = 1 및 d = 1.24가 사용되었습니다(섹션 1 및 그림 3 참조).

1. 프로브 분기에서 50:50 OC 1의 다른 출력을 EDFA 3 및 50:50 OC 3에 연결합니다.
2. 50:50 OC 3의 출력 중 하나를 PC와 MZM 2에 연결합니다. MZM 2의 출력이 최대화되도록 편광을 조정합니다.
3. BFS - d∙Δν_B0 및 16dBm 진폭으로 RFG 2의 RF 신호를 MZM 2에 적용합니다. OSA에서 변조 스펙트럼을 확인하고 바이어스 전압을 조정하여 반송파 진폭을 최소화합니다.
4. MZM 2의 출력을 광 스위치(OS 1)의 입력, 50:50 OC 4의 입력 중 하나 및 FBG 2에 연결합니다.
5. OSA에서 광 신호를 확인하고 반송파와 저주파 측파대가 차단되도록 FBG 2 중심 파장을 조정합니다( 그림 4A 참조). 그러면 손실 1 프로브 분기의 설정이 완료됩니다.
6. 50:50 OC 3의 다른 출력을 PC와 MZM 3에 연결합니다. MZM 3의 출력이 최대화되도록 편광을 조정합니다.
7. MZM 3에서 BFS + d∙Δν_B0 및 16dBm 진폭으로 RFG 3의 RF 신호를 적용합니다. OSA에서 변조 스펙트럼을 확인하고 바이어스 전압을 조정하여 반송파 진폭을 최소화합니다.
8. MZM 3의 출력을 스위치 기능(OS 2)과 50:50 OC 4의 다른 입력이 있는 가변 광 감쇠기(VOA)에 연결합니다. 손실 프로브 주파수 간의 오프셋이 FBG 2 전송 창(수 GHz)에 비해 상대적으로 작다는 점을 고려할 때 MZM 3의 반송파와 저주파 측파대도 FBG 2에 의해 차단됩니다. 그러면 손실 2 프로브 분기의 설정이 완료됩니다.
9. OS 1을 닫고 OS 2를 연 다음 손실 3 프로브의 전력이 -14dBm(m = 1)이 되도록 EDFA 1 전류 값을 I_l로 설정합니다.
10. OS 1을 열고 OS 2를 닫은 다음 손실 2 프로브의 전력도 -14dBm이 되도록 VOA의 감쇠를 조정합니다.

5. 제안된 전체 BOTDA 설정 및 데이터 처리를 사용한 측정

1. OS 1을 닫고 OS 2를 닫은 다음 EDFA 1, EDFA 2, EDFA 3 및 EDFA 4의 현재 값을 각각 I₂₀, I_g, _{I l} 및 I₄로 설정합니다. BFS ± 90MHz 범위에서 RFG 1의 주파수를 1MHz 단위로 스캔합니다. RFG 2 및 RFG 3의 주파수는 이에 따라 스캔됩니다. 각 스캔 단계 후에 프로그램의 추적을 기록합니다.
2. 3.2단계에서와 같이 로컬 Brillouin 이득을 계산하고 측정된 노이즈가 있는 BGS를 중첩된 Lorentzian 함수에 피팅하여 각 광섬유 섹션에서 엔지니어링된 BGS를 검색합니다.
3. N = 48회에 대해 5.1단계와 5.2단계를 반복하고 i^번째 과정에서 섬유 ν_Bpi(z)를 따라 추정된 피크(BFS) 주파수 분포를 모두 수집합니다(그림 5A 참조).
4. BFS 추정 오차를 48개 측정의 각 광섬유 섹션에서 피팅된 BFS의 표준 편차로 계산합니다( 그림 5B 참조).

결과

그림 3은 시뮬레이션 결과를 보여줍니다. 그림 1A에서 η < 3 점이 있으면 엔지니어링된 BGS에서 더 작은 주파수 오류(더 높은 측정 분해능)를 나타냅니다. 값이 낮을수록 이점이 커집니다. 최소 비율은 m = 1이었으며, 이는 다중 펌프 방식 대신 다중 프로브를 수행할 수 있음을 나?...

토론

실험 중 가장 중요한 단계는 m = 1이고 두 Brillouin 손실 스펙트럼 간의 대칭이 달성되도록 세 개의 프로브 파워를 균등화하는 것입니다. 4.9 및 4.10 단계에서 제시된 바와 같이 Cir 포트 2의 전력계를 사용한 별도의 전력 확인 외에도 디지타이저에서 전력 이퀄라이제이션을 보다 정확하게 확인할 수 있습니다. RF 1 주파수를 ~11GHz(광섬유 BFS)로 설정하고 EDFA 3을 끄면 피크 ...

자료

Name	Company	Catalog Number	Comments
Current controller for laser diode	ILX Lightwave	LDX3220
Digitizer	Acqiris SA	U5309A-1039
Erbium doped fiber amplifier 1	Photop	PTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2	LiComm	OFA-TCH
Erbium doped fiber amplifier 3	Calmar Optcom	AMP-ST30
Erbium doped fiber amplifier 4	Photop	PTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1	Advanced Optics Solutions	T-FBG
Fiber Bragg grating 2	Advanced Optics Solutions	T-FBG
Fiber under test	ofs
Isolator	General Photonics	S-15-NTSS
Laser diode	3SP Group	A1905 LMI
Mach-Zehnder modulator 1	Avanex	IM10
Mach-Zehnder modulator 2	Avanex	IM10
Mach-Zehnder modulator 3	Avanex	IM10
Nanosecond driving board for semiconductor optical amplifier	Highland Technology	T160-9 (28A160-9C)
Optical coupler 10:90	Newport		Benchtop coupler/WDM
Optical coupler 50:50	Newport		Benchtop coupler/WDM
Optical spectrum analyzer	Hewlett Packard	86145A
Optical switch 1	JDSU	SN12-1075NC
Photodiode	Thorlabs	D400FC
Polarization scrambler	General Photonics	PSY-101
Pulase generator	Hewlett Packard	8082A
Radio function generator 1	Anritsu	MG3692C
Radio function generator 2	Agilent Technology	E8257D
Radio function generator 3	HTM	T2100
Semiconductor optical amplifier	Thorlabs	SOA1013SXS
Temperature controller for laser diode	ILX Lightwave	LDT5948
Temperature controller for semiconductor optical amplifier	Tektronix	TED200
Variable optical attenuator	JDSU	mVOA-A1	With optical switch function