Otimizando analisadores ópticos no domínio do tempo Brillouin com base na engenharia de espectro de ganho

Resumo

Um protocolo para analisadores ópticos no domínio do tempo de Brillouin baseado na engenharia do espectro de ganho é apresentado. Melhorias no desempenho de detecção, incluindo faixa de detecção e resolução de mensuração, são alcançadas e o excesso de ruído de intensidade de Brillouin é estudado. O protocolo apresenta uma nova maneira de melhorar o desempenho da detecção de Brillouin distribuído.

Resumo

Demonstrado é um método exclusivo para detectar o aprimoramento do desempenho em analisadores ópticos no domínio do tempo (BOTDA) Brillouin. Um espectro de ganho de Brillouin (BGS) é sobreposto a dois espectros de perda de Brillouin simétricos (BLS). Isso leva a uma forma de espectro de engenharia complexa que é mais resistente ao ruído do sistema de detecção. Em vez de apenas uma interação bomba e sonda como na configuração convencional do BOTDA, três ondas de sonda óptica são exploradas, com uma sonda localizada no BGS e as outras duas simetricamente no BLS. Devido à resistência e insensibilidade da forma do espectro projetado ao ruído, o desempenho de detecção é aprimorado em 60% e a resolução de medição é dobrada.

Introdução

A detecção de fibra distribuída (DFS) é um mecanismo exclusivo que emprega uma fibra inteira como meio de detecção. Tem atraído muito interesse devido à baixa perda de fibras; tamanho pequeno; e a capacidade de ser facilmente incorporado em várias estruturas, como barragens, pontes e edifícios, para realizar a vigilância ambiental como um sistema nervoso artificial. Em comparação com a aplicação de vários sensores pontuais tradicionais, como grades de Bragg de fibra (FBG), ele fornece uma solução mais eficiente e econômica em uma ampla gama de tarefas de detecção em larga escala, como monitoramento de infraestrutura e integridade estrutural¹.

Os sensores distribuídos atuais exploram diferentes mecanismos de dispersão dentro da fibra para medir a temperatura e a distribuição de deformação. Dentre eles, o DFS baseado no espalhamento de Brillouin é o mais atraente devido às vantagens marcantes do espalhamento de Brillouin estimulado (SBS), como alta relação sinal-ruído (SNR), baixo limiar e sensibilidade à temperatura² e à deformação³. O SBS pode ser classicamente descrito como uma interação entre as ondas contínuas ópticas incidentes (CW), ou seja, a bomba, e a onda da sonda CW de contrapropagação por meio de uma onda acústica. De acordo com a conservação de energia e momento, a onda da sonda é reduzida em frequência para a bomba. Essa mudança é chamada de mudança de frequência de Brillouin (BFS). Considerando o tempo de vida finito de uma onda acústica de 10 ns, há uma distribuição espectral finita da onda refratada, também chamada de espectro de ganho de Brillouin (BGS), na qual o BFS é a diferença de frequência entre a onda da bomba e a frequência do centro de pico. A interação entre as ondas leva a uma região de ganho de redução de frequência e uma região de perda de frequência para cima, onde a onda da sonda é amplificada e atenuada, respectivamente. Para uma fibra monomodo padrão (SSMF) na banda C, o BFS é de aproximadamente 11 GHz e o BGS tem uma forma lorentziana com uma largura total ultraestreita na metade do máximo (FWHM) de 10-30 MHz, que pode ser reduzida ainda mais para 3,4 MHz com técnicas específicas 4,5,6,7. Com base nessas características, o SBS também pode ser aplicado em filtros fotônicos de micro-ondas ^8,9,10, filtros ópticos¹¹, luz lenta e rápida 12,13,14 e espectroscopia óptica de alta resolução ^7,15.

Uma das aplicações SBS mais promissoras é a detecção distribuída de Brillouin. Esses sensores exploram a dependência do BFS da temperatura e da tensão. O primeiro a ser demonstrado foi o analisador óptico de Brillouin no domínio do tempo (BOTDA) ¹⁶, que é a técnica de detecção de Brillouin distribuída no domínio do tempo mais consolidada. Ele difere da interação CW-SBS convencional na medida em que explora a interação SBS entre uma onda de bomba pulsada e uma sonda CW para que as informações ambientais sejam interrogadas localmente em cada seção de fibra. A frequência da bomba ou sonda geralmente é fixa enquanto a sonda ou a frequência da bomba é escaneada nas proximidades do BFS. A potência da sonda é registrada para reconstrução BGS e o BFS é idealmente a frequência de pico do BGS local em cada seção de fibra. No entanto, devido ao inevitável ruído do sistema, o pico de BGS geralmente é ambíguo e um algoritmo de ajuste deve ser aplicado¹⁷, o que leva a um certo erro de estimativa na frequência¹⁸ e influencia a resolução do mensurando.

Estatisticamente, o erro de estimativa do BFS é inversamente proporcional à relação sinal-ruído (SNR) do sistema. A maneira mais direta de melhorar o SNR é aumentar a potência da bomba e da sonda. No entanto, estes são limitados pela instabilidade de modulação (IM)¹⁹ e efeitos não locais (NLE)^20,21 a ~20 dBm e -14 dBm, respectivamente. Numerosas técnicas, como codificação²² e amplificação em linha baseada em Raman²³ foram propostas para quebrar esses limites. Recentemente, foi relatado que esse erro de frequência pode ser minimizado com a escolha de um algoritmo de ajuste adequado²⁴. Da mesma forma, as medições que exploram a fase de Brillouin e um algoritmo de ajuste linear também são relatadas como tendo um erro de frequência reduzido²⁵, o que indica o potencial de um BGS bem projetado para melhorar o desempenho de detecção. Outra opção para melhorar o SNR é a redução de ruído. No entanto, de acordo com o ponto de vista tradicional, o ruído do sistema de detecção vem principalmente do detector (ou seja, ruído de modo comum, incluindo ruído escuro, ruído de tiro, etc.)^26,27 e a melhora é menos provável.

A ideia básica deste artigo é projetar o BGS pela superposição de um BGS convencional com dois espectros de perda de Brillouin simétricos (BLS) (ver Figura 1). Em comparação com um espectro BGS convencional, que segue uma forma Lorentziana, o espectro projetado é mais nítido e robusto com o mesmo nível de ruído do sistema. Assim, o ruído tem menor influência na determinação da frequência de pico. Isso pode ser verificado coletando e ajustando os dados de medição do BGS um número estatisticamente significativo de vezes. Devido a essa melhor resistência ao ruído, são alcançadas melhorias no desempenho de detecção, incluindo a faixa de detecção em 60% e resolução de medição dobrada, ou seja, um erro de frequência reduzido em 50%. Devido ao envolvimento da medição com a interação de perda de Brillouin em parte do BGS projetado, é feita uma comparação direta do ruído traço com e sem interação de Brillouin. Devido à evasão do excesso de ruído de Brillouin, o traço com o BGS projetado é muito mais claro.

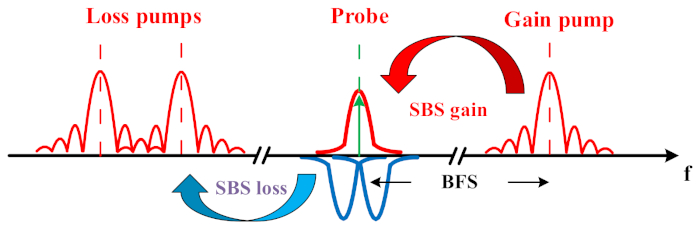
Figura 1: Esquema de um BGS projetado pela superposição de um ganho de Brillouin e dois espectros de perda de Brillouin simétricos. Clique aqui para ver uma versão maior desta figura.

Protocolo

1. Seleção de parâmetros otimizados para a engenharia de espectro via simulação

1. Modele o BGS g_SBS (ν,z) com as equações ^28,29
   
   conforme implementado, por exemplo, pelo script MATLAB suplementar.
   NOTA: Aqui, G(ν) é o coeficiente de ganho complexo, calculado no script como G_complex dentro da função SBS_g para o BGS convencional ou função SBS_gl para o BGS projetado; g(ν,z) é o complexo local de Brillouin ganho; e g_SBS e φ_SBS são a parte real e imaginária de g(ν,z) e simbolizam a resposta de fase BGS e SBS no local z da extremidade de lançamento da bomba, respectivamente. No script, g_SBS é simbolizado pelas variáveis SBS_g_log e SBS_gl_log para o BGS convencional e projetado em escala logarítmica, respectivamente. P_p = 20 dBm (P_pump no script) é a potência de pico de pulso da bomba na extremidade de lançamento da fibra; ν_B é o BFS (normalizado no script); g₀ = 0,2 ^{W-1 m-1} (g₀ no script) é o coeficiente de ganho de Brillouin; Δν_B = 50 MHz (gamma_B no script) é o FWHM do BGS; α = 0,2 dB/km é o coeficiente de perda de fibra e é representado por alpha_log e alpha_lin como o valor em escala logarítmica e linear no script, respectivamente; ν é a frequência de onda da sonda de modo que o desvio de frequência da bomba e da sonda ν - ν_B é varrido de -250 MHz a 250 MHz. O deslocamento de frequência da bomba e da sonda é representado no script como o vetor global f. O termo g₁ = mg₀ é o fator de perda; 2d∙Δ_{ν B} é o deslocamento de frequência entre as duas perdas; e L_eff = 10 m (L_eff no script) é o comprimento da interação de Brillouin para largura de pulso de 100 ns. A forma espectral projetada pode ser facilmente ajustada ajustando dois fatores normalizados, m e d. O BGS convencional pode ser modelado simplesmente por m = 0.
2. Adicione ruído aleatório (ou seja, ruído gaussiano branco aditivo) com o mesmo nível no BGS convencional e projetado. Ajustar o parâmetro noise_level no script pode alterar o nível de ruído.
3. Ajuste o BGS ruidoso convencional com a função Lorentziana (função Lorentz_g_gain_fun no script) e o BGS ruidoso projetado com a função Lorentziana sobreposta (função Lorentz_gl_gain_fun no script) (consulte a Figura 2A).
4. Determine o deslocamento da frequência de pico devido ao ruído para o BGS convencional e projetado (Figura 2B).
5. Repita as etapas 1.2-1.4 para N = 500 e colete todos os deslocamentos de frequência de pico Δf_ci e Δf_pi (representados por delta_g_g e delta_g_gl no script, respectivamente) para o BGS convencional e projetado no i^ésimo processo, respectivamente.

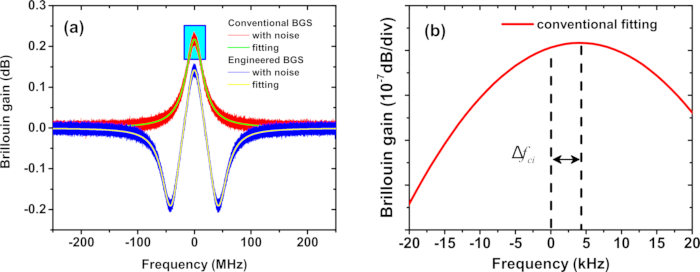
Figura 2: BGS simulado. (A) Demonstração da adaptação de um BGS Lorentziano típico (vermelho) e projetado (azul) na simulação. (B) O pico do BGS Lorentziano de (A). Δf_ci representa o erro de estimativa BFS para o BGS convencional na i^ésima medição. Clique aqui para ver uma versão maior desta figura.

6. Calcular o rácio do desvio-padrão dos erros de estimativa do BFS induzidos pelo ruído como:
   
7. Plote η como uma função de m e d (ver Figura 3A). Encontre o valor mínimo η_min e os m e d correspondentes. A vantagem da precisão da estimativa será mantida ao longo de toda a fibra²⁸.
8. Ajuste o valor de z (ou seja, o comprimento da fibra, também z no script) na Equação (2) de 0 km a 60 km, passo 50 m e repita os passos 1.1-1.7 com alguns valores m e d selecionados. Em seguida, a razão do desvio padrão em função do comprimento da fibra pode ser adquirida (ver Figura 3B).

2. Prepare e teste a configuração convencional do BOTDA (bloco destacado na Figura 4B)

1. Ligue o diodo laser (LD) e verifique a funcionalidade do LD com o analisador de espectro óptico (OSA). Normalmente, um comprimento de onda em torno de 1.550 nm é usado.
2. Conecte o LD com o acoplador óptico (OC) 10:90. Verifique a potência da saída de 10% OC. Se a potência for superior a 13 dBm (a potência máxima de entrada do embaralhador de polarização [Pol.S.]), diminua a potência de saída LD diminuindo a corrente LD.
3. Conecte a saída de 10% OC com o Pol.S. Para evitar o desvanecimento da polarização¹, defina a frequência de embaralhamento para 1 kHz.
4. Verifique a potência da saída do Pol.S. Se a potência for superior a -3 dBm (o limite máximo de potência de entrada do amplificador óptico semicondutor [SOA]), adicione atenuadores até que o requisito de energia seja atendido. Conecte o Pol.S. com o SOA.
5. Aplique o sinal do trem de pulso elétrico com largura de pulso de 100 ns e taxa de repetição de 4 kHz do gerador de pulso (PG) no SOA. Certifique-se de que a amplitude do sinal de pulso seja maior que o limite de lógica transistor-transistor (TTL) do SOA (ou seja, 4 dBm) e que a taxa de repetição satisfaça o requisito de ida e volta³⁰.
6. Conecte a saída do SOA com a fibra dopada com érbio amplifier (EDFA 1) e opere o EDFA no modo de controle automático de corrente (ACC). Conecte a saída do EDFA 1 à porta 1 do circulador (Cir).
7. Verifique o sinal de pulso óptico da porta 2 do Cir no digitalizador conectando-o ao fotodiodo (PD). Para evitar qualquer dano ao PD, é necessária atenuação suficiente.
8. Calcule a potência de pico do pulso óptico pela forma de onda medida no digitalizador. A potência de pico óptica P_o é estimada de acordo com
   
   onde V_E é a tensão de pico do pulso elétrico e R _{e R f} são a responsividade e transresistência do PD. Leve em consideração a atenuação da proteção neste cálculo para que seja avaliada uma potência correta da bomba de entrada na fibra em teste (FUT, 10,6 km).
9. Observe o valor atual de EDFA I₂₀ quando a potência de pico de pulso óptico calculada atingir 20 dBm (limiar MI¹⁹). A taxa de extinção (ER) do trem de pulso óptico pode ser avaliada de acordo com a conservação de energia:
   
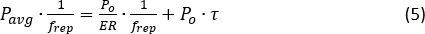
   onde P_média é a potência média óptica do trem de pulso; f_rep é a taxa de repetição; e τ é a largura do pulso. O ER do SOA é geralmente superior a 30 dBm, evitando eficientemente NLE^31,32.
   NOTA: Desligue o EDFA antes de desconectar o PD e continuar a construir o sistema.
10. Conecte a porta 2 do Cir com uma extremidade do FUT para concluir a configuração do ramal da bomba. Verifique se o sistema sofrerá de MI verificando o espectro da outra extremidade do FUT no OSA e definindo o EDFA em um valor de corrente constante, I₂₀. Se o espectro detectado for o mesmo (em forma, não necessariamente em amplitude) que o medido na etapa 2.1, o sistema está livre de MI. Caso contrário, quando for observado alargamento óbvio do espectro ou divisão de pico³³ , reduza a corrente EDFA 1 para manter a forma do espectro.
11. Conecte a saída de 90% do OC a um OC 50:50 1 e conecte uma das saídas do OC 1 ao modulador Mach-Zehnder (MZM 1) por meio de um controlador de polarização (PC). Defina a polarização corretamente, para que a saída de MZM 1 seja maximizada (alinhamento de polarização).
12. Aplique o sinal de radiofrequência (RF) do gerador de RF (RFG 1) com o BFS do FUT (para SSMF em torno de 11 GHz) e amplitude de 16 dBm ao MZM 1. Defina a tensão de polarização CC do MZM 1 para que a portadora seja suprimida ao mínimo.
13. Conecte a saída do MZM 1 com grade de Bragg de fibra (FBG 1). Verifique o espectro de saída do FBG 1 no OSA para que o FBG 1 esteja configurado para bloquear a banda lateral de frequência superior e a portadora.
14. Conecte a saída do FBG 1 ao EDFA 2, outro 50:50 OC 2 e um isolador (ISO) consecutivamente.
15. Opere o EDFA 2 também no modo ACC e defina o valor atual para _Ig, de modo que a potência de saída do ISO seja inferior a -14 dBm, minimizando NLE²⁰. Desligue o EDFA antes de desconectar o medidor de energia e continue a construção do sistema. Conecte a saída ISO à outra extremidade do FUT para concluir a criação de configuração da ramificação da sonda de ganho.
16. Conecte a porta Cir 3 ao EDFA 4 (para pré-amplificação³⁴) e PD. Defina o EDFA para o modo ACC. O valor atual I₄ deve permitir que a potência de saída do EDFA seja 4 menor que o limite de entrada do PD. Conecte a saída de RF PD a um filtro passa-baixo de RF de 10 MHz^35,36. Conecte a saída do filtro ao digitalizador.
17. Conecte o gatilho do digitalizador com a saída sincronizada (ou inversa) do gerador de pulsos. Defina os parâmetros do digitalizador da seguinte forma: Taxa de amostragem: 500 MSa/s; média: 4.096 vezes; Número de amostras: 10.000.
18. Defina o valor atual de EDFA 1, EDFA 2 e EDFA 4 para I₂₀, I_g e I₄, respectivamente. Execute um programa de gravação de rastreamento. Verifique o traço medido no digitalizador. Se a amplitude do traço seguir o decaimento exponencial, o sistema de detecção está livre de MI. Caso contrário, reduza o valor atual do EDFA 1.

3. Medição usando a configuração convencional BOTDA e processamento de dados

1. Defina os valores de EDFA 1 e EDFA 2 para I₂₀ e I_g, respectivamente. Varra a frequência de RFG 1 na faixa de BFS ± 90 MHz com passos de 1 MHz. Registre o traço do programa de gravação após cada etapa de digitalização.
2. Calcule o ganho de Brillouin local dividindo a amplitude do traço (no período de interação de Brillouin) por cada deslocamento DC (período de interação não Brillouin).
3. Recupere o BGS em cada seção de fibra ajustando o BGS ruidoso medido com o encaixe Lorentziano. Determinar o FWHM do BGS convencional Δν_B0 a partir do acessório.
4. Repita as etapas 3.1 e 3.2 para N = 48 vezes e colete todas as distribuições de frequência de pico estimadas (BFS) ao longo da fibra ν_Bci(z) no ^i-ésimo processo (ver Figura 5A).
5. Calcule o erro de estimativa do BFS como o desvio padrão do BFS ajustado em cada seção de fibra nas 48 medições (consulte a Figura 5B).

4. Preparando o restante da configuração

NOTA: Neste caso, foram utilizados m = 1 e d = 1,24, de acordo com os resultados da simulação (ver secção 1 e Figura 3).

1. Conecte a outra saída do 50:50 OC 1 no ramo da sonda com o EDFA 3 e o 50:50 OC 3.
2. Conecte uma das saídas de 50:50 OC 3 a um PC e MZM 2. Ajuste a polarização para que a saída do MZM 2 seja maximizada.
3. Aplique o sinal de RF do RFG 2 com BFS - d∙Δν_B0 e amplitude de 16 dBm no MZM 2. Verifique o espectro de modulação no OSA e ajuste a tensão de polarização para minimizar a amplitude da portadora.
4. Conecte a saída do MZM 2 à entrada de um switch óptico (OS 1), uma das entradas de 50:50 OC 4 e o FBG 2.
5. Verifique o sinal óptico no OSA e ajuste o comprimento de onda central do FBG 2 para que a portadora e a banda lateral de frequência mais baixa sejam bloqueadas (consulte a Figura 4A). A configuração da ramificação de sonda de perda 1 será concluída.
6. Conecte a outra saída do 50:50 OC 3 a um PC e MZM 3. Ajuste a polarização para que a saída do MZM 3 seja maximizada.
7. Aplique o sinal de RF do RFG 3 com BFS + d∙Δν_B0 e amplitude de 16 dBm em MZM 3. Verifique o espectro de modulação no OSA e ajuste a tensão de polarização para minimizar a amplitude da portadora.
8. Conecte a saída do MZM 3 a um atenuador óptico variável (VOA) com uma função de comutação (OS 2) e a outra entrada de 50:50 OC 4. Considerando que o deslocamento entre as frequências da sonda de perda é relativamente pequeno em comparação com a janela de transmissão do FBG 2 (vários GHz), a portadora e a banda lateral de frequência mais baixa do MZM 3 também serão bloqueadas pelo FBG 2. A configuração da ramificação de sonda de perda 2 será concluída.
9. Feche o OS 1, abra o OS 2 e defina o valor atual do EDFA 3 para I_l de modo que a potência da sonda de perda 1 seja igual a -14 dBm (m = 1).
10. Abra o OS 1, feche o OS 2 e ajuste a atenuação do VOA para que a potência da sonda de perda 2 também seja igual a -14 dBm.

5. Medição usando a configuração completa proposta do BOTDA e processamento de dados

1. Feche o OS 1, feche o OS 2 e defina o valor atual de EDFA 1, EDFA 2, EDFA 3 e EDFA 4 para I₂₀, I_g, I_l e I₄, respectivamente. Varra a frequência do RFG 1 na faixa de BFS ± 90 MHz em passos de 1 MHz. As frequências de RFG 2 e RFG 3 são verificadas de forma correspondente. Registre o rastreamento do programa após cada etapa de verificação.
2. Calcule o ganho de Brillouin local como na etapa 3.2 e recupere o BGS projetado em cada seção de fibra, ajustando o BGS ruidoso medido com a função Lorentziana sobreposta.
3. Repita as etapas 5.1 e 5.2 para N = 48 vezes e colete todas as distribuições de frequência de pico estimadas (BFS) ao longo da fibra ν_Bpi(z) no ^i-ésimo processo (ver Figura 5A).
4. Calcule o erro de estimativa do BFS como o desvio padrão do BFS ajustado em cada seção de fibra nas 48 medições (consulte a Figura 5B).

Resultados

A Figura 3 mostra os resultados da simulação. Pontos com η < 1 na Figura 3A indicam um erro de frequência menor (maior resolução de medição) com o BGS projetado. Quanto menor o valor, maior a vantagem. A razão mínima foi em m = 1, indicando que um esquema multissonda em vez de multibomba pode ser realizado (ver Discussão). A Figur...

Discussão

A etapa mais crítica durante o experimento é a equalização das três potências da sonda para que m = 1 e a simetria entre os dois espectros de perda de Brillouin sejam alcançados. Além da verificação de potência separada usando o medidor de potência na porta Cir 2, conforme apresentado nas etapas 4.9 e 4.10, a equalização de potência pode ser verificada com mais precisão no digitalizador. Ao definir a frequência RF 1 para ~ 11 GHz (o BFS da fibra) e desligar o ED...

Materiais

Name	Company	Catalog Number	Comments
Current controller for laser diode	ILX Lightwave	LDX3220
Digitizer	Acqiris SA	U5309A-1039
Erbium doped fiber amplifier 1	Photop	PTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2	LiComm	OFA-TCH
Erbium doped fiber amplifier 3	Calmar Optcom	AMP-ST30
Erbium doped fiber amplifier 4	Photop	PTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1	Advanced Optics Solutions	T-FBG
Fiber Bragg grating 2	Advanced Optics Solutions	T-FBG
Fiber under test	ofs
Isolator	General Photonics	S-15-NTSS
Laser diode	3SP Group	A1905 LMI
Mach-Zehnder modulator 1	Avanex	IM10
Mach-Zehnder modulator 2	Avanex	IM10
Mach-Zehnder modulator 3	Avanex	IM10
Nanosecond driving board for semiconductor optical amplifier	Highland Technology	T160-9 (28A160-9C)
Optical coupler 10:90	Newport		Benchtop coupler/WDM
Optical coupler 50:50	Newport		Benchtop coupler/WDM
Optical spectrum analyzer	Hewlett Packard	86145A
Optical switch 1	JDSU	SN12-1075NC
Photodiode	Thorlabs	D400FC
Polarization scrambler	General Photonics	PSY-101
Pulase generator	Hewlett Packard	8082A
Radio function generator 1	Anritsu	MG3692C
Radio function generator 2	Agilent Technology	E8257D
Radio function generator 3	HTM	T2100
Semiconductor optical amplifier	Thorlabs	SOA1013SXS
Temperature controller for laser diode	ILX Lightwave	LDT5948
Temperature controller for semiconductor optical amplifier	Tektronix	TED200
Variable optical attenuator	JDSU	mVOA-A1	With optical switch function