Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.
Method Article
Bestimmung der mechanischen Festigkeit ultrafeinkörniger Metalle
In diesem Artikel
Zusammenfassung
Das hier vorgestellte Protokoll beschreibt die Hochdruck-Radial-Diamant-Amboss-Zell-Experimente und die Analyse der damit verbundenen Daten, die für die Erzielung der mechanischen Festigkeit der Nanomaterialien mit einem signifikanten Durchbruch zum traditionellen Ansatz unerlässlich sind.
Zusammenfassung
Die mechanische Verstärkung von Metallen ist die langjährige Herausforderung und das beliebte Thema der Materialwissenschaften in Industrie und Wissenschaft. Die Größenabhängigkeit der Festigkeit der Nanometalle hat großes Interesse geweckt. Die Charakterisierung der Festigkeit von Materialien auf der unteren Nanometerskala war jedoch eine große Herausforderung, da die traditionellen Techniken nicht mehr effektiv und zuverlässig werden, wie Nano-Einrückung, Mikrosäulenkompression, Zugfestigkeit usw. Das aktuelle Protokoll verwendet radiale Diamant-Amboss-Zellen (rDAC) Röntgenbeugungstechniken (XRD), um differentielle Spannungsänderungen zu verfolgen und die Festigkeit ultrafeiner Metalle zu bestimmen. Es wird festgestellt, dass ultrafeine Nickelpartikel eine signifikantere Streckgrenze aufweisen als gröbere Partikel, und die Größenverstärkung von Nickel setzt sich bis auf 3 nm fort. Diese wichtige Erkenntnis hängt immens von effektiven und zuverlässigen Charakterisierungstechniken ab. Es wird erwartet, dass die rDAC XRD-Methode eine bedeutende Rolle bei der Untersuchung und Erforschung der Nanomaterialmechanik spielen wird.
Einleitung
Die Beständigkeit gegen plastische Verformung bestimmt die Festigkeit der Materialien. Die Festigkeit der Metalle steigt in der Regel mit den abnehmenden Korngrößen. Dieses Phänomen der Größenstärkung kann gut durch die traditionelle Hall-Petch-Beziehungstheorie vom Millimeter- bis zum Submikron-Regime1,2 veranschaulicht werden, die auf dem dislokationsvermittelten Verformungsmechanismus von massengroßen Metallen basiert, d.h. Versetzungen häufen sich an Korngrenzen (GBs) an und behindern ihre Bewegungen, was zur mechanischen Verstärkung in Metallen führt 3,4.
Im Gegensatz dazu wurde in den letzten zwei Jahrzehnten eine mechanische Erweichung, die oft als inverse Hall-Petch-Beziehung bezeichnet wird, für feine Nanometalle berichtet 5,6,7,8,9,10. Daher ist die Festigkeit der Nanometalle immer noch rätselhaft, da eine kontinuierliche Härtung für Korngrößen bis hinunter zu ~ 10 nm 11,12 festgestellt wurde, während die Fälle von Größenerweichung unter 10 nm auch 7,8,9,10 gemeldet wurden. Die Hauptschwierigkeit oder Herausforderung für dieses diskutierte Thema besteht darin, statistisch reproduzierbare Messungen der mechanischen Eigenschaften ultrafeiner Nanometalle durchzuführen und eine zuverlässige Korrelation zwischen der Festigkeit und der Korngröße der Nanometalle herzustellen. Ein weiterer Teil der Schwierigkeit ergibt sich aus der Mehrdeutigkeit der plastischen Verformungsmechanismen der Nanometalle. Es wurden verschiedene Defekte oder Prozesse im Nanobereich berichtet, darunter Versetzungen 13,14, Verformungspartnerschaften15,16,17, Stapelfehler 15,18, GB-Migration 19, GB-Gleiten 5,6,20,21, Kornrotation22,23,24, Atombindungsparameter25,26,27,28 usw. Welche jedoch die plastische Verformung dominiert und damit die Festigkeit von Nanometallen bestimmt, ist noch unklar.
Für diese oben genannten Probleme sind traditionelle Ansätze der mechanischen Festigkeitsprüfung, wie Zugversuch29, Vickers-Härtetest 30,31, Nano-Eindringtest 32, Mikrosäulenkompression33,34,35 usw., weniger effektiv, da die hohe Qualität großer Stücke nanostrukturierter Materialien so schwer herzustellen ist und herkömmliche Eindringkörper viel größer sind als einzelne Nanopartikel von Materialien (für die B. Einzelteilchenmechanik). In dieser Studie führen wir radiale DAC XRD-Techniken36,37,38 in die Materialwissenschaften ein, um in situ die Fließspannung und Deformationstexturierung von Nanonickel verschiedener Korngrößen zu verfolgen, die in früheren Studien im Bereich der Geowissenschaften verwendet werden. Es wurde festgestellt, dass die mechanische Verstärkung auf bis zu 3 nm ausgedehnt werden kann, viel kleiner als die zuvor berichteten größten Größen von Nanometallen, was das Regime der konventionellen Hall-Petch-Beziehung erweitert, was die Bedeutung der rDAC XRD-Techniken für die Materialwissenschaft impliziert.
Protokoll
1. Probenvorbereitung
- Erhalten Sie 3 nm, 20 nm, 40 nm, 70 nm, 100 nm, 200 nm und 500 nm Nickelpulver aus kommerziellen Quellen (siehe Materialtabelle). Die morphologische Charakterisierung ist in Abbildung 1 dargestellt.
- Bereiten Sie 8 nm Nickelpartikel vor, indem Sie 3 nm Nickelpartikel mit einem Reaktionskessel erhitzen (siehe Materialtabelle).
- Geben Sie ~ 20 ml absolutes Ethanol und ~ 50 mg 3 nm Nickelpulver in den Reaktionskessel. HINWEIS: Die gesamte Lösung sollte nicht ~ 70% des Wasserkochervolumens erreichen.
- Den Reaktionskessel 24 h auf 80 °C erhitzen.
- Kühlen Sie die Lösung auf Raumtemperatur ab und lassen Sie eine kleine Lösung auf ein Kupfernetz fallen (TEM-Raster, siehe Materialtabelle).
- Legen Sie das getrocknete Kupfernetz in die TEM-Kammer (Transmission Electron Microscopy) und beobachten Sie die Probenmorphologie unter 200 kV Spannung Elektronenstrahl.
HINWEIS: Das Kupfernetz wurde für ~ 5 min an der Luft getrocknet oder verwendete ein Trocknungslicht von 5 min. - Messen Sie die Partikelgrößenverteilung aus den TEM-Bildern manuell.
HINWEIS: Die Partikelgrößenmessung kann auch mit jeder frei verfügbaren Software wie Image J durchgeführt werden. - Nehmen Sie die Lösung heraus und verdampfen Sie das Ethanol bei Raumtemperatur; Dann ist der Rest des schwarzen Feststoffs das reine Nickelpulver mit einer durchschnittlichen Partikelgröße von 8 nm.
- 12 nm Nickelpulver zubereiten
- Wiederholen Sie Schritt 1.2, ändern Sie jedoch "absolutes Ethanol" und "80 °C für 24 h" in "absolutes Isopropanol" und "150 °C für 12 h", um das reine Nickelpulver mit dem durchschnittlichen Partikel von 12 nm zu erhalten.
2. Hochdruck-Radial-DAC-XRD-Messungen
- Machen Sie röntgentransparente Bor-Epoxid-Dichtung mit einer Laserbohrmaschine (siehe Materialtabelle).
- Bereiten Sie Kapton (eine Art Kunststoff) unterstützende Dichtungen vor
HINWEIS: Kapton ist ein Polyimid-Folienmaterial (siehe Materialtabelle).- Schneiden Sie den inneren Kreis mit einer Laserbohrmaschine mit den genannten Parametern: 35% Laserleistung, drei Durchgänge, 0,4 mm/s (Schnittgeschwindigkeit).
- Schneiden Sie das äußere Rechteck mit den Parametern: 80% der Laserleistung, zwei Durchgänge, 1,2 mm/s (Schnittgeschwindigkeit). Das rechteckige Maß beträgt 8 x 1,4 mm.
- Bereiten Sie Bor-Epoxid-Dichtungen aus einer größeren Borscheibe mit einem Durchmesser von ~ 10 mm vor.
HINWEIS: Die Borscheibe wird hergestellt, indem die Mischung aus amorphem Borpulver und Epoxidkleber36 komprimiert wird.- Polieren Sie die Rohscheiben mit Schleifpapier manuell auf eine Dicke von 60-100 μm.
HINWEIS: Das Schleifpapier ist von ~ 400 Mesh bis ~ 1000 Mesh. - Schneiden Sie die inneren Kreise mit einer Laserbohrmaschine mit den genannten Parametern: 35% Laserleistung, drei Durchgänge, 0,4 mm/s (Schnittgeschwindigkeit).
- Schneiden Sie den äußeren Kreis mit einer Laserbohrmaschine: 30% Laserleistung, ein Durchgang, 0,4 mm/s (Schnittgeschwindigkeit). Wiederholen und stoppen Sie sofort, wenn es sich löst.
- Polieren Sie die Rohscheiben mit Schleifpapier manuell auf eine Dicke von 60-100 μm.
- Montage der Dichtungen
- Legen Sie eine Kapton-Stützdichtung (vorbereitet in Schritt 2.1.1) auf einen Glasschieber.
- Platzieren Sie eine gebohrte Bordichtung auf dem inneren Loch der Kapton-Dichtung. Stellen Sie sicher, dass sich das größere Ende der Bordichtung oben befindet.
- Legen Sie einen weiteren sauberen Glasschieber auf die Oberseite. Halten Sie es fest und drücken Sie es, bis die Dichtung fest in das Loch der Kapton-Dichtung eingeführt ist.
- Lagern Sie die gefertigten Dichtungsbaugruppen zwischen zwei sauberen Glasobjektträgern und wickeln Sie sie für die zukünftige Verwendung mit Klebeband ein.
HINWEIS: Der Dichtungsdurchmesser, Ø = Diamantculetgröße + 150 μm. Zur besseren Reproduzierbarkeit können für das Laserbohren und Schneiden während der Dichtungsvorbereitung die gleichen Aufbauten verwendet werden (ggf. mit kleinen Anpassungen, wenn etwas Falsches gefunden wird). Für eine gute Größenanpassung beträgt der Durchmesser der für das Laserschneiden eingegebenen Dichtungen Ø + 23 μm, während der Durchmesser des Innenlochs der Kapton-Stützdichtungen (für das Laserschneiden eingegeben) Ø - 23 μm beträgt.
- Bereiten Sie Kapton (eine Art Kunststoff) unterstützende Dichtungen vor
- Radiales Laden von DAC-Experimenten
- Montieren Sie die Dichtungsbaugruppe
- Markieren Sie auf dem Monitor des sehenden Computers (der an das optische Mikroskop angeschlossen ist) einen Punkt, um die Mitte des Diamanten (den Kolbendiamanten des DAC) zu lokalisieren.
- Montieren Sie die Bor-Epoxid-Dichtung (vorbereitet in Schritt 2.1) und die Markierung in der Mitte des Dichtungslochs.
- Verwenden Sie einen Glasschieber, um die Dichtungsanordnung so nach unten zu drücken, dass die Dichtung fest auf dem Diamanten des Kolbens sitzt.
HINWEIS: Ein DAC hat zwei identische Diamantenstücke. Im Allgemeinen wird der obere als Zylinderdiamant und der untere als Kolbendiamant bezeichnet.
- Reinigung und Verdichtung des Dichtungsaufbaus
- Laden Sie Proben mit einer Stückgröße kleiner als das Dichtungsloch, so dass es keinen Überlauf von Materialien auf der Dichtungsoberfläche gibt.
HINWEIS: Die Proben hier sind die Kandidatenmaterialien, die wir in unseren Experimenten untersucht haben. In dieser Studie handelt es sich bei den Proben um Ni-Pulver unterschiedlicher Größe und Pt-Chips. - Schließen Sie die Zelle nach dem Laden eines neuen Probenstücks, um Kompaktheit zu erreichen.
- Laden Sie Proben mit einer Stückgröße kleiner als das Dichtungsloch, so dass es keinen Überlauf von Materialien auf der Dichtungsoberfläche gibt.
- Beladung von weichen Materialien (z.B. Gold)
- Laden Sie nur ein Stück der weichen Probe (machen Sie das weiche Material zu einem kleinen Bruchteil der belasteten Materialien).
- Verwenden Sie harte amorphe Materialien, um das Dichtungsloch für eine gute Kompaktheit zu füllen.
- Beladung von Materialien mit niedriger Ordnungszahl (wie Spinell, Pyrop, Serpentin)
- Mischen Sie die Probe mit 10% Pt oder Au. Füllen Sie das Dichtungsloch mit der Mischung, jedoch ohne Überlauf.
- Falls erforderlich, legen Sie harte amorphe Materialien für eine gute Kompaktheit auf die Oberseite.
- Montieren Sie die Dichtungsbaugruppe
- Röntgenbeugungsstudie
- Montieren Sie die röntgentransparente Bor-Kapton-Dichtung (vorbereitet in Schritt 2.1) mit einer Dicke von 100 μm und einem Kammerloch von 60 μm auf der Oberseite von 300 μm Dilet aus DAC mit Unterstützung der Tone.
- Legen Sie ein kleines Stück Pt-Chip als Druckkalibrant auf die Ni-Probe.
HINWEIS: Es wurde kein Druckmedium verwendet, um die Differenzspannung zwischen axial und radial zu maximieren. - Verwenden Sie ein monochromatisches Synchrotronröntgen (siehe Materialtabelle) mit einer Energie von 25 oder 30 keV, um die Röntgenbeugungsexperimente durchzuführen.
- Fokussieren Sie den Röntgenstrahl auf eine Oberfläche von ~ 30 x 30 μm2 auf der Probe.
- Sammeln Sie die Röntgenbeugungsmuster in Druckintervallen von 1-2 GPa durch eine zweidimensionale Bildplatte (siehe Materialtabelle) mit einer Auflösung von 100 μm/Pixel. Das verwendete Setup ist in Abbildung 2 und Abbildung 3 dargestellt.
- Die experimentelle Datenanalyse
- Verarbeiten Sie jedes Röntgenbeugungsbild in eine Datei mit 72 Spektren über 5° azimutale Schritte mit Fit2d 37,38,39,40,41,42.
HINWEIS: Ein zweidimensionales Beugungsbild enthält 360°-Informationen. Um die Spannungs- und Texturinformationen zu analysieren, ist es notwendig, in 72 Dateien mit 5° azimutalen Informationen zu trennen, die in jeder Datei enthalten sind. Fit2d ist die Software zur Analyse von Röntgenbeugungsdaten 37,38,39,40,41,42. - Verfeinern Sie das Beugungsmuster mit der Rietveld-Methode in der MAUD37-Software. Die Gitterdehnung jeder Gitterebene wurde durch Anpassung des Musters37,40 erhalten.
- Berechnen Sie die Differenzspannung und Streckgrenze nach der Gitterdehnungstheorie 38 und dem von Mises-Streckgrenze38,39 nach Schritt 2.5.
- Verarbeiten Sie jedes Röntgenbeugungsbild in eine Datei mit 72 Spektren über 5° azimutale Schritte mit Fit2d 37,38,39,40,41,42.
- Die Gitterdehnungstheorie für die experimentelle Datenanalyse
- Bestimmen Sie die Differenzspannung (die Differenz zwischen diesen maximalen (σ22 = σ33) und minimalen Spannungskomponenten (σ11), die eine untere Schätzung der Streckgrenze der Streckgrenze eines Materials 38, σy, basierend auf dem von Mises-Streckgrenze gemäß Gleichung (1)38 liefert:
(1) t= σ11-σ 33<2τ= σy. - Erhalten Sie die richtungsabhängige abweichende Dehnung Qhkl, indem Sie die d-Abstände aus verschiedenen Beugungsrichtungen mit der folgenden Gleichung (2)38 messen:
(2)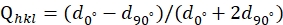
wobei d 0° und d 90° die d-Abstände sind, die von Ψ = 0° bzw. Ψ = 90° (dem Winkel zwischen dem Beugungsvektor und der Lastachse) gemessen werden. - Leiten Sie dann den Wert von t mit Gleichung (3)38 ab:
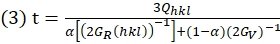
wobei G R(hkl) und Gv der Schubmodul der Aggregate unter der Bedingung Reuss (ISO-Spannung) bzw. Voigt (ISO-Dehnung) sind; α ist der Faktor, der das relative Gewicht der Reuss- und Voigt-Bedingungen40 bestimmt.
HINWEIS: Unter Berücksichtigung der komplizierten Spannungs-/Dehnungsbedingungen der aktuellen Experimente wird in dieser Studie α = 0,5 verwendet. - Für ein kubisches System berechnen Sie GR(hkl) und Gvwie folgt mit den Gleichungen 4-638,40,41:
(4)
(5)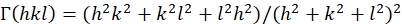
(6)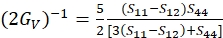
wobei S ij die einkristallelastischen Nachgiebigkeiten sind und aus den elastischen Steifigkeitskonstanten Cij von Werkstoffen erhalten werden können.
- Bestimmen Sie die Differenzspannung (die Differenz zwischen diesen maximalen (σ22 = σ33) und minimalen Spannungskomponenten (σ11), die eine untere Schätzung der Streckgrenze der Streckgrenze eines Materials 38, σy, basierend auf dem von Mises-Streckgrenze gemäß Gleichung (1)38 liefert:
3. TEM-Messungen
- Bereiten Sie dünn unter Druck stehende Ni-Folien für TEM mit einem FIB-System (Focused Ion Beam) vor (siehe Materialverzeichnis). Um mögliche Artefakte während des Ionenfräsens der Probe zu reduzieren, legen Sie eine schützende Pt-Schicht mit der im REM mit einer Dicke von ~ 1 μm ausgestatteten Pt-Pistole auf den Kandidatenbereich ab.
- Führen Sie TEM-Messungen an einem 300-kV-aberrationskorrigierten Transmissionselektronenmikroskop durch, das mit RAADF- (High Angle Annular Dark-Field) und Hellfeld-Detektoren (BF) ausgestattet ist.
- Nehmen Sie hochauflösende TEM-Bilder auf.
Ergebnisse
Bei hydrostatischer Kompression sollten ungerollte Röntgenbeugungslinien gerade und nicht gekrümmt sein. Unter nicht-hydrostatischem Druck erhöht jedoch die Krümmung (Ellipsizität der XRD-Ringe, die sich in der Nichtlinearität der entlang des Azimutwinkels aufgetragenen Linien niederschlägt) das ultrafeinkörnige Nickel bei ähnlichen Drücken signifikant an (Abbildung 4). Bei einem ähnlichen Druck ist die Differenzdehnung des 3 nm großen Nickels am höchsten. Die Ergebnisse der mec...
Diskussion
Computersimulationen wurden häufig eingesetzt, um den Korngrößeneffekt auf die Stärke von Nanometallen 5,6,16,17,27,42 zu untersuchen. Es wurde vorgeschlagen, dass perfekte Versetzungen, Teilversetzungen und GB-Verformungen eine entscheidende Rolle bei den Verformungsmechanismen der Nanomaterialien spielen. In einer Molek...
Offenlegungen
Die Autoren haben nichts offenzulegen.
Danksagungen
Wir danken der Unterstützung der National Natural Science Foundation of China (NSFC) unter den Fördernummern 11621062, 11772294, U1530402 und 11811530001. Diese Forschung wurde teilweise auch von der China Postdoctoral Science Foundation (2021M690044) unterstützt. Diese Forschung nutzte die Ressourcen der Advanced Light Source, einer DOE Office of Science User Facility unter der Vertragsnummer DE-AC02-05CH11231, und der Shanghai Synchrotron Radiation Facility. Diese Forschung wurde teilweise von COMPRES, dem Konsortium für Materialeigenschaftsforschung in den Geowissenschaften im Rahmen der NSF-Kooperationsvereinbarung EAR 1606856, unterstützt.
Materialien
| Name | Company | Catalog Number | Comments |
| 20 nm Ni | Nanomaterialstore | SN1601 | Flammable |
| 3 nm Ni | nanoComposix | Flammable | |
| 40, 70, 100, 200, 500 nm Ni | US nano | US1120 | Flammable |
| Absolute ethanol | as the solution to make 8 nm Ni | ||
| Absolute isopropanol | as the solution to make 12 nm Ni | ||
| Amorphous boron powder | alfa asear | ||
| Copper mesh | Beijing Zhongjingkeyi Technology Co., Ltd. | TEM grid | |
| Epoxy glue | |||
| Ethanol | clean experimental setup | ||
| Focused ion beam | FEI | ||
| Glass slide | |||
| Glue tape | Scotch | ||
| Kapton | DuPont | Polyimide film material | |
| Laser drilling machine | located in high pressure lab of ALS | ||
| Monochromatic synchrotron X-ray | Beamline 12.2.2, Advanced Light Source (ALS), Lawrence Berkeley National Laboratory | X-ray energy: 25-30 keV | |
| Optical microscope | Leica | to mount the gasket and load samples | |
| Pt powder | thermofisher | 38374 | |
| Reaction kettle | Xian Yichuang Co.,Ltd. | 50 mL | |
| Sand paper | from 400 mesh to 1000 mesh | ||
| Transmission Electron Microscopy | FEI | Titan G2 60-300 | |
| Two-dimension image plate | ALS, BL 12.2.2 | mar 345 |
Referenzen
- Hall, E. O. The Deformation and ageing of mild steel.3. Discussion of results. Proceedings of the Physical Society of London Section B. 64 (381), 747-753 (1951).
- Conrad, H. Effect of grain size on the lower yield and flow stress of iron and steel. Acta Metallurgica. 11 (1), 75-77 (1963).
- Kanninen, M. F., Rosenfield, A. R. Dynamics of dislocation pile-up formation. The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics. 20 (165), 569-587 (1969).
- Thompson, A. A. W. Yielding in nickel as a function of grain or cell size. Acta Metallurgica. 23 (11), 1337-1342 (1975).
- Schiotz, J., Di Tolla, F. D., Jacobsen, K. W. Softening of nanocrystalline metals at very small grain sizes. Nature. 391 (6667), 561-563 (1998).
- Schiotz, J., Jacobsen, K. W. A maximum in the strength of nanocrystalline copper. Science. 301 (5638), 1357-1359 (2003).
- Conrad, H., Narayan, J. Mechanism for grain size softening in nanocrystalline Zn. Applied Physics Letters. 81 (12), 2241-2243 (2002).
- Chokshi, A. H., Rosen, A., Karch, J., Gleiter, H. On the validity of the hall-petch relationship in nanocrystalline materials. Scripta Metallurgica. 23 (10), 1679-1683 (1989).
- Sanders, P. G., Eastman, J. A., Weertman, J. R. Elastic and tensile behavior of nanocrystalline copper and palladium. Acta Materialia. 45 (10), 4019-4025 (1997).
- Conrad, H., Narayan, J. On the grain size softening in nanocrystalline materials. Scripta Materialia. 42 (11), 1025-1030 (2000).
- Chen, J., Lu, L., Lu, K. Hardness and strain rate sensitivity of nanocrystalline Cu. Scripta Materialia. 54 (11), 1913-1918 (2006).
- Knapp, J. A., Follstaedt, D. M. Hall-Petch relationship in pulsed-laser deposited nickel films. Journal of Materials Research. 19 (1), 218-227 (2004).
- Kumar, K. S., Suresh, S., Chisholm, M. F., Horton, J. A., Wang, P. Deformation of electrodeposited nanocrystalline nickel. Acta Materialia. 51 (2), 387-405 (2003).
- Chen, B., et al. Texture of Nanocrystalline Nickel: Probing the lower size limit of dislocation activity. Science. 338 (6113), 1448-1451 (2012).
- Chen, M. W., et al. Deformation twinning in nanocrystalline aluminum. Science. 300 (5623), 1275-1277 (2003).
- Yamakov, V., Wolf, D., Phillpot, S. R., Gleiter, H. Deformation twinning in nanocrystalline Al by molecular-dynamics simulation. Acta Materialia. 50 (20), 5005-5020 (2002).
- Yamakov, V., Wolf, D., Phillpot, S. R., Mukherjee, A. K., Gleiter, H. Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation. Nature Materials. 1 (1), 45-49 (2002).
- Yamakov, V., Wolf, D., Salazar, M., Phillpot, S. R., Gleiter, H. Length-scale effects in the nucleation of extended dislocations in nanocrystalline Al by molecular-dynamics simulation. Acta Materialia. 49 (14), 2713-2722 (2001).
- Shan, Z. W., et al. Grain boundary-mediated plasticity in nanocrystalline nickel. Science. 305 (5684), 654-657 (2004).
- Li, H., et al. Strain-Dependent Deformation Behavior in Nanocrystalline Metals. Physical Review Letters. 101 (1), 015502 (2008).
- Van Swygenhoven, H., Derlet, P. M. Grain-boundary sliding in nanocrystalline fcc metals. Physical Review B. 64 (22), 224105 (2001).
- Ovid’ko, I. A. Deformation of nanostructures. Science. 295 (5564), 2386 (2002).
- Murayama, M., Howe, J. M., Hidaka, H., Takaki, S. Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe. Science. 295 (5564), 2433 (2002).
- Wang, L., et al. Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum. Nature Communications. 5, 4402 (2014).
- Edalati, K., et al. Influence of dislocation-solute atom interactions and stacking fault energy on grain size of single-phase alloys after severe plastic deformation using high-pressure torsion. Acta Materialia. 69, 68-77 (2014).
- Edalati, K., Horita, Z. High-pressure torsion of pure metals: Influence of atomic bond parameters and stacking fault energy on grain size and correlation with hardness. Acta Materialia. 59 (17), 6831-6836 (2011).
- Yamakov, V., Wolf, D., Phillpot, S. R., Mukherjee, A. K., Gleiter, H. Deformation-mechanism map for nanocrystalline metals by molecular-dynamics simulation. Nature Materials. 3 (1), 43-47 (2004).
- Starink, M. J., Cheng, X., Yang, S. Hardening of pure metals by high-pressure torsion: A physically based model employing volume-averaged defect evolutions. Acta Materialia. 61 (1), 183-192 (2013).
- Yang, T., et al. Ultrahigh-strength and ductile superlattice alloys with nanoscale disordered interfaces. Science. 369 (6502), 427 (2020).
- Hu, J., Shi, Y. N., Sauvage, X., Sha, G., Lu, K. Grain boundary stability governs hardening and softening in extremely fine nanograined metals. Science. 355 (6331), 1292 (2017).
- Yue, Y., et al. Hierarchically structured diamond composite with exceptional toughness. Nature. 582 (7812), 370-374 (2020).
- Li, X. Y., Jin, Z. H., Zhou, X., Lu, K. Constrained minimal-interface structures in polycrystalline copper with extremely fine grains. Science. 370 (6518), 831 (2020).
- Yan, S., et al. Crystal plasticity in fusion zone of a hybrid laser welded Al alloys joint: From nanoscale to macroscale. Materials and Design. 160, 313-324 (2018).
- Khalajhedayati, A., Pan, Z., Rupert, T. J. Manipulating the interfacial structure of nanomaterials to achieve a unique combination of strength and ductility. Nature Communications. 7 (1), 10802 (2016).
- Chen, L. Y., et al. Processing and properties of magnesium containing a dense uniform dispersion of nanoparticles. Nature. 528 (7583), 539-543 (2015).
- Zhou, X., et al. High-pressure strengthening in ultrafine-grained metals. Nature. 579 (7797), 67-72 (2020).
- Lutterotti, L., Vasin, R., Wenk, H. -. R. Rietveld texture analysis from synchrotron diffraction images. I. Calibration and basic analysis. Powder Diffraction. 29 (1), 76-84 (2014).
- Singh, A. K., Balasingh, C., Mao, H. K., Hemley, R. J., Shu, J. F. Analysis of lattice strains measured under nonhydrostatic pressure. Journal of Applied Physics. 83 (12), 7567-7575 (1998).
- Hemley, R. J., et al. X-ray imaging of stress and strain of diamond, iron, and tungsten at megabar pressures. Science. 276 (5316), 1242-1245 (1997).
- Merkel, S., et al. Deformation of polycrystalline MgO at pressures of the lower mantle. Journal of Geophysical Research-Solid Earth. 107, 2271 (2002).
- Singh, A. K. The lattice strains in a specimen (cubic system) compressed nonhydrostatically in an opposed Anvil device. Journal of Applied Physics. 73 (9), 4278-4286 (1993).
- Van Swygenhoven, H., Derlet, P. M., Frøseth, A. G. Stacking fault energies and slip in nanocrystalline metals. Nature Materials. 3 (6), 399-403 (2004).
- Chung, H. Y., et al. Synthesis of ultra-incompressible superhard rhenium diboride at ambient pressure. Science. 316 (5823), 436-439 (2007).
- Jo, M., et al. Theory for plasticity of face-centered cubic metals. Proceedings of the National Academy of Sciences. 111 (18), 6560 (2014).
- Klueh, R. L. Miniature tensile test specimens for fusion reactor irradiation studies. Nuclear Engineering and Design, Fusion. 2 (3), 407-416 (1985).
- Konopík, P., Farahnak, P., Rund, M., Džugan, J., Rzepa, S. Applicability of miniature tensile test in the automotive sector. IOP Conference Series: Materials Science and Engineering. 461, 012043 (2018).
- Yang, J., et al. Strength enhancement of nanocrystalline tungsten under high pressure. Matter and Radiation at Extremes. 5 (5), 058401 (2020).
- Chen, B. Exploring nanomechanics with high-pressure techniques. Matter and Radiation at Extremes. 5 (6), (2020).
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten