Determinazione della resistenza meccanica dei metalli a grana ultra fine

Riepilogo

Il protocollo qui presentato descrive gli esperimenti radiali ad alta pressione diamante-incudine-cella e analizza i relativi dati, che sono essenziali per ottenere la resistenza meccanica dei nanomateriali con una svolta significativa rispetto all'approccio tradizionale.

Abstract

Il rafforzamento meccanico dei metalli è la sfida di lunga data e l'argomento popolare della scienza dei materiali nelle industrie e nel mondo accademico. La dipendenza dalle dimensioni della forza dei nanometalli ha attirato molto interesse. Tuttavia, caratterizzare la resistenza dei materiali su scala nanometrica inferiore è stata una grande sfida perché le tecniche tradizionali diventano non più efficaci e affidabili, come la nano-indentazione, la compressione del micropilastro, la trazione, ecc. L'attuale protocollo utilizza tecniche di diffrazione a raggi X (XRD) radial diamond-anvil cell (rDAC) per tracciare i cambiamenti di stress differenziale e determinare la forza dei metalli ultrafini. Si è scoperto che le particelle di nichel ultrafini hanno una resistenza allo snervamento più significativa rispetto alle particelle più grossolane e il rafforzamento delle dimensioni del nichel continua fino a 3 nm. Questa scoperta vitale dipende immensamente da tecniche di caratterizzazione efficaci e affidabili. Si prevede che il metodo rDAC XRD svolgerà un ruolo significativo nello studio e nell'esplorazione della meccanica dei nanomateriali.

Introduzione

La resistenza alla deformazione plastica determina la resistenza dei materiali. La forza dei metalli di solito aumenta con la diminuzione delle dimensioni dei grani. Questo fenomeno di rafforzamento delle dimensioni può essere ben illustrato dalla tradizionale teoria della relazione Hall-Petch dal millimetro fino al regime submicron ^1,2, che si basa sul meccanismo di deformazione mediato dalla dislocazione dei metalli di grandi dimensioni, cioè le dislocazioni si accumulano ai confini del grano (GB) e ostacolano i loro movimenti, portando al rafforzamento meccanico nei metalli ^3,4.

Al contrario, l'ammorbidimento meccanico, spesso indicato come la relazione inversa Hall-Petch, è stato riportato per nanometalli fini negli ultimi due decenni 5,6,7,8,9,10. Pertanto, la forza dei nanometalli è ancora sconcertante poiché è stato rilevato un indurimento continuo per granulometrie fino a ~ 10 nm^11,12, mentre i casi di ammorbidimento delle dimensioni al di sotto del regime di 10 nm sono stati segnalati anche ^7,8,9,10. La principale difficoltà o sfida per questo argomento dibattuto è quella di effettuare misurazioni statisticamente riproducibili sulle proprietà meccaniche dei nanometalli ultrafini e stabilire una correlazione affidabile tra la resistenza e la granulometria dei nanometalli. Un'altra parte della difficoltà deriva dall'ambiguità nei meccanismi di deformazione plastica dei nanometalli. Sono stati segnalati vari difetti o processi su scala nanometrica, tra cui lussazioni^13,14, gemellaggio di deformazione 15,16,17, errori di impilamento^15,18, migrazione GB¹⁹, GB scorrevoli ^5,6,20,21, rotazione del grano 22,23,24, parametri del legame^atomico 25,26,27,28, ecc. Tuttavia, quale domina la deformazione plastica e quindi determina la forza dei nanometalli non è ancora chiaro.

Per questi problemi di cui sopra, gli approcci tradizionali di esame della resistenza meccanica, come la prova di trazione²⁹, la prova di durezza Vickers^30,31, la prova di nano-indentazione³², la compressione del micropilare ^33,34,35, ecc. sono meno efficaci perché l'alta qualità di grandi pezzi di materiali nanostrutturati è così difficile da fabbricare e il penetratore convenzionale è molto più grande della singola nanoparticella di materiali (per il meccanica a particella singola). In questo studio, introduciamo le tecniche radiali DAC XRD 36,37,38 alla scienza dei materiali per tracciare in situ lo stress di snervamento e la testurizzazione della deformazione del nano nichel di varie granulometrie, che vengono utilizzati nel campo delle geoscienze in studi precedenti. È stato scoperto che il rafforzamento meccanico può essere esteso fino a 3 nm, molto più piccolo delle dimensioni più sostanziali precedentemente riportate di nanometalli, il che amplia il regime della relazione convenzionale Hall-Petch, implicando il significato delle tecniche RDAC XRD per la scienza dei materiali.

Protocollo

1. Preparazione del campione

1. Ottenere polvere di nichel da 3 nm, 20 nm, 40 nm, 70 nm, 100 nm, 200 nm e 500 nm da fonti commerciali (vedere Tabella dei materiali). La caratterizzazione morfologica è mostrata in Figura 1.
2. Preparare particelle di nichel da 8 nm riscaldando particelle di nichel da 3 nm utilizzando un bollitore di reazione (vedere Tabella dei materiali).
   1. Mettere ~ 20 ml di etanolo assoluto e ~ 50 mg di polvere di nichel 3 nm nel bollitore di reazione. NOTA: l'intera soluzione non dovrebbe raggiungere ~ 70% del volume del bollitore.
   2. Riscaldare il bollitore di reazione a 80 °C per 24 ore.
   3. Raffreddare la soluzione a temperatura ambiente e far cadere una piccola soluzione su una rete di rame (griglia TEM, vedere Tabella dei materiali).
   4. Inserire la rete di rame essiccata nella camera di microscopia elettronica a trasmissione (TEM) e osservare la morfologia del campione sotto il fascio di elettroni con tensione di 200 kV.
      NOTA: La rete di rame è stata essiccata all'aria per ~ 5 minuti o ha utilizzato una luce di asciugatura di 5 minuti.
   5. Misurare manualmente la distribuzione granulometrica dalle immagini TEM.
      NOTA: La misurazione delle dimensioni delle particelle può anche essere effettuata utilizzando qualsiasi software disponibile gratuitamente come Image J.
   6. Estrarre la soluzione e vaporizzare l'etanolo a temperatura ambiente; quindi, il resto del solido nero è la polvere di nichel puro con una dimensione media delle particelle di 8 nm.
3. Preparare 12 nm di polvere di nichel
   1. Ripetere il passaggio 1.2, ma modificare "etanolo assoluto" e "80 °C per 24 ore" in "isopropanolo assoluto" e "150 °C per 12 ore" per ottenere la polvere di nichel pura con la particella media di 12 nm.

2. Misurazioni radiali DAC XRD ad alta pressione

1. Realizzare una guarnizione trasparente in boro-epossidico a raggi X utilizzando una perforatrice laser (vedere Tabella dei materiali).
   1. Preparare le guarnizioni di supporto Kapton (una sorta di plastica)
      NOTA: Kapton è un materiale in film di poliimmide (vedi Tabella dei materiali).
      1. Tagliare il cerchio interno con una foratrice laser utilizzando i parametri menzionati: 35% di potenza laser, tre passaggi, 0,4 mm/s (velocità di taglio).
      2. Tagliare il rettangolare esterno utilizzando i parametri: 80% della potenza del laser, due passate, 1,2 mm/s (velocità di taglio). La dimensione rettangolare è 8 x 1,4 mm.
   2. Preparare guarnizioni di boro-epossidiche da un disco di boro più grande con un diametro di ~ 10 mm.
      NOTA: Il disco di boro è realizzato comprimendo la miscela di polvere di boro amorfo e colla epossidica³⁶.
      1. Lucidare manualmente i dischi grezzi ad uno spessore di 60-100 μm con carta vetrata.
         NOTA: la carta vetrata va da ~ 400 mesh a ~ 1000 mesh.
      2. Tagliare i cerchi interni con una foratrice laser utilizzando i parametri menzionati: 35% di potenza laser, tre passaggi, 0,4 mm/s (velocità di taglio).
      3. Tagliare il cerchio esterno con una foratrice laser: 30% della potenza laser, una passata, 0,4 mm/s (velocità di taglio). Ripeti e fermati immediatamente quando si stacca.
   3. Assemblare le guarnizioni
      1. Posizionare una guarnizione di supporto Kapton (preparata al punto 2.1.1) su una slitta di vetro.
      2. Posizionare una guarnizione di boro forata sul foro interno della guarnizione Kapton. Assicurarsi che l'estremità più grande della guarnizione di boro sia nella parte superiore.
      3. Metti un'altra diapositiva di vetro pulita sulla parte superiore. Tenerlo saldamente e premerlo fino a quando la guarnizione non è saldamente inserita nel foro della guarnizione Kapton.
      4. Conservare i gruppi di guarnizioni fabbricati tra due vetrini puliti e avvolgerli con nastro adesivo per un uso futuro.
         NOTA: Diametro guarnizione, Ø = dimensione del culet diamantato + 150 μm. Per una migliore riproducibilità, le stesse configurazioni possono essere utilizzate (possibilmente con piccole regolazioni se qualcosa non va) per la foratura laser e il taglio durante la preparazione della guarnizione. Per una buona corrispondenza delle dimensioni, il diametro delle guarnizioni inserite per il taglio laser è Ø + 23 μm mentre il diametro del foro interno delle guarnizioni di supporto Kapton (inserite per il taglio laser) è Ø - 23 μm.
2. Caricamento dell'esperimento DAC radiale
   1. Montare il gruppo guarnizione
      1. Sul monitor del computer di visualizzazione (collegato al microscopio ottico), contrassegnare un punto per individuare il centro del diamante (il diamante a pistone del DAC).
      2. Montare la guarnizione in boro-epossidico (preparata al punto 2.1) e il segno al centro del foro della guarnizione.
      3. Utilizzare una slitta di vetro per premere verso il basso l'assieme della guarnizione in modo che la guarnizione si fissi saldamente sul diamante del pistone.
         NOTA: un DAC ha due pezzi identici di diamanti. Generalmente, quello superiore è chiamato diamante del cilindro e quello inferiore è chiamato diamante del pistone.
   2. Pulizia e compattazione della configurazione della guarnizione
      1. Caricare campioni con una dimensione del pezzo inferiore al foro della guarnizione in modo tale che non vi sia trabocco di materiali sulla superficie della guarnizione.
         NOTA: i campioni qui indicano i materiali candidati che abbiamo studiato nei nostri esperimenti. In questo studio, i campioni sono polveri ni di dimensioni diverse e chip Pt.
      2. Chiudere la cella dopo il caricamento di un nuovo pezzo di campione per ottenere compattezza.
   3. Caricamento di materiali morbidi (come l'oro)
      1. Caricare solo un pezzo del campione morbido (rendere il materiale morbido come una piccola frazione dei materiali caricati).
      2. Utilizzare materiali amorfi duri per riempire il foro della guarnizione per una buona compattezza.
   4. Caricamento di materiali a basso numero atomico (come spinello, piropo, serpentina)
      1. Mescolare il campione con 10% Pt o Au. Riempire il foro della guarnizione con la miscela ma senza traboccare.
      2. Se necessario, mettere materiali amorfi duri sulla parte superiore per una buona compattezza.
3. Studio di diffrazione a raggi X
   1. Montare la guarnizione in boro trasparente a raggi X-Kapton (preparata al punto 2.1) con uno spessore di 100 μm e un foro della camera di 60 μm sulla parte superiore del culet da 300 μm di DAC con il supporto delle argille.
   2. Posizionare un piccolo pezzo di chip Pt sopra il campione Ni come calibrante di pressione.
      NOTA: non è stato utilizzato alcun mezzo di pressione per massimizzare la sollecitazione differenziale tra assiale e radiale.
   3. Utilizzare una radiografia di sincrotrone monocromatica (vedere Tabella dei materiali) con un'energia di 25 o 30 keV per condurre gli esperimenti di diffrazione a raggi X.
   4. Focalizzare il fascio di raggi X su una superficie di ~30 x 30 μm² sul campione.
   5. Raccogliere i modelli di diffrazione a raggi X a intervalli di pressione di 1-2 GPa da una piastra immagine bidimensionale (vedere Tabella dei materiali) con una risoluzione di 100 μm/pixel. L'impostazione utilizzata è illustrata nella Figura 2 e nella Figura 3.
4. L'analisi dei dati sperimentali
   1. Elabora ogni immagine di diffrazione a raggi X in un file contenente 72 spettri su passi azimutali di 5° utilizzando Fit2d 37,38,39,40,41,42.
      NOTA: un'immagine di diffrazione bidimensionale contiene informazioni a 360°. Per analizzare le informazioni sullo stress e sulla texture, è necessario separare in 72 file con informazioni azimutali a 5° contenute in ciascuno di essi. Fit2d è il software utilizzato per analizzare i dati di diffrazione a raggi X 37,38,39,40,41,42.
   2. Perfeziona il modello di diffrazione con il metodo Rietveld nel software MAUD³⁷. La deformazione reticolare di ciascun piano reticolare è stata ottenuta adattando il modello^37,40.
   3. Calcolare la sollecitazione differenziale e la resistenza allo snervamento secondo la teoria della deformazione reticolare³⁸ e il criterio di resa di von Mises ^38,39 seguendo il passaggio 2.5.
5. La teoria della deformazione reticolare per l'analisi dei dati sperimentali
   1. Determinare la sollecitazione differenziale (la differenza tra questi componenti di sollecitazione massima (σ₂₂ = σ₃₃) e minima (σ₁₁)) che fornisce una stima del limite inferiore del limite inferiore del carico di snervamento di un materiale³⁸, σ_y, in base al criterio di resa di von Mises seguendo l'equazione (1)³⁸:
      (1) t= σ_{11-σ 33}<2τ= σ_y.
   2. Ottenere la deformazione deviatoria Q_hkl dipendente dalla direzione misurando le d-spaziature da diverse direzioni di diffrazione con la seguente equazione (2)³⁸:
      (2)
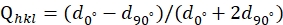
      dove d_0° e d_90° sono le d-spaziature misurate rispettivamente da Ψ = 0° e Ψ = 90° (l'angolo tra il vettore di diffrazione e l'asse di carico).
   3. Quindi, derivare il valore di t usando l'equazione (3)³⁸:
      
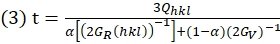
      dove G_R(hkl) e G_v sono il modulo di taglio degli aggregati rispettivamente nella condizione di Reuss (iso-stress) e nella condizione di Voigt (iso-deformazione); α è il fattore per determinare il peso relativo delle condizioni di Reuss e Voigt⁴⁰.
      NOTA: Considerando le complicate condizioni di stress/deformazione degli esperimenti in corso, in questo studio viene utilizzato α = 0,5.
   4. Per un sistema cubico, calcolare G_R(hkl) e G_vcome segue usando le equazioni 4-6 38,40,41:
      (4)
      (5)
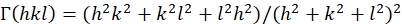
      (6)
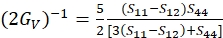
      dove S_ij sono le conformità elastiche a cristallo singolo e possono essere ottenute dalle costanti di rigidità elastica C_ij dei materiali.

3. Misure TEM

1. Preparare sottili fogli di Ni pressurizzati per TEM utilizzando un sistema a fascio ionico focalizzato (FIB) (vedere Tabella dei materiali). Per ridurre possibili artefatti durante la fresatura ionica del campione, depositare uno strato protettivo di Pt utilizzando la pistola Pt equipaggiata nel SEM con uno spessore di ~ 1 μm sulla regione candidata.
2. Eseguire misurazioni TEM su un microscopio elettronico a trasmissione corretto per aberrazione da 300 kV dotato di rivelatori ad alto angolo anulare a campo oscuro (HAADF) e a campo luminoso (BF).
3. Scatta immagini TEM ad alta risoluzione.

Risultati

Sotto compressione idrostatica, le linee di diffrazione a raggi X srotolate devono essere diritte, non curve. Tuttavia, sotto pressione non idrostatica, la curvatura (ellitticità degli anelli XRD, che si traduce nella non linearità delle linee tracciate lungo l'angolo azimutale) aumenta significativamente il nichel a grana ultrafine a pressioni simili (Figura 4). A una pressione simile, la deformazione differenziale del nichel di 3 nm è la più alta. I risultati della resistenza meccanica...

Discussione

Le simulazioni computazionali sono state ampiamente utilizzate per studiare l'effetto granulometrico sulla forza dei nanometalli ^{5,6,16,17,27,42}. Dislocazioni perfette, lussazioni parziali e deformazione GB sono state proposte per svolgere un ruolo decisivo nei meccanismi di deformazione dei nanomateriali. In una simulazione ...

Materiali

Name	Company	Catalog Number	Comments
20 nm Ni	Nanomaterialstore	SN1601	Flammable
3 nm Ni	nanoComposix		Flammable
40, 70, 100, 200, 500 nm Ni	US nano	US1120	Flammable
Absolute ethanol			as the solution to make 8 nm Ni
Absolute isopropanol			as the solution to make 12 nm Ni
Amorphous boron powder	alfa asear
Copper mesh	Beijing Zhongjingkeyi Technology Co., Ltd.		TEM grid
Epoxy glue
Ethanol			clean experimental setup
Focused ion beam	FEI
Glass slide
Glue tape	Scotch
Kapton	DuPont		Polyimide film material
Laser drilling machine			located in high pressure lab of ALS
Monochromatic synchrotron X-ray	Beamline 12.2.2, Advanced Light Source (ALS), Lawrence Berkeley National Laboratory		X-ray energy: 25-30 keV
Optical microscope	Leica		to mount the gasket and load samples
Pt powder	thermofisher	38374
Reaction kettle	Xian Yichuang Co.,Ltd.		50 mL
Sand paper			from 400 mesh to 1000 mesh
Transmission Electron Microscopy	FEI		Titan G2 60-300
Two-dimension image plate	ALS, BL 12.2.2		mar 345