Для просмотра этого контента требуется подписка на Jove Войдите в систему или начните бесплатную пробную версию.
Method Article
Определение механической прочности сверхмелкозернистых металлов
В этой статье
Резюме
Представленный здесь протокол описывает радиальные эксперименты высокого давления с алмазно-наковальней и анализ связанных с ними данных, которые необходимы для получения механической прочности наноматериалов со значительным прорывом к традиционному подходу.
Аннотация
Механическое упрочнение металлов является давней проблемой и популярной темой материаловедения в промышленности и научных кругах. Размерная зависимость прочности нанометаллов вызывает большой интерес. Тем не менее, характеристика прочности материалов в нижнем нанометровом масштабе была большой проблемой, потому что традиционные методы становятся более неэффективными и надежными, такие как нано-углубление, микросвильное сжатие, растяжение и т. Д. Текущий протокол использует методы рентгеновской дифракции (XRD) радиальной алмазно-наковальни (rDAC) для отслеживания дифференциальных изменений напряжений и определения прочности ультратонких металлов. Установлено, что ультрадисперсные частицы никеля обладают более значительным пределом текучести, чем более грубые частицы, а усиление размера никеля продолжает снижаться до 3 нм. Этот жизненно важный вывод в огромной степени зависит от эффективных и надежных методов характеристики. Ожидается, что метод rDAC XRD будет играть значительную роль в изучении и изучении механики наноматериалов.
Введение
Устойчивость к пластической деформации определяет прочность материалов. Прочность металлов обычно увеличивается с уменьшением размеров зерен. Это явление усиления размеров может быть хорошо проиллюстрировано традиционной теорией отношений Холла-Петча от миллиметра до субмикронного режима 1,2, которая основана на дислокационно-опосредованном механизме деформации объемных металлов, то есть дислокации накапливаются на границах зерен (ГБ) и препятствуют их движениям, что приводит к механическому усилению в металлах 3,4.
Напротив, механическое размягчение, часто называемое обратным соотношением Холла-Петча, было зарегистрировано для тонких нанометаллов за последние два десятилетия 5,6,7,8,9,10. Таким образом, прочность нанометаллов все еще вызывает недоумение, поскольку непрерывное затвердевание было обнаружено для размеров зерен до ~ 10 нм11,12, в то время как случаи размягчения размера ниже режима 10 нм также были зарегистрированы 7,8,9,10. Основная трудность или вызов для этой обсуждаемой темы заключается в том, чтобы провести статистически воспроизводимые измерения механических свойств ультрадисперсных нанометаллов и установить надежную корреляцию между прочностью и размером зерен нанометаллов. Другая часть сложности связана с неоднозначностью механизмов пластической деформации нанометаллов. Сообщалось о различных дефектах или процессах на наноуровне, включая дислокации 13,14, деформацию побратимства 15,16,17, ошибки укладки 15,18, миграцию GB19, скольжение GB 5,6,20,21, вращение зерна 22,23,24, параметры атомной связи 25,26,27,28 и т.д. Однако какой из них доминирует в пластической деформации и, таким образом, определяет прочность нанометаллов, до сих пор неясно.
Для этих вышеуказанных вопросов традиционные подходы к исследованию механической прочности, такие как испытание на растяжение29, испытание на твердость по Виккерсу 30,31, тест на наноиндентацию32, микропилларное сжатие 33,34,35 и т. Д., Менее эффективны, потому что высокое качество больших кусков наноструктурированных материалов настолько сложно изготовить, а обычный индентер намного больше, чем одна наночастица материалов (для механика одиночных частиц). В этом исследовании мы вводим радиальные методы DAC XRD 36,37,38 в материаловедение для in situ отслеживания пределов текучести и текстурирования деформации наноникеля различных размеров зерен, которые использовались в области геонаук в предыдущих исследованиях. Было обнаружено, что механическое усиление может быть расширено до 3 нм, что намного меньше, чем ранее сообщенные наиболее существенные размеры нанометаллов, что расширяет режим обычных отношений Холла-Петча, подразумевая значение методов rDAC XRD для материаловедения.
протокол
1. Пробоподготовка
- Получение никелевого порошка 3 нм, 20 нм, 40 нм, 70 нм, 100 нм, 200 нм и 500 нм из коммерческих источников (см. Таблицу материалов). Характеристика морфологии показана на рисунке 1.
- Получение частиц никеля 8 нм путем нагревания 3 нм частиц никеля с помощью реакционного чайника (см. Таблицу материалов).
- Поместите ~20 мл абсолютного этанола и ~50 мг порошка никеля 3 нм в реакционный чайник. ПРИМЕЧАНИЕ: Весь раствор не должен достигать ~70% от объема чайника.
- Нагревайте реакционный чайник при 80 °C в течение 24 ч.
- Охладите раствор до комнатной температуры и опустите немного раствора на одну медную сетку (сетка ТЭМ, см. Таблица материалов).
- Поместите высушенную медную сетку в камеру просвечивающей электронной микроскопии (ТЭМ) и наблюдайте морфологию образца под напряжением электронного пучка 200 кВ.
ПРИМЕЧАНИЕ: Медную сетку сушили на воздухе в течение ~5 мин или использовали сушильный свет 5 мин. - Измерьте распределение частиц по размерам по изображениям ТЕА вручную.
ПРИМЕЧАНИЕ: Измерение размера частиц также может быть выполнено с использованием любого свободно доступного программного обеспечения, такого как Image J. - Вынуть раствор и испарить этанол при комнатной температуре; тогда остальная часть черного твердого тела представляет собой чистый никелевый порошок со средним размером частиц 8 нм.
- Приготовить 12 нм никелевого порошка
- Повторите этап 1.2, но замените "абсолютный этанол" и "80 °C в течение 24 ч" на "абсолютный изопропанол" и "150 °C в течение 12 ч" для получения чистого никелевого порошка со средней частицей 12 нм.
2. Радиальные измерения XRD ЦАП высокого давления
- Сделайте рентгеновскую прозрачную борно-эпоксидную прокладку с помощью лазерного сверлильного станка (см. Таблицу материалов).
- Подготовьте Каптон (разновидность пластика) поддерживающие прокладки
ПРИМЕЧАНИЕ: Каптон представляет собой полиимидный пленочный материал (см. Таблицу материалов).- Вырежьте внутренний круг лазерным сверлильным станком, используя указанные параметры: мощность лазера 35%, три прохода, 0,4 мм/с (скорость резания).
- Вырезать наружный прямоугольник можно по параметрам: 80% мощности лазера, два прохода, 1,2 мм/с (скорость резания). Прямоугольный размер составляет 8 х 1,4 мм.
- Приготовьте борно-эпоксидные прокладки из более крупного борного диска диаметром ~10 мм.
ПРИМЕЧАНИЕ: Борный диск изготавливается путем сжатия смеси аморфного порошка бора и эпоксидного клея36.- Отполируйте необработанные диски до толщины 60-100 мкм наждачной бумагой вручную.
ПРИМЕЧАНИЕ: Наждачная бумага от ~400 меш до ~1000 меш. - Вырежьте внутренние круги лазерным сверлильным станком, используя указанные параметры: мощность лазера 35%, три прохода, 0,4 мм/с (скорость резания).
- Вырежьте внешний круг с помощью лазерного сверлильного станка: 30% мощности лазера, один проход, 0,4 мм/с (скорость резания). Повторите и немедленно остановитесь, когда он оторвется.
- Отполируйте необработанные диски до толщины 60-100 мкм наждачной бумагой вручную.
- Сборка прокладок
- Поместите опорную прокладку Kapton (подготовленную на этапе 2.1.1) на стеклянную горку.
- Поместите просверленную прокладку бора на внутреннее отверстие прокладки Kapton. Убедитесь, что больший конец борной прокладки находится наверху.
- Положите еще один чистый стеклянный слайд сверху. Крепко держите его и прижимайте до тех пор, пока прокладка не будет прочно вставлена в отверстие прокладки Kapton.
- Храните изготовленные прокладки в сборе между двумя чистыми стеклянными слайдами и оберните их клеевой лентой для дальнейшего использования.
ПРИМЕЧАНИЕ: Диаметр прокладки, Ø = размер алмазного кулета + 150 мкм. Для лучшей воспроизводимости можно использовать одни и те же установки (возможно, с небольшими корректировками, если что-то окажется не так) для лазерного сверления и резки во время подготовки прокладки. Для хорошего соответствия размеров диаметр прокладок, вводимых для лазерной резки, составляет Ø + 23 мкм, а диаметр внутреннего отверстия опорных прокладок Kapton (вводимых для лазерной резки) составляет Ø - 23 мкм.
- Подготовьте Каптон (разновидность пластика) поддерживающие прокладки
- Радиальная загрузка эксперимента ЦАП
- Монтаж прокладки в сборе
- На мониторе просматривающего компьютера (подключенном к оптическому микроскопу) отметьте точку, чтобы найти центр алмаза (поршневой алмаз ЦАП).
- Установите борно-эпоксидную прокладку (подготовленную на этапе 2.1) и метку в центре отверстия прокладки.
- Используйте стеклянную горку, чтобы прижать узел прокладки таким образом, чтобы прокладка прочно застыла на алмазе поршня.
ПРИМЕЧАНИЕ: ЦАП имеет два одинаковых куска алмазов. Как правило, верхний называется цилиндрическим алмазом, а нижний называется поршневым алмазом.
- Очистка и уплотнение прокладки
- Загружайте образцы с куском размером меньше отверстия прокладки, чтобы не было переполнения материалов на поверхности прокладки.
ПРИМЕЧАНИЕ: Образцы здесь означают материалы-кандидаты, которые мы изучали в наших экспериментах. В этом исследовании образцы представляют собой порошки Ni разного размера и чипсы Pt. - Закройте ячейку после загрузки нового образца для достижения компактности.
- Загружайте образцы с куском размером меньше отверстия прокладки, чтобы не было переполнения материалов на поверхности прокладки.
- Загрузка мягких материалов (таких как золото)
- Загрузите только один кусок мягкого образца (сделайте мягкий материал небольшой частью загруженных материалов).
- Используйте твердые аморфные материалы для заполнения отверстия прокладки для хорошей компактности.
- Загрузка материалов с низким атомным номером (таких как шпинель, пироп, серпентин)
- Смешайте образец с 10% Pt или Au. Заполните отверстие прокладки смесью, но без перелива.
- При необходимости сверху нанесите твердые аморфные материалы для хорошей компактности.
- Монтаж прокладки в сборе
- Рентгеноструктурное исследование
- Установите рентгеновскую прозрачную прокладку бора-каптона (подготовленную на стадии 2.1) толщиной 100 мкм и камерное отверстие 60 мкм поверх 300 мкм кулета ЦАП с опорой глины.
- Поместите небольшой кусочек чипа Pt поверх образца Ni в качестве калибра давления.
ПРИМЕЧАНИЕ: Для максимизации дифференциального напряжения между осевым и радиальным напряжением среда давления не использовалась. - Используйте монохроматический синхротронный рентгеновский луч (см. Таблицу материалов) с энергией 25 или 30 кэВ для проведения экспериментов по дифракции рентгеновских лучей.
- Сфокусируйте рентгеновский луч на площади поверхности образца ~30 x 30мкм2 .
- Соберите рентгеновские дифракционные картины с интервалами давления 1-2 ГПа с помощью двухмерной графической пластины (см. Таблицу материалов) с разрешением 100 мкм/пиксель. Используемая установка показана на рисунках 2 и 3.
- Анализ экспериментальных данных
- Обработайте каждое рентгеновское дифракционное изображение в файл, содержащий 72 спектра на азимутальных шагах 5°, используя Fit2d 37,38,39,40,41,42.
ПРИМЕЧАНИЕ: Двумерное дифракционное изображение содержит информацию 360°. Для анализа информации о напряжении и текстуре необходимо разделить на 72 файла с азимутальной информацией 5°, содержащейся в каждом. Fit2d - это программное обеспечение, используемое для анализа данных дифракции рентгеновских лучей 37,38,39,40,41,42. - Уточните дифракционную картину с помощью метода Ритвельда в программном обеспечении MAUD37. Деформация решетки каждой плоскости решетки была получена путем подгонки рисунка 37,40.
- Рассчитайте дифференциальное напряжение и предел текучести в соответствии с теорией деформациирешетки 38 и критерием выхода фон Мизеса 38,39 после шага 2.5.
- Обработайте каждое рентгеновское дифракционное изображение в файл, содержащий 72 спектра на азимутальных шагах 5°, используя Fit2d 37,38,39,40,41,42.
- Теория деформации решетки для анализа экспериментальных данных
- Определите дифференциальное напряжение (разницу между этими максимальными (σ22 = σ33) и минимальными напряжениями (σ11) компонентами), которое обеспечивает нижнюю оценку предела текучести материала38, σy, на основе критерия урожайности фон Мизеса по уравнению (1)38:
(1) t= σ11-σ 33<2τ= σy. - Получение зависящей от направления девиаторной деформации Qhkl путем измерения d-интервалов от различных направлений дифракции по следующему уравнению (2)38:
(2)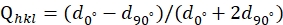
где d0° и d90° - d-интервалы, измеренные от Ψ = 0° и Ψ = 90° (угол между вектором дифракции и осью нагрузки), соответственно. - Затем выведем значение t с помощью уравнения (3)38:
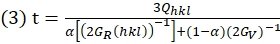
где GR(hkl) и Gv - модуль сдвига агрегатов в условиях Ройсса (изо-напряжение) и Фойгта (изо-деформация) соответственно; α является фактором для определения относительного веса условий Ройсса и Фойгта40.
ПРИМЕЧАНИЕ: Учитывая сложные условия напряжения/деформации текущих экспериментов, в данном исследовании используется α = 0,5. - Для кубической системы вычислите GR(hkl) и Gvследующим образом, используя уравнения 4-6 38,40,41:
(4)
(5)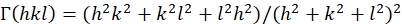
(6)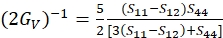
где Sij — монокристаллические упругие соответствия и могут быть получены из констант упругой жесткости Cij материалов.
- Определите дифференциальное напряжение (разницу между этими максимальными (σ22 = σ33) и минимальными напряжениями (σ11) компонентами), которое обеспечивает нижнюю оценку предела текучести материала38, σy, на основе критерия урожайности фон Мизеса по уравнению (1)38:
3. Измерения ТЕА
- Подготовка тонкой никелевой фольги под давлением для ТЭМ с использованием системы сфокусированного ионного пучка (FIB) (см. Таблицу материалов). Чтобы уменьшить возможные артефакты во время ионного фрезерования образца, нанесите защитный слой Pt с помощью пистолета Pt, оснащенного в SEM толщиной ~ 1 мкм на области-кандидате.
- Выполняйте измерения ТЭМ на электронном микроскопе с коррекцией аберрации 300 кВ, оснащенном высокоугловыми кольцевыми детекторами темного поля (HAADF) и яркого поля (BF).
- Делайте снимки с высоким разрешением TEM.
Результаты
При гидростатическом сжатии развернутые рентгеновские дифракционные линии должны быть прямыми, а не изогнутыми. Однако при негидростатическом давлении кривизна (эллиптичность XRD-колец, которая переводится в нелинейность линий, построенных по азимутальному углу) значительно увеличив...
Обсуждение
Вычислительное моделирование широко используется для изучения влияния размера зерна на прочность нанометаллов 5,6,16,17,27,42. Было предложено, чтобы идеальные дислокации, частичные ...
Раскрытие информации
Авторам нечего раскрывать.
Благодарности
Мы признаем поддержку со стороны Национального фонда естественных наук Китая (NSFC) по номерам грантов 11621062, 11772294, U1530402 и 11811530001. Это исследование также было частично поддержано Китайским постдокторским научным фондом (2021M690044). В этом исследовании использовались ресурсы Advanced Light Source, который является пользовательским объектом Управления науки Министерства энергетики США по контрактному номеру DE-AC02-05CH11231 и Шанхайской установки синхротронного излучения. Это исследование было частично поддержано COMPRES, Консорциумом по исследованию свойств материалов в науках о Земле в соответствии с Соглашением о сотрудничестве NSF EAR 1606856.
Материалы
| Name | Company | Catalog Number | Comments |
| 20 nm Ni | Nanomaterialstore | SN1601 | Flammable |
| 3 nm Ni | nanoComposix | Flammable | |
| 40, 70, 100, 200, 500 nm Ni | US nano | US1120 | Flammable |
| Absolute ethanol | as the solution to make 8 nm Ni | ||
| Absolute isopropanol | as the solution to make 12 nm Ni | ||
| Amorphous boron powder | alfa asear | ||
| Copper mesh | Beijing Zhongjingkeyi Technology Co., Ltd. | TEM grid | |
| Epoxy glue | |||
| Ethanol | clean experimental setup | ||
| Focused ion beam | FEI | ||
| Glass slide | |||
| Glue tape | Scotch | ||
| Kapton | DuPont | Polyimide film material | |
| Laser drilling machine | located in high pressure lab of ALS | ||
| Monochromatic synchrotron X-ray | Beamline 12.2.2, Advanced Light Source (ALS), Lawrence Berkeley National Laboratory | X-ray energy: 25-30 keV | |
| Optical microscope | Leica | to mount the gasket and load samples | |
| Pt powder | thermofisher | 38374 | |
| Reaction kettle | Xian Yichuang Co.,Ltd. | 50 mL | |
| Sand paper | from 400 mesh to 1000 mesh | ||
| Transmission Electron Microscopy | FEI | Titan G2 60-300 | |
| Two-dimension image plate | ALS, BL 12.2.2 | mar 345 |
Ссылки
- Hall, E. O. The Deformation and ageing of mild steel.3. Discussion of results. Proceedings of the Physical Society of London Section B. 64 (381), 747-753 (1951).
- Conrad, H. Effect of grain size on the lower yield and flow stress of iron and steel. Acta Metallurgica. 11 (1), 75-77 (1963).
- Kanninen, M. F., Rosenfield, A. R. Dynamics of dislocation pile-up formation. The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics. 20 (165), 569-587 (1969).
- Thompson, A. A. W. Yielding in nickel as a function of grain or cell size. Acta Metallurgica. 23 (11), 1337-1342 (1975).
- Schiotz, J., Di Tolla, F. D., Jacobsen, K. W. Softening of nanocrystalline metals at very small grain sizes. Nature. 391 (6667), 561-563 (1998).
- Schiotz, J., Jacobsen, K. W. A maximum in the strength of nanocrystalline copper. Science. 301 (5638), 1357-1359 (2003).
- Conrad, H., Narayan, J. Mechanism for grain size softening in nanocrystalline Zn. Applied Physics Letters. 81 (12), 2241-2243 (2002).
- Chokshi, A. H., Rosen, A., Karch, J., Gleiter, H. On the validity of the hall-petch relationship in nanocrystalline materials. Scripta Metallurgica. 23 (10), 1679-1683 (1989).
- Sanders, P. G., Eastman, J. A., Weertman, J. R. Elastic and tensile behavior of nanocrystalline copper and palladium. Acta Materialia. 45 (10), 4019-4025 (1997).
- Conrad, H., Narayan, J. On the grain size softening in nanocrystalline materials. Scripta Materialia. 42 (11), 1025-1030 (2000).
- Chen, J., Lu, L., Lu, K. Hardness and strain rate sensitivity of nanocrystalline Cu. Scripta Materialia. 54 (11), 1913-1918 (2006).
- Knapp, J. A., Follstaedt, D. M. Hall-Petch relationship in pulsed-laser deposited nickel films. Journal of Materials Research. 19 (1), 218-227 (2004).
- Kumar, K. S., Suresh, S., Chisholm, M. F., Horton, J. A., Wang, P. Deformation of electrodeposited nanocrystalline nickel. Acta Materialia. 51 (2), 387-405 (2003).
- Chen, B., et al. Texture of Nanocrystalline Nickel: Probing the lower size limit of dislocation activity. Science. 338 (6113), 1448-1451 (2012).
- Chen, M. W., et al. Deformation twinning in nanocrystalline aluminum. Science. 300 (5623), 1275-1277 (2003).
- Yamakov, V., Wolf, D., Phillpot, S. R., Gleiter, H. Deformation twinning in nanocrystalline Al by molecular-dynamics simulation. Acta Materialia. 50 (20), 5005-5020 (2002).
- Yamakov, V., Wolf, D., Phillpot, S. R., Mukherjee, A. K., Gleiter, H. Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation. Nature Materials. 1 (1), 45-49 (2002).
- Yamakov, V., Wolf, D., Salazar, M., Phillpot, S. R., Gleiter, H. Length-scale effects in the nucleation of extended dislocations in nanocrystalline Al by molecular-dynamics simulation. Acta Materialia. 49 (14), 2713-2722 (2001).
- Shan, Z. W., et al. Grain boundary-mediated plasticity in nanocrystalline nickel. Science. 305 (5684), 654-657 (2004).
- Li, H., et al. Strain-Dependent Deformation Behavior in Nanocrystalline Metals. Physical Review Letters. 101 (1), 015502 (2008).
- Van Swygenhoven, H., Derlet, P. M. Grain-boundary sliding in nanocrystalline fcc metals. Physical Review B. 64 (22), 224105 (2001).
- Ovid’ko, I. A. Deformation of nanostructures. Science. 295 (5564), 2386 (2002).
- Murayama, M., Howe, J. M., Hidaka, H., Takaki, S. Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe. Science. 295 (5564), 2433 (2002).
- Wang, L., et al. Grain rotation mediated by grain boundary dislocations in nanocrystalline platinum. Nature Communications. 5, 4402 (2014).
- Edalati, K., et al. Influence of dislocation-solute atom interactions and stacking fault energy on grain size of single-phase alloys after severe plastic deformation using high-pressure torsion. Acta Materialia. 69, 68-77 (2014).
- Edalati, K., Horita, Z. High-pressure torsion of pure metals: Influence of atomic bond parameters and stacking fault energy on grain size and correlation with hardness. Acta Materialia. 59 (17), 6831-6836 (2011).
- Yamakov, V., Wolf, D., Phillpot, S. R., Mukherjee, A. K., Gleiter, H. Deformation-mechanism map for nanocrystalline metals by molecular-dynamics simulation. Nature Materials. 3 (1), 43-47 (2004).
- Starink, M. J., Cheng, X., Yang, S. Hardening of pure metals by high-pressure torsion: A physically based model employing volume-averaged defect evolutions. Acta Materialia. 61 (1), 183-192 (2013).
- Yang, T., et al. Ultrahigh-strength and ductile superlattice alloys with nanoscale disordered interfaces. Science. 369 (6502), 427 (2020).
- Hu, J., Shi, Y. N., Sauvage, X., Sha, G., Lu, K. Grain boundary stability governs hardening and softening in extremely fine nanograined metals. Science. 355 (6331), 1292 (2017).
- Yue, Y., et al. Hierarchically structured diamond composite with exceptional toughness. Nature. 582 (7812), 370-374 (2020).
- Li, X. Y., Jin, Z. H., Zhou, X., Lu, K. Constrained minimal-interface structures in polycrystalline copper with extremely fine grains. Science. 370 (6518), 831 (2020).
- Yan, S., et al. Crystal plasticity in fusion zone of a hybrid laser welded Al alloys joint: From nanoscale to macroscale. Materials and Design. 160, 313-324 (2018).
- Khalajhedayati, A., Pan, Z., Rupert, T. J. Manipulating the interfacial structure of nanomaterials to achieve a unique combination of strength and ductility. Nature Communications. 7 (1), 10802 (2016).
- Chen, L. Y., et al. Processing and properties of magnesium containing a dense uniform dispersion of nanoparticles. Nature. 528 (7583), 539-543 (2015).
- Zhou, X., et al. High-pressure strengthening in ultrafine-grained metals. Nature. 579 (7797), 67-72 (2020).
- Lutterotti, L., Vasin, R., Wenk, H. -. R. Rietveld texture analysis from synchrotron diffraction images. I. Calibration and basic analysis. Powder Diffraction. 29 (1), 76-84 (2014).
- Singh, A. K., Balasingh, C., Mao, H. K., Hemley, R. J., Shu, J. F. Analysis of lattice strains measured under nonhydrostatic pressure. Journal of Applied Physics. 83 (12), 7567-7575 (1998).
- Hemley, R. J., et al. X-ray imaging of stress and strain of diamond, iron, and tungsten at megabar pressures. Science. 276 (5316), 1242-1245 (1997).
- Merkel, S., et al. Deformation of polycrystalline MgO at pressures of the lower mantle. Journal of Geophysical Research-Solid Earth. 107, 2271 (2002).
- Singh, A. K. The lattice strains in a specimen (cubic system) compressed nonhydrostatically in an opposed Anvil device. Journal of Applied Physics. 73 (9), 4278-4286 (1993).
- Van Swygenhoven, H., Derlet, P. M., Frøseth, A. G. Stacking fault energies and slip in nanocrystalline metals. Nature Materials. 3 (6), 399-403 (2004).
- Chung, H. Y., et al. Synthesis of ultra-incompressible superhard rhenium diboride at ambient pressure. Science. 316 (5823), 436-439 (2007).
- Jo, M., et al. Theory for plasticity of face-centered cubic metals. Proceedings of the National Academy of Sciences. 111 (18), 6560 (2014).
- Klueh, R. L. Miniature tensile test specimens for fusion reactor irradiation studies. Nuclear Engineering and Design, Fusion. 2 (3), 407-416 (1985).
- Konopík, P., Farahnak, P., Rund, M., Džugan, J., Rzepa, S. Applicability of miniature tensile test in the automotive sector. IOP Conference Series: Materials Science and Engineering. 461, 012043 (2018).
- Yang, J., et al. Strength enhancement of nanocrystalline tungsten under high pressure. Matter and Radiation at Extremes. 5 (5), 058401 (2020).
- Chen, B. Exploring nanomechanics with high-pressure techniques. Matter and Radiation at Extremes. 5 (6), (2020).
Перепечатки и разрешения
Запросить разрешение на использование текста или рисунков этого JoVE статьи
Запросить разрешениеСмотреть дополнительные статьи
This article has been published
Video Coming Soon
Авторские права © 2025 MyJoVE Corporation. Все права защищены