Caracterización de metamateriales elásticos disipativos producidos por fabricación aditiva

Resumen

Los polímeros fabricados aditivamente se han utilizado ampliamente para producir metamateriales elásticos. Sin embargo, el comportamiento viscoelástico de estos polímeros a frecuencias ultrasónicas sigue siendo poco estudiado. Este estudio reporta un protocolo para estimar las propiedades viscoelásticas de polímeros impresos en 3D y muestra cómo usarlos para analizar la dinámica de los metamateriales.

Resumen

El comportamiento viscoelástico puede ser beneficioso para mejorar la dinámica sin precedentes de los metamateriales poliméricos o, por el contrario, afectar negativamente a sus mecanismos de control de ondas. Por lo tanto, es crucial caracterizar adecuadamente las propiedades viscoelásticas de un metamaterial polimérico en sus frecuencias de trabajo para comprender los efectos viscoelásticos. Sin embargo, la viscoelasticidad de los polímeros es un fenómeno complejo, y los datos sobre los módulos de almacenamiento y pérdida a frecuencias ultrasónicas son extremadamente limitados, especialmente en el caso de los polímeros fabricados aditivamente. En este trabajo se presenta un protocolo para caracterizar experimentalmente las propiedades viscoelásticas de polímeros fabricados aditivamente y utilizarlos en el análisis numérico de metamateriales poliméricos. Específicamente, el protocolo incluye la descripción del proceso de fabricación, procedimientos experimentales para medir las propiedades térmicas, viscoelásticas y mecánicas de polímeros fabricados aditivamente, y un enfoque para usar estas propiedades en simulaciones de elementos finitos de la dinámica de metamateriales. Los resultados numéricos se validan en pruebas de transmisión ultrasónica. Para ejemplificar el protocolo, el análisis se centra en el acrilonitrilo butadieno estireno (ABS) y tiene como objetivo caracterizar el comportamiento dinámico de un metamaterial simple hecho a partir de él mediante el uso de impresión tridimensional (3D) de modelado por deposición fundida (FDM). El protocolo propuesto será útil para muchos investigadores para estimar las pérdidas viscosas en los metamateriales elásticos poliméricos impresos en 3D, lo que mejorará la comprensión de las relaciones entre los materiales y las propiedades de los metamateriales viscoelásticos y, finalmente, estimulará el uso de piezas de metamateriales poliméricos impresas en 3D en diversas aplicaciones.

Introducción

Los polímeros revelan una respuesta viscoelástica en mayor o menor medida. Esto significa que, además del comportamiento elástico descrito por los módulos elásticos (almacenamiento), tienen componentes viscosos (pérdida). Las pérdidas viscosas causan un retraso en el desarrollo de la tensión bajo la tensión aplicada y viceversa. Bajo excitación dinámica, los componentes de tensión desfasados se disipan a través del calor, reduciendo así la energía de las ondas acústicas que se propagan en un medio viscoelástico. Este fenómeno se conoce como amortiguación viscosa.

La viscosidad se origina a nivel molecular debido a movimientos relativos o rotaciones locales de enlaces en cadenas poliméricas y, por lo tanto, se rige por la composición química, la estructura y las conexiones de las cadenas poliméricas. La movilidad molecular depende de la temperatura y la velocidad de deformación, lo que da como resultado un comportamiento de los materiales viscoelásticos impulsado por la temperatura y el tiempo. Todo esto hace que la viscoelasticidad sea un fenómeno inherentemente complejo que tiene una firma única para cada material. Una forma factible de aproximar tal comportamiento implica modelar un material viscoelástico como un sistema mecánico compuesto por resortes (hookeanos) y dashpots (newtonianos)¹. Aunque este enfoque descuida por completo la estructura molecular de un material y toda la complejidad de un proceso de relajación real, puede proporcionar resultados adecuados para polímeros duros^{con pérdidas} viscosas comparativamente bajas.

La clave para obtener un modelo mecánico adecuado es ajustar los parámetros de los resortes y tableros a los datos experimentales para los módulos de almacenamiento y pérdida de un polímero viscoelástico 3,4,5,6,7,8. Este trabajo describe un conjunto de métodos para determinar los módulos viscoelásticos de polímeros fabricados aditivamente y utilizarlos en la caracterización de la dinámica de metamateriales elásticos. Con esto, nuestro objetivo es cerrar la brecha entre las propiedades de los materiales y la dinámica impulsada por la estructura de los metamateriales, lo que permite un diseño más robusto y confiable de metamateriales para las frecuencias de trabajo objetivo.

Los metamateriales elásticos son una clase de materiales de ingeniería, a menudo estructurados periódicamente, que pueden manipular las ondas acústicas en los sólidos de una manera inusual pero controlable⁹. La manipulación de ondas se implementa principalmente mediante la adaptación de bandas prohibidas, es decir, los rangos de frecuencia en los que está prohibida la propagación de ondas⁴. La dinámica única de los metamateriales elásticos se rige por una arquitectura afinada representada por celdas unitarias de forma compleja, especialmente para configuraciones tridimensionales. Tal complejidad estructural a menudo solo se puede lograr utilizando la fabricación aditiva, lo que hace que el análisis de viscoelasticidad sea especialmente relevante para los metamateriales elásticos fabricados aditivamente. Sin embargo, la mayoría de los estudios actuales han utilizado modelos de viscosidad demasiado simplificados, como el modelo de Maxwell^10,11 o el modelo de Kelvin-Voigt¹¹. Debido a que estos modelos no pueden describir ningún material viscoelástico real², las conclusiones derivadas de su uso no pueden considerarse fiables. Por lo tanto, existe una necesidad imperiosa de modelos más realistas que repliquen las propiedades del material viscoelástico a frecuencias ultrasónicas. Varios estudios han abordado esta necesidad ^6,8,12 y han reportado serias limitaciones de los solucionadores comerciales de elementos finitos debido a la alta carga computacional¹³, especialmente cuando se trata de geometrías complejas y/o altas frecuencias¹⁴ y la restricción de considerar la relajación de un solo módulo (en realidad, ambos módulos de un medio isótropo bajo relajación). Otro método de análisis, por ejemplo, la expansión de onda plana, puede reducir la carga computacional¹⁵, pero requiere una descripción analítica de la geometría del dispersor, lo que limita su aplicabilidad. El enfoque de expansión de onda plana extendida^16,17 aborda esta limitación, pero agrega complejidad computacional. Los métodos de expansión de onda de Bloch¹⁸ y matriz de transferencia¹⁹ solo pueden considerar estructuras periódicas de dimensiones finitas, que pueden describirse analíticamente. El enfoque de elemento espectral^20,21 ofrece eficiencia computacional, pero su aplicabilidad se limita a frecuencias muy bajas por debajo de la primera banda prohibida. Por lo tanto, además de la falta de datos experimentales para el almacenamiento y los módulos de pérdida a temperatura ambiente y altas frecuencias (por encima de 100 Hz), que son condiciones de trabajo comunes para los metamateriales elásticos 20,22,23,24, el análisis de su dinámica sigue siendo un desafío. Este trabajo tiene como objetivo llenar estos vacíos mediante el resumen de las técnicas experimentales (y numéricas) para la caracterización de polímeros viscoelásticos fabricados aditivamente y metamateriales elásticos hechos de ellos.

Este enfoque se ilustra mediante el análisis de un análogo continuo unidimensional (1D) simple de un modelo periódico de masa-resorte hecho de polímero de acrilonitrilo butadieno estireno (ABS) de uso común y producido por una impresión 3D de modelado de deposición fundida (FDM) (Sección 1), para el cual se pueden determinar experimentalmente las temperaturas de descomposición y transición vítrea (Sección 2) y derivar las curvas maestras para los módulos de almacenamiento y pérdida a temperatura ambiente de referencia (Sección 3). Además, los módulos mecánicos cuasiestáticos pueden estimarse en ensayos de tracción (Sección 4) y vincularse a sus homólogos dinámicos. A continuación, se describe el método numérico para modelar las características dinámicas de un metamaterial (Sección 5), y los resultados numéricos obtenidos se validan experimentalmente en experimentos de transmisión (Sección 6). Finalmente, se discute la aplicabilidad y limitaciones de los métodos propuestos a partir de los hallazgos.

Protocolo

1. 3D procedimiento de impresión para muestras de polímeros

NOTA: La impresión 3D de muestras de polímeros en una impresora 3D FDM incluye una fase preparatoria, un proceso de impresión y un posprocesamiento.

1. Preparación del modelo
   1. Cree un modelo 3D de una geometría de muestra en cualquier software que admita el diseño asistido por ordenador (CAD) y expórtelo como un archivo STL, OBJ o STEP.
      NOTA: Para los metamateriales, el software común es un paquete de elementos finitos comercial (COMSOL Multiphysics, Abaqus, SolidWorks, etc.) o de código abierto (Elmer, MSLattice, etc.) o un software CAD (Grasshopper, Fusion 360, SketchUp, 3DMECMET, GrabCAD, etc.) para geometrías complejas.
   2. Abra el archivo exportado en una cortadora para construir un modelo real para la impresión 3D basado en el modelo digital generado. Especifique los ajustes de impresión, como la orientación de la muestra (para reducir la necesidad de soporte), la velocidad y la temperatura de impresión (regidas por la elección de un filamento), la densidad de relleno para las piezas sólidas (100% para las muestras de metamateriales), la altura de la capa, el eventual soporte para las piezas de resaca, etc.
      NOTA: Los valores específicos para estos ajustes dependen del modelo de una impresora 3D y se pueden encontrar en los manuales correspondientes.
   3. Almacene la geometría cortada y la configuración especificada en un archivo de código G enviado a la impresora 3D a través de una conexión de red o una unidad USB externa.
2. Preparación de una impresora 3D
   1. Antes de comenzar el proceso de impresión 3D, limpie la cama de impresión con alcohol y un paño de microfibra.
   2. Aplique una capa de adhesivo (por ejemplo, laca para el cabello, pegamento o adhesivo de lecho de vidrio) en el área de la cama de impresión donde se imprimirá la muestra en 3D.
   3. Cargue un filamento en una boquilla, de acuerdo con un manual para la impresora 3D, y asegúrese de que se extruya correctamente.
   4. Inicie el proceso de impresión 3D siguiendo las instrucciones de la impresora 3D.
3. Proceso de impresión 3D y post-procesamiento
   1. Asegúrese de que la impresora 3D alcance el valor especificado de la temperatura de la cama antes de comenzar el proceso de impresión.
   2. Una vez finalizada la impresión 3D, deja que la temperatura de la cama de impresión se reduzca a temperatura ambiente (RT) y retira con cuidado la muestra impresa en 3D.
   3. Corta la capa de soporte o ala o lávala para obtener una estructura final limpia.

2. Análisis termogravimétrico (TGA) y calorimetría diferencial de barrido (DSC)

NOTA: Las técnicas TGA y DSC siguen un protocolo similar que incluye la carga de la muestra, la definición de parámetros experimentales y las condiciones de prueba, que son seguidas por el procesamiento de datos.

1. Carga de muestras
   NOTA: Asegúrese de que la muestra esté en forma de polvo o en trozos pequeños para que el peso total no exceda los 5 mg (aproximadamente la mitad del peso de un grano de sal de mesa).
   1. Abra la puerta de la cámara del horno TGA, coloque la bandeja de muestras de aluminio/platino en la bandeja de equilibrio y tara la balanza.
   2. Transfiera la muestra a la bandeja de muestras con cuidado con una espátula.
   3. Registre la masa de la muestra (generalmente 2-5 mg) y cierre la puerta de la cámara del horno.
2. Parámetros experimentales
   1. Defina los parámetros experimentales específicos, incluido el rango de temperatura, la velocidad de calentamiento y la atmósfera (gas nitrógeno).
   2. Especifique parámetros adicionales (por ejemplo, paso de tiempo, velocidad de rampa) e inicie el experimento.
3. Pruebas experimentales
   1. TGA: Controle continuamente la masa de la muestra mientras varía la temperatura o el tiempo y observe las variaciones en el peso, que pueden indicar procesos como la descomposición, la oxidación o la desorción.
   2. DSC: Evalúe continuamente el flujo de calor en función de la temperatura o el tiempo y observe cualquier pico endotérmico o exotérmico que pueda significar transiciones de fase, cristalización, fusión o reacciones químicas.
4. Recopilación y análisis de datos
   1. Exporte datos como archivos binarios "ASCII" o "mat" de MATLAB para trazarlos utilizando herramientas como OriginPro, MATLAB, etc.
   2. Examine la curva TGA medida en busca de cambios de paso que indiquen transiciones en el comportamiento de pérdida de masa de la muestra y se caractericen por cambios repentinos en la pendiente de la curva. Identifique la temperatura correspondiente a una pérdida de masa del 5% de la muestra como temperatura de descomposición. Los picos de la curva de termogravimetría derivada (DTG) indican los puntos de máxima tasa de pérdida de masa.
   3. En el análisis de la curva DSC, identifique los puntos de inflexión caracterizados por cambios en la pendiente de la curva, ya que reflejan cambios en el caudal de calor asociados con diferentes transiciones de fase que ocurren dentro de la muestra. Localice la temperatura de inicio de cada punto de inflexión, que representa el punto en el eje de temperatura donde comienza el cambio de pendiente. Para la determinación de la temperatura de transición vítrea (T_g), el punto de inflexión corresponde al punto medio de la región de transición donde la curva se desvía de la línea de base.
      NOTA: Una curva de referencia bien definida garantiza una calibración adecuada del instrumento. Si la línea de base no es plana, podría indicar la inestabilidad de un instrumento, el manejo inadecuado de la muestra o la contaminación. La nitidez de la curva indica la homogeneidad y pureza de la muestra. Es común extraer datos del segundo ciclo de experimentos DSC para evitar la influencia de cualquier impureza o tensión residual dentro de la muestra en los resultados.

3. Análisis mecánico dinámico (DMA) para la caracterización de materiales

NOTA: La caracterización de las propiedades viscoelásticas de un polímero con un analizador mecánico dinámico implica asegurar una muestra en una de las varias configuraciones de prueba enumeradas en la Tabla 1. El protocolo del experimento DMA incluye los siguientes pasos.

1. Preparación de la muestra
   1. Fabrica muestras de prueba de forma cúbica utilizando una prensa en caliente, moldeo, corte o impresión 3D. Asegúrese de que los bordes de la muestra sean paralelos y suaves. Use papel abrasivo si es necesario. Evite formar burbujas de aire en el material.
   2. Consulte la Tabla 2 para conocer las dimensiones de la muestra de prueba para cuatro configuraciones de prueba.
      NOTA: El siguiente protocolo se centra únicamente en el procedimiento para la configuración de prueba de voladizo único que se adapta bien a los polímeros impresos en 3D (duros). Un protocolo similar se aplica a las otras configuraciones de prueba.
2. Experimento de diseño
   1. Defina el rango de temperatura para la prueba, la temperatura de transición vítrea y la temperatura de fusión del material (según DSC).
      NOTA: Para garantizar resultados precisos, evite operar a temperaturas que sean 20 °C más altas o más bajas que el punto de transición vítrea.
   2. Elija una velocidad de calentamiento de 1-3 °C/min. Elija el valor de deformación más bajo para obtener resultados óptimos. Los desplazamientos típicos varían entre 5 μm y 50 μm. Por lo general, un punto de partida de 10 μm es apropiado. Configure los parámetros para el barrido de frecuencia y la velocidad de calentamiento.
3. Calibración
   1. Elija la configuración de prueba de un solo voladizo y desconecte el horno quitando las abrazaderas ubicadas en las paredes laterales.
   2. Ajuste la pinza fija a la longitud de medición necesaria (de acuerdo con las dimensiones de la muestra) retirándola y volviéndola a instalar en la máquina DMA.
      1. Asegúrese de que los tornillos de la abrazadera móvil estén bien apretados e inmóviles. Asegúrese de que la abrazadera no toque el termopar.
   3. Inicie el proceso de calibración para garantizar que los cálculos de fuerza no incluyan el peso de la geometría de medición. Realice la calibración en cada arranque de la máquina o interruptor de una configuración de prueba.
4. Sujeción de la muestra
   1. Afloje los tornillos de la papelería y las abrazaderas ajustables cuando el modo de estacionamiento esté activado. El estacionamiento se refiere a restringir el movimiento de la abrazadera ajustable para evitar daños al instrumento durante la sujeción.
   2. Deslice la muestra de prueba por un lado y apóyela en las roscas de las abrazaderas. Utilice una llave dinamométrica para atornillar las abrazaderas ajustables, seguidas de las abrazaderas estacionarias, con el esfuerzo suficiente para sujetar la muestra sin soporte adicional.
   3. Revise la muestra para ver si hay alguna desalineación.
   4. Para verificar la idoneidad de la sujeción de la muestra y la funcionalidad del procedimiento, inicie una oscilación manual. Esto ejerce una fuerza variable sobre la muestra sin registrar los datos.
      NOTA: Si el módulo de almacenamiento de la muestra permanece por debajo del 0,1% (o la fuerza dinámica por debajo de 5 N), entonces la técnica y el sujetamiento se consideran adecuados.
5. Realización de la medición
   1. Vuelva a instalar el horno colocándolo sobre la configuración de prueba e ingrese la temperatura inicial manualmente. Abra la válvula de nitrógeno líquido en una revolución completa y espere al menos 3 minutos después de alcanzar la temperatura deseada.
   2. Inicie las mediciones y sígalas en la pantalla de una computadora.
   3. Una vez finalizadas las mediciones y la temperatura del horno vuelva a ser ambiente, cierre la válvula de nitrógeno. Retire el horno y la muestra, y no reutilice la muestra para realizar más pruebas.
6. Análisis de datos
   1. Guarde los datos, seleccione las curvas y cáptelas a una temperatura de referencia utilizando los factores de desplazamiento adecuados para obtener una curva maestra a la temperatura de referencia.
   2. Represente las propiedades mecánicas especificadas (por ejemplo, módulo de almacenamiento, módulo de pérdida, tangente δ) frente a la frecuencia para la curva de superposición tiempo-temperatura (TTS). El eje horizontal generalmente representa la frecuencia en una escala logarítmica.
   3. Analice las variaciones de las propiedades mecánicas con frecuencia.
      NOTA: Los materiales poliméricos duros a menudo exhiben módulos viscoelásticos que se adhieren a una correlación de ley de potencia con la frecuencia indicada por un cambio de pendiente en un gráfico logarítmico-logarítmico. La intersección de las curvas de módulos de pérdida y almacenamiento significa la frecuencia de cruce, lo que sugiere un cambio en las propiedades viscoelásticas predominantes de un polímero. Dentro de rangos de frecuencia específicos, las características mecánicas del material pueden permanecer independientes de la frecuencia, es decir, una zona de meseta donde el material se comporta principalmente de manera elástica.
   4. Exporte datos como archivos binarios "ASCII" o "mat" de MATLAB para trazarlos utilizando herramientas como OriginPro, MATLAB, etc.

4. Ensayos de tracción acoplados a la correlación digital de imágenes (DIC)

NOTA: Este protocolo se describe para el funcionamiento del sistema Q400 DIC (LIMESS Messtechnik & Software GmbH, Alemania) utilizando el software Istra4D.

1. Preparación de la muestra
   1. Fabricar una muestra de prueba, según la designación D638-14, utilizando una técnica de fabricación aditiva.
   2. Aplique un patrón de moteado con aerosoles o tratamiento de superficie para crear una superficie lisa adecuada para el análisis DIC, asegurando un tamaño de moteado ideal de 3-5 píxeles de diámetro.
      
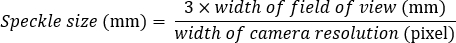
      Por ejemplo, si el ancho del campo de visión es de 80 mm y la resolución de la cámara es de 2000 píxeles de ancho, el cálculo sería:
      
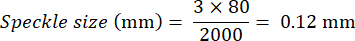
2. Configuración experimental
   1. Monte la muestra en la máquina de ensayo de tracción correctamente asegurándose de que la alineación y el agarre sean adecuados para evitar el deslizamiento durante el ensayo.
   2. Conecte el hardware DIC al software.
   3. Instala cámaras de alta resolución para capturar imágenes de la superficie del espécimen. Asegúrese de que las cámaras tengan un campo de visión suficiente para capturar toda la región de interés.
   4. Configure la iluminación adecuada para garantizar una iluminación uniforme en toda la superficie de la muestra. Evite las sombras o los reflejos que puedan afectar a la calidad de la imagen.
3. Calibración
   1. Inicie un nuevo proceso de calibración y ajuste la paleta de colores a GrayMinMax.
   2. Seleccione una lente apropiada y abra la apertura por completo. Ajuste el tiempo de exposición (por ejemplo, 50 ms) para capturar imágenes con menos puntos rojos.
   3. Ajuste el enfoque y la apertura para obtener puntos rojos mínimos en la superficie de la muestra de prueba.
   4. Elija una calibración y adquiera imágenes de calibración, asegurándose de que la placa esté inclinada en todas las direcciones.
   5. Guarde los datos de calibración.
4. Prueba experimental
   1. Capture las imágenes iniciales del espécimen en su estado original sin ninguna carga.
   2. Comience a aplicar una carga de tracción a la muestra a una velocidad controlada de acuerdo con los estándares de prueba.
   3. Capture simultáneamente imágenes de la superficie de la muestra a intervalos regulares o de forma continua durante todo el proceso de prueba.
   4. Transfiera las imágenes capturadas a una computadora equipada con el software DIC para su análisis. Utilice el software para correlacionar imágenes entre fotogramas consecutivos, rastreando los desplazamientos y deformaciones de la superficie.
5. Análisis y post-procesamiento
   1. Seleccione la serie de imágenes deseada en el explorador de proyectos. Inicie un nuevo análisis haciendo clic en Nueva evaluación y defina un nombre para el análisis.
   2. Ajuste los parámetros de análisis (tamaño de faceta, espaciado de cuadrícula, etc.) en la pestaña Configuración de evaluación . Establezca el espaciado de cuadrícula en aproximadamente un tercio del tamaño de faceta para una precisión de análisis óptima.
   3. Utilice máscaras para definir áreas de interés o exclusión (Polígono 1 en la Figura 6A) dentro del análisis. Valide la búsqueda de puntos de inicio en la pestaña Puntos de inicio haciendo clic en Inicio. Asegúrese de que todos los pasos estén marcados con un semicírculo verde para la asignación automática.
   4. Comience el análisis navegando a la pestaña Control y haciendo clic en Iniciar. Supervise el progreso del análisis, asegurándose de que todos los pasos de la imagen estén marcados con un círculo completo verde una vez finalizados con éxito.
   5. Analice los resultados de DIC para calcular los campos de deformación y desplazamiento a través de la superficie de la muestra utilizando los módulos disponibles en el software. Extraiga características mecánicas relevantes como curvas de tensión-deformación, módulo de Young, resistencia máxima a la tracción, etc.
   6. Procese posteriormente los datos utilizando las técnicas necesarias (por ejemplo, filtrado, suavizado) para mejorar la precisión y la legibilidad.
   7. Interpretar los resultados para concluir el comportamiento del material en condiciones de carga de tracción.

5. Estudios de elementos finitos para la dinámica de ondas en metamateriales

NOTA: A continuación se muestra la descripción del procedimiento basado en elementos finitos para el análisis de transmisión de un metamaterial elástico utilizando el software comercial de elementos finitos COMSOL Multiphysics.

1. Preparación del modelo
   1. Comience utilizando el Asistente para modelos para crear un nuevo modelo. Seleccione la dimensión de espacio 3D y agregue el estudio Mecánica de sólidos . En la ventana de estudio, elija el estudio de dominio de frecuencia para el análisis de transmisión.
   2. Defina los parámetros relevantes y asígneles valores en la pestaña Definiciones globales . Cree la geometría de un modelo de metamaterial utilizando las herramientas disponibles. El modelo suele estar compuesto por un conjunto de celdas unitarias interconectadas.
   3. Haga clic con el botón derecho en los componentes para acceder a la pestaña Definiciones y, a continuación, seleccione Sondeos y elija Sondeo de límites. Asigne un límite en el modelo a esta sonda de límite donde se calculará la pérdida de transmisión. Defina la expresión matemática para estimar la relación entre la energía de onda transmitida y la energía de entrada en esta sonda de límite de la siguiente manera:
      
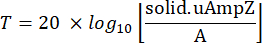
      donde T es la relación de transmisión, A es la amplitud de excitación en el plano incidente y sólido.uAmpZ son los componentes de desplazamiento en el plano de salida, a lo largo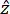 de .
   4. Para evitar la generación de ondas reflejadas espurias desde los límites del dominio, defina una capa perfectamente coincidente (PML) haciendo clic con el botón derecho en la pestaña Definiciones y asignando propiedades PML a los bloques geométricos que rodean la geometría del metamaterial. El tamaño de PML debe ser lo suficientemente grande como para atenuar los reflejos no deseados, generalmente de 2 a 6 veces la longitud de onda de la onda entrante. Alternativamente, para modelar la extensión periódica de un medio, aplique condiciones de contorno periódicas en caras perpendiculares a la dirección de la periodicidad y habilite la función Continuidad .
   5. Asigne propiedades de material a la geometría haciendo clic con el botón derecho en la pestaña Materiales y agregando materiales de la biblioteca. Como alternativa, seleccione una propiedad de material en blanco que requiera la especificación manual de las propiedades de material requeridas.
   6. En la pestaña Componente , la configuración de física predeterminada asigna un comportamiento de material elástico lineal a la geometría analizada. Para incorporar propiedades viscoelásticas, haga clic con el botón derecho en la pestaña Materiales elásticos lineales y seleccione el modelo de material de viscoelasticidad. El modelo generalizado de Maxwell es una opción adecuada debido a su capacidad para cumplir con los datos experimentales obtenidos de las pruebas DMA. Introduzca el tensor desviador obtenido del cálculo basado en los resultados de DMA.
   7. Haga clic con el botón derecho en la pestaña Desplazamiento prescrito y seleccione una parte del modelo para que se excite dinámicamente desde la ventana gráfica . Visualizando la validación experimental de los resultados de transmisión en una prueba de cabeceo y captura con elementos piezoeléctricos, asigne la amplitud del desplazamiento fuera del plano en la posición esperada de un elemento piezoeléctrico.
   8. Genere una malla adecuada para el modelo analizado con el tamaño del elemento de malla obedeciendo la regla de que debe haber al menos 5-7 elementos finitos para resolver la longitud de onda más pequeña bajo consideración. Para ello, defina la malla manualmente o asigne configuraciones de malla controladas por la física. La función de malla de barrido es más compatible con la configuración de PML para definir su comportamiento de absorción.
2. Configuración de los parámetros de estudio de Mecánica de sólidos para un modelo viscoelástico
   1. En el caso de los polímeros reológicos simples, los efectos inducidos por la temperatura sobre las propiedades viscoelásticas de un polímero pueden traducirse directamente en un cambio en la escala de tiempo mediante la aplicación de un factor de desplazamiento. Elija una función de cambio adecuada en el menú desplegable. Seleccione Ninguno si los efectos de la temperatura ya se tienen en cuenta en los resultados de DMA que se van a utilizar.
   2. Seleccione un modelo viscoelástico apropiado, por ejemplo, el modelo de Maxwell generalizado, una opción común para materiales viscoelásticos debido a su capacidad para capturar el comportamiento de relajación medido experimentalmente. Introduzca los valores del tensor desviador en función de los cálculos.
   3. Un método para calcular el tiempo de relajación (τ) a partir de los resultados de DMA consiste en identificar el valor máximo o máximo en la curva del módulo de pérdida, que corresponde al proceso de relajación en el material. Estime la frecuencia (f) asociada con este pico para calcular el tiempo de relajación, τ = 1/(2πf).
   4. Para el procedimiento general para estimar los parámetros de los datos experimentales de ajuste del modelo de Maxwell generalizado, utilice la herramienta de ajuste incorporada que se puede encontrar en la pestaña Estimación de parámetros . Realice el ajuste con un solucionador de optimización que permita la comparación de la predicción del modelo actual con los datos experimentales en tiempo real.
3. Cálculo del estudio
   1. En la biblioteca de estudios, en la opción Agregar estudio , seleccione Dominio de frecuencia e introduzca el rango de frecuencia objetivo. Defina el número de frecuencias intermedias en este rango de frecuencias.
   2. Calcule el estudio pulsando el botón Calcular .
4. Análisis y procesamiento de datos
   1. Una vez completado el cálculo, haga clic con el botón derecho en la pestaña Resultados y seleccione la función Grupo de trazado 1D . Haga clic con el botón derecho del ratón en el grupo de trazados 1D creado y elija Global en las opciones.
   2. En la pestaña Datos del eje Y de la ventana Configuración , introduzca la expresión matemática para la pérdida de transmisión. Como alternativa, introduzca el apodo asignado al sondeo de límite en los pasos anteriores.
   3. Elija el parámetro para el eje X en el menú desplegable de la pestaña Datos del eje X y trace los datos. Identifique las bandas prohibidas de frecuencia en el gráfico como los rangos de frecuencia con una caída de transmisión de al menos 10 dB en comparación con la transmisión de referencia. A continuación, exporte los datos brutos como mat o csv y utilice herramientas gráficas (por ejemplo, MATLAB, Origin Pro, MS Excel, etc.) para generar gráficos para su posterior análisis.

6. Pruebas de transmisión pitch-catch con vibrómetro Doppler láser sin contacto (LDV)

NOTA: El procedimiento experimental implica la configuración de la prueba, la adquisición de la señal transmitida y el posprocesamiento de los datos medidos.

1. Preparación experimental
   1. Elija una fuente de excitación adecuada basada en predicciones numéricas para un rango de frecuencia operativa.
      1. Si las frecuencias de funcionamiento superan los 75 kHz, elija un transductor ultrasónico, limpie su superficie y cúbrala uniformemente con una capa delgada de acoplante (diferente para los transductores de onda longitudinal y de corte²⁵) antes de colocarlo sobre una muestra.
      2. Para la excitación de baja frecuencia (<50 kHz), elija un disco piezoeléctrico de diámetro adecuado (3-50 kHz) o un agitador vibratorio (0-10 kHz) como fuente de excitación. Los discos piezoeléctricos deben pegarse a una muestra probada para garantizar un acoplamiento adecuado.
   2. Asegúrese de que la muestra de prueba esté limpia y colocada de forma segura. Aplique una cinta reflectante a la muestra de prueba en el punto previsto de adquisición de la señal para una mejor detección de la señal por parte del láser.
   3. Ajuste la posición y el ángulo del láser LDV para dirigirlo hacia la cinta reflectante asegurándose de que el láser esté dirigido estrictamente perpendicular a la cinta reflectante y que la distancia de separación esté configurada en un valor óptimo según lo prescrito en el manual de LDV. Asegúrese de aislar la mesa base, donde se guarda el espécimen, de cualquier objeto que pueda inducir ruido eléctrico o acústico.
   4. Cree un circuito eléctrico conectando una computadora a un generador de señal, seguido de un amplificador, que está conectado a un piezoeléctrico. El LDV está conectado a un sistema de adquisición u osciloscopio. El sistema de adquisición de datos está, a su vez, conectado a un ordenador. Una vez que se establezca una conexión adecuada, comience la prueba.
2. Generación y adquisición de señales
   NOTA: Los procedimientos de generación y adquisición de señales se ejemplifican mediante el uso del software SBench6.
   1. Cree dos proyectos separados para la generación y adquisición de señales seleccionando el hardware adecuado en el cuadro de diálogo Administrador de inicio para un generador y un digitalizador. Haga clic en Iniciar para iniciar el proceso en la pestaña Modo de entrada y elija un modo de grabación. Preseleccione el modo Estándar Único , lo que permite el ajuste de parámetros como Memsize (número de muestras por canal).
      NOTA: Un valor inicial recomendado es de 32 kS. El pre-disparo y el post-disparo se refieren al número de muestras que deben grabarse antes y después del modo de disparo, según sea necesario.
   2. Establezca la frecuencia de muestreo deseada en la pestaña Reloj . De forma predeterminada, se aplica la frecuencia de muestreo máxima para el modo de grabación seleccionado.
   3. Configure el modo de activación en la pestaña Desencadenador . Elija un modo adecuado, como la activación del software para la adquisición inmediata después de que la tarjeta de licencia esté lista. Se puede acceder a todos los canales de entrada en la pestaña Canal de entrada .
   4. Para iniciar una grabación de una sola toma, haga clic en el botón de flecha verde que se mueve hacia la derecha. La grabación se detiene automáticamente al alcanzar el Memsize especificado. También puedes optar por la grabación en bucle sin fin. Finalice la grabación con el botón Detener . Las grabaciones se muestran en una pantalla analógica.
      NOTA: Cuando la tarjeta del generador está conectada, la pestaña Modo de entrada en la ventana del generador cambia al modo de salida.
   5. Utilice la opción Easy Generator del software de medición para generar funciones de excitación simples como ondas sinusoidales o pulsos rectangulares.
      1. Alternativamente, emplee un generador de funciones para generar funciones matemáticas arbitrarias. Para ello, vaya a la pestaña Nuevo , elija Cálculos de señal y elija la opción Generador de funciones .
      2. Asegúrese de que la frecuencia de muestreo coincida con la frecuencia de temporización interna. Defina la longitud de la señal e inicie la señal, que luego se mostrará en la pantalla analógica. Una función matemática se puede escribir en el campo de fórmula o cargarse como un archivo .txt .
   6. Realice una transformada rápida de Fourier (FFT) en la señal seleccionando Cálculos de señal en Canales de entrada y eligiendo FFT. Elija una función de ventana adecuada (por ejemplo, rectangular, Hanning, Hamming, etc.) para el cálculo de FFT. Para verificar la precisión de la señal generada, calcule su transformada rápida de Fourier (FFT) y confirme si el pico se alinea con la frecuencia asignada a la señal.
   7. Inspeccione la configuración para garantizar un funcionamiento adecuado antes de comenzar la prueba apuntando el láser LDV a la fuente de vibración (por ejemplo, transductor ultrasónico, agitador, etc.), enviando una señal y calculando FFT. En otra ventana del software de medición, asigne una tarjeta de licencia del digitalizador y observe la señal recibida. Haga coincidir los resultados de FFT en ambas ventanas antes de continuar con el experimento.
   8. Comience el experimento apuntando el láser LDV al punto deseado de adquisición en la muestra de metamaterial. Genere una señal, registre los datos y guárdelos.
3. Análisis y procesamiento de datos
   1. Analice los datos de respuesta de frecuencia en la ventana del digitalizador para identificar las bandas prohibidas de frecuencia para validar los resultados numéricos.
   2. Exporte datos como archivos binarios ASCII o mat de MATLAB para trazarlos utilizando herramientas como OriginPro, MATLAB, etc.

Resultados

El protocolo descrito se ilustra mediante la fabricación y caracterización de muestras en forma de hueso y metamateriales hechos de acrilonitrilo butadieno estireno (ABS). Las geometrías de las muestras son las siguientes. Las dimensiones de las muestras en forma de hueso de perro para los ensayos de tracción siguen la designación D638-14. La estructura del metamaterial representa un análogo continuo de un modelo unidimensional de masa-resorte (Archivo Suplementario 1) que está compuesto por 10 discos de radio de 7 mm y 2 mm de espesor ubicados periódicamente a 20 mm, que se unen mediante vigas delgadas de sección transversal cuadrada de 2 mm x 2 mm. El archivo STL para la estructura de hueso de perro utilizada para ensayos de tracción se puede encontrar en el Archivo Suplementario 2.

Impresión 3D de muestras de polímeros
Se siguen los pasos de la sección 1 para fabricar el metamaterial y las muestras en forma de hueso utilizando una impresora 3D FDM de dos boquillas. En el software del cortador, el filamento de acrilonitrilo butadieno estireno (ABS) se asigna para la boquilla 1, mientras que la boquilla 2 está apagada ya que las muestras se producen a partir de un solo material sin soporte. Se utilizan los siguientes ajustes de impresión: densidad de relleno del 100%, patrón de relleno lineal de 0,2 mm de altura de capa, temperatura del inyector de 245 °C, temperatura del lecho de 100 °C, velocidad de impresión de 40 mm/s y velocidad del ventilador del 3%. Las geometrías cortadas se muestran en la Figura 1A. Para mantener las piezas fijas durante el proceso de impresión, se aplica una fina capa de pegamento sobre la superficie de la cama de impresión. Una vez finalizada la impresión (Figura 1B), las estructuras impresas en 3D se retiran después de que la cama de impresión se enfríe a temperatura ambiente. Las muestras finales impresas en 3D se muestran en la Figura 1C.

TGA y DSC
El TGA del polímero ABS indica un proceso de descomposición de una sola etapa, ver Figura 2A. La temperatura de inicio de la descomposición medida es de 390 °C, y la descomposición completa se produce alrededor de 420 °C. Se observa una pérdida de peso del 5% de la muestra de prueba correspondiente a 363,6 °C, que sirvió como límite superior de temperatura para la prueba DSC. Los resultados de DTG revelan una tasa máxima de descomposición a 404,5 °C. La Figura 2B muestra los resultados de la prueba DSC realizada en un rango de temperatura de 40 °C a 270 °C, indicando una temperatura de transición vítrea (T_g) de 100,4 °C y una temperatura de fusión (T_m) de 216,5 °C.

DMA
La temperatura de transición vítrea (T_g) de DSC sirve como límite superior de temperatura para la prueba DMA siguiendo el objetivo de este trabajo de caracterizar el ABS a temperatura ambiente. El DMA se realizó utilizando el DMA 8000, ver Figura 3, en tres muestras, cada una de patrón de relleno lineal alineado a 0° (tipo 1) y 45° (tipo 2) a la referencia 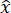de la impresora 3D. Se emplea un barrido de frecuencia de 0,1 a 100 Hz con temperaturas que varían entre 5 °C y 60 °C. La velocidad de calentamiento se ajustó a 2 °C/min, y la temperatura se incrementó en incrementos de 5 °C con una pausa isotérmica de 5 min en cada paso. Las curvas obtenidas a 12 temperaturas diferentes se desplazaron a una temperatura de referencia de 25 °C utilizando la ecuación de Williams-Landel-Ferry (WLF). Los resultados concluyentes de la superposición de tiempo-temperatura para muestras de tipo 1 y tipo 2 (Figura 4) revelan una línea plana para el módulo de almacenamiento y el módulo de pérdida en el rango de frecuencia de ^10-7 a 10⁸ Hz. Se observan algunas desviaciones en el módulo de pérdida y en la tangente (δ) en ciertos puntos de la curva TTS.

Ensayos de tracción
Las pruebas de tracción se llevaron a cabo utilizando una máquina de tracción máxima (UTM), ver Figura 5, con una capacidad de carga máxima de 1 kN. Los parámetros de prueba incluyeron una fuerza máxima de 980 N y un tiempo de rampa de 60 s. Se estableció un tiempo de recuperación de 10 s y la máquina de prueba de tracción registró 10 puntos de datos de fuerza por segundo. Las cámaras de alta resolución de un sistema DIC capturaron 30 imágenes por fotograma, y el análisis se centró en la región sombreada identificada como polígono 1 en la Figura 6A. Los valores medios de deformación principal dentro de la región sombreada son 1,317 (deformación por tracción) y -0,454 (deformación por compresión). En la Figura 6B se muestran los resultados de la relación de Poisson, con un valor medio observado de 0,37. En la Figura 6C se muestran los resultados para el módulo de Young, calculado a partir de la pendiente de la curva de descarga que muestra la recuperación elástica, que arroja un valor de 0,543 GPa.

Análisis de elementos finitos
La Figura 7A presenta la geometría de un metamaterial considerado para el análisis de transmisión, donde el "Plano de salida" indica la sonda para medir las señales transmitidas. La curva de transmisión estimada numéricamente se muestra en la Figura 7B, para un desplazamiento de excitación fuera del plano de 1 μm a lo largo 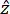del plano incidente mostrado para el modelo en la Figura 7A. Las caídas en el nivel de transmisión superiores a 20 dB, indicadas por una región sombreada, representan bandas prohibidas de frecuencia en varias gamas de frecuencias.

Pruebas de transmisión de pitch-catch
La Figura 8 muestra la configuración utilizada para la prueba de transmisión de cabeceo-captura realizada en un análogo continuo 1D simple de un modelo periódico de masa-resorte hecho de polímero ABS de uso común (Figura 9A), utilizando LDV sin contacto. La Figura 9B muestra los resultados de la prueba de transmisión de cabeceo-captura en el dominio de la frecuencia para la muestra de ABS impresa en 3D idéntica a la que se muestra en la Figura 7A. Se utilizó el disco piezoeléctrico apantallado de Ag de base cerámica de frecuencia de resonancia radial de 200 kHz (diámetro 10 mm y espesor 0,2 mm) para aplicar una señal de barrido de frecuencia de 4 kHz a 40 kHz. La señal transmitida se adquirió en la^10ª celda unitaria desde el lado de excitación. Los datos registrados en el dominio del tiempo se transformaron al dominio de la frecuencia mediante la aplicación de la transformada rápida de Fourier. Los datos procesados revelan una caída de señal de más de 20 dB en varias frecuencias, lo que indica las bandas prohibidas de frecuencia que se resaltan en azul en la Figura 9B.

Figura 1: Impresión 3D de muestras de polímeros. (A) Geometría cortada en el software de corte. (B) Proceso de impresión 3D en curso. (C) Muestra de ABS impresa en 3D para pruebas de tracción según la norma ASTM D638. Haga clic aquí para ver una versión más grande de esta figura.

Figura 2: Análisis termogravimétrico (TGA) y calorimetría diferencial de barrido (DSC). Resultados de caracterización térmica del polímero ABS en (A) TGA y DTG y (B) DSC. Haga clic aquí para ver una versión más grande de esta figura.

Figura 3: Análisis mecánico dinámico. (A) Instrumento DMA y partes importantes. (B) Imagen de la configuración de prueba de un solo voladizo (sin muestra). (C) Imagen de una muestra sujetada en la configuración de prueba de un solo voladizo. Haga clic aquí para ver una versión más grande de esta figura.

Figura 4: Resultados de la superposición tiempo-temperatura. Resultados de TTS para polímeros ABS impresos en 3D con un patrón de relleno lineal alineado a 0° (tipo 1) y 45° (tipo 2) con respecto a la referencia de la impresora 3D: módulo de almacenamiento, módulo de pérdida y tan(δ). Haga clic aquí para ver una versión más grande de esta figura.

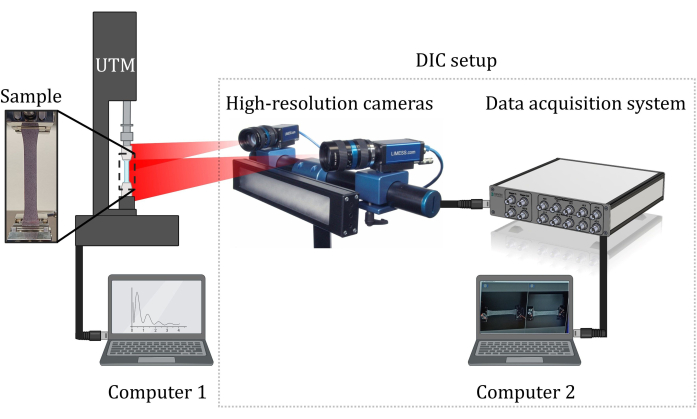
Figura 5: Configuración de la prueba de tracción. Diagrama de la configuración de prueba de tracción, incluida la máquina de tracción universal (UTM) junto con una configuración DIC. También se muestra una vista ampliada de la muestra para resaltar el patrón de manchas en la muestra. Haga clic aquí para ver una versión más grande de esta figura.

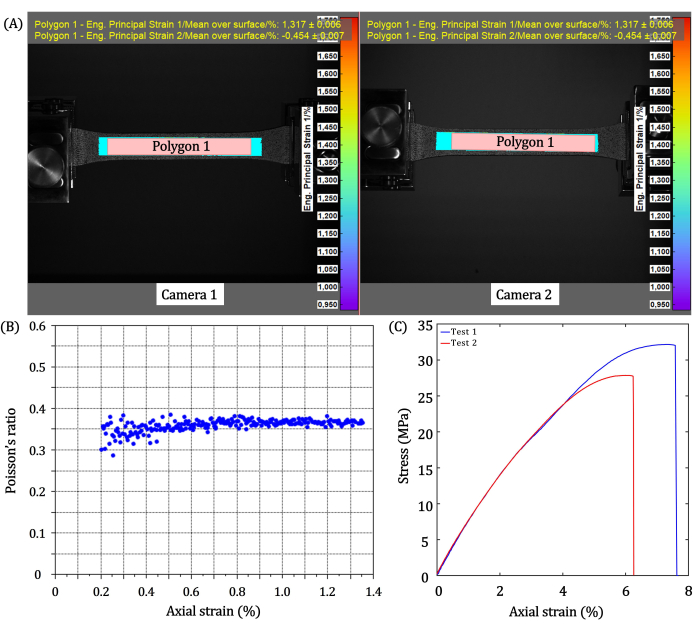
Figura 6: Resultados de los ensayos de tracción. (A) Imagen de la muestra de ensayo adquirida por ambas cámaras de la configuración DIC. El polígono 1 es el área considerada para los cálculos; La muestra se extrajo de izquierda a derecha. (B) Resultados para la relación de Poisson. (C) Comportamiento de tensión-deformación de las muestras en forma de hueso ABS impresas en 3D (tipo 2) probadas a 50 mm/min (Prueba 1) y 5 mm/min (Prueba 2). Las pruebas se realizaron en cuatro muestras. Haga clic aquí para ver una versión más grande de esta figura.

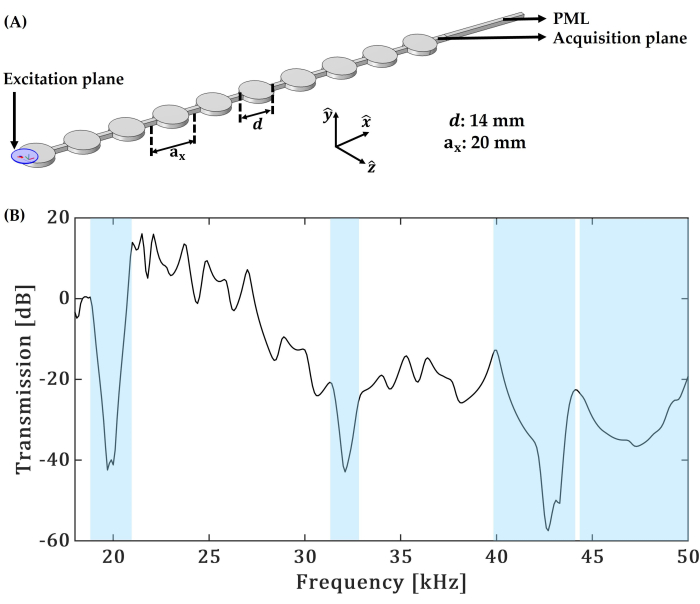
Figura 7: Análisis de elementos finitos. (A) Un modelo geométrico para cálculos numéricos de transmisión; a_x es la dimensión de la celda unitaria, d es el diámetro del disco y PML representa la capa perfectamente adaptada. (B) Resultados numéricos para los cálculos de transmisión, las regiones sombreadas representan la banda prohibida de frecuencias. Haga clic aquí para ver una versión más grande de esta figura.

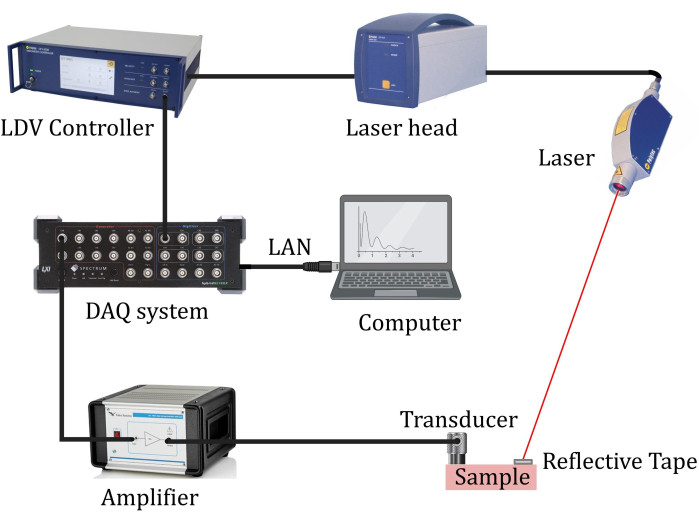
Figura 8: Configuración del experimento de transmisión de pitch-catch. Configuración de pruebas para experimentos de transmisión de cabeceo-captura con un vibrómetro láser Doppler sin contacto utilizado para medir vibraciones mecánicas transmitidas a través de una muestra. Haga clic aquí para ver una versión más grande de esta figura.

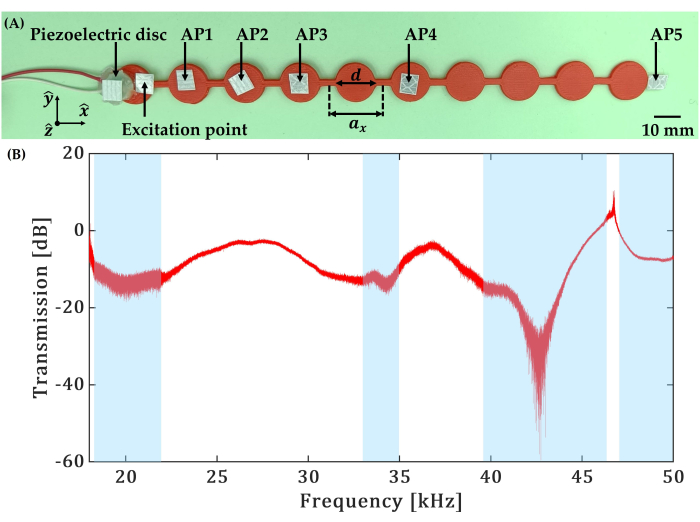
Figura 9: Resultados del experimento de transmisión de brea-captura. (A) Una foto de la estructura del metamaterial de tamaño de celda unitaria a_x = 20 mm con diámetro de disco d = 14 mm probado en el experimento de transmisión de brea-captura. Se utiliza un disco piezoeléctrico de frecuencia de resonancia radial de 200 kHz para excitar las vibraciones estructurales y se pega cinta reflectante para su adquisición en diferentes puntos (AP1, AP2, AP3, AP4 y AP5) de la estructura. (B) Resultados experimentales de la prueba de transmisión de lanzamiento-captura. Los registros del incidente y de la señal transmitida se realizaron en el punto de excitación y en el punto de adquisición 5 (AP5), respectivamente. Las regiones sombreadas representan la banda prohibida de frecuencia estimada experimentalmente. Haga clic aquí para ver una versión más grande de esta figura.

Configuración de la prueba	Muestras de prueba
Voladizo simple	La mayoría de las muestras, excepto las películas delgadas de menos de 0,1 mm
Doble voladizo	Materiales comparativamente blandos si los datos individuales en voladizo son ruidosos
Flexión de tres puntos	Muestras muy rígidas y grandes
Tensión	Películas muy finas de <0,2 mm de espesor

Tabla 1: Configuraciones de prueba adecuadas para diferentes muestras de prueba para DMA, clasificadas en función de la rigidez de la muestra.

Configuraciones de prueba	Longitud (mm)	Ancho (mm)	Espesor (mm)
Voladizo simple	05–25	04–12	0.10–4.00
Doble voladizo	25–45	04–12	0.10–4.00
Flexión de tres puntos	25–45	04–12	0.50–4.00
Tensión	10–25	04–10	0.01–0.20

Tabla 2: Dimensiones de las muestras de ensayo para diferentes configuraciones de ensayo en la técnica DMA.

Fichero suplementario 1: Fichero STL para estructura periódica 1D. Haga clic aquí para descargar este archivo.

Archivo complementario 2: Archivo STL para la estructura de hueso de perro utilizada para ensayos de tracción. Haga clic aquí para descargar este archivo.

Discusión

El procedimiento de impresión 3D descrito en la sección 1 se aplica a la mayoría de las impresoras 3D FDM de tamaño de mesa. Sin embargo, la impresión 3D a partir de ABS puede ser complicada porque este polímero es sensible a los cambios de temperatura. El calentamiento o enfriamiento desigual puede provocar la contracción de las piezas ya impresas, lo que provoca deformaciones, grietas o delaminación. Para evitar estos problemas, se sugiere identificar primero la configuración de impresión adecuada en función de una hoja de datos del proveedor. A continuación, se aconseja evitar fuertes variaciones de temperatura cerca de la pieza impresa durante el proceso de impresión. Se puede lograr encerrando la impresora 3D con una caja o una cámara para mantener un ambiente cálido y estable.

El análisis termogravimétrico (TGA) tiene como objetivo identificar la temperatura a la que se inicia la descomposición del material, ya que esta temperatura rige la temperatura máxima segura para la calorimetría diferencial de barrido (DSC). El TGA funciona según el principio de medir la pérdida de masa de un material en función de la temperatura. El DSC, a su vez, mide los parámetros térmicos clave de un material, incluida la temperatura de transición vítrea, el punto de fusión y las temperaturas de recristalización. Funciona según el principio de detección de cambios de energía asociados con las transiciones de fase. Por lo tanto, las pruebas TGA y DSC sirven como técnicas complementarias a la DMA.

Es crucial analizar cuidadosamente T_m del gráfico DSC, ya que someter el analizador mecánico dinámico a una muestra fundida puede dañar el termopar del instrumento. Antes de cargar la muestra, es necesario asegurarse de que la bandeja no esté contaminada. La contaminación de la muestra con sustancias extrañas puede afectar a las propiedades térmicas e introducir artefactos en las curvas TGA y DSC. La identificación cuidadosa de T_g y T_m es crucial, ya que sirven como parámetros importantes para DMA.

DMA mide la variación de las propiedades del material de la muestra de prueba con la temperatura, dentro del rango de frecuencia especificado por el usuario. El instrumento DMA puede realizar tales mediciones dentro del rango de frecuencia de 0.01-600 Hz. La variación de las propiedades del material de polímeros reológicos simples a valores de frecuencia fuera de este rango se puede predecir utilizando la superposición de tiempo-temperatura⁷. De esta manera, se obtienen las propiedades viscoelásticas de los materiales: módulo de pérdida y viscosidad compleja. Sin embargo, el funcionamiento a temperaturas cercanas a T_m puede dañar el analizador mecánico dinámico y debe evitarse. Además, operar a temperaturas cercanas a T_g, puede resultar en resultados inconsistentes y poco confiables. Además, tenga en cuenta que la alineación adecuada de la muestra es esencial, asegurándose de que la muestra esté recta y tenga bordes lisos y paralelos sin defectos en la superficie. El termopar no debe tocar las pinzas en ningún punto de la medición para evitar daños.

Las tendencias casi planas de las curvas de módulos de almacenamiento y pérdida de la Figura 4 revelan que el ABS impreso con FDM exhibe principalmente un comportamiento elástico a temperatura ambiente. La planitud de la curva para la tangente del ángulo de fase (δ), que es la relación entre el módulo de almacenamiento y el módulo de pérdida, indica que la T_g del material no se encuentra dentro del rango de temperatura medido. Además, los datos de las dos muestras de prueba con diferentes orientaciones del patrón de impresión son indistinguibles, lo que sugiere que no hay un efecto significativo del patrón de impresión en los módulos. Se puede atribuir a las pérdidas viscosas excepcionalmente bajas en ABS y al 100% de densidad de relleno, que enmascaran cualquier efecto del patrón. Tenga en cuenta, sin embargo, que estos resultados son más una excepción que una regla para los polímeros impresos en 3D, ya que las pérdidas viscosas en otros filamentos no son despreciables. Estas pérdidas enfatizan la importancia de realizar el DMA para polímeros impresos en 3D.

Los ensayos de tracción son una técnica ampliamente adoptada para la caracterización mecánica de materiales. Proporciona módulos mecánicos cuasiestáticos, por ejemplo, el módulo de Young y la relación de Poisson, para un material de la muestra de prueba, a menudo de forma ósea (Figura 1B). La técnica de correlación de imágenes digitales (DIC) se puede agregar para garantizar el posicionamiento adecuado de una muestra de prueba y para capturar imágenes de su superficie deformada en cada paso de carga, así como para procesar las imágenes para analizar los campos de deformación y desplazamiento. Aunque la integración de DIC produce un mayor nivel de precisión en los resultados, puede generar varios desafíos si no se maneja adecuadamente. Es importante aplicar un buen patrón de moteado, con un residuo 3D inferior a 0,4/píxel, mientras se prepara la muestra para DIC. Asegúrese de que la muestra esté bien enfocada y utilice las placas de calibración adecuadas que se adapten mejor al campo de visión de la cámara. El módulo de Young determinado a partir de los ensayos de tracción en este estudio, 0,543 GPa, concuerda bien con el valor reportado (0,751 GPa) por Samykano et ^al.26. El UTM utilizado para las pruebas puede tener limitaciones en términos de precisión, resolución o capacidad, lo que puede afectar a la calidad y fiabilidad de los resultados. Una preparación incorrecta de la muestra, incluido el montaje o el mecanizado incorrectos, puede causar errores en la medición. El deslizamiento de la muestra se puede evitar mediante el uso de papeles abrasivos para un mejor contacto entre la muestra y las mordazas del UTM. Además, muchos materiales tienen propiedades mecánicas anisotrópicas. La falta de atención al comportamiento anisotrópico puede llevar a predicciones inexactas.

Las simulaciones numéricas para estimar las bandas prohibidas son esenciales para definir adecuadamente las frecuencias de trabajo para las pruebas de transmisión de brea-captura ^4,8,27. Los datos calculados que se muestran en la Figura 7B son esperables para la configuración del metamaterial analizado que se muestra en la Figura 7A. Específicamente, la curva de transmisión fuera de la frecuencia de banda prohibida oscila alrededor de un valor constante con los picos de oscilación correspondientes a las frecuencias naturales del medio periódico de tamaño finito²⁷. Dentro de la banda prohibida, la transmisión se reduce fuertemente, lo que valida la capacidad de este metamaterial para atenuar las ondas acústicas.

El procedimiento de simulación reportado (sección 5) es general y no se limita a la geometría analizada o al comportamiento viscoelástico específico. Otras estructuras de metamateriales hechas de diversos materiales viscoelásticos pueden probarse con éxito en el análisis de transmisión 7,8,20,22,24. El comportamiento del material se limita al elástico lineal de la viscoelástica, ya que los materiales no lineales no pueden analizarse en el dominio de la frecuencia⁴. Tenga en cuenta que el análisis de transmisión en otros paquetes de elementos finitos puede requerir otros pasos de implementación y terminología o comandos diferentes para acciones similares. Además, las condiciones de contorno periódicas y PML pueden estar ausentes, lo que requiere la búsqueda de alternativas para reducir las reflexiones de onda espurias de los límites del dominio.

Las pruebas de transmisión de pitch-catch tienen como objetivo estimar la porción de la energía de la onda acústica transmitida a través de una muestra de (meta)material e identificar (validar) las frecuencias de banda prohibida. Es conveniente establecer una prueba de este tipo basada en datos numéricos preliminares de transmisión, que permitan identificar un rango de frecuencia de operación que, a su vez, permita la selección de una fuente de excitación adecuada 8,20,22,24. El equipo típico para las pruebas de transmisión incluye un generador de señales para generar una señal de excitación, un amplificador para aumentar la intensidad de la señal, elementos piezoeléctricos (por ejemplo, un disco piezoeléctrico o un transductor piezocerámico) para transformar las señales eléctricas en movimientos mecánicos y viceversa, y un sistema de adquisición de datos para registrar las señales transmitidas⁷. Un elemento piezoeléctrico está estrechamente conectado a una muestra probada para excitar una señal, mientras que el otro se utiliza para recibir una señal transmitida. El segundo elemento piezoeléctrico se sustituye aquí por un vibrómetro láser Doppler (LDV) para mediciones sin contacto que proporcionan una mejor calidad de las señales registradas debido a la sensibilidad extremadamente alta del láser.

El promedio de la señal transmitida medido está en buena concordancia con las predicciones numéricas (Figura 7B y Figura 9B), como puede esperarse de una muestra con pérdidas viscosas extremadamente bajas. Los datos mostrados en el dominio de la frecuencia se superponen con ruido debido a la alta sensibilidad del láser. Las ventajas y la flexibilidad de utilizar LDV para la adquisición de datos son claras. Además de las mediciones sin contacto y los datos precisos, el LDV permite medir la señal en el lado de excitación enfocando el láser en la muestra en las proximidades de un disco piezoeléctrico. Esto ofrece la posibilidad de evaluar la relación entre las señales transmitidas y las señales de entrada, como en la simulación numérica, lo que es especialmente útil para metamateriales de estructura compleja que exhiben un nivel elevado de reflexiones de onda internas.

Se puede concluir que el protocolo propuesto para caracterizar metamateriales viscoelásticos puede ser útil para los investigadores que trabajan en este campo de rápido desarrollo para adquirir datos para una amplia gama de materiales fabricados aditivamente y utilizar estos datos en el análisis de la dinámica de los metamateriales. Dado que las excepcionales propiedades de amortiguación que ofrecen los polímeros debido a los efectos viscoelásticos los convierten en la opción preferida sobre los metamateriales metálicos o cerámicos, una comprensión más profunda de estos efectos es esencial para aumentar aún más las aplicaciones de los metamateriales en la guía de ondas acústicas, el camuflaje, la acústica subacuática, la absorción de sonido, las imágenes médicas, la recolección de energía y muchos otros.

Materiales

Name	Company	Catalog Number	Comments
Acrylonitrile Butadiene Styrene (ABS)	BASF	https://www.xometry.com/resources/3d-printing/abs-3d-printing-filament/	Print temperature: 225-245 °C
COMSOL Multiphysics 6.0	COMSOL	https://www.comsol.com/product-download/6.0	Finite element software
DAQ system for DIC	Dantec Dynamics	https://www.dantecdynamics.com/components/daq-controllers/
Discovery DSC 25	TA Instruments	https://www.tainstruments.com/dsc-25/	Software: Trios; Pan: Aluminium
DMA 8000	Perkin Elmer	https://www.perkinelmer.com/product/dma-8000-analyzer-qtz-window-ssti-clamp-n5330101	Software: PerkinElmer
DN2.813-04 Spectrum hybridNetbox	Spectrum Instrumentation	https://spectrum-instrumentation.com/products/details/DN2813-04.php	4-channel signal generator and digitizer; Software used: SBench6
FDM 3D printer Ultimaker 3.0	Ultimaker	https://ultimaker.com/3d-printers/s-series/ultimaker-s3/	Slicer: Ultimaker Cura
Polytec laser unit OFV 534	Polytec GmbH	https://www.polytec.com/eu/vibrometry/products	Laser and laser head, as a set
Polytec OFV-5000 vibrometer controller	Polytec GmbH	https://www.polytec.com/eu/vibrometry/products	LDV controller
Power amplifier Type 2718	Bruel & Kjaer	https://www.bksv.com/en/instruments/vibration-testing-equipment/vibration-amplifiers/exciters/power-amplifier-type-2718	Power output capability of 75 VA
PRYY-0110	PI Ceramic	https://www.piceramic.com/en/products/piezoceramic-components/disks-rods-and-cylinders/piezoelectric-discs-1206710	Ceramic-based, Ag-screened piezoelectric discs
Q400 DIC	Limess Messtechnik & Software GmbH	https://www.limess.com/en/products/q400-digital-image-correlation	Software: Istra4D
Thermogravimetric Discovery TGA 550	TA Instruments	https://www.tainstruments.com/tga-550/	Software: Trios; Pan: Aluminium
UniVert 1kN Tensile testing machine	Cell Scale biomaterials testing	https://www.cellscale.com/products/univert/	Software: UniVert; load cell capacity: 1 kN
WMA-300 High speed high voltage amplifier	Falco Systems	https://www.falco-systems.com/High_voltage_amplifier_WMA-300.html	50x amplification up to +150 V and -150 V with respect to ground