Charakterisierung dissipativer, elastischer Metamaterialien, die durch additive Fertigung hergestellt werden

Zusammenfassung

Additiv gefertigte Polymere werden in großem Umfang zur Herstellung elastischer Metamaterialien verwendet. Das viskoelastische Verhalten dieser Polymere bei Ultraschallfrequenzen ist jedoch noch wenig untersucht. Diese Studie berichtet über ein Protokoll zur Abschätzung der viskoelastischen Eigenschaften von 3D-gedruckten Polymeren und zeigt, wie sie zur Analyse der Metamaterialdynamik verwendet werden können.

Zusammenfassung

Viskoelastisches Verhalten kann von Vorteil sein, um die beispiellose Dynamik von Polymer-Metamaterialien zu verbessern oder im Gegensatz dazu ihre Wellenkontrollmechanismen negativ zu beeinflussen. Es ist daher von entscheidender Bedeutung, die viskoelastischen Eigenschaften eines Polymermetamaterials bei seinen Arbeitsfrequenzen richtig zu charakterisieren, um viskoelastische Effekte zu verstehen. Die Viskoelastizität von Polymeren ist jedoch ein komplexes Phänomen, und die Daten zu Speicher- und Verlustmodulen bei Ultraschallfrequenzen sind insbesondere bei additiv gefertigten Polymeren äußerst begrenzt. In dieser Arbeit wird ein Protokoll vorgestellt, um die viskoelastischen Eigenschaften additiv gefertigter Polymere experimentell zu charakterisieren und in der numerischen Analyse von Polymermetamaterialien zu nutzen. Konkret umfasst das Protokoll die Beschreibung des Herstellungsprozesses, experimentelle Verfahren zur Messung der thermischen, viskoelastischen und mechanischen Eigenschaften additiv gefertigter Polymere sowie einen Ansatz, um diese Eigenschaften in Finite-Elemente-Simulationen der Metamaterialdynamik zu nutzen. Die numerischen Ergebnisse werden in Ultraschall-Transmissionstests validiert. Um das Protokoll zu veranschaulichen, konzentriert sich die Analyse auf Acrylnitril-Butadien-Styrol (ABS) und zielt darauf ab, das dynamische Verhalten eines einfachen Metamaterials, das daraus hergestellt wird, unter Verwendung von dreidimensionalem (3D) Fused Deposition Modeling (FDM)-Druck zu charakterisieren. Das vorgeschlagene Protokoll wird für viele Forscher hilfreich sein, um viskose Verluste in 3D-gedruckten polymerelastischen Metamaterialien abzuschätzen, was das Verständnis der Material-Eigenschafts-Beziehungen für viskoelastische Metamaterialien verbessern und schließlich die Verwendung von 3D-gedruckten Polymer-Metamaterialteilen in verschiedenen Anwendungen anregen wird.

Einleitung

Polymere zeigen mehr oder weniger stark eine viskoelastische Reaktion. Das bedeutet, dass sie zusätzlich zu dem elastischen Verhalten, das durch elastische (Speicher-)Module beschrieben wird, viskose (Verlust-)Komponenten aufweisen. Viskose Verluste führen zu einer Verzögerung der Spannungsentwicklung unter ausgeübter Dehnung und umgekehrt. Unter dynamischer Anregung werden phasenverschobene Spannungskomponenten durch Wärme abgeführt, wodurch die Energie der akustischen Wellen, die sich in einem viskoelastischen Medium ausbreiten, reduziert wird. Dieses Phänomen wird als viskose Dämpfung bezeichnet.

Die Viskosität entsteht auf molekularer Ebene aufgrund von Relativbewegungen oder lokalen Rotationen von Bindungen in Polymerketten und wird daher durch die chemische Zusammensetzung, Struktur und Verbindungen der Polymerketten bestimmt. Die molekulare Mobilität hängt von der Temperatur und der Verformungsrate ab, was zu einem temperatur- und zeitgesteuerten Verhalten von viskoelastischen Materialien führt. All dies macht die Viskoelastizität zu einem von Natur aus komplexen Phänomen, das für jedes Material eine einzigartige Signatur hat. Ein praktikabler Weg, ein solches Verhalten zu approximieren, besteht darin, ein viskoelastisches Material als mechanisches System zu modellieren, das aus (Hookeschen) Federn und (Newtonschen) Dashpots besteht¹. Obwohl dieser Ansatz die molekulare Struktur eines Materials und die ganze Komplexität eines realen Relaxationsprozesses völlig vernachlässigt, kann er für harte Polymere mit vergleichsweise geringen viskosen Verlusten adäquate Ergebnisse liefern².

Der Schlüssel zu einem adäquaten mechanischen Modell liegt in der Abstimmung der Parameter der Federn und Dashpots auf experimentelle Daten für die Speicher- und Verlustmodule eines viskoelastischen Polymers 3,4,5,6,7,8. Diese Arbeit beschreibt eine Reihe von Methoden, um die viskoelastischen Module von additiv gefertigten Polymeren zu bestimmen und sie zur Charakterisierung der Dynamik elastischer Metamaterialien einzusetzen. Auf diese Weise wollen wir die Lücke zwischen Materialeigenschaften und der strukturgetriebenen Dynamik von Metamaterialien schließen und so ein robusteres und zuverlässigeres Design von Metamaterialien für die angestrebten Arbeitsfrequenzen ermöglichen.

Elastische Metamaterialien sind eine Klasse von technischen, oft periodisch strukturierten Materialien, die akustische Wellen in Festkörpern auf ungewöhnliche, aber kontrollierbare Weise manipulieren können⁹. Die Wellenmanipulation wird hauptsächlich durch das Zuschneiden von Bandlücken - den Frequenzbereichen, in denen die Wellenausbreitung verboten ist⁴ - realisiert. Die einzigartige Dynamik elastischer Metamaterialien wird durch eine fein abgestimmte Architektur bestimmt, die durch komplex geformte Elementarzellen dargestellt wird, insbesondere für dreidimensionale Konfigurationen. Eine solche strukturelle Komplexität kann oft nur mit Hilfe der additiven Fertigung realisiert werden, was die Viskoelastizitätsanalyse besonders relevant für additiv gefertigte elastische Metamaterialien macht. Die meisten aktuellen Studien haben jedoch stark vereinfachte Modelle der Viskosität verwendet, wie z. B. das Maxwell^10,11 oder das Kelvin-Voigt-Modell¹¹. Da diese Modelle kein reales viskoelastisches Material² beschreiben können, können die daraus abgeleiteten Schlussfolgerungen nicht als zuverlässig angesehen werden. Daher besteht ein dringender Bedarf an realistischeren Modellen, die viskoelastische Materialeigenschaften bei Ultraschallfrequenzen nachbilden. Mehrere Studien haben sich mit diesem Bedarf befasst ^6,8,12 und über schwerwiegende Einschränkungen kommerzieller Finite-Elemente-Löser aufgrund der hohen¹³ Rechenlast berichtet, insbesondere wenn es sich um komplexe Geometrien und/oder hohe Frequenzen¹⁴ handelt, und die Einschränkung, die Relaxation eines einzelnen Moduls (in Wirklichkeit beide Module eines isotropen Mediums unter Relaxation) zu berücksichtigen. Eine andere Analysemethode, z. B. die Ausdehnung der ebenen Welle, kann den Rechenaufwand¹⁵ reduzieren, erfordert jedoch eine analytische Beschreibung der Streugeometrie, was ihre Anwendbarkeit einschränkt. Der Ansatz der erweiterten ebenen Wellenexpansion^16,17 behebt diese Einschränkung, erhöht jedoch die Rechenkomplexität. Die Bloch-Wellenexpansion¹⁸ und die Transfermatrix-Methode¹⁹ können nur periodische Strukturen endlicher Dimensionen berücksichtigen, die analytisch beschrieben werden können. Der spektrale Elementansatz^20,21 bietet Recheneffizienz, aber seine Anwendbarkeit ist auf sehr niedrige Frequenzen unterhalb der ersten Bandlücke beschränkt. Neben dem Mangel an experimentellen Daten für Speicher- und Verlustmodule bei Raumtemperatur und hohen Frequenzen (über 100 Hz), die für elastische Metamaterialien 20,22,23,24 üblich sind, bleibt die Analyse ihrer Dynamik eine Herausforderung. Ziel dieser Arbeit ist es, diese Lücken zu schließen, indem die experimentellen (und numerischen) Techniken zur Charakterisierung von additiv gefertigten viskoelastischen Polymeren und daraus hergestellten elastischen Metamaterialien zusammengefasst werden.

Dieser Ansatz wird durch die Analyse eines einfachen eindimensionalen (1D) kontinuierlichen Analogons eines periodischen Masse-Feder-Modells veranschaulicht, das aus häufig verwendetem Acrylnitril-Butadien-Styrol (ABS)-Polymer hergestellt und durch einen Fused-Deposition Modeling (FDM) 3D-Druck hergestellt wurde (Abschnitt 1), für das man experimentell die Zersetzungs- und Glasübergangstemperaturen bestimmen (Abschnitt 2) und die Masterkurven für Lager- und Verlustmodule bei Referenzraumtemperatur ableiten kann (Abschnitt 3). Darüber hinaus können die quasi-statischen mechanischen Module in Zugversuchen (Abschnitt 4) abgeschätzt und mit ihren dynamischen Gegenstücken verknüpft werden. Anschließend wird die numerische Methode zur Modellierung der dynamischen Eigenschaften eines Metamaterials beschrieben (Abschnitt 5), und die erhaltenen numerischen Ergebnisse werden in Transmissionsexperimenten experimentell validiert (Abschnitt 6). Abschließend werden die Anwendbarkeit und Grenzen der vorgeschlagenen Methoden auf der Grundlage der Ergebnisse diskutiert.

Protokoll

1. 3D Druckverfahren für Polymerproben

HINWEIS: Der 3D-Druck von Polymerproben auf einem FDM-3D-Drucker umfasst eine Vorbereitungsphase, einen Druckprozess und eine Nachbearbeitung.

1. Vorbereitung des Modells
   1. Erstellen Sie ein 3D-Modell einer Beispielgeometrie in einer beliebigen Software, die Computer-Aided Design (CAD) unterstützt, und exportieren Sie es als STL-, OBJ- oder STEP-Datei.
      HINWEIS: Bei Metamaterialien handelt es sich bei der gängigen Software um ein kommerzielles (COMSOL Multiphysics, Abaqus, SolidWorks usw.) oder Open-Source-Finite-Elemente-Paket (Elmer, MSLattice usw.) oder CAD-Software (Grasshopper, Fusion 360, SketchUp, 3DMECMET, GrabCAD usw.) für komplexe Geometrien.
   2. Öffnen Sie die exportierte Datei in einem Slicer, um auf der Grundlage des generierten digitalen Modells ein tatsächliches Modell für den 3D-Druck zu erstellen. Legen Sie die Druckeinstellungen fest, z. B. die Ausrichtung der Probe (um den Bedarf an Unterstützung zu reduzieren), die Druckgeschwindigkeit und -temperatur (abhängig von der Wahl eines Filaments), die Fülldichte für feste Teile (100 % für Metamaterialproben), die Schichthöhe, die eventuelle Unterstützung für Katerteile usw.
      HINWEIS: Spezifische Werte für diese Einstellungen hängen vom Modell eines 3D-Druckers ab und sind in den entsprechenden Handbüchern zu finden.
   3. Speichern Sie die geschnittene Geometrie und die angegebenen Einstellungen in einer G-Code-Datei, die über eine Netzwerkverbindung oder ein externes USB-Laufwerk an den 3D-Drucker gesendet wird.
2. Vorbereitung eines 3D-Druckers
   1. Bevor du mit dem 3D-Druckprozess beginnst, reinige das Druckbett mit Alkohol und einem Mikrofasertuch.
   2. Trage eine Schicht Klebstoff (z. B. Haarspray, Kleber oder Glasbettkleber) auf den Druckbettbereich auf, in dem das Muster 3D-gedruckt wird.
   3. Laden Sie ein Filament in eine Düse hoch, gemäß einer Anleitung für den 3D-Drucker, und stellen Sie sicher, dass es richtig extrudiert wird.
   4. Starten Sie den 3D-Druckprozess gemäß den Anweisungen für den 3D-Drucker.
3. 3D-Druckverfahren und Nachbearbeitung
   1. Stellen Sie sicher, dass der 3D-Drucker den angegebenen Wert der Betttemperatur erreicht, bevor Sie den Druckvorgang starten.
   2. Sobald der 3D-Druck beendet ist, lass die Temperatur des Druckbetts auf Raumtemperatur (RT) sinken und entferne die 3D-gedruckte Probe vorsichtig.
   3. Schneiden Sie die Stütz- oder Krempenschicht aus oder waschen Sie sie weg, um eine saubere Endstruktur zu erhalten.

2. Thermogravimetrische Analyse (TGA) und dynamische Differenzkalorimetrie (DSC)

HINWEIS: Die TGA- und DSC-Techniken folgen einem ähnlichen Protokoll, das das Laden der Probe, die Definition experimenteller Parameter und die Testbedingungen umfasst, denen die Datenverarbeitung folgt.

1. Laden von Proben
   HINWEIS: Achten Sie darauf, dass die Probe in Pulverform oder in kleinen Stücken vorliegt, so dass das Gesamtgewicht 5 mg (etwa die Hälfte des Gewichts eines Korns Kochsalz) nicht überschreitet.
   1. Öffnen Sie die TGA-Ofenkammertür, positionieren Sie die Aluminium-/Platin-Probenschale auf der Waage und tarieren Sie die Waage.
   2. Übertragen Sie die Probe vorsichtig mit einem Spatel auf die Probenwanne.
   3. Notieren Sie die Probenmasse (in der Regel 2-5 mg) und schließen Sie die Ofenkammertür.
2. Experimentelle Parameter
   1. Definieren Sie die spezifischen experimentellen Parameter, einschließlich Temperaturbereich, Heizrate und Atmosphäre (Stickstoffgas).
   2. Geben Sie zusätzliche Parameter an (z. B. Zeitschritt, Rampenrate) und starten Sie das Experiment.
3. Experimentelle Tests
   1. TGA: Überwachen Sie kontinuierlich die Probenmasse bei Schwankungen der Temperatur oder Zeit und notieren Sie Schwankungen des Gewichts, die auf Prozesse wie Zersetzung, Oxidation oder Desorption hinweisen können.
   2. DSC: Bewerten Sie kontinuierlich den Wärmefluss in Abhängigkeit von Temperatur oder Zeit und notieren Sie endotherme oder exotherme Peaks, die möglicherweise auf Phasenübergänge, Kristallisation, Schmelzen oder chemische Reaktionen hinweisen.
4. Datenerhebung und -analyse
   1. Exportieren Sie Daten als binäre "ASCII"- oder MATLAB-"mat"-Dateien zum Plotten mit Tools wie OriginPro, MATLAB usw.
   2. Untersuchen Sie die gemessene TGA-Kurve auf Schrittänderungen, die auf Übergänge im Massenverlustverhalten der Probe hinweisen und durch plötzliche Verschiebungen in der Steigung der Kurve gekennzeichnet sind. Als Zersetzungstemperatur ist die Temperatur zu identifizieren, die einem Massenverlust der Probe von 5 % entspricht. Die Spitzen der abgeleiteten Thermogravimetrie (DTG)-Kurve geben die Punkte mit der maximalen Rate des Massenverlusts an.
   3. Identifizieren Sie bei der Analyse der DSC-Kurve die Wendepunkte, die durch Änderungen in der Steigung der Kurve gekennzeichnet sind, da sie Änderungen des Wärmedurchflusses widerspiegeln, die mit verschiedenen Phasenübergängen innerhalb der Probe verbunden sind. Lokalisieren Sie die Anfangstemperatur jedes Wendepunkts, die den Punkt auf der Temperaturachse darstellt, an dem die Änderung der Steigung beginnt. Bei der Bestimmung der Glasübergangstemperatur (T_g) entspricht der Wendepunkt dem Mittelpunkt des Übergangsbereichs, an dem die Kurve von der Basislinie abweicht.
      HINWEIS: Eine gut definierte Basislinienkurve gewährleistet die korrekte Kalibrierung des Geräts. Wenn die Basislinie nicht flach ist, kann dies auf die Instabilität eines Instruments, eine unsachgemäße Probenhandhabung oder eine Kontamination hinweisen. Die Schärfe der Kurve gibt die Homogenität und Reinheit der Probe an. Es ist üblich, Daten aus dem zweiten Zyklus von DSC-Experimenten zu extrahieren, um den Einfluss von Verunreinigungen oder Eigenspannungen innerhalb der Probe auf die Ergebnisse zu vermeiden.

3. Dynamisch-mechanische Analyse (DMA) zur Materialcharakterisierung

HINWEIS: Um die viskoelastischen Eigenschaften eines Polymers mit einem dynamisch-mechanischen Analysator zu charakterisieren, muss eine Probe in einem der verschiedenen in Tabelle 1 aufgeführten Prüfaufbauten gesichert werden. Das Protokoll des DMA-Experiments umfasst die folgenden Schritte.

1. Probenvorbereitung
   1. Stellen Sie Testmuster in quaderförmiger Form mit einer Heißpresse, Formen, Schneiden oder 3D-Druck her. Stellen Sie sicher, dass die Probenkanten parallel und glatt sind. Verwenden Sie bei Bedarf Schleifpapier. Vermeiden Sie die Bildung von Luftblasen im Material.
   2. In Tabelle 2 finden Sie die Abmessungen des Prüfmusters für vier Testkonfigurationen.
      HINWEIS: Das folgende Protokoll konzentriert sich ausschließlich auf das Verfahren für die Einzel-Cantilever-Testkonfiguration, die sich gut für 3D-gedruckte (harte) Polymere eignet. Ein ähnliches Protokoll gilt für die anderen Testkonfigurationen.
2. Entwerfen des Experiments
   1. Definieren Sie den Temperaturbereich für die Prüfung, die Glasübergangstemperatur und die Schmelztemperatur des Materials (basierend auf DSC).
      HINWEIS: Um genaue Ergebnisse zu gewährleisten, vermeiden Sie den Betrieb bei Temperaturen, die 20 °C höher oder niedriger als der Glasübergangspunkt sind.
   2. Wählen Sie eine Aufheizrate von 1-3 °C/min. Wählen Sie den niedrigsten Dehnungswert, um optimale Ergebnisse zu erzielen. Typische Verschiebungen variieren zwischen 5 μm und 50 μm. In der Regel ist ein Startpunkt von 10 μm sinnvoll. Konfigurieren Sie die Parameter für den Frequenzdurchlauf und die Heizrate.
3. Kalibrierung
   1. Wählen Sie die Testkonfiguration mit einem Ausleger und trennen Sie den Ofen, indem Sie die Klemmen an den Seitenwänden entfernen.
   2. Stellen Sie die feste Klemme auf die erforderliche Messlänge (entsprechend den Abmessungen der Probe) ein, indem Sie sie aus- und wieder an der DMA-Maschine installieren.
      1. Stellen Sie sicher, dass die Schrauben an der beweglichen Klemme fest angezogen und unbeweglich sind. Achten Sie darauf, dass die Klemme das Thermoelement nicht berührt.
   3. Starten Sie den Kalibrierungsprozess, um sicherzustellen, dass die Kraftberechnungen das Gewicht der Messgeometrie nicht berücksichtigen. Führen Sie die Kalibrierung bei jedem Start der Maschine oder beim Wechsel einer Testkonfiguration durch.
4. Einspannen der Probe
   1. Lösen Sie die Schrauben des Briefpapiers und der verstellbaren Klemmen, wenn der Parkmodus aktiviert ist. Unter Parken versteht man die Einschränkung der Bewegung der verstellbaren Klemme, um Schäden am Instrument beim Klemmen zu vermeiden.
   2. Schieben Sie das Prüfmuster durch eine Seite und legen Sie es auf die Gewinde der Klemmen. Verwenden Sie einen Drehmomentschlüssel, um die verstellbaren Klemmen zu verschrauben, gefolgt von den stationären Klemmen, mit gerade genug Kraftaufwand, um die Probe ohne zusätzliche Unterstützung zu halten.
   3. Überprüfen Sie die Probe auf Fehlausrichtungen.
   4. Um die Angemessenheit der Probenklemmung und die Funktionalität des Verfahrens zu überprüfen, wird eine manuelle Oszillation eingeleitet. Dadurch wird eine variable Kraft auf die Probe ausgeübt, ohne dass die Daten aufgezeichnet werden.
      HINWEIS: Wenn der Speichermodul der Probe unter 0,1 % (oder die dynamische Kraft unter 5 N) bleibt, gelten die Technik und die Klemmung als ausreichend.
5. Durchführung der Messung
   1. Setzen Sie den Ofen wieder ein, indem Sie ihn über die Testkonfiguration legen und die Anfangstemperatur manuell eingeben. Öffnen Sie das Flüssigstickstoffventil in einer vollen Umdrehung und warten Sie mindestens 3 Minuten, nachdem Sie die gewünschte Temperatur erreicht haben.
   2. Starten Sie die Messungen und verfolgen Sie sie auf einem Computerbildschirm.
   3. Nachdem die Messungen abgeschlossen sind und die Ofentemperatur wieder auf Umgebungstemperatur zurückkehrt, schließen Sie das Stickstoffventil. Entfernen Sie den Ofen und die Probe und verwenden Sie die Probe nicht für weitere Tests.
6. Datenanalyse
   1. Speichern Sie die Daten, wählen Sie die Kurven aus, und verschieben Sie sie mit geeigneten Verschiebungsfaktoren auf eine Referenztemperatur, um eine Masterkurve mit der Referenztemperatur zu erhalten.
   2. Zeichnen Sie die spezifizierten mechanischen Eigenschaften (z. B. Speichermodul, Verlustmodul, Tan δ) gegen die Frequenz für die Zeit-Temperatur-Überlagerungskurve (TTS) auf. Die horizontale Achse stellt die Frequenz in der Regel auf einer logarithmischen Skala dar.
   3. Analysieren Sie die Schwankungen der mechanischen Eigenschaften mit der Häufigkeit.
      HINWEIS: Harte Polymermaterialien weisen häufig viskoelastische Module auf, die einer Potenzgesetzkorrelation mit der Frequenz entsprechen, die durch eine Steigungsänderung in einem logarithmischen Diagramm angezeigt wird. Der Schnittpunkt von Verlust- und Speichermodulkurven gibt die Übergangsfrequenz an, was auf eine Verschiebung der vorherrschenden viskoelastischen Eigenschaften eines Polymers hindeutet. Innerhalb bestimmter Frequenzbereiche können die mechanischen Eigenschaften des Materials frequenzunabhängig bleiben, d.h. eine Plateauzone, in der sich das Material überwiegend elastisch verhält.
   4. Exportieren Sie Daten als binäre "ASCII"- oder MATLAB-"mat"-Dateien zum Plotten mit Tools wie OriginPro, MATLAB usw.

4. Zugversuch gekoppelt mit digitaler Bildkorrelation (DIC)

HINWEIS: Dieses Protokoll ist für den Betrieb des Q400 DIC Systems (LIMESS Messtechnik & Software GmbH, Deutschland) mit der Software Istra4D beschrieben.

1. Probenvorbereitung
   1. Herstellung eines Prüfmusters gemäß der Bezeichnung D638-14 unter Verwendung eines additiven Fertigungsverfahrens.
   2. Tragen Sie ein Speckle-Muster mit Sprays oder Oberflächenbehandlung auf, um eine glatte Oberfläche zu erzeugen, die für die DIC-Analyse geeignet ist und eine ideale Speckle-Größe von 3-5 Pixeln Durchmesser gewährleistet.
      
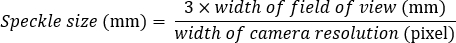
      Wenn die Breite des Sichtfelds beispielsweise 80 mm und die Kameraauflösung 2000 Pixel beträgt, lautet die Berechnung wie folgt:
      
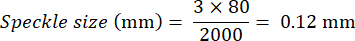
2. Versuchsaufbau
   1. Montieren Sie die Probe ordnungsgemäß in der Zugprüfmaschine, indem Sie auf eine korrekte Ausrichtung und Greifung achten, um ein Verrutschen während der Prüfung zu verhindern.
   2. Verbinden Sie die DIC-Hardware mit der Software.
   3. Richten Sie hochauflösende Kameras ein, um Bilder der Oberfläche der Probe aufzunehmen. Stellen Sie sicher, dass die Kameras über ein ausreichendes Sichtfeld verfügen, um den gesamten Interessenbereich zu erfassen.
   4. Konfigurieren Sie die geeignete Beleuchtung, um eine gleichmäßige Beleuchtung über die Oberfläche der Probe zu gewährleisten. Vermeiden Sie Schatten oder Blendung, die die Bildqualität beeinträchtigen könnten.
3. Kalibrierung
   1. Starten Sie einen neuen Kalibrierungsprozess und passen Sie die Farbpalette an GrayMinMax an.
   2. Wählen Sie ein geeignetes Objektiv aus und öffnen Sie die Blende vollständig. Passen Sie die Belichtungszeit (z. B. 50 ms) an, um Bilder mit weniger roten Punkten aufzunehmen.
   3. Passen Sie Fokus und Blende an, um minimale rote Punkte auf der Oberfläche des Prüflings zu erhalten.
   4. Wählen Sie eine Kalibrierung und erfassen Sie Kalibrierungsbilder, wobei Sie sicherstellen, dass die Platte in alle Richtungen geneigt ist.
   5. Speichern Sie die Kalibrierdaten.
4. Experimenteller Test
   1. Nehmen Sie erste Bilder der Probe in ihrem ursprünglichen Zustand ohne Belastung auf.
   2. Beginnen Sie mit dem Aufbringen einer Zugbelastung auf die Probe mit einer kontrollierten Geschwindigkeit gemäß den Prüfnormen.
   3. Erfassen Sie gleichzeitig Bilder der Probenoberfläche in regelmäßigen Abständen oder kontinuierlich während des gesamten Prüfprozesses.
   4. Übertragen Sie die aufgenommenen Bilder zur Analyse auf einen Computer, der mit der DIC-Software ausgestattet ist. Verwenden Sie die Software, um Bilder zwischen aufeinanderfolgenden Frames zu korrelieren und Oberflächenverschiebungen und Verformungen zu verfolgen.
5. Analyse und Nachbearbeitung
   1. Wählen Sie die gewünschte Bildserie aus dem Projektexplorer aus. Starten Sie eine neue Analyse, indem Sie auf Neue Auswertung klicken, und legen Sie einen Namen für die Analyse fest.
   2. Passen Sie die Analyseparameter (Facettengröße, Rasterabstand usw.) auf der Registerkarte Auswertungseinstellungen an. Legen Sie den Rasterabstand auf etwa ein Drittel der Facettengröße fest, um eine optimale Analysegenauigkeit zu erzielen.
   3. Verwenden Sie Masken, um Interessen- oder Ausschlussbereiche (Polygon 1 in Abbildung 6A) innerhalb der Analyse zu definieren. Validieren Sie die Startpunktsuche auf der Registerkarte Startpunkte , indem Sie auf Start klicken. Stellen Sie sicher, dass alle Schritte mit einem grünen Halbkreis für die automatische Zuweisung markiert sind.
   4. Beginnen Sie die Analyse, indem Sie zur Registerkarte Steuerung navigieren und auf Start klicken. Überwachen Sie den Analysefortschritt und stellen Sie sicher, dass alle Bildschritte nach erfolgreichem Abschluss mit einem grünen Vollkreis markiert sind.
   5. Analysieren Sie die DIC-Ergebnisse, um Dehnungs- und Verschiebungsfelder über die Oberfläche der Probe mit den in der Software verfügbaren Modulen zu berechnen. Extrahieren Sie relevante mechanische Eigenschaften wie Spannungs-Dehnungs-Kurven, Elastizitätsmodul, Zugfestigkeit usw.
   6. Verarbeiten Sie die Daten mit den erforderlichen Techniken (z. B. Filtern, Glätten), um die Genauigkeit und Lesbarkeit zu verbessern.
   7. Interpretieren Sie die Ergebnisse, um auf das Materialverhalten unter Zugbelastungsbedingungen zu schließen.

5. Finite-Elemente-Studien zur Wellendynamik in Metamaterialien

HINWEIS: Im Folgenden finden Sie eine Beschreibung des Finite-Elemente-basierten Verfahrens zur Transmissionsanalyse eines elastischen Metamaterials mit der kommerziellen Finite-Elemente-Software COMSOL Multiphysics.

1. Vorbereitung des Modells
   1. Beginnen Sie mit dem Modell-Assistenten , um ein neues Modell zu erstellen. Wählen Sie die Dimension 3D-Raum aus, und fügen Sie die Studie Festkörpermechanik hinzu. Wählen Sie im Studienfenster die Studie Frequenzbereich für die Transmissionsanalyse aus.
   2. Definieren Sie relevante Parameter und weisen Sie ihnen auf der Registerkarte Globale Definitionen Werte zu. Erstellen Sie die Geometrie eines Metamaterialmodells mit den verfügbaren Werkzeugen. Das Modell besteht in der Regel aus einem Satz miteinander verbundener Elementarzellen.
   3. Klicken Sie mit der rechten Maustaste auf Komponenten, um auf die Registerkarte Definitionen zuzugreifen, und wählen Sie dann Sonden und dann Boundary Probe aus. Weisen Sie dieser Begrenzungssonde eine Begrenzung auf dem Modell zu, an der der Übertragungsverlust berechnet werden soll. Definieren Sie den mathematischen Ausdruck zur Schätzung des Verhältnisses der übertragenen Wellenenergie zur Eingangsenergie an dieser Grenzsonde wie folgt:
      
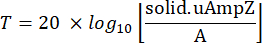
      wobei T das Übersetzungsverhältnis ist, A die Amplitude der Anregung in der einfallenden Ebene und solid.uAmpZ Komponenten der Verschiebung in der Ausgangsebene sind, entlang .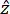
   4. Um die Erzeugung von störenden reflektierten Wellen von den Domänengrenzen zu vermeiden, definieren Sie eine perfekt angepasste Schicht (PML), indem Sie mit der rechten Maustaste auf die Registerkarte Definitionen klicken und den geometrischen Blöcken, die die Metamaterialgeometrie umgeben, PML-Eigenschaften zuweisen. Die PML-Größe sollte groß genug sein, um unerwünschte Reflexionen zu dämpfen, typischerweise das 2-6-fache der Wellenlänge der eingehenden Welle. Um die periodische Ausdehnung eines Mediums zu modellieren, wenden Sie alternativ periodische Randbedingungen an Flächen senkrecht zur Periodizitätsrichtung an, und aktivieren Sie die Funktion Kontinuität.
   5. Weisen Sie der Geometrie Materialeigenschaften zu, indem Sie mit der rechten Maustaste auf die Registerkarte Materialien klicken und Materialien aus der Bibliothek hinzufügen. Alternativ können Sie eine leere Materialeigenschaft auswählen, für die die erforderlichen Materialeigenschaften manuell angegeben werden müssen.
   6. Auf der Registerkarte Komponente weisen die Standardeinstellungen für die Physik der analysierten Geometrie lineares elastisches Materialverhalten zu. Um viskoelastische Eigenschaften zu integrieren, klicken Sie mit der rechten Maustaste auf die Registerkarte Lineare elastische Materialien , und wählen Sie das Viskoelastizitätsmaterialmodell aus. Das verallgemeinerte Maxwell-Modell ist eine geeignete Wahl, da es in der Lage ist, experimentelle Daten aus DMA-Tests zu erfüllen. Geben Sie den abweichenden Tensor ein, der sich aus der Berechnung auf der Grundlage der DMA-Ergebnisse ergibt.
   7. Klicken Sie mit der rechten Maustaste auf die Registerkarte Vorgegebene Verschiebung , und wählen Sie im Grafikfenster einen Teil des Modells aus, der dynamisch angeregt werden soll. Um die Übertragungsergebnisse in einem Pitch-Catch-Test mit Piezoelementen experimentell zu validieren, wird die Amplitude der Verschiebung außerhalb der Ebene an der erwarteten Position eines Piezoelements zugewiesen.
   8. Generieren Sie ein geeignetes Netz für das analysierte Modell, wobei die Größe des Netzelements der Regel entspricht, dass mindestens 5-7 finite Elemente vorhanden sein müssen, um die kleinste berücksichtigte Wellenlänge aufzulösen. Definieren Sie dazu das Netz manuell oder weisen Sie physikalisch gesteuerte Netzeinstellungen zu. Die Funktion "Sweeping-Netz" ist besser mit den PML-Einstellungen kompatibel, um deren Absorptionsverhalten zu definieren.
2. Konfigurieren der Parameter der Festkörpermechanik-Studie für ein viskoelastisches Modell
   1. Bei rheologischen einfachen Polymeren können temperaturinduzierte Effekte auf die viskoelastischen Eigenschaften eines Polymers durch Anwendung eines Verschiebungsfaktors direkt in eine Verschiebung der Zeitskala übersetzt werden. Wählen Sie eine geeignete Schichtfunktion aus dem Dropdown-Menü aus. Wählen Sie Keine , wenn die Temperatureffekte bereits in den zu verwendenden DMA-Ergebnissen berücksichtigt sind.
   2. Wählen Sie ein geeignetes viskoelastisches Modell, z. B. das generalisierte Maxwell-Modell, das aufgrund seiner Fähigkeit, experimentell gemessenes Relaxationsverhalten zu erfassen, eine gängige Wahl für viskoelastische Materialien ist. Geben Sie die Werte für den abweichenden Tensor auf der Grundlage von Berechnungen ein.
   3. Eine Methode zur Berechnung der Relaxationszeit (τ) aus DMA-Ergebnissen besteht darin, den Spitzen- oder Maximalwert in der Verlustmodulkurve zu identifizieren, der dem Relaxationsprozess im Material entspricht. Schätzen Sie die Häufigkeit (f), die mit diesem Peak verbunden ist, um die Relaxationszeit zu berechnen, τ = 1/(2πf).
   4. Verwenden Sie für das allgemeine Verfahren zum Schätzen der Parameter der experimentellen Daten zur generalisierten Maxwell-Modellanpassung das integrierte Anpassungswerkzeug, das sich auf der Registerkarte Parameterschätzung befindet. Führen Sie die Anpassung mit einem Optimierungssolver durch, der den Vergleich der aktuellen Modellvorhersage mit den experimentellen Daten in Echtzeit ermöglicht.
3. Berechnung der Studie
   1. Wählen Sie in der Studienbibliothek in der Option Studie hinzufügen die Option Frequenzbereich aus und geben Sie den Zielfrequenzbereich ein. Definieren Sie die Anzahl der Zwischenfrequenzen in diesem Frequenzbereich.
   2. Berechnen Sie die Studie, indem Sie auf die Schaltfläche Berechnen klicken.
4. Datenanalyse und -aufbereitung
   1. Nachdem die Berechnung abgeschlossen ist, klicken Sie mit der rechten Maustaste auf die Registerkarte Ergebnisse und wählen Sie die Funktion 1D-Diagrammgruppe aus. Klicken Sie mit der rechten Maustaste auf die erstellte 1D-Plotgruppe und wählen Sie Global aus den Optionen.
   2. Geben Sie auf der Registerkarte Daten der Y-Achse des Fensters Einstellungen den mathematischen Ausdruck für den Übertragungsverlust ein. Alternativ können Sie den Spitznamen eingeben, der der Begrenzungssonde in den vorherigen Schritten zugewiesen wurde.
   3. Wählen Sie den Parameter für die X-Achse aus dem Dropdown-Menü auf der Registerkarte Daten der X-Achse aus und zeichnen Sie die Daten. Identifizieren Sie die Frequenzbandlücken im Diagramm als die Frequenzbereiche mit mindestens 10 dB Übertragungsabfall im Vergleich zur Referenzübertragung. Exportieren Sie anschließend die Rohdaten als mat oder csv und verwenden Sie grafische Tools (z. B. MATLAB, Origin Pro, MS Excel usw.), um Diagramme für die weitere Analyse zu erstellen.

6. Pitch-Catch-Transmissionstests mit berührungslosem Laser-Doppler-Vibrometer (LDV)

HINWEIS: Das experimentelle Verfahren umfasst den Aufbau des Testaufbaus, die Erfassung des übertragenen Signals und die Nachbearbeitung der Messdaten.

1. Experimentelle Vorbereitung
   1. Wählen Sie eine geeignete Anregungsquelle auf der Grundlage numerischer Vorhersagen für einen Betriebsfrequenzbereich.
      1. Wenn die Betriebsfrequenzen 75 kHz überschreiten, wählen Sie einen Ultraschallwandler, reinigen Sie seine Oberfläche und bedecken Sie ihn gleichmäßig mit einer dünnen Schicht eines Koppelmittels (unterschiedlich bei Longitudinal- und Scherwellenwandlern²⁵), bevor Sie ihn auf eine Probe auflegen.
      2. Für die niederfrequente Anregung (<50 kHz) wählen Sie eine piezoelektrische Scheibe mit geeignetem Durchmesser (3-50 kHz) oder einen Schwingungsschüttler (0-10 kHz) als Anregungsquelle. Die piezoelektrischen Scheiben müssen auf eine geprüfte Probe geklebt werden, um eine korrekte Kopplung zu gewährleisten.
   2. Stellen Sie sicher, dass der Prüfling sauber und sicher positioniert ist. Bringen Sie ein reflektierendes Band an der vorgesehenen Stelle der Signalerfassung auf dem Prüfling an, um die Signalerfassung durch den Laser zu verbessern.
   3. Passen Sie die Position und den Winkel des LDV-Lasers so an, dass er auf das reflektierende Band gerichtet ist, indem Sie sicherstellen, dass der Laser streng senkrecht zum reflektierenden Band gerichtet ist und der Abstandsabstand auf einen optimalen Wert eingestellt ist, wie im LDV-Handbuch vorgeschrieben. Stellen Sie sicher, dass der Basistisch, auf dem die Probe aufbewahrt wird, von Gegenständen isoliert ist, die elektrische oder akustische Geräusche verursachen könnten.
   4. Erstellen Sie eine elektrische Schaltung, indem Sie einen Computer an einen Signalgenerator anschließen, gefolgt von einem Verstärker, der mit einem Piezo verbunden ist. Das LDV wird an ein Erfassungssystem oder Oszilloskop angeschlossen. Das Datenerfassungssystem ist wiederum mit einem Computer verbunden. Sobald eine ordnungsgemäße Verbindung hergestellt ist, beginnen Sie mit dem Test.
2. Signalerzeugung und -erfassung
   HINWEIS: Die Verfahren zur Signalerzeugung und -erfassung werden anhand der SBench6-Software veranschaulicht.
   1. Erstellen Sie zwei separate Projekte für die Signalerzeugung und -erfassung, indem Sie im Start-Manager-Dialog die richtige Hardware für einen Generator und einen Digitalisierer auswählen. Klicken Sie auf Start , um den Vorgang auf der Registerkarte Eingabemodus zu starten, und wählen Sie einen Aufnahmemodus aus. Wählen Sie den Standard-Single-Modus vor, um Parameter wie Memsize (Anzahl der Samples pro Kanal) anzupassen.
      HINWEIS: Ein empfohlener Startwert liegt bei 32 kS. Pre-Trigger und Post-Trigger beziehen sich auf die Anzahl der Samples, die je nach Bedarf vor und nach dem Trigger-Modus aufgenommen werden sollen.
   2. Stellen Sie die gewünschte Abtastrate auf der Registerkarte Uhr ein. Standardmäßig wird die maximale Abtastrate für den ausgewählten Aufnahmemodus angewendet.
   3. Konfigurieren Sie den Auslösemodus auf der Registerkarte Auslöser . Wählen Sie einen geeigneten Modus, z. B. Software-Triggerung für den sofortigen Erwerb, nachdem die Lizenzkarte bereit ist. Alle Eingangskanäle sind auf der Registerkarte Eingabekanal zugänglich.
   4. Um eine Single-Shot-Aufnahme zu starten, klicken Sie auf den grünen Pfeil nach rechts. Die Aufzeichnung stoppt automatisch, wenn die angegebene Memsize erreicht ist. Alternativ können Sie sich auch für Endlosschleifenaufnahmen entscheiden. Beenden Sie die Aufnahme mit der Schaltfläche Stopp . Die Aufzeichnungen werden auf einem analogen Display angezeigt.
      HINWEIS: Wenn die Generatorkarte angeschlossen ist, wechselt die Registerkarte "Eingabemodus " im Generatorfenster in den Ausgabemodus.
   5. Verwenden Sie die Option Easy Generator der Messsoftware, um einfache Anregungsfunktionen wie Sinuswellen oder Rechteckimpulse zu erzeugen.
      1. Alternativ können Sie einen Funktionsgenerator verwenden, um beliebige mathematische Funktionen zu generieren. Navigieren Sie dazu zur Registerkarte Neu , wählen Sie Signalberechnungen und wählen Sie die Option Funktionsgenerator .
      2. Stellen Sie sicher, dass die Abtastrate mit der internen Taktrate übereinstimmt. Definieren Sie die Länge des Signals und starten Sie das Signal, das dann auf der Analoganzeige angezeigt wird. Eine mathematische Funktion kann in das Formelfeld eingegeben oder als .txt Datei geladen werden.
   6. Führen Sie eine schnelle Fourier-Transformation (FFT) für das Signal durch, indem Sie unter Eingangskanäle die Option Signalberechnungen und dann FFT auswählen. Wählen Sie eine geeignete Fensterfunktion (z.B. rechteckig, Hanning, Hamming, etc.) für die FFT-Berechnung. Um die Genauigkeit des generierten Signals zu überprüfen, berechnen Sie seine schnelle Fourier-Transformation (FFT) und bestätigen Sie, ob der Peak mit der dem Signal zugewiesenen Frequenz übereinstimmt.
   7. Überprüfen Sie die Konfiguration, um einen ordnungsgemäßen Betrieb sicherzustellen, bevor Sie den Test starten, indem Sie den LDV-Laser auf die Schwingungsquelle (z. B. Ultraschallwandler, Shaker usw.) richten, ein Signal senden und die FFT berechnen. Weisen Sie in einem anderen Fenster der Messsoftware eine Digitizer-Lizenzkarte zu und beobachten Sie das empfangene Signal. Gleichen Sie die FFT-Ergebnisse in beiden Fenstern ab, bevor Sie mit dem Experiment fortfahren.
   8. Beginnen Sie das Experiment, indem Sie den LDV-Laser auf den gewünschten Aufnahmepunkt auf der Metamaterialprobe richten. Generieren Sie ein Signal, zeichnen Sie die Daten auf und speichern Sie sie.
3. Datenanalyse und -aufbereitung
   1. Analysieren Sie die Frequenzgangdaten im Digitizer-Fenster, um Frequenzbandlücken für die Validierung numerischer Ergebnisse zu identifizieren.
   2. Exportieren Sie Daten als binäre ASCII - oder MATLAB-MAT-Dateien zum Plotten mit Tools wie OriginPro, MATLAB usw.

Ergebnisse

Das beschriebene Protokoll wird durch die Herstellung und Charakterisierung von knochenförmigen und Metamaterialproben aus Acrylnitril-Butadien-Styrol (ABS) veranschaulicht. Die Geometrien der Proben sind wie folgt. Die Abmessungen der knochenförmigen Proben für die Zugversuche folgen der Bezeichnung D638-14. Die Metamaterialstruktur stellt ein kontinuierliches Analogon eines eindimensionalen Masse-Feder-Modells dar (Zusatzdatei 1), das aus 10 Scheiben mit einem Radius von 7 mm und einer Dicke von 2 mm besteht, die sich periodisch bei 20 mm befinden und durch dünne Balken mit quadratischem Querschnitt von 2 mm x 2 mm verbunden sind. Die STL-Datei für die Hundeknochenstruktur, die für den Zugversuch verwendet wird, befindet sich in der Zusatzdatei 2.

3D-Druck von Polymerproben
Die Schritte von Abschnitt 1 werden befolgt, um das Metamaterial und die knochenförmigen Proben mit einem FDM-Zweidüsen-3D-Drucker herzustellen. In der Slicer-Software wird für Düse 1 Acrylnitril-Butadien-Styrol (ABS)-Filament zugewiesen, während Düse 2 ausgeschaltet ist, da die Proben ohne Unterstützung aus einem einzigen Material hergestellt werden. Folgende Druckeinstellungen kommen zum Einsatz: Infill-Dichte von 100 %, lineares Infill-Muster von 0,2 mm Schichthöhe, Düsentemperatur von 245 °C, Betttemperatur von 100 °C, Druckgeschwindigkeit von 40 mm/s und Lüfterdrehzahl von 3 %. Die geschnittenen Geometrien sind in Abbildung 1A dargestellt. Um die Teile während des Druckvorgangs fixiert zu halten, wird eine dünne Schicht Kleber auf die Druckbettoberfläche aufgetragen. Sobald der Druck abgeschlossen ist (Abbildung 1B), werden die 3D-gedruckten Strukturen entfernt, nachdem das Druckbett auf Raumtemperatur abgekühlt wurde. Die endgültigen 3D-gedruckten Muster sind in Abbildung 1C dargestellt.

TGA und DSC
Die TGA des ABS-Polymers deutet auf einen einstufigen Zersetzungsprozess hin, siehe Abbildung 2A. Die gemessene Anfangstemperatur der Zersetzung beträgt 390 °C, wobei die vollständige Zersetzung bei etwa 420 °C erfolgt. Man beobachtet einen Gewichtsverlust von 5 % der Probe entsprechend 363,6 °C, was als obere Temperaturgrenze für den DSC-Test diente. Die DTG-Ergebnisse zeigen eine maximale Zersetzungsrate bei 404,5 °C. Abbildung 2B zeigt die Ergebnisse des DSC-Tests, der über einen Temperaturbereich von 40 °C bis 270 °C durchgeführt wurde und eine Glasübergangstemperatur (T_g) von 100,4 °C und eine Schmelztemperatur (T_m) von 216,5 °C anzeigt.

DMA
Die Glasübergangstemperatur (T_g) aus DSC dient als obere Temperaturgrenze für den DMA-Test im Anschluss an das Ziel dieser Arbeit, ABS bei Raumtemperatur zu charakterisieren. Die DMA wurde mit dem DMA 8000 (siehe Abbildung 3) an drei Proben durchgeführt, die jeweils ein lineares Füllmuster aufweisen, das bei 0° (Typ 1) und 45° (Typ 2) zur Referenz 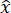des 3D-Druckers ausgerichtet ist. Es wird ein Frequenzdurchlauf von 0,1 bis 100 Hz mit Temperaturen zwischen 5 °C und 60 °C verwendet. Die Heizrate wurde auf 2 °C/min eingestellt und die Temperatur in Schritten von 5 °C mit einer isothermen Pause von 5 Minuten bei jedem Schritt erhöht. Die Kurven, die bei 12 verschiedenen Temperaturen erhalten wurden, wurden mit der Williams-Landel-Ferry-Gleichung (WLF) auf eine Referenztemperatur von 25 °C verschoben. Die schlüssigen Ergebnisse der Zeit-Temperatur-Überlagerung für Typ-1- und Typ-2-Proben (Abbildung 4) zeigen eine flache Linie für den Speichermodul und den Verlustmodul im Frequenzbereich von 10-7 bis 10,8 Hz. An bestimmten Stellen der TTS-Kurve werden einige Abweichungen im Verlustmodul und in der Bräune (δ) beobachtet.

Zugversuch
Die Zugversuche wurden mit einer Zugmaschine (UTM) durchgeführt, siehe Abbildung 5, mit einer maximalen Tragfähigkeit von 1 kN. Zu den Prüfparametern gehörten eine maximale Kraft von 980 N und eine Rampenzeit von 60 s. Es wurde eine Erholungszeit von 10 s eingestellt, und die Zugprüfmaschine zeichnete 10 Datenpunkte für die Kraft pro Sekunde auf. Die hochauflösenden Kameras eines DIC-Systems nahmen 30 Bilder pro Bild auf, und die Analyse konzentrierte sich auf den schattierten Bereich, der in Abbildung 6A als Polygon 1 identifiziert wurde. Die durchschnittlichen Hauptdehnungswerte im schattierten Bereich betragen 1,317 (Zugdehnung) und -0,454 (Druckdehnung). Abbildung 6B zeigt die Ergebnisse für die Poissonzahl mit einem beobachteten Mittelwert von 0,37. Abbildung 6C zeigt die Ergebnisse für den Elastizitätsmodul, berechnet aus der Steigung der Entlastungskurve, die eine elastische Rückgewinnung zeigt, was einen Wert von 0,543 GPa ergibt.

Finite-Elemente-Analyse
Abbildung 7A zeigt die Geometrie eines Metamaterials, das für die Transmissionsanalyse berücksichtigt wird, wobei die "Ausgangsebene" die Sonde zur Messung der übertragenen Signale anzeigt. Die numerisch geschätzte Transmissionskurve ist in Abbildung 7B für eine Anregungsverschiebung außerhalb der Ebene von 1 μm entlang 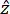der Einfallsebene dargestellt, die für das Modell in Abbildung 7A gezeigt ist. Die Abfall des Übertragungspegels von mehr als 20 dB, dargestellt durch einen schattierten Bereich, stellen Frequenzbandlücken in verschiedenen Frequenzbereichen dar.

Pitch-Catch-Getriebetests
Abbildung 8 zeigt den Aufbau des Pitch-Catch-Übertragungstests, der an einem einfachen kontinuierlichen 1D-Analogon eines periodischen Masse-Feder-Modells aus häufig verwendetem ABS-Polymer (Abbildung 9A) unter Verwendung von berührungslosem LDV durchgeführt wurde. Abbildung 9B zeigt die Ergebnisse des Pitch-Catch-Übertragungstests im Frequenzbereich für das 3D-gedruckte ABS-Muster, die mit dem in Abbildung 7A gezeigten identisch sind. Die piezoelektrische Scheibe auf Keramikbasis mit Ag-Schirm und einer radialen Resonanzfrequenz von 200 kHz (Durchmesser 10 mm und Dicke 0,2 mm) wurde verwendet, um ein Frequenz-Sweep-Signal von 4 kHz bis 40 kHz aufzulegen. Das gesendete Signal wurde an der 10^{. Elementarzelle} von der Anregungsseite erfasst. Die aufgezeichneten Zeitbereichsdaten wurden mit Hilfe der Fast-Fourier-Transformation in den Frequenzbereich transformiert. Die verarbeiteten Daten zeigen einen Signalabfall von mehr als 20 dB bei verschiedenen Frequenzen, was auf die Frequenzbandlücken hinweist, die in Abbildung 9B blau hervorgehoben sind.

Abbildung 1: 3D-Druck von Polymerproben. (A) Geschnittene Geometrie in der Slicer-Software. (B) Laufender 3D-Druckprozess. (C) 3D-gedruckte ABS-Probe für Zugtests gemäß der ASTM-Norm D638. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

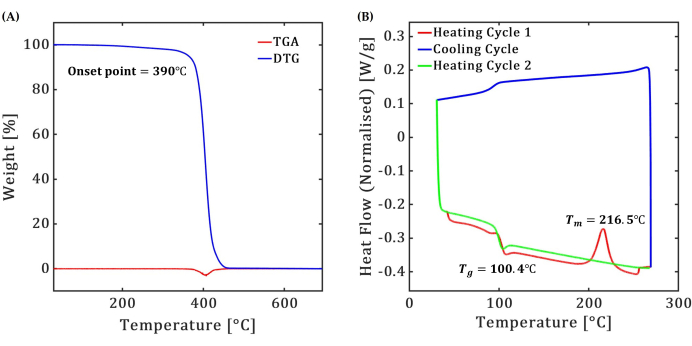
Abbildung 2: Thermogravimetrische Analyse (TGA) und dynamische Differenzkalorimetrie (DSC). Ergebnisse der thermischen Charakterisierung des ABS-Polymers in (A) TGA- und DTG- und (B) DSC-Tests. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Abbildung 3: Dynamisch-mechanische Analyse. (A) DMA-Instrument und wichtige Teile. (B) Bild der Konfiguration des Single-Cantilever-Tests (ohne Probe). (C) Bild einer eingespannten Probe in der Konfiguration mit einem Ausleger. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

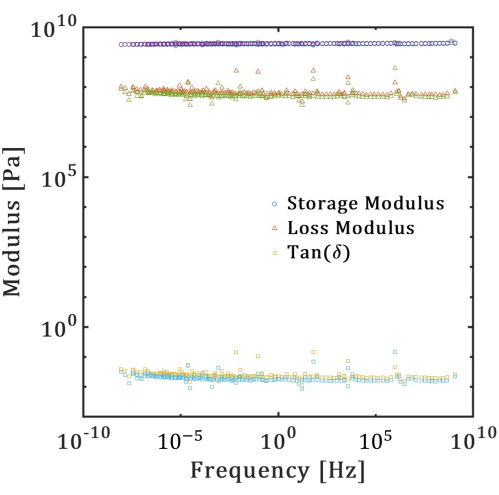
Abbildung 4: Ergebnisse der Zeit-Temperatur-Überlagerung. TTS-Ergebnisse für ABS-Polymere, die mit einem linearen Füllmuster 3D-gedruckt wurden, das bei 0° (Typ 1) und 45° (Typ 2) an der Referenz 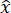des 3D-Druckers ausgerichtet ist: Speichermodul, Verlustmodul und tan(δ). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

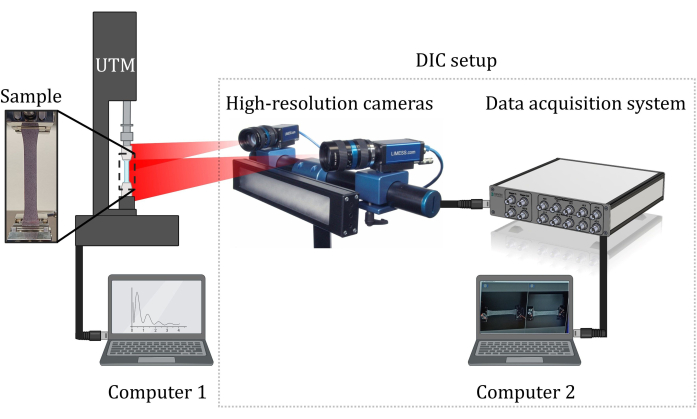
Abbildung 5: Aufbau des Zugversuchs. Schematische Darstellung des Zugversuchsaufbaus, einschließlich der universellen Zugmaschine (UTM) in Verbindung mit einem DIC-Aufbau. Eine vergrößerte Ansicht der Probe wird ebenfalls angezeigt, um das Speckle-Muster auf der Probe hervorzuheben. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

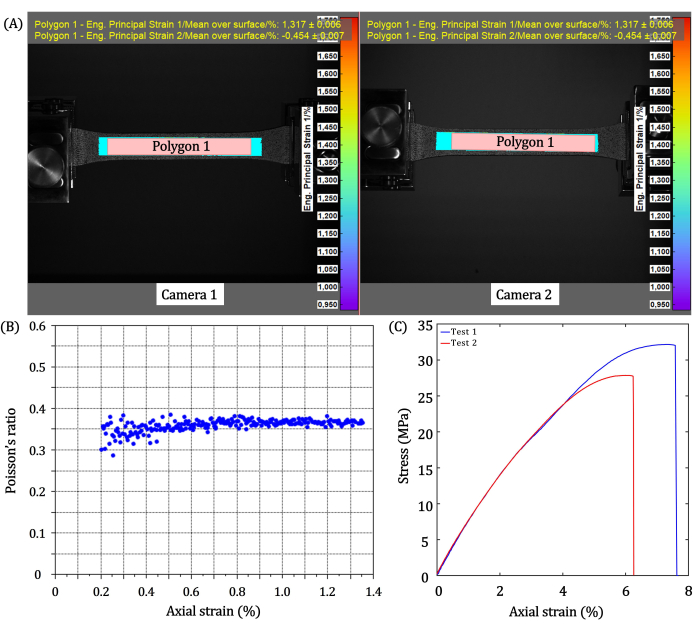
Abbildung 6: Ergebnisse des Zugversuchs. (A) Bild des Prüfmusters, das von beiden Kameras des DIC-Aufbaus aufgenommen wurde. Polygon 1 ist die Fläche, die für Berechnungen berücksichtigt wird. Die Probe wurde von links nach rechts gezogen. (B) Ergebnisse für die Poissonzahl. (C) Spannungs-Dehnungs-Verhalten der 3D-gedruckten knochenförmigen ABS-Proben (Typ 2), getestet bei 50 mm/min (Test 1) und 5 mm/min (Test 2). Die Tests wurden an vier Proben durchgeführt. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Abbildung 7: Finite-Elemente-Analyse. (A) ein geometrisches Modell für numerische Berechnungen der Übertragung; a_x ist die Dimension der Elementarzelle, d ist der Durchmesser der Scheibe und PML steht für Perfect Matched Layer. (B) Numerische Ergebnisse für Übertragungsberechnungen, schattierte Bereiche stellen die Frequenzbandlücke dar. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

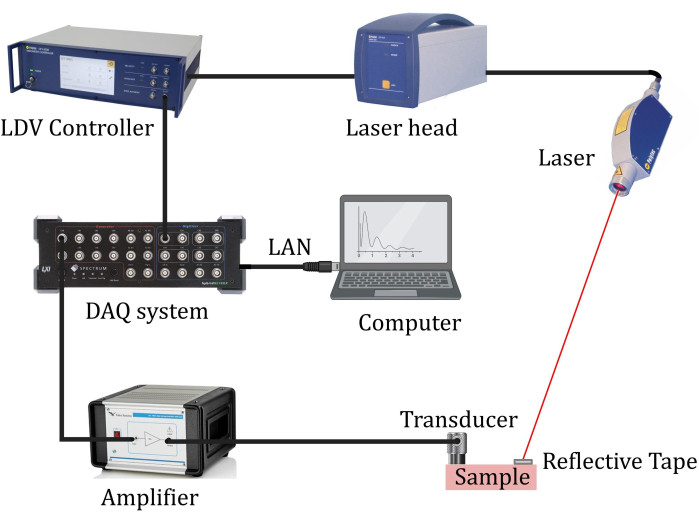
Abbildung 8: Aufbau des Pitch-Catch-Getriebeexperiments. Versuchsaufbau für Pitch-Catch-Transmissionsexperimente mit einem berührungslosen Laser-Doppler-Vibrometer zur Messung mechanischer Schwingungen, die durch eine Probe übertragen werden. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

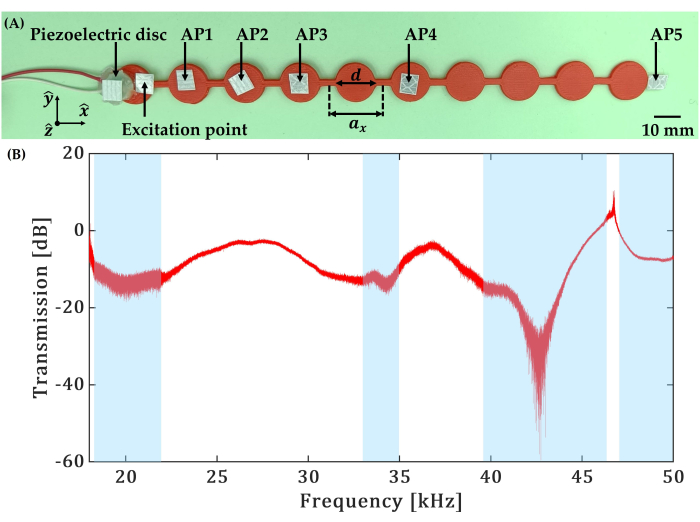
Abbildung 9: Ergebnisse des Pitch-Catch-Transmissionsexperiments. (A) Ein Foto der Metamaterialstruktur von Elementarzellen der Größe a_x = 20 mm mit dem Scheibendurchmesser d = 14 mm, getestet im Pitch-Catch-Transmissionsexperiment. Eine piezoelektrische Scheibe mit einer radialen Resonanzfrequenz von 200 kHz wird verwendet, um strukturelle Schwingungen anzuregen, und reflektierendes Band wird zur Erfassung an verschiedenen Punkten (AP1, AP2, AP3, AP4 und AP5) der Struktur eingeklebt. (B) Experimentelle Ergebnisse des Pitch-Catch-Getriebetests. Die Aufzeichnungen für den Einfall und das gesendete Signal wurden jeweils am Anregungspunkt und am Erfassungspunkt 5 (AP5) durchgeführt. Schattierte Bereiche stellen eine experimentell geschätzte Frequenzbandlücke dar. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Konfiguration testen	Prüfmuster
Einzelner Ausleger	Die meisten Proben, außer dünne Schichten unter 0,1 mm
Doppelter Ausleger	Vergleichsweise weiche Materialien, wenn die einzelnen Auslegerdaten verrauscht sind
Dreipunkt-Biegen	Sehr steife und große Proben
Spannung	Sehr dünne Schichten mit einer Dicke <0,2 mm

Tabelle 1: Testkonfigurationen, die für verschiedene Testproben auf DMA geeignet sind, klassifiziert anhand der Probensteifigkeit.

Konfigurationen testen	Länge (mm)	Breite (mm)	Dicke (mm)
Einzelner Ausleger	05–25	04–12	0.10–4.00
Doppelter Ausleger	25–45	04–12	0.10–4.00
Dreipunkt-Biegen	25–45	04–12	0.50–4.00
Spannung	10–25	04–10	0.01–0.20

Tabelle 2: Abmessungen von Prüflingen für verschiedene Testkonfigurationen in der DMA-Technik.

Ergänzende Datei 1: STL-Datei für periodische 1D-Struktur. Bitte klicken Sie hier, um diese Datei herunterzuladen.

Ergänzende Datei 2: STL-Datei für die Hundeknochenstruktur, die für Zugversuche verwendet wird. Bitte klicken Sie hier, um diese Datei herunterzuladen.

Diskussion

Das in Abschnitt 1 beschriebene 3D-Druckverfahren gilt für die meisten FDM-3D-Drucker im Tischformat. Der 3D-Druck aus ABS kann jedoch schwierig sein, da dieses Polymer empfindlich auf Temperaturänderungen reagiert. Ungleichmäßiges Erhitzen oder Abkühlen kann zum Schrumpfen bereits gedruckter Teile führen, was zu Verformungen, Rissen oder Delamination führt. Um diese Probleme zu vermeiden, wird empfohlen, zunächst die richtigen Druckeinstellungen anhand eines Datenblatts des Lieferanten zu ermitteln. Als nächstes wird empfohlen, starke Temperaturschwankungen in der Nähe des gedruckten Teils während des Druckvorgangs zu vermeiden. Dies kann erreicht werden, indem der 3D-Drucker mit einer Box oder einer Kammer umschlossen wird, um eine stabile warme Umgebung zu gewährleisten.

Die thermogravimetrische Analyse (TGA) zielt dabei darauf ab, die Temperatur zu identifizieren, bei der die Materialzersetzung beginnt, da diese Temperatur die maximal sichere Temperatur für die dynamische Differenzkalorimetrie (DSC) bestimmt. Die TGA arbeitet nach dem Prinzip, den Massenverlust eines Materials in Abhängigkeit von der Temperatur zu messen. Der DSC wiederum misst wichtige thermische Parameter eines Materials, darunter die Glasübergangstemperatur, den Schmelzpunkt und die Rekristallisationstemperaturen. Es basiert auf dem Prinzip der Erkennung von Energieänderungen, die mit Phasenübergängen verbunden sind. Somit dienen TGA- und DSC-Tests als komplementäre Techniken zu DMA.

Es ist wichtig, T_m aus dem DSC-Diagramm sorgfältig zu analysieren, da das Thermoelement des Geräts beschädigt werden kann, wenn der dynamisch-mechanische Analysator einer geschmolzenen Probe ausgesetzt wird. Vor dem Laden der Probe muss sichergestellt werden, dass die Pfanne nicht kontaminiert ist. Eine Kontamination der Probe mit Fremdstoffen kann die thermischen Eigenschaften beeinträchtigen und Artefakte in den TGA- und DSC-Kurven einführen. Eine sorgfältige Identifizierung von T_g und T_m ist von entscheidender Bedeutung, da sie als wichtige Parameter für DMA dienen.

DMA misst die Variation der Materialeigenschaften des Prüflings mit der Temperatur innerhalb des benutzerdefinierten Frequenzbereichs. Das DMA-Gerät kann solche Messungen im Frequenzbereich von 0,01-600 Hz durchführen. Die Variation der Materialeigenschaften von rheologischen einfachen Polymeren bei Frequenzwerten außerhalb dieses Bereichs kann mit Hilfe der Zeit-Temperatur-Superposition⁷ vorhergesagt werden. Auf diese Weise erhält man die viskoelastischen Eigenschaften von Materialien - Verlustmodul und komplexe Viskosität. Der Betrieb bei Temperaturen nahe T_m kann jedoch den dynamisch-mechanischen Analysator beschädigen und muss vermieden werden. Außerdem kann der Betrieb bei Temperaturen in der Nähe von T_g zu inkonsistenten und unzuverlässigen Ergebnissen führen. Beachten Sie auch, dass die richtige Ausrichtung der Probe unerlässlich ist, um sicherzustellen, dass die Probe gerade ist und glatte, parallele Kanten ohne Oberflächenfehler aufweist. Das Thermoelement darf die Klemmen an keiner Stelle der Messung berühren, um Beschädigungen zu vermeiden.

Die fast flachen Trends für die Kurven der Speicher- und Verlustmodule in Abbildung 4 zeigen, dass das FDM-gedruckte ABS vor allem bei Raumtemperatur ein elastisches Verhalten zeigt. Die Ebenheit der Kurve für den Tangens des Phasenwinkels (δ), d. h. das Verhältnis von Speichermodul zu Verlustmodul, zeigt an, dass der T_g des Materials nicht innerhalb des gemessenen Temperaturbereichs liegt. Außerdem sind die Daten für die beiden Testmuster mit unterschiedlichen Orientierungen des Druckmusters nicht unterscheidbar, was auf keinen signifikanten Einfluss des Druckmusters auf die Moduli hindeutet. Dies ist auf außergewöhnlich niedrige viskose Verluste im ABS und eine Füllungsdichte von 100 % zurückzuführen, die jeden Effekt der Strukturierung überdecken. Beachten Sie jedoch, dass diese Ergebnisse für 3D-gedruckte Polymere eher eine Ausnahme als eine Regel sind, da die viskosen Verluste in anderen Filamenten nicht vernachlässigbar sind. Diese Verluste unterstreichen die Bedeutung der Leitung des DMA für 3D-gedruckte Polymere.

Die Zugprüfung ist eine weit verbreitete Technik zur mechanischen Charakterisierung von Werkstoffen. Es liefert quasi-statische mechanische Module, z. B. den Elastizitätsmodul und die Poissonzahl, für ein Material der Prüfprobe, oft von knochenähnlicher Form (Abbildung 1B). Die Technik der digitalen Bildkorrelation (DIC) kann hinzugefügt werden, um die korrekte Positionierung einer Prüfprobe sicherzustellen und Bilder ihrer verformten Oberfläche bei jedem Ladeschritt zu erfassen sowie die Bilder zur Analyse von Dehnungs- und Verschiebungsfeldern zu verarbeiten. Obwohl die Integration von DIC zu einer höheren Genauigkeit der Ergebnisse führt, kann sie zu mehreren Herausforderungen führen, wenn sie nicht richtig gehandhabt wird. Es ist wichtig, bei der Probenvorbereitung für DIC ein gutes Speckle-Muster mit einem 3D-Residuum von weniger als 0,4/Pixel anzuwenden. Stellen Sie sicher, dass die Probe gut fokussiert ist, und verwenden Sie die richtigen Kalibrierplatten, die am besten zum Sichtfeld der Kamera passen. Der Elastizitätsmodul, der in dieser Studie durch Zugversuche bestimmt wurde, 0,543 GPa, stimmt gut mit dem von Samykano et al. berichteten Wert (0,751 GPa) ^überein.26. UTM, die für Tests verwendet wird, kann Einschränkungen in Bezug auf Genauigkeit, Auflösung oder Kapazität aufweisen, die sich auf die Qualität und Zuverlässigkeit der Ergebnisse auswirken können. Eine falsche Probenvorbereitung, einschließlich unsachgemäßer Montage oder Bearbeitung, kann zu Fehlern bei der Messung führen. Ein Verrutschen der Probe kann durch die Verwendung von Schleifpapieren für einen besseren Kontakt zwischen der Probe und den Backen der UTM vermieden werden. Darüber hinaus haben viele Materialien anisotrope mechanische Eigenschaften. Mangelnde Aufmerksamkeit für anisotropes Verhalten kann zu ungenauen Vorhersagen führen.

Numerische Simulationen zur Abschätzung von Bandlücken sind unerlässlich, um die Arbeitsfrequenzen für Pitch-Catch-Übertragungstests richtig zu definieren ^4,8,27. Die berechneten Daten, die in Abbildung 7B gezeigt werden, sind für die analysierte Metamaterialkonfiguration in Abbildung 7A erwartbar. Insbesondere oszilliert die Übertragungskurve außerhalb der Bandlückenfrequenz um einen konstanten Wert, wobei die Schwingungsspitzen den Eigenfrequenzen des endlichen periodischen Mediums²⁷ entsprechen. Innerhalb der Bandlücke ist die Transmission stark reduziert, was die Fähigkeit dieses Metamaterials zur Dämpfung akustischer Wellen bestätigt.

Das beschriebene Simulationsverfahren (Abschnitt 5) ist allgemein und nicht auf die analysierte Geometrie oder das spezifische viskoelastische Verhalten beschränkt. Weitere Metamaterialstrukturen aus verschiedenen viskoelastischen Materialien können in der Transmissionsanalytik 7,8,20,22,24 erfolgreich getestet werden. Das Materialverhalten ist auf die lineare Elastizität oder Viskoelastizität beschränkt, da nichtlineare Materialien im Frequenzbereich⁴ nicht analysiert werden können. Beachten Sie, dass die Übertragungsanalyse in anderen Finite-Elemente-Paketen möglicherweise andere Implementierungsschritte und eine andere Terminologie oder Befehle für ähnliche Aktionen erfordert. Außerdem können periodische Randbedingungen und PML fehlen, was die Suche nach Alternativen zur Reduzierung von Störwellenreflexionen von den Domänengrenzen erfordert.

Die Pitch-Catch-Übertragungstests zielen darauf ab, den Anteil der akustischen Wellenenergie abzuschätzen, der durch eine (Meta-)Materialprobe übertragen wird, und Bandlückenfrequenzen zu identifizieren (zu validieren). Es ist zweckmäßig, einen solchen Test auf der Grundlage vorläufiger numerischer Übertragungsdaten einzurichten, der es ermöglicht, einen Betriebsfrequenzbereich zu identifizieren, der wiederum die Auswahl einer geeigneten Anregungsquelle 8,20,22,24 ermöglicht. Typische Geräte für Übertragungsprüfungen umfassen einen Signalgenerator zur Erzeugung eines Anregungssignals, einen Verstärker zur Erhöhung der Signalintensität, Piezoelemente (z. B. eine piezoelektrische Scheibe oder einen piezokeramischen Wandler) zur Umwandlung elektrischer Signale in mechanische Bewegungen und umgekehrt sowie ein Datenerfassungssystem zur Aufzeichnung übertragener Signale⁷. Ein Piezoelement ist fest mit einer getesteten Probe verbunden, um ein Signal anzuregen, während das andere(n) verwendet wird/werden, um ein gesendetes Signal zu empfangen. Das zweite Piezoelement wird hier durch ein Laser-Doppler-Vibrometer (LDV) für berührungslose Messungen ersetzt, die aufgrund der extrem hohen Empfindlichkeit des Lasers eine bessere Qualität der aufgezeichneten Signale liefern.

Das gemittelte gemessene Sendesignal stimmt gut mit den numerischen Vorhersagen (Abbildung 7B und Abbildung 9B) überein, wie sie für eine Probe mit extrem niedrigen viskosen Verlusten zu erwarten ist. Die gezeigten Frequenzbereichsdaten werden aufgrund der hohen Empfindlichkeit des Lasers durch Rauschen überlagert. Die Vorteile und die Flexibilität des Einsatzes von LDV für die Datenerfassung liegen auf der Hand. Zusätzlich zu berührungslosen Messungen und genauen Daten ermöglicht das LDV die Messung des Signals auf der Anregungsseite, indem der Laser auf die Probe in der Nähe einer piezoelektrischen Scheibe fokussiert wird. Dies bietet eine Möglichkeit, das Verhältnis von übertragenen zu den Eingangssignalen wie in der numerischen Simulation zu bewerten, was besonders für komplex strukturierte Metamaterialien nützlich ist, die ein erhöhtes Maß an internen Wellenreflexionen aufweisen.

Daraus lässt sich schließen, dass das vorgeschlagene Protokoll zur Charakterisierung viskoelastischer Metamaterialien für Forscher, die in diesem sich schnell entwickelnden Bereich arbeiten, hilfreich sein kann, um Daten für ein breites Spektrum additiv gefertigter Materialien zu sammeln und diese Daten für die Analyse der Metamaterialdynamik zu nutzen. Da Polymere aufgrund ihrer außergewöhnlichen Dämpfungseigenschaften aufgrund viskoelastischer Effekte eine bevorzugte Wahl gegenüber metallischen oder keramischen Metamaterialien sind, ist ein tieferes Verständnis dieser Effekte unerlässlich, um die Anwendungen von Metamaterialien in den Bereichen akustische Wellenführung, Tarnung, Unterwasserakustik, Schallabsorption, medizinische Bildgebung, Energy Harvesting und viele andere weiter zu verbessern.

Materialien

Name	Company	Catalog Number	Comments
Acrylonitrile Butadiene Styrene (ABS)	BASF	https://www.xometry.com/resources/3d-printing/abs-3d-printing-filament/	Print temperature: 225-245 °C
COMSOL Multiphysics 6.0	COMSOL	https://www.comsol.com/product-download/6.0	Finite element software
DAQ system for DIC	Dantec Dynamics	https://www.dantecdynamics.com/components/daq-controllers/
Discovery DSC 25	TA Instruments	https://www.tainstruments.com/dsc-25/	Software: Trios; Pan: Aluminium
DMA 8000	Perkin Elmer	https://www.perkinelmer.com/product/dma-8000-analyzer-qtz-window-ssti-clamp-n5330101	Software: PerkinElmer
DN2.813-04 Spectrum hybridNetbox	Spectrum Instrumentation	https://spectrum-instrumentation.com/products/details/DN2813-04.php	4-channel signal generator and digitizer; Software used: SBench6
FDM 3D printer Ultimaker 3.0	Ultimaker	https://ultimaker.com/3d-printers/s-series/ultimaker-s3/	Slicer: Ultimaker Cura
Polytec laser unit OFV 534	Polytec GmbH	https://www.polytec.com/eu/vibrometry/products	Laser and laser head, as a set
Polytec OFV-5000 vibrometer controller	Polytec GmbH	https://www.polytec.com/eu/vibrometry/products	LDV controller
Power amplifier Type 2718	Bruel & Kjaer	https://www.bksv.com/en/instruments/vibration-testing-equipment/vibration-amplifiers/exciters/power-amplifier-type-2718	Power output capability of 75 VA
PRYY-0110	PI Ceramic	https://www.piceramic.com/en/products/piezoceramic-components/disks-rods-and-cylinders/piezoelectric-discs-1206710	Ceramic-based, Ag-screened piezoelectric discs
Q400 DIC	Limess Messtechnik & Software GmbH	https://www.limess.com/en/products/q400-digital-image-correlation	Software: Istra4D
Thermogravimetric Discovery TGA 550	TA Instruments	https://www.tainstruments.com/tga-550/	Software: Trios; Pan: Aluminium
UniVert 1kN Tensile testing machine	Cell Scale biomaterials testing	https://www.cellscale.com/products/univert/	Software: UniVert; load cell capacity: 1 kN
WMA-300 High speed high voltage amplifier	Falco Systems	https://www.falco-systems.com/High_voltage_amplifier_WMA-300.html	50x amplification up to +150 V and -150 V with respect to ground