Method Article
חישוב ריכוזי האטמוספירה של אשכולות מולקולאריים מ- ab , כימיה תרמו
In This Article
Summary
ריכוזים אטמוספריים של אשכולות מולקולריים מאוגדים חלש יכול להיות מחושב מן התכונות התרמוכימיים של מבני אנרגיה נמוכה שנמצאו באמצעות מתודולוגיה לדגימה מרובת צעדים מבצעות ניצול אלגוריתם גנטי ו-למחצה אמפירית ו ab כימיה קוונטית.
Abstract
המחקר החישובית של היווצרות וצמיחה של אירוסולים אטמוספרי דורש משטח מדויק של אנרגיה של גיבס חופשי, אשר ניתן להשיג מתוך מבנה אלקטרוני בשלב הדלק וחישובי תדירות רטט. כמויות אלה תקפות עבור אלה אשכולות אטמוספריים שהגאומטריות מתאימות למינימום על משטחי האנרגיה הפוטנציאליים שלהם. אנרגיה חופשית של גיבס של מבנה האנרגיה המינימלי ניתן להשתמש כדי לחזות ריכוזי אטמוספריים של האשכול תחת מגוון של מצבים כגון טמפרטורה ולחץ. אנו מציגים הליך זול מבחינה חישובית שנבנה על האלגוריתם הגנטי המבוסס מבצעות דיגום ואחריו סדרה של חישובי הקרנה מדויקת יותר ויותר. ההליך מתחיל על ידי יצירת והתפתחות הגיאומטריות של קבוצה גדולה של תצורות באמצעות דגמים למחצה אמפיריים ולאחר מכן מזקק את המבנים הייחודיים המתקבלים בסדרה של רמות ab ברמה גבוהה של התאוריה. לבסוף, תיקוני תרמודינמיים מחושבים עבור הקבוצה המתקבלת של מבני אנרגיה מינימלית ומשמשים לחישוב האנרגיות החופשיות של גיבס של היווצרות, קבועים בשיווי משקל וריכוזים אטמוספריים. אנו מציגים את היישום של הליך זה לחקר אשכולות גליצין רטוב בתנאי הסביבה.
Introduction
הפרמטר בלתי בטוח ביותר במחקרים אטמוספריים של שינוי האקלים הוא בדיוק במידה שבה חלקיקים ענן משקפים קרינת השמש נכנסות. אירוסולים, אשר חלקיקים החומר מושעה גז, הטופס חלקיקי ענן הנקרא ענן עיבוי גרעיני (CCN) כי פיזור קרינה נכנסות, ובכך מניעת ספיגת שלה ואת החימום הבא של האטמוספירה1. הבנה מפורטת של אפקט זה קירור נטו דורש הבנה של הצמיחה של אירוסולים לתוך CCNs, אשר בתורו דורש הבנה של הצמיחה של אשכולות מולקולריים קטנים לתוך חלקיקי תרסיס. העבודה האחרונה הציעה כי היווצרות תרסיס היא ביוזמת אשכולות מולקולריים של 3 ננומטר בקוטר או פחות2; עם זאת, המשטר בגודל זה קשה לגשת באמצעות טכניקות ניסיוני3,4. לכן, הגישה למידול חישובית רצויה כדי להתגבר על הגבלה ניסויית זו.
באמצעות גישת המידול שלנו שתוארה להלן, אנו יכולים לנתח את התפתחותם של כל אשכול הנוזלים. מכיוון שאנו מעוניינים בתפקיד המים בהיווצרות מולקולות ביולוגיות גדולות ממרכיבים קטנים יותר בסביבות קדם-ביוטי, אנו ממחישים את הגישה שלנו עם גליצין. האתגרים שאירעו וכלים הדרושים לטיפול בשאלות מחקר אלה דומים מאוד לאלה המעורבים בחקר אירוסולים אטמוספריים ואשכולות הפרניקליציה5,6,7,8,9,10,11,12,13,14,15. כאן, אנו בודקים אשכולות גליצין מבודדים החל ממולקולה גליסין מבודדת ואחריה סדרה של תוספות חורגות של עד חמש מולקולות מים. המטרה הסופית היא לחשב את ריכוזי שיווי משקל של מבחינה מעשית (H2O)n = 0-5 אשכולות באטמוספירה בטמפרטורת החדר ברמת הים ולחות יחסית (RH) של 100%.
מספר קטן של אשכולות אלה sub-ננומטר מולקולרי לגדול לתוך אשכול קריטי מטאפיטטיות (1-3 nm בקוטר) גם על ידי הוספת מולקולות אדים אחרים או קרוש על אשכולות קיימים. אשכולות קריטיים אלה יש פרופיל צמיחה חיובית המובילה היווצרות של הרבה יותר גדול (עד 50-100 ננומטר) ענן עיבוי גרעיני (CCN), אשר משפיעים ישירות על יעילות המשקעים של עננים, כמו גם את היכולת שלהם לשקף את האור האירוע. לכן, לאחר הבנה טובה של התרמודינמיקה של אשכולות מולקולריים והפצות שיווי משקל שלהם צריך להוביל תחזיות מדויקות יותר של ההשפעה של אירוסולים על האקלים העולמי.
מודל תיאורי של היווצרות תרסיס דורש תרמודינמיקה מדויקת של היווצרות אשכול מולקולרי. מיחשוב של תרמודינמיקה מדויקת של היווצרות אשכול מולקולרי דורש זיהוי של התצורות היציבות ביותר, אשר כרוכה במציאת המיזימה הגלובלית והמקומית על משטח האנרגיה הפוטנציאלי של האשכול (PES)16. תהליך זה נקרא מבצעות דיגום ניתן להשיג באמצעות מגוון רחב של טכניקות, כולל אלה המבוססים על דינמיקה מולקולרית (MD)17,18,19,20, מונטה קרלו (MC)21,22, ו אלגוריתמים גנטיים (GA)23,24,25.
פרוטוקולים שונים פותחו במהלך השנים כדי להשיג את המבנה ואת התרמודינמיקה של הידרטים אטמוספריים ברמה גבוהה של תאוריה. פרוטוקולים אלה שונים בבחירה של (i) מבצעות שיטת דגימה, (ii) הטבע של שיטה ברמה נמוכה המשמש בדגימה מבצעות, ו (iii) את ההיררכיה של שיטות ברמה גבוהה המשמשים למקד את התוצאות בשלבים הבאים.
שיטות הדיגום מבצעות כללו אינטואיציה כימית26, דגימה אקראית27,28, דינמיקה מולקולרית (MD)29,30, באסין מקפץ (BH)31, ו אלגוריתם גנטי (GA)24,25,32. השיטות השכיחות ביותר ברמה נמוכה המועסקים בשיטות דיגום אלה הן שדות כוח או מודלים למחצה אמפיריים כגון PM6, PM7 ו-SCC-DFTB. אלה מלווה לעתים קרובות על ידי חישובי DFT עם ערכות בסיס יותר ויותר פונקציות אמינות יותר מאשר השלבים הגבוהים של יעקב סולם33. במקרים מסוימים, אלה מלווה בשיטות פונקציית גל גבוהות יותר כגון MP2, ccsd (t), והמחיר היעיל dlpno-ccsd (t)34,35.
קילדגארד ואח '36 פיתחה שיטה שיטתית שבה מולקולות מים מתווספים בנקודות על הספירות של פיבונאצ ' י37 סביב אשכולות קטנים יותר או בלתי מנוזלים כדי ליצור מועמדים עבור אשכולות גדולים יותר. מועמדים בלתי פיזיים ויתירים יוסרו על בסיס ספי הקשר הקרוב ומרחק ממוצע-כיכר השורש בין מגבשי שונים. מיטובי הבאים באמצעות שיטת PM6 semi-אמפירית והיררכיה של שיטות הפונקציה של DFT ו-גל משמשות כדי לקבל סט של מגבשי אנרגיה נמוכה ברמה גבוהה של תאוריה.
מושבת הדבורים המלאכותית (ABC) האלגוריתם38 היא גישה מבצעות דגימה חדשה שיושמה לאחרונה על ידי ג'אנג ואח '. כדי ללמוד אשכולות מולקולריים בתוכנית בשם abcluster39. Kubecka ואח '40 בשימוש abcluster עבור מבצעות דיגום ואחריו מיטוב ברמה נמוכה באמצעות מחייב הדוקה Gfn-xtb שיטה חצי אמפירית41. הם מעודנים עוד יותר את המבנים והאנרגיות באמצעות שיטות DFT ולאחריהן האנרגיות הסופיות באמצעות DLPNO-CCSD (T).
ללא קשר לשיטה, מבצעות דיגום מתחיל בחלוקה אקראית או לא אקראית של נקודות על ה-PES. כל נקודה מקבילה לגיאומטריה ספציפית של האשכול המולקולרי הנדון ונוצרת על ידי שיטת הדגימה. לאחר מכן המינימום המקומי הקרוב ביותר נמצא עבור כל נקודה על ידי ביצוע "במורד" כיוון על פסי. הסדרה של קיצון כך נמצא מתאים הגיאומטריות האלה של האשכול המולקולרי כי הם יציבים, לפחות לזמן מה. כאן, צורת ה-PES והערכת האנרגיה בכל נקודה על פני השטח תהיה רגישה לתיאור הפיזי של המערכת, שבה תיאור פיזי מדויק יותר מביא לחישוב אנרגיה יקר יותר מבחינה חישובית. אנו נשתמש באופן ספציפי בשיטת ה-GA המיושמת בתוכנית של אוגולם25 , אשר הוחלה בהצלחה על מגוון רחב של מיטוב גלובלי ובעיות מבצעות דיגום42,43,44,45, כדי ליצור את הערכה הראשונית של נקודות דגימה. פסי יהיה מתואר על ידי PM7 דגם46 מיושם בתוכנית MOPAC201647. שילוב זה מועסק משום שהוא מייצר מגוון רחב יותר של נקודות בהשוואה ל-MD ו-MC שיטות ומוצא את קיצון המקומית מהר יותר מאשר תיאורים מפורטים יותר של PES.
הקבוצה של קיצון מקומי אופטימיזציה של GA נלקחים כמו הגאומטריות ההתחלתית לסדרה של שלבי הקרנה, אשר להוביל לקבוצה של אנרגיה נמוכה לשקר מינימלי. חלק זה של הפרוטוקול מתחיל על ידי אופטימיזציה של הקבוצה הייחודית של מבני GA-מיטוב באמצעות התיאוריה הפונקציונלית (DFT) עם סט בסיס קטן. קבוצה זו של מיטוב יהיה בדרך כלל לתת קבוצה קטנה יותר של מבנים מינימלי ייחודי מקומי אשר מעוצב באופן מפורט יותר לעומת המבנים ממוטב למחצה של GA. לאחר מכן, סיבוב נוסף של מיטובי DFT מבוצעים על קבוצה קטנה יותר של מבנים באמצעות ערכת בסיס גדולה יותר. שוב, שלב זה בדרך כלל לתת קבוצה קטנה של מבנים ייחודיים אשר מעוצב באופן מפורט יותר בהשוואה לשלב DFT בסיס קטן. הקבוצה הסופית של מבנים ייחודיים ממוטבת לאחר מכן להתכנסות הדוקה יותר ותדרי התנודה ההרמונית מחושבים. לאחר שלב זה יש לנו את כל מה שאנחנו צריכים כדי לחשב את ריכוזי האיזון של האשכולות באטמוספירה. הגישה הכוללת מסוכמת באיור 1. נשתמש בקירוב PW9148 כללית-מעבר הדרגתי (gga) exchange-מתאם פונקציונלי ביישום Gaussian0949 של dft יחד עם שתי וריאציות של מערכת pople50 בסיס (6-31 + g * עבור צעד בסיס קטן 6-311 + + g * * עבור צעד בסיס גדול). השילוב המסוים הזה של המתאם הפונקציונלי והתפקודי של מתאם החליפין נבחר בשל הצלחתו הקודמת במחשוב באנרגיות מדויקות של גיבס ללא היסוס של היווצרות אשכולות אטמוספריים51,52.
פרוטוקול זה מניח שלמשתמש יש גישה לאשכול מחשוב בעל ביצועים גבוהים (HPC) עם מערכת האצווה הניידת53 (PBS), MOPAC2016 (http://openmopac.net/MOPAC2016.html)47, אוגולם (Https://www.ogolem.org)25, גאוס 09 (Https://gaussian.com)49, ו openbabel54 (http://openbabel.org/wiki/Main_Page) התוכנה המותקנת בעקבות הוראות ההתקנה הספציפיות שלהם. כל שלב בפרוטוקול זה משתמש גם בקבוצה של מעטפת in-house ו-פיתון 2.7 סקריפטים אשר יש לשמור בספרייה הכלולה במשתנה הסביבה $PATH של המשתמש. כל המודולים הסביבתיים הדרושים והרשאות הביצוע כדי להפעיל את כל התוכניות הנ ל יש לטעון גם לתוך ההפעלה של המשתמש. השימוש בדיסק ובזיכרון על-ידי קוד ה-GA (OGOLEM גולם) והקודים החצי-אמפיריים (מוגאק) קטנים מאוד על-ידי תקני משאבי מחשב מודרניים. השימוש בזיכרון ובדיסק הכולל עבור OGOLEM גולם/מוורק תלוי במספר הליכי האשכולות שבהם ברצונו להשתמש ואפילו אז, השימוש במשאבים יהיה קטן בהשוואה ליכולות של רוב מערכות ה-HPC. צורכי המשאב של שיטות QM תלויים בגודל האשכולות וברמת התאוריה שבשימוש. היתרון בשימוש בפרוטוקול זה הוא שאדם יכול לשנות את רמת התאוריה כדי להיות מסוגל לחשב את הערכה הסופית של מבני אנרגיה נמוכה, לזכור כי בדרך כלל חישובים מהירים יותר להוביל לחוסר ודאות יותר בדיוק של התוצאות.
למען הבהירות, המחשב המקומי של המשתמש יהיה מכונה "מחשב מקומי" ואילו באשכול ה-HPC יש להם גישה כאל "אשכול מרוחק".
Protocol
1. מציאת מבנה האנרגיה המינימלי של גליצין ומים מבודדים
הערה: המטרה כאן היא two-קיפול: (i) כדי להשיג מבני אנרגיה מינימלית של מים מבודדים ומולקולות גליצין לשימוש באלגוריתם הגנטי מבצעות דיגום, (ii) ולחשב את תיקוני תרמודינמיים על האנרגיות בשלב הגז של מולקולות אלה לשימוש בחישוב ריכוזי אטמוספריים.
- במחשב המקומי, פתח הפעלה חדשה של אבוגדרו.
- לחץ על לבנות > הוסף ≫ פפטיד ובחר בסדר מתוך חלון הוספת פפטיד כדי ליצור מונומר גליצין בחלון הפריט החזותי.
- לחץ על סיומות ≫ גאוסיאנית וערוך את השורה הראשונה בתיבת הטקסט כדי לקרוא את ' pw91pw91/6-311 + + G * * Int (Acc2E = 12, ultrafine) scf (conver = 12) לבחור (הדוק, maxcyc = 300) freq '. לחץ על צור ושמור את קובץ הקלט כ- glycine.com.
- אנא שימו לב כי אם המולקולה כוללת גמישות משמעותית ביותר, כמו גליצין עושה55, זה קריטי לבצע בדיקות קונפורמציה כדי לזהות את המבנה המינימלי הגלובלי ומגבשי שקרים נמוכים אחרים. OpenBabel54 מספק כלי החיפוש מאוד חסון ניצול אלגוריתמים שונים ושדות כוח מהיר. בעוד הקונגבונים מורשים להירגע ולהמיר במהלך החישובים של GA והבאים, זה לפעמים הכרחי כדי להפעיל חישובי GA מרובים, כל אחד מתחיל עם conformers שעבר שונים.
- במחשב המקומי, פתח הפעלה חדשה באבוגדרו.
- לחץ על בניית > הוסף ≫ קטע וחפש אחר "מים" מחלון הוספת המקטע כדי לקבל את הקואורדינטות של המים.
- לחץ על סיומות ≫ גאוסיאנית וערוך את השורה הראשונה בתיבת הטקסט כדי לקרוא את ' pw91pw91/6-311 + + G * * Int (Acc2E = 12, ultrafine) scf (conver = 12) לבחור (הדוק, maxcyc = 300) freq '. לחץ על צור ושמור את קובץ הקלט כ- water.com.
- העבר את שני קבצי ה -. com לאשכול המרוחק. לאחר שתתחבר לאשכול המרוחק, התקשר לגאוס 09 בסקריפט של שליחת אצווה כדי להתחיל בחישוב. כאשר החישובים מסיימים, יש לחלץ את הקואורדינטות הקרטזיות (קבצי. xyz ) של מבני האנרגיה המינימליים על-ידי קריאה ל-openbabel. עבור גליצין, הפקודה לביצוע היא:
אובאבל-ig09 גליצין יומן הרישום-אוקסיז > גליצין. xyz
אלה שני קבצי . xyz ישמשו את ה-GA מבצעות לדגימה בשלב הבא.
2. גנטי-אלגוריתם מבוסס מבצעות דיגום של מאוד (H2O)n = 1-5 אשכולות
הערה: המטרה כאן היא להשיג קבוצה של מבנים בעלי אנרגיה נמוכה עבור הרמה (H2O)n = 1-5 ברמת התאוריה הזולה והחצי אמפירית, באמצעות PM746 מודל מיושם ב-מערכתה47. הכרחי שלספריית העבודה יהיה הארגון והמבנה המדויקים כפי שמוצג באיור 2. הדבר מבטיח שהמעטפת המותאמת אישית והסקריפטים של פייתון יעבדו ללא תקלות.
- העתק את כל קבצי ה-script הנחוצים לאשכול המרוחק והוסף את מיקומם ל-$PATH
- שימו את כל קבצי הסקריפטים והתבניות בתיקייה (למשל. סקריפטים) והעתיקו אותו לאשכול המרוחק
- ודא שכל קבצי ה-script הם קובץ הפעלה
- הוסף את המיקום של ספריית ה-script למשתנה הסביבתי $PATH על-ידי הזנת הפקודות הבאות במסוף. מיקום ברירת המחדל של קבצי ה-script מוגדר כ-$HOME/Joat-gomas, אך ניתן להגדיר משתנה סביבתי שנקרא $SCRIPTS _HOME הצבעה על הספריה המכילה את קבצי ה-script ולהוסיף $SCRIPTS _HOME לנתיב של אחד
- מעטפת Bash:
ייצוא SCRIPTS_HOME =/path/to/scripts
ייצוא נתיב = $ {SCRIPTS_HOME}: $ {PATH} - Tcsh/מעטפת Csh:
setenv SCRIPTS_HOME/path/to/סקריפטים
שביל setenv $ {SCRIPTS_HOME}: $ {PATH}
- מעטפת Bash:
- באשכול המרוחק, הגדר והפעל חישוב GA:
- צור מדריך בשם "בסדר -h2o " כאשר n הוא מספר מולקולות המים.
- צור ספריית מספרית בשם GA תחת המדריך הדוחה-h2o-n כדי להפעיל חישובי אלגוריתם גנטי.
- העתק את קבצי הקלט של אוגולם (למשל. pm7. אוגו), ונומרים קואורדינטות קרטזיות (למשל. גליצין. xyz, מים. xyz) ו-מכתב השליחה של ה-pbs אצווה (למשל. הפעל. PBS) לתוך ספריית ה- GA .
- בצע את השינויים הדרושים בקובץ הקלט ובקובץ השליחה באצווה של OGOLEM גולם.
- שלח את החישוב. כאשר החישוב מתחיל, ה-OGOLEM גולם ייצור ספריה חדשה בשם הקידומת של קובץ הקלט של OGOLEM גולם (Eg. pm7) בספריית ה-GA ותאחסן שם קואורדינטות חדשות שנוצרו שם.
- לאחר השלמת החישוב, יש לקמפל את האנרגיות והקבועים הסיבוב, ולהשתמש במידע זה כדי לקבוע מהם המבנים הייחודיים לאנרגיה נמוכה:
- שינוי הספרייה כדי לשנות את המדריך -h2o-n/GA/pm7
- חלץ את האנרגיות וחשב את הקבועים של האשכולות הממוטבים ב-GA באמצעות הפקודה:
getRotConsts-GA. csh N 0 99
כאשר N הוא מספר האטומים באשכול המולקולרי ו-' 0 99 ' מציין כי גודל מאגר ה-GA הוא 100, עם אינדקסים הפועלים מ -0 עד 99. פעולה זו תיצור קובץ הנקרא rotConstsData_C המכיל רשימה ממוינת של כל תצורות האשכולות הממוטב ב-GA, האנרגיות שלהם והקבועים הסיבוב שלהם. - בצע את הפקודה:
similarityAnalysis.py pm7 rotConstsData_C
כאשר pm7 ישמש כתווית למתן שמות קבצים, כדי לחפש ולשמור את האשכולות הייחודיים של מיטוב GA. פעולה זו תיצור קובץ בשם uniqueStructures-pm7. data המכיל רשימה ממוינת של התצורות הייחודיות של מיטוב GA. זוהי רשימה של מבנים מינימליים מקומיים ייחודיים עבור האשכול הטוב ביותר (H2O)n ממוטב ברמה PM7 של תאוריה, ומבנים אלה מוכנים כעת להיות מעודן באמצעות dft.
- גש אל המדריך הטוב ביותר -h2o-n/GA ושילוב התוצאות ממספר רב של מפעיל GA הדומה לשימוש בסקריפט combine-GA. csh . התחביר הוא:
combine-GA. csh < תווית > < רשימת הספריות עם הפעלת GA >
במקרה ספציפי זה, הפקודה:
combine-GA. csh pm7 pm7
יפיק רשימה חדשה של מבנים ייחודיים בשם 'uniqueStructures-pm7. data' בספרייה הזאת -h2o-n/GA .
3. עידון באמצעות שיטת QM עם ערכת בסיס קטנה
הערה: המטרה כאן היא למקד את הדגימה המבצעות שלn = 1-5 אשכולות באמצעות תיאור קוונטי מכני טוב יותר כדי לקבל קבוצה קטנה אך מדויקת יותר של מבנה האשכולות (H2O)n = 1-5 מבני אשכול.2 המבנים המתחילים עבור שלב זה הם התפוקות של שלב 2.
- הכן והפעל את חישוב DFT שהוגדר בסיס קטן:
- צור ספריית מע בשם QM תחת המדריך הדוחה-h2o-n . תחת הספריה QM, צור ספריית מע אחרת בשם pw91-sb.
- העתק את רשימת המבנים הייחודיים (uniqueStructures-pm7. data) מהספריה הזאת -h2o-n/GA לספריית QM/pw91-sb .
- לשנות את המדריך זה מכוערת-h2o-n/QM/pw91-sb.
- הפעל את הבסיס הקטן להגדיר DFT מבצעות דגימה סקריפט באמצעות הפקודה:
run-pw91-sb. csh uniqueStructures-pm7. נתונים sb תור 10
כאשר sb היא תווית עבור קבוצת חישובים זו, התור הוא התור המועדף באשכול המחשוב ו-10 מציין ש-10 חישובים יקובצו למשימת אצווה אחת. קובץ script זה יפיק באופן אוטומטי את הקלט עבור גאוס 09 ויגיש את כל החישובים. הזן ' מבחן ' עבור ' תור ' כדי לבצע מרוץ יבש.
- לאחר השלמת החישובים שהוגשו, לחלץ ולנתח את התוצאות.
- חלץ את האנרגיות וחשב את הקבועים הרוטציה של האשכולות הממוטבים בסיס קטן באמצעות הפקודה:
getRotConsts-dft-sb. csh pw91 N
כאשר pw91 מציין שנעשה שימוש בצפיפות הPW91, ו-N הוא מספר האטומים באשכול. שתיצור קובץ בשם rotConstsData_C. - כעת זהה את המבנים הייחודיים באמצעות הפקודה:
similarityAnalysis.py sb rotConstsData_C
כאשר sb משמש כתווית למתן שמות קבצים. כעת תהיה רשימה של תצורות ייחודיות הממוטב ברמת PW91/6-31 + G * התיאוריה שנשמרה בקובץ uniqueStructures-sb. data.
- חלץ את האנרגיות וחשב את הקבועים הרוטציה של האשכולות הממוטבים בסיס קטן באמצעות הפקודה:
- גש לספרייה הראשית -h2o-n/QM ותשלב את התוצאות ממספר מסלולים של QM מרובים באמצעות script combine-QM. csh . התחביר הוא:
combine-QM. csh < תווית > < רשימת הספריות עם ה-QM calcs >
במקרה ספציפי זה, הפקודה:
combine-QM. csh sb pw91-sb
יפיק רשימה חדשה של מבנים ייחודיים בשם 'uniqueStructures-sb. data' בספרייה הזאת -h2o-n/QM .
4. עידון נוסף באמצעות שיטת QM עם ערכת בסיס גדולה
הערה: המטרה כאן היא לחדד עוד יותר את הדגימות המבצעות של ה-H2O)n = 1-5 אשכולות באמצעות תיאור קוונטי טוב יותר מכני. המבנים המתחילים עבור שלב זה הם התפוקות של שלב 3.
- שליחת חישובים אמינים יותר באמצעות ערכת בסיס גדולה יותר.
- צור ספריית מע בשם pw91-lb תחת ספריית QM .
- העתק את רשימת המבנים הייחודיים (uniqueStructures-sb. data) מתוך הספרייה הראשית -h2o-n/qm לספריה הזאת -H2O-ליברות/qm/pw91-lb ולשנות את הספריה.
- הפעל את הסקריפט בסיס גדול DFT מבצעות דגימה עם הפקודה:
run-pw91-lb. csh uniqueStructures-sb. נתונים תור ליברות 10
כאשר lb הוא תווית עבור קבוצת חישובים זו, התור הוא התור המועדף באשכול המחשוב ו-10 מציין ש-10 חישובים יקובצו למשימת אצווה אחת. קובץ script זה יפיק באופן אוטומטי את הקלט עבור גאוס 09 ויגיש את כל החישובים. הזן ' מבחן ' עבור ' תור ' כדי לבצע בדיקות לרוץ יבש.
- לאחר השלמת החישובים שהוגשו, חלץ ונתח את הנתונים
- חשב את הקבועים הסיבוב של האשכולות המותאמים לבסיס הגדול באמצעות הפקודה:
getRotConsts-dft-lb. csh pw91 N
כאשר pw91 מציין שנעשה שימוש בצפיפות הPW91, ו-N הוא מספר האטומים באשכול. - כעת זהה את המבנים הייחודיים באמצעות הפקודה:
similarityAnalysis.py ליברות rotConstsData_C
כאשר lb משמש כתווית למתן שמות קבצים. כעת יש לך רשימה של תצורות ייחודיות אופטימיזציה ב PW91/6-311 + + G * * רמת התיאוריה שנשמרה בקובץ uniqueStructures-lb. data.
- חשב את הקבועים הסיבוב של האשכולות המותאמים לבסיס הגדול באמצעות הפקודה:
5. סופי אנרגיה וחישובי תיקון תרמודינמי
הערה: המטרה כאן היא להשיג את המבנה והאנרגיות של מבנה הרטט (H2O)n = 1-5 אשכולות באמצעות ערכת בסיס גדולה ורשת אינטגרציה בעלת בדיקת אולטרה-כימית כדי לחשב את התיקונים הרצויים התרמוכימיים.
- החל בתוצאות מהשלב הקודם, שלח חישובים אמינים יותר.
- צור ספריית מע הנקראת ultrafine תחת הספריה QM/pw91-lb. לאחר מכן העתק את רשימת המבנים הייחודיים (uniqueStructures-lb. data) מהספריה qm/pw91-Lb לספריה qm/pw91-lb/ultrafine ושנה לספריה זו.
- שלח את קובץ ה-DFT הגדול במיוחד בעזרת הפקודה:
run-pw91-lb-ultrafine. csh uniqueStructures-lb. התור לנתונים 10
כאשר uf היא תווית עבור קבוצת חישובים זו, התור הוא התור המועדף באשכול המחשוב ו-10 מציין ש-10 חישובים יקובצו למשימת אצווה אחת. קובץ script זה יפיק באופן אוטומטי את הקלט עבור גאוס 09 ויגיש את כל החישובים. הזן ' מבחן ' עבור ' תור ' כדי לבצע בדיקות לרוץ יבש.
- לאחר השלמת החישובים שהוגשו, חלץ ונתח את הנתונים
- חלץ את האנרגיות וחשב את הקבועים הרוטציה של האשכולות המותאמים לבסיס הגדול באמצעות הפקודה:
getRotConsts-dft-lb-ultrafine. csh pw91 N
כאשר pw91 מציין שנעשה שימוש בצפיפות הPW91, ו-N הוא מספר האטומים באשכול. - כעת זהה את המבנים הייחודיים באמצעות הפקודה:
similarityAnalysis.py uf rotConstsData_C
כאשר uf משמש כתווית למתן שמות קבצים. כעת יש לך רשימה של תצורות ייחודיות ממוטבת ב PW91/6-311 + + G * * רמת התיאוריה שנשמרה בקובץ uniqueStructures-uf. data.
- חלץ את האנרגיות וחשב את הקבועים הרוטציה של האשכולות המותאמים לבסיס הגדול באמצעות הפקודה:
- בצע חילוץ סופי של מידע הדרוש לחישוב תיקוני תרמודינמיים. השתמש במידע זה כדי לחשב את התיקונים התרמודינמיים.
- חלץ את האנרגיות האלקטרוניות הסופיות, הקבועים והתדרים התנובותית, והשתמש בהם לחישוב תיקוני תרמודינמיים באמצעות הפקודה:
run-thermo-pw91. csh uniqueStructures-uf. נתונים - העתק/הדבק את פלט שורת הפקודה לגיליון 'Raw_Energies' בגיליון האלקטרוני של Excel בשם 'gly-h2o-n. xlsx'. אתה צריך לעשות את זה עבור ונומרים (גליצין ומים), כמו גם חבר האנרגיה הנמוך ביותר של כל מימה (בסדר-h2o-n, שם n = 1, 2,...).
- כאשר האנרגיות הגולמי מתווספות לגיליון הראשון של הגיליון האלקטרוני 'gly-h2o-n. xlsx', הגליונות הבאים של 'Binding_Energies'ו'Hydrate_Distribution' מתעדכנים אוטומטית. בפרט, הגיליון 'Hydrate_Distribution' מניב ריכוז שיווי משקל של הידרטים בטמפרטורות שונות (למשל. 298.15 k), לחות יחסית (20%, 50%, 100%) וריכוזים ראשוניים של מים ([H2O]) ו גליצין ([גליצין]). התיאוריה שמאחורי חישובים אלה מתוארת בשלב הבא.
- חלץ את האנרגיות האלקטרוניות הסופיות, הקבועים והתדרים התנובותית, והשתמש בהם לחישוב תיקוני תרמודינמיים באמצעות הפקודה:
6. ריכוזים אטמוספריים של מיחשוב (H2O)n = 0-5 אשכולות בטמפרטורת החדר במפלס הים
הערה: פעולה זו מבוצעת על-ידי העתקת הנתונים התרמודינמיים שנוצרו בשלב הקודם לגיליון אלקטרוני וחישוב האנרגיות החופשיות של גיבס של מחות רציפים. לאחר מכן, האנרגיות החופשיות של גיבס משמשות לחישוב קבועים של שיווי משקל עבור כל מחות רציפים. לבסוף, קבוצה של משוואות לינאריות נפתרות כדי לקבל את ריכוז האיזון של הידרטים עבור ריכוז נתון של מונמרים, טמפרטורה ולחץ.
- התחל על ידי הגדרת מערכת של יוויי כימיים עבור הידרציה רציפה של גליצין כמוצג להלן:
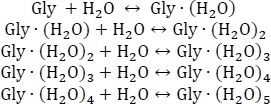
- לחשב את הקבועים שיווי משקל kn באמצעות kn = e-ΔGn/(KBT), כאשר n הוא הרמה של שתיה, ΔGn הוא שינוי אנרגיה של גיבס חינם של תגובת השתיהn, KB הוא קבוע של בולצמן, ו T הוא טמפרטורה.
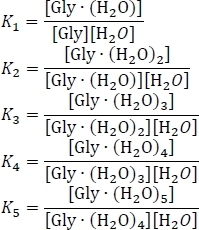
- הגדר את המשוואה לשימור מסה, תוך שימוש בהנחה כי סכום ריכוזי השיווי משקל של אשכולות הנוזלים והלא-מנוזלים שווים לריכוז הראשוני של גליצין מבודד [מכוער]0. שכתב מערכת זו של שש משוואות בו, תוך שימוש בסידור אלגברי של הביטויים הקבועים של שיווי משקל, כ
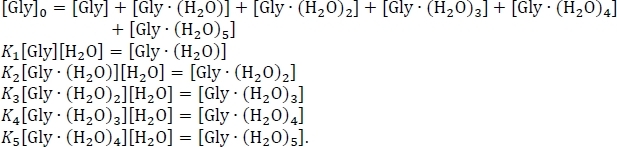
- לפתור את המערכת של משוואות המוצג לעיל כדי לקבל את ריכוזי שיווי משקל של מאוד (H2O)n = 0-5 באמצעות ערך ניסיוני56,57,58 לריכוז של גליצין באטמוספירה, [מכוער]0 = 2.9 x 106 ס"מ-3, ואת ריכוז המים באטמוספירה ב 100% לחות יחסית וטמפרטורה של 298.15 K59, [H2O] = 7.7 x 1017 ס"מ-3.
תוצאות
הסט הראשון של התוצאות מפרוטוקול זה צריך להיות קבוצה של מבנים בעלי אנרגיה נמוכה (H2O)n = 1-5 נמצא באמצעות הליך הדגימה מבצעות. מבנים אלה כבר אופטימיזציה ב PW91/6-311 + + G * * ברמה של התיאוריה הם הניחו להיות מדויקים למטרת הנייר הזה. אין ראיות להציע כי PW91/6-311 + + G * * בעקביות הערכות או מעריכים את האנרגיה המחייב של אשכולות אלה. יכולתה לנבא אנרגיות מחייבות ביחס ל-MP2/cbs32 ו [dlpno-] ccsd (T)/cbs60,61 האומדנים והניסוי52 מראה הרבה תנודות. הדבר נכון גם לגבי מרבית הפונקציונלים האחרים. באופן כללי, כל ערך של n = 1 – 5 אמור להניב קומץ של מבנים בעלי אנרגיה נמוכה בטווח של כ-5 קק ל מול1 של מבנה האנרגיה הנמוכה ביותר. כאן, אנו מתמקדים במבנה הראשון שהופק על ידי סקריפט run-thermo-pw91. csh לקיצור. איור 3 מראה את האנרגיה החשמלית הנמוכה ביותר של איזומטר (H2O)n = 0-5 אשכולות. ניתן לראות כי הרשת קשר מימן גדל במורכבות כמו מספר מולקולות מים עליות, ואפילו עובר מרשת מישורי בעיקר למבנה תלת מימדי כמו כלוב ב n = 5. שאר הטקסט משתמש באנרגיות ובכמויות תרמודינמיים המתאימות לחמשת האשכולות הספציפיים.
טבלה 1 מכילה את הכמויות התרמודינמיים הדרושות לביצוע הפרוטוקול. Table 2 מציג דוגמה לפלט של הסקריפט run-thermo-pw91. csh שבו האנרגיות האלקטרוניות, הרטט תיקונים בנקודות אפס, והתיקונים התרמודינמיים בשלוש טמפרטורות שונות מודפסים. עבור כל אשכול (שורה), E [PW91/6-311 + + g * *] מתאים את האנרגיות האלקטרוניות של שלב הדלק ב PW91/6-311 + + g * * ברמת התאוריה המחושבת על רשתות שילוב ultrafine ביחידות של hartree, כמו גם אנרגיה ויברציה של נקודת אפס (zpve) ביחידות של קק ל-1 בכל טמפרטורה, 216.65 K, 273.15 K, ו 298.15 K, התיקונים התרמודינמיים מפורטים, ∆ H האנתלפיית של היווצרות ביחידות של קק ל-1, S האנטרופיה של היווצרות יחידות של Cal מול-1, ו ∆ G של גיבס אנרגיה חופשית של היווצרות ביחידות של קק ל-1. טבלה 3 מראה חישוב לדוגמה של השינוי הכולל של גיבס אנרגיה חופשית של לחות, כמו גם עבור מחות רציפה. מיחשוב לדוגמה של השינוי הכולל של גיבס באנרגיה חופשית של מחות לתגובה
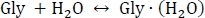
מתחיל במחשוב של אנרגיה אלקטרונית EPW91 as
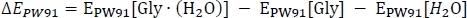
כאשר EPW91[מ∙ (H 2O)] נלקח מטבלה 2 עמודה C, ו-ePW91[מכוערת] ו-ePW91[H2O] נלקחים מטבלה 1 טור B. לאחר מכן אנו מחשבים את השלב הכולל הגז האנרגיה שינוי ΔE(0) על-ידי כלילת השינוי באנרגיה רטט נקודת אפס של התגובה כמו
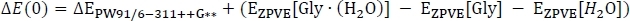
כדי לקבל עמודה D. כאן, ΔEPW91/6-311 + + G * * נלקח מטבלה 3 עמודה C, Ezpve[מאוד ∙ (H2O)] מטבלה 2 עמודה D, ו-EZpve[מכוערת] ו-ezpve[H2O] מטבלה 1 עמודה C. למען הקיצור, אנחנו נתקדם לתוך אשכולות טמפרטורת החדר, אז אנחנו לדלג על 216.65 K ו 273.15 K נתונים. בטמפרטורת החדר, אנו לאחר מכן לחשב את השינוי אנתלפיה של התגובה ΔH על ידי תיקון האנרגיה שלב שינוי בצריכת הגז כמו
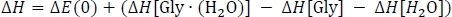
כאשרΔ E(0) נלקח מטבלה 3 עמודה D, ΔH[מאוד ∙ (h2O)] נלקח מטבלה 2 עמודה K, ו Δh[מכוערת] ו-Δh[H2O] נלקחים מטבלה 1 טור J. לבסוף, אנו מחשבים את שינוי האנרגיה של גיבס חינם של התגובה ΔG כמו
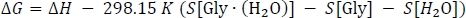
כאשרΔ H נלקח מטבלה 3 עמודה אני, s[מ∙ (h2o)] נלקח מטבלה 2 עמודה L , ו-s [השני] ו -s[h2 o] נלקחים מטבלה 1 עמודה K. שים לב שערכי האנטרופיה חייבים להיות מומרים ליחידות של קק ל מול1 K- 1 במהלך שלב זה.
כעת יש לנו את הכמויות הדרושות כדי לחשב את ריכוזי האטמוספירה של גליצין הרטוב כפי שמוצג בשלב 6. התוצאות אמורות להידמות לנתונים המוצגים בטבלה 4, אך יש לצפות בהבדלים מספריים קטנים. טבלה 4 מראה את ריכוזי שיווי משקל שנמצאו מתוך ניסוח של מערכת של שש משוואות בשלב 6.2 לתוך משוואת מטריצה אחת והפתרון הבא שלה. אנו מתחילים בהכרה בכך שמערכת המשוואות יכולה להיכתב כ
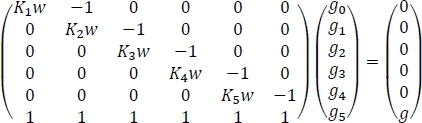
כאשר Kn הוא קבוע שיווי משקל עבור המיםהרציפים של גליצין, w הוא ריכוז המים באטמוספירה, g הוא הריכוז הראשוני של גליצין מבודדים באטמוספירה, ו- gn הוא ריכוז שיווי משקל של מאוזן (H2O)n. אם נשכתב את המשוואה לעיל כ- Ax = b, נקבל x = a-1b שבו a-1 הוא ההופכי של מטריצה a. ניתן לחשב היפוך זה בקלות באמצעות פונקציות מוכללות של גליונות אלקטרוניים כפי שמוצג בטבלה 4 כדי לקבל את התוצאות הסופיות.
איור 4 מראה את הריכוז השיווי משקל של גליצין הרטוב מחושב בטבלה 4 כפונקציה של טמפרטורה ב 100% לחות יחסית ו 1 לחץ אטמוספרה. זה מראה כי, כמו הטמפרטורה יורדת מ 298.15 K כדי 216.65 K, את הריכוז של גליצין בלתי מנוזלים (n = 0) פוחתת ואלה של הגדלת גליצין רטוב. גליצין דימים (n = 2) במיוחד מגדיל באופן דרמטי עם ירידה בטמפרטורה בעוד השינוי בריכוז של הידרטים אחרים הוא מורגש פחות. הקורלציה ההפוכה בין טמפרטורה לבין ריכוז מימה היא עקבית עם הציפייה כי התחתון אנרגיה חופשית של גיבס של הידרסים בטמפרטורות נמוכות יותר לטובת היווצרות של הידרטים.
איור 5 ממחיש את התלות היחסית לחות של ריכוז האיזון של גליצין הידרוטים ב 298.15 k ו 1 לחץ האטמוספירה. זה בבירור מוכיח כי כמו RH עולה מ 20% עד 100%, הריכוז של הידרטים (n > 0) להגדיל על חשבון של גליצין בלתי רטוב (n = 0). שוב הקורלציה הישירה בין הלחות היחסית והריכוז של הידרטים היא עקבית עם הרעיון כי הנוכחות של מולקולות מים יותר ב-RH גבוה יותר מקדמת את היווצרות של הידרטים.
בהתאם למוצג, פרוטוקול זה נותן הבנה איכותית של אוכלוסיות גליצין הרטוב באטמוספירה. בהנחה הריכוז הראשוני של גליצין מבודד של 2,900,000 מולקולות לסנטימטר מעוקב, אנו רואים כי גליצין לא רטוב (n = 0) הוא המינים הנפוצים ביותר ביותר ברוב התנאים למעט T = 216.65 K ו RH = 100%. הדימיים (n = 2), אשר יש הרציף הנמוך ביותר של גיבס אנרגיה חופשית של לחות בכל שלוש הטמפרטורות, הוא מימה הנפוץ ביותר בתנאים הנחשבים כאן. המונמים (n = 1) והידרטים גדולים יותר (n ≥ 3) צפויים להימצא בכמויות זניח. לאחר בדיקה של איור 3, השפע של n = 1 – 4 אשכולות יכול להיות קשור ליציבות ולמתח ברשת קשר מימן של אשכולות. אשכולות אלה יש את מולקולות המים מימן בונדד החומצה קרבוקסילית של גליצין בגיאומטריה הקרובה דומה לאלה של מבנים שונים מימן בונדד טבעת, מה שהופך אותם יציבים במיוחד.
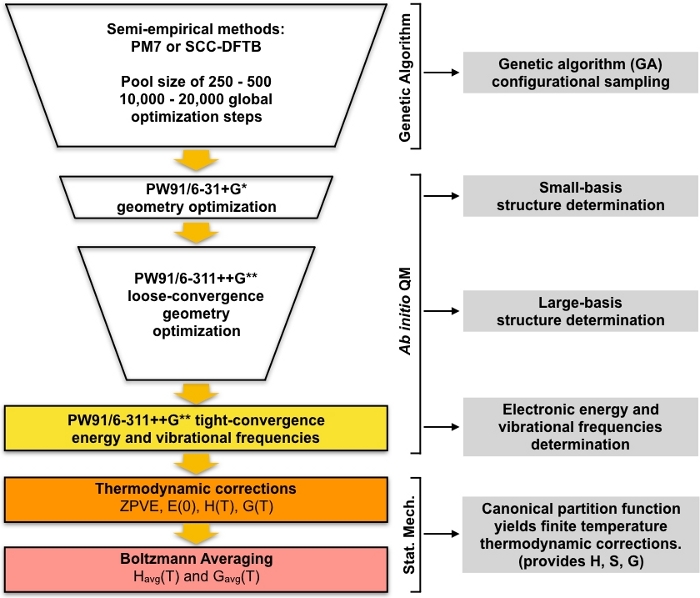
איור 1: תיאור סכמטי של הפרוצדורה הנוכחית. בריכה גדולה של מבנים לנחש שנוצר על ידי האלגוריתם הגנטי (GA) הוא מעודן על ידי סדרה של מיטוב הגיאומטריה PW91 עד קבוצה של מבנים התכנס מתקבלים. תדרי הרטט של מבנים אלה מחושבים ומשמשים לחישוב האנרגיה החופשית של גיבס היווצרות, אשר בתורו משמש לחישוב ריכוזי שיווי משקל של אשכולות בתנאי הסביבה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
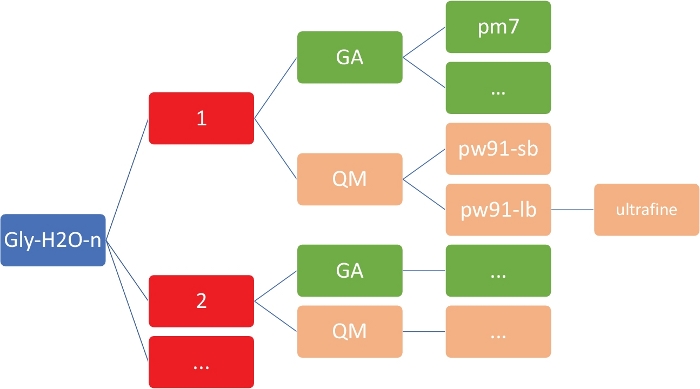
איור 2: מבנה הספריות המייצג עבור כל אשכול. הסקריפטים בתוך הבית הכלולים בפרוטוקול זה דורשים את מבנה הספריות המוצג לעיל, כאשר n הוא מספר מולקולות מים. עבור כל n ב -לנגלי-h2o-n, קיימות ספריות המשנה הבאות: ga עבור אלגוריתם גנטי עם מדריך GA/PM7, QM עבור מכניקת הקוונטים עם QM/pw91-SB עבור pw91/6-31 + g *, QM/pw91-LB עבור pw91/6-311 + + G *, ו QM/pw91-lb/ultrafine עבור אופטימיזציות וויברציה הסופי על רשתות אינטגרציה ultrafine. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
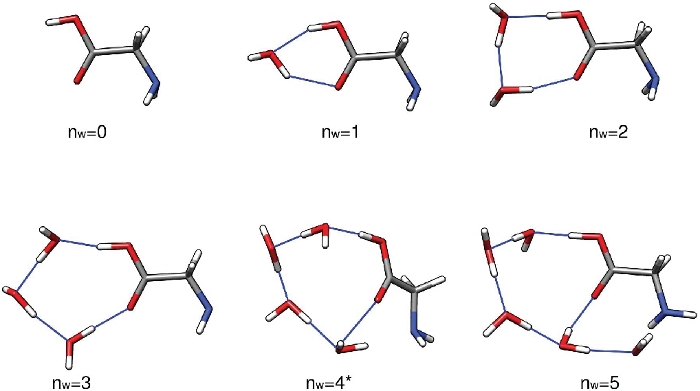
איור 3: נציג מבני אנרגיה נמוכה ביותר (H2O)n = 0-5. אשכולות אלה היו אנרגיה אלקטרונית קיצון גלובל אופטימיזציה ב PW91/6-311 + + G * רמה של תיאוריה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
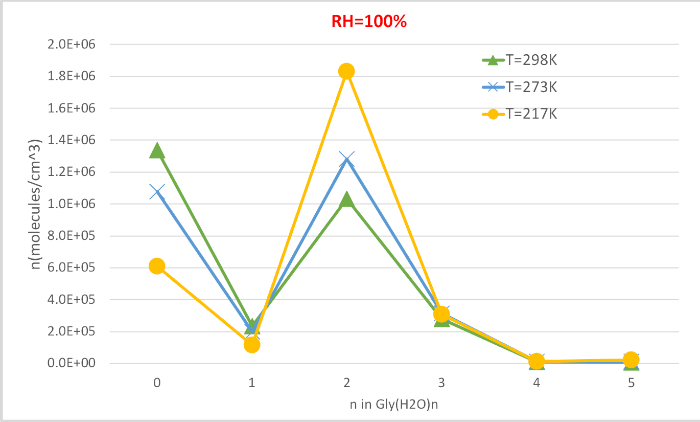
איור 4: התלות בטמפ ' (H2O)n = 0-5 כ- 100% לחות יחסית ולחץ כספומט אחד. ריכוז הידרטים ניתן ביחידות של מולקולות ס"מ-3. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
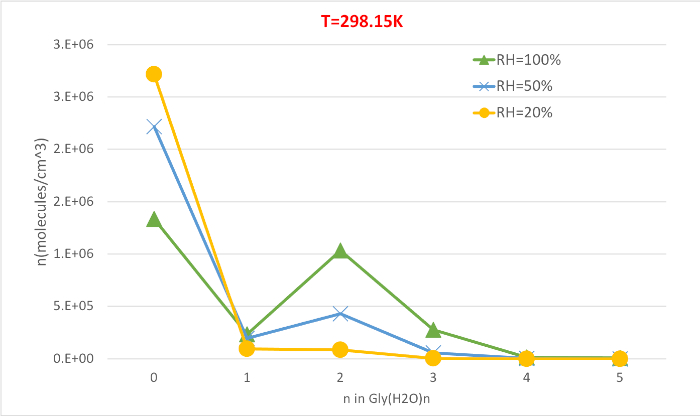
איור 5: התלות בלחות יחסית של השעה (H2O)n = 0-5 כ- 298.15 K ו-1 לחץ כספומט. ריכוז הידרטים ניתן ביחידות של מולקולות ס"מ-3. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.
| E [PW91/6-311 + + G * *] | 216.65 K | 273.15 K | 298.15 K | ||||||||
| ליברות-UF | מיכל הורנשטיין | ∆ H | S | ∆ G | ∆ H | S | ∆ G | ∆ H | S | ∆ G | |
| מים | -76.430500 | 13.04 | 1.72 | 42.59 | 5.54 | 2.17 | 44.44 | 3.08 | 2.37 | 45.14 | 1.96 |
| גליצין | -284.434838 | 48.55 | 2.65 | 69.53 | 36.14 | 3.70 | 73.81 | 32.09 | 4.22 | 75.61 | 30.22 |
שולחן 1: אנרגיות מונומר. אנרגיות אלקטרוניות נמצאות ביחידות של הארטרי ואילו כל הכמויות האחרות נמצאות ביחידות של קק ל מול-1. מים וגליצין היו ממוטבים ב-PW91/6-311 + + G * * ברמת התאוריה והרטט תדרים. תיקונים תרמודינמיים עבור לחץ של 1 כספומט וטמפרטורה של 298.15 K חושבו באמצעות script thermo.pl.
| E [PW91/6-311 + + G * *] | היכל האפס | 216.65 K | 273.15 K | 298.15 K | ||||||||
| n | שם | ליברות-UF | מיכל הורנשטיין | ∆ H | S | ∆ G | ∆ H | S | ∆ G | ∆ H | S | ∆ G |
| 1 | ובכן-h2o-1 | -360.88481 | 63.96 | 3.61 | 80.12 | 50.22 | 5.12 | 86.27 | 45.52 | 5.85 | 88.83 | 43.33 |
| 2 | ובכן-h2o-2 | -437.33763 | 79.33 | 4.53 | 90.86 | 64.17 | 6.46 | 98.78 | 58.81 | 7.40 | 102.06 | 56.30 |
| 3 | ובכן-h2o-3 | -513.78620 | 94.52 | 5.67 | 105.08 | 77.42 | 8.08 | 114.94 | 71.19 | 9.23 | 119.00 | 68.27 |
| 4 | -h2o-4 | -590.23667 | 109.80 | 6.03 | 104.98 | 91.30 | 8.78 | 116.21 | 84.40 | 10.11 | 120.87 | 81.14 |
| מיכל 5 | -h2o-5 | -666.68845 | 125.80 | 7.26 | 121.70 | 106.69 | 10.47 | 134.83 | 99.44 | 12.01 | 140.24 | 96.00 |
טבלה 2: אנרגיות מצרר. האנרגיות של האנרגיה הנמוכה ביותר (H2O)n = 1-5 מבנים שנמצאו תוך שימוש בהליך המתואר באיור 1. אנרגיות אלקטרוניות נמצאות ביחידות של הארטרי ואילו כל הכמויות האחרות נמצאות ביחידות של קק ל מול-1.
| כולל לחות: בnH2O + מ<-> מכוערת (H2O) n | לחות רציפה: מאוד (H2O) n-1 + H2O <-> (H2O) n | ||||||||||||||||
| E [PW91/6-311 + + G * *] | 216.65 | 273.15 | 298.15 | 216.65 | 273.15 | 298.15 | |||||||||||
| n | שם מערכת | ליברות-UF | ∆ E (0) | ∆ H (T) | ∆ G (T) | ∆ H (T) | ∆ G (T) | ∆ H (T) | ∆ G (T) | ליברות-UF | ∆ E (0) | ∆ H (T) | ∆ G (T) | H (T) | ∆ G (T) | ∆ H (T) | ∆ G (T) |
| 1 | ובכן-h2o-1 | -12.22 | -9.85 | -10.61 | -3.68 | -10.61 | -1.87 | -10.59 | -1.07 | -12.22 | -9.85 | -10.61 | -3.68 | -10.61 | -1.87 | -10.59 | -1.07 |
| 2 | ובכן-h2o-2 | -26.22 | -21.53 | -23.10 | -9.27 | -23.11 | -5.66 | -23.09 | -4.06 | -14.00 | -11.68 | -12.49 | -5.59 | -12.50 | -3.79 | -12.50 | -2.99 |
| 3 | ובכן-h2o-3 | -37.56 | -30.72 | -32.88 | -12.90 | -32.87 | -7.69 | -32.82 | -5.38 | -11.34 | -9.19 | -9.78 | -3.63 | -9.76 | -2.03 | -9.73 | -1.32 |
| 4 | -h2o-4 | -50.10 | -40.34 | -43.48 | -15.87 | -43.54 | -8.71 | -43.51 | -5.55 | -12.54 | -9.62 | -10.60 | -2.97 | -10.67 | -1.02 | -10.69 | -0.17 |
| מיכל 5 | -h2o-5 | -63.45 | -51.41 | -55.42 | -20.58 | -55.51 | -11.48 | -55.48 | -7.45 | -13.35 | -11.07 | -11.94 | -4.71 | -11.97 | -2.77 | -11.97 | -1.90 |
שולחן 3: אנרגיות מלחות. האנרגיה הכוללת של הידרציה והאנרגיה של הידרציה רציפה (H2O)n = 1-5 ביחידות של קק ל מול-1. כאן, E [PW91/6-311 + + G * *] הוא השינוי באנרגיה האלקטרונית, ∆ E (0) הוא האנרגיה ויברציה של נקודת אפס (zpve) מתוקן שינוי באנרגיה, ∆ H (t) הוא שינוי אנתלפיה בטמפרטורה T, ו ∆ G (t) הוא שינוי אנרגיה של גיבס חינם של שחות של כל מכוערת (H2O)n = 1-5 אשכול.
| שיווי משקל התפלגות מימה כפונקציה של טמפרטורה ולחות יחסית | |||||||||
| T = 298.15 K | T = 273.15 K | T = 216.65 K | |||||||
| בשבילך (H2O) n | RH = 100% | RH = 50% | RH = 20% | RH = 100% | RH = 50% | RH = 20% | RH = 100% | RH = 50% | RH = 20% |
| 0 | 1.3 e + 06 | 2.2 e + 06 | 2.7 e + 06 | 1.1 e + 06 | 2.0 e + 06 | 2.7 e + 06 | 6.1 e + 05 | 1.5 e + 06 | 2.5 e + 06 |
| 1 | 2.3 e + 05 | 1.9 e + 05 | 9.5 e + 04 | 2.0 e + 05 | 1.9 e + 05 | 9.9 e + 04 | 1.2 e + 05 | 1.5 e + 05 | 9.5 e + 04 |
| 2 | 1.0 e + 06 | 4.3 e + 05 | 8.4 e + 04 | 1.3 e + 06 | 6.1 e + 05 | 1.3 e + 05 | 1.8 e + 06 | 1.1 e + 06 | 3.0 e + 05 |
| 3 | 2.8 e + 05 | 5.8 e + 04 | 4.5 e + 03 | 3.2 e + 05 | 7.4 e + 04 | 6.3 e + 03 | 3.1 e + 05 | 9.6 e + 04 | 1.0 e + 04 |
| 4 | 1.1 e + 04 | 1.1 e + 03 | 3.4 e + 01 | 1.3 e + 04 | 1.5 e + 03 | 5.0 e + 01 | 1.1 e + 04 | 1.8 e + 03 | 7.5 e + 01 |
| מיכל 5 | 7.5 e + 03 | 3.9 e + 02 | 4.9 e + 00 | 1.2 e + 04 | 7.2 e + 02 | 9.7 e + 00 | 2.4 e + 04 | 1.9 e + 03 | 3.1 e + 01 |
שולחן 4: שיווי משקל ריכוזי מימה של מאוד (H2O)n = 0-5 כטמפרטורת פונקציה (T = 298.15 k, 273.15 k, 216.65 k) ולחות יחסית (RH = 100%, 50%, 20%). ריכוז הידרטים ניתן ביחידות של מולקולות cm-3 בהנחה ערכים ניסיוניים56,57,58, of [מכוערת]0 = 2.9 x 106 ס"מ-3 ו [H2O] = 7.7 x 1017 ס"מ-3, 1.6 x 1017 ס"מ-3 ו- 9.9 x 1014 ס"מ-3 ב 100% לחות יחסית ו T = 298.15 k, 273.15 k, ו 216.65 k, בהתאמה59.
קבצים משלימים. אנא לחץ כאן כדי להוריד קבצים אלה.
Discussion
הדיוק של הנתונים שנוצרו על-ידי פרוטוקול זה תלוי בעיקר בשלושה דברים: (i) מגוון התצורות שנדגמו על-ידי שלב 2, (ii) הדיוק של המבנה האלקטרוני של המערכת, (iii) והדיוק של התיקונים התרמודינמיים. ניתן לטפל בכל אחד מהגורמים הללו על-ידי שינוי השיטה על-ידי עריכת קבצי ה-script הכלולים. הגורם הראשון הוא בקלות להתגבר עם שימוש במאגר הראשונית גדול יותר של מבנים שנוצר באופן אקראי, חזרות רבות יותר של ה-GA, והגדרה משוחרר יותר של הקריטריונים המעורבים ב-GA. בנוסף, ניתן להשתמש בשיטה שונה למחצה אמפירית, כגון צפיפות עצמית לחיוב-הכריכה הדוקה (SCC-DFTB)62 דגם ופוטנציאל הרסיס האפקטיבי (efp)63 דגם כדי לחקור את ההשפעות של תיאורים פיזיים שונים. המגבלה העיקרית כאן היא חוסר היכולת של השיטה כדי ליצור או לשבור קשרים קוולנטי, כלומר ונומרים קפואים. הליך ה-GA מוצא את התנוחות היחסיות היציבות ביותר של המונמרים הקפואים האלה בהתאם לתיאור החצי-אמפירי.
הדיוק של המבנה האלקטרוני של המערכת ניתן לשפר במגוון דרכים, כל אחד עם עלות חישובית שלה. ניתן לבחור בצפיפות טובה יותר, כגון M06-2x64 ו-wB97X-V 65, או שיטה קוונטית מכנית (QM), כגון מולר-פלסט66,67,ב68 (mpn) ובשילוב שיטות ביחד-אשכול69 (CC), כדי לשפר את התיאור הפיזי של המערכת. בהיררכיה של הפונקציונאלים, הביצועים משתפרים בדרך כלל על המעבר מתוך מערך מדומה של מעבר הדרגתי (GGA) ומתפקד כמו PW91 לגבי פונקציונלים מופרדים בטווח כגון פונקציונליות היברידית wB97X-D ו-meta-GGA כמו M06-2X.
החיסרון של שיטות DFT הוא שהתכנסות שיטתית כלפי ערך מדויק אינה אפשרית; עם זאת, שיטות DFT זולות מבחינה חישובית ויש מגוון רחב של פונקציונלים למגוון רחב של יישומים.
אנרגיות המחושבות באמצעות שיטות של פונקציית גל כגון MP2 ו-CCSD (T) בשילוב עם ערכות מתאם עקביות בסיס מספר הקרדינל הגדל ([אוג-] cc-pV [D, T, Q,...] Z) מתכנסים לקראת המגבלה שלהם להגדיר בסיס שיטתי, אבל העלות החישובית של כל חישוב הופך אוסרני כמו גודל המערכת גדל. עידון נוסף של המבנה האלקטרוני ניתן לבצע באמצעות ערכות בסיס בקורלציה מפורשת70 ועל ידי הארכת להגדיר בסיס שלם (CBS)71 הגבלה. העבודה האחרונה שלנו עולה כי צפיפות מותאם במפורש בקורלציה מפורשת בסדר השני (DF-MP2-F12) פרעתיות גישה מניב אנרגיות מתקרב זה של MP2/CBS חישובים32. שינוי הפרוטוקול הנוכחי לשימוש בשיטות מבנה אלקטרוניות שונות כרוך בשני שלבים: (i) להכין קובץ קלט של תבנית בעקבות התחביר שניתן על-ידי התוכנה, (ii) ולערוך את קבצי ה -run-pw91-sb. csh, run-pw91-lb. csh וrun-pw91-lb-ultrafine. csh כדי להפיק את התחביר הנכון של קובץ הקלט,
לבסוף, רמת הדיוק של התיקונים התרמודינמיים תלויה בשיטת המבנה האלקטרונית, כמו גם בתיאור של ה-PES סביב המינימום הגלובלי. תיאור מדויק של ה-pes דורש את המיחשוב של נגזרים מסדר שלישי וגבוה יותר של ה-pes ביחס לdisplacements בדרגות הגרעיניות של החופש, כגון שדה הכוח הקווארטי72,73 (qff), שהוא משימה יקרה במיוחד. הפרוטוקול הנוכחי משתמש הערכה מתנד הרמוני על תדרי רטט, וכתוצאה מכך הצורך לחשב רק עד הנגזרות השני של פסי. גישה זו הופכת להיות בעייתית במערכות עם אנהרמוניה גבוהה, כגון מולקולות מאוד מאוד ופוטנציאליות סימטרית כפולה, בשל ההבדל הגדול ב-PES האמיתי ובפס הרמוני. יתר על כן, העלות של בעל איכות גבוהה PES מתוך שיטת המבנה האלקטרוני תובעניים מבחינה חישובית רק תרכובות בעיה של עלות לחישובי תדירות ויברליות. גישה אחת כדי להתגבר על זה היא להשתמש באנרגיות האלקטרוניות מתוך חישוב מבנה אלקטרוני באיכות גבוהה יחד עם תדירויות ויברליות שחושבו על פסי איכות נמוכה יותר, וכתוצאה מכך איזון בין עלות ודיוק. ניתן לשנות את הפרוטוקול הנוכחי כדי להשתמש בתיאורי PES שונים כמתואר בפיסקה הקודמת; עם זאת, ניתן גם לערוך את מילות החיפוש בתדירות הרטט בסקריפטים ובתבניות כדי לחשב תדרים הרמוניים ויברtional.
שני נושאים קריטיים עבור כל פרוטוקול דגימה מבצעות הם השיטה הראשונית לדגימת משטח האנרגיה הפוטנציאלי והקריטריונים המשמשים לזיהוי כל אשכול. עשינו שימוש נרחב במגוון שיטות בעבודתנו הקודמת. בגיליון הראשון, השיטה הראשונית לדגימת משטח האנרגיה הפוטנציאלי, עשינו את הבחירה בשימוש ב-GA עם שיטות חצי-אמפילתיות המבוססות על גורמים אלה. מבצעות דיגום באמצעות אינטואיציה כימית26, דגימה אקראית, ודינמיקה מולקולרית (MD)29,30, לא למצוא הבנה גלובל קיצון באופן קבוע עבור אשכולות גדולים יותר 10 monomers, כפי שצפינו במחקרים שלנו של אשכולות מים18. השתמשנו בהצלחה מקפץ באגן (BH) כדי ללמוד את PES מורכבים של (H2O)1174, אבל זה דרש את ההכללה הידנית של כמה פוטנציאלי אנרגיה נמוכה איזוers האלגוריתם BH לא מצא. השוואה של הביצועים של BH ו-GA במציאת המינימום הגלובלי של אשכולות מים, (H2O)n = 10-20 הפגינו כי GA בעקביות למצוא את המינימום הגלובלי מהר יותר מאשר BH75. GA כפי שיושם ב-OGOLEM גולם ו אשכול הוא רב-תכליתי מאוד, כי זה יכול להיות מיושם על כל אשכול מולקולרי והוא יכול ממשק עם מספר עצום של חבילות עם שדה כוח קלאסי, חצי אמפירי, צפיפות תפקודית, ויכולות ab מאותחל . הבחירה של PM7 היא מונעת על ידי המהירות שלה ודיוק סביר. כמעט לכל שיטה אחרת למחצה אמפירית היה עלות חישובית גבוהה באופן משמעותי.
באשר לסוגיה השנייה, בחנו באמצעות קריטריונים שונים כדי לזהות מבנים ייחודיים החל מאנרגיות אלקטרוניות, רגעים דיפול, חפיפה של RMSDs וקבועים סיבוב. באמצעות רגעים דיפול הוכיחה קשה, כי הן מרכיבי הרגע דיפול היו תלויים באוריינטציה של המולקולה ואת הרגע דיפול הכולל היה רגיש מאוד הבדלים הגיאומטריה באופן כזה, כי היה קשה להגדיר את הסף לקבוע מבנים הם אותו או ייחודי. שילוב של אנרגיות אלקטרוניות וקבועים ברוטציה הוכחו כשימושיים ביותר.
הקריטריונים הנוכחיים לתתעב שני מבנים ייחודיים מבוססים על סף הבדלי אנרגיה של 0.10 קק ל מול1 וההפרש התמידי של 1%. לכן, שני מבנים נחשבים שונים אם האנרגיות שלהם שונות יותר מ-0.10 קק ל מול-1 (~ 0.00015 a.u.) וכל אחד משלושת הקבועים שלהם (A, B, C) שונים על-ידי יותר מ-1%. בחינות פנימיות משמעותיות לאורך השנים מצאו את הסכום לבחירה הגיונית. הגישה המבצעות שלנו ומתודולוגיה לסינון הוחל על אשכולות מאוגדים מאוד חלש כגון פחמימנים polyארומטיים משלימה עם מים76,77 כמו גם מאוגד מאוד הידרוארי גופרתי המכילים אמוניה ו אמינים32. עבור אשכולות שבהם יש מדינות פרוטונציה שונות להיחשב, הגישה הטובה ביותר היא להפעיל חישובי GA שונים, כל אחד מתחיל עם ונומרים במדינות פרוטונציה שונות. זה מבטיח כי מבנים עם מדינות פרוטונציה שונות נחשבים בזהירות. עם זאת, חישובי DFT ברמה נמוכה מאפשרים לעתים קרובות פרוטונציה מדינות לשנות במהלך האופטימיזציה של הגיאומטריה, ובכך מניב את המצב היציב ביותר פרוטונציה ללא קשר לגיאומטריה ההתחלתית.
שיטות הדגימה שלנו GA מבצעות צריך לעבוד היטב גם עבור מולקולות תקליטונים כל עוד קודי GA מפנים עם כללי, שיטות ללא פרמטרים המאפשרים ונומרים לאמץ תצורות שונות במהלך הפעלת GA. לדוגמה, ממשק GA עם PM7 יאפשר מבנים של monomers לשנות, אבל אם הקשרים שלהם לשבור כפי שקורה כאשר פרוטונציה מדינות לשנות, המבנים עלולים להיות מושלך כמועמדים לא מקובלים.
שקלנו דרכים שונות לתקן את החסרונות של הקירוב ההרמוני, במיוחד אלה הנובעים מתדרי תנודה נמוכים. השילוב בין הקירוב המדומה למתודולוגיה הנוכחית אינו קשה. עם זאת, יש עדיין שאלות על השיטה המדומה, במיוחד כשמדובר בתדר החיתוך שמתחתיו זה יהיה להחיל. כמו כן, אין עבודות בדיקה קפדנית בוחנת את המהימנות של קירוב מדומה-RRHO, אף על פי שחוכמה קונבנציונלית מרמזת שהיא צריכה להיות שיפור על-פני קירוב RRHO.
הפרוטוקול המוצג כך עשוי להיות כללית לכל מערכת של אשכולות בלתי מאוגדים בשלב הגז מולקולרי הפאזה. ניתן להכליל אותה גם לשימוש בכל שיטה שהיא למחצה אמפירית, שיטת מבנה אלקטרונית ותוכנה, ושיטת ניתוח והתנודה של התוכנה על-ידי עריכת קבצי ה-script והתבניות. ההנחה היא שהמשתמש מרגיש בנוח עם ממשק שורת הפקודה של לינוקס, scripting של פיתון ומחשוב בעלי ביצועים גבוהים. התחביר הלא מוכר והמראה של מערכת ההפעלה Linux וחוסר ניסיון בסקריפטים הוא המכשול הגדול ביותר בפרוטוקול זה, והוא המקום שבו תלמידים חדשים נאבקים ביותר. פרוטוקול זה שימש בהצלחה במגוון יישומים במשך שנים בקבוצה שלנו, בעיקר התמקדות בהשפעות של חומצה גופרתית ואמוניה על היווצרות תרסיס. שיפורים נוספים בפרוטוקול זה יכלול ממשק חזק יותר לתוכנות מבנה אלקטרוני יותר, יישומים חלופיים של האלגוריתם הגנטי, ואולי שימוש בשיטות חדשות יותר לחישובים מהירים יותר של אנרגיות אלקטרוניות ויברליות. היישומים הנוכחיים שלנו בפרוטוקול זה הם בוחנים את החשיבות של חומצות אמינו בשלבים המוקדמים של היווצרות התרסיסים באטמוספירה הנוכחית ובהיווצרות מולקולות ביולוגיות גדולות יותר בסביבות קדם-ביוביוטית.
Disclosures
לא.
Acknowledgements
פרויקט זה נתמך על ידי מענקים צ'ה-1229354, צ'ה-1662030, צ'ה-1721511, ו צ'ה-1903871 מקרן המדע הלאומי (GCS), הפרס המלומד ארנולד ומייבל בקמן (AGG), ומלגת בארי מ. גולדוטר (AGG). נעשה שימוש במשאבי מחשוב בעלי ביצועים גבוהים של קונסורציום מרקורי (http://www.mercuryconsortium.org).
Materials
| Name | Company | Catalog Number | Comments |
| Avogadro | https://avogadro.cc | Open-source molecular visualization program | |
| Gaussian [09/16] Software | http://www.gaussian.com/ | Commercial ab initio electronic structure program | |
| MOPAC 2016 | http://openmopac.net/MOPAC2016.html | Open-source semi-empirical program | |
| OGOLEM Software | https://www.ogolem.org | Genetic algorithm-based global optimization program | |
| OpenBabel | http://openbabel.org/wiki/Main_Page | Open-source cheminformatics library | |
| calcRotConsts.py | Shields Group, Department of Chemistry, Furman University | Python script to compute rotational constants | |
| calcSymmetry.csh | Shields Group, Department of Chemistry, Furman University | Shell script to calculate symmetry number of a molecule given Cartesian coordinates | |
| combine-GA.csh | Shields Group, Department of Chemistry, Furman University | Shell script to combine energy and rotational constants from different GA directories | |
| combine-QM.csh | Shields Group, Department of Chemistry, Furman University | Shell script to combine energy and rotational constants from different QM directories | |
| gaussianE.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract Gaussian 09 energies | |
| gaussianFreqs.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract Gaussian 09 vibrational frequencies | |
| getrotconsts | Shields Group, Department of Chemistry, Furman University | Executable to calculate rotational constants given a molecule's Cartesian coordinates | |
| getRotConsts-dft-lb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of large basis DFT optimized structures | |
| getRotConsts-dft-lb-ultrafine.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of ultrafine DFT optimized structures | |
| getRotConsts-dft-sb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of small basis DFT optimized structures | |
| getRotConsts-GA.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of genetic algorithm optimized structures | |
| global-minimum-coords.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of global minimum structures of gly-(h2o)n, where n=0-5 | |
| make-thermo-gaussian.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract data from Gaussian output files and make input files for the thermo.pl script | |
| ogolem-input-file.ogo | Shields Group, Department of Chemistry, Furman University | Ogolem sample input file | |
| ogolem-submit-script.pbs | Shields Group, Department of Chemistry, Furman University | PBS batch submission file for Ogolem calculations | |
| README.docx | Shields Group, Department of Chemistry, Furman University | Clarifications to help readers use the scripts effectively | |
| runogolem.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run OGOLEM | |
| run-pw91-lb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of large basis DFT optimization calculations | |
| run-pw91-lb-ultrafine.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of ultrafine DFT optimization calculations | |
| run-pw91-sb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of small basis DFT optimization calculations | |
| run-thermo-pw91.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute the thermodynamic corrections for a batch of DFT optimized structures | |
| similarityAnalysis.py | Shields Group, Department of Chemistry, Furman University | Python script to determine unique structures based on rotational constants and energies | |
| symmetry | Shields Group, Department of Chemistry, Furman University | Executable to calculate molecular symmetry given Cartesian coordinates | |
| symmetry.c | (C) 1996, 2003 S. Patchkovskii, Serguei.Patchkovskii@sympatico.ca | C code to determine the molecular symmstry of a molecule given Cartesian coordinates | |
| template-marcy.pbs | Shields Group, Department of Chemistry, Furman University | Template for a PBS submit script which uses OGOLEM | |
| template-pw91.com | Shields Group, Department of Chemistry, Furman University | Template Gaussian 09 input | |
| template-pw91-HL.com | Shields Group, Department of Chemistry, Furman University | Template Gaussian 09 input for ultrafine DFT optimization | |
| thermo.pl | https://www.nist.gov/mml/csd/chemical-informatics-research-group/products-and-services/program-computing-ideal-gas | Perl open-source script to compute ideal gas thermodynamic corrections | |
| gly-h2o-n.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet for the complete protocol | |
| table-1.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-2.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-3.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-4.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| water.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of water | |
| glycine.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of glycine |
References
- Foster, P., Ramaswamy, V., Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., Tignor, M., Miller, H. L. . Climate Change 2007 The Scientific Basis. , (2007).
- Kulmala, M., et al. Toward direct measurement of atmospheric nucleation. Science. 318 (5847), 89-92 (2007).
- Sipila, M., et al. The role of sulfuric acid in atmospheric nucleation. Science. 327 (5970), 1243-1246 (2010).
- Jiang, J., et al. First measurement of neutral atmospheric cluster and 1 - 2 nm particle number size distributions during nucleation events. Aerosol Science and Technology. 45 (4), (2011).
- Dunn, M. E., Pokon, E. K., Shields, G. C. Thermodynamics of forming water clusters at various Temperatures and Pressures by Gaussian-2, Gaussian-3, Complete Basis Set-QB3, and Complete Basis Set-APNO model chemistries; implications for atmospheric chemistry. Journal of the American Chemical Society. 126 (8), 2647-2653 (2004).
- Pickard, F. C., Pokon, E. K., Liptak, M. D., Shields, G. C. Comparison of CBSQB3, CBSAPNO, G2, and G3 thermochemical predictions with experiment for formation of ionic clusters of hydronium and hydroxide ions complexed with water. Journal of Chemical Physics. 122, 024302 (2005).
- Pickard, F. C., Dunn, M. E., Shields, G. C. Comparison of Model Chemistry and Density Functional Theory Thermochemical Predictions with Experiment for Formation of Ionic Clusters of the Ammonium Cation Complexed with Water and Ammonia; Atmospheric Implications. Journal of Physical Chemistry A. 109 (22), 4905-4910 (2005).
- Alongi, K. S., Dibble, T. S., Shields, G. C., Kirschner, K. N. Exploration of the Potential Energy Surfaces, Prediction of Atmospheric Concentrations, and Vibrational Spectra of the HO2•••(H2O)n (n=1-2) Hydrogen Bonded Complexes. Journal of Physical Chemistry A. 110 (10), 3686-3691 (2006).
- Allodi, M. A., Dunn, M. E., Livada, J., Kirschner, K. N. Do Hydroxyl Radical-Water Clusters, OH(H2O)n, n=1-5, Exist in the Atmosphere. Journal of Physical Chemistry A. 110 (49), 13283-13289 (2006).
- Kirschner, K. N., Hartt, G. M., Evans, T. M., Shields, G. C. In Search of CS2(H2O)n=1-4 Clusters. Journal of Chemical Physics. 126, 154320 (2007).
- Hartt, G. M., Kirschner, K. N., Shields, G. C. Hydration of OCS with One to Four Water Molecules in Atmospheric and Laboratory Conditions. Journal of Physical Chemistry A. 112 (19), 4490-4495 (2008).
- Morrell, T. E., Shields, G. C. Atmospheric Implications for Formation of Clusters of Ammonium and 110 Water Molecules. Journal of Physical Chemistry A. 114 (12), 4266-4271 (2010).
- Temelso, B., et al. Quantum Mechanical Study of Sulfuric Acid Hydration: Atmospheric Implications. Journal of Physical Chemistry A. 116 (9), 2209 (2012).
- Husar, D. E., Temelso, B., Ashworth, A. L., Shields, G. C. Hydration of the Bisulfate Ion: Atmospheric Implications. Journal of Physical Chemistry A. 116 (21), 5151-5163 (2012).
- Bustos, D. J., Temelso, B., Shields, G. C. Hydration of the Sulfuric Acid – Methylamine Complex and Implications for Aerosol Formation. Journal of Physical Chemistry A. 118 (35), 7430-7441 (2014).
- Wales, D. J., Scheraga, H. A. Global optimization of clusters, crystals, and biomolecules. Science. 27 (5432), 1368-1372 (1999).
- Day, M. B., Kirschner, K. N., Shields, G. C. Global search for minimum energy (H2O)n clusters, n = 3 - 5. The Journal of Physical Chemistry A. 109 (30), 6773-6778 (2005).
- Shields, R. M., Temelso, B., Archer, K. A., Morrell, T. E., Shields, G. C. Accurate predictions of water cluster formation, (H2O)n=2-10. The Journal of Physical Chemistry A. 114 (43), 11725-11737 (2010).
- Temelso, B., Archer, K. A., Shields, G. C. Benchmark structures and binding energies of small water clusters with anharmonicity corrections. The Journal of Physical Chemistry A. 115 (43), 12034-12046 (2011).
- Temelso, B., Shields, G. C. The role of anharmonicity in hydrogen-bonded systems: The case of water clusters. The Journal of Chemical Theory and Computation. 7 (9), 2804-2817 (2011).
- Von Freyberg, B., Braun, W. Efficient search for all low energy conformations of polypeptides by Monte Carlo methods. The Journal of Computational Chemistry. 12 (9), 1065-1076 (1991).
- Rakshit, A., Yamaguchi, T., Asada, T., Bandyopadhyay, P. Understanding the structure and hydrogen bonding network of (H2O)32 and (H2O)33: An improved Monte Carlo temperature basin paving (MCTBP) method of quantum theory of atoms in molecules (QTAIM) analysis. RSC Advances. 7 (30), 18401-18417 (2017).
- Deaven, D. M., Ho, K. M. Molecular geometry optimization with a genetic algorithm. Physical Review Letters. 75, 288-291 (1995).
- Hartke, B. Application of evolutionary algorithms to global cluster geometry optimization. Applications of Evolutionary Computation in Chemistry. , (2004).
- Dieterich, J. M., Hartke, B. OGOLEM: Global cluster structure optimization for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach. Molecular Physics. 108 (3-4), 279-291 (2010).
- Herb, J., Nadykto, A. B., Yu, F. Large ternary hydrogen-bonded pre-nucleation clusters in the Earth's atmosphere. Chemical Physics Letters. 518, 7-14 (2011).
- Ortega, I. K., et al. From quantum chemical formation free energies to evaporation rates. Atmospheric Chemistry and Physics. 12 (1), 225-235 (2012).
- Elm, J., Bilde, M., Mikkelsen, K. V. Influence of Nucleation Precursors on the Reaction Kinetics of Methanol with the OH Radical. Journal of Physical Chemistry A. 117 (30), 6695-6701 (2013).
- Loukonen, V., et al. Enhancing effect of dimethylamine in sulfuric acid nucleation in the presence of water - a computational study. Atmospheric Chemistry and Physics. 10 (10), 4961-4974 (2010).
- Temelso, B., Phan, T. N., Shields, G. C. Computational study of the hydration of sulfuric acid dimers: implications for acid dissociation and aerosol formation. Journal of Physical Chemistry A. 116 (39), 9745-9758 (2012).
- Jiang, S., et al. Study of Cl-(H2O)n (n = 1-4) using basin-hopping method coupled with density functional theory. Journal of Computational Chemistry. 35 (2), 159-165 (2014).
- Temelso, B., et al. Effect of mixing ammonia and alkylamines on sulfate aerosol formation. Journal of Physical Chemistry A. 122 (6), 1612-1622 (2018).
- Perdew, J. P., Ruzsinszky, A., Tao, J. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. Journal of Chemical Physics. 123, 062201 (2005).
- Riplinger, C., Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. Journal of Chemical Physics. 138, 034106 (2013).
- Riplinger, C., Pinski, P., Becker, U., Valeev, E. F., Neese, F. Sparse maps--A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. Journal of Chemical Physics. 144 (2), 024109 (2016).
- Kildgaard, J. V., Mikkelsen, K. V., Bilde, M., Elm, J. Hydration of atmospheric molecular clusters: a new method for systematic configurational sampling. Journal of Physical Chemistry A. 122 (22), 5026-5036 (2018).
- González, &. #. 1. 9. 3. ;. Measurement of areas on a sphere Using Fibonacci and latitude-longitude lattices. Mathematical Geosciences. 42, 49-64 (2010).
- Karaboga, D., Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing. 8 (1), 687-697 (2008).
- Zhang, J., Doig, M. Global optimization of rigid molecules using the artificial bee colony algorithm. Physical Chemistry Chemical Physics. 18 (4), 3003-3010 (2016).
- Kubecka, J., Besel, V., Kurten, T., Myllys, N., Vehkamaki, H. Configurational sampling of noncovalent (atmospheric) molecular clusters: sulfuric acid and guanidine. Journal of Physical Chemistry A. 123 (28), 6022-6033 (2019).
- Grimme, S., Bannwarth, C., Shushkov, P. A Robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent Interactions of large molecular systems parametrized for all spd-block elements (Z = 1-86). Journal of Chemical Theory and Computation. 13 (5), 1989-2009 (2017).
- Buck, U., Pradzynski, C. C., Zeuch, T., Dieterich, J. M., Hartke, B. A size resolved investigation of large water clusters. Physical Chemistry Chemical Physics. 16 (15), 6859 (2014).
- Forck, R. M., et al. Structural diversity in sodium doped water trimers. Physical Chemistry Chemical Physics. 14 (25), 9054-9057 (2012).
- Witt, C., Dieterich, J. M., Hartke, B. Cluster structures influenced by interaction with a surface. Physical Chemistry Chemical Physics. 20 (23), 15661-15670 (2018).
- Freitbert, A., Dieterich, J. M., Hartke, B. Exploring self-organization of molecular tether molecules on a gold surface by global structure optimization. The Journal of Computational Chemistry. 40 (22), 1978-1989 (2019).
- Stewart, J. J. P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. The Journal of Molecular Modeling. 19 (1), 1-32 (2013).
- Burke, K., Perdew, J. P., Wang, Y. Derivation of a generalized gradient approximation: The PW91 density functional. Electronic Density Functional Theory. , 81-111 (1998).
- Frisch, M. J., et al. . Gaussian 09, Revision A.02. , (2016).
- Ditchfield, R., Hehre, W. J., Pople, J. A. Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. The Journal of Chemical Physics. 54 (2), 724 (1971).
- Elm, J., Bilde, M., Mikkelsen, K. V. Assessment of density functional theory in predicting structures and free energies of reaction of atmospheric prenucleation clusters. The Journal of Chemical Theory and Computation. 8 (6), 2071-2077 (2012).
- Elm, J., Mikkelsen, K. V. Computational approaches for efficiently modelling of small atmospheric clusters. Chemical Physics Letters. 615, 26-29 (2014).
- Bayucan, A., et al. . PBS Portable Batch System. , (1999).
- O'Boyle, N. M., et al. Open Babel: An open chemical toolbox. Journal of Cheminformatics. 3, 33 (2011).
- Csaszar, A. G. Conformers of gaseous glycine. Journal of the American Chemical Society. 114 (24), 9568-9575 (1992).
- Zhang, Q., Anastasio, C. Free and combined amino compounds in atmospheric fine particles (PM2.5) and fog waters from Northern California. Atmospheric Environment. 37 (16), 2247-2258 (2003).
- Matsumoto, K., Uematsu, M. Free amino acids in marine aerosols over the western North Pacific Ocean. Atmospheric Environment. 39 (11), 2163-2170 (2005).
- Mandalakis, M., Apostolaki, M., Stephanou, E. G. Trace analysis of free and combined amino acids in atmospheric aerosols by gas chromatography-mass spectrometry. Journal of Chromatography A. 1217 (1), 143-150 (2010).
- Seinfeld, J. H., Pandis, S. N. . Atmospheric Chemistry and Physics, 3rd Ed. , (2016).
- Myllys, N., Elm, J., Halonen, R., Kurten, T., Vehkamaki, H. Coupled cluster evaluation of atmospheric acid-base clusters with up to 10 molecules. The Journal of Physical Chemistry A. 120 (4), 621-630 (2016).
- Elm, J., Bilde, M., Mikkelsen, K. V. Assessment of binding energies of atmospherically relevant clusters. Physical Chemistry Chemical Physics. 15 (39), (2013).
- Elstner, M. The SCC-DFTB method and its application to biological systems. Theoretical Chemistry Accounts. 116 (1-3), 316-325 (2006).
- Kaliman, I. A., Slipchenko, L. V. LIBEFP: A new parallel implementation of the effective fragment potential method as a portable software library. The Journal of Computational Chemistry. 34 (26), 2284-2292 (2013).
- Zhao, Y., Truhlar, D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and trasition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theoretical Chemistry Accounts. 120 (1-3), 215-241 (2008).
- Mardirossian, N., Head-Gordon, M. wB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy. Physical Chemistry Chemical Physics. 16 (21), 9904-9924 (2014).
- Head-Gordon, M., Pople, J. A., Frisch, M. J. MP2 energy evaluation by direct methods. Chemical Physics Letters. 153 (6), 503-506 (1988).
- Pople, J. A., Seeger, R., Krishnan, R. Variational configuration interaction methods and comparison with perturbation theory. The International Journal of Quantum Chemistry. 12, 149-163 (1977).
- Pople, J. A., Binkley, J. S., Seeger, R. Theoretical models incorporating electron correlation. The International Journal of Quantum Chemistry. 10 (10), 1-19 (1976).
- Monkhorst, H. J. Calculation of properties with the coupled-cluster method. The International Journal of Quantum Chemistry. 12 (11), 421-432 (1977).
- Klopper, W., Manby, F. R., Ten-No, S., Valeev, E. F. R12 methods in explicitly correlated molecular electronic structure theory. International Reviews in Physical Chemistry. 25, 427-468 (2006).
- Hattig, C. Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core-valence and quintuple-z basis sets for H to Ar and QZVPP basis sets for Li to Kr. Physical Chemistry Chemical Physics. 7 (1), 59-66 (2005).
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. The Journal of Chemical Physics. 122, 014108 (2005).
- Barone, V. Vibrational zero-point energies and thermodynamic functions beyond the harmonic approximation. The Journal of Chemical Physics. 120 (7), 3059-3065 (2004).
- Temelso, B., et al. Exploring the Rich Potential Energy Surface of (H2O)11 and Its Physical Implications. Journal of Chemical Theory and Computation. 14 (2), 1141-1153 (2018).
- Kabrede, H., Hentschke, R. Global minima of water clusters (H2O)N, N≤25, described by three empirical potentials. Journal of Physical Chemistry B. 107 (16), (2003).
- Steber, A. L., et al. Capturing the Elusive Water Trimer from the Stepwise Growth of Water on the Surface of a Polycyclic Aromatic Hydrocarbon Acenaphthene. Journal of Physical Chemistry Letters. 8 (23), 5744-5750 (2017).
- Perez, C., et al. Corrannulene and its complex with water: A tiny cup of water. Physical Chemistry Chemical Physics. 19 (22), 14214-14223 (2017).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved