Method Article
Calcul des concentrations atmosphériques de grappes moléculaires de la thermochimie ab initio
Dans cet article
Résumé
Les concentrations atmosphériques de grappes moléculaires faiblement liées peuvent être calculées à partir des propriétés thermochimiques des structures à faible énergie trouvées grâce à une méthodologie d’échantillonnage configuration en plusieurs étapes utilisant un algorithme génétique et une chimie quantique semi-empirique et ab initio.
Résumé
L’étude informatique de la formation et de la croissance des aérosols atmosphériques nécessite une surface d’énergie sans Gibbs précise, qui peut être obtenue à partir de la structure électronique de phase gazeuse et des calculs de fréquence vibratoire. Ces quantités sont valables pour les amas atmosphériques dont les géométries correspondent au minimum sur leurs surfaces énergétiques potentielles. L’énergie libre Gibbs de la structure énergétique minimale peut être utilisée pour prédire les concentrations atmosphériques de l’amas dans une variété de conditions telles que la température et la pression. Nous présentons une procédure computationnellement peu coûteuse construite sur un échantillonnage configurationnel basé sur un algorithme génétique suivi d’une série de calculs de dépistage de plus en plus précis. La procédure commence par générer et faire évoluer les géométries d’un grand ensemble de configurations à l’aide de modèles semi-empiriques puis affine les structures uniques résultantes à une série de niveaux ab initio de haut niveau de la théorie. Enfin, les corrections thermodynamiques sont calculées pour l’ensemble résultant de structures d’énergie minimale et utilisées pour calculer les énergies libres Gibbs de formation, les constantes d’équilibre, et les concentrations atmosphériques. Nous présentons l’application de cette procédure à l’étude des grappes de glycine hydratées dans des conditions ambiantes.
Introduction
Le paramètre le plus incertain dans les études atmosphériques sur le changement climatique est la mesure exacte dans laquelle les particules de nuages reflètent le rayonnement solaire entrant. Les aérosols, qui sont des particules suspendues dans un gaz, forment des particules de nuages appelées noyaux de condensation des nuages (CCN) qui dispersent le rayonnement entrant, empêchant ainsi son absorption et le chauffage subséquent de l’atmosphère1. Une compréhension détaillée de cet effet de refroidissement net nécessite une compréhension de la croissance des aérosols en CCN, ce qui nécessite une compréhension de la croissance des petits amas moléculaires en particules d’aérosols. Des travaux récents ont suggéré que la formation d’aérosols est initiée par des grappes moléculaires de 3 nm de diamètre ou moins2; cependant, ce régime de taille est difficile d’accès en utilisant des techniques expérimentales3,4. Par conséquent, une approche de modélisation computationnelle est souhaitée afin de surmonter cette limitation expérimentale.
En utilisant notre approche de modélisation décrite ci-dessous, nous pouvons analyser la croissance de n’importe quel cluster hydraté. Parce que nous nous intéressons au rôle de l’eau dans la formation de grandes molécules biologiques à partir de petits constituants dans des environnements prébiotiques, nous illustrerons notre approche avec la glycine. Les défis rencontrés et les outils nécessaires pour répondre à ces questions de recherche sont très similaires à ceux impliqués dans l’étude des aérosols atmosphériques et des grappes de prénucléation5,6,7,8,9,10,11,12,13,14,15. Ici, nous examinons les amas de glycine hydratés à partir d’une molécule de glycine isolée suivie d’une série d’ajouts étape de jusqu’à cinq molécules d’eau. L’objectif final est de calculer les concentrations d’équilibre des grappes Gly (H2O)n-0-5 dans l’atmosphère à température ambiante au niveau de la mer et une humidité relative (RH) de 100 %.
Un petit nombre de ces amas moléculaires sous-nanomètres se développent en un amas critique métastable (1-3 nm de diamètre) soit en ajoutant d’autres molécules de vapeur ou en coagulant sur des amas existants. Ces grappes critiques ont un profil de croissance favorable menant à la formation de noyaux de condensation de nuages beaucoup plus grands (jusqu’à 50-100 nm) (CCN), qui affectent directement l’efficacité des précipitations des nuages ainsi que leur capacité à refléter la lumière incidente. Par conséquent, avoir une bonne compréhension de la thermodynamique des amas moléculaires et de leurs distributions d’équilibre devrait conduire à des prédictions plus précises de l’impact des aérosols sur le climat mondial.
Un modèle descriptif de formation d’aérosols nécessite une thermodynamique précise de la formation de grappes moléculaires. Le calcul de la thermodynamique précise de la formation des grappes moléculaires nécessite l’identification des configurations les plus stables, ce qui implique de trouver les minima globaux et locaux sur la surface énergétique potentielle de l’amas (PES)16. Ce processus est appelé échantillonnage de configuration et peut être réalisé grâce à une variété de techniques, y compris celles basées sur la dynamique moléculaire (MD)17,18,19,20, Monte Carlo (MC)21,22, et les algorithmes génétiques (GA)23,24,25.
Différents protocoles ont été développés au fil des ans pour obtenir la structure et la thermodynamique des hydrates atmosphériques à un niveau élevé de théorie. Ces protocoles différaient dans le choix de (i) méthode d’échantillonnage configurationnel, (ii) la nature de la méthode de bas niveau utilisée dans l’échantillonnage de configuration, et (iii) la hiérarchie des méthodes de niveau supérieur utilisées pour affiner les résultats dans les étapes suivantes.
Les méthodes d’échantillonnage configurationnels comprenaient l’intuition chimique26, l’échantillonnage aléatoire27,28, la dynamique moléculaire (MD)29,30, le saut de bassin (BH)31, et l’algorithme génétique (GA)24,25,32. Les méthodes de faible niveau les plus courantes utilisées avec ces méthodes d’échantillonnage sont les champs de force ou les modèles semi-empiriques tels que pm6, PM7 et SCC-DFTB. Ceux-ci sont souvent suivis par des calculs DFT avec des ensembles de base de plus en plus grands et des fonctions plus fiables des échelons supérieurs de l’échelle de Jacob33. Dans certains cas, ceux-ci sont suivis par des méthodes de fonction d’onde de niveau supérieur telles que MP2, CCSD (T), et le DLPNO-CCSD(T)34,35.
Kildgaard et coll.36 ont développé une méthode systématique où des molécules d’eau sont ajoutées à des points sur les sphères Fibonacci37 autour de plus petits amas hydratés ou non hydratés pour générer des candidats pour de plus grands groupes. Les candidats non physiques et redondants sont supprimés en fonction des seuils de contact étroits et de la distance carrée par les racines entre les différents conformistes. Les optimisations ultérieures utilisant la méthode semi-empirique PM6 et une hiérarchie des méthodes DFT et de fonction d’onde sont utilisées pour obtenir un ensemble de conformations à faible énergie à un niveau élevé de théorie.
L’algorithme38 de la colonie d’abeilles artificielles (ABC) est une nouvelle approche d’échantillonnage configurationnel qui a récemment été mise en œuvre par Zhang et coll. pour étudier les grappes moléculaires dans le cadre d’un programme appelé ABCluster39. Kubecka et coll.40 ont utilisé ABCluster pour l’échantillonnage configuration, suivis de réoptimisations de bas niveau à l’aide de la méthode semi-empirique GFN-xTB41. Ils ont en outre affiné les structures et les énergies à l’aide de méthodes DFT suivies d’énergies finales à l’aide de DLPNO-CCSD (T).
Quelle que soit la méthode, l’échantillonnage de configuration commence par une distribution aléatoire ou non-générée de points sur le PSE. Chaque point correspond à une géométrie spécifique du cluster moléculaire en question et est généré par la méthode d’échantillonnage. Ensuite, le minimum local le plus proche se trouve pour chaque point en suivant la direction «descente» sur le PSE. L’ensemble de minima ainsi trouvé correspondent à ces géométries de l’amas moléculaire qui sont stables, au moins pendant un certain temps. Ici, la forme du PSE et l’évaluation de l’énergie à chaque point de la surface seront sensibles à la description physique du système où une description physique plus précise entraîne un calcul de l’énergie plus coûteux. Nous utiliserons spécifiquement la méthode GA mise en œuvre dans le programme OGOLEM25, qui a été appliquée avec succès à une variété de problèmes d’optimisation globale et d’échantillonnage de configuration42,43,44,45, pour générer l’ensemble initial de points d’échantillonnage. Le PSE sera décrit par le modèlePM7 46 mis en œuvre dans le programme MOPAC201647. Cette combinaison est utilisée parce qu’elle génère une plus grande variété de points par rapport aux méthodes MD et MC et trouve les minima locaux plus rapidement que les descriptions plus détaillées du PSE.
L’ensemble des minima locaux optimisés par les GA sont pris comme les géométries de départ pour une série d’étapes de dépistage, qui conduisent à un ensemble d’énergie minimale de faible altitude. Cette partie du protocole commence par l’optimisation de l’ensemble de structures uniques optimisées par les GA à l’aide de la théorie fonctionnelle de la densité (DFT) avec un petit ensemble de base. Cet ensemble d’optimisations donnera généralement un plus petit ensemble de structures minimales locales uniques qui sont modélisés plus en détail par rapport aux structures semi-empiriques optimisées par les GA. Ensuite, une autre série d’optimisations DFT sont effectuées sur ce plus petit ensemble de structures en utilisant un ensemble de base plus large. Encore une fois, cette étape donnera généralement un plus petit ensemble de structures uniques qui sont modélisés plus en détail par rapport à la petite base DFT étape. L’ensemble final de structures uniques est ensuite optimisé pour une convergence plus serrée et les fréquences vibratoires harmoniques sont calculées. Après cette étape, nous avons tout ce dont nous avons besoin pour calculer les concentrations d’équilibre des grappes dans l’atmosphère. L’approche globale est résumée schématiquement à la figure 1. Nous utiliserons la corrélation d’échange PW9148 de gradient généralisé (GGA) fonctionnelle dans la mise en œuvre de la DFT gaussian0949 ainsi que deux variantes de l’ensemble de base Pople50 (6-31 GD POUR la petite étape de base et 6-311 GD pour la grande étape de base). Cette combinaison particulière de l’ensemble fonctionnel et de base de corrélation d’échange a été choisie en raison de son succès précédent dans l’informatique précis Gibbs énergies libres de formation pour les amas atmosphériques51,52.
Ce protocole suppose que l’utilisateur a accès à un cluster informatique haute performance (HPC) avec le système de lots portable53 (PBS), MOPAC2016 (http://openmopac.net/MOPAC2016.html)47, OGOLEM (https://www.ogolem.org)25, Gaussian 09 (https://gaussian.com)49, et OpenBabel54 (http://openbabel.org/wiki/Main_Page) logiciel installé suivant leurs instructions d’installation spécifiques. Chaque étape de ce protocole utilise également un ensemble de scripts en coquille interne et Python 2.7 qui doivent être enregistrés à un répertoire qui est inclus dans la variable environnementale $PATH de l’utilisateur. Tous les modules environnementaux nécessaires et les autorisations d’exécution pour exécuter tous les programmes ci-dessus doivent également être chargés dans la session de l’utilisateur. L’utilisation du disque et de la mémoire par le code GA (OGOLEM) et les codes semi-empiriques (MOPAC) sont très faibles par les normes modernes de ressources informatiques. La mémoire globale et l’utilisation du disque pour OGOLEM/MOPAC dépend du nombre de threads que l’on veut utiliser, et même alors, l’utilisation des ressources sera faible par rapport aux capacités de la plupart des systèmes HPC. Les besoins en ressources des méthodes de QM dépendent de la taille des grappes et du niveau de théorie utilisé. L’avantage de l’utilisation de ce protocole est que l’on peut varier le niveau de théorie pour être en mesure de calculer l’ensemble final de structures à faible énergie, en gardant à l’esprit que les calculs généralement plus rapides conduisent à plus d’incertitude dans l’exactitude des résultats.
Par souci de clarté, l’ordinateur local de l’utilisateur sera appelé «ordinateur local» tandis que le cluster HPC auquel il a accès sera appelé «cluster à distance».
Protocole
1. Trouver la structure énergétique minimale de la glycine et de l’eau isolées
REMARQUE : L’objectif ici est double : (i) d’obtenir des structures énergétiques minimales de molécules d’eau et de glycine isolées pour une utilisation dans l’échantillonnage de configuration de l’algorithme génétique, (ii) et de calculer les corrections thermodynamiques aux énergies de phase gazeuse de ces molécules pour une utilisation dans le calcul des concentrations atmosphériques.
- Sur votre ordinateur local, ouvrez une nouvelle session d’Avogadro.
- Cliquez sur Build 'gt; Insert 'gt; Peptide et sélectionnez Gly à partir de la fenêtre Insert Peptide pour générer un monomer de glycine dans la fenêtre de visualisation.
- Cliquez sur Extensions 'gt; Gaussian et éditez la première ligne dans la boîte de texte pour lire 'pw91pw91/6-311'G’int (Acc2E'12,UltraFine) scf (conver'12) optez (serré, maxcyc'300) freq'. Cliquez sur Générer et enregistrer le fichier d’entrée comme glycine.com.
- Veuillez noter que si la molécule a une flexibilité conformationnelle significative, comme la glycine le fait55,il est essentiel d’effectuer une analyse conformationnelle pour identifier la structure minimale globale et d’autres conformistes de faible altitude. OpenBabel54 fournit des outils de recherche conformationnel robustes utilisant différents algorithmes et champs de force rapide. Bien que les conformistes soient autorisés à se détendre et à s’interconvertir pendant les calculs de l’AG et des calculs ultérieurs, il est parfois nécessaire d’exécuter plusieurs calculs d’AG, chacun commençant par une conformation différente.
- Sur votre ordinateur local, ouvrez une nouvelle session à Avogadro.
- Cliquez sur Build 'gt; Insert 'gt; Fragment et la recherche de "eau" à partir de la fenêtre Insert Fragment pour obtenir les coordonnées de l’eau.
- Cliquez sur Extensions 'gt; Gaussian et éditez la première ligne dans la boîte de texte pour lire 'pw91pw91/6-311'G’int (Acc2E'12,UltraFine) scf (conver'12) optez (serré, maxcyc'300) freq'. Cliquez sur Générer et enregistrer le fichier d’entrée comme water.com.
- Transférez les deux fichiers .com au cluster distant. Une fois que vous vous connectez dans le cluster distant, appelez Gaussian 09 dans un script de soumission de lots pour commencer le calcul. Lorsque les calculs se terminent, extraire les coordonnées cartésiennes (fichiers.xyz) des structures énergétiques minimales en appelant OpenBabel. Pour la glycine, la commande à exécuter est :
obabel -ig09 glycine.log -oxyz -gt; glycine.xyz
Ces deux fichiers .xyz seront utilisés par l’échantillonnage de configuration GA dans la prochaine étape.
2. Échantillonnage de configuration basé sur l’algorithme génétique des clusters Gly (H2O)n-1-5
REMARQUE: L’objectif ici est d’obtenir un ensemble de structures à faible consommation d’énergie pour Gly (H2O)n '1-5 au niveau semi-empirique peu coûteux de la théorie, en utilisant le modèle PM746 mis en œuvre dans MOPAC47. Il est impératif que le répertoire de travail ait l’organisation et la structure exactes, comme le montre la figure 2. Il s’agit de s’assurer que la coque personnalisée et les scripts Python fonctionnent sans échecs.
- Copiez tous les scripts nécessaires au cluster distant et ajoutez leur emplacement à $PATH
- Mettez tous les scripts et les fichiers de modèle à un dossier (par exemple les scripts) et copiez-le au cluster distant
- Assurez-vous que tous les scripts sont exécutables
- Ajoutez l’emplacement du répertoire des scripts à la variable environnementale $PATH en entrant les commandes suivantes dans un terminal. L’emplacement par défaut des scripts est réglé pour $HOME/JoVE-démo/scripts, cependant, on peut définir une variable environnementale appelée $SCRIPTS-HOME pointant vers le répertoire contenant les scripts et ajouter $SCRIPTS-HOME à son chemin
- Coquille de bash :
l’exportation SCRIPTS_HOMEMD/chemin/aux scripts
exportation PATHMD$$'SCRIPTS_HOME':$'PATH' - Tcsh/Csh coquille:
setenv SCRIPTS_HOME /path/to/scripts
setenv PATH $SCRIPTS_HOME: $'PATH'
- Coquille de bash :
- Sur le cluster distant, configurez et exécutez un calcul GA :
- Créer un répertoire appelé gly-h2o-n où n est le nombre de molécules d’eau.
- Créez une sous-direction appelée GA sous le répertoire gly-h2o-n pour exécuter des calculs d’algorithme génétique.
- Copiez les fichiers d’entrée OGOLEM (par exemple pm7.ogo), les coordonnées cartésiennes monomers (Eg. glycine.xyz, water.xyz) et le script de soumission de lots PBS (par exemple run.pbs) dans le répertoire de l’AG.
- Apporter les modifications nécessaires au fichier d’entrée OGOLEM et au fichier de soumission par lots.
- Soumettez le calcul. Lorsque le calcul commencera, OGOLEM créera un nouvel annuaire nommé préfixe du fichier d’entrée OGOLEM (par exemple pm7) dans l’annuaire de l’AG et y stockera les coordonnées nouvellement générées.
- Une fois le calcul terminé, compilez les énergies et les constantes de rotation, et utilisez cette information pour déterminer quelles sont les structures uniques à faible énergie :
- Changez d’annuaire en gly-h2o-n/GA/pm7 et
- Extraire les énergies et calculer les constantes de rotation des clusters optimisés par les GA avec la commande :
getRotConsts-GA.csh N 0 99
où N est le nombre d’atomes dans l’amas moléculaire et «0 99» indique que la taille du pool GA est de 100, avec des indices allant de 0 à 99. Cela générera un fichier appelé rotConstsData_C qui contient une liste triée de toutes les configurations de clusters optimisées par les GA, de leurs énergies et de leurs constantes de rotation. - Exécuter la commande:
similarityAnalysis.py pm7 rotConstsData_C
où pm7 sera utilisé comme une étiquette de nommage de fichiers, pour trouver et enregistrer les clusters uniques optimisés par les GA. Cela générera un fichier appelé uniqueStructures-pm7.data qui contient une liste triée des configurations uniques optimisées par les GA. Il s’agit d’une liste de structures minimales locales uniques pour le Gly (H2O)n cluster optimisé au niveau PM7 de la théorie, et ces structures sont maintenant prêtes à être raffinées à l’aide de DFT.
- Montez à l’annuaire gly-h2o-n/GA et combinez les résultats de plusieurs courses comparables en GA à l’aide du script combine-GA.csh. La syntaxe est :
combine-GA.csh 'lt;label’gt; 'lt;list of directories with GA runs’gt;
Dans ce cas particulier, la commande :
combine-GA.csh pm77
générera une nouvelle liste de structures uniques nommée 'uniqueStructures-pm7.data' dans le répertoire gly-h2o-n/GA.
3. Raffinement à l’aide de la méthode QM avec un petit ensemble de base
REMARQUE : L’objectif ici est d’affiner l’échantillonnage configuré des clusters Gly(H2O)n'1-5 en utilisant une meilleure description quantique-mécanique pour obtenir un ensemble plus petit mais plus précis de structures de cluster Gly(H2O)n-1-5. Les structures de départ de cette étape sont les sorties de l’étape 2.
- Préparer et exécuter le calcul DFT de petite base :
- Créez une sous-direction appelée QM sous l’annuaire gly-h2o-n. Sous l’annuaire QM, créez une autre sous-direction nommée pw91-sb.
- Copiez la liste des structures uniques(uniqueStructures-pm7.data) de l’annuaire gly-h2o-n/GA à l’annuaire QM/pw91-sb.
- Changez d’annuaire à ce gly-h2o-n/QM/pw91-sb.
- Exécutez le script d’échantillonnage configurationnel DFT de petit jeu de base à l’aide de la commande :
run-pw91-sb.csh uniqueStructures-pm7.data sb QUEUE 10
lorsque sb est une étiquette pour cet ensemble de calculs, QUEUE est la file d’attente préférée sur le cluster informatique, et 10 indique que 10 calculs doivent être regroupés en un seul travail par lots. Ce script générera automatiquement les entrées de Gaussian 09 et soumettra tous les calculs. Entrez 'test' pour que le 'QUEUE' fasse une course à sec.
- Une fois les calculs soumis terminés, extraire et analyser les résultats.
- Extraire les énergies et calculer les constantes de rotation des clusters optimisés à petite base à l’aide de la commande :
getRotConsts-dft-sb.csh pw91 N
où pw91 indique que la densité PW91 fonctionnelle a été utilisée, et N est le nombre d’atomes dans l’amas. Cela créera un fichier nommé rotConstsData_C. - Maintenant, identifiez les structures uniques avec la commande :
similarityAnalysis.py sb rotConstsData_C
où sb est utilisé comme une étiquette de nommage de fichiers. Il y aura maintenant une liste de configurations uniques optimisées au niveau de théorie PW91/6-31-GMD enregistré dans le fichier uniqueStructures-sb.data.
- Extraire les énergies et calculer les constantes de rotation des clusters optimisés à petite base à l’aide de la commande :
- Montez à l’annuaire gly-h2o-n/QM et combinez les résultats de plusieurs courses comparables de QM à l’aide du script combine-QM.csh. La syntaxe est :
combine-QM.csh -lt;label’gt; 'lt;list of directories with QM calcs’gt;
Dans ce cas particulier, la commande :
combine-QM.csh sb pw91-sb
générera une nouvelle liste de structures uniques nommée 'uniqueStructures-sb.data' dans l’annuaire gly-h2o-n/QM.
4. Amélioration supplémentaire de la méthode QM avec un ensemble de base
REMARQUE : L’objectif ici est d’affiner davantage l’échantillonnage de configuration des clusters Gly(H2O)n'1-5 à l’aide d’une meilleure description quantique-mécanique. Les structures de départ de cette étape sont les sorties de l’étape 3.
- Soumettez des calculs plus fiables à l’aide d’un ensemble de base plus large.
- Créez une sous-direction appelée pw91-lb sous l’annuaire QM.
- Copiez la liste des structures uniques(uniqueStructures-sb.data) de l’annuaire gly-h2o-n/QM à l’annuaire gly-h2o-n/QM/pw91-lb et changez à cet annuaire.
- Exécutez le script d’échantillonnage configurationnel DFT à grande base avec la commande :
run-pw91-lb.csh uniqueStructures-sb.data lb QUEUE 10
lorsque lb est une étiquette pour cet ensemble de calculs, QUEUE est la file d’attente préférée sur le cluster informatique, et 10 indique que 10 calculs doivent être regroupés en un seul travail par lots. Ce script générera automatiquement les entrées de Gaussian 09 et soumettra tous les calculs. Entrez «test» pour le «QUEUE» de faire un test de course à sec.
- Une fois les calculs soumis terminés, extraire et analyser les données
- Calculez les constantes de rotation des clusters optimisés à grande base avec la commande :
getRotConsts-dft-lb.csh pw91 N
où pw91 indique que la densité PW91 fonctionnelle a été utilisée, et N est le nombre d’atomes dans l’amas. - Maintenant, identifiez les structures uniques avec la commande :
similarityAnalysis.py lb rotConstsData_C
où lb est utilisé comme une étiquette de nommage de fichiers. Vous disposez maintenant d’une liste de configurations uniques optimisées au niveau de théorie PW91/6-311-GMD enregistré dans le fichier uniqueStructures-lb.data.
- Calculez les constantes de rotation des clusters optimisés à grande base avec la commande :
5. Calculs de correction finales de l’énergie et de la thermodynamique
REMARQUE : L’objectif ici est d’obtenir la structure vibratoire et les énergies des clusters Gly(H2O)n'1-5 à l’aide d’un grand ensemble de base et d’une grille d’intégration ultrafine afin de calculer les corrections thermochimiques souhaitées.
- En commençant par les résultats de l’étape précédente, soumettez des calculs plus fiables.
- Créez une sous-direction appelée ultrafine sous l’annuaire QM/pw91-lb. Ensuite, copiez la liste des structures uniques(uniqueStructures-lb.data) de l’annuaire QM/pw91-lb à l’annuaire QM/pw91-lb/ultrafine et changez à cet annuaire.
- Soumettez le script DFT ultrafin avec la commande :
run-pw91-lb-ultrafine.csh uniqueStructures-lb.data uf QUEUE 10
lorsque l’uf est une étiquette pour cet ensemble de calculs, QUEUE est la file d’attente préférée sur le cluster informatique, et 10 indique que 10 calculs doivent être regroupés en un seul travail par lots. Ce script générera automatiquement les entrées de Gaussian 09 et soumettra tous les calculs. Entrez «test» pour le «QUEUE» de faire un test de course à sec.
- Une fois les calculs soumis terminés, extraire et analyser les données
- Extraire les énergies et calculer les constantes de rotation des clusters optimisés à grande base avec la commande :
getRotConsts-dft-lb-ultrafine.csh pw91 N
où pw91 indique que la densité PW91 fonctionnelle a été utilisée, et N est le nombre d’atomes dans l’amas. - Maintenant, identifiez les structures uniques avec la commande :
similarityAnalysis.py uf rotConstsData_C
où l’uf est utilisé comme étiquette de nommage de fichiers. Vous disposez maintenant d’une liste de configurations uniques optimisées au niveau de théorie PW91/6-311-GMD enregistré dans le fichier uniqueStructures-uf.data.
- Extraire les énergies et calculer les constantes de rotation des clusters optimisés à grande base avec la commande :
- Effectuez une extraction finale de l’information nécessaire pour calculer les corrections thermodynamiques. Utilisez ces informations pour calculer les corrections thermodynamiques.
- Extraire les énergies électroniques finales, les constantes de rotation et les fréquences vibratoires, et utilisez-les pour calculer les corrections thermodynamiques à l’aide de la commande :
run-thermo-pw91.csh uniqueStructures-uf.data - Copiez/coller la sortie de la ligne de commande à la feuille de la feuille de calcul Excel deRaw_Energiesnommée «gly-h2o-n.xlsx». Vous auriez besoin de le faire pour les monomers (glycine et eau) ainsi que le membre le plus faible de l’énergie de chaque hydrate (gly-h2o-n, où n '1,2, ...).
- Comme les énergies brutes sont ajoutées à la première feuille de la feuille de calcul 'gly-h2o-n.xlsx', les feuilles suivantes 'Binding_Energies' et 'Hydrate_Distribution'sont automatiquement mises à jour. En particulier, la feuille de« Hydrate_Distribution» donne la concentration d’équilibre des hydrates à des températures différentes (298,15 km), l’humidité relative (20 %, 50 %, 100 %) et les concentrations initiales d’eau ([H2O]) et de glycine ([glycine]). La théorie derrière ces calculs est décrite dans l’étape suivante.
- Extraire les énergies électroniques finales, les constantes de rotation et les fréquences vibratoires, et utilisez-les pour calculer les corrections thermodynamiques à l’aide de la commande :
6. Calcul des concentrations atmosphériques des amas Gly (H2O)n-0-5 à température ambiante au niveau de la mer
REMARQUE : Ceci est accompli en copiant d’abord les données thermodynamiques générées dans l’étape précédente dans une feuille de calcul et en calculant les énergies libres Gibbs de l’hydratation séquentielle. Ensuite, les énergies libres Gibbs sont utilisées pour calculer les constantes d’équilibre pour chaque hydratation séquentielle. Enfin, un ensemble d’équations linéaires sont résolus pour obtenir la concentration d’équilibre des hydrates pour une concentration donnée de monomères, de température et de pression.
- Commencez par mettre en place un système d’équilibre chimique pour l’hydratation séquentielle de la glycine comme indiqué ci-dessous:
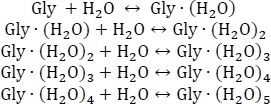
- Calculez les constantes d’équilibre Kn en utilisant Kn 'e'Gn'(kBT), où n est le niveau d’hydratation, Gn est le changement d’énergie libre Gibbs de la réaction d’hydratation ne, k B est la constante de Boltzmann, et T est la température.
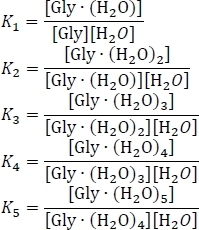
- Mettre en place l’équation pour la conservation de la masse, en utilisant l’hypothèse que la somme des concentrations d’équilibre des grappes de glycine hydratées et non hydratées équivaut à la concentration initiale de glycine isolée [Gly]0. Réécrire ce système de six équations simultanées, en utilisant un certain réarrangement algébrique des expressions constantes d’équilibre,
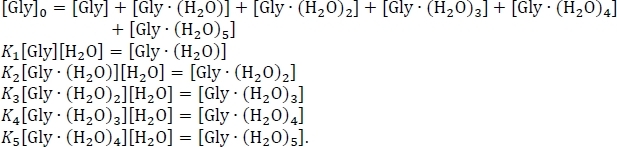
- Résoudre le système d’équations indiqués ci-dessus pour obtenir les concentrations d’équilibre de Gly (H2O)n 0-5 en utilisant une valeur expérimentale56,57,58 pour la concentration de glycine dans l’atmosphère, [Gly]0 x 2,9 x 106 cm-3, et la concentration d’eau dans l’atmosphère à 100% humidité relative et une température de 298,15 K59, [H2O] - 7,7 x 1017 cm-3.
Résultats
La première série de résultats de ce protocole devrait être un ensemble de structures à faible consommation d’énergie de Gly (H2O)n'1-5 trouvé par la procédure d’échantillonnage configurationnel. Ces structures ont été optimisées au niveau de théorie PW91/6-311 et sont supposées exactes aux fins du présent document. Rien n’indique que PW91/6-311 GMD sous-estime ou surestime constamment l’énergie contraignante de ces grappes. Sa capacité à prédire les énergies contraignantes par rapport à MP2/CBS32 et [DLPNO-]CCSD(T)/CBS60,61 estimations et l’expérience52 montre beaucoup de fluctuations. Il en va de même pour la plupart des autres fonctions de densité. En général, chaque valeur de n 1 à 5 devrait donner une poignée de structures à faible énergie dans un rayon d’environ 5 kcal mol-1 de la structure la plus faible en énergie. Ici, nous nous concentrons sur la première structure produite par le script run-thermo-pw91.csh pour la brièveté. La figure 3 montre les plus faibles isomères d’énergie électronique des grappes Gly (H2O)n-0-5. On peut voir que le réseau de liaisons d’hydrogène augmente en complexité à mesure que le nombre de molécules d’eau augmente, et passe même d’un réseau principalement planaire à une structure tridimensionnelle en forme de cage à n 5. Le reste de ce texte utilise les énergies et les quantités thermodynamiques correspondant à ces cinq clusters spécifiques.
Le tableau 1 contient les quantités thermodynamiques nécessaires à l’application du protocole. Le tableau 2 montre un exemple de la sortie du script run-thermo-pw91.csh où les énergies électroniques, les corrections vibratoires à zéro point et les corrections thermodynamiques à trois températures différentes sont imprimées. Pour chaque cluster (ligne), le niveau de théorie E[PW91/6-311-G] correspond aux énergies électroniques de phase gazeuse du niveau de théorie PW91/6-311-GMD calculé sur les réseaux d’intégration ultrafin dans les unités de Hartree, ainsi qu’à l’énergie vibratoire zéro point(ZPVE) dans les unités de m mol kcal-1. À chaque température, 216,65 K, 273,15 K, et 298,15 K, les corrections thermodynamiques sont énumérées, H l’enthalpie de formation dans les unités de kcal mol-1, S l’entropie de formation dans les unités de cal mol-1, et G l’énergie sans Gibbs de formation dans les unités de m mol kcal-1. Le tableau 3 montre un exemple de calcul du changement total d’énergie libre Gibbs de l’hydratation, ainsi que pour l’hydratation séquentielle. Un exemple de calcul du changement total d’énergie libre Gibbs de l’hydratation pour la réaction
commence par le calcul de l’énergie électronique EPW91 comme
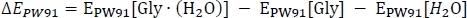
où EPW91[Gly(H2O)] est tiré de la colonne C du tableau 2, et EPW91[Gly] et EPW91[H2O] sont tirés de la colonne B du tableau 1. Ensuite, nous calculons le changement énergétique de phase totale du gaz'E(0) en incluant le changement dans l’énergie vibratoire zéro point de la réaction comme
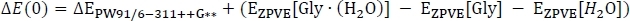
pour obtenir la colonne D. Ici, leTPS91/6-311-GMD est tiré de la colonne C du tableau 3, de l’EZPVE[Gly (H2O)] de la colonne D du tableau 2, et de l’EZPVE[Gly] et de l’EZPVE[H2O] de la colonne C du tableau 1. Pour des raisons de brièveté, nous passerons à des grappes de température ambiante, donc nous passons sur les données de 216,65 K et 273,15 K. À température ambiante, nous calculons ensuite le changement d’enthalpie de la réactionH en corrigeant le changement d’énergie de phase de gaz
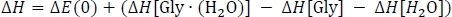
où l’onpuise dans la colonne du tableau 3 D,le H[GlyMD(H2O)] est tiré de la colonne K du tableau 2, et les articlesde H[Gly] etH[H2O] sont tirés de la colonne J du tableau 1. Enfin, nous calculons le changement d’énergie libre Gibbs de la réactionG comme
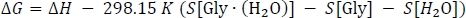
où le tableau 2 est tiré de la colonne du tableau 3 I, S[GlyMD(H2O)] est tiré de la colonne L du tableau 2, et S[Gly] et S[H2O] sont tirés de la colonne K. Note ici que les valeurs d’entropie doivent être converties en unités de mol kcal-1 K-1 pendant cette étape.
Nous avons maintenant les quantités nécessaires pour calculer les concentrations atmosphériques de glycine hydratée comme le montre l’étape 6. Les résultats devraient ressembler aux données présentées au tableau 4,mais il faut s’attendre à de petites différences numériques. Le tableau 4 montre les concentrations d’hydrate d’équilibre trouvées à partir de la formulation du système de six équations de l’étape 6.2 en une seule équation de matrice et sa solution subséquente. Nous commençons par reconnaître le fait que le système d’équations peut être
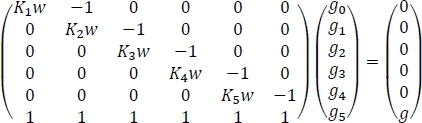
où Kn est la constanted’équilibre pour l’hydratation séquentielle n de glycine, w est la concentration d’eau dans l’atmosphère, g est la concentration initiale de glycine isolée dans l’atmosphère, et gn est la concentration d’équilibre de Gly (H2O)n. Si nous réécrivons l’équation ci-dessus comme Ax b, nous obtenons x 'A'1b où A'1 est l’inverse de la matrice A. Cet inverse peut être facilement calculé à l’aide de fonctions intégrées de feuilles de calcul comme indiqué dans le tableau 4 pour obtenir les résultats finaux.
La figure 4 montre la concentration d’équilibre de la glycine hydratée calculée dans le tableau 4 en fonction de la température à 100 % d’humidité relative et à 1 pression de l’atmosphère. Il montre que, comme la température diminue de 298,15K à 216.65K, la concentration de glycine non hydratée (n '0) diminue et ceux de la glycine hydratée augmente. Le dihydrate de glycine (n-2) augmente considérablement avec la température décroissante tandis que le changement dans la concentration d’autres hydrates est moins perceptible. Ces corrélations inverses entre la température et la concentration d’hydrates sont compatibles avec l’attente que les énergies libres inférieures De Gibbs d’hydratations à des températures plus basses favorisent la formation d’hydrates.
La figure 5 illustre la dépendance relative à l’humidité de la concentration d’équilibre des hydrates de glycine à 298,15 K et 1 pression de l’atmosphère. Il démontre clairement qu’à mesure que les RH augmentent de 20 % à 100 %, la concentration d’hydrates (n-gt;0) augmente au détriment de la glycine non hydratée (n-0). Une fois de plus, la corrélation directe entre l’humidité relative et la concentration des hydrates est compatible avec l’idée que la présence d’un plus grand nombre de molécules d’eau à un RH plus élevé favorise la formation d’hydrates.
Tel que présenté, ce protocole donne une compréhension qualitative des populations de glycine hydratées dans l’atmosphère. En supposant une concentration initiale de glycine isolée de 2,9 millions de molécules par centimètre cube, nous constatons que la glycine non hydratée (n-0) est l’espèce la plus abondante dans la plupart des conditions, à l’exception de T-216.65K et RH-100%. Le dihydrate (n'2), qui a l’énergie sans Gibbs séquentielle la plus faible de l’hydratation à toutes les trois températures, est l’hydrate le plus abondant dans les conditions considérées ici. On prévoit que les hydrates monohydrat (n-1) et les plus grands hydrates (n'3) se trouveraient en quantités négligeables. Lors de l’inspection de la figure 3, l’abondance des grappes n 1-4 peut être liée à la stabilité et à la souche du réseau de liaisons hydrogène des grappes. Ces grappes ont les molécules d’eau de l’hydrogène collé à la mésety d’acide carboxylique de la glycine dans une géométrie ressemblant étroitement à celles de diverses structures d’anneau à hydrogène, ce qui les rend particulièrement stables.
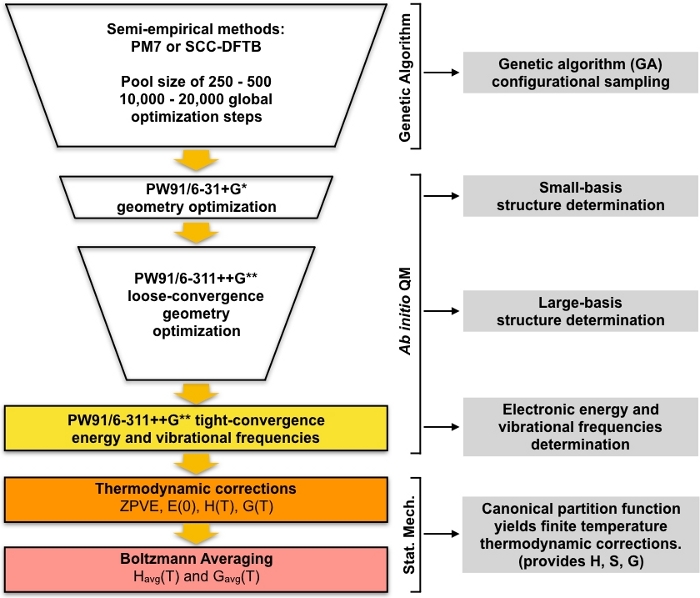
Figure 1 : Description schématique de la procédure actuelle. Un grand bassin de structures de devinettes générées par l’algorithme génétique (GA) est affiné par une série d’optimisations de géométrie PW91 jusqu’à ce qu’un ensemble de structures convergentes soient obtenus. Les fréquences vibratoires de ces structures sont calculées et utilisées pour calculer l’énergie libre Gibbs de formation, qui est à son tour utilisée pour calculer les concentrations d’équilibre des amas dans des conditions ambiantes. S’il vous plaît cliquez ici pour voir une version plus grande de ce chiffre.
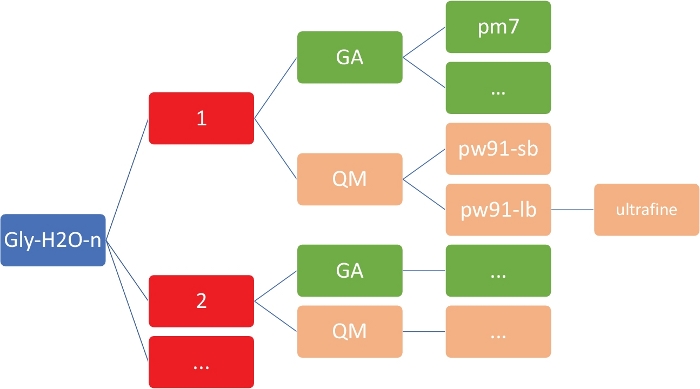
Figure 2 : Structure d’annuaire représentative pour chaque cluster. Les scripts internes inclus dans ce protocole nécessitent la structure du répertoire indiqué ci-dessus, où n est le nombre de molécules d’eau. Pour chaque n en gly-h2o-n, il y a les sous-directeurs suivants : GA pour algorithme génétique avec un répertoire GA/pm7, QM pour la mécanique quantique avec QM/pw91-sb pour PW91/6-31-GMD, QM/pw91-lb pour PW91/6-311 GMD, et QM/pw91-lb/ultrafine pour les optimisations et les calculs vibratoires finaux sur les grilles d’intégration ultrafines. S’il vous plaît cliquez ici pour voir une version plus grande de ce chiffre.
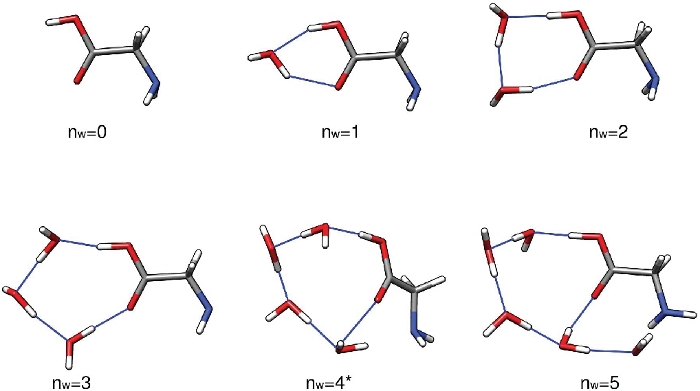
Figure 3 : Structures représentatives à faible consommation d’énergie de Gly(H2O)n'0-5. Ces grappes étaient les minima mondiaux d’énergie électronique optimisés au niveau de théorie PW91/6-311-G. S’il vous plaît cliquez ici pour voir une version plus grande de ce chiffre.
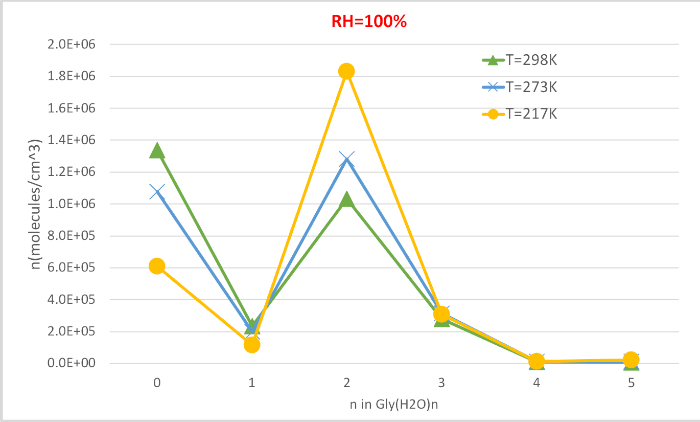
Figure 4 : Dépendance à la température de Gly (H2O)n-0-5 comme humidité relative de 100 % et 1 pression au guichet. La concentration des hydrates est donnée dans des unités de molécules cm-3. S’il vous plaît cliquez ici pour voir une version plus grande de ce chiffre.
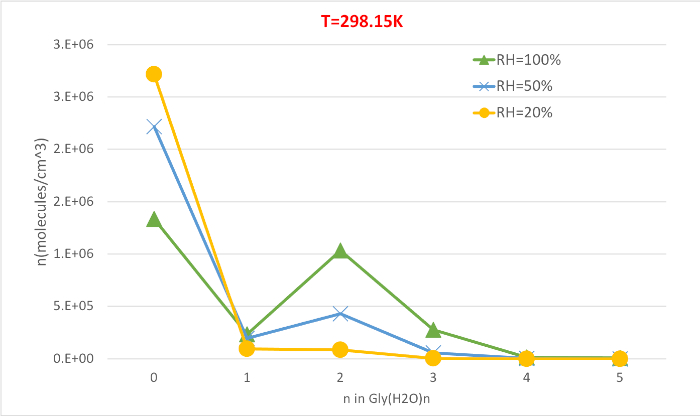
Figure 5 : Dépendance relative à l’humidité de Gly (H2O)n-0-5 comme 298,15 K et 1 pression au guichet. La concentration des hydrates est donnée dans des unités de molécules cm-3. S’il vous plaît cliquez ici pour voir une version plus grande de ce chiffre.
| E[PW91/6-311-G] | 216,65 K | 273,15 K | 298,15 K | ||||||||
| LB-UF | ZPVE (ZPVE) | H | S | G G | H | S | G G | H | S | G G | |
| Eau | -76.430500 | 13.04 | 1.72 | 42.59 | 5.54 | 2.17 | 44.44 | 3.08 | 2.37 | 45.14 | 1.96 |
| Glycine | -284.434838 | 48.55 | 2.65 | 69.53 | 36.14 | 3.70 | 73.81 | 32.09 | 4.22 | 75.61 | 30.22 |
Tableau 1 : Énergies monomer. Les énergies électroniques sont dans les unités de Hartree tandis que toutes les autres quantités sont dans des unités de mol kcal-1. L’eau et la glycine ont été optimisées au niveau de théorie et de fréquences vibratoires PW91/6-311-GMD. Les corrections thermodynamiques pour une pression de 1 atm et la température de 298,15 K ont été calculées à l’aide du script thermo.pl.
| E[PW91/6-311-G] | 0 K | 216,65 K | 273,15 K | 298,15 K | ||||||||
| ¡n | Nom | LB-UF | ZPVE (ZPVE) | H | S | G G | H | S | G G | H | S | G G |
| 1 | gly-h2o-1 | -360.88481 | 63.96 | 3.61 | 80.12 | 50.22 | 5.12 | 86.27 | 45.52 | 5.85 | 88.83 | 43.33 |
| 2 | gly-h2o-2 | -437.33763 | 79.33 | 4.53 | 90.86 | 64.17 | 6.46 | 98.78 | 58.81 | 7.40 | 102.06 | 56.30 |
| 3 | gly-h2o-3 | -513.78620 | 94.52 | 5.67 | 105.08 | 77.42 | 8.08 | 114.94 | 71.19 | 9.23 | 119.00 | 68.27 |
| 4 | gly-h2o-4 | -590.23667 | 109.80 | 6.03 | 104.98 | 91.30 | 8.78 | 116.21 | 84.40 | 10.11 | 120.87 | 81.14 |
| 5 | gly-h2o-5 | -666.68845 | 125.80 | 7.26 | 121.70 | 106.69 | 10.47 | 134.83 | 99.44 | 12.01 | 140.24 | 96.00 |
Tableau 2 : Énergies de cluster. Les énergies des structures Gly (H2O)n-1-5 à faible énergie trouvées à l’aide de notre procédure décrites dans la figure 1. Les énergies électroniques sont dans les unités de Hartree tandis que toutes les autres quantités sont dans des unités de mol kcal-1.
| Hydratation totale: Gly nH2O 'lt;-gt; Gly (H2O)n | Hydratation séquentielle: Gly (H2O)n-1 - H2O 'lt;-gt; Gly (H2O)n | ||||||||||||||||
| E[PW91/6-311-G] | 216.65 | 273.15 | 298.15 | 216.65 | 273.15 | 298.15 | |||||||||||
| ¡n | nom du système | LB-UF | E (0) | H (T) | G (T) | H (T) | G (T) | H (T) | G (T) | LB-UF | E (0) | H (T) | G (T) | H(T) | G (T) | H (T) | G (T) |
| 1 | gly-h2o-1 | -12.22 | -9.85 | -10.61 | -3.68 | -10.61 | -1.87 | -10.59 | -1.07 | -12.22 | -9.85 | -10.61 | -3.68 | -10.61 | -1.87 | -10.59 | -1.07 |
| 2 | gly-h2o-2 | -26.22 | -21.53 | -23.10 | -9.27 | -23.11 | -5.66 | -23.09 | -4.06 | -14.00 | -11.68 | -12.49 | -5.59 | -12.50 | -3.79 | -12.50 | -2.99 |
| 3 | gly-h2o-3 | -37.56 | -30.72 | -32.88 | -12.90 | -32.87 | -7.69 | -32.82 | -5.38 | -11.34 | -9.19 | -9.78 | -3.63 | -9.76 | -2.03 | -9.73 | -1.32 |
| 4 | gly-h2o-4 | -50.10 | -40.34 | -43.48 | -15.87 | -43.54 | -8.71 | -43.51 | -5.55 | -12.54 | -9.62 | -10.60 | -2.97 | -10.67 | -1.02 | -10.69 | -0.17 |
| 5 | gly-h2o-5 | -63.45 | -51.41 | -55.42 | -20.58 | -55.51 | -11.48 | -55.48 | -7.45 | -13.35 | -11.07 | -11.94 | -4.71 | -11.97 | -2.77 | -11.97 | -1.90 |
Tableau 3 : Énergies d’hydratation. L’énergie totale de l’hydratation et de l’énergie de l’hydratation séquentielle pour Gly (H2O)n 1-5 dans les unités de kcal mol-1. Ici, E[PW91/6-311-G] est le changement dans l’énergie électronique, E(0) est l’énergie vibratoire zéro point (ZPVE) changement corrigé de l’énergie, H(T) est le changement enthalpy à la température T, et G(T) est le changement d’énergie libre Gibbs de l’hydratation de chaque Gly (H2O)n '1-5 cluster.
| Répartition des hydrates d’équilibre en fonction de la température et de l’humidité relative | |||||||||
| T-298.15K | T-273.15K | T-216.65K | |||||||
| Gly (H2O)n | RH 100% | RH-50% | RH-20% | RH 100% | RH-50% | RH-20% | RH 100% | RH-50% | RH-20% |
| 0 | 1.3E 06 | 2.2E-06 | 2.7E 06 | 1.1E-06 | 2.0E 06 | 2.7E 06 | 6.1E-05 | 1.5E 06 | 2.5E 06 |
| 1 | 2.3E 05 | 1.9E 05 | 9.5E-04 | 2.0E 05 | 1.9E 05 | 9.9E-04 | 1.2E 05 | 1.5E 05 | 9.5E-04 |
| 2 | 1.0E 06 | 4.3E 05 | 8.4E 04 | 1.3E 06 | 6.1E-05 | 1.3E 05 | 1.8E 06 | 1.1E-06 | 3.0E 05 |
| 3 | 2.8E 05 | 5.8E 04 | 4.5E 03 | 3.2E 05 | 7.4E 04 | 6.3E 03 | 3.1E-05 | 9.6E-04 | 1.0E 04 |
| 4 | 1.1E-04 | 1.1E 03 | 3.4E 01 | 1.3E 04 | 1.5E 03 | 5.0E 01 | 1.1E-04 | 1.8E 03 | 7.5E 01 |
| 5 | 7.5E 03 | 3.9E 02 | 4.9E 00 | 1.2E 04 | 7.2E 02 | 9.7E-00 | 2.4E 04 | 1.9E 03 | 3.1E-01 |
Tableau 4 : Les concentrations d’hydrates d’équilibre de Gly (H2O)n-0-5 en fonction de la température de la fonction (T-298.15K, 273.15K, 216.65K) et l’humidité relative (RH-100%, 50%, 20%). La concentration des hydrates est donnée dans des unités de molécules cm-3 en supposant des valeurs expérimentales56,57,58, de [Gly]0 - 2,9 x 106 cm-3 et [H2O] - 7,7 x 101017 cm-3, 1,6 x 1017 cm-3 et 9,9 x 1014 cm-3 à 100% humidité relative et T 298,15 K, 273,15 K, et 216,65 K, respectivement59.
Fichiers supplémentaires. S’il vous plaît cliquez ici pour télécharger ces fichiers.
Discussion
L’exactitude des données générées par ce protocole dépend principalement de trois choses : (i) la variété des configurations échantillonnées par l’étape 2, (ii) la précision de la structure électronique du système, (iii) et la précision des corrections thermodynamiques. Chacun de ces facteurs peut être abordé en modifiant la méthode en éditant les scripts inclus. Le premier facteur est facilement surmonté avec l’utilisation d’un plus grand bassin initial de structures générées au hasard, des itérations plus nombreuses de l’AG, et une définition plus souple des critères impliqués dans l’AG. En outre, on peut utiliser une méthode semi-empirique différente comme le modèle de fixation serrée-fonctionnelle de densité de charge auto-cohérente (SCC-DFTB)62 modèle et le potentiel de fragment efficace (EFP)63 modèle afin d’explorer les effets de différentes descriptions physiques. La principale limitation ici est l’incapacité de la méthode à former ou briser les liaisons covalentes, ce qui signifie que les monomères sont gelés. La procédure d’AG ne trouve que les positions relatives les plus stables de ces monomères congelés selon la description semi-empirique.
L’exactitude de la structure électronique du système peut être améliorée de diverses façons, chacune avec son coût de calcul. On peut choisir une meilleure densité fonctionnelle, comme M06-2X64 et wB97X-V65, ou mécanique quantique (QM) méthode comme le M-ller-Plesset66,67,68 (MPn) théories de perturbation et couplé-cluster69 (CC) méthodes afin d’améliorer la description physique du système. Dans la hiérarchie des fonctions, les performances s’améliorent généralement en passant de fonctions d’approximation généralisée-gradient (GGA) comme PW91 aux fonctions hybrides séparées à la portée comme wB97X-D et méta-GGA fonctions hybrides comme M06-2X.
L’inconvénient des méthodes DFT est qu’une convergence systématique vers une valeur précise n’est pas possible; cependant, les méthodes DFT sont computationnellement peu coûteuses et il y a une grande variété de fonctions pour une grande variété d’applications.
Energies calculées à l’aide de méthodes de fonction d’onde comme MP2 et CCSD(T) en conjonction avec des ensembles de base cohérents de corrélation de nombre cardinal croissant ([aug-]cc-pV[D,T,Q,...] Z) convergent vers leur limite complète de base définie systématiquement, mais le coût de calcul de chaque calcul devient prohibitif à mesure que la taille du système augmente. Un plus grand raffinement de la structure électronique peut être réalisé en utilisant des ensembles de base explicitement corrélés70 et en extrapolant à la limite de base complète (CBS)71. Nos travaux récents suggèrent qu’une approche perturbative de second ordre explicitement corrélée et en corrélation explicite de densité M’ller-Plesset (DF-MP2-F12) donne des énergies approchant celle des calculs MP2/CBS32. La modification du protocole actuel pour utiliser différentes méthodes de structure électronique comporte deux étapes : (i) préparer un fichier d’entrée de modèle suivant la syntaxe donnée par le logiciel, (ii) et modifier les scripts run-pw91-sb.csh, run-pw91-lb.csh, et exécuter-pw91-lb-ultrafine.csh scripts pour générer la syntaxe fichier d’entrée correcte ainsi que le script de soumettre correctement pour le logiciel.
Enfin, l’exactitude des corrections thermodynamiques dépend de la méthode de la structure électronique ainsi que de la description du PSE autour du minimum global. Une description précise du PSE exige le calcul des dérivés de troisième et plus haut débit du PSE en ce qui concerne les déplacements dans les degrés nucléaires de liberté, tels que le champ de la force quartique72,73 (QFF), ce qui est une tâche exceptionnellement coûteuse. Le protocole actuel utilise l’approximation harmonique des oscillateurs aux fréquences vibratoires, ce qui entraîne la nécessité de calculer seulement jusqu’à la deuxième dérivé du PSE. Cette approche devient problématique dans les systèmes à forte harmonie, tels que les molécules très disquettes et les potentiels symétriques à double puits en raison de la grande différence dans le vrai PSE et le PSE harmonique. En outre, le coût d’avoir un PSE de haute qualité à partir d’une méthode de structure électronique exigeante en calcul ne fait qu’aggraver le problème du coût des calculs de fréquence vibratoire. Une approche pour surmonter cela est d’utiliser les énergies électroniques à partir d’un calcul de structure électronique de haute qualité avec des fréquences vibratoires calculées sur un PSE de qualité inférieure, résultant en un équilibre entre le coût et la précision. Le protocole actuel peut être modifié pour utiliser différentes descriptions de PSE telles que décrites dans le paragraphe précédent; cependant, on peut également modifier les mots-clés de fréquence vibratoire dans les scripts et les modèles pour calculer les fréquences vibratoires anharmoniques.
Deux questions cruciales pour tout protocole d’échantillonnage de configuration sont la méthode initiale pour l’échantillonnage de la surface énergétique potentielle et les critères utilisés pour identifier chaque cluster. Nous avons fait un usage intensif d’une variété de méthodes dans nos travaux précédents. Pour le premier numéro, la méthode initiale pour l’échantillonnage de la surface énergétique potentielle, nous avons fait le choix d’utiliser l’AG avec des méthodes semi-empiriques basées sur ces facteurs. Échantillonnage configurationnel à l’aide de l’intuition chimique26, échantillonnage aléatoire, et la dynamique moléculaire (MD)29,30, ne parviennent pas à trouver des minima mondiaux putatifs régulièrement pour les grappes de plus de 10 monomers, comme nous l’avons observé dans nos études sur les grappes d’eau18. Nous avons utilisé avec succès le saut de bassin (BH) pour étudier le PES complexe de (H2O)1174, mais il a exigé l’inclusion manuelle de certains isomers potentiels à faible énergie l’algorithme BH n’a pas trouvé. Une comparaison de la performance de BH et GA dans la recherche du minimum mondial de grappes d’eau, (H2O)n '10-20 a démontré que l’AG a toujours trouvé le minimum mondial plus rapide que BH75. GA tel qu’il est mis en œuvre dans OGOLEM et CLUSTER est très polyvalent parce qu’il peut être appliqué à n’importe quel cluster moléculaire et il peut l’interface avec un grand nombre de paquets avec champ de force classique, semi-empirique, densité fonctionnelle, et ab initio capacités. Le choix du PM7 est motivé par sa vitesse et sa précision raisonnable. Pratiquement n’importe quelle autre méthode semi-empirique aurait un coût de calcul significativement plus élevé.
En ce qui concerne le deuxième numéro, nous avons exploré en utilisant différents critères pour identifier des structures uniques allant des énergies électroniques, des moments dipole, des RMSD qui se chevauchent et des constantes de rotation. L’utilisation de moments dipole s’est avérée difficile parce que les composants du moment dipole dépendaient de l’orientation de la molécule et le moment total de dipole était très sensible aux différences de géométrie de telle sorte qu’il était difficile de fixer des seuils déterminant est que les structures sont les mêmes ou uniques. Une combinaison d’énergies électroniques et de constantes de rotation s’est avérée la plus utile.
Les critères actuels pour juger deux structures uniques sont basés sur un seuil de différence d’énergie de 0,10 kcal mol-1 et une différence constante de rotation de 1%. Par conséquent, deux structures sont considérées comme différentes si leurs énergies diffèrent de plus de 0,10 kcal mol-1 (0,00015 a.u.) ET l’une de leurs trois constantes de rotation (A, B, C) diffèrent de plus de 1%. D’importants repères internes au fil des ans ont conclu que ces seuils étaient des choix raisonnables. Notre approche d’échantillonnage configurationnel et notre méthodologie de dépistage ont été appliquées à des grappes très faiblement liées telles que les hydrocarbures polyaromatiques complexes avec de l’eau76,77 ainsi que des hydrates de sulfate sternary fortement liés contenant de l’ammoniac et des amines32. Pour les grappes où il ya différents états de protonation à considérer, la meilleure approche est d’exécuter divers calculs d’AG, chacun commençant par des monomères dans différents états de protonation. Cela garantit que les structures avec différents états de protonation sont soigneusement examinées. Cependant, les calculs DFT de bas niveau permettent souvent aux états de protonation de changer au cours de l’optimisation de la géométrie, produisant ainsi l’état de protonation le plus stable indépendamment de la géométrie de départ.
Nos méthodes d’échantillonnage configurationnelle GA devraient bien fonctionner même pour les molécules disquettes tant que les codes GA sont interatronisés avec des méthodes générales non paramétrisées qui permettent aux monomères d’adopter différentes configurations au cours de la course GA. Par exemple, l’interaction de l’AG avec le PM7 permettrait aux structures des monomères de changer, mais si leurs liens se brisent comme cela se produirait lorsque les États protonation changent, les structures peuvent être rejetées en tant que candidats inacceptables.
Nous avons examiné différentes façons de corriger les lacunes de l’approximation harmonique, en particulier celles résultant de basses fréquences vibratoires. Il n’est pas difficile d’intégrer l’approximation quasi harmonique dans la méthodologie actuelle. Cependant, il ya encore des questions sur la méthode quasi-harmonique, en particulier quand il s’agit de la fréquence de coupure ci-dessous laquelle il sera appliqué. En outre, il n’y a pas d’ouvrages de benchmarking rigoureux examinant la fiabilité de l’approximation quasi-RRHO, même si la sagesse conventionnelle suggère qu’il devrait être une amélioration par rapport à l’approximation RRHO.
Le protocole ainsi présenté peut être généralisé à n’importe quel système de clusters moléculaires de phase de gaz non liés. Il peut également être généralisé d’utiliser n’importe quelle méthode semi-empirique, méthode de structure électronique et logiciel, et méthode d’analyse vibratoire et logiciel en éditant les scripts et les modèles. Cela suppose que l’utilisateur est à l’aise avec l’interface Linux de ligne de commande, le script Python, et l’informatique haute performance. La syntaxe et l’apparence inconnues du système d’exploitation Linux et le manque d’expérience de script est le plus grand piège dans ce protocole et est l’endroit où les nouveaux étudiants luttent le plus. Ce protocole a été utilisé avec succès dans une variété d’implémentations pendant des années dans notre groupe, principalement en se concentrant sur les effets de l’acide sulfurique et l’ammoniac sur la formation d’aérosols. D’autres améliorations à ce protocole impliqueront une interface plus robuste à plus de logiciels de structure électronique, des implémentations alternatives de l’algorithme génétique, et peut-être l’utilisation de nouvelles méthodes pour des calculs plus rapides des énergies électroniques et vibratoires. Nos applications actuelles de ce protocole explorent l’importance des acides aminés dans les premiers stades de la formation d’aérosols dans l’atmosphère actuelle et dans la formation de molécules biologiques plus grandes dans des environnements prébiotiques.
Déclarations de divulgation
Aucun.
Remerciements
Ce projet a été soutenu par des subventions CHE-1229354, CHE-1662030, CHE-1721511 et CHE-1903871 de la National Science Foundation (GCS), l’Arnold and Mabel Beckman Foundation Beckman Scholar Award (AGG), et la bourse Barry M. Goldwater (AGG). Des ressources informatiques haute performance du Consortium MERCURY (http://www.mercuryconsortium.org) ont été utilisées.
matériels
| Name | Company | Catalog Number | Comments |
| Avogadro | https://avogadro.cc | Open-source molecular visualization program | |
| Gaussian [09/16] Software | http://www.gaussian.com/ | Commercial ab initio electronic structure program | |
| MOPAC 2016 | http://openmopac.net/MOPAC2016.html | Open-source semi-empirical program | |
| OGOLEM Software | https://www.ogolem.org | Genetic algorithm-based global optimization program | |
| OpenBabel | http://openbabel.org/wiki/Main_Page | Open-source cheminformatics library | |
| calcRotConsts.py | Shields Group, Department of Chemistry, Furman University | Python script to compute rotational constants | |
| calcSymmetry.csh | Shields Group, Department of Chemistry, Furman University | Shell script to calculate symmetry number of a molecule given Cartesian coordinates | |
| combine-GA.csh | Shields Group, Department of Chemistry, Furman University | Shell script to combine energy and rotational constants from different GA directories | |
| combine-QM.csh | Shields Group, Department of Chemistry, Furman University | Shell script to combine energy and rotational constants from different QM directories | |
| gaussianE.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract Gaussian 09 energies | |
| gaussianFreqs.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract Gaussian 09 vibrational frequencies | |
| getrotconsts | Shields Group, Department of Chemistry, Furman University | Executable to calculate rotational constants given a molecule's Cartesian coordinates | |
| getRotConsts-dft-lb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of large basis DFT optimized structures | |
| getRotConsts-dft-lb-ultrafine.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of ultrafine DFT optimized structures | |
| getRotConsts-dft-sb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of small basis DFT optimized structures | |
| getRotConsts-GA.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of genetic algorithm optimized structures | |
| global-minimum-coords.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of global minimum structures of gly-(h2o)n, where n=0-5 | |
| make-thermo-gaussian.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract data from Gaussian output files and make input files for the thermo.pl script | |
| ogolem-input-file.ogo | Shields Group, Department of Chemistry, Furman University | Ogolem sample input file | |
| ogolem-submit-script.pbs | Shields Group, Department of Chemistry, Furman University | PBS batch submission file for Ogolem calculations | |
| README.docx | Shields Group, Department of Chemistry, Furman University | Clarifications to help readers use the scripts effectively | |
| runogolem.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run OGOLEM | |
| run-pw91-lb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of large basis DFT optimization calculations | |
| run-pw91-lb-ultrafine.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of ultrafine DFT optimization calculations | |
| run-pw91-sb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of small basis DFT optimization calculations | |
| run-thermo-pw91.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute the thermodynamic corrections for a batch of DFT optimized structures | |
| similarityAnalysis.py | Shields Group, Department of Chemistry, Furman University | Python script to determine unique structures based on rotational constants and energies | |
| symmetry | Shields Group, Department of Chemistry, Furman University | Executable to calculate molecular symmetry given Cartesian coordinates | |
| symmetry.c | (C) 1996, 2003 S. Patchkovskii, Serguei.Patchkovskii@sympatico.ca | C code to determine the molecular symmstry of a molecule given Cartesian coordinates | |
| template-marcy.pbs | Shields Group, Department of Chemistry, Furman University | Template for a PBS submit script which uses OGOLEM | |
| template-pw91.com | Shields Group, Department of Chemistry, Furman University | Template Gaussian 09 input | |
| template-pw91-HL.com | Shields Group, Department of Chemistry, Furman University | Template Gaussian 09 input for ultrafine DFT optimization | |
| thermo.pl | https://www.nist.gov/mml/csd/chemical-informatics-research-group/products-and-services/program-computing-ideal-gas | Perl open-source script to compute ideal gas thermodynamic corrections | |
| gly-h2o-n.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet for the complete protocol | |
| table-1.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-2.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-3.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-4.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| water.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of water | |
| glycine.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of glycine |
Références
- Foster, P., Ramaswamy, V., Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., Tignor, M., Miller, H. L. . Climate Change 2007 The Scientific Basis. , (2007).
- Kulmala, M., et al. Toward direct measurement of atmospheric nucleation. Science. 318 (5847), 89-92 (2007).
- Sipila, M., et al. The role of sulfuric acid in atmospheric nucleation. Science. 327 (5970), 1243-1246 (2010).
- Jiang, J., et al. First measurement of neutral atmospheric cluster and 1 - 2 nm particle number size distributions during nucleation events. Aerosol Science and Technology. 45 (4), (2011).
- Dunn, M. E., Pokon, E. K., Shields, G. C. Thermodynamics of forming water clusters at various Temperatures and Pressures by Gaussian-2, Gaussian-3, Complete Basis Set-QB3, and Complete Basis Set-APNO model chemistries; implications for atmospheric chemistry. Journal of the American Chemical Society. 126 (8), 2647-2653 (2004).
- Pickard, F. C., Pokon, E. K., Liptak, M. D., Shields, G. C. Comparison of CBSQB3, CBSAPNO, G2, and G3 thermochemical predictions with experiment for formation of ionic clusters of hydronium and hydroxide ions complexed with water. Journal of Chemical Physics. 122, 024302 (2005).
- Pickard, F. C., Dunn, M. E., Shields, G. C. Comparison of Model Chemistry and Density Functional Theory Thermochemical Predictions with Experiment for Formation of Ionic Clusters of the Ammonium Cation Complexed with Water and Ammonia; Atmospheric Implications. Journal of Physical Chemistry A. 109 (22), 4905-4910 (2005).
- Alongi, K. S., Dibble, T. S., Shields, G. C., Kirschner, K. N. Exploration of the Potential Energy Surfaces, Prediction of Atmospheric Concentrations, and Vibrational Spectra of the HO2•••(H2O)n (n=1-2) Hydrogen Bonded Complexes. Journal of Physical Chemistry A. 110 (10), 3686-3691 (2006).
- Allodi, M. A., Dunn, M. E., Livada, J., Kirschner, K. N. Do Hydroxyl Radical-Water Clusters, OH(H2O)n, n=1-5, Exist in the Atmosphere. Journal of Physical Chemistry A. 110 (49), 13283-13289 (2006).
- Kirschner, K. N., Hartt, G. M., Evans, T. M., Shields, G. C. In Search of CS2(H2O)n=1-4 Clusters. Journal of Chemical Physics. 126, 154320 (2007).
- Hartt, G. M., Kirschner, K. N., Shields, G. C. Hydration of OCS with One to Four Water Molecules in Atmospheric and Laboratory Conditions. Journal of Physical Chemistry A. 112 (19), 4490-4495 (2008).
- Morrell, T. E., Shields, G. C. Atmospheric Implications for Formation of Clusters of Ammonium and 110 Water Molecules. Journal of Physical Chemistry A. 114 (12), 4266-4271 (2010).
- Temelso, B., et al. Quantum Mechanical Study of Sulfuric Acid Hydration: Atmospheric Implications. Journal of Physical Chemistry A. 116 (9), 2209 (2012).
- Husar, D. E., Temelso, B., Ashworth, A. L., Shields, G. C. Hydration of the Bisulfate Ion: Atmospheric Implications. Journal of Physical Chemistry A. 116 (21), 5151-5163 (2012).
- Bustos, D. J., Temelso, B., Shields, G. C. Hydration of the Sulfuric Acid – Methylamine Complex and Implications for Aerosol Formation. Journal of Physical Chemistry A. 118 (35), 7430-7441 (2014).
- Wales, D. J., Scheraga, H. A. Global optimization of clusters, crystals, and biomolecules. Science. 27 (5432), 1368-1372 (1999).
- Day, M. B., Kirschner, K. N., Shields, G. C. Global search for minimum energy (H2O)n clusters, n = 3 - 5. The Journal of Physical Chemistry A. 109 (30), 6773-6778 (2005).
- Shields, R. M., Temelso, B., Archer, K. A., Morrell, T. E., Shields, G. C. Accurate predictions of water cluster formation, (H2O)n=2-10. The Journal of Physical Chemistry A. 114 (43), 11725-11737 (2010).
- Temelso, B., Archer, K. A., Shields, G. C. Benchmark structures and binding energies of small water clusters with anharmonicity corrections. The Journal of Physical Chemistry A. 115 (43), 12034-12046 (2011).
- Temelso, B., Shields, G. C. The role of anharmonicity in hydrogen-bonded systems: The case of water clusters. The Journal of Chemical Theory and Computation. 7 (9), 2804-2817 (2011).
- Von Freyberg, B., Braun, W. Efficient search for all low energy conformations of polypeptides by Monte Carlo methods. The Journal of Computational Chemistry. 12 (9), 1065-1076 (1991).
- Rakshit, A., Yamaguchi, T., Asada, T., Bandyopadhyay, P. Understanding the structure and hydrogen bonding network of (H2O)32 and (H2O)33: An improved Monte Carlo temperature basin paving (MCTBP) method of quantum theory of atoms in molecules (QTAIM) analysis. RSC Advances. 7 (30), 18401-18417 (2017).
- Deaven, D. M., Ho, K. M. Molecular geometry optimization with a genetic algorithm. Physical Review Letters. 75, 288-291 (1995).
- Hartke, B. Application of evolutionary algorithms to global cluster geometry optimization. Applications of Evolutionary Computation in Chemistry. , (2004).
- Dieterich, J. M., Hartke, B. OGOLEM: Global cluster structure optimization for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach. Molecular Physics. 108 (3-4), 279-291 (2010).
- Herb, J., Nadykto, A. B., Yu, F. Large ternary hydrogen-bonded pre-nucleation clusters in the Earth's atmosphere. Chemical Physics Letters. 518, 7-14 (2011).
- Ortega, I. K., et al. From quantum chemical formation free energies to evaporation rates. Atmospheric Chemistry and Physics. 12 (1), 225-235 (2012).
- Elm, J., Bilde, M., Mikkelsen, K. V. Influence of Nucleation Precursors on the Reaction Kinetics of Methanol with the OH Radical. Journal of Physical Chemistry A. 117 (30), 6695-6701 (2013).
- Loukonen, V., et al. Enhancing effect of dimethylamine in sulfuric acid nucleation in the presence of water - a computational study. Atmospheric Chemistry and Physics. 10 (10), 4961-4974 (2010).
- Temelso, B., Phan, T. N., Shields, G. C. Computational study of the hydration of sulfuric acid dimers: implications for acid dissociation and aerosol formation. Journal of Physical Chemistry A. 116 (39), 9745-9758 (2012).
- Jiang, S., et al. Study of Cl-(H2O)n (n = 1-4) using basin-hopping method coupled with density functional theory. Journal of Computational Chemistry. 35 (2), 159-165 (2014).
- Temelso, B., et al. Effect of mixing ammonia and alkylamines on sulfate aerosol formation. Journal of Physical Chemistry A. 122 (6), 1612-1622 (2018).
- Perdew, J. P., Ruzsinszky, A., Tao, J. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. Journal of Chemical Physics. 123, 062201 (2005).
- Riplinger, C., Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. Journal of Chemical Physics. 138, 034106 (2013).
- Riplinger, C., Pinski, P., Becker, U., Valeev, E. F., Neese, F. Sparse maps--A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. Journal of Chemical Physics. 144 (2), 024109 (2016).
- Kildgaard, J. V., Mikkelsen, K. V., Bilde, M., Elm, J. Hydration of atmospheric molecular clusters: a new method for systematic configurational sampling. Journal of Physical Chemistry A. 122 (22), 5026-5036 (2018).
- González, &. #. 1. 9. 3. ;. Measurement of areas on a sphere Using Fibonacci and latitude-longitude lattices. Mathematical Geosciences. 42, 49-64 (2010).
- Karaboga, D., Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing. 8 (1), 687-697 (2008).
- Zhang, J., Doig, M. Global optimization of rigid molecules using the artificial bee colony algorithm. Physical Chemistry Chemical Physics. 18 (4), 3003-3010 (2016).
- Kubecka, J., Besel, V., Kurten, T., Myllys, N., Vehkamaki, H. Configurational sampling of noncovalent (atmospheric) molecular clusters: sulfuric acid and guanidine. Journal of Physical Chemistry A. 123 (28), 6022-6033 (2019).
- Grimme, S., Bannwarth, C., Shushkov, P. A Robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent Interactions of large molecular systems parametrized for all spd-block elements (Z = 1-86). Journal of Chemical Theory and Computation. 13 (5), 1989-2009 (2017).
- Buck, U., Pradzynski, C. C., Zeuch, T., Dieterich, J. M., Hartke, B. A size resolved investigation of large water clusters. Physical Chemistry Chemical Physics. 16 (15), 6859 (2014).
- Forck, R. M., et al. Structural diversity in sodium doped water trimers. Physical Chemistry Chemical Physics. 14 (25), 9054-9057 (2012).
- Witt, C., Dieterich, J. M., Hartke, B. Cluster structures influenced by interaction with a surface. Physical Chemistry Chemical Physics. 20 (23), 15661-15670 (2018).
- Freitbert, A., Dieterich, J. M., Hartke, B. Exploring self-organization of molecular tether molecules on a gold surface by global structure optimization. The Journal of Computational Chemistry. 40 (22), 1978-1989 (2019).
- Stewart, J. J. P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. The Journal of Molecular Modeling. 19 (1), 1-32 (2013).
- Burke, K., Perdew, J. P., Wang, Y. Derivation of a generalized gradient approximation: The PW91 density functional. Electronic Density Functional Theory. , 81-111 (1998).
- Frisch, M. J., et al. . Gaussian 09, Revision A.02. , (2016).
- Ditchfield, R., Hehre, W. J., Pople, J. A. Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. The Journal of Chemical Physics. 54 (2), 724 (1971).
- Elm, J., Bilde, M., Mikkelsen, K. V. Assessment of density functional theory in predicting structures and free energies of reaction of atmospheric prenucleation clusters. The Journal of Chemical Theory and Computation. 8 (6), 2071-2077 (2012).
- Elm, J., Mikkelsen, K. V. Computational approaches for efficiently modelling of small atmospheric clusters. Chemical Physics Letters. 615, 26-29 (2014).
- Bayucan, A., et al. . PBS Portable Batch System. , (1999).
- O'Boyle, N. M., et al. Open Babel: An open chemical toolbox. Journal of Cheminformatics. 3, 33 (2011).
- Csaszar, A. G. Conformers of gaseous glycine. Journal of the American Chemical Society. 114 (24), 9568-9575 (1992).
- Zhang, Q., Anastasio, C. Free and combined amino compounds in atmospheric fine particles (PM2.5) and fog waters from Northern California. Atmospheric Environment. 37 (16), 2247-2258 (2003).
- Matsumoto, K., Uematsu, M. Free amino acids in marine aerosols over the western North Pacific Ocean. Atmospheric Environment. 39 (11), 2163-2170 (2005).
- Mandalakis, M., Apostolaki, M., Stephanou, E. G. Trace analysis of free and combined amino acids in atmospheric aerosols by gas chromatography-mass spectrometry. Journal of Chromatography A. 1217 (1), 143-150 (2010).
- Seinfeld, J. H., Pandis, S. N. . Atmospheric Chemistry and Physics, 3rd Ed. , (2016).
- Myllys, N., Elm, J., Halonen, R., Kurten, T., Vehkamaki, H. Coupled cluster evaluation of atmospheric acid-base clusters with up to 10 molecules. The Journal of Physical Chemistry A. 120 (4), 621-630 (2016).
- Elm, J., Bilde, M., Mikkelsen, K. V. Assessment of binding energies of atmospherically relevant clusters. Physical Chemistry Chemical Physics. 15 (39), (2013).
- Elstner, M. The SCC-DFTB method and its application to biological systems. Theoretical Chemistry Accounts. 116 (1-3), 316-325 (2006).
- Kaliman, I. A., Slipchenko, L. V. LIBEFP: A new parallel implementation of the effective fragment potential method as a portable software library. The Journal of Computational Chemistry. 34 (26), 2284-2292 (2013).
- Zhao, Y., Truhlar, D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and trasition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theoretical Chemistry Accounts. 120 (1-3), 215-241 (2008).
- Mardirossian, N., Head-Gordon, M. wB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy. Physical Chemistry Chemical Physics. 16 (21), 9904-9924 (2014).
- Head-Gordon, M., Pople, J. A., Frisch, M. J. MP2 energy evaluation by direct methods. Chemical Physics Letters. 153 (6), 503-506 (1988).
- Pople, J. A., Seeger, R., Krishnan, R. Variational configuration interaction methods and comparison with perturbation theory. The International Journal of Quantum Chemistry. 12, 149-163 (1977).
- Pople, J. A., Binkley, J. S., Seeger, R. Theoretical models incorporating electron correlation. The International Journal of Quantum Chemistry. 10 (10), 1-19 (1976).
- Monkhorst, H. J. Calculation of properties with the coupled-cluster method. The International Journal of Quantum Chemistry. 12 (11), 421-432 (1977).
- Klopper, W., Manby, F. R., Ten-No, S., Valeev, E. F. R12 methods in explicitly correlated molecular electronic structure theory. International Reviews in Physical Chemistry. 25, 427-468 (2006).
- Hattig, C. Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core-valence and quintuple-z basis sets for H to Ar and QZVPP basis sets for Li to Kr. Physical Chemistry Chemical Physics. 7 (1), 59-66 (2005).
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. The Journal of Chemical Physics. 122, 014108 (2005).
- Barone, V. Vibrational zero-point energies and thermodynamic functions beyond the harmonic approximation. The Journal of Chemical Physics. 120 (7), 3059-3065 (2004).
- Temelso, B., et al. Exploring the Rich Potential Energy Surface of (H2O)11 and Its Physical Implications. Journal of Chemical Theory and Computation. 14 (2), 1141-1153 (2018).
- Kabrede, H., Hentschke, R. Global minima of water clusters (H2O)N, N≤25, described by three empirical potentials. Journal of Physical Chemistry B. 107 (16), (2003).
- Steber, A. L., et al. Capturing the Elusive Water Trimer from the Stepwise Growth of Water on the Surface of a Polycyclic Aromatic Hydrocarbon Acenaphthene. Journal of Physical Chemistry Letters. 8 (23), 5744-5750 (2017).
- Perez, C., et al. Corrannulene and its complex with water: A tiny cup of water. Physical Chemistry Chemical Physics. 19 (22), 14214-14223 (2017).
Réimpressions et Autorisations
Demande d’autorisation pour utiliser le texte ou les figures de cet article JoVE
Demande d’autorisationThis article has been published
Video Coming Soon