Method Article
Вычисление атмосферных концентраций молекулярных кластеров из термохимии ab initio
В этой статье
Резюме
Атмосферные концентрации слабо связанных молекулярных скоплений можно вычислить из термохимических свойств низкоэнергетических структур, найденных с помощью многоступенчатой методологии конфигурации выборки с использованием генетического алгоритма и полуэмпирической и ab initio квантовой химии.
Аннотация
Вычислительное исследование образования и роста атмосферных аэрозолей требует точной поверхности свободной энергии Гиббса, которая может быть получена из газовой фазы электронной структуры и вибрационных вычислений частоты. Эти количества действительны для тех атмосферных скоплений, геометрия которых соответствует минимуму по их потенциальным энергетическим поверхностям. Свободная энергия Гиббса минимальной энергетической структуры может быть использована для прогнозирования атмосферных концентраций скопления в различных условиях, таких как температура и давление. Мы представляем вычислительно недорогой процедуры, построенные на генетическом алгоритме на основе конфигурации выборки следуют ряд все более точные расчеты скрининга. Процедура начинается с генерации и развития геометрии большого набора конфигураций с использованием полуэмпирических моделей, а затем уточняет полученные уникальные структуры на ряде уровней теории ab initio высокого уровня. Наконец, термодинамические коррекции вычисляются для полученного набора минимальных энергетических структур и используются для вычисления свободных энергий образования, равновесных констант и атмосферных концентраций. Мы представляем применение этой процедуры для изучения гидратированных глицинных кластеров в условиях окружающей среды.
Введение
Наиболее неопределенным параметром в атмосферных исследованиях изменения климата является точная степень, в которой частицы облаков отражают поступающую солнечную радиацию. Аэрозоли, которые являются твердыми частицами, взвешенными в газе, образуют частицы облаков, называемые ядрами конденсации облаков (CCN), которые рассеивают поступающее излучение, тем самым предотвращая его поглощение и последующее нагревание атмосферы1. Детальное понимание этого эффекта чистого охлаждения требует понимания роста аэрозолей в CCNs, что, в свою очередь, требует понимания роста малых молекулярных скоплений в аэрозольные частицы. Недавняя работа показала, что образование аэрозолей инициируется молекулярными кластерами диаметром 3 нм или менее2; однако, этот режим размера трудно получить доступ с помощью экспериментальных методов3,4. Поэтому для преодоления этого экспериментального ограничения желательно принять подход к вычислительному моделированию.
Используя наш подход моделирования, описанный ниже, мы можем проанализировать рост любого гидратного кластера. Поскольку мы заинтересованы в роли воды в формировании крупных биологических молекул из небольших компонентов в добиотической среде, мы иллюстрируем наш подход глицином. Проблемы и инструменты, необходимые для решения этих вопросов исследования очень похожи на те, которые участвуют в изучении атмосферных аэрозолей и донуклеационных кластеров5,,6,,7,,8,9,,10,,11,12,13,14,15. Здесь мы исследуем гидратированные глицинные кластеры, начиная с изолированной молекулы глицина, за которыми следует серия пошаговых дополнений до пяти молекул воды. Конечная цель состоит в том, чтобы рассчитать равновесные концентрации скоплений Gly (H2O)n'0-5 в атмосфере при комнатной температуре на уровне моря и относительной влажности (RH) в 100%.
Небольшое число этих субнанометров молекулярных кластеров вырастают в метастабильное критическое скопление (1-3 нм в диаметре) либо путем добавления других молекул пара, либо свогуляющих на существующих кластерах. Эти критические кластеры имеют благоприятный профиль роста, ведущий к образованию гораздо больших (до 50-100 нм) ядер конденсации облаков (CCN), которые непосредственно влияют на эффективность осадков облаков, а также их способность отражать свет инцидента. Поэтому хорошее понимание термодинамики молекулярных скоплений и их равновесного распределения должно привести к более точным прогнозам воздействия аэрозолей на глобальный климат.
Описательная модель формирования аэрозолей требует точной термодинамики формирования молекулярного кластера. Вычисление точной термодинамики формирования молекулярного кластера требует идентификации наиболее стабильных конфигураций, что предполагает поиск глобальной и локальной минимальной на потенциальной энергетической поверхности кластера (PES)16. Этот процесс называется конфигурационной выборки и может быть достигнуто с помощью различных методов, в том числе на основе молекулярной динамики (MD)17,18,19,20, Монте-Карло (MC)21,22, и генетические алгоритмы (GA)23,24,25.
Различные протоколы были разработаны на протяжении многих лет для получения структуры и термодинамики атмосферных гидратов на высоком уровне теории. Эти протоколы отличались выбором (i) метода конфигурационной выборки, ii) характером метода низкого уровня, используемого в конфигурационной выборке, и iii) иерархией методов более высокого уровня, используемых для уточнения результатов в последующих шагах.
Конфигурационные методы отбора проб включали химическую интуицию26, случайную выборку27,,28,молекулярной динамики (MD)29,30, бассейн прыжков (BH)31, и генетический алгоритм (GA)24,25,32. Наиболее распространенными низкоуровневыми методами, используемыми с помощью этих методов отбора проб, являются силовые поля или полуэмпирические модели, такие как PM6, PM7 и SCC-DFTB. За ними часто следуют расчеты DFT с все более большими базовыми наборами и более надежными функциональными возможностями с более высоких ступеней лестницыИакова 33. В некоторых случаях за ними следуют методы волной более высокого уровня, такие как MP2, CCSD (T), а также экономически эффективные DLPNO-CCSD (T)34,35.
Kildgaard et al.36 разработали систематический метод, при котором молекулы воды добавляются в точках на сферах Фибоначчи37 вокруг небольших гидратированных или негидратированных кластеров для генерации кандидатов для больших кластеров. Нефизические и избыточные кандидаты удаляются на основе пороговых значений контакта и расстояния корня-квадрата между различными конформистами. Последующие оптимизации с использованием полуэмпирического метода PM6 и иерархии методов DFT и wavefunction используются для получения набора низкоэнергетических конформистов на высоком уровне теории.
Алгоритм искусственной пчелообразной колонии (ABC)38 представляет собой новый подход к выборке конфигурации, который недавно был реализован Чжан и др. для изучения молекулярных кластеров в программе под названием ABCluster39. Kubecka et al.40 использовали ABCluster для конфигурационной выборки с последующим низкоуровневым переоптимизацией с использованием герметичного полуэмпирического метода GFN-xTB41. Они дополнительно уточнили структуры и энергии с помощью методов DFT, а затем конечных энергий с использованием DLPNO-CCSD (T).
Независимо от метода, конфигурационная выборка начинается с случайно- или неслучайно генерируемого распределения точек на PES. Каждая точка соответствует конкретной геометрии рассматриваемого молекулярного кластера и генерируется методом выборки. Затем ближайший локальный минимум находится для каждой точки, следуя направлению «вниз» на PES. Таким образом, найденный набор минимы соответствует геометриям молекулярного скопления, которые стабильны, по крайней мере на некоторое время. Здесь форма PES и оценка энергии в каждой точке на поверхности будут чувствительны к физическому описанию системы, где более точное физическое описание приводит к более вычислительно-дорогому расчету энергии. Мы специально будем использовать метод GA, реализованный в программе OGOLEM25, который был успешно применен к различным глобальным проблемам оптимизации и конфигурации выборки42,,43,,44,,45, для создания первоначального набора точек отбора проб. PES будет описано PM7 модель46 реализованы в программе MOPAC201647. Эта комбинация используется потому, что она генерирует большее разнообразие точек по сравнению с методами MD и MC и находит локальные минимумы быстрее, чем более подробные описания PES.
Набор оптимизированных ГА локальных минимумов берется в качестве стартовой геометрии для серии скрининговых шагов, которые приводят к набору низколежащей минимальной энергии. Эта часть протокола начинается с оптимизации набора уникальных ОПтимизированных га структур с использованием плотной функциональной теории (DFT) с небольшим базовым набором. Этот набор оптимизаций, как правило, дает меньший набор уникальных локальных минимальных структур, которые моделируются более подробно по сравнению с ОПтимизированными ГА полуэмпирическими структурами. Затем на этом уменьшенном наборе структур выполняется еще один раунд оптимизации DFT с использованием более широкого базисного набора. Опять же, этот шаг, как правило, дают меньший набор уникальных структур, которые моделируются более подробно по сравнению с небольшой базой DFT шаг. Окончательный набор уникальных структур затем оптимизирован до более жесткой конвергенции и рассчитываются гармонические вибрационные частоты. После этого шага у нас есть все необходимое для вычисления равновесных концентраций скоплений в атмосфере. Общий подход обобщен диаграммонана на рисунке 1. Мы будем использовать PW9148 обобщенный градиент приближения (GGA) обмен-корреляции функциональных в Gaussian0949 реализации DFT вместе с двумя вариациями Pople50 базовый набор (6-31"G " для небольшой базовый шаг и 6-311 "G" для большого базисного шага). Данная комбинация валютно-корреляционного функционального и базисного набора была выбрана благодаря своему предыдущему успеху в вычислении точных свободных энергий образования Гиббса для атмосферных кластеров51,52.
Этот протокол предполагает, что пользователь имеет доступ к высокопроизводительным вычислительным (HPC) кластеру с портативной пакетной системой53 (PBS), MOPAC2016 (http://openmopac.net/MOPAC2016.html)47,OGOLEM (https://www.ogolem.org)25, Gaussian 09 (https://gaussian.com)49, и OpenBabel54 (http://openbabel.org/wiki/Main_Page программное обеспечение, установленное в соответствии с их конкретными инструкциями по установке. Каждый шаг в этом протоколе также использует набор внутренних оболочек и скриптов Python 2.7, которые должны быть сохранены в каталоге, который включен в $PATH экологической переменной пользователя. Все необходимые экологические модули и разрешения на выполнение всех вышеперечисленных программ также должны быть загружены в сеанс пользователя. Использование диска и памяти кодом GA (OGOLEM) и полуэмпирическими кодами (MOPAC) очень мало по современным стандартам компьютерных ресурсов. Общее использование памяти и диска для OGOLEM/MOPAC зависит от того, сколько потоков человек хочет использовать, и даже в этом случае использование ресурсов будет небольшим по сравнению с возможностями большинства систем HPC. Потребности в ресурсах методов КМ зависят от размера кластеров и уровня используемой теории. Преимущество использования этого протокола заключается в том, что можно варьировать уровень теории, чтобы иметь возможность вычислить окончательный набор низкоэнергетических структур, имея в виду, что обычно более быстрые расчеты приводят к большей неопределенности в точности результатов.
Для ясности локальный компьютер пользователя будет называться«локальным компьютером»,в то время как кластер HPC, к которому они имеют доступ, будет называться«удаленным кластером».
протокол
1. Поиск минимальной энергетической структуры изолированных глицина и воды
ПРИМЕЧАНИЕ: Цель здесь состоит в двух раз: i) получить минимальные энергетические структуры изолированных молекул воды и глицина для использования в генетическом алгоритме конфигурационных выборок, (ii) и вычислить термодинамические коррекции газовых фазовых энергий этих молекул для использования при расчете атмосферных концентраций.
- На локальном компьютере откройте новую сессию Avogadro.
- Нажмите Построить йgt; Вставить и пептид и выбрать Gly из окна вставить пептид для создания глицина мономер в окне визуализации.
- Нажмите На расширение (Acc2E-12,UltraFine) scf (conver-12) и отредконите первую строку в текстовом поле, чтобы прочитать:" pw91pw91/6-311-G'int (Acc2E-12,UltraFine) scf (conver-12) opt (жесткий, maxcyc'300) freq. Extensions > Gaussian Нажмите Generate и сохраните файл ввода вglycine.com.
- Пожалуйста, обратите внимание, что если молекула обладает значительной конформиальной гибкостью, так как глицин делает55,очень важно выполнить конформационный анализ для определения глобальной минимальной структуры и других низколежащих конформитов. OpenBabel54 предоставляет надежные конформационные поисковые инструменты с использованием различных алгоритмов и полей быстрой силы. В то время как конформии могут расслабиться и interconvert во время ГА и последующих расчетов, иногда необходимо запустить несколько расчетов ГА, каждый из которых начинается с другой конформера.
- На локальном компьютере откройте новую сессию в Avogadro.
- Нажмите Построить йgt; Вставить и фрагмент и поиск "воды" из окна Вставить Фрагмент, чтобы получить координаты воды.
- Нажмите На расширение (Acc2E-12,UltraFine) scf (conver-12) и отредконите первую строку в текстовом поле, чтобы прочитать:" pw91pw91/6-311-G'int (Acc2E-12,UltraFine) scf (conver-12) opt (жесткий, maxcyc'300) freq. Extensions > Gaussian Нажмите Generate и сохраните файл ввода в water.com.
- Перенесите два файла .com в удаленный кластер. Как только вы входите в удаленный кластер, позвоните Gaussian 09 в скрипте отправки пакетов, чтобы начать вычисление. Когда расчеты закончатся, извлеките декартовые координаты(файлы .xyz) минимальных энергетических структур, позвонив в OpenBabel. Для глицина, команда для выполнения является:
obabel -ig09 glycine.log -oxyz
Эти два файла .xyz будут использованы выборкой конфигурации GA на следующем этапе.
2. Генетическо-алгоритм-на основе конфигурационной выборки Gly (H2O)n-1-5 кластеров
ПРИМЕЧАНИЕ: Цель здесь состоит в том, чтобы получить набор низкоэнергетических структур для Gly (H2O)n'1-5 на недорогом полуэмпирическом уровне теории, используя модель PM746, реализованную в MOPAC47. Крайне важно, чтобы рабочий каталог имеет точную организацию и структуру, как показано на рисунке 2. Это необходимо для обеспечения того, чтобы пользовательские скрипты оболочки и Python работали без сбоев.
- Скопируйте все необходимые скрипты в удаленном кластере и добавьте их местоположение в $PATH
- Поместите все скрипты и файлы шаблонов в папку (например, скрипты) и скопируйте ее в удаленное кластер
- Убедитесь, что все скрипты исполняются
- Добавьте местоположение каталога скриптов в $PATH переменной окружающей среды, введя следующие команды в терминале. Расположение скриптов по умолчанию устанавливается для $HOME/JoVE-demo/scripts, однако можно определить экологическую переменную, называемую $SCRIPTS»HOME, указывая на каталог, содержащий сценарии, и добавить $SCRIPTS
- Bash оболочки:
экспорт SCRIPTS_HOME/путь/к/скриптам
экспорт ПАГЗ$SCRIPTS_HOME: $:PATH - Tcsh/Csh оболочка:
setenv SCRIPTS_HOME /путь/к/скриптам
setenv PATH $'SCRIPTS_HOME:$
- Bash оболочки:
- На удаленном кластере навлажьте и запустите расчет GA:
- Создайте каталог под названием gly-h2o-n, где n является число молекул воды.
- Создайте субдиректорпод название GA под каталогом gly-h2o-n для выполнения генетических вычислений алгоритмов.
- Копирование oGOLEM входных файлов (например, pm7.ogo), мономеров декартовых координат (например, glycine.xyz, water.xyz) и PBS пакетпредставления скрипа (например, run.pbs) в каталог ГА.
- Внести необходимые изменения в файл ввода OGOLEM и файл пакетной отправки.
- Отправить расчет. Когда начинается расчет, OGOLEM создаст новый каталог, названный в качестве префикса файла ввода OGOLEM (Например, pm7) в каталоге GA и хранит там вновь созданные координаты.
- Как только расчет завершен, составить энергии и константы вращения, и использовать эту информацию, чтобы определить, какие из них являются уникальными низкоэнергетическими структурами:
- Изменение каталога на gly-h2o-n/GA/pm7 и
- Извлеките энергии и вычислите вращающиеся константы оптимизированных га кластеров с командой:
getRotConsts-GA.csh N 0 99
где N — это количество атомов в молекулярном кластере и '0 99' указывает на то, что размер бассейна GA составляет 100, а индексы — от 0 до 99. Это позволит создать файл под названием rotConstsData_C который содержит отсортированный список всех оптимизированных конфигураций кластеров GA, их энергий и их констант вращения. - Выполните команду:
similarityAnalysis.py вечера 7 rotConstsData_C
где pm7 будет использоваться в качестве метки именования файлов, чтобы найти и сохранить уникальные кластеры, оптимизированные GA. Это позволит создать файл под названием uniqueStructures-pm7.data, который содержит отсортированный список уникальных ОПтимизированных конфигураций GA. Это список уникальных локальных минимальных структур для кластера Gly (H2O)n, оптимизированного на уровне теории PM7, и теперь эти структуры готовы к доработке с помощью DFT.
- Поднизись к каталогу gly-h2o-n/GA и объедините результаты нескольких сопоставимых ГА работает с помощью комбинированного-GA.csh скрипт. Синтаксис:
комбинат-GA.csh злт;метка йgt; lt;список каталогов с GA работает и gt;
В данном конкретном случае команда:
комбинат-GA.csh pm7 pm7
будет генерировать новый уникальный список структур под названием 'уникальныеструктуры-pm7.data' в каталоге gly-h2o-n/GA.
3. Уточнение с использованием метода ЗМ с небольшим набором основы
ПРИМЕЧАНИЕ: Цель здесь заключается в уточнении конфигурационной выборки кластеров Gly (H2O)n-1-5 с использованием лучшего квантово-механического описания для получения меньшего, но более точного набора кластерных структур Gly (H2O)n-1-5. Стартовые структуры для этого шага являются выходами Шага 2.
- Подготовьте и запустите небольшой базовый набор расчета DFT:
- Создайте субдиректорию под названием «ЗМ» под каталогом gly-h2o-n. Под каталогом ЗМ создайте еще один субдиректор под названием pw91-sb.
- Копируйте список уникальных структур(uniqueStructures-pm7.data) от каталога gly-h2o-n/GA до каталога зМ/pw91-sb.
- Изменение каталога, что гли-h2o-n / ЗМ / pw91-sb.
- Выполнить небольшой базовый набор DFT конфигурационный сценарий выборки с помощью команды:
run-pw91-sb.csh уникальныеСтруктуры-pm7.data sb ОЧЕРЕДЬ 10
где sb является меткой для этого набора вычислений, очередь является предпочтительной очередью в вычислительном кластере, а 10 указывает на то, что 10 вычислений должны быть сгруппированы в одно пакетное задание. Этот скрипт будет автоматически генерировать входные данные для Gaussian 09 и представить все расчеты. Введите 'тест' для 'QUEUE', чтобы сделать сухой пробег.
- Как только представленные расчеты будут завершены, извлеките и проанализируйте результаты.
- Извлеките энергии и вычислите вращающиеся константы малых базисных оптимизированных кластеров с помощью команды:
getRotConsts-dft-sb.csh pw91 N
где pw91 указывает на то, что использовался функционал плотности PW91, а N — это количество атомов в кластере. Это создаст файл под названием rotConstsData_C. - Теперь определите уникальные структуры с командой:
similarityAnalysis.py rotConstsData_C
где sb используется в качестве метки именования файлов. Теперь будет список уникальных конфигураций, оптимизированных на уровне теории PW91/6-31-G, сохраненных в файле uniqueStructures-sb.data.
- Извлеките энергии и вычислите вращающиеся константы малых базисных оптимизированных кластеров с помощью команды:
- Поднизись к каталогу gly-h2o-n/qM и объедините результаты нескольких сопоставимых трасс с помощью сценария комбайна -M.csh. Синтаксис:
комбинат-М.Кш злт;метка
В данном конкретном случае команда:
комбинат-M.csh sb pw91-sb
будет генерировать новый уникальный список структур под названием 'уникальныеструктуры-sb.data' в каталоге gly-h2o-n/'M.
4. Дальнейшее уточнение с использованием метода ЗМ с большим базовым набором
ПРИМЕЧАНИЕ: Цель здесь заключается в дальнейшем уточнении конфигурационной выборки кластеров Gly (H2O)n-1-5 с использованием лучшего квантово-механического описания. Стартовые структуры для этого шага являются выходами Шага 3.
- Отправить более надежные расчеты с использованием большего базиса.
- Создайте субдиректорпод название pw91-lb под каталогом qM.
- Копируйте список уникальных структур(uniqueStructures-sb.data) от каталога gly-h2o-n/'M до каталога gly-h2o-n/'m/pw91-lb и измените в этот каталог.
- Запустите большой базальный dFT примерный сценарий выборки с командой:
run-pw91-lb.csh уникальныеСтруктуры-sb.data lb ОЧЕРЕДЬ 10
где фунт является меткой для этого набора вычислений, очередь является предпочтительной очередью в вычислительном кластере, а 10 указывает на то, что 10 вычислений должны быть сгруппированы в одно пакетное задание. Этот скрипт будет автоматически генерировать входные данные для Gaussian 09 и представить все расчеты. Введите 'тест' для 'QUEUE', чтобы сделать сухой тест запуска.
- После завершения представленных расчетов извлекайте и анализируйте данные
- Вычислите вращающиеся константы больших базисных оптимизированных кластеров с помощью команды:
getRotConsts-dft-lb.csh pw91 N
где pw91 указывает на то, что использовался функционал плотности PW91, а N — это количество атомов в кластере. - Теперь определите уникальные структуры с командой:
similarityAnalysis.py фунтов rotConstsData_C
где фунт используется в качестве метки именования файлов. Теперь у вас есть список уникальных конфигураций, оптимизированных на уровне теории PW91/6-311, сохраненном в файле uniqueStructures-lb.data.
- Вычислите вращающиеся константы больших базисных оптимизированных кластеров с помощью команды:
5. Окончательные расчеты энергии и термодинамической коррекции
ПРИМЕЧАНИЕ: Цель здесь состоит в том, чтобы получить колебательное строение и энергии gly (H2O)n'1-5 кластеров с использованием большого базиса и ультратонкой интеграционной сетки для вычисления желаемых термохимических коррекций.
- Начиная с результатов предыдущего шага, предоставьте более надежные расчеты.
- Создайте субдиректорию, называемую ультратонкой в каталоге qM/pw91-lb. Затем скопируйте список уникальных структур(uniqueStructures-lb.data)из каталога qM/pw91-lb/ultrafine и измените в этот каталог. QM/pw91-lb/ultrafine
- Отправить сверхтонкий большой базой DFT-скрипт с командой:
run-pw91-lb-ultrafine.csh уникальныеСтруктуры-lb.data uf queue 10
где uf является меткой для этого набора вычислений, очередь является предпочтительной очередью в вычислительном кластере, а 10 указывает на то, что 10 вычислений должны быть сгруппированы в одно пакетное задание. Этот скрипт будет автоматически генерировать входные данные для Gaussian 09 и представить все расчеты. Введите 'тест' для 'QUEUE', чтобы сделать сухой тест запуска.
- После завершения представленных расчетов извлекайте и анализируйте данные
- Извлеките энергии и вычислите вращающиеся константы больших базисных оптимизированных кластеров с командой:
getRotConsts-dft-lb-ultrafine.csh pw91 N
где pw91 указывает на то, что использовался функционал плотности PW91, а N — это количество атомов в кластере. - Теперь определите уникальные структуры с командой:
similarityAnalysis.py уф-rotConstsData_C
где uf используется в качестве метки именования файлов. Теперь у вас есть список уникальных конфигураций, оптимизированных на уровне теории PW91/6-311, сохраненном в файле uniqueStructures-uf.data.
- Извлеките энергии и вычислите вращающиеся константы больших базисных оптимизированных кластеров с командой:
- Выполните окончательную экстракцию информации, необходимой для расчета термодинамических коррекций. Используйте эту информацию для расчета термодинамических коррекций.
- Извлекайте окончательные электронные энергии, вращающиеся константы и вибрационные частоты, и используйте их для расчета термодинамических коррекций с помощью команды:
run-thermo-pw91.csh уникальныеСтруктуры-uf.data - Копируйте/вставьте выход командной строки в'Raw_Energies'лист таблицы Excel под названием 'gly-h2o-n.xlsx'. Вам нужно будет сделать это для мономеров (глицин и вода), а также самый низкий энергетический член каждого гидрата (gly-h2o-n, где n'1,2, ...).
- По мере добавления необработанных энергий на первый лист таблицы'gly-h2o-n.xlsx'последующие листы 'Binding_Energies'и'Hydrate_Distribution'автоматически обновляются. В частности, лист«Hydrate_Distribution»дает равновесную концентрацию гидратов при различных температурах (например, 298.15K), относительную влажность (20%, 50%, 100%) и начальные концентрации воды (H2O) и глицина (Глицин). Теория, лежащая в основе этих расчетов, описана на следующем этапе.
- Извлекайте окончательные электронные энергии, вращающиеся константы и вибрационные частоты, и используйте их для расчета термодинамических коррекций с помощью команды:
6. Вычисление атмосферных концентраций скоплений Gly (H2O)n'0-5 при комнатной температуре на уровне моря
ПРИМЕЧАНИЕ: Это достигается путем первого копирования термодинамических данных, полученных в предыдущем шаге в электронную таблицу и расчета Гиббс свободных энергий последовательной гидратации. Затем свободные энергии Гиббса используются для расчета равновесных констант для каждой последовательной гидратации. Наконец, набор линейных уравнений решается, чтобы получить равновесную концентрацию гидратов для данной концентрации мономеров, температуры и давления.
- Начните с создания системы химического эквилибрии для последовательного гидратации глицина, как показано ниже:
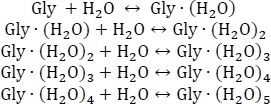
- Вычислите равновесные константы Kn используя Kn e-' Gn/(kBT), где n уровень гидратации, N n будет изменением энергии Gibbs свободнойреакцией энергии n th hydration, kB постоянн, и T температура.n
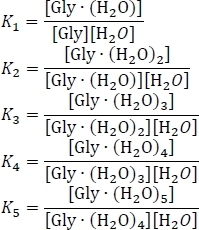
- Настроили уравнение для сохранения массы, используя предположение, что сумма равновесных концентраций гидратированных и негидратированных глициновых кластеров равна первоначальной концентрации изолированного глицина «Гли»0. Перепишите эту систему из шести одновременных уравнений, используя некоторые алгебраические перестановки равновесия постоянных выражений, как
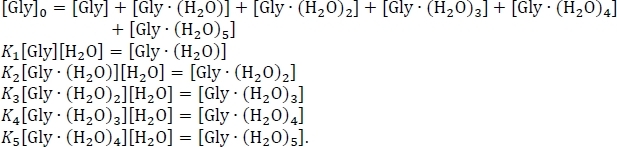
- Решите систему уравнений, показанных выше, чтобы получить равновесные концентрации Gly (H2O)n 0-5 с помощью экспериментального значения56,,57,58 для концентрации глицина в атмосфере, «Гли»0 , 2,9 х 106 см-3, и концентрация воды в атмосфере при 100% относительной влажности и температуре 298,15 K59, »H2O» 7,7 х 1017 см-3.
Результаты
Первый набор результатов этого протокола должен быть набором низкоэнергетических структур Gly (H2O)n'1-5, найденных в рамках конфигурационной процедуры отбора проб. Эти структуры были оптимизированы на уровне теории PW91/6-311 и считаются точными для целей настоящего документа. Нет никаких доказательств того, что PW91/6-311»G» постоянно недооценивает или переоценивает связывающую энергию этих кластеров. Его способность предсказывать связывающие энергии относительно MP2/CBS32 и «DLPNO-CCSD»(T)/CBS60,61 оценки и эксперимент52 показывает много колебаний. То же самое относится и к большинству других функций плотности. Как правило, каждое значение n no 1 - 5 должно дать несколько низкоэнергетических структур в пределах около 5 ккал мол-1 из низкой энергетической структуры. Здесь мы сосредоточимся на первой структуре, произведенной скриптом run-thermo-pw91.csh для краткости. На рисунке 3 показаны самые низкие электронные энергетические изомеры кластеров Gly (H2O)n'0-5. Видно, что сеть водородных связей растет в сложности по мере увеличения числа молекул воды, и даже переходит от преимущественно планарной сети к трехмерной клетке- как структура на n No 5. В остальной части этого текста используются энергии и термодинамические количества, соответствующие этим пяти конкретным скоплениям.
Таблица 1 содержит термодинамические количества, необходимые для выполнения протокола. В таблице 2 показан пример выхода сценария run-thermo-pw91.csh, где печатаются электронные энергии, вибрационные коррекции нулевой точки и термодинамические коррекции при трех различных температурах. Для каждого кластера (строки) E'PW91/6-311-G, соответствует электронной энергии газовой фазы на уровне PW91/6-311'G, рассчитанной на сверхтонких интеграционных сетках в единицах Hartree, а также в нулевую точку вибрационной энергии(PVE) в единицах ккал mol-1. При каждой температуре, 216,65 K, 273.15 K, и 298,15 K, термодинамические коррекции перечислены, ЗХ enthalpy формирования в единицах ккал мол-1, S энтропии формирования в единицах cal mol-1, и Г Гиббс свободной энергии формирования в единицах кккал мол-1. В таблице 3 показанпримерный расчет общего количества свободного изменения энергии Гиббса гидратации, а также последовательного гидратации. Пример вычисления полного изменения энергии Gibbs свободной гидратации для реакции
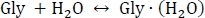
начинается с расчета электронной энергии EPW91 как
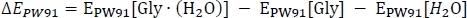
где EPW91(H2O) берется из колонки Таблицы 2 C, а EPW91«Гли» и EPW91» H2O » взяты из столбца Таблицы 1 B. Далее мы вычисляем общее изменение энергетической точки газаE(0), включив изменение в нулевую точку колебательной энергии реакции как
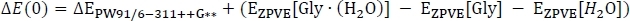
получить колонку D. Здесь, «EPW91/6»311 »G» берется из столбца таблицы 3 C, E«PVE»Gly » (H2O)» из столбца D, и E«PVE»и E«PVE» H2O » из столбца таблицы 1 C. Ради краткости, мы перейдем к кластерам комнатной температуры, поэтому мы пропустим данные 216,65 K и 273.15 K. При комнатной температуре мы затем вычисляем enthalpy изменение реакцииH путем коррекции изменения энергии газовой фазы как
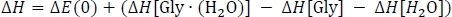
гдеиз столбца Таблицы 3 взята точка в год 3,h(H2O) берется из столбца таблицы 2 K, аH«Gly» и«H»H2O » взяты из столбца таблицы 1 J. Наконец, мы вычисляем Гиббса свободной изменения энергии реакции »G как
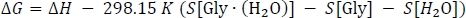
гдеиз столбца Таблицы 3 i, S«Gly» (H2O)) берется из столбца таблицы 2 L, а S«Gly» иSS2O » взяты из столбца таблицы 1 K. Обратите внимание, что значения энтропии должны быть преобразованы в единицы ккал-мола-1 K-1 во время этого шага. S
Теперь у нас есть необходимые количества для расчета атмосферных концентраций гидратированных глицинов, как показано в шаге 6. Результаты должны напоминать данные, приведенные в таблице 4,но следует ожидать небольших численных различий. В таблице 4 показаны равновесные концентрации гидратов, найденные в результате разработки системы шести уравнений в шаге 6.2 в одно матричного уравнения и его последующего решения. Мы начинаем с признания того факта, что система уравнений может быть написана как
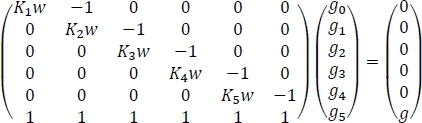
где Kn является равновесной постоянной для nй последовательной гидратации глицина, w является концентрация воды в атмосфере, г является начальной концентрацией изолированных глицин в атмосфере, и gn является равновесной концентрацией Gly (H2O)n. Если мы переписываем вышеупомянутое уравнение как Ax q b,мы получим−1 х 1b, где ANo1 является обратной матрицы A. Это обратное можно легко вычислить с помощью встроенных функций электронной таблицы, как показано в таблице 4 для получения окончательных результатов.
На рисунке 4 показана равновесная концентрация гидратного глицина, рассчитанная в таблице 4 как функция температуры при 100% относительной влажности и 1 атмосферном давлении. Это показывает, что, как температура снижается с 298.15K до 216.65K, концентрация неивлажного глицина (n'0) уменьшается и у гидратированных глицина увеличивается. Глицин дигидрат (n'2), в частности, резко возрастает при снижении температуры, в то время как изменение концентрации других гидратов менее заметно. Эти обратные корреляции между температурой и концентрацией гидратов согласуется с ожиданием, что более низкие энергии Гиббса свободных гидратов при более низких температурах благоприятствуют образованию гидратов.
Рисунок 5 иллюстрирует относительную зависимость влажности равновесной концентрации гидратов глицина при 298,15К и 1 атмосферном давлении. Это ясно показывает, что по мере увеличения RH с 20% до 100%, концентрация гидратов (n'gt;0) увеличивается за счет негидратированных глицинов (n'0). Вновь прямая корреляция между относительной влажностью и концентрацией гидратов согласуется с мыслью о том, что наличие большего количества молекул воды при более высоком RH способствует образованию гидратов.
Как представлено, этот протокол дает качественное понимание гидратированных популяций глицина в атмосфере. Предполагая, что первоначальная концентрация изолированного глицина составляет 2,9 миллиона молекул на кубический сантиметр, мы видим, что негидратированный глицин (n'0) является наиболее распространенным видом в большинстве условий, за исключением T 216.65K и RH'100%. Дигидрат (n'2), который имеет самую низкую последовательную энергию гидратации Гиббса при всех трех температурах, является наиболее распространенным гидратом в условиях, рассматриваемых здесь. По прогнозам, моногидраты (n-1) и более крупные гидраты (n-3) будут найдены в незначительных количествах. При осмотре рисунка 3,обилие n и 1-4 кластеров может быть связано со стабильностью и напряжением в сети водородных связей кластеров. Эти скопления имеют молекулы воды водорода связаны с carboxylic кислоты moiety глицина в геометрии, тесно напоминающей те из различных водородных связанных кольцевых структур, что делает их особенно стабильными.
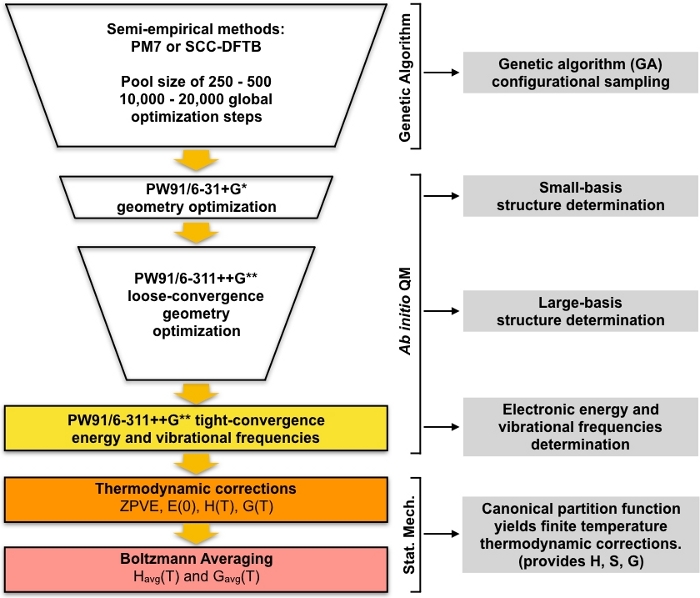
Рисунок 1: Схематическое описание текущей процедуры. Большой пул догадок, генерируемых генетическим алгоритмом (GA), уточняется с помощью серии оптимизаций геометрии PW91 до тех пор, пока не будет получен набор конвергентных структур. Вибрационные частоты этих структур вычисляются и используются для вычисления свободной энергии образования Гиббса, которая, в свою очередь, используется для расчета равновесных концентраций кластеров в условиях окружающей среды. Пожалуйста, нажмите здесь, чтобы просмотреть большую версию этой цифры.
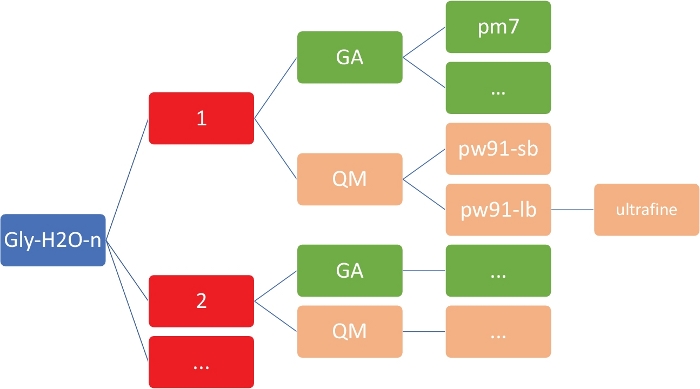
Рисунок 2: Структура каталога представителей для каждого кластера. Внутренние скрипты, включенные в этот протокол, требуют приведенной выше структуры каталога, где n — это количество молекул воды. Для каждого n в gly-h2o-n, Есть следующие субдиректора: GA для генетического алгоритма с каталогом GA/pm7, «ММ для квантовой механики с «M/pw91-sb» для PW91/6-31-G, «M/pw91», «M/pw91»/ultrafine для оптимизации и окончательных вибрационных вычислений на сверхтонких сетках. Пожалуйста, нажмите здесь, чтобы просмотреть большую версию этой цифры.
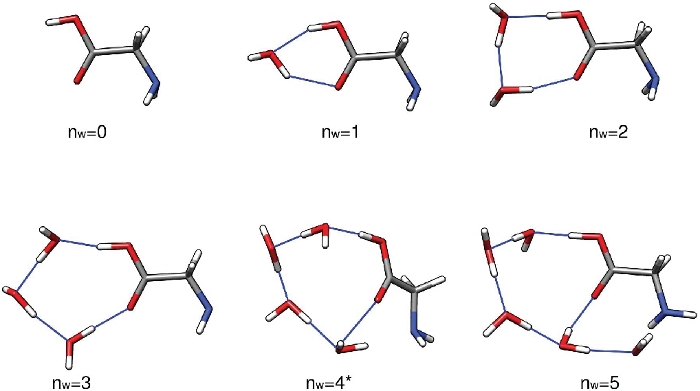
Рисунок 3: Представитель низкоэнергетических структур Gly (H2O)n'0-5. Эти кластеры были электронной энергетической глобальной минимальной, оптимизированной на уровне теории PW91/6-311. Пожалуйста, нажмите здесь, чтобы просмотреть большую версию этой цифры.
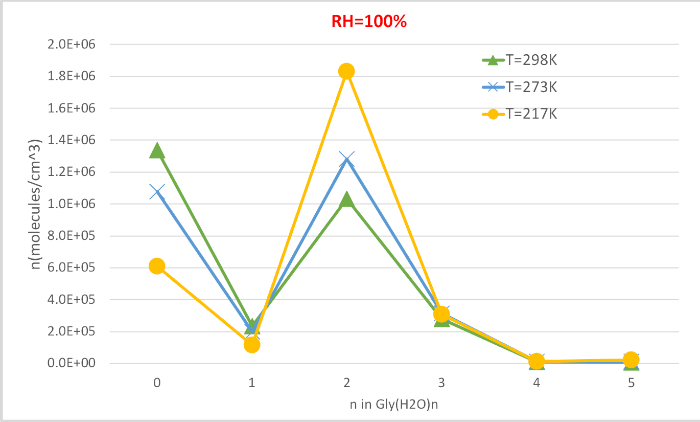
Рисунок 4: Температурная зависимость Gly (H2O)n'0-5 как 100% относительная влажность и давление 1 атм. Концентрация гидратов дается в единицах молекул см-3. Пожалуйста, нажмите здесь, чтобы просмотреть большую версию этой цифры.
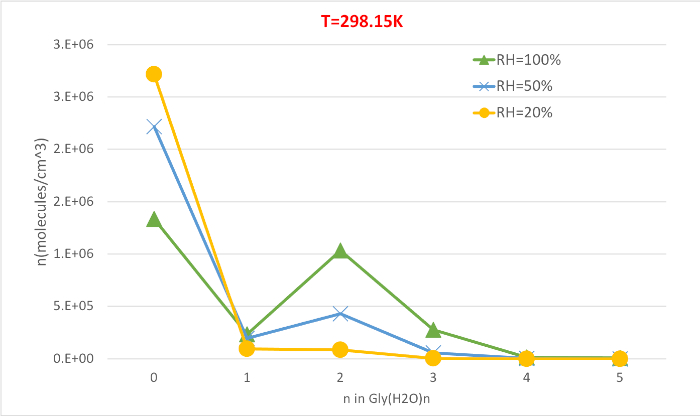
Рисунок 5: Относительная зависимость влажности Gly (H2O)n'0-5 как 298.15 K и давление 1 атм. Концентрация гидратов дается в единицах молекул см-3. Пожалуйста, нажмите здесь, чтобы просмотреть большую версию этой цифры.
| Е-PW91/6-311 | 216.65 K | 273.15 K | 298.15 K | ||||||||
| LB-UF | ЗПВЕ | ЗЧ | S | ЗГ | ЗЧ | S | ЗГ | ЗЧ | S | ЗГ | |
| Воды | -76.430500 | 13.04 | 1.72 | 42.59 | 5.54 | 2.17 | 44.44 | 3.08 | 2.37 | 45.14 | 1.96 |
| Глицин | -284.434838 | 48.55 | 2.65 | 69.53 | 36.14 | 3.70 | 73.81 | 32.09 | 4.22 | 75.61 | 30.22 |
Таблица 1: Мономерные энергии. Электронные энергии находятся в единицах Hartree в то время как все остальные количества находятся в единицах ккал мол-1. Вычислили воду и глицин на уровне теории и вибрационных частот PW91/6-311.G. С помощью thermo.pl скрипта были вычислены термодинамические коррекции давления 1 атм и температуры 298,15 К.
| Е-PW91/6-311 | 0 K | 216.65 K | 273.15 K | 298.15 K | ||||||||
| N | Имя | LB-UF | ЗПВЕ | ЗЧ | S | ЗГ | ЗЧ | S | ЗГ | ЗЧ | S | ЗГ |
| 1 | gly-h2o-1 | -360.88481 | 63.96 | 3.61 | 80.12 | 50.22 | 5.12 | 86.27 | 45.52 | 5.85 | 88.83 | 43.33 |
| 2 | gly-h2o-2 | -437.33763 | 79.33 | 4.53 | 90.86 | 64.17 | 6.46 | 98.78 | 58.81 | 7.40 | 102.06 | 56.30 |
| 3 | gly-h2o-3 | -513.78620 | 94.52 | 5.67 | 105.08 | 77.42 | 8.08 | 114.94 | 71.19 | 9.23 | 119.00 | 68.27 |
| 4 | gly-h2o-4 | -590.23667 | 109.80 | 6.03 | 104.98 | 91.30 | 8.78 | 116.21 | 84.40 | 10.11 | 120.87 | 81.14 |
| 5 | gly-h2o-5 | -666.68845 | 125.80 | 7.26 | 121.70 | 106.69 | 10.47 | 134.83 | 99.44 | 12.01 | 140.24 | 96.00 |
Таблица 2: Кластерные энергии. Энергии низшей энергии Gly (H2O)n'1-5 структур, найденных с помощью нашей процедуры, изложенной на рисунке 1. Электронные энергии находятся в единицах Hartree в то время как все остальные количества находятся в единицах ккал мол-1.
| Полная гидратация: Гли nH2O йlt;--gt; Gly (H2O)n | Секвенциальная гидратация: Гли (H2O)n-1 - H2O lt;-gt; Gly (H2O)n | ||||||||||||||||
| Е-PW91/6-311 | 216.65 | 273.15 | 298.15 | 216.65 | 273.15 | 298.15 | |||||||||||
| N | системное имя | LB-UF | Зе (0) | ЗГ (T) | ЗГ (T) | ЗГ (T) | ЗГ (T) | ЗГ (T) | ЗГ (T) | LB-UF | Зе (0) | ЗГ (T) | ЗГ (T) | H (T) | ЗГ (T) | ЗГ (T) | ЗГ (T) |
| 1 | gly-h2o-1 | -12.22 | -9.85 | -10.61 | -3.68 | -10.61 | -1.87 | -10.59 | -1.07 | -12.22 | -9.85 | -10.61 | -3.68 | -10.61 | -1.87 | -10.59 | -1.07 |
| 2 | gly-h2o-2 | -26.22 | -21.53 | -23.10 | -9.27 | -23.11 | -5.66 | -23.09 | -4.06 | -14.00 | -11.68 | -12.49 | -5.59 | -12.50 | -3.79 | -12.50 | -2.99 |
| 3 | gly-h2o-3 | -37.56 | -30.72 | -32.88 | -12.90 | -32.87 | -7.69 | -32.82 | -5.38 | -11.34 | -9.19 | -9.78 | -3.63 | -9.76 | -2.03 | -9.73 | -1.32 |
| 4 | gly-h2o-4 | -50.10 | -40.34 | -43.48 | -15.87 | -43.54 | -8.71 | -43.51 | -5.55 | -12.54 | -9.62 | -10.60 | -2.97 | -10.67 | -1.02 | -10.69 | -0.17 |
| 5 | gly-h2o-5 | -63.45 | -51.41 | -55.42 | -20.58 | -55.51 | -11.48 | -55.48 | -7.45 | -13.35 | -11.07 | -11.94 | -4.71 | -11.97 | -2.77 | -11.97 | -1.90 |
Таблица 3: Энергии гидратации. Общая энергия гидратации и энергия последовательной гидратации для Gly (H2O)n'1-5 в единицах ккал мол-1. Здесь, E'PW91/6-311 "ГЗ" является изменение в электронной энергии, "E(0) является нулевой точки колебательной энергии (ЗПВЕ) исправленные изменения в энергии, H(T) является enthalpy изменения при температуре T, и "G"T) является Гиббс свободного изменения энергии гидратации каждого Gly (H2O)n-1.
| Равномерное распределение гидратов в зависимости от температуры и относительной влажности | |||||||||
| T 298.15K | T 273.15K | T 216.65K | |||||||
| Гли (H2O)n | RH 100% | RH-50% | RH-20% | RH 100% | RH-50% | RH-20% | RH 100% | RH-50% | RH-20% |
| 0 | 1.3E-06 | 2.2E-06 | 2.7E-06 | 1.1E-06 | 2.0E-06 | 2.7E-06 | 6.1E-05 | 1.5E-06 | 2.5E-06 |
| 1 | 2.3E-05 | 1.9E-05 | 9.5E-04 | 2.0E-05 | 1.9E-05 | 9.9E-04 | 1.2E-05 | 1.5E-05 | 9.5E-04 |
| 2 | 1.0E-06 | 4.3E-05 | 8.4E-04 | 1.3E-06 | 6.1E-05 | 1.3E-05 | 1.8E-06 | 1.1E-06 | 3.0E-05 |
| 3 | 2.8E-05 | 5.8E-04 | 4.5E-03 | 3.2E-05 | 7.4E-04 | 6.3E-03 | 3.1E-05 | 9.6E-04 | 1.0E-04 |
| 4 | 1.1E-04 | 1.1E-03 | 3.4E-01 | 1.3E-04 | 1.5E-03 | 5.0E-01 | 1.1E-04 | 1.8E-03 | 7.5E-01 |
| 5 | 7.5E-03 | 3.9E-02 | 4.9E-00 | 1.2E-04 | 7.2E-02 | 9.7E-00 | 2.4E-04 | 1.9E-03 | 3.1E-01 |
Таблица 4: Равновесные увлажняемые концентрации Gly (H2O)n'0-5 в качестве функциональной температуры (T'298.15K, 273.15K, 216.65K) и относительная влажность (RH-100%, 50%, 20%). Концентрация гидратов дается в единицах молекул см-3 при условии экспериментальных значений56,,57,,58, из «Gly»0 , 2,9 х 106 см-3 и Х2O » 7,7 х 1017 см-3, 1,6 х 1017 см-3 и 9,9 х 1010 см-3 при 100% относительной влажности, 273.15 K и 216.65 K, соответственно59.
Дополнительные файлы. Пожалуйста, нажмите здесь, чтобы загрузить эти файлы.
Обсуждение
Точность данных, генерируемых этим протоколом, зависит главным образом от трех моментов: i) разнообразие конфигураций, отобранных шагом 2, (ii) точность юндаром структуры системы (iii) и точность термодинамических коррекций. Каждый из этих факторов может быть решен путем изменения метода путем редактирования включенных скриптов. Первый фактор легко преодолеть с помощью большего первоначального пула случайно генерируемых структур, более многочисленных итераций ГА и более слабого определения критериев, участвующих в ГА. Кроме того, можно использовать другой полуэмпирический метод, такой как самосогласованная плотность заряда-функциональная герметичная герметичная (SCC-DFTB)62 модель и эффективный фрагмент потенциал (EFP)63 модель для того, чтобы исследовать эффекты различных физических описаний. Основным ограничением здесь является неспособность метода формировать или ломать ковалентные связи, а это означает, что мономера заморожены. Процедура ГА находит только наиболее стабильные относительные позиции этих замороженных мономеров в соответствии с полуэмпирическим описанием.
Точность электронной структуры системы может быть улучшена различными способами, каждый из которых имеет свои вычислительные затраты. Можно выбрать более высокую плотность функциональных, таких как M06-2X64 и wB97X-V65, или квантово-механических (ЗМ) метод, таких как Мюллер-Плессет66,67,68 (MPn) возмущения теорий и совместно-кластер69 (CC) методы для улучшения физического описания системы. В иерархии функциональных функций, производительность, как правило, улучшается при переходе от обобщенного градиента приближения (GGA) функций, как PW91 в диапазоне разделенных гибридных функций, как wB97X-D и мета-GGA гибридных функций, как M06-2X.
Недостатком методов DFT является то, что систематическое сближение с точным значением невозможно; однако, методы DFT являются вычислительно недорогими и существует широкий спектр функций для широкого спектра приложений.
Энергия, рассчитанная с использованием методов волнообразов, таких как MP2 и CCSD(T) в сочетании с корреляционными последовательными базовыми наборами увеличения кардинального числа («Ауг-кк-пВ»,Т,...» В) сходятся к их полной основе установленного предела систематически, но вычислительная стоимость каждого расчета становится непомерно высокой по мере роста размера системы. Дальнейшее уточнение электронной структуры может быть достигнуто с помощью явно коррелированных базовых наборов70 и экстраполации на полный базовый набор (CBS)71 предел. Наша недавняя работа показывает, что плотность установлены явно коррелирует второго порядка Мюллер-Плессет (DF-MP2-F12) возмущенный подход дает энергии приближается к MP2 / CBS вычислений32. Изменение текущего протокола для использования различных методов электронной структуры включает в себя два шага: (i) подготовить шаблон входиного файла после синтаксиса, приведенного программным обеспечением, (ii) и откорректировать run-pw91-sb.csh, run-pw91-lb.csh, и run-pw91-lb-ultrafine.csh скрипты для создания правильного ввода.
Наконец, точность термодинамических коррекций зависит от метода электронной структуры, а также от описания PES вокруг глобального минимума. Точное описание PES требует вычисления производных ПЭУ третьего и более высокого порядка в отношении перемещений в ядерных степенях свободы, таких как поле квартической силы72,,73 (КФФ), что является исключительно дорогостоящей задачей. Текущий протокол использует гармоничное приближение осциллятора к вибрационным частотам, в результате чего необходимо вычислить только до вторых производных PES. Этот подход становится проблематичным в системах с высокой агармоничностью, таких как очень дискеты молекул и симметричных двойного потенциала из-за большой разницы в истинном PES и гармонических PES. Кроме того, стоимость высококачественного ПЭУ от вычислительно-требовательного метода электронной структуры только усугубляет проблему затрат на вибрационные частотные вычисления. Один из подходов к преодолению этого заключается в использовании электронных энергий от высококачественного электронного расчета структуры наряду с вибрационными частотами, вычисляемыми на более низком качестве PES, что приводит к балансу между стоимостью и точностью. Текущий протокол может быть изменен с целью использования различных описаний ПЭУ, описанных в предыдущем пункте; однако, можно также отсеивать биевания частотных ключевых слов в сценариях и шаблонах для вычисления агармонических вибрационных частот.
Двумя важнейшими вопросами для любого протокола выборки конфигурации являются первоначальный метод отбора проб потенциальной энергетической поверхности и критерии, используемые для определения каждого кластера. Мы широко использовали различные методы в нашей предыдущей работе. Для первого выпуска, первоначального метода отбора проб потенциальной энергетической поверхности, мы сделали выбор использования ГА с полуэмпирическими методами на основе этих факторов. Конфигурационная выборка с использованием химической интуиции26, случайная выборка, и молекулярной динамики (MD)29,30, не в состоянии найти ориентировочный глобальной минимы регулярно для кластеров больше, чем 10 мономеров, как мы наблюдали в наших исследованиях водных кластеров18. Мы успешно использовали бассейн прыжков (BH) для изучения сложных PES (H2O)1174, но это требует ручного включения некоторых потенциальных изомерителей низкой энергии алгоритм BH не нашли. Сравнение производительности BH и GA в поиске глобального минимума водных кластеров, (H2O)n'10-20 показали, что GA последовательно нашел глобальный минимум быстрее, чем BH75. GA, как реализовано в OGOLEM и CLUSTER является очень универсальным, потому что он может быть применен к любому молекулярному кластеру, и он может взаимодействовать с огромным количеством пакетов с классическим силовым полем, полуэмпирическими, функциональными плотностями и возможностями ab initio. Выбор PM7 определяется его скоростью и разумной точностью. Практически любой другой полуэмпирический метод будет иметь значительно более высокую вычислительную стоимость.
Что касается второго выпуска, мы изучили с использованием различных критериев для выявления уникальных структур, начиная от электронных энергий, дипольные моменты, перекрытия RMSDs и вращательных констант. Использование дипольные моменты оказалось трудным, потому что оба компонента диполи-момента зависели от ориентации молекулы, а общий дипольные моменты были очень чувствительны к геометрии различий таким образом, что было трудно установить пороги, определяющие структуры, одинаковые или уникальные. Сочетание электронных энергий и вращательных констант оказалось наиболее полезным.
Текущие критерии для того, чтобы считать две структуры уникальными, основаны на пороге разницы в энергии 0,10 ккалмол -1 и постоянной разнице в повороте в 1%. Таким образом, две структуры считаются различными, если их энергия отличается более чем на 0,10 ккал мол-1 (0,00015 a.u.) И любая из трех их вращательных констант (A, B, C) отличается более чем на 1%. Существенные внутренние ориентиры на протяжении многих лет сочли эти пороговые значения разумным выбором. Наш конфигурационный подход к выборке и методология скрининга были применены к очень слабо связанным кластерам, таким как полиароматические углеводороды, комплексированные с водой76,,77, а также сильно связанные тернарисные гидраты сульфата, содержащие аммиак и амины32. Для кластеров, где существуют различные состояния протонации, который следует учитывать, лучшим подходом является запуск различных расчетов ГА, каждый из которых начинается с мономеров в разных состояниях протонации. Это гарантирует тщательное обдумание структур с различными состояниями протонации. Однако низкоуровневые расчеты DFT часто позволяют состояниям протонации изменяться в ходе оптимизации геометрии, тем самым уступая наиболее стабильное состояние протонации независимо от стартовой геометрии.
Наши методы гамма-конфигурации выборки должны хорошо работать даже для дискетных молекул, пока коды GA взаимосвязаны с общими, непараметризированными методами, которые позволяют мономерам принимать различные конфигурации в ходе бега ГА. Например, взаимодействие ГА с PM7 позволит изменить структуры мономеров, но если их облигации прервутся, как это произойдет при смене состояний протонации, структуры могут быть отвергнуты как неприемлемые кандидаты.
Мы рассмотрели различные способы исправления недостатков гармонического приближения, особенно те, которые возникают из-за низких колебатевых частот. Включение квазигармонического приближения в нынешнюю методологию не сложно. Тем не менее, есть еще вопросы о квази-гармонический метод, особенно когда дело доходит до частоты отсечения, ниже которого он будет применяться. Кроме того, нет строгих контрольных работ, изучающих надежность приближения квази-RRHO, хотя общепринятая точка зрения предполагает, что это должно быть улучшением по сравнению с приближением RRHO.
Представленный таким образом протокол может быть обобщен любой системе молекулярных кластеров нековалентно связанных газовых фаз. Он также может быть обобщен использовать любой полуэмпирический метод, электронный метод структуры и программного обеспечения, а также метод вибрационного анализа и программного обеспечения путем редактирования скриптов и шаблонов. Это предполагает, что пользователь доволен интерфейсом командной строки Linux, скриптом Python и высокопроизводительными вычислениями. Незнакомый синтаксис и внешний вид операционной системы Linux и отсутствие опыта работы с криптами является самой большой ловушкой в этом протоколе и где новые студенты борются больше всего. Этот протокол успешно используется в различных реализациях в течение многих лет в нашей группе, в основном упором на влияние серной кислоты и аммиака на образование аэрозолей. Дальнейшие усовершенствования этого протокола будут включать в себя более надежный интерфейс для более электронной структуры программного обеспечения, альтернативные реализации генетического алгоритма, и, возможно, использование новых методов для более быстрых вычислений электронных и вибрационных энергий. Наши текущие применения этого протокола изучают важность аминокислот на ранних стадиях формирования аэрозолей в текущей атмосфере и в формировании более крупных биологических молекул в пребиотической среде.
Раскрытие информации
Ни один.
Благодарности
Этот проект был поддержан грантами CHE-1229354, CHE-1662030, CHE-1721511 и CHE-1903871 от Национального научного фонда (GCS), Арнольда и Мэйбл Бекман Фонд Бекман Стипендиат премии (AGG), и Барри М. Голдуотер стипендии (AGG). Использовались высокопроизводительные вычислительные ресурсы консорциума MERCURY (http://www.mercuryconsortium.org).
Материалы
| Name | Company | Catalog Number | Comments |
| Avogadro | https://avogadro.cc | Open-source molecular visualization program | |
| Gaussian [09/16] Software | http://www.gaussian.com/ | Commercial ab initio electronic structure program | |
| MOPAC 2016 | http://openmopac.net/MOPAC2016.html | Open-source semi-empirical program | |
| OGOLEM Software | https://www.ogolem.org | Genetic algorithm-based global optimization program | |
| OpenBabel | http://openbabel.org/wiki/Main_Page | Open-source cheminformatics library | |
| calcRotConsts.py | Shields Group, Department of Chemistry, Furman University | Python script to compute rotational constants | |
| calcSymmetry.csh | Shields Group, Department of Chemistry, Furman University | Shell script to calculate symmetry number of a molecule given Cartesian coordinates | |
| combine-GA.csh | Shields Group, Department of Chemistry, Furman University | Shell script to combine energy and rotational constants from different GA directories | |
| combine-QM.csh | Shields Group, Department of Chemistry, Furman University | Shell script to combine energy and rotational constants from different QM directories | |
| gaussianE.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract Gaussian 09 energies | |
| gaussianFreqs.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract Gaussian 09 vibrational frequencies | |
| getrotconsts | Shields Group, Department of Chemistry, Furman University | Executable to calculate rotational constants given a molecule's Cartesian coordinates | |
| getRotConsts-dft-lb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of large basis DFT optimized structures | |
| getRotConsts-dft-lb-ultrafine.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of ultrafine DFT optimized structures | |
| getRotConsts-dft-sb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of small basis DFT optimized structures | |
| getRotConsts-GA.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute rotational constants for a batch of genetic algorithm optimized structures | |
| global-minimum-coords.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of global minimum structures of gly-(h2o)n, where n=0-5 | |
| make-thermo-gaussian.csh | Shields Group, Department of Chemistry, Furman University | Shell script to extract data from Gaussian output files and make input files for the thermo.pl script | |
| ogolem-input-file.ogo | Shields Group, Department of Chemistry, Furman University | Ogolem sample input file | |
| ogolem-submit-script.pbs | Shields Group, Department of Chemistry, Furman University | PBS batch submission file for Ogolem calculations | |
| README.docx | Shields Group, Department of Chemistry, Furman University | Clarifications to help readers use the scripts effectively | |
| runogolem.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run OGOLEM | |
| run-pw91-lb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of large basis DFT optimization calculations | |
| run-pw91-lb-ultrafine.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of ultrafine DFT optimization calculations | |
| run-pw91-sb.csh | Shields Group, Department of Chemistry, Furman University | Shell script to run a batch of small basis DFT optimization calculations | |
| run-thermo-pw91.csh | Shields Group, Department of Chemistry, Furman University | Shell script to compute the thermodynamic corrections for a batch of DFT optimized structures | |
| similarityAnalysis.py | Shields Group, Department of Chemistry, Furman University | Python script to determine unique structures based on rotational constants and energies | |
| symmetry | Shields Group, Department of Chemistry, Furman University | Executable to calculate molecular symmetry given Cartesian coordinates | |
| symmetry.c | (C) 1996, 2003 S. Patchkovskii, Serguei.Patchkovskii@sympatico.ca | C code to determine the molecular symmstry of a molecule given Cartesian coordinates | |
| template-marcy.pbs | Shields Group, Department of Chemistry, Furman University | Template for a PBS submit script which uses OGOLEM | |
| template-pw91.com | Shields Group, Department of Chemistry, Furman University | Template Gaussian 09 input | |
| template-pw91-HL.com | Shields Group, Department of Chemistry, Furman University | Template Gaussian 09 input for ultrafine DFT optimization | |
| thermo.pl | https://www.nist.gov/mml/csd/chemical-informatics-research-group/products-and-services/program-computing-ideal-gas | Perl open-source script to compute ideal gas thermodynamic corrections | |
| gly-h2o-n.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet for the complete protocol | |
| table-1.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-2.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-3.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| table-4.xlsx | Shields Group, Department of Chemistry, Furman University | Excel spreadsheet | |
| water.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of water | |
| glycine.xyz | Shields Group, Department of Chemistry, Furman University | Cartesian coordinates of glycine |
Ссылки
- Foster, P., Ramaswamy, V., Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., Tignor, M., Miller, H. L. . Climate Change 2007 The Scientific Basis. , (2007).
- Kulmala, M., et al. Toward direct measurement of atmospheric nucleation. Science. 318 (5847), 89-92 (2007).
- Sipila, M., et al. The role of sulfuric acid in atmospheric nucleation. Science. 327 (5970), 1243-1246 (2010).
- Jiang, J., et al. First measurement of neutral atmospheric cluster and 1 - 2 nm particle number size distributions during nucleation events. Aerosol Science and Technology. 45 (4), (2011).
- Dunn, M. E., Pokon, E. K., Shields, G. C. Thermodynamics of forming water clusters at various Temperatures and Pressures by Gaussian-2, Gaussian-3, Complete Basis Set-QB3, and Complete Basis Set-APNO model chemistries; implications for atmospheric chemistry. Journal of the American Chemical Society. 126 (8), 2647-2653 (2004).
- Pickard, F. C., Pokon, E. K., Liptak, M. D., Shields, G. C. Comparison of CBSQB3, CBSAPNO, G2, and G3 thermochemical predictions with experiment for formation of ionic clusters of hydronium and hydroxide ions complexed with water. Journal of Chemical Physics. 122, 024302 (2005).
- Pickard, F. C., Dunn, M. E., Shields, G. C. Comparison of Model Chemistry and Density Functional Theory Thermochemical Predictions with Experiment for Formation of Ionic Clusters of the Ammonium Cation Complexed with Water and Ammonia; Atmospheric Implications. Journal of Physical Chemistry A. 109 (22), 4905-4910 (2005).
- Alongi, K. S., Dibble, T. S., Shields, G. C., Kirschner, K. N. Exploration of the Potential Energy Surfaces, Prediction of Atmospheric Concentrations, and Vibrational Spectra of the HO2•••(H2O)n (n=1-2) Hydrogen Bonded Complexes. Journal of Physical Chemistry A. 110 (10), 3686-3691 (2006).
- Allodi, M. A., Dunn, M. E., Livada, J., Kirschner, K. N. Do Hydroxyl Radical-Water Clusters, OH(H2O)n, n=1-5, Exist in the Atmosphere. Journal of Physical Chemistry A. 110 (49), 13283-13289 (2006).
- Kirschner, K. N., Hartt, G. M., Evans, T. M., Shields, G. C. In Search of CS2(H2O)n=1-4 Clusters. Journal of Chemical Physics. 126, 154320 (2007).
- Hartt, G. M., Kirschner, K. N., Shields, G. C. Hydration of OCS with One to Four Water Molecules in Atmospheric and Laboratory Conditions. Journal of Physical Chemistry A. 112 (19), 4490-4495 (2008).
- Morrell, T. E., Shields, G. C. Atmospheric Implications for Formation of Clusters of Ammonium and 110 Water Molecules. Journal of Physical Chemistry A. 114 (12), 4266-4271 (2010).
- Temelso, B., et al. Quantum Mechanical Study of Sulfuric Acid Hydration: Atmospheric Implications. Journal of Physical Chemistry A. 116 (9), 2209 (2012).
- Husar, D. E., Temelso, B., Ashworth, A. L., Shields, G. C. Hydration of the Bisulfate Ion: Atmospheric Implications. Journal of Physical Chemistry A. 116 (21), 5151-5163 (2012).
- Bustos, D. J., Temelso, B., Shields, G. C. Hydration of the Sulfuric Acid – Methylamine Complex and Implications for Aerosol Formation. Journal of Physical Chemistry A. 118 (35), 7430-7441 (2014).
- Wales, D. J., Scheraga, H. A. Global optimization of clusters, crystals, and biomolecules. Science. 27 (5432), 1368-1372 (1999).
- Day, M. B., Kirschner, K. N., Shields, G. C. Global search for minimum energy (H2O)n clusters, n = 3 - 5. The Journal of Physical Chemistry A. 109 (30), 6773-6778 (2005).
- Shields, R. M., Temelso, B., Archer, K. A., Morrell, T. E., Shields, G. C. Accurate predictions of water cluster formation, (H2O)n=2-10. The Journal of Physical Chemistry A. 114 (43), 11725-11737 (2010).
- Temelso, B., Archer, K. A., Shields, G. C. Benchmark structures and binding energies of small water clusters with anharmonicity corrections. The Journal of Physical Chemistry A. 115 (43), 12034-12046 (2011).
- Temelso, B., Shields, G. C. The role of anharmonicity in hydrogen-bonded systems: The case of water clusters. The Journal of Chemical Theory and Computation. 7 (9), 2804-2817 (2011).
- Von Freyberg, B., Braun, W. Efficient search for all low energy conformations of polypeptides by Monte Carlo methods. The Journal of Computational Chemistry. 12 (9), 1065-1076 (1991).
- Rakshit, A., Yamaguchi, T., Asada, T., Bandyopadhyay, P. Understanding the structure and hydrogen bonding network of (H2O)32 and (H2O)33: An improved Monte Carlo temperature basin paving (MCTBP) method of quantum theory of atoms in molecules (QTAIM) analysis. RSC Advances. 7 (30), 18401-18417 (2017).
- Deaven, D. M., Ho, K. M. Molecular geometry optimization with a genetic algorithm. Physical Review Letters. 75, 288-291 (1995).
- Hartke, B. Application of evolutionary algorithms to global cluster geometry optimization. Applications of Evolutionary Computation in Chemistry. , (2004).
- Dieterich, J. M., Hartke, B. OGOLEM: Global cluster structure optimization for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach. Molecular Physics. 108 (3-4), 279-291 (2010).
- Herb, J., Nadykto, A. B., Yu, F. Large ternary hydrogen-bonded pre-nucleation clusters in the Earth's atmosphere. Chemical Physics Letters. 518, 7-14 (2011).
- Ortega, I. K., et al. From quantum chemical formation free energies to evaporation rates. Atmospheric Chemistry and Physics. 12 (1), 225-235 (2012).
- Elm, J., Bilde, M., Mikkelsen, K. V. Influence of Nucleation Precursors on the Reaction Kinetics of Methanol with the OH Radical. Journal of Physical Chemistry A. 117 (30), 6695-6701 (2013).
- Loukonen, V., et al. Enhancing effect of dimethylamine in sulfuric acid nucleation in the presence of water - a computational study. Atmospheric Chemistry and Physics. 10 (10), 4961-4974 (2010).
- Temelso, B., Phan, T. N., Shields, G. C. Computational study of the hydration of sulfuric acid dimers: implications for acid dissociation and aerosol formation. Journal of Physical Chemistry A. 116 (39), 9745-9758 (2012).
- Jiang, S., et al. Study of Cl-(H2O)n (n = 1-4) using basin-hopping method coupled with density functional theory. Journal of Computational Chemistry. 35 (2), 159-165 (2014).
- Temelso, B., et al. Effect of mixing ammonia and alkylamines on sulfate aerosol formation. Journal of Physical Chemistry A. 122 (6), 1612-1622 (2018).
- Perdew, J. P., Ruzsinszky, A., Tao, J. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. Journal of Chemical Physics. 123, 062201 (2005).
- Riplinger, C., Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. Journal of Chemical Physics. 138, 034106 (2013).
- Riplinger, C., Pinski, P., Becker, U., Valeev, E. F., Neese, F. Sparse maps--A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. Journal of Chemical Physics. 144 (2), 024109 (2016).
- Kildgaard, J. V., Mikkelsen, K. V., Bilde, M., Elm, J. Hydration of atmospheric molecular clusters: a new method for systematic configurational sampling. Journal of Physical Chemistry A. 122 (22), 5026-5036 (2018).
- González, &. #. 1. 9. 3. ;. Measurement of areas on a sphere Using Fibonacci and latitude-longitude lattices. Mathematical Geosciences. 42, 49-64 (2010).
- Karaboga, D., Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Applied Soft Computing. 8 (1), 687-697 (2008).
- Zhang, J., Doig, M. Global optimization of rigid molecules using the artificial bee colony algorithm. Physical Chemistry Chemical Physics. 18 (4), 3003-3010 (2016).
- Kubecka, J., Besel, V., Kurten, T., Myllys, N., Vehkamaki, H. Configurational sampling of noncovalent (atmospheric) molecular clusters: sulfuric acid and guanidine. Journal of Physical Chemistry A. 123 (28), 6022-6033 (2019).
- Grimme, S., Bannwarth, C., Shushkov, P. A Robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent Interactions of large molecular systems parametrized for all spd-block elements (Z = 1-86). Journal of Chemical Theory and Computation. 13 (5), 1989-2009 (2017).
- Buck, U., Pradzynski, C. C., Zeuch, T., Dieterich, J. M., Hartke, B. A size resolved investigation of large water clusters. Physical Chemistry Chemical Physics. 16 (15), 6859 (2014).
- Forck, R. M., et al. Structural diversity in sodium doped water trimers. Physical Chemistry Chemical Physics. 14 (25), 9054-9057 (2012).
- Witt, C., Dieterich, J. M., Hartke, B. Cluster structures influenced by interaction with a surface. Physical Chemistry Chemical Physics. 20 (23), 15661-15670 (2018).
- Freitbert, A., Dieterich, J. M., Hartke, B. Exploring self-organization of molecular tether molecules on a gold surface by global structure optimization. The Journal of Computational Chemistry. 40 (22), 1978-1989 (2019).
- Stewart, J. J. P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. The Journal of Molecular Modeling. 19 (1), 1-32 (2013).
- Burke, K., Perdew, J. P., Wang, Y. Derivation of a generalized gradient approximation: The PW91 density functional. Electronic Density Functional Theory. , 81-111 (1998).
- Frisch, M. J., et al. . Gaussian 09, Revision A.02. , (2016).
- Ditchfield, R., Hehre, W. J., Pople, J. A. Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. The Journal of Chemical Physics. 54 (2), 724 (1971).
- Elm, J., Bilde, M., Mikkelsen, K. V. Assessment of density functional theory in predicting structures and free energies of reaction of atmospheric prenucleation clusters. The Journal of Chemical Theory and Computation. 8 (6), 2071-2077 (2012).
- Elm, J., Mikkelsen, K. V. Computational approaches for efficiently modelling of small atmospheric clusters. Chemical Physics Letters. 615, 26-29 (2014).
- Bayucan, A., et al. . PBS Portable Batch System. , (1999).
- O'Boyle, N. M., et al. Open Babel: An open chemical toolbox. Journal of Cheminformatics. 3, 33 (2011).
- Csaszar, A. G. Conformers of gaseous glycine. Journal of the American Chemical Society. 114 (24), 9568-9575 (1992).
- Zhang, Q., Anastasio, C. Free and combined amino compounds in atmospheric fine particles (PM2.5) and fog waters from Northern California. Atmospheric Environment. 37 (16), 2247-2258 (2003).
- Matsumoto, K., Uematsu, M. Free amino acids in marine aerosols over the western North Pacific Ocean. Atmospheric Environment. 39 (11), 2163-2170 (2005).
- Mandalakis, M., Apostolaki, M., Stephanou, E. G. Trace analysis of free and combined amino acids in atmospheric aerosols by gas chromatography-mass spectrometry. Journal of Chromatography A. 1217 (1), 143-150 (2010).
- Seinfeld, J. H., Pandis, S. N. . Atmospheric Chemistry and Physics, 3rd Ed. , (2016).
- Myllys, N., Elm, J., Halonen, R., Kurten, T., Vehkamaki, H. Coupled cluster evaluation of atmospheric acid-base clusters with up to 10 molecules. The Journal of Physical Chemistry A. 120 (4), 621-630 (2016).
- Elm, J., Bilde, M., Mikkelsen, K. V. Assessment of binding energies of atmospherically relevant clusters. Physical Chemistry Chemical Physics. 15 (39), (2013).
- Elstner, M. The SCC-DFTB method and its application to biological systems. Theoretical Chemistry Accounts. 116 (1-3), 316-325 (2006).
- Kaliman, I. A., Slipchenko, L. V. LIBEFP: A new parallel implementation of the effective fragment potential method as a portable software library. The Journal of Computational Chemistry. 34 (26), 2284-2292 (2013).
- Zhao, Y., Truhlar, D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and trasition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theoretical Chemistry Accounts. 120 (1-3), 215-241 (2008).
- Mardirossian, N., Head-Gordon, M. wB97X-V: A 10-parameter, range-separated hybrid, generalized gradient approximation density functional with nonlocal correlation, designed by a survival-of-the-fittest strategy. Physical Chemistry Chemical Physics. 16 (21), 9904-9924 (2014).
- Head-Gordon, M., Pople, J. A., Frisch, M. J. MP2 energy evaluation by direct methods. Chemical Physics Letters. 153 (6), 503-506 (1988).
- Pople, J. A., Seeger, R., Krishnan, R. Variational configuration interaction methods and comparison with perturbation theory. The International Journal of Quantum Chemistry. 12, 149-163 (1977).
- Pople, J. A., Binkley, J. S., Seeger, R. Theoretical models incorporating electron correlation. The International Journal of Quantum Chemistry. 10 (10), 1-19 (1976).
- Monkhorst, H. J. Calculation of properties with the coupled-cluster method. The International Journal of Quantum Chemistry. 12 (11), 421-432 (1977).
- Klopper, W., Manby, F. R., Ten-No, S., Valeev, E. F. R12 methods in explicitly correlated molecular electronic structure theory. International Reviews in Physical Chemistry. 25, 427-468 (2006).
- Hattig, C. Optimization of auxiliary basis sets for RI-MP2 and RI-CC2 calculations: Core-valence and quintuple-z basis sets for H to Ar and QZVPP basis sets for Li to Kr. Physical Chemistry Chemical Physics. 7 (1), 59-66 (2005).
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. The Journal of Chemical Physics. 122, 014108 (2005).
- Barone, V. Vibrational zero-point energies and thermodynamic functions beyond the harmonic approximation. The Journal of Chemical Physics. 120 (7), 3059-3065 (2004).
- Temelso, B., et al. Exploring the Rich Potential Energy Surface of (H2O)11 and Its Physical Implications. Journal of Chemical Theory and Computation. 14 (2), 1141-1153 (2018).
- Kabrede, H., Hentschke, R. Global minima of water clusters (H2O)N, N≤25, described by three empirical potentials. Journal of Physical Chemistry B. 107 (16), (2003).
- Steber, A. L., et al. Capturing the Elusive Water Trimer from the Stepwise Growth of Water on the Surface of a Polycyclic Aromatic Hydrocarbon Acenaphthene. Journal of Physical Chemistry Letters. 8 (23), 5744-5750 (2017).
- Perez, C., et al. Corrannulene and its complex with water: A tiny cup of water. Physical Chemistry Chemical Physics. 19 (22), 14214-14223 (2017).
Перепечатки и разрешения
Запросить разрешение на использование текста или рисунков этого JoVE статьи
Запросить разрешениеThis article has been published
Video Coming Soon
Авторские права © 2025 MyJoVE Corporation. Все права защищены