24.14 : Electrostatic Boundary Conditions
Consider an external electric field propagating through a homogeneous medium. When the electric field crosses the surface boundary of the medium, it undergoes a discontinuity. The electric field can be resolved into normal and tangential components. The amount by which the field changes at any boundary is given by the difference between the field components above and below the surface boundary.
The surface integral of an electric field is given by Gauss's law in integral form and is related to the total enclosed charge. Consider a Gaussian pillbox on the surface boundary. The surface integral of the field is the sum of the integrals over all the surfaces of the pillbox. If the thickness of the pillbox tends to zero, then the surface integral includes only the contributions of the pillbox faces above and below the boundary. Solving this gives the discontinuity of the normal component of the electric field at any surface boundary.
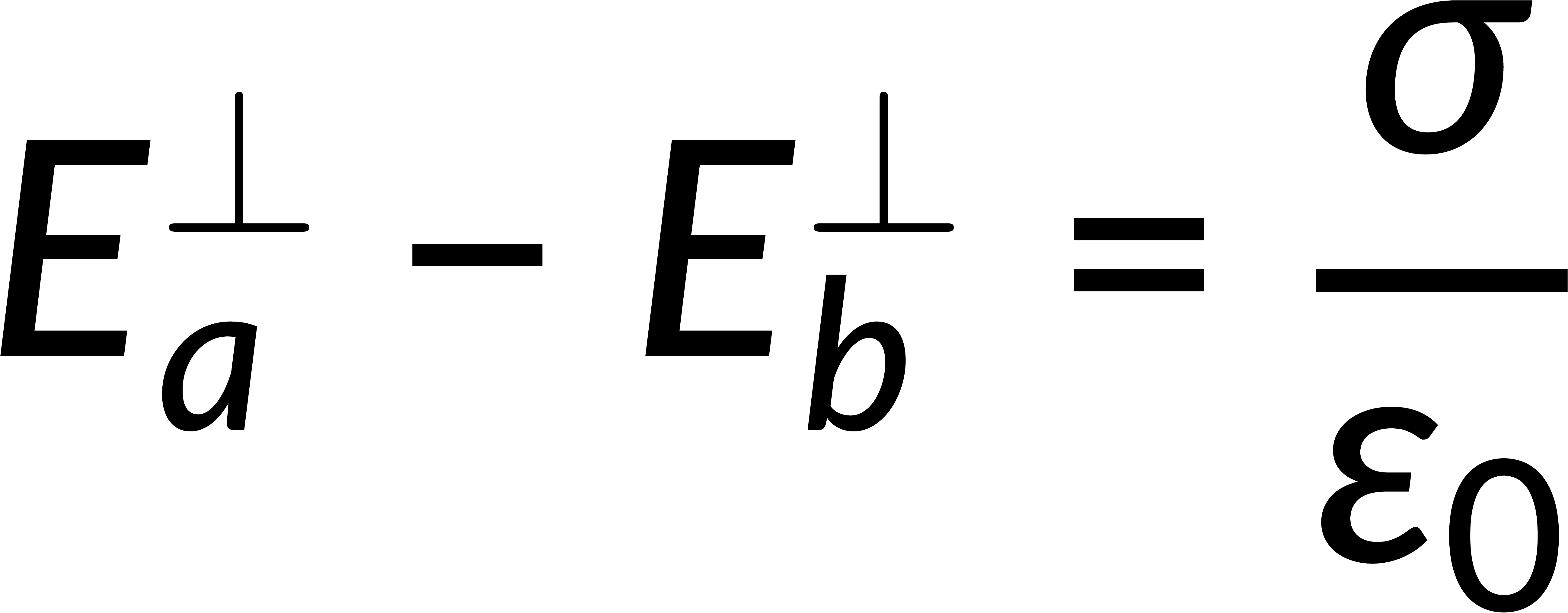
To estimate the discontinuity of the tangential component, consider a loop on the surface boundary. The integration of the electric field over this closed path is zero. Breaking this into the contributions from four parts of the loop and applying the condition that the thickness of the loop tends to zero implies that the tangential component of the electric field is continuous across the boundary.
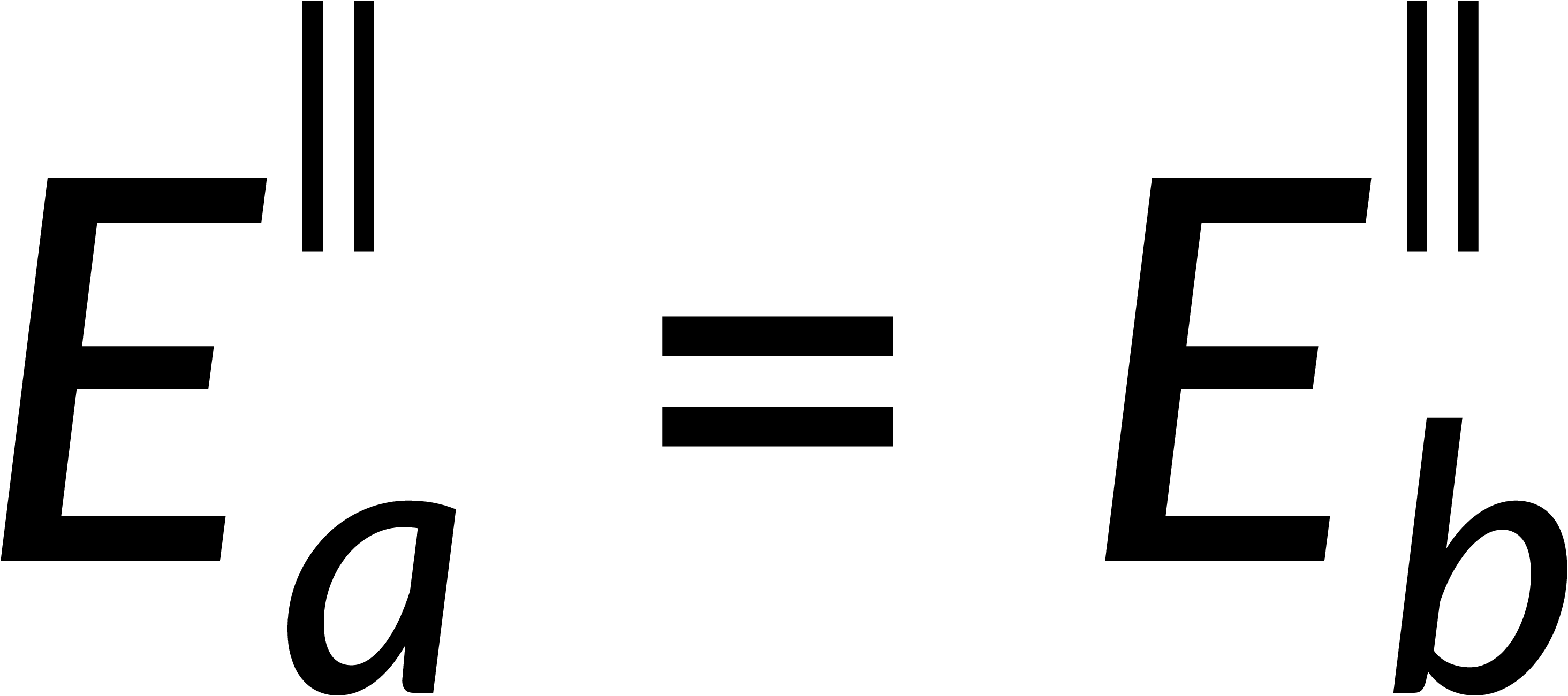
Combining the normal and tangential equations, the field at the boundary can be written by defining the unit vector perpendicular to the surface. It is known that the electric field is the negative gradient of the potential. The line integral of the field from below to above the boundary tends to zero, implying that the potential is continuous across any boundary.
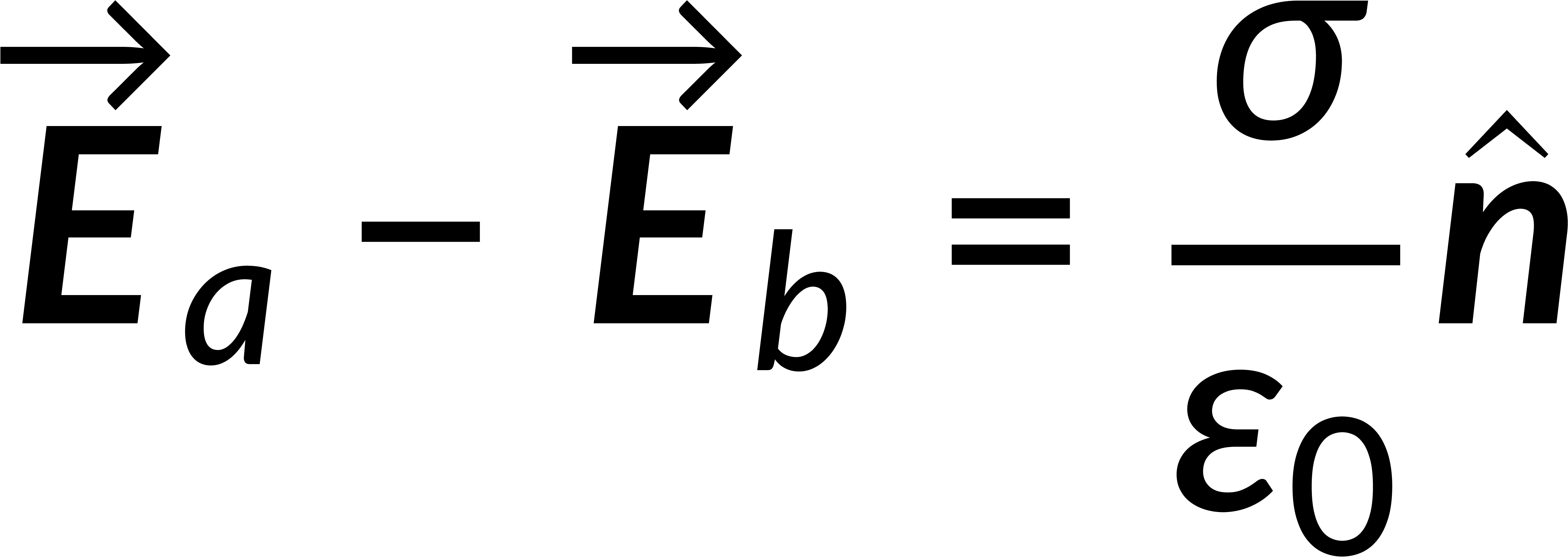
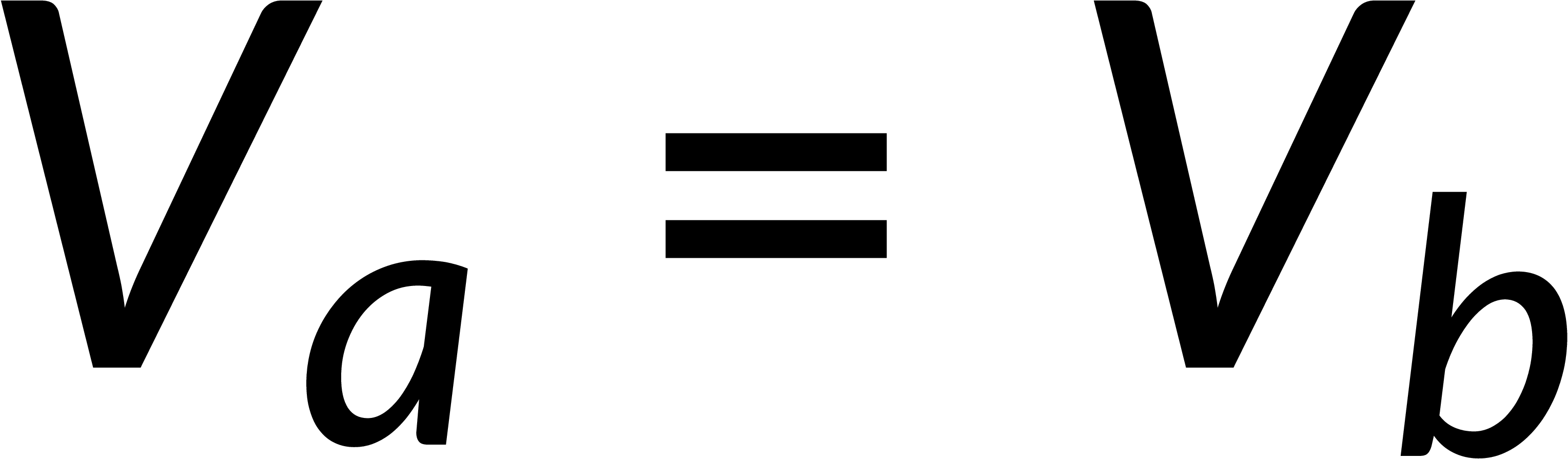
장에서 24:

Now Playing
24.14 : Electrostatic Boundary Conditions
Electric Potential
413 Views

24.1 : 전기 위치 에너지
Electric Potential
5.7K Views

24.2 : 균일한 전기장에서의 전기 위치 에너지
Electric Potential
4.6K Views

24.3 : 2점 전하의 전위 에너지
Electric Potential
4.4K Views

24.4 : 전위와 전위차
Electric Potential
4.3K Views

24.5 : 전기장에서 전위 찾기
Electric Potential
4.0K Views

24.6 : 전위 계산 I
Electric Potential
1.9K Views

24.7 : 전위 계산 II
Electric Potential
1.6K Views

24.8 : 등전위 표면(Equipotential Surfaces)과 필드 라인(Field Lines)
Electric Potential
3.6K Views

24.9 : 등전위 표면 및 도체
Electric Potential
3.3K Views

24.10 : 전위에서 전기장 결정
Electric Potential
4.3K Views

24.11 : 푸아송과 라플라스 방정식
Electric Potential
2.6K Views

24.12 : Van de Graaff 발전기
Electric Potential
1.7K Views

24.13 : 전하 분포와 관련된 에너지
Electric Potential
1.5K Views

24.15 : 두 번째 고유성 정리
Electric Potential
972 Views
Copyright © 2025 MyJoVE Corporation. 판권 소유