A Modeling and Simulation Method for Preliminary Design of an Electro-Variable Displacement Pump

Summary

A simulation model specifically supporting the preliminary design of an electro-variable displacement pump (EVDP) is developed and partially verified by experiments. The control performance, life, reliability, etc., can all be evaluated using the proposed model, which covers the main performance requirements under the EVDP preliminary design task.

Abstract

Electro-hydrostatic actuators (EHAs) have been considerably researched in academia, and their applications in various industrial fields are expanding. The variable-speed EHA has now taken priority over the variable-displacement EHA, but its driving motor and associated electronics encounter issues when applied in high-power applications: low-dynamics, high thermal dissipation, high price, etc. Therefore, a variable-displacement EHA equipped with an electro-variable displacement pump (EVDP) has been considered. The EVDP itself is a mechatronic system that integrates a piston pump, a ball screw, a gearbox, and a permanent magnet synchronous motor (PMSM). Consequently, the EVDP needs to be investigated to ensure its system-level performance when applied in an EHA. In addition to the previous research on the technical parameters of the EVDP, a dedicated design method is necessary for further reducing the cost of using the EVDP and exploring its performance potential. Here, a simulation based EVDP preliminary design method is selected for designing a 37 kW EVDP. Firstly, a previously proposed multidisciplinary model of the EVDP is extended by improving the parameter generation, including the EVDP life, reliability, control models, etc. Secondly, the proposed model is partially verified using a downsized prototype. Thirdly, the EVDP is simulated at a system level, supported by the proposed model. The EVDP performance is evaluated according to the specified design requirements. The temperature, bandwidth and accuracy, reliability and lifetime, etc., are all predicted for the EVDP. The simulation results demonstrate the EVDP's applicability in variable-displacement EHA. The proposed modeling and simulation method can be used to evaluate diverse EVDP performance and respond to general design requirements. The method can also support the resolution of the preliminary design challenges in terms of limited information and robustness. Therefore, the proposed method is appropriate for the realization of the simulation-based EVDP preliminary design method.

Introduction

Electro-hydrostatic actuators (EHAs) are receiving increasing interest for applications such as industrial presses, large mobile machinery, crane manipulators, and primary aircraft control due to their combination of the advantages of both electric actuators and hydraulic actuators¹. Two basic types of EHAs can be identified: variable-speed EHAs and variable-displacement EHAs². Currently, the variable-speed EHA is more popular than the variable-displacement EHA due to its higher efficiency and simplicity. However, along with the higher power level of the EHA, which is needed in heavy vehicles, such as heavy launch vehicles³ and submarines⁴, the driving motor and associated electronics of the variable-speed EHA have issues related to low dynamics, high thermal dissipation, high price, etc. Therefore, the variable-displacement EHA is being reconsidered for these high-power applications (>30 kW), as its control is realized via a low-power device that regulates the pump displacement.

One major concern that prevents variable-displacement EHA being taken as a priority is its cumbersome pump displacement control unit, which itself is a complete valve-controlled hydraulic system. The electro-variable displacement pump (EVDP) has been proposed to address this issue by using a compact electric displacement control unit. This design improves the compactness, efficiency, etc., of the variable-displacement EHA, which resolves the previous weakness to a certain degree. Therefore, the use of variable-displacement EHAs for high-power applications may be facilitated by using the newly proposed EVDP. However, the complexity of the EVDP is significantly greater compared to the conventional hydraulically controlled variable-displacement pump as it integrates components from several new disciplines. Consequently, specific EVDP-based research activities have emerged. Our research group started the EVDP research⁵ and has continued to develop it⁶. Liu developed the EVDP for EHA applications and performed experimental tests⁷. Some hydraulic companies also provide EVDP products. In addition to the research regarding the technical components of the EVDP, the design method for responding to real application requirements is also significant for enhancing the EVDP's competence by further reducing the cost of using EVDPs and exploring their performance potential. Hence, a specific EVDP preliminary design method is necessary for optimizing trade-offs in its system-level performance by analyzing its coupled disciplines. The simulation-based preliminary design is of interest for this type of multidisciplinary coupling of mechatronic products⁸.

Although no specific simulation models for EVDP preliminary design have been proposed due to it being a newly proposed concept, much research has been invested in related mechatronic products. A dynamic EHA model has been built to optimize the weight, efficiency, and control performance in preliminary design⁹, but the lifetime, reliability, thermal characteristics, etc., were not involved, which are essential performance indexes that should be considered in preliminary design. Another dynamic EHA model has also been used to optimize cost, efficiency, and control performance¹⁰, and a thermal model was subsequently developed to evaluate the thermal characteristics of the optimized EHA¹¹, but the reliability and lifetime were not considered. A comprehensive electro-mechanical actuator (EMA) preliminary design method has been presented¹². Specific models with different functions capable of analyzing different characteristics have been proposed for this method, and reliability and lifetime models have also been developed¹³. The mechanical strength, power capability, thermal performance, etc., could hereby be evaluated, but the control performance was not involved. Another EMA preliminary design method utilized a dynamic EMA model and associated component sizing models¹⁴. The cost, weight, fatigue life, power capacity, physical constraints, etc., were involved in the simulation analysis, but reliability and control performance were not included. A dynamic model was proposed for the optimization design of a hydraulic hybrid drive train¹⁵. The power capacity, efficiency, control, etc., could be simulated, but the reliability and life were not considered. Models for analyzing an EHA-based flight control actuation system have been proposed, within which simple power transmission equations and weight functions were used¹⁶. Considering that the models were used for vehicle-level and mission-level analyses, the limited attribute coverage of the models was appropriate. As a major component of the EHA, servo motors have attracted separate attention regarding modeling and design, and the results are also instructive for EHA model development. Thermal networks, weight models, etc., can also be considered for EHA modeling^17,18,19. The reviewed literature indicates that, even considering the results from products related to the EVDP, the developed models do not analyze all the influential performance attributes of the products for the preliminary design. The control performance, thermal performance, reliability, and lifetime are the attributes that have been most neglected in construction of the models. Therefore, this paper proposes a model package capable of analyzing all the most influential performance attributes for the EVDP preliminary design. The simulation analysis is also presented to better illustrate the model functions. This paper is an extension of a previous publication²⁰, as it improves the parameter generation, involves the lifetime model, reliability model, and control model, optimizes the calculation cost, validates the model, and conducts in-depth simulation analysis, etc.

The conventional hydraulic control unit of a variable-displacement piston pump is replaced with an electric actuator to improve the compactness and reduce heat dissipation, as shown in Figure 1. The electric actuator consists of a ball screw, a gearbox, and a permanent magnet synchronous motor (PMSM). The electric actuator connects the swashplate via a bar to regulate the pump displacement. When applied in EHAs, the EVDP swashplate rotational position is closed-loop controlled by modulating the PMSM. The electric actuator is integrated with the piston pump in a mutual case to form an integral component. This design submerges the electric actuator in the working fluid and hereby strengthens the multi-domain coupling effects.

As the EVDP is a typical multi-domain mechatronic product, its preliminary design plays an essential role in optimizing trade-offs in its system-level performance and outlining the component design requirements. The process is illustrated in Figure 2 based on the simulation-based design scheme^10,12. Step 1 firstly analyzes the selected EVDP architecture, as in Figure 1, and concludes the design parameters based on the specified performance requirements. Then, the design task is usually transformed into an optimization problem to explore the performance optimization of the EVDP. This is carried out by converting the design parameters into optimization variables and converting the performance requirements into objectives and constraints. It is worth noting that the design parameters need to be classified into active, driven, and empirical categories. Only the active parameters are used as optimization variables due to their independence features. The other two categories are automatically generated by estimation from the active parameters. Therefore, Step 2 develops the estimation models of the driven and empirical parameters. These estimation tools are used in each iteration of the optimization, as well as in Step 5 for formulating all the required simulation parameters. Step 3 builds the calculation models for each optimization objective or constraint, which reflects the required performance. These models should be computationally efficient; otherwise, the optimization calculation cost would be unacceptable. Step 4 performs the optimization calculation, which is usually multi-objective and multidisciplinary. It also deals with the parameter uncertainties in the preliminary design phase. Step 5 constructs an overall model of the designed EVDP and uses it for validating the optimization results by simulating the EVDP under typical duty cycles. This model is the ultimate tool for evaluating the preliminary design results. Therefore, this model should have the highest fidelity and involve all the influential characteristics in a tight coupling style. Finally, the preliminary design performance results and the system-level dimensioning results are obtained.

This paper focuses on the system modeling and simulation method of the EVDP, which involves conducting the parameter analysis in Step 1 and completing Steps 2 and 5. Firstly, the design parameters are derived based on the EVDP architecture and the design requirements, and they are classified into three sub-categories. Secondly, the estimation models for the non-active parameters are developed based on scaling laws, component catalogs, empirical functions, etc. Thirdly, the overall model of the EVDP is constructed using multidisciplinary coupling equations and additional lifetime and reliability sub-models, and the model is partially verified by experiments. Lastly, the previous sizing results are imported into the constructed model to perform simulation analysis under typical duty cycles. The system-level performance is deduced based on the simulation results. The parameter sensitivity and the robustness of the design are also evaluated. As a result, this paper develops a specific modeling and simulation method for EVDP preliminary design. The EVDP's performance for application in the EHA is comprehensively predicted. The proposed method stands as a practical tool for developing EVDPs and variable-displacement EHAs for high-power applications. The method can also be referred to for developing simulation tools for other types of mechatronic products. The EVDP in this paper refers to the electro-mechanically controlled variable-displacement pump, but the electro-hydraulically controlled variable-displacement pump is out of the scope of this paper.

Protocol

NOTE: Matlab and Simcenter Amesim (referred to as system simulation platform hereafter) were used in this protocol and are listed in the Table of Materials. However, the proposed protocol is not limited to implementation in these two software applications.

1. Selecting and classifying the EVDP design parameters (Step 1 in Figure 2).

1. Dismantle the architecture of the EVDP in Figure 1 into a piston pump unit, a ball screw, a gearbox, a PMSM, and a controller. Check the performance requirements of the EVDP.
   NOTE: Particularly in this paper, the requirements included power capacity, control performance, thermal performance, lifetime, reliability, efficiency, and weight.
2. Summarize the size parameters and specifications of the components of the EVDP. Analyze the parameters and specifications and select those related to the specified EVDP performance requirements.
   NOTE: The selected component parameters and specifications are the design parameters in the EVDP preliminary design, as shown in Table 1. Table 1 also includes the parameter classification results that were obtained through Step 1.3.
3. Classify the design parameters into active, driven, and empirical categories²¹, as listed in Table 1²⁰.
   1. Assign the independent parameters or specifications that are most representative of each component to the active category.
   2. Assign the parameters that can be derived from the active parameters to the driven category.
   3. Assign the other parameters that are calculated using empirical functions to the empirical category.
      NOTE: The thermal resistances are the group of parameters for thermal network modeling. Each thermal path is assigned with a thermal resistance. The quantity and values of the thermal parameters are finally decided upon by the thermal network architecture.

2. Developing the estimation models of the driven and empirical parameters (Step 2 in Figure 2).

NOTE: Carry out the estimation models of the driven and empirical parameters using Matlab based on the following methods. An individual script is built for each driven or empirical parameter.

1. Estimate the pump and motor-driven parameters from the active parameters using scaling laws^22,23.
   NOTE: The pump and motor-driven parameters are mostly geometry or weight-related, which usually meet the requirement of material and geometry similarities for using scaling laws.
   1. Define the scaling ratio of one arbitrary component parameter x as:
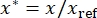        (1)
      where x is the concerned parameter and x_ref is the corresponding parameter of a reference component. Relate the active and driven parameters to the characteristic dimension of the component as:
        (2)
      where Y* is the scaling ratio of one active or driven parameter, l* is the scaling ratio of the characteristic dimension of the component, and α is the coefficient of the scaling ratio.
   2. Relate each driven parameter of the component to the active parameter by combining the respective Equation (2) of the specific driven parameter and the active parameters.
      NOTE: Some exemplified results are^22,2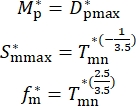3:
        (3)
      where the symbols of the equations refer to Table 1. Refer to the Table of Materials for the details of the piston pump and motor used in this protocol.
2. Estimate the driven parameters for the gearbox and the ball screw from the active parameters using component catalogs.
   NOTE: The active parameters of the gearbox and the ball screw are discrete values. Continuous variation of the active parameters is not possible due to mechanism constraints or high costs. Therefore, using off-the-shelf gearboxes or ball screws is preferable.
   1. Estimate the driven parameters of the gearbox by extracting those parameters from the gearbox datasheet that best match the defined ratio and nominal torque. Particularly in this paper, the gearhead (Table of Materials) was used for building the gearbox library in Matlab software. Use the nominal torque before the defined ratio for matching the gearbox based on the portfolio organization method of the specified gearhead (Table of Materials).
   2. Estimate the driven parameters for the ball screw by extracting those parameters from the ball screw datasheet that best match the defined lead and nominal load. Particularly in this paper, the ball screw (Table of Materials) was used for building the ball screw library in Matlab. Use the nominal load before the defined lead for matching the ball screw based on the portfolio organization method of the specified ball screw (Table of Materials).
3. Estimate the pump, the gearbox, and the ball screw efficiencies by empirical functions.
   NOTE: The efficiency parameters are not provided by the datasheets of the pump, the gearbox, and the ball screw, so they are estimated by an empirical function-based method.
   1. Assume the pump volumetric efficiency and the pump mechanical efficiency at the nominal working point are 0.95 and 0.90, respectively. Use these two values to fit the empirical functions of the leakage and viscous friction at the nominal working point, as in Equation (4) and Equation (5)²⁴. Then derive the coefficients, E_pv and E_pm of the empirical functions. As a result, use the derived empirical functions to simulate the efficiency characteristics under full working conditions:
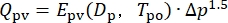        (4)
        (5)
      where Δp is the pump pressure difference, T_po is the temperature of the oil in the pump, D_p is the instant pump displacement, and S_p is the pump speed.
      NOTE: The efficiency data at the nominal working point of the off-the-shelf pumps can be obtained from the manufacturer, even though it was not the case in this paper. Then, the efficiency data can be used instead of the assumed data to improve the fidelity. The derived coefficients, which are under the nominal working point, are further regulated according to the instant working conditions (i.e., the displacement and the temperature).
   2. Use the maximum efficiency data of the gearbox or the ball screw to fit the viscous friction function under maximum load and maximum speed, as in Equation (6). Then, derive the viscous friction coefficient f. As a result, model the instant gearbox or ball screw efficiency as in Equation (7):
        (6)
        (7)
      where E_max, S_max, and F_max are the maximum efficiency, the maximum speed, and the maximum force of the gearbox or the ball screw obtained from the datasheet, respectively; E, S, and F are the instant efficiency, the instant speed, and the instant force of the gearbox or the ball screw during the simulation, respectively; and f is the viscous friction coefficient of the gearbox or the ball screw.
      NOTE: Assume the maximum efficiency of the ball screw is 0.90 due to the absence of any efficiency-related data. Update the efficiency function of the ball screw once efficiency-related data become available.
4. Estimate the thermal resistance parameters. Estimate the thermal resistances for the thermal network model developed in Step 3.3. using the empirical functions from thermodynamics theory. Classify the thermal resistances into two types: forced convection and conduction.
   NOTE: Define the thermal resistance between the EVDP shell and the environment as a constant value. This is because the current stage investigates the thermal characteristics inside the pump, while the detailed heat dissipation performance of the shell is the focus of the future thermal design.
   1. Estimate the thermal conduction resistance between the solid parts using Equation (8), which is based on the scaling law²³:
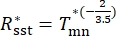        (8)
      where R_sst is the thermal resistance between two solid parts, and T_mn is the nominal torque of the servo motor.
      NOTE: Equation (8) is used only for estimating the thermal resistance of the winding-shell thermal conduction as it is the only solid-solid contact in the thermal network model.
   2. Estimate the thermal resistance of the forced convection between a solid part and a fluid part using Equation (9)^25,26:
        (9)
      where R_sft is the thermal resistance between a solid part and a fluid part; λ_f is the thermal conductivity of the fluid; L_a is the characteristic length of the heat exchange; C_Re and m are coefficients depending on the Reynolds number Re; Pr is the Prandtl number; and A_t is the heat exchange area.
      NOTE: L_a and other structural dimensions are estimated based on scaling laws, and the fluid velocity across the heat exchange area is instantly calculated from the simulation results of the pump flow.

3. Building the system simulation model (Step 5 in Figure 2).

NOTE: Build a multidisciplinary coupling model of the EVDP that can examine its full performance. The model architecture is shown in Figure 3, and the model is carried out in the co-simulation environment based on Matlab and the system simulation platform. Firstly, build the individual lumped model of each component or discipline. Then, assemble the component/discipline models according to Figure 3.

1. Build the weight model of the EVDP in Matlab.
   1. Calculate the weight of the EVDP by adding up the weights of each component, which are obtained from the weight estimation models in Step 2.
2. Conduct dynamic lumped parameter modeling of the EVDP in the system simulation platform.
   1. Build the electro-magnetic-motion model of the servo motor, the motion model of the mechanical transmission, the hydraulic-motion model of the piston pump unit, and the load torque model of the swashplate, as previously described²⁰.
   2. Model the system losses as in Equation (10):
      (10)
      where Q_mCu is the copper loss of the servo motor; Q_mr is the rotor loss of the servo motor; Q_pv and Q_pm are the volumetric loss and mechanical loss of the pump, respectively; Q_g is the gearbox loss; Q_s is the ball screw loss; i_m is the servo motor current; S_m is the servo motor speed; Δp is the pump pressure difference; T_po is the temperature of the oil in the pump; D_p is the pump displacement; S_p is the pump speed; f_g is the viscous friction coefficient of the gearbox; S_s is the gearbox input speed; and T_s is the torque of the ball screw.
   3. Model the fluid properties as in Equation (11). Identify the coefficients by fitting the fluid datasheet to Equation (11):
      (11)
      where ρ_f and ρ_f0 are the instant and reference density, respectively; C_p and C_p0 are the instant and reference specific heat, respectively; μ_f and μ_f0 are the instant and reference absolute viscosity, respectively; λ_f and λ_f0 are the instant and reference thermal conductivity, respectively; p_i is the instant pressure of the ith fluid node; T_i is the instant temperature of the ith fluid node; p₀ and T₀ are the reference pressure and temperature of the fluid properties; and a_m,n, b_m,n, c_m,n, and d_m,n are the coefficients.
   4. Model the pressure dynamics of the fluid volumes as in Equation (12)^27,28. Model the orifice as in Equation (4):
        (12)
      where p is the pressure of the fluid volume; B is the fluid bulk modulus; ρ is the fluid density; V is the fluid volume; and are the incoming and outgoing mass flow rate of the fluid volume, respectively; α_p is the volumetric expansion coefficient of the fluid; and T is the temperature of the fluid volume.
   5. Model the controller using a triple loop PID controller, as in Figure 4⁶. Tune the control parameters through several simulation trials when the simulation model and other simulation parameters are ready. Tune the control parameters from the inner loop to the outer loop by gradually increasing the gain values.
   6. Add a rotary spring and damper model between the driving speed source and the rotor of the pump. Add a linear spring and damper model between the input speed and the load mass of the ball screw.
      NOTE: This step enables equation causality in the piston pump unit model and ball screw model. Set the spring stiffness and damper rating to constant values that can drive the effects of these two blocks ignorable.
3. Conduct thermal modeling of the EVDP in the system simulation platform.
   1. Set a thermal network for the EVDP²⁰. Add the thermal load in Equation (10), except for Q_pv, to the corresponding thermal nodes.
   2. Model the thermal resistances for solid-solid heat exchange and solid-fluid heat exchange using the parameter functions in Step 2.4. Model the heat exchange of fluid-fluid nodes through exchanging their external enthalpy flow rates (refer to Step 3.3.4.)²⁹.
      NOTE: A reference thermal exchange structure and the dimensions of the EVDP are necessary for obtaining the parameters in Equation (9) based on scaling laws. The used EVDP thermal exchange structure is depicted in Figure 5.
   3. Model the temperature dynamics of the solid thermal nodes as in Equation (13):
        (13)
      where , m, and c_p are the heat flow rate, mass, and the specific heat of the solid node, respectively.
   4. Model the temperature dynamics of the fluid volumes as in Equation (14)^27,28:
        (14)
      where p, m, c_p, and α_p are the pressure, the mass, the specific heat, and the volumetric expansion coefficient of the fluid node, respectively; V and h are the volumes and the enthalpy of the fluid node, respectively; and h_in are mass flow rate and the enthalpy of the incoming flow, respectively; is the heat exchange rate; and W_s is the shaft work of the fluid node.
   5. Model the temperature dynamics of the orifices as in Equation (15). This also determines the heat load effects of Q_pv. Model the orifices as an ideal enthalpy transfer node, which transfers the incoming enthalpy directly to the outgoing enthalpy.
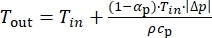        (15)
      where α_p, ρ, and c_p are the volumetric expansion coefficient, the density, and the specific heat of the fluid, respectively.
   6. Model the enthalpy transfers inside the pump as in Equation 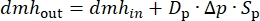(16):
        (16)
      where dmh_out and dmh_in are the outgoing and incoming enthalpy flow rate, respectively; and D_p, Δp, and S_p are the displacement, the pressure difference, and the speed of the pump, respectively.
4. For lifetime and reliability modeling, set the ball screw and the piston pump unit as the lifetime and reliability critical components. Use the smaller value of the evaluated lifetime/reliability of these two components as the EVDP lifetime/reliability performance. Carry out the models using the Matlab scripts.
   1. Use the fatigue life of the ball screw as its lifetime. Use the wear life of the piston pump unit as its lifetime. Model the ball screw and piston pump unit lifetime as in Equation (17) and Equation (18)^13,30:
        (17)
        (18)
      where F_ampi and F_meani are the load force amplitude and mean load of the ball screw derived from the load simulation results of the ball screw using rainflow counting; F_max is the maximum allowable load force of the ball screw; Δp_meani is the mean load pressure of the pump derived from the load pressure simulation results of the pump using rainflow counting; S_p is the pump speed; m is the quantity of the different cycles that are counted; n_i is the quantity of the ith cycle; N_i is the quantity of ith cycle that can run out of the component life; T_cyc is the duty cycle duration, from which the m cycles are identified; and p, α, and β are the experimental constants.
      NOTE: N_i is obtained by fitting its associated load stress, , to the linear log-log S-N curve, which is established using the maximum load data and nominal load-life data of the specific component. The log-log S-N curve can be improved when more lifetime data become available.
   2. Assume the reliability of the ball screw and the pump corresponding to its lifetime is 0.90. Define the reliability as calculated at the 50,000^th working hour. Model the ball screw and piston pump unit reliability as in Equation (19)¹³:
        (19)
      where R_ref is the reference reliability at the reference lifetime L_h,10 and L_{h,10 spec} is the specified working time to evaluate the reliability.
5. Assemble the model.
   1. Place all the necessary equations (introduced from Step 3.1-3.4) of each node in Figure 3 together to form the model block for each node. Conclude the input and output variables of each node.
      NOTE: Take the theoretical piston pump node as an example; it involves five equations: the driving torque considering the mechanical losses, the output flow without considering leakage (leakage is modeled separately by the orifices), the displacement variation according to the displacement control motion, the enthalpy transportation, and the load torque produced by the swashplate. The derived inputs are the driving speed, the pressure and temperature at the two ports, and the swashplate displacement. The derived outputs are the shaft angle, the load torque of the driving shaft, the output flow, the output enthalpy, and the load torque produced by the swashplate.
   2. Define the inputs and outputs of the overall EVDP model and perform the causality analysis of all the nodes. Add extra nodes when necessary to ensure that all the nodes are causally linked. Then, connect all the nodes to form the overall model of the EVDP, as in Figure 3.
      NOTE: The three fluid path nodes and two inner port nodes in Figure 3 were added to ensure the compatibility of the overall model causality. They are modeled as the orifices (Equation [4]).

4. Partial model verification (Step 5 in Figure 2).

NOTE: Use an EVDP prototype and its test rig to verify the modeling method in Step 3. Step 4 (model verification) was performed in this paper because the EVDP was newly developed, and the models were newly proposed. The EVDP prototype used in this paper was downsized compared to the one simulated in Step 5. The models validated based on the downsized prototype are considered applicable for simulating the same type of EVDP in other sizes. For future modeling and simulation tasks during preliminary design of the same type of EVDP, Step 4 can be omitted.

1. Conduct experimental setup.
   1. Build an EVDP prototype according to the schematics in Figure 1. Adapt the existing components to form the sub-components of the EVDP, such as the piston pump unit, the gearbox, the ball screw, and the servo motor.
      NOTE: a 7-piston pump featuring 7.4 mL/rev displacement was used for building the prototype in this paper. The maximum inclination of the swashplate was 18°. The nominal speed was 7000 rev/min, and the nominal pressure was 21 MPa. The ball screw lead was 1.59 x 10^-3 m, and the gearbox ratio was 2.47. The EVDP prototype is shown in Figure 6.
   2. Install the EVDP on a test rig consisting of a loading part and a control part³¹, as shown in Figure 7. Connect the three EVDP ports to the hydraulic circuit of the loading part. Connect the EVDP electric cables to the control part.
2. Conduct prototype testing.
   1. Start the auxiliary hydraulic power (9) by pushing the start button on the panel.
   2. Set the displacement of the EVDP to 2.5° in the textbox of the displacement command using the UI. Energize the mode valve (10) and tune the load control valves (12) to 3.5 MPa load pressure using the panel. Read and record the output flow of the EVDP from the panel.
   3. Set the EVDP displacement to -18°, -15°, -12°, -10°, -8°, -5°, -2.5°, 2.5°, 5°, 8°, 10°, 12°, 15°, and 18°, respectively. Record each output flow of the EVDP under each set displacement, as shown in Figure 8A.
   4. Set the EVDP displacement at 2.5° and adjust the load pressure to around 3.3 MPa, 5 MPa, 8 MPa, 10 MPa, 13 MPa, 15 MPa, 17 MPa, 18 MPa, 19 MPa, 20 MPa, and 21 MPa, respectively. Record the output flow of the EVDP under each pressure. Set the EVDP displacement at 5°, 8°, and 18°, respectively, and repeat the pressure setting of the 2.5° displacement test for each new displacement. Record the EVDP output flow under each testing point, as shown in Figure 8B.
   5. Deactivate the mode valve (10) by pushing the button on the panel. Set the sweeping frequency displacement command (from 0.02 Hz to 20.5 Hz at 2.5° amplitude) to the EVDP in the textbox of the UI. Record the EVDP displacement response and derive its magnitude and phase characteristics, as shown in Figure 9A.
3. Analyze the experimental results.
   1. Set the active parameters of the EVDP prototype to the built model in Step 3. The model generates other required simulation parameters automatically. Set the environment temperature and initial EVDP temperature at 40 °C. Run the simulation model under the same conditions as in the EVDP prototype test in Step 4.2 and record the simulation results.
   2. Plot the experimental results and simulation results of each condition group in the same figure, as shown in Figure 8 and Figure 9.
      NOTE: The maximum flow simulation error (2.2 L/min) happened at 2.5° displacement, which was 4.35% of the full EVDP flow. The simulation results of the frequency characteristics achieved good consistency with the experimental results under 10 Hz commands and showed higher errors over 10 Hz commands. The simulation accuracy was satisfactory.
      NOTE: The higher errors of the frequency characteristic simulation results over 10 Hz commands in Figure 9A arose from the parameter generation tools of the proposed model package. The simulation results achieved good accuracy when using real prototype parameters, as shown in Figure 9B. The parameter generation tools resulted in errors because the reference components used for estimating the parameters were not in the same series as the components of the prototype (in-house components were used for the EVDP prototype). Therefore, the simulation errors are not a concern when the selected components are in the same series as the reference components, but parameter uncertainties are also discussed in Step 5.

5. Simulation analysis (Step 5 in Figure 2).

NOTE: Perform the simulation analysis of the EVDP design option previously obtained by performing Steps 3 and 4 (optimization design) in Figure 2. Break down the simulation process, as shown in Figure 10.

1. Set active parameters and simulation settings.
   1. Use a set of previously obtained active parameters of the EVDP for the first simulation, where the EVDP nominal speed is 7000 rpm, the EVDP nominal pressure is 28 MPa, the maximum EVDP displacement is 12.3 mL/rev, the servo motor nominal voltage is 28 VDC, the servo motor nominal torque is 0.386 Nm, the gearbox is omitted, the ball screw nominal force is 5460 N, and the ball screw lead is 0.005 m.
   2. Use GJB1177-1991 15# aerospace hydraulic fluid as the working fluid in the simulation. Set the environment at a critical temperature of 70 °C. The heat exchange coefficient between the EVDP shell and the environment is constant at 20 W/m²/K.
   3. Set the duty cycle²⁰. Add a fluid heat sink to collect the EVDP return flow and supply flow to the inlet of the EVDP.
      NOTE: The heat sink emulates the downstream components in the real application. It contains 10 L fluid with a 5 m² heat exchange area, which maintains a 50 W/m²/K heat exchange coefficient with the environment. The strong heat dissipation of the fluid heat sink is used for dissipating all the EVDP output power as the EVDP output power is all converted into heat by the load control valve.
   4. Set the design parameters to ranges that cover the design space for performing the sensitivity analysis. Use the gearbox ratio as the exemplified parameter in this paper. Set the gearbox ratio range as 1-3.5 to investigate the effects of using continuous varying values for the gearbox ratio.
      NOTE: The range of the gearbox ratio was set by using the last series number as the lower bound and using the next series number as the upper bound. In this way, the effects of using continuous varying values of the gearbox ratio could be analyzed. As ratio 1 (not using gearbox) was the optimized gearbox ratio, the last series gearbox ratio did not exist. The lower bound of the range had to be 1 in this study. Ratio 3.5 did not need to be simulated again because it was already compared with the ratio of 1 in the previous optimization design and was discarded. At last, ratios 2 and 3 were selected for the sensibility analysis. Size the other components to comparable EVDP displacement control performance once the new gearbox ratio is defined to ensure a fair comparison³².
   5. Set the design parameters to ranges that cover their tolerances to perform the uncertainty analysis. Use the servo motor torque constant and the moment of inertia of the servo motor as the exemplified parameters in this paper. Set the range of the servo motor torque constant and the moment of inertia of the servo motor as 1 - 20% and 1 + 20% of their estimated values to check their estimation error effects on the EVDP frequency characteristics³³.
2. Run the simulation.
   1. Set the dynamic model and thermal model proposed in Step 3 (implemented in the system simulation platform) according to Step 5.1.2. Click on Parameter Mode > TFFD3-1 > filename for simple fluid characteristic data to import the oil property file. Click on Parameter Mode > THGCV0-1/THGCV0-2 > Temperature of the Fluid to set the environment temperature at 70 °C. Click on Parameter Mode > THGCV0-1/THGCV0-2 > Convective Heat Exchange Coefficient to set the environment temperature at (20 W/m²/K) / (50 W/m²/K).
   2. Input the active parameters in Step 5.1.1. to the parameter estimation models (implemented using Matlab) proposed in Step 2. Click on EDITOR > Run to run the script for generating all the necessary simulation parameters, as shown in Table 2.
      NOTE: The control parameters are obtained as illustrated in Step 3.2.5. rather than being automatically generated.
   3. Click EDITOR > Run in Matlab to run the script for calculating the weight and activating the dynamic and thermal models with the simulation parameters. The simulation results are automatically obtained by this script.
   4. Click EDITOR > Run in Matlab to run the script for calculating the EVDP lifetime and reliability performance from the saved simulation results.
3. Click Simulation Mode in the system simulation platform to check the simulation results. Derive other EVDP performance results from these time-domain simulation results (e.g., the swashplate control accuracy and bandwidth, the EVDP working temperature, the EVDP efficiency, and the EVDP power level).
4. Click Parameter Mode in the system simulation platform to set the simulation parameters specified in Steps 5.1.4. and 5.1.5. Click EDITOR > Run in Matlab to run the script for activating the dynamic and thermal models.Click Simulation Mode in the system simulation platform to check the simulation results of the sensitivity and uncertainty analyses.

Results

This section presents the results obtained from performing all the protocol steps, which constitute part of Step 1, all of Step 2, and all of Step 5 of the EVDP preliminary design method in Figure 2. The input information in the protocol includes the EVDP schematics in Figure 1, the optimized active parameters (clarified in Step 5.1.1.) of the EVDP from Step 4 of Figure 2, and the EVDP performance simulation tasks, which relate to t...

Discussion

The concept and other technical components of the EVDP have been presented in previous publications^6,31, demonstrating the applicability and advantages of the EVDP. Instead of studying the EVDP itself, this paper continued to study the design method in relation to future real application needs. A specific design method is necessary for this type of highly integrated and multidisciplinary coupling product, which calls for delicate performance trade-offs and optimi...

Materials

Name	Company	Catalog Number	Comments
Ball screw	NSK	PSS
EVDP prototype	Beijing Institute of Precision Mechatronics and Controls	customized	7.4 mL/rev, 7000 rpm, 21 Mpa
EVDP testrig	Beijing Institute of Precision Mechatronics and Controls	customized	Refer to Figure 7, can be adapted upon individual needs. Including Power PMAC controller, ELMO Whistle Driver, etc.
Gearhead	Maxon	GP
Matlab	Mathworks	R2020a
Permannet magnet synchronous motor	Maxon	393023
Piston pump	Bosch Rexroth	A10VZO
Simcenter Amesim	Siemens	2021.1	system simulation platform