A subscription to JoVE is required to view this content. Sign in or start your free trial.
Method Article
تحليل شكل الجسيمات ثلاثي الأبعاد باستخدام التصوير المقطعي المحوسب بالأشعة السينية: الإجراء التجريبي وخوارزميات التحليل لمساحيق المعادن
In This Article
Summary
حجم وشكل جزيئات المسحوق ليست كميات مستقلة. لا تقيس تقنيات القياس المعتادة هذه المعلمات المتشابكة في ثلاثة أبعاد (3D). يتم وصف تقنية قياس / تحليل ثلاثية الأبعاد ، بناء على التصوير المقطعي المحوسب بالأشعة السينية ، والتي يمكنها قياس الحجم والشكل وتصنيف جزيئات المسحوق وفقا لكلا المعلمين.
Abstract
يعد قياس توزيع حجم الجسيمات في المسحوق نشاطا شائعا في العلوم والصناعة. قياس توزيع شكل الجسيمات أقل شيوعا. ومع ذلك ، فإن شكل وحجم جزيئات المسحوق ليست كميات مستقلة. جميع تقنيات قياس الحجم / الشكل المعروفة إما تفترض شكلا كرويا أو تقيس الشكل في بعدين فقط. تقيس الطريقة القائمة على التصوير المقطعي المحوسب بالأشعة السينية (XCT) المعروضة هنا الحجم والشكل في 3D دون وضع أي افتراضات. بدءا من صورة ثلاثية الأبعاد للجسيمات ، يمكن للطريقة تصنيف الجسيمات رياضيا وفقا للشكل ، على سبيل المثال الجسيمات المكونة من عدة جزيئات أصغر ملحومة معا بدلا من الجسيمات المفردة التي ليست كروية بالضرورة. بالطبع ، فإن تحديد رقم واحد على أنه "حجم" أو "شكل" جسيم عشوائي غير كروي غير ممكن من حيث المبدأ ، مما يؤدي إلى العديد من الطرق لتقدير حجم الجسيمات وشكله عبر معلمات مختلفة مترابطة ، والتي يمكن إنشاؤها جميعا من هذا التوصيف ثلاثي الأبعاد الكامل في شكل متوسطات وتوزيعات. يتم وصف الإجراءات التجريبية اللازمة والتحليل الرياضي والتحليل الحاسوبي وإعطاء مثال لمسحوق المعادن. تقتصر هذه التقنية على الجسيمات التي يمكن تصويرها بواسطة XCT بحد أدنى حوالي 1000 فوكسل لكل حجم جسيم.
Introduction
يعد قياس توزيع حجم الجسيمات في المسحوق نشاطا شائعا في العلوم والصناعة1،2. يعد قياس توزيع شكل الجسيمات أقل شيوعا ، ولكن كلا من الحجم والشكل ، جنبا إلى جنب مع المواد التي تصنع منها الجسيمات ، يحددان خصائصها ، إما بمفردها أو في نوع من مادة المصفوفة3،4،5،6،7. تشمل المواد التي يكون حجم الجسيمات وشكلها موضع أهمية الأسمنت البورتلاندي والرمل والحصى8،9،10،11،12،13،14،15،16،17،18،19،20،21،22 ، 23 ، مساحيق معدنية لتعدين المساحيق وتصنيع المواد المضافة24،25،26 ، التربة القمرية27،28،29 ، إطارات السيارات الممزقة30 ، زجاج النفاياتالمكسر 31 ، الخلايا الجذعية32 ، والأنابيب النانوية الكربونية والجرافين33،34،35،36،37. ومع ذلك ، فإن شكل وحجم جزيئات المسحوق ليست كميات مستقلة26. على سبيل المثال ، لنفترض أن المرء لديه جسيم منتظم هندسيا يقال إن "حجمه" هو d. دون أن نقول ما إذا كان هذا الجسيم عبارة عن كرة أو مكعب أو قضيب رفيع بطول d ، لا يعرف المرء حقا كيف ينطبق الحجم على هذا الجسيم. بالقول إن الجسيم عبارة عن كرة أو مكعب أو قضيب ، فإن المرء يحدد شكل الجسيم حقا ، وبدون هذه المعلومات الإضافية ، فإن معلومات الحجم لا معنى لها.
بالنسبة لهذه الأمثلة الثلاثة ، يمكن تحديد حجم الجسيم للكرة أو المكعب أو القضيب الرفيع برقم واحد. ولكن حتى لو كان للقضيب مقطع عرضي دائري ، فسيحتاج المرء أيضا إلى قياس قطر هذا المقطع العرضي ، لذلك ستكون هناك حاجة حقا إلى معلمتين للحجم لجسيم القضيب الرفيع. ماذا عن الجسيمات على شكل أشكال بيضاوية أو صناديق مستطيلة؟ لكل من هذه ، هناك حاجة إلى ثلاثة أرقام لتحديد الحجم ، ولا يزال يجب إعطاء الشكل إما كمربع بيضاوي الشكل أو مستطيل حتى يكون لمعلمات الحجم الثلاثة معنى. بالنسبة للجسيم ذي الشكل العشوائي ، ستكون هناك حاجة إلى عدد لا حصر له من معلمات الحجم (على سبيل المثال ، طول الحبال عبر الجسيم) لتوصيف "حجم" الجسيم بالكامل ، ومع ذلك ستكون هذه لا معنى لها بدون "توصيف الشكل" ، مع معرفة الزوايا بالنسبة لمركز كتلة الجسيم التي تم رسم هذه الأوتار.
هناك العديد من التقنيات المستخدمة لقياس توزيع حجم الجسيمات في المسحوق ، باستخدام مبادئ فيزيائية مختلفة1،2. ومع ذلك ، فإن ما لا يتم التعرف عليه عادة هو أنه من أجل استخراج حجم الجسيمات ، يجب استخدام معلومات حول شكل الجسيمات ، سواء كانت مفترضة أو مقاسة. يمكن تصنيف التقنيات الحالية على النحو التالي: (I) قياسات لحجم الجسيمات ثلاثية الأبعاد (3D) مع افتراض الشكل ثلاثي الأبعاد ، و (II) قياسات لكل من الحجم والشكل ولكن فقط لإسقاطات ثنائية الأبعاد (2D) ، باستخدام تقنيات تحليل الصور ثنائية الأبعاد. بالنسبة للجسيمات الكروية ، فإن جميع الإسقاطات ثنائية الأبعاد عبارة عن دوائر ، بنفس قطر الجسيمات الأصلية ، وكل تقنيات القياس هذه ، سواء من الفئة الأولى أو الثانية ، ضمن عدم اليقين في القياس ، تعطي نفس النتائج للمجالات المثالية. بالنسبة للجسيمات غير الكروية ، فإن الإسقاطات ثنائية الأبعاد أقل ارتباطا بالجسيمات الأصلية. إذا كان للجسيم مسامية داخلية لا تكسر سطح الجسيمات ، فلن يتم قياس هذه المسام على الإطلاق بأي من تقنيات القياس ثلاثية الأبعاد أو ثنائية الأبعاد. تشمل الفئة الأولى حيود الليزر وحجم الاستشعار الكهربائي (ESV) 38 وتحليل الغربال والترسيب. وتغطي الفئة الثانية الفحص المجهري الإلكتروني للإرسال والمسح الضوئي ، والفحص المجهري للقوة الذرية ، وتحليل الصور الديناميكية والثابتة بالتقنيات البصرية. لا تقيس أي من الفئتين بدقة حجم وشكل الجسيمات غير الكروية في 3D.
منذ حوالي عام 200239 ، تم تطوير طريقة جديدة لتحليل الجسيمات40،41،42،43،44،45 تصور جسيما ثلاثي الأبعاد في 3D ، ثم تستخدم عدة أشكال من التحليل الرياضي لتمثيل وتصنيف كل جسيم. يتم حفظ صورة ثلاثية الأبعاد لكل جسيم على حدة ، والتي يمكن مقارنتها بالمعلومات الهندسية والرياضية التي يتم حفظها أيضا لكل جسيم. يمكن استخدام هذه المعلومات الرياضية لإعادة توليد الجسيم حسب الرغبة في أي نوع من النماذج ثلاثية الأبعاد46،47،48،49 ، في أي مكان واتجاه ، أو لتوليد جسيمات افتراضية مجبرة على الحصول على نفس الإحصائيات50،51. تعتمد طريقة تحليل الجسيمات هذه على عمليات مسح XCT للجسيمات المنتشرة في الإيبوكسي أو بعض الوسائط الأخرى المماثلة. يتم تشغيل عمليات المسح XCT بواسطة برنامج متخصص يستخدم خوارزمية الاحتراق52،53،54،55،56 لتحديد الجسيمات ، ثم إما تركيب السلسلة التوافقية الكروية أو عد الفوكسل لتوليد وتخزين شكل وحجم الجسيمات ، والصور ثلاثية الأبعاد للجسيمات ، وفي الخطوة الثانية ، المعلومات الهندسية لكل جسيم. يحتوي كل جسيم تم تحليله على تسمية أبجدية رقمية فريدة ، والتي تستخدم لتتبع كل جسيم ، والمعلومات حول كل جسيم ، وربط كل جسيم بصورته ثلاثية الأبعاد. خلال عملية التحليل هذه ، يتم تحليل المسام الموجودة داخل الجسيم ويتم تخزين المسامية الكلية في هذا الجسيم المعين ، نظرا لأن إعادة بناء XCT تعطي عرضا ثلاثي الأبعاد كاملا للعينة.
تم العثور على ثلاثة معلمات هندسية للحجم / الشكل (من بين العديد منها) لتكون مفيدة بشكل خاص في تحليل وتصنيف الجسيمات في 3D: الطول ، L ، العرض ، W ، والسمك ، يتم تعريف T. L على أنه أطول مسافة من نقطة السطح إلى نقطة السطح عبر الجسيم ، يتم تعريف W بالمثل على أنه L مع القيد الإضافي ، يجب أن يكون متجه الوحدة على طول W عموديا على متجه الوحدة على طول L ، و T يتم تعريفه أيضا بالمثل على أنه L مع القيد الإضافي المتمثل في أن متجه الوحدة على طول T يجب أن يكون عموديا على كل من متجه الوحدة على طول L ومتجه الوحدة على طول W12. تحدد هذه المعلمات الثلاث الحد الأدنى من المربع المستطيل أو المحيط الذي يحتوي فقط على الجسيم ، وتعطي نسب هذه المعلمات الثلاثة معلومات قيمة ولكنها تقريبية عن الشكل حول كل جسيم. يمكن إجراء توزيعات لأي من هذه. من الممكن أن يرتبط W ارتباطا جيدا ب "الأحجام" المقاسة بتحليل الغربال57 ، بينما ترتبط "الأحجام" المقاسة بحيود الليزر بمزيج من L و W و T31.
أخيرا ، يتم فحص الصور ثلاثية الأبعاد لعينة اختبار من 100-200 من الجسيمات بصريا لتحديد مكان القطع في L / T التي تمكن الطريقة من التمييز بين الجسيمات المفردة شبه الكروية (SnS) ، والجسيمات غير الكروية (NS) ، والتي يمكن أن تكون جسيمات متعددة ملحومة معا ، أو ما هي جسيمات مفردة بشكل واضح ولكن ذات شكل غريب.
Protocol
ملاحظة: تمت كتابة البروتوكول التالي لجزيئات مسحوق المعادن ذات الحجم ، وفقا لتقريب القطر الكروي المكافئ للحجم (VESD ، قطر الكرة بنفس حجم الجسيم) ، بين 10 ميكرومتر و 100 ميكرومتر. افترض أن المعدن له كثافة بوحدات جم / سم3. يجب ارتداء القفازات أثناء خطوات تحضير العينة ، جنبا إلى جنب مع حماية العين. من المهم قراءة جميع الخطوات الواردة في البروتوكول 1 ، حيث يجب أن تكون بعض المعدات جاهزة قبل بدء البروتوكول.
1. تحضير خليط مسحوق الايبوكسي
- تحضير ما يقرب من 25 جم من الايبوكسي سريع المعالجة (5 دقائق) في طبق صغير يمكن التخلص منه. تعمل قوارب رقائق الألومنيوم بشكل جيد لهذا الغرض. يأتي الإيبوكسي الجيد للاستخدام في غلاف فقاعي ، مع فصل الراتنج عن المقسى ، الذي تكون كثافته المعالجة ρe g / cm3.
- استخدم M جراما من المسحوق ، من عينة أكبر من المسحوق مهتزة جيدا ، حيث تم تصميم M لإعطاء جزء حجمي يبلغ حوالي 10٪ بمجرد خلط M grams في الإيبوكسي. تم تصميم هذا لتجنب الموقف الذي تكون فيه الجسيمات قريبة جدا من بعضها البعض لدرجة أن فحص XCT يحددها بشكل خاطئ على أنها جسيمات متعددة حقيقية مرتبطة بإحكام. المعادلة التي تحدد M هي:
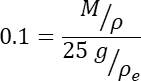
- امزج المسحوق المعدني بقوة في الإيبوكسي ، يدويا ، باستخدام قضيب تحريك يمكن التخلص منه - عصا خشبية بسيطة تعمل بشكل جيد - لمدة 30 ثانية تقريبا ، وهي طويلة بما يكفي لتفريق المسحوق بشكل كاف. هذه العملية ، التي تتم بشكل جيد ، تجعل تحليل الصور للجسيمات الفردية أكثر وضوحا.
- بعد الخلط ، اكشط خليط اللزج في كتلة مضغوطة بأكبر قدر ممكن من الرأسي ، لتكون جاهزا للخطوة التالية. من المهم إعداد الخطوات التالية مسبقا ، حيث لن يتبقى الكثير من الوقت قبل أن تصلب الإيبوكسي.
- استخدم مضخة تفريغ صغيرة متصلة بخرطوم بلاستيكي بطول 0.5 متر ، مع إدخال فوهة في الطرف المفتوح للخرطوم تتناسب بشكل مريح مع قش بوليمر يبلغ قطره الداخلي حوالي 3 مم.
ملاحظة: قش الكوكتيل ، المتوفر بسهولة في محلات البقالة ، يعمل بشكل جيد مع قش البوليمر بقطر 3 مم ويبلغ طوله حوالي 150 مم. بالنسبة للفوهة ، عادة ما يكون الطرف المقطوع للماصة البلاستيكية التي تستخدم لمرة واحدة من 1 مل إلى 2 مل فعالا. عندما تتناسب الفوهة مع الخرطوم البلاستيكي ، يجب شد بعض الأشرطة الكهربائية بإحكام حول المفصل لضمان إحكام الإغلاق. يجب أن يكون 25 جم من مسحوق الايبوكسي بلس أكثر من كاف لملء قشتين كاملتين. - أدخل الفوهة في المصاصة ، مع إمساك الفوهة ونهاية القشة بقوة معا. أدخل الطرف الحر من القشة في كتلة مسحوق الايبوكسي المدمجة وقم بتشغيل مضخة التفريغ.
ملاحظة: احتفظ بالطرف الحر من القش مغمورا في خليط مسحوق الايبوكسي لتجنب إدخال فقاعات الهواء في القشة - ستكون بعض فقاعات الهواء موجودة دائما ، لكن هذا الإجراء يقلل من وجودها. يجب ملء القش في حدود 10 مم من الأعلى - يمكن رؤية خط التعبئة من خلال القش الشفاف. عندما تمتلئ القشة الأولى ، قم بإيقاف تشغيل مضخة التفريغ وإزالة القشة من الفوهة. - امسح خليط الإيبوكسي من نهاية ملء القش وادفع طرفي القش إلى كتلة صغيرة من الطين لملء طرفي القش حتى لا يتسرب خليط مسحوق الايبوكسي أثناء المعالجة. ضع القشة 2 على الفوهة وكرر ذلك ، أولا باستخدام قضيب الخلط لتجميع خليط مسحوق الايبوكسي معا إذا لزم الأمر.
- بعد معالجة الإيبوكسي الموجود في القشتين ، قم بقطع نهايات القش ، حيث كان مانع التسرب من الطين ، بشفرة حلاقة ثم قم بقطع كل قش إلى نصفين لإعطاء أربع عينات. استخدم ماصة واحدة كعينة # 1 ل XCT ، مثبتة عموديا بحيث تخترق الأشعة السينية المقطع العرضي الدائري للقشة.
2. أداة XCT
ملاحظة: تفترض هذه الخطوات الإلمام بأداة XCT التي يختارها المستخدم.
- استخدم جهدا عاليا ، عادة 100 كيلو فولت أو أعلى ، حيث يوجد تباين جيد بين مصفوفة الإيبوكسي وجزيئات المسحوق المعدني ولا داعي لحل أي شيء داخل مصفوفة الإيبوكسي ، والتي تتطلب عادة جهدا منخفضا حوالي 40 كيلو فولت. استخدم مسحا ضوئيا كاملا بزاوية 360درجة ، بحجم فوكسل يبلغ حوالي 1 ميكرومتر. يجب أن تكون النسبة بين أصغر حجم للجسيمات التي تم أخذها في الاعتبار وحجم الفوكسل المستخدم 8-1039 كحد أدنى.
- خذ ما يكفي من مجالات الرؤية ، على أكثر من عينة واحدة ، لإعطاء جسيمات كافية للتحليل. إذا تم اتباع إرشادات تحضير العينة ، فستكون 2 إلى 8 FOVs كافية. عادة ما يكون الحد الأدنى من 1000 جسيم كافيا لتحليل صحيح للشكل / الحجم ، لكن المزيد من الجسيمات تؤدي إلى منحنيات توزيع أكثر سلاسة وإحصائيات أفضل. يتم ترقيم الشرائح المعاد بناؤها من 0 إلى nz-1 ، من أسفل إلى أعلى مجال الرؤية ، حيث nz هو العدد الإجمالي للشرائح المعاد بناؤها.
- احفظ شرائح المقطع العرضي الرأسي لكل مجال رؤية على حدة ، بتنسيق 8 بت (على سبيل المثال ، tiff) مع ملاحظة حجم البكسل لكل مجموعة صور (nx x ny) ، وعدد هذه الشرائح (nz) ، وحجم voxel بالميكرومتر (v). تنسيق 8 بت مناسب لهذه الأنواع من الصور الرمادية ذات المصفوفة المعدنية البسيطة من الجسيمات المعدنية والإيبوكسي ، والتي يسهل تقسيمها.
3. تجميع الشرائح التي تنتمي إلى كل مجال رؤية في بنية مجهرية 3D ASCII
ملاحظة: يطلق على برنامج C المستخدم في NIST اسم tiff2array.c وغالبا ما يستخدم مع ملفات tiff ولكن يمكنه التعامل مع تنسيقات 8 بت الأخرى. يمكن تجميعها كما هي ، مع الملف القابل للتنفيذ المسمى tiff2array. يقرأ هذا البرنامج في كل صورة ، من الأسفل إلى الأعلى ، ويحولها إلى تنسيق ascii (من 0 إلى 255 مقياس رمادي) ثم يكديسها في نهاية الملف الرئيسي.
- إذا كانت الصور المعاد إنشاؤها بتنسيق tiff ، على سبيل المثال ، وتم ترقيمها على التوالي من الأسفل إلى الأعلى ، فاستخدم بناء الجملة التالي في أمر طرف السطر: tiff2array * .tiff. هذا الملف الرئيسي ، أو ملف البنية المجهرية ، هو تمثيل ثلاثي الأبعاد لمجال الرؤية. إذا كان المتغير a (i ، j ، k) هو المقياس الرمادي في الموضع (i ، j ، k) ، حيث k هو رقم الشريحة ، k = 1 إلى nz ، و (i ، j) هو البكسل في شريحة kth ، حيث يتم قياس i من اليسار إلى اليمين ويتم قياس j من أعلى إلى أسفل.
ملاحظة: جميع البرامج المطلوبة في البروتوكول متاحة في قسم المعلومات التكميلية في هذه الورقة عبر رابط إلى قاعدة بيانات NIST الموجودة في https://doi.org/10.18434/M32265. - بالنسبة إلى P FOVs ، قم بإنشاء ملف صغير يسمى particle-class-sysconfig.dat ، مع خطوط P ، حيث يقرأ كل سطر ، ل pth (p = 1 ، P) FOV:
اسم الملف nx ny nz v b c
حيث اسم الملف = تعريف مكون من 12 حرفا لمجال رؤية معين ، و b = 1 للمسح الداخلي و 0 للمسح الخارجي ، و c = عدد المراحل الموجودة في الصور. عند إجراء الفحص الداخلي ، عادة ما تكون هناك ثلاث مراحل (c = 3): 1) الايبوكسي ، 2) المناطق السوداء التي تشير إلى الجزء الخارجي من المسح الدائري وفقاعات الهواء ، و 3) الجسيمات الأكثر إشراقا. في بعض الأحيان قد تبدو أربع مراحل للعين على أنها افتراض أكثر منطقية ، وبالتالي ج = 4. قيم c 3 أو 4 هما الخياران الوحيدان. تخبر قيمة c برنامج تحليل الجسيمات الذي تمت كتابة خوارزمية التجزئة التلقائية Otsu ، المكتوبة في الأصل للصور ذات المرحلتين ولكن يمكن تمديدها بسهولة إلى أي عدد من المراحل ، لاستخدامها لتقسيم الصور تلقائيا في مجال رؤيةمعين 26،58. يجب أن تحتوي ملفات البنية المجهرية التي سيتم استخدامها في البرنامج التالي على أسماء مكونة من 12 حرفا تشبه تماما اسم الملف المدرج في ملف FOV-name-sysconfig.dat ، متبوعا بالامتداد .mic. - قم بتشغيل برنامج تحليل الجسيمات pp-Otsu.f ، باستخدام إدخال ملف particle-class-sysconfig.dat وملفات البنية المجهرية المختلفة ، Filename.mic. قم بإجراء تغييرين فقط على هذا البرنامج لنظام جديد ، وكلها مميزة بتعليق "USER" في مصدر Fortran: أسماء الملفات لملفات الإخراج العامة (تغيير اسم فئة الجسيمات العامة) وعدد FOVs المدرجة في particle-class-sysconfig.dat. البرنامج pp-Otsu.f موجود في Fortran ، وهو عددي ، وعادة ما يتم تجميعه في Fortran 77 ، على الرغم من أن Fortran 90 يجب أن يعمل بشكل جيد. يجب تجميعها وجميع برامج Fortran الأخرى الموضحة أدناه بدقة مزدوجة (-r8) للحصول على نتائج دقيقة.
- بالإضافة إلى ذلك ، نظرا لأن pp-Otsu.f يعمل مع الملفات الكبيرة ، أضف دائما المعلمات (أو ما يعادلها) -mcmodel = medium و -Mlarge_arrays إلى التجميع. يحتوي الملف الإضافي ، gauss120.dat ، على الأوزان والنقاط لتربيع غاوسي مكون من 120 نقطة المستخدم على نطاق واسع في pp-Otsu.f ، ويجب أن يكون في نفس الدليل مثل pp-Otsu.f. جميع البرامج الموضحة أدناه مكتوبة في Fortran 77 باستثناء برامج MPI المكتوبة في Fortran 90.
- اعرض ملفات الجسيمات التي تعد المخرجات الرئيسية من pp-Otsu.f ، والتي قد تستغرق عدة ساعات لتشغيلها على معالج واحد إذا كان هناك آلاف الجسيمات المراد تحليلها. وتشمل هذه الملفات بأسماء مثل Particle-class-name-anm-particle-number.dat ، والتي تحتوي على قائمة المعاملات المعقدة (ن = 0،26) ، بوحدات ميكرومتر أو في أي وحدة v ، للجسيمات التي تم الحكم عليها على أنها على شكل نجمةكافية 39 وبالتالي يمكن توسيعها في وظائف التوافقيات الكروية (تسمى جسيمات SH). تتضمن ملفات الجسيمات أيضا ملفات مثل Particle-class-name-part-particle- number.dat ، والتي تحتوي على عدد voxels في الجسيم وجميع مواضع voxel (بإحداثيات voxel) للجسيمات غير القادرة على وصفها بالتوسعات التوافقية الكروية (تسمى الجسيمات nonSH).
- اعرض الملفين ، أحدهما ل SH والآخر للجسيمات غير SH ، والتي تعطي مسامية جميع الجسيمات الموجودة ، حتى لو كانت المسامية صفرا ، مع عبارة المسامية في أسماء الملفات. يجب إعطاء برنامج إضافي ، porosity-analyze.f ، عدد الأسطر في كل ملف مسامية وأسماء ملفاتها - أسماء الملفات المراد تغييرها موجودة في بداية الكود المصدري. الإخراج من هذا البرنامج هو الملفان Particle-class-intern-poros-analysis.txt و Particle-class-intern-poros-list.txt. ينشئ ملف التحليل المعلومات الموضحة في الجدول 2 في قسم النتائج التمثيلية، ويقدم ملف القائمة المعلومات اللازمة لإنشاء الشكل 5 في قسم النتائج التمثيلية.
- اعرض ملفات صور tiff الثلاثة التي تعرض شريحة واحدة من مجال الرؤية الأول الذي تم أخذه في الاعتبار. تظهر الشريحة الأولى (OriA-0500.tiff) k = 500 شريحة من مجال الرؤية الأول في ملف particle-class-sysconfig.dat ، دون أي معالجة للصور ، ويعرض ملف الصورة الثاني نفس الصورة ولكن الآن مجزأة ومتدرجة (PixA-0500.tiff). إذا تم تطبيق أي تقسيم محدود لمستجمعات المياه ، فإن ملف الصورة الثالث يعرض نتائج هذه الخوارزمية (LWSA-0500.tiff). عادة لا يتم تطبيق خطوة معالجة الصور هذه ، وبالتالي فإن ملف الصورة الثالث هو نفسه الثاني. يتم إنشاء هذه الصور كخطوة للتحقق من الأخطاء في التجميع الأصلي للبنية المجهرية ثلاثية الأبعاد وتجزئة صورة Otsu التلقائية. يتم إنشاء ملف إخراج عام (particle-class-name-particles-data.dat) يسرد جميع المعلومات المساعدة لمعالجة كل جسيم. يتم استخدام هذا الملف كمرجع فقط، ولكن يتم كتابة وحدات تخزين voxel وتسميات الأرقام لجميع الجسيمات التي تمت معالجتها في نهاية هذا الملف.
- لكل جسيم معالج ، سواء كان SH أو غير SH ، اعرض ملف صورة 3D VRML ، مع اصطلاح التسمية particle-name-particle-number.wrl. بالنسبة لجزيئات SH ، يحتوي ملف صورة VRML هذا على صورتين جنبا إلى جنب ، وصورة فوكسل للجسيم الأصلي ، وصورة أكثر سلاسة باستخدام معاملات SH. بالنسبة للجسيمات غير SH ، يتم تخزين صورة voxel فقط.
4. إنشاء معلومات هندسية لجميع جسيمات SH وغير SH
- قبل مزيد من المعالجة ، قم بعمل قائمة بأسماء ملفات Particle-class-name-anm-particle-number.dat ، تسمى anm.lis ، وقائمة بجسيمات Particle-class-name-part-particle-number.dat غير SH ، تسمى nonSH.lis. قم بتشغيل البرنامج الصغير number.f ، بعد أن تم تحريره أولا للحصول على العدد الصحيح من الملفات في anm.lis. يؤدي هذا إلى تغيير ملف anm.lis ليكون له رقم الجسيم في كل سطر من ملف القائمة ، بالإضافة إلى اسم الملف ، ليحل محل الملف السابق.
- استخدم البرنامج part-lwt-listnum-unitvector.f لإنشاء وتقييم المعلومات الهندسية لجسيمات SH. هذا برنامج متوازي ل MPI ، حيث يمكن أن يكون هناك الآلاف من جسيمات SH ليتم تقييمها ، وقد يستغرق عمل جسيم واحد فقط في كل مرة أياما. التغييرات الوحيدة في هذا البرنامج التي يجب إجراؤها عند معالجة فئة جسيمات جديدة هي عدد Ntot لملفات Particle-class-name-anm-particle number.dat ، ومعلومات تسمية فئة الجسيمات لملف الإخراج (Particle-class-name-un-geom-len.dat). يحتوي البرنامج على تعليقات (USER) في الأماكن القليلة التي تحتاج إلى تغيير لنوع جسيمات جديد. Particle-type-info-un-SH-geom-len.dat يوحد ملف الإخراج الجسيمات من كل مجال رؤية ، ولكل سطر الهيكل التالي.
معاملات SH اسم الملف ، x1 ، x2 ، y1 ، y2 ، z1 ، z2 ، الحجم ، مساحة السطح ، نسبة SA ، انحناء ، نسبة nnn ، غاوس ، عنصر نائب ، L ، W ، T ، L / T ، W / T ، T / T ، لحظة مكونات موتر القصور الذاتي ، متجه الوحدة L ، ثيتا ، زوايا فاي ، متجه وحدة W ، ثيتا ، زوايا فاي ، متجه الوحدة T ، زوايا ثيتا ، فاي
x1 هي الحد الأدنى لقيمة x على سطح الجسيم و x2 هو الحد الأقصى وبالمثل ل y و z. تحدد هذه "مربع المدى" الذي يحيط بالجسيم في اتجاهه المقاس42. يستخدم مربع المدى في تطبيقات أخرى46،47،48،49. نسبة SA هي مساحة سطح الجسيم مقسومة على مساحة سطح الكرة المكافئة للحجم. Curv هو متوسط الانحناء المتكامل المقلوب والتطبيع بحيث يكون مساويا للقطر عندما يكون الجسيم كرة مثالية. النسبة هي أثر عزم موتر القصور الذاتي مقسوما على أثر عزم موتر القصور الذاتي للكرة المكافئة للحجم. nnn هو الحد الأقصى لعدد معاملات SH (n = 0 ، nnn) التي يجب استخدامها عند العمل مع الجسيم المحدد. غاوس هو الانحناء الغوسي المتكامل ، مقسوما على 4π ، والذي يجب أن يساوي 1 لجسم مغلق. تحدد النقطة التي يختلف عندها غاوس عن الوحدة بأكثر من 5٪ الحد الأقصى لعدد معاملات SH (n = nnn) التي يجب استخدامها عند إعادة إنشاء الجسيم. L و W و T هي طول الجسيم وعرضه وسمكه، وقد تم تعريفها في قسم المقدمة. يتم سرد المكونات المستقلة لعزم موتر القصور الذاتي على النحو التاليI 11 و I22 و I33 و I13 و I23 و I12. أخيرا ، يتم سرد متجه الوحدة ل L ، بترتيب إحداثيات x و y و z ، متبوعة بالزوايا القطبية الكروية θ (الزاوية من المحور z الموجب) و Φ (زاوية الدوران حول المحور z ، المحددة على أنها صفر عند المحور x الموجب وتكون موجبة عكس اتجاه عقارب الساعة). تتبع معلمات W و T ، مدرجة بنفس الطريقة. - استخدم البرنامج nonSH-lwt-un-scalar.f لحساب معلمات L و W و T للجسيمات غير SH ، والتي تعمل على قائمة أسماء الملفات nonSH.lis ، وكذلك تسجيل متجهات الوحدة المقترنة. التغييرات الوحيدة التي يجب إجراؤها في هذا الملف لفئة جسيمات جديدة هي عدد أسماء الملفات في nonSH.lis، وأسماء ملفات الإخراج. يحتوي الإخراج الرئيسي من هذا البرنامج ، المسمى Particle-name-info-nonSH-len.dat ، على كل سطر بالتنسيق:
اسم الملف ، المجلد ، L W T A1 ، A2 ، A3 (متجهات وزوايا وحدة LWT)
حيث A1 و A2 و A3 هي الزوايا النهائية (بالدرجات - 90درجة مئوية) بين متجهات الوحدة ل L و W و W و T و L و T ، والتي يتم تضمينها كفحص للخطأ لخوارزمية الحساب L و W و T ، حيث يجب أن تكون هذه الزوايا صفرا للحصول على حساب مثالي. متجهات وزوايا الوحدات L و W و T بنفس التنسيق بالنسبة لجسيمات SH.
5. حدد مجموعة فرعية من جسيمات SH وغير SH لتحديد قطع SnS و NS L / T بصريا
ملاحظة: تتكون جسيمات SH ، بشكل عام ، من جسيمات كروية مفردة ، وجسيمات مفردة غير كروية (بيضاوية الشكل أو مكسورة بطريقة ما أو شكل عشوائي) ، وجسيمات مزدوجة ، وجسيمات متعددة (أكثر من جسيمين مرتبطين ببعضهما البعض). يمكن أن تكون الجسيمات المكونة للجسيمات المتعددة كروية أو غير كروية. تحتوي الجسيمات غير SH بشكل عام على عدد قليل من الجسيمات الكروية المفردة ، على الرغم من أنها تحتوي بشكل أساسي على مسام كبيرة اخترقت السطح ، والباقي في الغالب عبارة عن جزيئات مزدوجة ومتعددة26. يتم تحديد ذلك من خلال عرض عينة عشوائية من كلا النوعين من الجسيمات بقيم L / T من 1 إلى 2. يصبح هذا الفحص البصري خطوة مهمة لتمكين تصنيف SnS و NS.
- قم بتشغيل البرنامج (VRML-select-multi-single.f) الذي يقرأ ملفات Particle-type-info-SH-geom-len.dat و Particle-name-info-nonSH-len.dat ، ويختار 10 جسيمات في كل فاصل L / T بحجم 0.1 ، أي (1،1.1) ، (1.1،1.2) ، إلخ. يخزن هذا ما يصل إلى 100 جسيم SH مع L / T تتراوح من 1 إلى 2 ، وما يصل إلى 100 جسيم غير SH بنفس نطاق L / T . يتم إنشاء ملفين نصيين (*SH-VRML-list.txt و *nonSH-VRML-list.txt) يسردان قيم L/T والأسماء الجذرية لملفات صور VRML التي تم العثور عليها. يجب وضعها في جدول بيانات من نوع ما وترتيبها وفقا لقيمة L / T.
- افحص الصور ثلاثية الأبعاد لكل من هذه الجسيمات بصريا لتحديد النطاق الكلي للأشكال ، بدءا من أقل جسيمات قيمة L / T . يتم تقييم الجسيمات من حيث ما إذا كانت جسيمات مكسورة ، أو جسيمات مزدوجة ، أو جسيمات متعددة ، أو غير منتظمة (على سبيل المثال ، ليست كروية جدا) ، وما إذا كانت تحتوي على أقمار صناعية ، وهي جسيمات أصغر بكثير ، متصلة بالجسيم الرئيسي. يتم الحكم على القمر الصناعي على أنه يجعل الجسيم الرئيسي جسيما مزدوجا أو متعدد إذا كان القمر الصناعي (الأقمار الصناعية) أكثر من 1/5 قطر الجسيم الرئيسي. تم العثور على القيمة التقريبية ل L / T التي تفصل الجسيمات المفردة شبه الكروية (SnS) عن الجسيمات المتعددة وغير الكروية (NS) ، والتي يمكن أن تكون مختلفة قليلا بالنسبة لجسيمات SH وغير SH. يحدد الجسيم المزدوج أو المتعدد الأول الذي تم العثور عليه قيمة القطع لكل من جسيمات SH وغير SH.
ملاحظة: تتضمن المادة التكميلية، الموجودة في https://doi.org/10.18434/M32265، ملف جدول بيانات للجسيمات التي تم فحصها، لمعرفة كيفية تحديد قيم القطع هذه. هناك بعض عدم اليقين ودرجة من الذاتية في هذه الأرقام ، والتي يمكن تقييمها عن طريق اختيار مجموعة مختلفة من 100 SH و 100 جسيم غير SH ، مع L / T بين 1 و 2 ، لتقييم قيم القطع. وجد العمل الأخير أن عدم اليقين هذا كانصغيرا 26 ولم يؤثر على النتائج بشكل كبير.
6. إنشاء بيانات إسقاط ثنائية الأبعاد من الجسيمات ثلاثية الأبعاد
ملاحظة: أجهزة تحليل الجسيمات التجارية الوحيدة الحالية التي تقيس شكل الجسيمات على الإطلاق تفعل ذلك باستخدام إسقاطات ثنائية الأبعاد. يمكن تحليل بيانات XCT لإعطاء توقعات ثنائية الأبعاد تعسفية ، وتوليد بيانات يمكن مطابقتها كميا مع نتائج هذه الأدوات التجارية. يتم إجراء الإسقاطات ثنائية الأبعاد من كل من جسيمات SH و nonSH ويتم دمجها ، دون محاولة للتصنيف إلى فئات 2D SnS و NS ، لأنه من غير المعروف في الوقت الحالي كيفية تحديد هذه الفئات لإسقاطات 2D.
- استخدم البرنامجين ، (proj-mpi-SH-LWT.f) لجسيمات SH و (proj2D-nonSH-LWT.f) للجسيمات غير SH ، لإنشاء ثلاثة إسقاطات متعامدة لكل جسيم ، على طول اتجاه متجهات وحدة LWT الثلاثة ، ثم إنشاء معاملات فورييه لمخطط الإسقاط. تستخدم هذه المعاملات لحساب كميات ثنائية الأبعاد مختلفة مثل المساحة والمحيط والأطوال المختلفة ونسب العرض إلى الارتفاع.
- يتم إنشاء سلسلة من النقاط (x ، y) وتخزينها لكل إسقاط ، مع تسميتها باسم ملف الجسيمات و 1 للإسقاط على طول متجه الوحدة L ، و 2 للإسقاط على طول متجه الوحدة W ، و 3 للإسقاط على طول متجه الوحدة T . قم بإدخالها في أي برنامج رسم بياني يقبل هذا الإدخال ، مع التأكد من أن حدود المحور x و y يجب أن تكون متماثلة ، وأن كل محور له نفس الطول المادي.
- قم بتخزين معاملات فورييه باصطلاح تسمية ملف مماثل ، ولكن يتم إيقاف تشغيل هذه الميزة ، افتراضيا ، باستخدام التعليقات. التغييرات الوحيدة التي تم إجراؤها في أي من هذين البرنامجين (موضع البرنامج المميز ب "USER") هي العدد الإجمالي للجسيمات التي يجب أخذها في الاعتبار (Ntot) ، وأسماء ملفات الإدخال والإخراج ، والتي يجب أن تعكس فئة الجسيمات التي يتم تحليلها.
- الإخراج الرئيسي من التشغيل (proj-mpi-SH-LWT.f) و (proj2D-nonSH-LWT.f) هو ملفات بيانات الإسقاط ، مع اصطلاح التسمية Particle-class-info-SH-proj.dat و Particle-class-info-nonSH-proj.dat. يمكن حساب مجموعة متنوعة من الكميات ثنائية الأبعاد ، بما في ذلك بعضها المستخدم بواسطة أداتين تجاريتين مختلفتين (Horiba Camsizer59 و Malvern MORPHOLOGI G360). في كلتا الحالتين ، تحسب البرامج إصدارا ثنائي الأبعاد من L و W ، يسمى L2D و W2D.
- يسرد هيكل ملف الإخراج ، لكل جسيم ، ومنطقة ، ومحيط ، و Xcmax ، و Xcmin ، و Fermax ، و Fermin ، و W2D ، و L2D ، و WM ، و LM ، حيث Fermax و Fermin هما الحد الأقصى والحد الأدنى لأقطار Feret و Xcmax و Xcmin يتم تعريفهما من أقطار الوتر المأخوذة في اتجاهاتمختلفة 59. يمكن أن يظهر نظريا أن L2D هي نفس كمية Xcmax ، والتي يمكن رؤيتها أيضا في ملفات البيانات. المعلمات LM و WM هي إصدارات من L2D و W2D محددة بشكل مختلف قليلا في دليل Malvern MORPHOLOGI G360. تنسيق الملف هو: اسم / رقم الجسيمات ، المساحة ، المحيط ، Fermin ، Fermax ، Xcmin ، Xcmax ، W2D ، L2D ، theta ، WM ، LM ، slo ، و nnnF ، حيث nnnF هو عدد معاملات فورييه المستخدمة لتمثيل إسقاط الجسيمات. كمية ثيتا هي الزاوية ، بالدرجات ، التي يصنعها المحور الذي يحدد WM و LM بالمحور x 60. الكمية البطيئة هي فقط نسبة جيب ثيتا إلى جيب تمام ثيتا. لا يتم استخدام أي من الكميتين في تحليل الجسيمات الموصوف هنا ويتم تضمينهما فقط كفحص للحساب. تأتي بيانات كل جسيم في مجموعات من ثلاثة ، سطر واحد لكل من الإسقاطات الثلاثة ، (1،2،3) = (L ، W ، T).
7. معالجة البيانات الهندسية للجسيمات ثلاثية الأبعاد و 2D لإنتاج رسوم بيانية مختلفة
- استخدم أي برنامج يحبه المستخدم لمعالجة بيانات حجم الجسيمات وشكلها. مهما كان البرنامج المستخدم ، يجب اتباع إجراء معين.
- بالنسبة للبيانات ثلاثية الأبعاد، ادمج بيانات SH وغير SH في قوائم SnS وNS، باستخدام قيم قطع L/T المحددة مسبقا لكل فئة جسيمات. وينبغي حساب التوزيعات والمتوسطات لجسيمات SnS وNS بشكل منفصل، وكذلك لبيانات SnS وNS مجتمعة، لجميع المعلمات الهندسية ذات الأهمية، مثل L وW وT وL/T وL/W والقطر الكروي المكافئ للحجم، وغيرها.
- بالنسبة لبيانات الإسقاط ثنائي الأبعاد، اجمع بين بيانات SH وغير SH. هناك ثلاثة إسقاطات ثنائية الأبعاد لكل جسيم ثلاثي الأبعاد ، مأخوذة على طول متجهات الوحدة ل L و W و T. يجب أن يؤدي الجمع بين هذه الإسقاطات الثلاثة إلى نتائج مشابهة لتقنية تجريبية تقوم بتدوير الجسيمات بشكل عشوائي قبل إجراء إسقاط. على سبيل المثال ، يحاكي استخدام بيانات متجه الوحدة L فقط تقنية تجريبية يتم فيها محاذاة الجسيمات تقريبا على طول أطول اتجاهها ، عموديا على اتجاه الإسقاط وموازيا لاتجاه الضوء / الإسقاط القوي في جهاز نموذجي.
النتائج
بدأت ASTM برنامج اختبار الكفاءة (AMPM ، تعدين مسحوق التصنيع الإضافي) لمسحوق المعادن المستخدم في اندماج طبقة مسحوق الليزر ، حيث يقوم المشاركون بإجراء بطارية من اختبارات مسحوق المعادن القياسية وتقوم ASTM بتجميع التوزيع الإحصائي لهذه النتائج في تقرير للمشاركين61. ي?...
Discussion
الطريقة المستندة إلى XCT لتوصيف حجم وشكل الجسيمات المعدنية ثلاثية الأبعاد لها تطبيقات أكثر ممكنة ولكن أيضا بعض القيود. سيتم معالجة القيود أولا.
يتم استخدام الايبوكسي سريع المعالجة بحيث تكون لزوجة الإيبوكسي عالية بما يكفي لمنع المسحوق من الاستقرار تحت الج?...
Disclosures
المؤلفون ليس لديهم ما يكشفون عنه.
Acknowledgements
يود المؤلفون أن يقروا بالدعم طويل الأمد ل NIST لتحليل المسحوق ثلاثي الأبعاد.
Materials
| Name | Company | Catalog Number | Comments |
| Epoxy | Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/ | Hardman Part # 4001 | case of 100 |
References
- Allen, T. . Powder Sampling and Particle Size Determination, 1st edition. , (2003).
- Rodriguez, J., Edeskär, T., Knutsson, S. Particle shape quantities and measurement techniques: a review. Electron Journal of Geotechnical Engineering. , 18 (2013).
- Garboczi, E. J., Douglas, J. F. Intrinsic conductivity of objects having arbitrary shape and conductivity. Physical Review E. 53, 6169-6180 (1996).
- Mansfield, M. L., Douglas, J. F., Garboczi, E. J. Intrinsic viscosity and the electrical polarizability of arbitrarily shaped objects. Physical Review E. 64, 61401-61416 (2001).
- Garboczi, E. J., Douglas, J. F., Bohn, R. B. A hybrid finite element-analytical method for determining the intrinsic elastic moduli of particles having moderately extended shapes and a wide range of elastic properties. Mechanics of Materials. 38, 786-800 (2006).
- Garboczi, E. J., Douglas, J. F. Elastic Moduli of Composites Containing a Low Concentration of Complex-Shaped Particles Having a General Property Contrast with the Matrix. Mechanics of Materials. 5, 53-65 (2012).
- Audus, D. J., Hassan, A. M., Garboczi, E. J., Hudson, S. D., Douglas, J. F. Interplay of particle shape and suspension properties: A study of cube-like particles. Soft Matter. 11, 3360-3366 (2015).
- Garboczi, E. J., Bullard, J. W. Shape analysis of a reference cement. Cement and Concrete Research. 34, 1933-1937 (2004).
- Masad, E., Saadeh, S., Al-Rousan, T., Garboczi, E. J., Little, D. Computations of particle surface characteristics using optical and x-ray CT images. Computational Materials Science. 34, 406-424 (2005).
- Cheok, G. S., Stone, W. C., Garboczi, E. J. Using LADAR to characterize the 3-D shape of aggregates: Preliminary results. Cement and Concrete Research. 36, 1072-1075 (2006).
- Mahmoud, E., Gates, L., Masad, E., Garboczi, E. J. Comprehensive Evaluation of AIMS Texture, Angularity, and Dimensions Measurements. Journal of Materials in Civil Engineering. 22, 369-379 (2010).
- Erdoğan, S. T., Nie, X., Stutzman, P. E., Garboczi, E. J. Micrometer-scale 3-D imaging of eight cements: Particle shape, cement chemistry, and the effect of particle shape on laser diffraction size analysis. Cement and Concrete Research. 40, 731-739 (2010).
- Holzer, L., Flatt, R., Erdoğan, S. T., Nie, X., Garboczi, E. J. Shape comparison between 0.4 µm to 2.0 µm and 20 µm to 60 µm cement particles. Journal of the American Ceramic Society. 93, 1626-1633 (2010).
- Erdoğan, S. T., Fowler, D. W., Garboczi, E. J. Shape and size of microfine aggregates: X-ray microcomputed tomography vs. laser diffraction. Powder Technology. 177, 53-63 (2007).
- Garboczi, E. J., Liu, X., Taylor, M. A. The Shape of a Blasted and Crushed Rock Material over More than Three Orders of Magnitude: 20 µm to 60 mm. Powder Technology. 229, 84-89 (2012).
- Cepuritis, R., Wigum, B. J., Garboczi, E. J., Mørtsell, E., Jacobsen, S. Filler from crushed aggregate for concrete: Pore structure, specific surface, particle shape and size distribution. Cement and Concrete Composites. 54, 2-16 (2014).
- Cepuritis, R., Garboczi, E. J., Jacobsen, S., Snyder, K. A. Comparison of 2-D and 3-D shape analysis of concrete aggregate fines from VSI crushing. Powder Technology. 309, 110-125 (2017).
- Cepuritis, R., Garboczi, E. J., Jacobsen, S. Three-dimensional shape analysis of concrete aggregate fines produced by VSI crushing. Powder Technology. 308, 410-421 (2017).
- Cepuritis, R., Garboczi, E. J., Ferraris, C. F., Jacobsen, S., Sørensen, B. E. Measurement of particle size distribution and specific surface area for crushed concrete aggregate fines. Advanced Powder Technology. 28, 7065 (2017).
- Erdogan, S. T., Forster, A. M., Stutzman, P. E., Garboczi, E. J. Particle-based characterization of Ottawa sand: Shape, size, mineralogy, and elastic moduli. Cement and Concrete Composites. 83, 36-44 (2017).
- Olivas, A., et al. Certification of SRM 2493: Standard Reference Mortar for Rheological Measurements. NIST Special Publication. , 260 (2017).
- Martys, N., Peltz, W., George, W., Toman, B., Garboczi, E. J. . Certification of SRM 2497: Standard Reference Concrete for Rheological Measurement, NIST SP1237. , (2019).
- Estephane, P., Garboczi, E. J., Bullard, J. W., Wallevik, O. H. Three-dimensional shape characterization of fine sands and the influence of particle shape on the packing and workability of mortars. Cement and Concrete Composites. 97, 125-142 (2019).
- Slotwinski, J. A., et al. Characterization of Metal Powders Used for Additive Manufacturing. Journal of Research of the National Institute of Standards and Technology. 119, (2014).
- Grell, W. A., et al. Effect of powder oxidation on the impact toughness of electron beam melting Ti-6Al-4V. Additive Manufacturing. 17, 123-134 (2017).
- Garboczi, E. J., Hrabe, N. Particle shape and size analysis for metal powders used for additive manufacturing: Technique description and application to a gas-atomized Ti64 powder and a plasma-atomized Ti64 powder. Additive Manufacturing. 31, 100965 (2020).
- Garboczi, E. J. Three-Dimensional Shape Analysis of JSC-1A Simulated Lunar Regolith Particles. Powder Technology. 207, 96-103 (2011).
- Chiaramonti, A. N., Goguen, J. D., Garboczi, E. J. Quantifying the 3-Dimensional Shape of Lunar Regolith Particles Using X-Ray Computed Tomography and Scanning Electron Microscopy at Sub-λ Resolution. Microscopy and Microanalysis. 23, (2017).
- Escobar-Cerezo, J., et al. An Experimental Scattering Matrix for Lunar Regolith Simulant JSC-1A at Visible Wavelengths. The Astrophysical Journal Supplement Series. 235, 19 (2018).
- Hu, M., Zhang, T., Stansbury, J., Neal, J., Garboczi, E. J. Determination of Porosity and Thickness of Biofilm Attached on Irregular-Shaped Media. Journal of Environmental Engineering. 139 (7), 923-931 (2013).
- Garboczi, E. J., Riding, K. A., Mirzahosseini, M. Particle shape effects on particle size measurement for crushed waste glass. Advanced Powder Technology. 28, 648-657 (2017).
- Baidya, S., et al. Analysis of Different Computational Techniques for Calculating the Polarizability Tensors of Stem Cells with Realistic Three-Dimensional Morphologies. IEEE Transactions on Biomedical Engineering. , (2018).
- Vargas-Lara, F., Hassan, A. M., Garboczi, E. J., Douglas, J. F. Intrinsic Conductivity of Carbon Nanotubes and Graphene Sheets Having a Realistic Geometry. Journal of Chemical Physics. 143, 204902 (2015).
- Hassan, A. M., Vargas-Lara, F., Douglas, J. F., Garboczi, E. J. Electromagnetic Resonances of Individual Single-Walled Carbon Nanotubes with Realistic Shapes: A Characteristic Modes Approach. IEEE Transactions on Antennas and Propagation. 64, 2743 (2016).
- Durbhakula, K. C., et al. Electromagnetic Scattering From Individual Crumpled Graphene Flakes: A Characteristic Modes Approach. IEEE Transactions on Antennas and Propagation. 65, 6035 (2017).
- Hassan, A. M., et al. Electromagnetic Scattering from Multiple Single-Walled Carbon Nanotubes Having Tumbleweed Configurations. IEEE Transactions on Antennas and Propagation. 65, (2017).
- Malavé, V., Killgore, J. P., Garboczi, E. J., Berger, J. R. Decoupling the effects of surface topography and material heterogeneity on indentation modulus: A simple numerical linear-elastic model. International Journal of Solids and Structures. 124, 235-243 (2017).
- Garboczi, E. J. The influence of particle shape on the results of the electrical sensing zone method as explained by the particle intrinsic conductivity. Powder Technology. 322, 32-40 (2017).
- Garboczi, E. J. Three-dimensional mathematical analysis of particle shape using x-ray tomography and spherical harmonics: Application to aggregates used in concrete. Cement and Concrete Research. 32, 1621-1638 (2002).
- Erdoğan, S. T., et al. Three-dimensional shape analysis of coarse aggregates: New techniques for and preliminary results on several different coarse aggregates and reference rocks. Cement and Concrete Research. 36, 1619-1627 (2006).
- Taylor, M. A., Garboczi, E. J., Erdoğan, S. T., Fowler, D. W. Some properties of irregular particles in 3-D. Powder Technology. 162, 1-15 (2006).
- Garboczi, E. J., Bullard, J. W. Contact function, uniform-thickness shell volume, and convexity measure for 3D star-shaped random particles. Powder Technology. 237, 191-201 (2013).
- Bullard, J. W., Garboczi, E. J. Defining shape measures for 3D star-shaped particles: Sphericity, roundness, and dimensions. Powder Technology. 249, 241-252 (2013).
- Jia, X., Garboczi, E. J. Advances in shape measurement in the digital world. Particuology. 26, 19-31 (2016).
- Garboczi, E. J., Bullard, J. W. 3D analytical mathematical models of random star-shape particles via a combination of X-ray computed microtomography and spherical harmonic analysis. Advanced Powder Technology. 28, 325-339 (2017).
- Qian, Z., Garboczi, E. J., Ye, G., Schlangen, E. Anm: A geometrical model for the composite structure of mortar and concrete using real-shape particles. Materials and Structures. 49 (1), 149-158 (2015).
- Thomas, S., Lu, Y., Garboczi, E. J. Improved model for 3-D virtual concrete: Anm model. Journal of Computing in Civil Engineering. , (2015).
- Zuo, Y., Qian, Z., Garboczi, E. J., Ye, G. Numerical simulation of the initial particle parking structure of cement/geopolymer paste and the dissolution of amorphous silica using real-shape particles. Construction and Building Materials. 185, 206-219 (2018).
- Lu, Y., Islam, A., Thomas, S., Garboczi, E. J. Three-dimensional mortar models using real-shaped sand particles and uniform thickness interfacial transition zones: Artifacts seen in 2D slices. Construction and Building Materials. 236, 117590 (2020).
- Grigoriu, M., Garboczi, E. J., Kafali, C. Spherical harmonic-based random fields for aggregates used in concrete. Powder Technology. 166, 123-138 (2006).
- Liu, X., Garboczi, E. J., Grigoriu, M., Lu, Y., Erdoğan, S. T. Spherical harmonic-based random fields based on real particle 3D data: Improved numerical algorithm and quantitative comparison to real particles. Powder Technology. 207, 78-86 (2011).
- Stauffer, D., Aharony, A. . Introduction To Percolation Theory: Revised, second edition. , (1994).
- Bentz, D. P., Garboczi, E. J. Percolation of phases in a three-dimensional cement paste microstructural model. Cement and Concrete Research. 21, 325-344 (1991).
- Garboczi, E. J., Snyder, K. A., Douglas, J. F., Thorpe, M. F. Geometrical percolation threshold of overlapping ellipsoids. Physical Review E. 52, 819-828 (1995).
- Garboczi, E. J., Bentz, D. P., Stauffer, D. Computer simulation and percolation theory applied to concrete, in. Annual Reviews of Computational Physics VII. , 85-123 (2000).
- Garboczi, E. J. Percolation phase diagrams for multi-phase models built on the overlapping sphere model. Physica A: Statistical Mechanics and its Applications. 442, 156-168 (2016).
- Fernlund, J. M. R. The effect of particle form on sieve analysis: a test by image analysis. Engineering Geology. 50 (1), 111-124 (1998).
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Transactions on Systems, Man, and Cybernetics. 9, 62-66 (1979).
- . Horiba Available from: https://www.horiba.com/fileadmin/uploads/Scientific/Documents/PSA/Manuals/CAMSIZER_Characteristics_Nov2009.pdf (2020)
- . Malvern MORPHOLOGI G3 Available from: https://www.malvernpanalytical.com/en/support/product-support/morphologi-range/morphologi-g3 (2020)
- . ASTM Available from: https://www.astm.org/STATQA/Additive_Manufacturinng_Powder_Metallurgy.htm (2020)
- Bain, E., Garboczi, E. J., Seppala, J., Parker, T., Migler, K. AMB2018-04: Benchmark Physical Property Measurements for Powder Bed Fusion Additive Manufacturing of Polyamide 12. Integrating Materials and Manufacturing Innovation. , (2019).
- du Plessis, A., Sperling, P., Beerlink, A., du Preez, W., le Roux, S. G. Standard method for microCT-based additive manufacturing quality control 4: Metal powder analysis. MethodsX. 5, 1336-1345 (2018).
- DeCost, B. L., Jain, J., Rollett, A. D., Holm, E. A. Computer vision and machine learning for autonomous characterization for AM powder feedstocks. JOM. 69, 456-465 (2017).
- DeCost, B. L., Holm, E. A. Characterizing powder materials using keypoint-based computer vision methods. Computational Materials Science. 126, 438-445 (2017).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionExplore More Articles
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved