Análisis tridimensional de la forma de las partículas mediante tomografía computarizada de rayos X: procedimiento experimental y algoritmos de análisis para polvos metálicos

Resumen

El tamaño y la forma de las partículas de polvo no son cantidades independientes. Las técnicas de medición habituales no miden estos parámetros entrelazados en tres dimensiones (3D). Se describe una técnica de medición/análisis 3D, basada en la tomografía computarizada de rayos X, que permite medir el tamaño y la forma y clasificar las partículas de polvo según ambos parámetros.

Resumen

Medir la distribución del tamaño de las partículas en un polvo es una actividad común en la ciencia y la industria. La medición de la distribución de la forma de las partículas es mucho menos común. Sin embargo, la forma y el tamaño de las partículas de polvo no son cantidades independientes. Todas las técnicas conocidas de medición de tamaño/forma asumen una forma esférica o miden la forma solo en dos dimensiones. El método basado en tomografía computarizada de rayos X (XCT) que se presenta aquí mide tanto el tamaño como la forma en 3D sin hacer ninguna suposición. A partir de una imagen 3D de partículas, el método puede clasificar matemáticamente las partículas según su forma, por ejemplo, partículas compuestas por varias partículas más pequeñas soldadas entre sí, en lugar de partículas individuales que no son necesariamente esféricas. Por supuesto, definir un solo número como el "tamaño" o la "forma" de una partícula no esférica aleatoria no es posible en principio, lo que lleva a muchas formas de estimar el tamaño y la forma de la partícula a través de varios parámetros interrelacionados, que se pueden generar a partir de esta caracterización 3D completa en forma de promedios y distribuciones. Se describen los procedimientos experimentales necesarios, el análisis matemático y el análisis informático y se da un ejemplo de un polvo metálico. La técnica se limita a partículas que pueden ser fotografiadas por XCT con un mínimo de aproximadamente 1000 vóxeles por volumen de partícula.

Introducción

La medición de la distribución del tamaño de las partículas en un polvo es una actividad común en la ciencia y la industria ^1,2.  La medición de la distribución de la forma de las partículas es menos común, pero tanto el tamaño como la forma, junto con el material del que están hechas las partículas, determinan sus propiedades, ya sea solas o en algún tipo de material de matriz 3,4,5,6,7. Los materiales cuyo tamaño y forma de partícula son de interés incluyen cemento Portland, arena y grava 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22^{, 23}, polvos metálicos para pulvimetalurgia y fabricación aditiva 24,25,26, suelo lunar 27,28,29, neumáticos de automóviles triturados³⁰, vidrio de desecho triturado³¹, células madre³² y nanotubos de carbono y grafeno 33,34,35,36,37 . Sin embargo, la forma y el tamaño de las partículas de polvo no son cantidades independientes²⁶. Por ejemplo, supongamos que uno tiene una partícula geométricamente regular cuyo "tamaño" se dice que es d. Sin decir si esta partícula es una esfera, un cubo o una varilla delgada de longitud d, no se sabe realmente cómo se aplica el tamaño a esta partícula. Al decir que la partícula es una esfera, un cubo o una varilla, en realidad se está especificando la forma de la partícula, y sin esta información adicional, la información sobre el tamaño no tiene sentido.

Para estos tres ejemplos, una esfera, un cubo o una varilla delgada, el tamaño de partícula se puede especificar con un solo número. Pero incluso si la varilla tuviera una sección transversal circular, también sería necesario medir el diámetro de esta sección transversal, por lo que realmente se necesitarían dos parámetros de tamaño para la partícula delgada de la varilla. ¿Qué pasa con las partículas con forma de elipsoides o cajas rectangulares? Para cada uno de estos, se necesitan tres números para especificar el tamaño, y aún así la forma debe darse como un elipsoide o una caja rectangular para que los tres parámetros de tamaño tengan significado. Para una partícula de forma aleatoria, se necesitaría un número infinito de parámetros de tamaño (por ejemplo, la longitud de las cuerdas a través de la partícula) para caracterizar completamente el "tamaño" de la partícula y, sin embargo, estos no tendrían sentido sin una "caracterización de la forma", sabiendo en qué ángulos relativos al centro de masa de la partícula se dibujaron estas cuerdas.

Existen muchas técnicas utilizadas para medir la distribución del tamaño de las partículas en un polvo, empleando diferentes principios físicos ^1,2. Lo que generalmente no se reconoce, sin embargo, es que para extraer el tamaño de la partícula, se debe utilizar información sobre la forma de la partícula, ya sea supuesta o medida. Las técnicas actuales se pueden clasificar en: (I) mediciones del tamaño de partícula tridimensional (3D) asumiendo la forma 3D, y (II) mediciones de tamaño y forma, pero solo de proyecciones bidimensionales (2D), utilizando técnicas de análisis de imágenes 2D. Para las partículas esféricas, todas las proyecciones 2D son círculos, con el mismo diámetro que las partículas originales, y todas estas técnicas de medición, tanto de Clase I como de Clase II, dentro de la incertidumbre de medición, dan los mismos resultados para esferas perfectas. En el caso de las partículas no esféricas, las proyecciones 2D están mucho menos relacionadas con las partículas originales. Si una partícula tiene una porosidad interna que no rompe la superficie de la partícula, estos poros no se medirán en absoluto mediante ninguna de estas técnicas de medición 3D o 2D. La clase I incluye difracción láser, volumen de detección eléctrica (ESV)³⁸, análisis de tamices y sedimentación; y la Clase II cubre la microscopía electrónica de transmisión y barrido, la microscopía de fuerza atómica y el análisis de imágenes dinámicas y estáticas con técnicas ópticas. Ninguna de las dos clases mide con precisión el tamaño y la forma de las partículas no esféricas en 3D.

Desde alrededor de 2002³⁹, se ha desarrollado un nuevo método de análisis de partículas 40,41,42,43,44,45 que toma imágenes de una partícula 3D en 3D, y luego utiliza varias formas de análisis matemático para representar y clasificar cada partícula. Se guarda una imagen 3D para cada partícula individual, que se puede comparar con la información geométrica y matemática que también se guarda para cada partícula. Esta información matemática se puede utilizar para regenerar la partícula como se desee en cualquier tipo de modelo 3D 46,47,48,49, en cualquier ubicación y orientación, o para generar partículas virtuales que se ven obligadas a tener las mismas estadísticas^50,51. Este método de análisis de partículas se basa en escaneos XCT de partículas dispersas en epoxi o algún otro medio similar. Los escaneos XCT son operados por un software especializado que emplea el algoritmo de grabación 52,53,54,55,56 para identificar partículas, y luego el ajuste de series armónicas esféricas o el conteo de vóxeles para generar y almacenar la forma y el tamaño de las partículas, imágenes 3D de las partículas y, en un segundo paso, información geométrica para cada partícula. Cada partícula analizada tiene una etiqueta alfanumérica única, que se utiliza para rastrear cada partícula, la información sobre cada partícula y vincular cada partícula a su imagen 3D. Durante este proceso de análisis, se analizan los poros que se encuentran dentro de una partícula y se almacena la porosidad total en esa partícula en particular, ya que la reconstrucción XCT brinda una vista 3D completa de una muestra.

Se ha encontrado que tres (de muchos) parámetros geométricos de tamaño/forma son particularmente útiles para analizar y clasificar partículas en 3D: la longitud, L, el ancho, W y el grosor, T. L se define como la distancia más larga de punto a punto de superficie a través de una partícula, W se define de manera similar a L con la restricción adicional de que el vector unitario a lo largo de W debe ser perpendicular al vector unitario a lo largo de L, y T también se define de manera similar a L con la restricción adicional de que el vector unitario a lo largo de T debe ser perpendicular tanto al vector unitario a lo largo de L como al vector unitario a lo largo de W¹². Estos tres parámetros definen el rectángulo o cuadro delimitador mínimo que contiene la partícula, y las proporciones de estos tres parámetros proporcionan información valiosa pero aproximada sobre la forma de cada partícula. Se pueden hacer distribuciones de cualquiera de estos. Es posible que W se correlacione bien con los "tamaños" medidos con el análisis de tamiz⁵⁷, mientras que los "tamaños" medidos con difracción láser se correlacionan con una mezcla de L, W y T³¹.

Por último, las imágenes 3D de una muestra de prueba de 100-200 de las partículas se comprueban visualmente para determinar dónde están los puntos de corte en L/T que permiten al método distinguir entre partículas individuales, casi esféricas (SnS) y no esféricas (NS), que podrían ser múltiples partículas soldadas entre sí, o lo que son claramente partículas individuales pero con una forma extraña.

Protocolo

NOTA: El siguiente protocolo está escrito para partículas de polvo metálico con tamaño, de acuerdo con una aproximación de diámetro esférico equivalente en volumen (VESD, diámetro de la esfera con el mismo volumen que la partícula), entre 10 μm y 100 μm. Supongamos que el metal tiene una densidad en unidades de g/cm³. Se deben usar guantes durante los pasos de preparación de la muestra, junto con protección para los ojos. Es importante leer todos los pasos del Protocolo 1, ya que algunos equipos deben estar listos antes de iniciar el Protocolo.

1. Preparación de la mezcla epoxi-polvo

1. Prepare aproximadamente 25 g de un epoxi de curado rápido (5 min) en un plato pequeño desechable. Los botes de papel de aluminio funcionan bien para este propósito. Un buen epoxi para usar viene en un plástico de burbujas, con la resina separada del endurecedor, cuya densidad curada es ρ_e g/cm³.
2. Use M gramos de polvo, de una muestra más grande de polvo bien agitada, donde M está diseñado para dar una fracción de volumen de aproximadamente el 10% una vez que los M gramos se mezclan con el epoxi. Esto está diseñado para evitar la situación en la que las partículas están tan cerca unas de otras que el escaneo XCT las identifica erróneamente como multipartículas reales que están firmemente unidas. La ecuación que define M es:
   
   
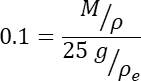
3. Mezcle el polvo metálico vigorosamente en el epoxi, manualmente, usando una varilla de agitación desechable (un simple palo de madera para manualidades funciona bien) durante unos 30 s, el tiempo suficiente para dispersar el polvo adecuadamente. Este proceso, bien hecho, hace que el análisis de imágenes de las partículas individuales sea mucho más sencillo.
   1. Después de mezclar, raspe la mezcla viscoplástica en un grupo compacto con la mayor extensión vertical posible, para estar listo para el siguiente paso. Es importante tener los siguientes pasos preparados con anticipación, ya que no quedará mucho tiempo antes de que el epoxi se endurezca.
4. Utilice una pequeña bomba de vacío conectada a una manguera de plástico de 0,5 m de largo, con una boquilla insertada en el extremo abierto de la manguera que encaje perfectamente en una pajita de polímero de unos 3 mm de diámetro interior.
   NOTA: Las pajitas de cóctel, fácilmente disponibles en las tiendas de comestibles, funcionan bien para la pajita de polímero de 3 mm de diámetro y tienen una longitud de aproximadamente 150 mm. En el caso de una boquilla, el extremo de corte de una pipeta de plástico desechable de 1 mL a 2 mL suele ser eficaz. Donde la boquilla encaja en la manguera de plástico, un poco de cinta aislante debe estirarse firmemente alrededor de la junta para garantizar un sello hermético. Los 25 g de epoxi más polvo deberían ser más que suficientes para llenar dos pajitas completas.
5. Inserte la boquilla en la pajita, sosteniendo la boquilla y el extremo de la pajita firmemente apretados. Inserte el extremo libre de la pajita en el grupo compacto de polvo epoxi y encienda la bomba de vacío.
   NOTA: Mantenga el extremo libre de la pajita sumergido en la mezcla de epoxi y polvo para evitar introducir burbujas de aire en la pajita: siempre habrá algunas burbujas de aire, pero este procedimiento minimiza su presencia. Las pajitas deben llenarse hasta 10 mm de la parte superior: la línea de llenado se puede ver a través de la pajita translúcida. Cuando se llene la primera pajita, apague la bomba de vacío y retire la pajita de la boquilla.
6. Limpie la mezcla de epoxi del extremo de relleno de la pajita y empuje ambos extremos de la pajita en un pequeño trozo de arcilla para llenar ambos extremos de la pajita para que no se filtre la mezcla de epoxi y polvo durante el curado. Coloque la^2ª pajita en la boquilla y repita, primero usando la varilla mezcladora para juntar la mezcla de epoxi y polvo si es necesario.
7. Después de curar el epoxi en las dos pajitas, corte los extremos de la pajita, donde estaba el sellador de arcilla, con una navaja y luego corte cada pajita por la mitad para dar cuatro muestras. Utilice una pajita como muestra #1 para la XCT, montada verticalmente de modo que los rayos X penetren a través de la sección transversal circular de la pajita.

2. El instrumento XCT

NOTA: Estos pasos asumen familiaridad con el instrumento XCT elegido por el usuario.

1. Utilice un voltaje alto, generalmente 100 kV o más, ya que hay un buen contraste entre la matriz epoxi y las partículas de polvo metálico y no es necesario resolver nada dentro de la matriz epoxi, lo que normalmente requeriría voltajes bajos alrededor de 40 kV. Utilice un escaneo completo de 360^grados , con un tamaño de vóxel de aproximadamente 1 μm. La relación entre el tamaño de partícula más pequeño considerado y el tamaño de vóxel utilizado debe ser un mínimo de 8-10³⁹.
2. Tome suficientes FOV, en más de una muestra, para proporcionar suficientes partículas para el análisis. Si se siguen las pautas de preparación de la muestra, de 2 a 8 FOV serán suficientes. Normalmente, un mínimo de 1000 partículas es suficiente para un análisis de forma/tamaño válido, pero más partículas dan como resultado curvas de distribución más suaves y mejores estadísticas. Los segmentos reconstruidos se numeran del 0 al nz-1, de abajo hacia arriba del campo de visión, donde nz es el número total de segmentos reconstruidos.
   1. Guarde los cortes de la sección transversal vertical para cada FOV individualmente, en formato de 8 bits (por ejemplo, tiff) anotando el tamaño de píxel de cada conjunto de imágenes (nx x ny), el número de estos cortes (nz) y el tamaño del vóxel en micrómetros (v). El formato de 8 bits es adecuado para este tipo de imágenes simples de escala de grises de matriz epoxi de partículas metálicas, que son fáciles de segmentar.

3. Ensamblaje de los segmentos pertenecientes a cada campo de visión en una microestructura ASCII 3D

NOTA: El programa C que se utiliza en el NIST se llama tiff2array.c y se utiliza con mayor frecuencia con archivos tiff, pero puede manejar otros formatos de 8 bits. Se puede compilar tal cual, con el ejecutable llamado tiff2array. Este programa lee cada imagen, de abajo hacia arriba, las convierte a formato ascii (escala de grises de 0 a 255) y luego las apila al final de un archivo maestro.

1. Si las imágenes reconstruidas están en formato tiff, por ejemplo, y están numeradas consecutivamente de abajo hacia arriba, utilice la siguiente sintaxis en un comando de terminal de línea: tiff2array *.tiff. Este archivo maestro, o archivo de microestructura, es una representación 3D del campo de visión. Si la variable a(i,j,k) es la escala de grises en la posición (i,j,k), donde k es el número del corte, k = 1 a nz, y (i,j) es el píxel en el corte k-ésimo, donde i se mide de izquierda a derecha y j se mide de arriba a abajo.
   NOTA: Todo el software necesario en el Protocolo está disponible en la sección de Información Complementaria de este documento a través de un enlace a una base de datos del NIST ubicada en https://doi.org/10.18434/M32265.
2. Para los P FOVs, haga un pequeño archivo llamado particle-class-sysconfig.dat, con líneas P, donde cada línea lee, para el pth (p = 1,P) FOV:
   Nombre de archivo nx ny nz v b c
   donde Nombre de archivo = una identificación de 12 caracteres para un campo de visión en particular, b = 1 para un escaneo interior y 0 para un escaneo exterior, y c = el número de fases presentes en las imágenes. Cuando se realiza un escaneo interior, generalmente hay tres fases (c = 3) presentes: 1) el epoxi, 2) las regiones negras que indican el exterior del escaneo circular y las burbujas de aire, y 3) las partículas más brillantes. A veces, cuatro fases pueden parecer a simple vista una suposición más razonable, por lo que c = 4. Los valores de c de 3 o 4 son las dos únicas opciones. El valor de c le dice al software de análisis de partículas qué algoritmo de segmentación automática Otsu, originalmente escrito para imágenes bifásicas pero fácilmente extendido a cualquier número de fases, para usar para segmentar automáticamente las imágenes en un FOV^{particular 26,58}. Los archivos de microestructura que se utilizarán en el siguiente programa de software deben tener nombres de 12 caracteres que sean exactamente los mismos que el nombre de archivo que figura en el archivo FOV-name-sysconfig.dat, seguido de la extensión .mic.
3. Ejecute el software de análisis de partículas pp-Otsu.f, utilizando como entrada el archivo particle-class-sysconfig.dat y los diversos archivos de microestructura, Filename.mic. Realice solo dos cambios en este programa para un nuevo sistema, todos los cuales están marcados con un comentario "USUARIO" en la fuente de Fortran: los nombres de archivo para los archivos de salida generales (cambie el nombre general de la clase de partículas) y el número de FOV enumerados en particle-class-sysconfig.dat. El programa pp-Otsu.f está en Fortran, es escalar, y generalmente se compila en Fortran 77, aunque Fortran 90 debería funcionar bien. Éste, y todos los demás programas de Fortran que se describen a continuación, deben compilarse en doble precisión (-r8) para obtener resultados precisos.
   1. Además, dado que pp-Otsu.f trabaja con archivos grandes, siempre agregue los parámetros (o su equivalente) -mcmodel=medium y -Mlarge_arrays a la compilación. Un archivo auxiliar, gauss120.dat, contiene los pesos y puntos para una cuadratura gaussiana de 120 puntos utilizada ampliamente en pp-Otsu.f, y debe estar en el mismo directorio que pp-Otsu.f. Todos los programas que se describen a continuación están escritos en Fortran 77, excepto los programas MPI, que están escritos en Fortran 90.
4. Vea los archivos de partículas que son las principales salidas de pp-Otsu.f, que pueden tardar varias horas en ejecutarse en un solo procesador si hay miles de partículas para analizar. Estos incluyen archivos con nombres como Particle-class-name-anm-particle-number.dat, que contienen la lista de los coeficientes complejos (n = 0,26), con unidades de micrómetros o en las unidades que v tenga, para las partículas juzgadas como adecuadamente en forma de estrella³⁹ y, por lo tanto, capaces de expandirse en funciones armónicas esféricas (llamadas partículas SH). Los archivos de partículas también incluyen archivos como Particle-class-name-part-particle- number.dat, que contienen el número de vóxeles en la partícula y todas las posiciones de vóxeles (en coordenadas de vóxeles) para partículas que no pueden describirse mediante expansiones armónicas esféricas (llamadas partículas no SH).
5. Vea los dos archivos, uno para las partículas SH y otro para las partículas no SH, que dan las porosidades de todas las partículas encontradas, incluso si la porosidad es cero, con la frase porosidad en los nombres de archivo. Un programa adicional, porosity-analyze.f, debe recibir el número de líneas en cada archivo de porosidad y sus nombres de archivo: los nombres de los archivos que se cambiarán están al comienzo del código fuente. La salida de este programa son los dos archivos Particle-class-intern-poros-analysis.txt y Particle-class-intern-poros-list.txt. El archivo de análisis genera la información que se muestra en la Tabla 2 en la sección Resultados representativos, y el archivo de lista proporciona la información necesaria para generar la Figura 5 en la sección Resultados representativos.
6. Vea los tres archivos de imagen tiff que muestran una porción del primer campo de visión considerado. El primer corte (OriA-0500.tiff) muestra el corte k = 500 del primer campo de visión en el archivo particle-class-sysconfig.dat , sin ningún procesamiento de imagen, y el segundo archivo de imagen muestra la misma imagen pero ahora segmentada y con umbral (PixA-0500.tiff). Si se aplica alguna división de cuenca hidrográfica limitada, el tercer archivo de imagen muestra los resultados de este algoritmo (LWSA-0500.tiff). Por lo general, este paso de procesamiento de imagen no se aplica, por lo que el tercer archivo de imagen es el mismo que el segundo. Estas imágenes se generan como un paso de comprobación de errores en el ensamblaje original de la microestructura 3D y la segmentación automática de la imagen Otsu. Se crea un archivo de salida general (particle-class-name-particles-data.dat) que enumera toda la información auxiliar para el procesamiento de cada partícula. Este archivo solo se utiliza como referencia, pero los volúmenes de vóxeles y las etiquetas numéricas de todas las partículas procesadas se escriben al final de este archivo.
7. Para cada partícula procesada, ya sea SH o no SH, vea el archivo de imagen VRML 3D, con la convención de nomenclatura particle-name-particle-number.wrl. En el caso de las partículas SH, este archivo de imagen VRML contiene dos imágenes una al lado de la otra, una imagen de vóxel de la partícula original y una imagen renderizada más suave con los coeficientes SH. En el caso de las partículas que no son SH, solo se almacena la imagen del vóxel.

4. Generar información geométrica para todas las partículas SH y no SH

1. Antes de continuar con el procesamiento, haga una lista de los nombres de archivo Particle-class-name-anm-particle-number.dat , llamada anm.lis, y una lista de las partículas Particle-class-name-part-particle-number.dat no SH , llamada nonSH.lis. Ejecute el pequeño número de programa.f, después de haber sido editado primero para tener el número correcto de archivos en anm.lis. Esto cambia el archivo anm.lis para que tenga el número de la partícula en cada línea del archivo de lista, así como el nombre del archivo, reemplazando el archivo anterior.
2. Utilice el programa part-lwt-listnum-unitvector.f para generar y evaluar información geométrica para las partículas SH. Este es un programa paralelo de MPI, ya que puede haber miles de partículas SH para evaluar, y solo hacer una partícula a la vez puede llevar días. Los únicos cambios en este programa que deben realizarse al procesar una nueva clase de partículas son el número Ntot de los archivos de number.dat Particle-class-class-name-anm-particle y la información de nomenclatura de la clase de partículas para el archivo de salida (Particle-class-name-un-geom-len.dat). El programa tiene comentarios (USER) en los pocos lugares que necesitan ser cambiados para un nuevo tipo de partícula. El archivo de salida Particle-type-info-un-SH-geom-len.dat une las partículas de cada campo de visión y cada línea tiene la siguiente estructura.
   
   Nombre de archivo de coeficientes SH, x1, x2, y1, y2, z1, z2, volumen, área de superficie, relación SA, curva, relación, nnn, gauss, marcador de posición, L, W, T, L/T, W/T, T/T, componentes del tensor de momento de inercia, vector unitario L, theta, ángulos phi, vector unitario W, theta, ángulos phi, vector unitario T, theta, ángulos phi
   
   x1 es el valor mínimo de x en la superficie de la partícula y x2 es el máximo, y de manera similar para y y z. Estos definen una "caja de extensión" que simplemente encierra la partícula en su orientación medida⁴². El cuadro de extensión se utiliza en otras aplicaciones 46,47,48,49. La relación SA es el área superficial de la partícula dividida por el área superficial de la esfera de volumen equivalente. La curvatura es la curvatura media integrada invertida y normalizada para que sea igual al diámetro cuando la partícula es una esfera perfecta. La relación es la traza del tensor de momento de inercia dividida por la traza del tensor de momento de inercia para la esfera de volumen equivalente. nnn es el número máximo de coeficientes SH (n = 0, nnn) que se deben usar cuando se trabaja con la partícula dada. Gauss es la curvatura gaussiana integrada, dividida por 4π, que debería ser igual a 1 para un objeto cerrado. El punto en el que Gauss varía de la unidad en más del 5% define el número máximo de coeficientes SH (n= nnn) que se deben utilizar al recrear la partícula. L, W, T son la longitud, el ancho y el grosor de la partícula, y se definieron en la sección Introducción. Los componentes independientes del tensor de momento de inercia se enumeran como I₁₁, I₂₂, I₃₃, I₁₃, I₂₃, I₁₂. Finalmente, se enumera el vector unitario para L, en el orden de las coordenadas x, y y z, seguido de los ángulos polares esféricos θ (ángulo desde el eje z positivo) y Φ (ángulo de rotación alrededor del eje z, definido como cero en el eje x positivo y es positivo en sentido contrario a las agujas del reloj). Los parámetros para W y T son los siguientes, enumerados de la misma manera.
3. Utilice el programa nonSH-lwt-un-scalar.f para calcular los parámetros L, W y T para las partículas nonSH, operando en la lista de nombres de archivo nonSH.lis , y también registre los vectores unitarios asociados. Los únicos cambios que deben realizarse en este archivo para una nueva clase de partículas es el número de nombres de archivo en nonSH.lis y los nombres de archivo de salida. La salida principal de este programa, llamada Particle-name-info-nonSH-len.dat, tiene cada línea en el formato:
   
   Volumen del nombre de archivo: L, W, T, a1, a2, a3 (LWT, unidad, vectores y ángulos)
   
   donde a1, a2 y a3 son los ángulos finales (en grados - 90^o) entre los vectores unitarios para L y W, W y T, y L y T, que se incluyen como una verificación de error para el algoritmo de cálculo L, W y T , ya que estos ángulos deben ser todos cero para un cálculo perfecto. Los vectores y ángulos unitarios L, W y T están en el mismo formato que para las partículas SH.

5. Seleccione un subconjunto de partículas SH y no SH para determinar visualmente los puntos de corte SnS y NS L/T

NOTA: Las partículas SH, en general, comprenden partículas esféricas simples, partículas no esféricas individuales (elipsoidales o rotas de alguna manera o de una forma aleatoria), partículas dobles y partículas múltiples (más de dos partículas unidas entre sí). Las partículas que componen las múltiples partículas pueden ser esféricas o no esféricas. Las partículas no SH generalmente tienen unas pocas partículas esféricas individuales, aunque principalmente con poros grandes que han atravesado la superficie, y el resto son en su mayoría partículas dobles y múltiples²⁶. Esto se determina observando una muestra aleatoria de ambos tipos de partículas con valores de L/T de 1 a 2. Esta inspección visual se convierte en un paso importante para permitir la clasificación SnS y NS.

1. Ejecute el programa (VRML-select-multi-single.f) que lee los archivos Particle-type-info-SH-geom-len.dat y Particle-name-info-nonSH-len.dat , y selecciona 10 partículas en cada intervalo L/T de tamaño 0.1, es decir, (1,1.1), (1.1,1,1), etc. Esto almacena hasta 100 partículas SH con un rango de L/T de 1 a 2, y hasta 100 partículas no SH con el mismo rango de L/T . Se generan dos archivos de texto (*SH-VRML-list.txt y *nonSH-VRML-list.txt) que enumeran los valores L/T y los nombres raíz de los archivos de imagen VRML encontrados. Estos deben colocarse en una hoja de cálculo de algún tipo y ordenarse de acuerdo con el valor L/T.
2. Examine visualmente las imágenes 3D de cada una de estas partículas para determinar la gama general de morfologías, comenzando por las partículas de menor valor L/T . Las partículas se evalúan en términos de si son partículas rotas, partículas dobles, partículas múltiples, irregulares (por ejemplo, no muy esféricas) y si tienen satélites, que son partículas mucho más pequeñas, unidas a la partícula principal. Se considera que un satélite convierte la partícula principal en una partícula doble o múltiple si el satélite o satélites tienen más de 1/5 del diámetro de la partícula principal. Se encuentra el valor aproximado de L/T que separa las partículas individuales casi esféricas (SnS) de las partículas múltiples y muy no esféricas (NS), que pueden ser un poco diferentes para las partículas SH y no SH. La primera partícula doble o múltiple encontrada determina el valor de corte para las partículas SH y no SH.
   NOTA: El Material Suplementario, ubicado en https://doi.org/10.18434/M32265, incluye un archivo de hoja de cálculo para las partículas examinadas, para ver cómo se determinaron estos valores de corte. Existe cierta incertidumbre y un grado de subjetividad en estos números, que se pueden evaluar eligiendo un conjunto diferente de 100 partículas SH y 100 no SH, con L/T entre 1 y 2, para evaluar los valores de corte. Trabajos recientes encontraron que esta incertidumbre era pequeña²⁶ y no afectó significativamente los resultados.

6. Genere datos de proyección 2D a partir de las partículas 3D

NOTA: Los únicos analizadores de partículas comerciales actuales que miden la forma de las partículas lo hacen con proyecciones 2D. Los datos XCT se pueden analizar para dar proyecciones 2D arbitrarias, generando datos que se pueden comparar cuantitativamente con los resultados de estos instrumentos comerciales. Las proyecciones 2D se realizan a partir de las partículas SH y no SH y se combinan, sin intentar clasificarlas en categorías 2D SnS y NS, ya que no se sabe en la actualidad cómo definir estas clases para las proyecciones 2D.

1. Utilice los dos programas, (proj-mpi-SH-LWT.f) para las partículas SH y (proj2D-nonSH-LWT.f) para las partículas no SH, para generar tres proyecciones ortogonales para cada partícula, a lo largo de la dirección de los tres vectores unitarios LWT , y luego genere coeficientes de Fourier para el contorno de la proyección. Estos coeficientes se utilizan para calcular varias cantidades 2D, como el área, el perímetro y varias longitudes y relaciones de aspecto.
2. Se genera y almacena una serie de puntos (x,y) para cada proyección, etiquetados con el nombre del archivo de partículas y 1 para la proyección a lo largo del vector unitario L , 2 para la proyección a lo largo del vector unitario W y 3 para la proyección a lo largo del vector unitario T . Introdúzcalos en cualquier programa de gráficos que acepte esta entrada, asegurándose de que los límites de los ejes x e y sean los mismos, y que cada eje tenga la misma longitud física.
3. Almacene los coeficientes de Fourier con una convención de nomenclatura de archivos similar, pero esta función está desactivada, de forma predeterminada, mediante comentarios. Los únicos cambios realizados en cualquiera de estos programas (posición del programa marcada con "USER") es el número total de partículas a considerar (Ntot), y los nombres de los archivos de entrada y salida, que deben reflejar la clase de partículas que se está analizando.
4. La salida principal de la ejecución (proj-mpi-SH-LWT.f) y (proj2D-nonSH-LWT.f) son archivos de datos de proyección, con convención de nomenclatura Particle-class-info-SH-proj.dat y Particle-class-info-nonSH-proj.dat. Se puede calcular una variedad de cantidades 2D, incluidas algunas utilizadas por dos instrumentos comerciales diferentes (Horiba Camsizer⁵⁹ y Malvern MORPHOLOGI G3⁶⁰). En ambos casos, los programas calculan una versión 2D de L y W, llamada L2D y W2D.
5. Las listas de estructura de archivos de salida, para cada partícula, área, perímetro, Xcmax, Xcmin, Fermax, Fermin, W2D, L2D, WM y LM, donde Fermax y Fermin son los diámetros de Feret máximo y mínimo y Xcmax y Xcmin se definen a partir de los diámetros de cuerda tomados en varias direcciones ⁵⁹. Teóricamente se puede demostrar que L2D es la misma cantidad que Xcmax, lo que también se puede ver en los archivos de datos. Los parámetros LM y WM son versiones de L2D y W2D definidas de forma ligeramente diferente en el manual⁶⁰ de Malvern MORPHOLOGI G3. El formato de archivo es: Nombre/número de partícula, área, perímetro, Fermín, Fermax, Xcmin, Xcmax, W2D, L2D, theta, WM, LM, slo y nnnF, donde nnnF es el número de coeficientes de Fourier utilizados para representar la proyección de la partícula. La cantidad theta es el ángulo, en grados, que forma el eje que define WM y LM con el eje^{x 60}. La cantidad slo es simplemente la relación entre el seno de theta y el coseno de theta. Ninguna de las dos cantidades se utiliza en el análisis de partículas descrito aquí y solo se incluyen como una verificación en el cálculo. Los datos de cada partícula vienen en conjuntos de tres, una línea para cada una de las tres proyecciones, (1,2,3) = (L,W,T).

7. Procesamiento de datos geométricos de partículas 3D y 2D para producir varios gráficos

1. Utilice cualquier software que le guste al usuario para procesar los datos de tamaño y forma de partícula. Independientemente del software que se utilice, se debe seguir un determinado procedimiento.
2. Para los datos 3D, combine los datos SH y no SH en listas SnS y NS, utilizando los valores de corte L/T previamente determinados para cada clase de partícula. Las distribuciones y los promedios deben calcularse para las partículas SnS y NS por separado, y también para los datos combinados de SnS y NS, para todos los parámetros geométricos de interés, como L, W, T, L/T, W/T, L/W, diámetro esférico equivalente al volumen y otros.
3. Para los datos de proyección 2D, combine los datos SH y no SH. Hay tres proyecciones 2D para cada partícula 3D, tomadas a lo largo de los vectores unitarios para L, W y T. La combinación de estas tres proyecciones debería dar resultados similares a una técnica experimental que rota aleatoriamente las partículas antes de hacer una proyección. El uso exclusivo de los datos vectoriales unitarios L , por ejemplo, simula una técnica experimental en la que las partículas están alineadas aproximadamente a lo largo de su dirección más larga, perpendiculares a la dirección de caída y paralelas a la dirección de la luz/proyección estroboscópica en un dispositivo típico.

Resultados

ASTM ha iniciado un programa de pruebas de aptitud (AMPM, Fabricación Aditiva de Pulvimetalurgia) para el polvo metálico utilizado para la fusión de lecho de polvo láser, donde los participantes llevan a cabo una batería de pruebas estándar de polvo metálico y ASTM compila la distribución estadística de estos resultados en un informe para los participantes⁶¹. Las muestras de polvo metálico se distribuyen dos veces al año a todos los participantes. El pe...

Discusión

El método basado en XCT para caracterizar el tamaño y la forma 3D de las partículas metálicas tiene más aplicaciones posibles, pero también algunas limitaciones. Primero se abordarán las limitaciones.

Se utiliza un epoxi de curado rápido para que la viscosidad del epoxi sea lo suficientemente alta como para evitar que el polvo se asiente por gravedad mientras el epoxi se cura, o al menos reducir el tiempo durante el cual podría ocurrir la sedimentaci?...

Materiales

Name	Company	Catalog Number	Comments
Epoxy	Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/	Hardman Part # 4001	case of 100