Трехмерный анализ формы частиц с помощью рентгеновской компьютерной томографии: экспериментальная методика и алгоритмы анализа металлических порошков

Резюме

Размер и форма частиц порошка не являются независимыми величинами. Обычные методы измерения не измеряют эти взаимосвязанные параметры в трех измерениях (3D). Описан метод 3D-измерения/анализа, основанный на рентгеновской компьютерной томографии, которая позволяет измерять размер и форму и классифицировать частицы порошка в соответствии с обоими параметрами.

Аннотация

Измерение распределения частиц в порошке по размерам является обычным занятием в науке и промышленности. Измерение распределения частиц по форме встречается гораздо реже. Однако форма и размер частиц порошка не являются независимыми величинами. Все известные методы измерения размера/формы либо принимают сферическую форму, либо измеряют форму только в двух измерениях. Представленный здесь метод, основанный на рентгеновской компьютерной томографии (XCT), измеряет размер и форму в 3D без каких-либо предположений. Начиная с 3D-изображения частиц, метод может математически классифицировать частицы в соответствии с формой, например, частицы, состоящие из нескольких более мелких частиц, сваренных вместе, в отличие от отдельных частиц, которые не обязательно имеют сферическую форму. Конечно, определение одного числа как «размера» или «формы» случайной несферической частицы невозможно в принципе, что приводит к множеству способов оценки размера и формы частицы с помощью различных взаимосвязанных параметров, которые могут быть сгенерированы из этой полной трехмерной характеристики в виде средних значений и распределений. Описаны необходимые экспериментальные процедуры, математический и компьютерный анализ, а также приведен пример для металлического порошка. Этот метод ограничен частицами, которые могут быть визуализированы с помощью XCT с минимальным содержанием около 1000 вокселей на объем частицы.

Введение

Измерение распределения частиц в порошке по размерам является обычным занятием в науке и промышленности ^1,2.  Измерение распределения формы частиц встречается реже, но и размер, и форма, а также материал, из которого они изготовлены, определяют их свойства, либо отдельно, либо в каком-либо матричном материале 3,4,5,6,7. Материалы, размер и форма частиц которых представляют интерес, включают портландцемент, песок и гравий 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22^{, 23}, металлические порошки для порошковой металлургии и аддитивного производства 24,25,26, лунный грунт 27,28,29, измельченные автомобильные шины ³⁰, измельченное стекло³¹, стволовые клетки³², углеродные нанотрубки и графен 33,34,35,36,37. Однако форма и размер частиц порошка не являются независимыми величинами²⁶. Например, предположим, что у нас есть геометрически правильная частица, «размер» которой называется d. Не говоря о том, является ли эта частица сферой, кубом или тонким стержнем длины d, на самом деле не известно, как размер относится к этой частице. Когда мы говорим, что частица представляет собой сферу, куб или стержень, мы на самом деле определяем форму частицы, а без этой дополнительной информации информация о размере не имеет смысла.

Для этих трех примеров, сферы, куба или тонкого стержня, размер частиц может быть указан одним числом. Но даже если бы стержень имел круглое сечение, нужно было бы также измерить диаметр этого поперечного сечения, поэтому для частицы тонкого стержня действительно понадобились бы два параметра размера. А как насчет частиц в форме эллипсоидов или прямоугольных коробок? Для каждого из них необходимо указать три числа, чтобы указать размер, и все же форма должна быть задана либо в виде эллипсоида, либо в виде прямоугольного прямоугольника, чтобы три параметра размера имели значение. Для частицы случайной формы потребовалось бы бесконечное количество параметров размера (например, длина хорд на частице), чтобы полностью охарактеризовать «размер» частицы, и все же они были бы бессмысленны без «характеристики формы», зная, под какими углами относительно центра масс частицы были проведены эти хорды.

Существует множество методов, используемых для измерения распределения частиц по размерам в порошке, использующих различные физические принципы ^1,2. Однако обычно не признается, что для определения размера частиц необходимо использовать информацию о форме частиц, как предполагаемую, так и измеренную. Современные методы можно классифицировать следующим образом: (I) измерения трехмерного (3D) размера частиц с принятием трехмерной формы, и (II) измерения как размера, так и формы, но только двумерных (2D) проекций, с использованием методов анализа 2D-изображений. Для сферических частиц все двумерные проекции представляют собой круги того же диаметра, что и исходные частицы, и все эти методы измерения, как класса I, так и класса II, в пределах неопределенности измерения, дают одинаковые результаты для идеальных сфер. Для несферических частиц двумерные проекции гораздо менее тесно связаны с исходными частицами. Если частица имеет внутреннюю пористость, которая не разрушает поверхность частицы, эти поры вообще не будут измеряться с помощью любого из этих методов 3D или 2D измерения. Класс I включает лазерную дифракцию, электрическое зондирование объема (ESV)³⁸, ситовой анализ и седиментацию; а класс II охватывает просвечивающую и сканирующую электронную микроскопию, атомно-силовую микроскопию, а также динамический и статический анализ изображений с помощью оптических методов. Ни один из классов точно не измеряет размер и форму несферических частиц в 3D.

Примерно с 2002 года был разработан новый метод анализа частиц 40,41,42,43,44,45, который отображает трехмерную частицу в 3D, а затем использует несколько форм математического анализа для представления и классификации каждой частицы. Для каждой отдельной частицы сохраняется 3D-изображение, которое можно сравнить с геометрической и математической информацией, которая также сохраняется для каждой частицы. Эта математическая информация может быть использована для повторной генерации частицы по желанию в любом виде 3D-модели 46,47,48,49, в любом месте и ориентации, или для генерации виртуальных частиц, которые вынуждены иметь ту же статистику ^50,51. Этот метод анализа частиц основан на сканировании XCT частиц, диспергированных в эпоксидной смоле или какой-либо другой подобной среде. Сканирование XCT осуществляется с помощью специализированного программного обеспечения, которое использует алгоритм горения 52,53,54,55,56 для идентификации частиц, а затем либо подгонку сферических гармонических рядов или воксельный подсчет для генерации и хранения формы и размера частиц, 3D-изображения частиц и, на втором этапе, геометрическую информацию для каждой частицы. Каждая анализируемая частица имеет уникальную буквенно-цифровую метку, которая используется для отслеживания каждой частицы, информации о каждой частице и привязки каждой частицы к ее 3D-изображению. В процессе этого анализа анализируются поры, которые находятся внутри частицы, и сохраняется общая пористость этой конкретной частицы, поскольку реконструкция XCT дает полное 3D-изображение образца.

Три (из многих) геометрических параметра размера/формы оказались особенно полезными при анализе и классификации частиц в 3D: длина L, ширина, W, и толщина, T. L определяется как самое длинное расстояние от точки поверхности до поверхности частицы, W определяется аналогично L , с дополнительным ограничением: единичный вектор вдоль W должен быть перпендикулярен единичному вектору вдоль L, и T также определяется аналогично L с дополнительным ограничением, что единичный вектор вдоль T должен быть перпендикулярен как единичному вектору вдоль L , так и единичному вектору вдоль W¹². Эти три параметра определяют минимальный прямоугольник или ограничивающий прямоугольник, который содержит только частицу, а отношения этих трех параметров дают ценную, но приблизительную информацию о форме каждой частицы. Распределения могут быть сделаны из любого из них. Возможно, что W хорошо коррелирует с «размерами», измеренными с помощью ситового анализа⁵⁷, в то время как «размеры», измеренные с помощью лазерной дифракции, коррелируют со смесью L, W и T³¹.

Наконец, 3D-изображения тестового образца из 100-200 частиц визуально проверяются, чтобы определить, где находятся пороги в L/T, которые позволяют методу различать одиночные, почти сферические (SnS) частицы и несферические (NS) частицы, которые могут быть несколькими частицами, сваренными вместе, или явно одиночные частицы, но со странной формой.

протокол

ПРИМЕЧАНИЕ: Следующий протокол составлен для частиц металлического порошка с размером, в соответствии с приближением объемного эквивалента сферического диаметра (VESD, диаметр сферы с тем же объемом, что и частица), от 10 мкм до 100 мкм. Предположим, что металл имеет плотность в единицах г/^см3. На этапах подготовки образца следует надевать перчатки, а также средства защиты глаз. Важно прочитать все шаги в Протоколе 1, так как некоторое оборудование должно быть готово до начала работы Протокола.

1. Приготовление эпоксидно-порошковой смеси

1. Приготовьте примерно 25 г быстротвердеющей (5 мин) эпоксидной смолы в небольшой одноразовой посуде. Для этой цели хорошо подходят лодки из алюминиевой фольги. Хорошая эпоксидная смола для использования поставляется в пузырчатой пленке, где смола отделена от отвердителя, плотность отверждения которого составляет ρ_e г/^см3.
2. Используйте M граммов порошка из хорошо встряхнутого большего образца порошка, где M предназначен для получения объемной доли около 10% после смешивания M граммов с эпоксидной смолой. Это сделано для того, чтобы избежать ситуации, когда частицы находятся настолько близко друг к другу, что сканирование XCT ошибочно идентифицирует их как настоящие мультичастицы, которые прочно прикреплены. Уравнение, определяющее М, выглядит следующим образом:
   
   
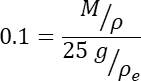
3. Энергично перемешайте металлический порошок с эпоксидной смолой вручную, используя одноразовый стержень для перемешивания - простая деревянная палочка для поделки отлично подойдет - в течение примерно 30 секунд, достаточно долго, чтобы порошок адекватно рассеялся. Этот процесс, если он выполнен правильно, значительно упрощает анализ изображений отдельных частиц.
   1. После смешивания соскребите вязкопластичную смесь в компактный комок с максимально возможной вертикальной протяженностью, чтобы быть готовым к следующему этапу. Важно заранее подготовить следующие шаги, так как до затвердевания эпоксидной смолы останется не так много времени.
4. Используйте небольшой вакуумный насос, подключенный к пластиковому шлангу длиной 0,5 м, с насадкой, вставленной в открытый конец шланга, которая будет плотно прилегать к полимерной соломинке внутреннего диаметра около 3 мм.
   ПРИМЕЧАНИЕ: Коктейльные соломинки, легко доступные в продуктовых магазинах, хорошо подходят для полимерной соломинки диаметром 3 мм и имеют длину около 150 мм. Для сопла обычно эффективен отрезанный конец одноразовой пластиковой пипетки объемом от 1 мл до 2 мл. Там, где сопло входит в пластиковый шланг, вокруг соединения следует плотно натянуть изоленту, чтобы обеспечить герметичное уплотнение. 25 г эпоксидной смолы и порошка должно быть более чем достаточно, чтобы заполнить две полные соломинки.
5. Вставьте насадку в соломинку, крепко удерживая насадку и конец соломинки вместе. Вставьте свободный конец соломинки в компактный комок эпоксидного порошка и включите вакуумный насос.
   ПРИМЕЧАНИЕ: Держите свободный конец соломинки погруженным в эпоксидно-порошковую смесь, чтобы избежать попадания пузырьков воздуха внутрь соломинки - некоторые пузырьки воздуха будут присутствовать всегда, но эта процедура сводит к минимуму их присутствие. Соломинки должны быть заполнены с точностью до 10 мм от верха - линия наполнения видна через полупрозрачную соломинку. Когда первая соломинка будет заполнена, выключите вакуумный насос и выньте соломинку из насадки.
6. Сотрите эпоксидную смесь с заполняющего конца соломинки и вдавите оба конца соломинки в небольшой комок глины, чтобы заполнить оба конца соломинки так, чтобы эпоксидно-порошковая смесь не вытекала во время отверждения. Поместите^2-ю соломинку на сопло и повторите, сначала используя стержень для смешивания, чтобы собрать эпоксидно-порошковую смесь вместе, если это необходимо.
7. После того, как эпоксидная смола в двух соломинках затвердеет, отрежьте бритвой концы соломинки, где был герметик для глины, а затем разрежьте каждую соломинку пополам, чтобы получить четыре образца. Используйте одну соломинку в качестве образца #1 для XCT, установленную вертикально так, чтобы рентгеновские лучи проникали через круглое поперечное сечение соломинки.

2. Инструмент XCT

ПРИМЕЧАНИЕ: Эти шаги предполагают знакомство с выбранным пользователем инструментом XCT.

1. Используйте высокое напряжение, обычно 100 кВ или выше, так как существует хороший контраст между эпоксидной матрицей и частицами металлического порошка, и нет необходимости что-либо устранять внутри эпоксидной матрицы, что обычно требует низкого напряжения около 40 кВ. Используйте полное сканирование на 360^{градусов} с размером вокселя около 1 мкм. Соотношение между наименьшим рассматриваемым размером частиц и используемым размером вокселей должно быть минимум 8-10:³⁹.
2. Возьмите достаточное количество FOV для более чем одного образца, чтобы получить достаточное количество частиц для анализа. Если следовать рекомендациям по подготовке образцов, будет достаточно от 2 до 8 FOV. Как правило, минимум 1000 частиц достаточно для корректного анализа формы/размера, но большее количество частиц приводит к более плавным кривым распределения и лучшей статистике. Восстановленные срезы нумеруются от 0 до nz-1, снизу вверх поля зрения, где nz — общее количество восстановленных срезов.
   1. Сохраняйте вертикальные срезы поперечного сечения для каждого поля зрения отдельно, в 8-битном формате (например, tiff), отмечая размер каждого набора изображений в пикселях (nx x ny), количество этих срезов (nz) и размер вокселов в микрометрах (v). Формат 8 бит подходит для таких простых изображений серого цвета с металлическими частицами и эпоксидной матрицей, которые легко сегментировать.

3. Сборка срезов, принадлежащих каждому полю зрения, в 3D ASCII микроструктуру

ПРИМЕЧАНИЕ: Программа на C, используемая в NIST, называется tiff2array.c и чаще всего используется с файлами tiff, но может работать и с другими 8-битными форматами. Он может быть скомпилирован как есть, с помощью исполняемого файла с именем tiff2array. Эта программа считывает каждое изображение, снизу вверх, преобразует их в формат ascii (от 0 до 255 оттенков серого), а затем складывает их в конце мастер-файла.

1. Например, если восстановленные изображения имеют формат tiff и нумеруются последовательно снизу вверх, используйте следующий синтаксис в команде линейного терминала: tiff2array *.tiff. Этот мастер-файл, или файл микроструктуры, представляет собой 3D-представление поля зрения. Если переменная a(i,j,k) — это шкала серого в положении (i,j,k), где k — номер среза, k = 1 до nz, а (i,j) — пиксель в k-м срезе, где i измеряется слева направо, а j — сверху вниз.
   ПРИМЕЧАНИЕ: Все программное обеспечение, необходимое для Протокола, доступно в разделе «Дополнительная информация» данного документа по ссылке на базу данных NIST, расположенную по адресу https://doi.org/10.18434/M32265.
2. Для P FOV создайте небольшой файл с именем particle-class-sysconfig.dat, с P строками, где каждая строка читается, для pth (p=1,P) FOV:
   Имя файла nx ny nz v b c
   где Filename = 12-символьная идентификация для конкретного поля зрения, b = 1 для внутреннего сканирования и 0 для внешнего сканирования, а c = количество фаз, присутствующих на изображениях. Когда выполняется внутреннее сканирование, обычно присутствуют три (c = 3) фазы: 1) эпоксидная смола, 2) черные области, обозначающие внешнюю сторону кругового сканирования и пузырьки воздуха, и 3) более яркие частицы. Иногда четыре фазы могут показаться более разумным предположением, и поэтому c = 4. Значения для c 3 или 4 являются единственными двумя вариантами. Значение c сообщает программному обеспечению для анализа частиц, какой алгоритм автоматической сегментации Otsu, первоначально написанный для двухфазных изображений, но легко расширенный до любого числа фаз, использовать для автоматической сегментации изображений в определенном поле зрения ^26,58. Файлы микроструктуры, которые будут использоваться в следующей программе, должны иметь 12-символьные имена, точно такие же, как имя файла, указанное в файле FOV-name-sysconfig.dat, за которым следует расширение .mic.
3. Запустите программу для анализа частиц pp-Otsu.f, используя в качестве входных данных файл particle-class-sysconfig.dat и различные файлы микроструктуры Filename.mic. Внесите только два изменения в эту программу для новой системы, все из которых помечены комментарием "USER" в исходном коде Fortran: имена файлов для общих выходных файлов (измените общее имя класса частиц) и количество FOV, перечисленных в particle-class-sysconfig.dat. Программа pp-Otsu.f находится на языке Fortran, является скалярной и обычно компилируется на Fortran 77, хотя Fortran 90 должен работать нормально. Она, как и все другие программы на языке Форран, описанные ниже, должна быть скомпилирована с двойной точностью (-r8) для получения точных результатов.
   1. Кроме того, поскольку pp-Otsu.f работает с большими файлами, всегда добавляйте в компиляцию параметры (или их эквиваленты) -mcmodel=medium и -Mlarge_arrays. Вспомогательный файл gauss120.dat содержит веса и точки для 120-точечной квадратуры Гаусса, широко используемой в pp-Otsu.f, и должен находиться в том же каталоге, что и pp-Otsu.f. Все описанные ниже программы написаны на языке Fortran 77, за исключением программ MPI, которые написаны на языке Fortran 90.
4. Просмотр файлов частиц, которые являются основными выходными данными pp-Otsu.f, выполнение которых на одном процессоре может занять несколько часов, если в нем есть тысячи частиц, подлежащих анализу. К ним относятся файлы с именами, такими как Particle-class-name-anm-particle-number.dat, которые содержат список комплексных коэффициентов (n = 0,26), с единицами измерения микрометров или в любых других единицах v, для частиц, которые считаются адекватно звездообразными³⁹ и, таким образом, способными расширяться в сферических гармонических функциях (называемых частицами SH). Файлы частиц также включают файлы типа Particle-class-name-part-particle-number.dat, которые содержат количество вокселей в частице и все позиции вокселей (в координатах вокселей) для частиц, которые не могут быть описаны сферическими гармоническими разложениями (называемых неSH-частицами).
5. Просмотрите два файла, один для частиц SH и один для частиц, не относящихся к SH, которые содержат пористость всех найденных частиц, даже если пористость равна нулю, с фразой porosity в именах файлов. Дополнительная программа, porosity-analyze.f, должна получить количество строк в каждом файле porosity и их имена - имена файлов, которые необходимо изменить, находятся в начале исходного кода. Результатом работы этой программы являются два файла Particle-class-intern-poros-analysis.txt и Particle-class-intern-poros-list.txt. Файл анализа генерирует информацию, показанную в таблице 2, в разделе «Репрезентативные результаты», а файл списка предоставляет информацию, необходимую для создания рисунка 5 в разделе «Репрезентативные результаты».
6. Просмотрите три файла изображений в формате tiff, показывающие один срез первого рассмотренного поля зрения. Первый срез (OriA-0500.tiff) показывает k = 500 среза первого поля зрения в файле particle-class-sysconfig.dat без какой-либо обработки изображений, а второй файл изображения показывает то же изображение, но теперь сегментированное и пороговое (PixA-0500.tiff). Если применяется какое-либо ограниченное разделение водораздела, то третий файл изображения показывает результаты этого алгоритма (LWSA-0500.tiff). Обычно этот этап обработки изображения не применяется, поэтому третий файл изображения такой же, как и второй. Эти изображения генерируются в качестве этапа проверки на наличие ошибок при первоначальной сборке 3D-микроструктуры и автоматической сегментации изображения Оцу. Создается общий выходной файл (particle-class-name-particles-data.dat), в котором перечисляется вся вспомогательная информация для обработки каждой частицы. Этот файл используется только в качестве справочного, но воксельные объемы и метки номеров всех обработанных частиц записываются в конце этого файла.
7. Для каждой обработанной частицы, будь то SH или не SH, просмотрите файл изображения 3D VRML с соглашением об именовании particle-name-particle-number.wrl. Для частиц SH этот файл изображения VRML содержит два изображения, расположенных рядом, воксельное изображение исходной частицы и более гладкое визуализированное изображение с использованием коэффициентов SH. Для частиц, отличных от SH, сохраняется только воксельное изображение.

4. Создание геометрической информации для всех частиц SH и других частиц

1. Перед дальнейшей обработкой составьте список Particle-class-name-anm-particle-number.dat имен файлов с именем anm.lis, а список частиц non-SH Particle-class-name-part-particle-number.dat с именем nonSH.lis. Запустите маленькую программу number.f, предварительно отредактировав нужное количество файлов в anm.lis. Это изменяет файл anm.lis , чтобы в нем был указан номер частицы в каждой строке файла списка, а также имя файла, заменяя предыдущий файл.
2. Используйте программу part-lwt-listnum-unitvector.f для генерации и оценки геометрической информации для частиц SH. Это параллельная программа MPI, поскольку в ней могут быть оценены тысячи частиц SH, а выполнение только одной частицы за раз может занять несколько дней. Единственными изменениями в этой программе, которые необходимо внести при обработке нового класса частиц, являются Ntot количество файлов Particle-class-name-anm-particle number.dat и информация об именовании класса частиц для выходного (Particle-class-name-un-geom-len.dat) файла. В программе есть комментарии (USER) в нескольких местах, которые необходимо изменить для нового типа частиц. Выходной файл Particle-type-info-un-SH-geom-len.dat объединяет частицы из каждого поля зрения, и каждая строка имеет следующую структуру.
   
   Имя файла коэффициентов SH, x1, x2, y1, y2, z1, z2, объем, площадь поверхности, коэффициент SA, кривая, отношение, nnn, гаусс, заполнитель, L, W, T, L/T, W/T, T/T, момент инерционных тензорных компонент, единичный вектор L, тета, фи углы, единичный вектор W, тета, фи углы, T единичный вектор, тета, фи углы
   
   x1 — минимальное значение x на поверхности частицы, а x2 — максимальное и аналогично для y и z. Они определяют «коробку экстента», которая просто заключает частицу в ее измеренную ориентацию⁴². Поле экстента используется в других приложениях 46,47,48,49. Коэффициент SA — это площадь поверхности частицы, деленная на площадь поверхности сферы, эквивалентной объему. Кривая — это интегрированная средняя кривизна, инвертированная и нормализованная таким образом, что она равна диаметру, когда частица является идеальной сферой. Отношение — это след тензора момента инерции, деленный на след тензора момента инерции для объемно-эквивалентной сферы. nnn — максимальное количество коэффициентов SH (n=0, nnn), которое должно использоваться при работе с данной частицей. Гаусс — это интегрированная гауссова кривизна, деленная на 4π, которая должна быть равна 1 для замкнутого объекта. Точка, в которой Гаусс отклоняется от единицы более чем на 5%, определяет максимальное количество коэффициентов SH (n = nnn), которые должны использоваться при воссоздании частицы. L, W, T — длина, ширина и толщина частицы, которые были определены в разделе «Введение». Независимые компоненты тензора момента инерции перечислены как I₁₁, I₂₂, I₃₃, I₁₃, I₂₃, I₁₂. Наконец, перечисляется единичный вектор для L в порядке координат x, y и z, за которым следуют сферические полярные углы θ (угол от положительной оси z) и Φ (угол поворота вокруг оси z, определенный равным нулю по положительной оси x и положительный против часовой стрелки). Далее следуют параметры для W и T, перечисленные таким же образом.
3. Используйте программу nonSH-lwt-un-scalar.f для вычисления параметров L, W и T для частиц, отличных от SH, работающих со списком имен файлов, отличных от SH.lis , а также для записи связанных с ними единичных векторов. Единственные изменения, которые необходимо внести в этот файл для нового класса частиц, - это количество имен файлов в nonSH.lis, а также имена выходных файлов. Основной вывод этой программы, называемый Particle-name-info-nonSH-len.dat, имеет каждую строку в формате:
   
   Имя файла: volume: L, W, T, A1, a2, a3 (единицы измерения LWT, векторы и углы)
   
   где a1, a2 и a3 — конечные углы (в градусах - 90^o) между единичными векторами для L и W, W и T, а также L и T, которые включены в качестве проверки на ошибку для алгоритма вычисления L, W и T , поскольку все эти углы должны быть равны нулю для идеального вычисления. Единичные векторы и углы L, W и T имеют тот же формат, что и для частиц SH.

5. Выберите подмножество частиц SH и других частиц для визуального определения предсечных значений SnS и NS L/T.

Примечание: Частицы SH, как правило, состоят из одиночных сферических частиц, одиночных несферических (эллипсоидальных или разбитых каким-либо образом или случайной формы) частиц, двойных частиц и множественных (более двух частиц, соединенных вместе) частиц. Частицы, составляющие множество частиц, могут быть сферическими или несферическими. Частицы, отличные от SH, обычно имеют несколько одиночных сферических частиц, хотя в основном с большими порами, которые прорвались на поверхность, а остальные в основном состоят из двойных и множественных^{частиц26}. Это определяется путем просмотра случайной выборки обоих видов частиц со значениями L/T от 1 до 2. Такой визуальный осмотр становится важным этапом для обеспечения классификации SnS и NS.

1. Запустите программу (VRML-select-multi-single.f), которая считывает файлы Particle-type-info-SH-geom-len.dat и Particle-name-info-nonSH-len.dat , и выбирает по 10 частиц в каждом интервале L/T размером 0.1, т.е. (1,1.1), (1.1,1.2) и т.д. Он хранит до 100 частиц SH с L/T в диапазоне от 1 до 2 и до 100 частиц без SH с тем же диапазоном L/T . Генерируются два текстовых файла (*SH-VRML-list.txt и *nonSH-VRML-list.txt) со списком значений L/T и корневых имен найденных файлов изображений VRML. Они должны быть помещены в какую-либо таблицу и упорядочены в соответствии со значением L/T.
2. Визуально изучите 3D-изображения каждой из этих частиц, чтобы определить общий диапазон морфологий, начиная с частиц с наименьшим значением L/T . Частицы оцениваются с точки зрения того, являются ли они раздробленными частицами, двойными частицами, множественными частицами, неправильными (например, не очень сферическими) и имеют ли они спутники, которые представляют собой гораздо более мелкие частицы, прикрепленные к основной частице. Считается, что спутник делает главную частицу двойной или кратной частицей, если диаметр спутника (спутников) превышает 1/5 диаметра главной частицы. Найдено приблизительное значение L/T , которое отделяет одиночные, почти сферические (SnS) частицы от множественных и очень несферических частиц (NS), которые могут немного отличаться для SH и неSH частиц. Первая найденная двойная или множественная частица определяет пороговое значение как для SH, так и для неSH частиц.
   ПРИМЕЧАНИЕ: Дополнительный материал, расположенный по адресу https://doi.org/10.18434/M32265, включает в себя файл электронной таблицы для исследованных частиц, чтобы увидеть, как были определены эти пороговые значения. В этих числах присутствует некоторая неопределенность и некоторая степень субъективности, которые можно оценить, выбрав другой набор из 100 частиц SH и 100 частиц, не содержащих SH, с L/T от 1 до 2, для оценки пороговых значений. Недавняя работа показала, что эта неопределенность^{была невелика} и не оказала существенного влияния на результаты.

6. Создание данных 2D-проекции из 3D-частиц

ПРИМЕЧАНИЕ: Единственные современные коммерческие анализаторы частиц, которые измеряют форму частиц, делают это с помощью 2D-проекций. Данные XCT могут быть проанализированы для получения произвольных 2D-прогнозов, генерируя данные, которые могут быть количественно сопоставлены с результатами этих коммерческих инструментов. 2D-проекции создаются как из SH, так и из других частиц и объединяются, без попытки классификации по категориям 2D SnS и NS, поскольку в настоящее время неизвестно, как определить эти классы для 2D-проекций.

1. Используйте две программы (proj-mpi-SH-LWT.f) для частиц SH и (proj2D-nonSH-LWT.f) для частиц, отличных от SH, чтобы построить три ортогональные проекции для каждой частицы вдоль направления трех единичных векторов LWT , а затем сгенерировать коэффициенты Фурье для контура проекции. Эти коэффициенты используются для вычисления различных 2D-величин, таких как площадь, периметр, а также различные длины и соотношения сторон.
2. Для каждой проекции генерируется и сохраняется ряд точек (x,y), помеченных именем файла частиц и 1 для проекции вдоль единичного вектора L , 2 для проекции вдоль единичного вектора W и 3 для проекции вдоль единичного вектора T . Введите их в любую графическую программу, которая принимает эти данные, убедившись, что пределы осей x и y должны быть одинаковыми, а каждая ось имеет одинаковую физическую длину.
3. Храните коэффициенты Фурье с аналогичным соглашением об именовании файлов, но по умолчанию эта функция отключена с помощью комментариев. Единственными изменениями, внесенными в любую из этих программ (позиция программы отмечена "USER"), являются общее количество рассматриваемых частиц (Ntot), а также имена входных и выходных файлов, которые должны отражать класс анализируемых частиц.
4. Основными выходными данными работы (proj-mpi-SH-LWT.f) и (proj2D-nonSH-LWT.f) являются файлы данных проекции с соглашением об именовании Particle-class-info-SH-proj.dat и Particle-class-info-nonSH-proj.dat. Можно рассчитать различные 2D-величины, в том числе те, которые используются двумя различными коммерческими инструментами (Horiba Camsizer⁵⁹ и Malvern MORPHOLOGI G3⁶⁰). В обоих случаях программы вычисляют двумерную версию L и W, называемую L2D и W2D.
5. Структура выходного файла перечисляет для каждой частицы, области, периметра Xcmax, Xcmin, Fermax, Fermin, W2D, L2D, WM и LM, где Fermax и Fermin — максимальный и минимальный диаметры Feret, а Xcmax и Xcmin определяются из диаметров хорд, взятых в различных направлениях⁵⁹. Теоретически можно показать, что L2D является той же величиной, что и Xcmax, что также можно увидеть в файлах данных. Параметры LM и WM являются версиями L2D и W2D, определенными немного иначе в Malvern MORPHOLOGI G3 manual⁶⁰. Формат файла: Particle name/number, area, perimeter, Fermin, Fermax, Xcmin, Xcmax, W2D, L2D, theta, WM, LM, slo и nnnF, где nnnF — это количество коэффициентов Фурье, используемых для представления проекции частицы. Величина тета — это угол в градусах, который проходит ось, определяющая WM и LM, с осью x ⁶⁰. Величина slo — это просто отношение синуса тета к косинусу тета. Ни одна из этих величин не используется в описанном здесь анализе частиц и включается только в качестве проверки расчетов. Данные для каждой частицы поступают в виде наборов по три, по одной линии для каждой из трех проекций, (1,2,3) = (L,W,T).

7. Обработка 3D и 2D геометрических данных частиц для создания различных графиков

1. Используйте любое программное обеспечение, которое нравится пользователю для обработки данных о размере и форме частиц. Какое бы программное обеспечение ни использовалось, необходимо соблюдать определенную процедуру.
2. Для 3D-данных объедините данные SH и non-SH в списки SnS и NS, используя ранее определенные значения L/T для каждого класса частиц. Распределения и средние значения должны быть вычислены для частиц SnS и NS отдельно, а также для объединенных данных SnS и NS для всех интересующих геометрических параметров, таких как L, W, T, L/T, W /T, L/W, эквивалентный объему сферический диаметр и другие.
3. Для данных 2D-проекции объедините данные SH и другие данные. Существует три 2D-проекции для каждой 3D-частицы, взятые вдоль единичных векторов для L, W и T. Объединение всех трех проекций должно дать результаты, аналогичные экспериментальной технике, которая случайным образом вращает частицы перед тем, как сделать проекцию. Использование только данных L-вектора, например, моделирует экспериментальную методику, в которой частицы грубо выровнены вдоль их самого длинного направления, перпендикулярно направлению падения и параллельно стробоскопу/направлению проекции в типичном устройстве.

Результаты

Компания ASTM инициировала программу проверки квалификации (AMPM, Additive Manufacturing Powder Metallurgy) для металлического порошка, используемого для лазерного сплавления порошкового слоя, в рамках которой участники проводят серию стандартных испытаний металлического порошка, а ASTM с?...

Обсуждение

Метод определения 3D-размера и формы металлических частиц на основе XCT имеет больше возможных применений, но также и некоторые ограничения. Ограничения будут устранены в первую очередь.

Быстроотверждаемая эпоксидная смола используется для того, чтобы в...

Материалы

Name	Company	Catalog Number	Comments
Epoxy	Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/	Hardman Part # 4001	case of 100