Analyse tridimensionnelle de la forme des particules à l’aide de la tomodensitométrie à rayons X : procédure expérimentale et algorithmes d’analyse pour les poudres métalliques

Résumé

La taille et la forme des particules de poudre ne sont pas des quantités indépendantes. Les techniques de mesure habituelles ne mesurent pas ces paramètres entrelacés en trois dimensions (3D). Une technique de mesure/analyse 3D, basée sur la tomographie à rayons X, est décrite, qui permet de mesurer la taille et la forme et de classer les particules de poudre en fonction des deux paramètres.

Résumé

La mesure de la distribution granulométrique des particules dans une poudre est une activité courante dans la science et l’industrie. La mesure de la distribution de la forme des particules est beaucoup moins courante. Cependant, la forme et la taille des particules de poudre ne sont pas des quantités indépendantes. Toutes les techniques de mesure de taille/forme connues prennent une forme sphérique ou mesurent la forme en deux dimensions seulement. La méthode basée sur la tomodensitométrie à rayons X (XCT) présentée ici mesure à la fois la taille et la forme en 3D sans faire d’hypothèses. À partir d’une image 3D de particules, la méthode permet de classer mathématiquement les particules en fonction de leur forme, par exemple des particules composées de plusieurs particules plus petites soudées ensemble, par opposition à des particules uniques qui ne sont pas nécessairement sphériques. Bien sûr, définir un nombre unique comme la « taille » ou la « forme » d’une particule non sphérique aléatoire n’est pas possible en principe, ce qui conduit à de nombreuses façons d’estimer la taille et la forme des particules via divers paramètres interconnectés, qui peuvent tous être générés à partir de cette caractérisation 3D complète sous forme de moyennes et de distributions. Les procédures expérimentales nécessaires, l’analyse mathématique et l’analyse informatique sont décrites et un exemple est donné pour une poudre métallique. La technique est limitée aux particules qui peuvent être imagées par XCT avec un minimum d’environ 1000 voxels par volume de particules.

Introduction

La mesure de la distribution granulométrique des particules dans une poudre est une activité courante dans la science et l’industrie ^1,2.  La mesure de la distribution de la forme des particules est moins courante, mais la taille et la forme, ainsi que le matériau à partir duquel les particules sont fabriquées, déterminent leurs propriétés, seules ou dans une sorte de matériau matriciel 3,4,5,6,7. Les matériaux dont la taille et la forme des particules sont intéressantes comprennent le ciment Portland, le sable et le gravier 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22^{, 23}, poudres métalliques pour la métallurgie des poudres et la fabrication additive 24,25,26, sol lunaire 27,28,29, pneus automobiles déchiquetés ³⁰, déchets de verre broyés³¹, cellules souches³², nanotubes de carbone et graphène 33,34,35,36,37. Cependant, la forme et la taille des particules de poudre ne sont pas des quantités indépendantes²⁶. Par exemple, supposons que l’on ait une particule géométriquement régulière dont la « taille » est dite d. Sans dire si cette particule est une sphère, un cube ou une fine tige de longueur d, on ne sait pas vraiment comment la taille s’applique à cette particule. En disant que la particule est une sphère, un cube ou une tige, on spécifie en réalité la forme de la particule, et sans cette information supplémentaire, l’information sur la taille n’a aucun sens.

Pour ces trois exemples, une sphère, un cube ou une tige mince, la taille des particules peut être spécifiée par un seul nombre. Mais même si la tige avait une section transversale circulaire, il faudrait également mesurer le diamètre de cette section transversale, de sorte que deux paramètres de taille seraient vraiment nécessaires pour la particule mince de la tige. Qu’en est-il des particules en forme d’ellipsoïdes ou des boîtes rectangulaires ? Pour chacun d’entre eux, trois chiffres sont nécessaires pour spécifier la taille, et la forme doit toujours être donnée sous la forme d’un ellipsoïde ou d’une boîte rectangulaire pour que les trois paramètres de taille aient un sens. Pour une particule de forme aléatoire, un nombre infini de paramètres de taille (par exemple, la longueur des cordes à travers la particule) seraient nécessaires pour caractériser complètement la « taille » de la particule, et pourtant ceux-ci n’auraient aucun sens sans une « caractérisation de forme », sachant à quels angles par rapport au centre de masse de la particule ces cordes ont été dessinées.

Il existe de nombreuses techniques utilisées pour mesurer la distribution granulométrique des particules dans une poudre, en utilisant différents principes physiques ^1,2. Ce que l’on ne reconnaît généralement pas, cependant, c’est que pour extraire la taille des particules, il faut utiliser des informations sur la forme des particules, qu’elles soient supposées ou mesurées. Les techniques actuelles peuvent être classées comme suit : (I) mesures de la taille des particules tridimensionnelles (3D) en supposant une forme 3D, et (II) mesures de la taille et de la forme, mais uniquement des projections bidimensionnelles (2D), à l’aide de techniques d’analyse d’images 2D. Pour les particules sphériques, toutes les projections 2D sont des cercles, avec le même diamètre que les particules d’origine, et toutes ces techniques de mesure, à la fois de classe I et de classe II, dans l’incertitude de mesure, donnent les mêmes résultats pour des sphères parfaites. Pour les particules non sphériques, les projections 2D sont beaucoup moins étroitement liées aux particules d’origine. Si une particule a une porosité interne qui ne brise pas la surface de la particule, ces pores ne seront pas du tout mesurés par l’une de ces techniques de mesure 3D ou 2D. La classe I comprend la diffraction laser, le volume de détection électrique (ESV)³⁸, l’analyse par tamisage et la sédimentation ; et la classe II couvre la microscopie électronique à transmission et à balayage, la microscopie à force atomique et l’analyse d’images dynamiques et statiques avec des techniques optiques. Aucune des deux classes ne mesure avec précision la taille et la forme des particules non sphériques en 3D.

Depuis environ 2002³⁹, une nouvelle méthode d’analyse des particules a été développée 40,41,42,43,44,45 qui permet d’imager une particule 3D en 3D, puis d’utiliser plusieurs formes d’analyse mathématique pour représenter et classer chaque particule. Une image 3D est enregistrée pour chaque particule individuelle, qui peut être comparée aux informations géométriques et mathématiques également enregistrées pour chaque particule. Cette information mathématique peut être utilisée pour régénérer la particule à volonté dans n’importe quel type de modèle 3D 46,47,48,49, à n’importe quel endroit et orientation, ou pour générer des particules virtuelles qui sont forcées d’avoir les mêmes statistiques ^50,51. Cette méthode d’analyse des particules est basée sur des balayages XCT de particules dispersées dans de l’époxy ou un autre support similaire. Les balayages XCT sont opérés par un logiciel spécialisé qui utilise l’algorithme de gravure 52,53,54,55,56 pour identifier les particules, puis soit l’ajustement de séries harmoniques sphériques, soit le comptage de voxels pour générer et stocker la forme et la taille des particules, des images 3D des particules et, dans un second temps, des informations géométriques pour chaque particule. Chaque particule analysée possède une étiquette alphanumérique unique, qui est utilisée pour suivre chaque particule, les informations sur chaque particule et relier chaque particule à son image 3D. Au cours de ce processus d’analyse, les pores qui se trouvent à l’intérieur d’une particule sont analysés et la porosité totale de cette particule particulière est stockée, car la reconstruction XCT donne une vue 3D complète d’un échantillon.

Trois paramètres géométriques de taille/forme (parmi tant d’autres) se sont avérés particulièrement utiles pour l’analyse et la classification des particules en 3D : la longueur, L, la largeur, W et l’épaisseur, T. L est défini comme la plus longue distance de surface à point de surface à travers une particule, W est défini de la même manière que L avec la contrainte supplémentaire que le vecteur unitaire le long de W doit être perpendiculaire au vecteur unitaire le long de L, et T est également défini de la même manière que L avec la contrainte supplémentaire que le vecteur unitaire le long de T doit être perpendiculaire à la fois au vecteur unitaire le long de L et au vecteur unitaire le long de W¹². Ces trois paramètres définissent le rectangle ou la boîte englobante minimale qui contient uniquement la particule, et les rapports de ces trois paramètres fournissent des informations précieuses mais approximatives sur la forme de chaque particule. Des distributions peuvent être faites de n’importe lequel d’entre eux. Il est possible que W soit bien corrélé avec les « tailles » mesurées avec l’analyse par tamisage⁵⁷, tandis que les « tailles » mesurées avec la diffraction laser sont corrélées à un mélange de L, W et T³¹.

Enfin, les images 3D d’un échantillon d’essai de 100 à 200 particules sont vérifiées visuellement pour déterminer où se trouvent les seuils en L/T qui permettent à la méthode de distinguer les particules simples et quasi sphériques (SnS) et les particules non sphériques (NS), qui peuvent être plusieurs particules soudées ensemble, ou ce qui sont clairement des particules uniques mais avec une forme étrange.

Protocole

REMARQUE : Le protocole suivant est écrit pour les particules de poudre métallique dont la taille, selon une approximation du diamètre sphérique équivalent-volume (VESD, diamètre de la sphère avec le même volume que la particule), est comprise entre 10 μm et 100 μm. Supposons que le métal ait une masse volumique en g/cm³. Des gants doivent être portés pendant les étapes de préparation de l’échantillon, ainsi qu’une protection oculaire. Il est important de relire toutes les étapes du Protocole 1, car certains équipements doivent être prêts avant de commencer le Protocole.

1. Préparation du mélange époxy-poudre

1. Préparez environ 25 g d’un époxy à durcissement rapide (5 min) dans un petit plat jetable. Les bateaux en aluminium fonctionnent bien à cet effet. Un bon époxy à utiliser est livré dans un papier bulle, avec la résine séparée du durcisseur, dont la densité durcie est de ρ_e g / cm³.
2. Utilisez M grammes de poudre, à partir d’un échantillon plus grand de poudre bien secoué, où M est conçu pour donner une fraction volumique d’environ 10 % une fois que les M grammes sont mélangés à l’époxy. Ceci est conçu pour éviter la situation où les particules sont si proches les unes des autres que le balayage XCT les identifie à tort comme de véritables multiparticules fermement attachées. L’équation définissant M est :
   
   
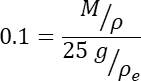
3. Mélangez vigoureusement la poudre métallique dans l’époxy, manuellement, à l’aide d’une tige d’agitation jetable - un simple bâton d’artisanat en bois fonctionne très bien - pendant environ 30 s, assez longtemps pour disperser la poudre de manière adéquate. Ce processus, bien fait, rend l’analyse d’image des particules individuelles beaucoup plus simple.
   1. Après le mélange, grattez le mélange viscoplastique en un amas compact avec autant d’étendue verticale que possible, afin d’être prêt pour l’étape suivante. Il est important d’avoir les étapes suivantes préparées à l’avance, car il ne restera pas beaucoup de temps avant que l’époxy ne durcisse.
4. Utilisez une petite pompe à vide reliée à un tuyau en plastique de 0,5 m de long, avec une buse insérée dans l’extrémité ouverte du tuyau qui s’insère parfaitement dans une paille en polymère d’environ 3 mm de diamètre intérieur.
   REMARQUE : Les pailles à cocktail, facilement disponibles dans les épiceries, fonctionnent bien pour la paille en polymère de 3 mm de diamètre et ont une longueur d’environ 150 mm. Pour une buse, l’extrémité tronçonnée d’une pipette en plastique jetable de 1 mL à 2 mL est généralement efficace. Lorsque la buse s’insère dans le tuyau en plastique, du ruban isolant doit être tendu fermement autour du joint pour assurer une étanchéité à l’air. Les 25 g de poudre époxy plus devraient être plus que suffisants pour remplir deux pailles complètes.
5. Insérez la buse dans la paille, en tenant la buse et l’extrémité de la paille fermement pincées ensemble. Insérez l’extrémité libre de la paille dans la touffe compacte de poudre époxy et allumez la pompe à vide.
   REMARQUE : Gardez l’extrémité libre de la paille immergée dans le mélange époxy-poudre pour éviter d’introduire des bulles d’air dans la paille - certaines bulles d’air seront toujours présentes, mais cette procédure minimise leur présence. Les pailles doivent être remplies à moins de 10 mm du haut - la ligne de remplissage est visible à travers la paille translucide. Lorsque la première paille est remplie, éteignez la pompe à vide et retirez la paille de la buse.
6. Essuyez le mélange époxy de l’extrémité de remplissage de la paille et enfoncez les deux extrémités de la paille dans un petit morceau d’argile afin de remplir les deux extrémités de la paille afin qu’aucun mélange époxy-poudre ne s’échappe pendant le durcissement. Placez la 2ème^{paille sur} la buse et répétez, en utilisant d’abord la tige de mélange pour rassembler le mélange époxy-poudre si nécessaire.
7. Une fois que l’époxy des deux pailles est durci, coupez les extrémités de la paille, là où se trouvait le scellant d’argile, avec un rasoir, puis coupez chaque paille en deux pour donner quatre échantillons. Utilisez une paille comme échantillon #1 pour le XCT, montée verticalement de manière à ce que les rayons X pénètrent à travers la section transversale circulaire de la paille.

2. L’instrument XCT

REMARQUE : Ces étapes supposent une familiarité avec l’instrument XCT choisi par l’utilisateur.

1. Utilisez une tension élevée, généralement de 100 kV ou plus, car il y a un bon contraste entre la matrice époxy et les particules de poudre métallique et il n’est pas nécessaire de résoudre quoi que ce soit à l’intérieur de la matrice époxy, ce qui nécessiterait normalement des basses tensions d’environ 40 kV. Utilisez^{un balayage complet} à 360°, avec une taille de voxel d’environ 1 μm. Le rapport entre la plus petite taille de particule considérée et la taille de voxel utilisée doit être d’au moins 8-10³⁹.
2. Prélever suffisamment de FFO, sur plus d’un échantillon, pour donner suffisamment de particules pour l’analyse. Si les directives de préparation des échantillons sont suivies, 2 à 8 FOV seront suffisants. En règle générale, un minimum de 1000 particules est suffisant pour une analyse de forme/taille valide, mais plus il y a de particules, plus les courbes de distribution sont lisses et les statistiques sont meilleures. Les tranches reconstruites sont numérotées de 0 à nz-1, de bas en haut du FOV, où nz est le nombre total de tranches reconstruites.
   1. Enregistrez les tranches de section transversale verticale pour chaque FOV individuellement, au format 8 bits (par exemple, tiff) en notant la taille en pixels de chaque ensemble d’images (nx x ny), le nombre de ces tranches (nz) et la taille du voxel en micromètres (v). Le format 8 bits est adéquat pour ces types d’images simples en niveaux de gris de matrice de particules métalliques-époxy, qui sont faciles à segmenter.

3. Assemblage des tranches appartenant à chaque FOV en une microstructure ASCII 3D

REMARQUE : Le programme C utilisé au NIST s’appelle tiff2array.c et est le plus souvent utilisé avec les fichiers tiff, mais peut gérer d’autres formats 8 bits. Il peut être compilé tel quel, avec l’exécutable nommé tiff2array. Ce programme lit chaque image, de bas en haut, les convertit au format ascii (échelle de gris de 0 à 255) puis les empile à la fin d’un fichier maître.

1. Si les images reconstruites sont au format tiff, par exemple, et sont numérotées consécutivement de bas en haut, utilisez la syntaxe suivante dans une commande de terminal de ligne : tiff2array *.tiff. Ce fichier maître, ou fichier de microstructure, est une représentation 3D du FOV. Si la variable a(i,j,k) est l’échelle de gris à la position (i,j,k), où k est le numéro de la tranche, k = 1 à nz, et (i,j) est le pixel de la kème tranche, où i est mesuré de gauche à droite et j est mesuré de haut en bas.
   REMARQUE : Tous les logiciels nécessaires au protocole sont disponibles dans la section Informations supplémentaires de ce document via un lien vers une base de données du NIST située à l’https://doi.org/10.18434/M32265.
2. Pour les champs de vision P, créez un petit fichier appelé particle-class-sysconfig.dat, avec P lignes, où chaque ligne se lit comme suit, pour le champ de vision pth (p=1,P) :
   Nom de fichier nx ny nz v b c
   où Nom de fichier = une identification de 12 caractères pour un champ de vision particulier, b = 1 pour un balayage intérieur et 0 pour un balayage extérieur, et c = le nombre de phases présentes dans les images. Lorsqu’un balayage intérieur est effectué, il y a généralement trois phases (c = 3) présentes : 1) l’époxy, 2) les régions noires indiquant l’extérieur du balayage circulaire et les bulles d’air, et 3) les particules les plus brillantes. Parfois, quatre phases peuvent sembler à l’œil nu être une hypothèse plus raisonnable et donc c = 4. Les valeurs de c de 3 ou 4 sont les deux seuls choix. La valeur de c indique au logiciel d’analyse de particules quel algorithme de segmentation automatique Otsu, écrit à l’origine pour les images biphasiques mais facilement étendu à n’importe quel nombre de phases, à utiliser pour segmenter automatiquement les images dans un champ de vision particulier^{de 26,58}. Les fichiers de microstructure qui seront utilisés dans le prochain logiciel doivent avoir des noms de 12 caractères qui sont exactement les mêmes que le nom de fichier indiqué dans le fichier FOV-name-sysconfig.dat, suivi de l’extension .mic.
3. Exécutez le logiciel d’analyse de particules pp-Otsu.f, en utilisant en entrée le fichier particle-class-sysconfig.dat et les différents fichiers de microstructure, Filename.mic. N’apportez que deux modifications à ce programme pour un nouveau système, toutes marquées par un commentaire « USER » dans la source Fortran : les noms de fichiers pour les fichiers de sortie généraux (changer le nom général de la classe de particules) et le nombre de FOV listés dans particle-class-sysconfig.dat. Le programme pp-Otsu.f est en Fortran, est scalaire et est généralement compilé en Fortran 77, bien que Fortran 90 devrait fonctionner correctement. Ce programme, ainsi que tous les autres programmes Fortran décrits ci-dessous, doivent être compilés en double précision (-r8) pour des résultats précis.
   1. De plus, comme pp-Otsu.f fonctionne avec des fichiers volumineux, ajoutez toujours les paramètres (ou leur équivalent) -mcmodel=medium et -Mlarge_arrays à la compilation. Un fichier auxiliaire, gauss120.dat, contient les poids et les points d’une quadrature gaussienne de 120 points largement utilisée dans pp-Otsu.f, et doit se trouver dans le même répertoire que pp-Otsu.f. Tous les programmes décrits ci-dessous sont écrits en Fortran 77, à l’exception des programmes MPI, qui sont écrits en Fortran 90.
4. Affichez les fichiers de particules qui sont les principales sorties de pp-Otsu.f, qui peuvent prendre plusieurs heures à fonctionner sur un seul processeur s’il y a des milliers de particules à analyser. Il s’agit notamment de fichiers portant des noms tels que Particle-class-name-anm-particle-number.dat, qui contiennent la liste des coefficients complexes (n = 0,26), avec des unités de micromètres ou dans n’importe quelle unité v , pour les particules jugées adéquatement en forme d’étoile³⁹ et donc capables d’être développées dans des fonctions harmoniques sphériques (appelées particules SH). Les fichiers de particules incluent également des fichiers tels que Particle-class-name-part-particle- number.dat, qui contiennent le nombre de voxels dans la particule et toutes les positions de voxels (en coordonnées de voxel) pour les particules qui ne peuvent pas être décrites par des expansions harmoniques sphériques (appelées particules nonSH).
5. Affichez les deux fichiers, l’un pour les particules SH et l’autre pour les particules nonSH, qui donnent les porosités de toutes les particules trouvées, même si la porosité est nulle, avec l’expression porosité dans les noms de fichiers. Un programme supplémentaire, porosity-analyze.f, doit recevoir le nombre de lignes dans chaque fichier de porosité et leurs noms de fichiers - les noms de fichiers à modifier se trouvent au début du code source. La sortie de ce programme sont les deux fichiers Particle-class-intern-poros-analysis.txt et Particle-class-intern-poros-list.txt. Le fichier d’analyse génère les informations indiquées dans le tableau 2 de la section Résultats représentatifs, et le fichier de liste fournit les informations nécessaires à la génération de la figure 5 dans la section Résultats représentatifs.
6. Affichez les trois fichiers d’image tiff montrant une tranche du premier FOV considéré. La première tranche (OriA-0500.tiff) montre la tranche k = 500 du premier FOV dans le fichier particle-class-sysconfig.dat , sans aucun traitement d’image, et le deuxième fichier image montre la même image mais maintenant segmentée et seuillée (PixA-0500.tiff). Si une division limitée du bassin versant est appliquée, le troisième fichier image affiche les résultats de cet algorithme (LWSA-0500.tiff). Habituellement, cette étape de traitement d’image n’est pas appliquée, de sorte que le troisième fichier image est le même que le deuxième. Ces images sont générées comme une étape de vérification des erreurs sur l’assemblage original de la microstructure 3D et la segmentation automatique de l’image Otsu. Un fichier de sortie général (particle-class-name-particles-data.dat) est créé répertoriant toutes les informations auxiliaires pour le traitement de chaque particule. Ce fichier n’est utilisé qu’à titre de référence, mais les volumes de voxels et les étiquettes numériques de toutes les particules traitées sont écrits à la fin de ce fichier.
7. Pour chaque particule traitée, qu’elle soit SH ou non, affichez le fichier image VRML 3D, avec la convention de nommage particle-name-particle-number.wrl. Pour les particules SH, ce fichier image VRML contient deux images côte à côte, une image en voxel de la particule d’origine et une image rendue plus lisse à l’aide des coefficients SH. Pour les particules nonSH, seule l’image du voxel est stockée.

4. Générer des informations géométriques pour toutes les particules SH et non-SH

1. Avant de poursuivre le traitement, dressez une liste des noms de fichiers Particle-class-name-anm-particle-number.dat , appelée anm.lis, et une liste des particules Particle-class-name-part-particle-number.dat nonSH, appelées nonSH.lis. Exécutez le petit programme number.f, après avoir été modifié pour avoir le bon nombre de fichiers dans anm.lis. Cela change le fichier anm.lis pour avoir le numéro de la particule sur chaque ligne du fichier de liste, ainsi que le nom du fichier, remplaçant le fichier précédent.
2. Utilisez le programme part-lwt-listnum-unitvector.f pour générer et évaluer des informations géométriques pour les particules SH. Il s’agit d’un programme parallèle MPI, car il peut y avoir des milliers de particules SH à évaluer, et ne faire qu’une seule particule à la fois peut prendre des jours. Les seules modifications de ce programme qui doivent être apportées lors du traitement d’une nouvelle classe de particules sont le numéro Ntot des fichiers number.dat Particle-class-name-anm-particle et les informations de nommage de la classe de particules pour le fichier de sortie (Particle-class-name-un-geom-len.dat). Le programme a des commentaires (USER) aux quelques endroits qui doivent être modifiés pour un nouveau type de particule. Le fichier de sortie unit Particle-type-info-un-SH-geom-len.dat particules de chaque champ de vision, et chaque ligne a la structure suivante.
   
   Coefficients SH nom de fichier, x1, x2, y1, y2, z1, z2, volume, surface, rapport SA, courbure, rapport, nnn, gauss, espace réservé, L, W, T, L/T, W/T, T/T, composantes du moment d’inertie, vecteur unitaire L, thêta, angles phi, vecteur unitaire W, thêta, angles phi, vecteur unitaire T, thêta, angles phi
   
   x1 est la valeur minimale x à la surface de la particule et x2 est la valeur maximale et de même pour y et z. Ceux-ci définissent une « boîte d’étendue » qui entoure simplement la particule dans son orientation telle que mesurée⁴². La boîte d’extension est utilisée dans d’autres applications 46,47,48,49. Le rapport SA est la surface de la particule divisée par la surface de la sphère équivalente en volume. La courbure est la courbure moyenne intégrée, inversée et normalisée de sorte qu’elle est égale au diamètre lorsque la particule est une sphère parfaite. Le rapport est la trace du moment tenseur d’inertie divisée par la trace du moment tenseur d’inertie pour la sphère équivalente en volume. nnn est le nombre maximal de coefficients SH (n = 0, nnn) qui doivent être utilisés lors de l’utilisation d’une particule donnée. Gauss est la courbure gaussienne intégrée, divisée par 4π, qui devrait être égale à 1 pour un objet fermé. Le point où Gauss s’écarte de l’unité de plus de 5 % définit le nombre maximum de coefficients SH (n = nnn) qui doivent être utilisés lors de la recréation de la particule. L, W, T sont la longueur, la largeur et l’épaisseur de la particule, et ont été définis dans la section Introduction. Les composantes indépendantes du moment du tenseur d’inertie sont énumérées comme I₁₁, I₂₂, I₃₃, I₁₃, I₂₃, I₁₂. Enfin, le vecteur unitaire de L est indiqué, dans l’ordre des coordonnées x, y et z, suivi des angles polaires sphériques θ (angle par rapport à l’axe z positif) et Φ (angle de rotation autour de l’axe z, défini comme étant nul sur l’axe des x positifs et positif dans le sens inverse des aiguilles d’une montre). Les paramètres de W et T suivent, listés de la même manière.
3. Utilisez le programme nonSH-lwt-un-scalar.f pour calculer les paramètres L, W et T des particules nonSH, fonctionnant sur la liste de noms de fichiers nonSH.lis , et enregistrez également les vecteurs unitaires associés. Les seules modifications qui doivent être apportées dans ce fichier pour une nouvelle classe de particules sont le nombre de noms de fichiers dans nonSH.lis et les noms de fichiers de sortie. La sortie principale de ce programme, nommée Particle-name-info-nonSH-len.dat, a chaque ligne au format :
   
   Nom de fichier : volume L W T a1 a2 a3 (unités LWT, vecteurs et angles)
   
   où a1, a2 et a3 sont les angles finaux (en degrés - 90^o) entre les vecteurs unitaires de L et W, W et T, et L et T, qui sont inclus en tant que vérification d’erreur pour l’algorithme de calcul L, W et T , puisque ces angles doivent tous être nuls pour un calcul parfait. Les vecteurs unitaires et les angles L, W et T sont dans le même format que pour les particules SH.

5. Sélectionnez un sous-ensemble de particules SH et non-SH pour déterminer visuellement les seuils SnS et NS L/T

REMARQUE : Les particules SH, en général, comprennent des particules sphériques simples, des particules simples non sphériques (ellipsoïdales ou brisées d’une manière ou d’une autre ou bien de forme aléatoire), des particules doubles et des particules multiples (plus de deux particules réunies). Les particules qui composent les multiples particules peuvent être sphériques ou non sphériques. Les particules nonSH ont généralement quelques particules sphériques simples, bien que principalement avec de grands pores qui ont percé jusqu’à la surface, et le reste est principalement constitué de particules doubles et multiples²⁶. Ceci est déterminé en visualisant un échantillon aléatoire des deux types de particules avec des valeurs de L/T de 1 à 2. Une telle inspection visuelle devient une étape importante pour permettre la classification SnS et NS.

1. Exécutez le programme (VRML-select-multi-single.f) qui lit les fichiers Particle-type-info-SH-geom-len.dat et Particle-name-info-nonSH-len.dat , et sélectionne 10 particules dans chaque intervalle L/T de taille 0,1, c’est-à-dire (1,1.1), (1.1,1.2), etc. Celui-ci stocke jusqu’à 100 particules SH avec un L/T compris entre 1 et 2, et jusqu’à 100 particules non-SH avec la même plage L/T . Deux fichiers texte sont générés (*SH-VRML-list.txt et *nonSH-VRML-list.txt) répertoriant les valeurs L/T et les noms racines des fichiers image VRML trouvés. Ceux-ci doivent être placés dans une sorte de feuille de calcul et ordonnés en fonction de la valeur L/T.
2. Examinez visuellement les images 3D de chacune de ces particules pour déterminer la gamme globale de morphologies, en commençant par les particules de la valeur L/T la plus faible. Les particules sont évaluées en fonction de savoir si elles sont des particules brisées, des particules doubles, des particules multiples, irrégulières (par exemple, pas très sphériques) et si elles ont des satellites, qui sont des particules beaucoup plus petites, attachés à la particule principale. On considère qu’un satellite fait de la particule principale une particule double ou multiple si le ou les satellites ont plus de 1/5 du diamètre de la particule principale. On trouve la valeur approximative de L/T qui sépare les particules simples et quasi sphériques (SnS) des particules multiples et très non sphériques (NS), qui peuvent être un peu différentes pour les particules SH et non SH. La première particule double ou multiple trouvée détermine la valeur limite pour les particules SH et non-SH.
   REMARQUE : Le matériel supplémentaire, situé à https://doi.org/10.18434/M32265, comprend un fichier tableur pour les particules examinées, afin de voir comment ces valeurs limites ont été déterminées. Il y a une certaine incertitude et un certain degré de subjectivité dans ces chiffres, qui peuvent être évalués en choisissant un ensemble différent de particules 100 SH et 100 particules non-SH, avec L/T entre 1 et 2, pour évaluer les valeurs limites. Des travaux récents ont révélé que cette incertitude était faible²⁶ et n’affectait pas les résultats de manière significative.

6. Générer des données de projection 2D à partir des particules 3D

REMARQUE : Les seuls analyseurs de particules commerciaux actuels qui mesurent la forme des particules le font avec des projections 2D. Les données XCT peuvent être analysées pour donner des projections 2D arbitraires, générant des données qui peuvent être quantitativement appariées aux résultats de ces instruments commerciaux. Les projections 2D sont faites à partir des particules SH et non-SH et sont combinées, sans tentative de classification dans les catégories 2D SnS et NS, car on ne sait pas à l’heure actuelle comment définir ces classes pour les projections 2D.

1. Utilisez les deux programmes, (proj-mpi-SH-LWT.f) pour les particules SH et (proj2D-nonSH-LWT.f) pour les particules nonSH, pour générer trois projections orthogonales pour chaque particule, le long de la direction des trois vecteurs unitaires LWT , puis générez des coefficients de Fourier pour le contour de la projection. Ces coefficients sont utilisés pour calculer diverses grandeurs 2D telles que la surface, le périmètre et diverses longueurs et rapports d’aspect.
2. Une série de points (x,y) est générée et stockée pour chaque projection, étiquetée avec le nom de fichier de particule et 1 pour la projection le long du vecteur unitaire L , 2 pour la projection le long du vecteur unitaire W et 3 pour la projection le long du vecteur unitaire T . Entrez-les dans n’importe quel programme graphique qui accepte cette entrée, en vous assurant que les limites des axes x et y doivent être les mêmes et que chaque axe a la même longueur physique.
3. Stockez les coefficients de Fourier avec une convention de nommage de fichier similaire, mais cette fonctionnalité est désactivée, par défaut, à l’aide de commentaires. Les seules modifications apportées dans l’un ou l’autre de ces programmes (position du programme marquée par « USER ») sont le nombre total de particules à prendre en compte (Ntot) et les noms de fichiers d’entrée et de sortie, qui doivent refléter la classe de particules analysée.
4. Les principales sorties de l’exécution (proj-mpi-SH-LWT.f) et (proj2D-nonSH-LWT.f) sont des fichiers de données de projection, avec la convention de nommage Particle-class-info-SH-proj.dat et Particle-class-info-nonSH-proj.dat. Une variété de grandeurs 2D peuvent être calculées, y compris certaines utilisées par deux instruments commerciaux différents (Horiba Camsizer⁵⁹ et Malvern MORPHOLOGI G3⁶⁰). Dans les deux cas, les programmes calculent une version 2D de L et W, appelée L2D et W2D.
5. La structure du fichier de sortie répertorie, pour chaque particule, aire, périmètre, Xcmax, Xcmin, Fermax, Fermin, W2D, L2D, WM et LM, où Fermax et Fermin sont les diamètres de Feret maximum et minimum et Xcmax et Xcmin sont définis à partir des diamètres de corde pris dans différentes directions⁵⁹. On peut théoriquement montrer que L2D est la même quantité que Xcmax, ce qui peut également être vu dans les fichiers de données. Les paramètres LM et WM sont des versions de L2D et W2D définies légèrement différemment dans le Malvern MORPHOLOGI G3 manual⁶⁰. Le format de fichier est le suivant : Nom/numéro de particule, aire, périmètre, Fermin, Fermax, Xcmin, Xcmax, W2D, L2D, theta, WM, LM, slo et nnnF, où nnnF est le nombre de coefficients de Fourier utilisés pour représenter la projection des particules. La quantité thêta est l’angle, en degrés, que l’axe qui définit WM et LM forme avec l’axe des x ⁶⁰. La quantité slo est simplement le rapport entre le sinus de thêta et le cosinus de thêta. Aucune des deux grandeurs n’est utilisée dans l’analyse des particules décrite ici et n’est incluse qu’à titre de vérification dans le calcul. Les données pour chaque particule sont présentées par ensembles de trois, une ligne pour chacune des trois projections, (1,2,3) = (L,W,T).

7. Traitement de données géométriques de particules 3D et 2D pour produire divers graphiques

1. Utilisez n’importe quel logiciel apprécié par l’utilisateur pour traiter les données de taille et de forme des particules. Quel que soit le logiciel utilisé, une certaine procédure doit être suivie.
2. Pour les données 3D, combinez les données SH et non-SH dans des listes SnS et NS, en utilisant les valeurs limites L/T précédemment déterminées pour chaque classe de particules. Les distributions et les moyennes doivent être calculées séparément pour les particules SnS et NS, ainsi que pour les données combinées SnS et NS, pour tous les paramètres géométriques d’intérêt, tels que L, W, T, L/T, W/T, L/W, le diamètre sphérique équivalent au volume, etc.
3. Pour les données de projection 2D, combinez les données SH et nonSH. Il y a trois projections 2D pour chaque particule 3D, prises le long des vecteurs unitaires pour L, W et T. La combinaison de ces trois projections devrait donner des résultats similaires à une technique expérimentale qui fait tourner les particules au hasard avant de faire une projection. L’utilisation uniquement des données vectorielles unitaires L , par exemple, simule une technique expérimentale dans laquelle les particules sont grossièrement alignées le long de leur direction la plus longue, perpendiculairement à la direction de chute et parallèlement à la direction de la lumière stroboscopique/projection dans un dispositif typique.

Résultats

L’ASTM a lancé un programme d’essais d’aptitude (AMPM, Additive Manufacturing Powder Metallurgy) pour la poudre métallique utilisée pour la fusion laser sur lit de poudre, où les participants effectuent une batterie d’essais standard sur poudre métallique et l’ASTM compile la distribution statistique de ces résultats dans un rapport aux participants⁶¹. Des échantillons de poudre métallique sont distribués deux fois par an à tous les participant...

Discussion

La méthode XCT pour caractériser la taille et la forme 3D des particules métalliques a plus d’applications possibles, mais aussi certaines limites. Les limitations seront abordées en premier.

Un époxy à durcissement rapide est utilisé de sorte que la viscosité de l’époxy soit suffisamment élevée pour empêcher la poudre de se déposer par gravité pendant le durcissement de l’époxy, ou du moins réduire le temps pendant lequel la sédimentati...

matériels

Name	Company	Catalog Number	Comments
Epoxy	Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/	Hardman Part # 4001	case of 100