Análise tridimensional da forma de partículas usando tomografia computadorizada de raios X: procedimento experimental e algoritmos de análise para pós metálicos

Resumo

O tamanho e a forma das partículas de pó não são quantidades independentes. As técnicas de medição usuais não medem esses parâmetros entrelaçados em três dimensões (3D). É descrita uma técnica de medição/análise 3D, baseada em tomografia computadorizada de raios-X, que pode medir tamanho e forma e classificar partículas de pó de acordo com ambos os parâmetros.

Resumo

Medir a distribuição de tamanho das partículas em um pó é uma atividade comum na ciência e na indústria. Medir a distribuição de forma das partículas é muito menos comum. No entanto, a forma e o tamanho das partículas de pó não são quantidades independentes. Todas as técnicas conhecidas de medição de tamanho/forma assumem uma forma esférica ou medem a forma apenas em duas dimensões. O método baseado em tomografia computadorizada de raios-X (XCT) apresentado aqui mede tamanho e forma em 3D sem fazer suposições. A partir de uma imagem 3D de partículas, o método pode classificar matematicamente as partículas de acordo com a forma, por exemplo, partículas compostas por várias partículas menores soldadas entre si, em oposição a partículas únicas que não são necessariamente esféricas. É claro que definir um único número como o "tamanho" ou "forma" de uma partícula aleatória não esférica não é possível em princípio, levando a muitas maneiras de estimar o tamanho e a forma das partículas por meio de vários parâmetros interligados, que podem ser gerados a partir dessa caracterização 3D completa na forma de médias e distribuições. Os procedimentos experimentais necessários, análise matemática e análise computacional são descritos e um exemplo é dado para um pó metálico. A técnica é limitada a partículas que podem ser visualizadas por XCT com um mínimo de cerca de 1000 voxels por volume de partícula.

Introdução

Medir a distribuição de tamanho das partículas em um pó é uma atividade comum na ciência e na indústria ^1,2.  Medir a distribuição da forma das partículas é menos comum, mas tanto o tamanho quanto a forma, juntamente com o material do qual as partículas são feitas, determinam suas propriedades, isoladamente ou em algum tipo de material de matriz 3,4,5,6,7. Os materiais cujo tamanho e forma de partícula são de interesse incluem cimento Portland, areia e cascalho 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22^{, 23}, pós metálicos para metalurgia do pó e manufatura aditiva 24,25,26, solo lunar 27,28,29, pneus automotivos triturados³⁰, resíduos de vidro triturados ³¹, células-tronco³² e nanotubos de carbono e grafeno 33,34,35,36,37. No entanto, a forma e o tamanho das partículas de pó não são quantidades independentes²⁶. Por exemplo, suponha que alguém tenha uma partícula geometricamente regular cujo "tamanho" é dito ser d. Sem dizer se essa partícula é uma esfera, um cubo ou uma haste fina de comprimento d, não se sabe realmente como o tamanho se aplica a essa partícula. Ao dizer que a partícula é uma esfera, cubo ou bastonete, está-se realmente especificando a forma da partícula e, sem essa informação extra, a informação de tamanho não tem sentido.

Para esses três exemplos, uma esfera, cubo ou haste fina, o tamanho da partícula pode ser especificado por um único número. Mas mesmo que a haste tivesse uma seção transversal circular, seria necessário medir também o diâmetro dessa seção transversal, portanto, dois parâmetros de tamanho seriam realmente necessários para a partícula fina da haste. E as partículas em forma de elipsóides ou caixas retangulares? Para cada um deles, três números são necessários para especificar o tamanho e, ainda assim, a forma deve ser fornecida como uma caixa elipsóide ou retangular para que os três parâmetros de tamanho tenham significado. Para uma partícula de formato aleatório, um número infinito de parâmetros de tamanho (por exemplo, o comprimento das cordas na partícula) seria necessário para caracterizar completamente o "tamanho" da partícula e, no entanto, isso não teria sentido sem uma "caracterização da forma", sabendo em quais ângulos em relação ao centro de massa da partícula essas cordas foram desenhadas.

Existem muitas técnicas usadas para medir a distribuição de tamanho das partículas em um pó, empregando diferentes princípios físicos ^1,2. O que geralmente não é reconhecido, no entanto, é que, para extrair o tamanho da partícula, informações sobre a forma da partícula, seja assumida ou medida, devem ser usadas. As técnicas atuais podem ser classificadas como: (I) medições de tamanho de partícula tridimensional (3D) assumindo forma 3D, e (II) medições de tamanho e forma, mas apenas de projeções bidimensionais (2D), usando técnicas de análise de imagem 2D. Para partículas esféricas, todas as projeções 2D são círculos, com o mesmo diâmetro das partículas originais, e todas essas técnicas de medição, tanto Classe I quanto Classe II, dentro da incerteza de medição, fornecem os mesmos resultados para esferas perfeitas. Para partículas não esféricas, as projeções 2D estão muito menos relacionadas às partículas originais. Se uma partícula tiver porosidade interna que não quebre a superfície da partícula, esses poros não serão medidos por nenhuma dessas técnicas de medição 3D ou 2D. A classe I inclui difração de laser, volume de detecção elétrica (ESV)³⁸, análise de peneira e sedimentação; e a Classe II abrange microscopia eletrônica de transmissão e varredura, microscopia de força atômica e análise de imagem dinâmica e estática com técnicas ópticas. Nenhuma das classes mede com precisão o tamanho e a forma de partículas não esféricas em 3D.

Desde cerca de 2002³⁹, um novo método de análise de partículas foi desenvolvido 40,41,42,43,44,45 que cria imagens de uma partícula 3D em 3D e, em seguida, usa várias formas de análise matemática para representar e classificar cada partícula. Uma imagem 3D é salva para cada partícula individual, que pode ser comparada com as informações geométricas e matemáticas que também são salvas para cada partícula. Essas informações matemáticas podem ser usadas para gerar novamente a partícula conforme desejado em qualquer tipo de modelo 3D 46,47,48,49, em qualquer local e orientação, ou para gerar partículas virtuais que são forçadas a ter as mesmas estatísticas ^50,51. Este método de análise de partículas é baseado em varreduras XCT de partículas dispersas em epóxi ou algum outro meio. As varreduras XCT são operadas por software especializado que emprega o algoritmo de queima 52,53,54,55,56 para identificar partículas e, em seguida, ajuste de série harmônica esférica ou contagem de voxels para gerar e armazenar a forma e o tamanho das partículas, imagens 3D das partículas e, em uma segunda etapa, informações geométricas para cada partícula. Cada partícula analisada tem um rótulo alfanumérico exclusivo, que é usado para rastrear cada partícula, as informações sobre cada partícula e vincular cada partícula à sua imagem 3D. Durante esse processo de análise, os poros que estão dentro de uma partícula são analisados e a porosidade total nessa partícula específica é armazenada, pois a reconstrução XCT fornece uma visão 3D completa de uma amostra.

Três (de muitos) parâmetros geométricos de tamanho/forma foram considerados particularmente úteis na análise e classificação de partículas em 3D: o comprimento, L, a largura, W e a espessura, T. L é definido como a maior distância de ponto a ponto de superfície através de uma partícula, W é definido de forma semelhante a L com a restrição adicional de que o vetor unitário ao longo de W deve ser perpendicular ao vetor unitário ao longo de L, e T também é definido de forma semelhante a L com a restrição adicional de que o vetor unitário ao longo de T deve ser perpendicular ao vetor unitário ao longo de L e ao vetor unitário ao longo de W¹². Esses três parâmetros definem a caixa retangular ou delimitadora mínima que contém apenas a partícula, e as proporções desses três parâmetros fornecem informações valiosas, mas aproximadas, sobre a forma de cada partícula. As distribuições podem ser feitas de qualquer um deles. É possível que W se correlacione bem com os "tamanhos" medidos com a análise de peneira⁵⁷, enquanto os "tamanhos" medidos com difração de laser se correlacionam com uma mistura de L, W e T³¹.

Finalmente, as imagens 3D de uma amostra de teste de 100-200 das partículas são verificadas visualmente para determinar onde estão os cortes em L / T que permitem ao método distinguir entre partículas únicas, quase esféricas (SnS) e partículas não esféricas (NS), que podem ser várias partículas soldadas juntas, ou o que são claramente partículas únicas, mas com uma forma estranha.

Protocolo

NOTA: O protocolo a seguir é escrito para partículas de pó metálico com tamanho, de acordo com uma aproximação de diâmetro esférico equivalente a volume (VESD, diâmetro da esfera com o mesmo volume que a partícula), entre 10 μm e 100 μm. Suponha que o metal tenha uma densidade em unidades de g/cm³. Luvas devem ser usadas durante as etapas de preparação da amostra, juntamente com proteção para os olhos. É importante ler todas as etapas do Protocolo 1, pois alguns equipamentos precisam estar prontos antes de iniciar o Protocolo.

1. Preparação da mistura epóxi-pó

1. Prepare aproximadamente 25 g de epóxi de cura rápida (5 min) em um pequeno prato descartável. Barcos de folha de alumínio funcionam bem para esse fim. Um bom epóxi para usar vem em plástico bolha, com a resina separada do endurecedor, cuja densidade de cura é ρ_e g/cm³.
2. Use M gramas do pó, de uma amostra maior de pó bem agitada, onde M é projetado para dar uma fração de volume de cerca de 10%, uma vez que os M gramas são misturados ao epóxi. Isso foi projetado para evitar a situação em que as partículas estão tão próximas umas das outras que a varredura XCT as identifica erroneamente como multipartículas reais que estão firmemente presas. A equação que define M é:
   
   
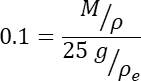
3. Misture o pó metálico vigorosamente no epóxi, manualmente, usando uma haste de agitação descartável - um simples bastão de madeira funciona bem - por cerca de 30 s, tempo suficiente para dispersar o pó adequadamente. Esse processo, bem feito, torna a análise de imagens das partículas individuais muito mais direta.
   1. Após a mistura, raspe a mistura viscoplástica em uma moita compacta com a maior extensão vertical possível, para estar pronta para a próxima etapa. É importante ter as etapas a seguir preparadas com antecedência, pois não haverá muito tempo antes que o epóxi endureça.
4. Use uma pequena bomba de vácuo conectada a uma mangueira de plástico de 0.5 m de comprimento, com um bico inserido na extremidade aberta da mangueira que se encaixará perfeitamente em um canudo de polímero de cerca de 3 mm de diâmetro interno.
   NOTA: Canudos de coquetel, facilmente disponíveis em supermercados, funcionam bem para o canudo de polímero de 3 mm de diâmetro e têm um comprimento de cerca de 150 mm. Para um bico, a extremidade de corte de uma pipeta de plástico descartável de 1 mL a 2 mL geralmente é eficaz. Onde o bico se encaixa na mangueira de plástico, um pouco de fita isolante deve ser esticada firmemente ao redor da junta para garantir uma vedação hermética. Os 25 g de epóxi mais pó devem ser mais do que suficientes para encher dois canudos completos.
5. Insira o bico no canudo, segurando o bico e a extremidade do canudo firmemente presos. Insira a extremidade livre do canudo na moita compacta de pó epóxi e ligue a bomba de vácuo.
   NOTA: Mantenha a extremidade livre do canudo imersa na mistura de epóxi em pó para evitar a introdução de bolhas de ar no canudo - algumas bolhas de ar estarão sempre presentes, mas este procedimento minimiza sua presença. Os canudos devem ser enchidos até 10 mm do topo - a linha de enchimento pode ser vista através do canudo translúcido. Quando o primeiro canudo estiver cheio, desligue a bomba de vácuo e remova o canudo do bico.
6. Limpe a mistura de epóxi da extremidade de enchimento do canudo e empurre ambas as extremidades do canudo em um pequeno pedaço de argila para preencher as duas extremidades do canudo para que nenhuma mistura de epóxi e pó vaze durante a cura. Coloque o^2º canudo no bico e repita, primeiro usando a vareta misturadora para reunir a mistura de epóxi e pó, se necessário.
7. Depois que o epóxi nos dois canudos estiver curado, corte as pontas do canudo, onde estava o selador de argila, com uma navalha e corte cada canudo ao meio para dar quatro amostras. Use um canudo como amostra # 1 para o XCT, montado verticalmente de modo que os raios X penetrem na seção transversal circular do canudo.

2. O instrumento XCT

NOTA: Essas etapas pressupõem familiaridade com o instrumento XCT escolhido pelo usuário.

1. Use uma alta tensão, geralmente 100 kV ou superior, pois há um bom contraste entre a matriz epóxi e as partículas de pó metálico e não há necessidade de resolver nada dentro da matriz epóxi, o que normalmente exigiria baixas tensões em torno de 40 kV. Use uma varredura completa de 360^o , com um tamanho de voxel de cerca de 1 μm. A razão entre o menor tamanho de partícula considerado e o tamanho do voxel usado deve ser de no mínimo 8-10³⁹.
2. Pegue FOVs suficientes, em mais de uma amostra, para fornecer partículas suficientes para análise. Se as diretrizes de preparação de amostras forem seguidas, 2 a 8 FOVs serão suficientes. Normalmente, um mínimo de 1000 partículas é suficiente para uma análise válida de forma/tamanho, mas mais partículas resultam em curvas de distribuição mais suaves e melhores estatísticas. As fatias reconstruídas são numeradas de 0 a nz-1, de baixo para cima do FOV, onde nz é o número total de fatias reconstruídas.
   1. Salve as fatias de seção transversal vertical para cada FOV individualmente, no formato de 8 bits (por exemplo, tiff) observando o tamanho do pixel de cada conjunto de imagens (nx x ny), o número dessas fatias (nz) e o tamanho do voxel em micrômetros (v). O formato de 8 bits é adequado para esses tipos de imagens simples em escala de cinza de matriz de partículas de metal-epóxi, que são fáceis de segmentar.

3. Montagem das fatias pertencentes a cada FOV em uma microestrutura 3D ASCII

NOTA: O programa C usado no NIST é chamado tiff2array.c e é usado com mais frequência com arquivos tiff, mas pode lidar com outros formatos de 8 bits. Ele pode ser compilado como está, com o executável chamado tiff2array. Este programa lê cada imagem, de baixo para cima, converte-as para o formato ascii (escala de cinza de 0 a 255) e as empilha no final de um arquivo mestre.

1. Se as imagens reconstruídas estiverem no formato tiff, por exemplo, e forem numeradas consecutivamente de baixo para cima, use a seguinte sintaxe em um comando de terminal de linha: tiff2array *.tiff. Este arquivo mestre, ou arquivo de microestrutura, é uma representação 3D do FOV. Se a variável a(i,j,k) é a escala de cinza na posição (i,j,k), onde k é o número da fatia, k = 1 a nz, e (i,j) é o pixel na k-ésima fatia, onde i é medido da esquerda para a direita e j é medido de cima para baixo.
   NOTA: Todo o software necessário no Protocolo está disponível na seção Informações Suplementares deste documento por meio de um link para um banco de dados do NIST localizado em https://doi.org/10.18434/M32265.
2. Para FOVs P, faça um pequeno arquivo chamado particle-class-sysconfig.dat, com linhas P, onde cada linha é lida, para o FOV pth (p = 1, P):
   Nome do arquivo nx ny nz v b c
   onde Nome do arquivo = uma identificação de 12 caracteres para um FOV específico, b = 1 para uma varredura interna e 0 para uma varredura externa e c = o número de fases presentes nas imagens. Quando uma varredura interna é feita, geralmente há três (c = 3) fases presentes: 1) o epóxi, 2) as regiões pretas indicando a parte externa da varredura circular e bolhas de ar e 3) as partículas mais brilhantes. Às vezes, quatro fases podem parecer aos olhos uma suposição mais razoável e, portanto, c = 4. Valores para c de 3 ou 4 são as duas únicas opções. O valor de c informa ao software de análise de partículas qual algoritmo de segmentação automática Otsu, originalmente escrito para imagens bifásicas, mas facilmente estendido a qualquer número de fases, usar para segmentar automaticamente as imagens em um determinado FOV^26,58. Os arquivos de microestrutura que serão usados no próximo programa de software devem ter nomes de 12 caracteres que sejam exatamente iguais ao nome do arquivo listado no arquivo FOV-name-sysconfig.dat, seguido pela extensão .mic.
3. Execute o software de análise de partículas pp-Otsu.f, usando como entrada o arquivo particle-class-sysconfig.dat e os vários arquivos de microestrutura, Filename.mic. Faça apenas duas alterações neste programa para um novo sistema, todas marcadas por um comentário "USER" na fonte Fortran: os nomes dos arquivos de saída gerais (altere o nome geral da classe de partículas) e o número de FOVs listados em particle-class-sysconfig.dat. O programa pp-Otsu.f está em Fortran, é escalar e geralmente é compilado em Fortran 77, embora Fortran 90 deva funcionar bem. Ele, e todos os outros programas Fortran descritos abaixo, devem ser compilados em precisão dupla (-r8) para obter resultados precisos.
   1. Além disso, como o pp-Otsu.f trabalha com arquivos grandes, sempre adicione os parâmetros (ou equivalentes) -mcmodel=medium e -Mlarge_arrays à compilação. Um arquivo auxiliar, gauss120.dat, contém os pesos e pontos para uma quadratura gaussiana de 120 pontos usada extensivamente em pp-Otsu.f, e deve estar no mesmo diretório que pp-Otsu.f. Todos os programas descritos abaixo são escritos em Fortran 77, exceto os programas MPI, que são escritos em Fortran 90.
4. Visualize os arquivos de partículas que são as principais saídas do pp-Otsu.f, que podem levar várias horas para serem executados em um único processador se houver milhares de partículas a serem analisadas. Estes incluem arquivos com nomes como Particle-class-name-anm-particle-number.dat, que contêm a lista dos coeficientes complexos (n = 0,26), com unidades de micrômetros ou em quaisquer unidades v seja, para as partículas consideradas adequadamente em forma de estrela³⁹ e, portanto, capazes de serem expandidas em funções harmônicas esféricas (chamadas partículas SH). Os arquivos de partículas também incluem arquivos como Particle-class-name-part-particle- number.dat, que contêm o número de voxels na partícula e todas as posições de voxels (em coordenadas de voxel) para partículas que não podem ser descritas por expansões harmônicas esféricas (chamadas de partículas não-SH).
5. Visualize os dois arquivos, um para as partículas SH e outro para as partículas não SH, que fornecem as porosidades de todas as partículas encontradas, mesmo que a porosidade seja zero, com a frase porosidade nos nomes dos arquivos. Um programa adicional, porosity-analyze.f, deve receber o número de linhas em cada arquivo de porosidade e seus nomes de arquivo - os nomes de arquivo a serem alterados estão no início do código-fonte. A saída deste programa são os dois arquivos Particle-class-intern-poros-analysis.txt e Particle-class-intern-poros-list.txt. O arquivo de análise gera as informações mostradas na Tabela 2 na seção Resultados Representativos, e o arquivo de lista fornece as informações necessárias para gerar a Figura 5 na seção Resultados Representativos.
6. Exiba os três arquivos de imagem tiff mostrando uma fatia do primeiro FOV considerado. A primeira fatia (OriA-0500.tiff) mostra a fatia k = 500 do primeiro FOV no arquivo particle-class-sysconfig.dat , sem nenhum processamento de imagem, e o segundo arquivo de imagem mostra a mesma imagem, mas agora segmentada e com limite (PixA-0500.tiff). Se qualquer divisão limitada da bacia hidrográfica for aplicada, o terceiro arquivo de imagem mostrará os resultados desse algoritmo (LWSA-0500.tiff). Normalmente, essa etapa de processamento de imagem não é aplicada, portanto, o terceiro arquivo de imagem é igual ao segundo. Essas imagens são geradas como uma etapa de verificação de erros na montagem original da microestrutura 3D e na segmentação automática da imagem Otsu. Um arquivo de saída geral (particle-class-name-particles-data.dat) é criado listando todas as informações auxiliares para o processamento de cada partícula. Este arquivo é usado apenas como referência, mas os volumes de voxel e os rótulos numéricos de todas as partículas processadas são escritos no final deste arquivo.
7. Para cada partícula processada, seja SH ou não, visualize o arquivo de imagem VRML 3D, com a convenção de nomenclatura particle-name-particle-number.wrl. Para partículas SH, este arquivo de imagem VRML contém duas imagens lado a lado, uma imagem voxel da partícula original e uma imagem renderizada mais suave usando os coeficientes SH. Para as partículas não SH, apenas a imagem de voxel é armazenada.

4. Gere informações geométricas para todas as partículas SH e não SH

1. Antes do processamento posterior, faça uma lista dos nomes de arquivo Particle-class-name-anm-particle-number.dat , chamada anm.lis, e uma lista das partículas de Particle-class-name-part-particle-number.dat nonSH, chamada nonSH.lis. Execute o pequeno número do programa.f, tendo sido editado primeiro para ter o número correto de arquivos em anm.lis. Isso altera o arquivo anm.lis para ter o número da partícula em cada linha do arquivo de lista, bem como o nome do arquivo, substituindo o arquivo anterior.
2. Use o programa part-lwt-listnum-unitvector.f para gerar e avaliar informações geométricas para as partículas SH. Este é um programa paralelo MPI, pois pode haver milhares de partículas SH a serem avaliadas, e fazer apenas uma partícula de cada vez pode levar dias. As únicas alterações neste programa que precisam ser feitas ao processar uma nova classe de partículas são o número Ntot de arquivos de number.dat Particle-class-name-anm-particle e as informações de nomenclatura da classe de partículas para o arquivo de saída (Particle-class-name-un-geom-len.dat). O programa tem comentários (USER) nos poucos locais que precisam ser alterados para um novo tipo de partícula. O arquivo de saída Particle-type-info-un-SH-geom-len.dat une partículas de cada FOV e cada linha tem a seguinte estrutura.
   
   Nome do arquivo, x1, x2, y1, y2, z1, z2, volume, área de superfície, razão SA, curv, razão, nnn, gauss, espaço reservado, L, W, T, L/T, W/T, T/T, componentes tensores de momento de inércia, vetor unitário L,, ângulos phi, vetor unitário W,, ângulos phi, vetor unitário T,, ângulos phi
   
   x1 é o valor mínimo de x na superfície da partícula e x2 é o máximo e da mesma forma para y e z. Eles definem uma "caixa de extensão" que apenas envolve a partícula em sua orientação medida⁴². A caixa de extensão é usada em outras aplicações 46,47,48,49. A razão SA é a área de superfície da partícula dividida pela área de superfície da esfera equivalente a volume. Curv é a curvatura média integrada invertida e normalizada para que seja igual ao diâmetro quando a partícula é uma esfera perfeita. Razão é o traço do tensor do momento de inércia dividido pelo traço do tensor do momento de inércia para a esfera equivalente ao volume. nnn é o número máximo de coeficientes SH (n=0, nnn) que devem ser usados ao trabalhar com a partícula dada. Gauss é a curvatura gaussiana integrada, dividida por 4π, que deve ser igual a 1 para um objeto fechado. O ponto em que Gauss varia da unidade em mais de 5% define o número máximo de coeficientes SH (n = nnn) que devem ser usados ao recriar a partícula. L, W, T são o comprimento, largura e espessura da partícula e foram definidos na seção Introdução. Os componentes independentes do tensor do momento de inércia são listados como I₁₁, I₂₂, I₃₃, I₁₃, I₂₃, I₁₂. Finalmente, o vetor unitário para L é listado, na ordem das coordenadas x, y e z, seguido pelos ângulos polares esféricos θ (ângulo do eixo z positivo) e Φ (ângulo de rotação em torno do eixo z, definido como zero no eixo x positivo e é positivo no sentido anti-horário). Os parâmetros para W e T seguem, listados da mesma maneira.
3. Use o programa nonSH-lwt-un-scalar.f para calcular os parâmetros L, W e T para as partículas nonSH, operando na lista de nomes de arquivos nonSH.lis , e também registrar os vetores unitários associados. As únicas alterações que precisam ser feitas neste arquivo para uma nova classe de partícula são o número de nomes de arquivo em nonSH.lis e os nomes de arquivo de saída. A saída principal deste programa, chamada Particle-name-info-nonSH-len.dat, tem cada linha no formato:
   
   Volume de nome de arquivo L W T a1 a2 a3 (vetores e ângulos de unidade LWT)
   
   onde a1, a2 e a3 são os ângulos finais (em graus - 90^o) entre os vetores unitários para L e W, W e T e L e T, que são incluídos como uma verificação de erro para o algoritmo de computação L, W e T , uma vez que esses ângulos devem ser todos zero para um cálculo perfeito. Os vetores e ângulos unitários L, W e T estão no mesmo formato das partículas SH.

5. Selecione um subconjunto de partículas SH e não SH para determinar visualmente os cortes de SnS e NS L/T

NOTA: As partículas SH, em geral, compreendem partículas esféricas únicas, partículas únicas não esféricas (elipsoidais ou quebradas de alguma forma ou então de forma aleatória), partículas duplas e partículas múltiplas (mais de duas partículas unidas). As partículas que compõem as múltiplas partículas podem ser esféricas ou não esféricas. As partículas não-SH geralmente têm algumas partículas esféricas únicas, embora principalmente com poros grandes que romperam a superfície, e o restante são principalmente partículas duplas e múltiplas²⁶. Isso é determinado pela visualização de uma amostra aleatória de ambos os tipos de partículas com valores de L/T de 1 a 2. Essa inspeção visual torna-se uma etapa importante para permitir a classificação SnS e NS.

1. Execute o programa (VRML-select-multi-single.f) que lê os arquivos Particle-type-info-SH-geom-len.dat e Particle-name-info-nonSH-len.dat e seleciona 10 partículas em cada intervalo L/T de tamanho 0,1, ou seja, (1,1.1), (1.1,1.2), etc. Isso armazena até 100 partículas SH com L/T variando de 1 a 2 e até 100 partículas não SH com a mesma faixa L/T . Dois arquivos de texto são gerados (*SH-VRML-list.txt e *nonSH-VRML-list.txt) listando os valores L/T e os nomes raiz dos arquivos de imagem VRML encontrados. Estes devem ser colocados em uma planilha de algum tipo e ordenados de acordo com o valor L / T.
2. Examine as imagens 3D de cada uma dessas partículas visualmente para determinar a gama geral de morfologias, começando pelas partículas de menor valor L/T . As partículas são avaliadas em termos de se são partículas quebradas, partículas duplas, partículas múltiplas, irregulares (por exemplo, não muito esféricas) e se possuem satélites, que são partículas muito menores, ligadas à partícula principal. Um satélite é considerado como fazendo da partícula principal uma partícula dupla ou múltipla se o (s) satélite (s) tiverem mais de 1/5 do diâmetro da partícula principal. O valor aproximado de L/T é encontrado que separa partículas únicas, quase esféricas (SnS) de partículas múltiplas e muito não esféricas (NS), que podem ser um pouco diferentes para as partículas SH e não SH. A primeira partícula dupla ou múltipla encontrada determina o valor de corte para partículas SH e não SH.
   NOTA: O Material Suplementar, localizado na https://doi.org/10.18434/M32265, inclui um arquivo de planilha para as partículas examinadas, para ver como esses valores de corte foram determinados. Há alguma incerteza e um grau de subjetividade nesses números, que podem ser avaliados escolhendo um conjunto diferente de 100 partículas SH e 100 não SH, com L/T entre 1 e 2, para avaliar os valores de corte. Trabalhos recentes descobriram que essa incerteza era pequena²⁶ e não afetou significativamente os resultados.

6. Gere dados de projeção 2D a partir das partículas 3D

NOTA: Os únicos analisadores de partículas comerciais atuais que medem a forma das partículas o fazem com projeções 2D. Os dados do XCT podem ser analisados para fornecer projeções 2D arbitrárias, gerando dados que podem ser quantitativamente combinados com os resultados desses instrumentos comerciais. As projeções 2D são feitas a partir das partículas SH e não-SH e são combinadas, sem nenhuma tentativa de classificação nas categorias SnS e NS 2D, uma vez que não se sabe atualmente como definir essas classes para projeções 2D.

1. Use os dois programas, (proj-mpi-SH-LWT.f) para as partículas SH e (proj2D-nonSH-LWT.f) para as partículas não-SH, para gerar três projeções ortogonais para cada partícula, ao longo da direção dos três vetores unitários LWT e, em seguida, gerar coeficientes de Fourier para o contorno da projeção. Esses coeficientes são usados para calcular várias quantidades 2D, como área, perímetro e vários comprimentos e proporções.
2. Uma série de pontos (x,y) são gerados e armazenados para cada projeção, rotulados com o nome do arquivo de partículas e 1 para a projeção ao longo do vetor unitário L , 2 para a projeção ao longo do vetor unitário W e 3 para a projeção ao longo do vetor unitário T . Insira-os em qualquer programa gráfico que aceite essa entrada, certificando-se de que os limites dos eixos de x e y sejam os mesmos e que cada eixo tenha o mesmo comprimento físico.
3. Armazene os coeficientes de Fourier com uma convenção de nomenclatura de arquivo semelhante, mas esse recurso está desativado, por padrão, usando comentários. As únicas alterações feitas em qualquer um desses programas (posição do programa marcada com "USER") são o número total de partículas a serem consideradas (Ntot) e os nomes dos arquivos de entrada e saída, que devem refletir a classe de partículas que está sendo analisada.
4. A saída principal da execução (proj-mpi-SH-LWT.f) e (proj2D-nonSH-LWT.f) são arquivos de dados de projeção, com Particle-class-info-SH-proj.dat de convenção de nomenclatura e Particle-class-info-nonSH-proj.dat. Uma variedade de quantidades 2D pode ser calculada, incluindo algumas usadas por dois instrumentos comerciais diferentes (Horiba Camsizer⁵⁹ e Malvern MORPHOLOGI G3⁶⁰). Em ambos os casos, os programas calculam uma versão 2D de L e W, chamada L2D e W2D.
5. A estrutura do arquivo de saída lista, para cada partícula, área, perímetro, Xcmax, Xcmin, Fermax, Fermin, W2D, L2D, WM e LM, onde Fermax e Fermin são os diâmetros máximo e mínimo de Feret e Xcmax e Xcmin são definidos a partir dos diâmetros de corda tomados em várias direções⁵⁹. Pode-se mostrar teoricamente que L2D é a mesma quantidade que Xcmax, o que também pode ser visto nos arquivos de dados. Os parâmetros LM e WM são versões de L2D e W2D definidas de forma ligeiramente diferente no manual⁶⁰ do Malvern MORPHOLOGI G3. O formato do arquivo é: Nome/número da partícula, área, perímetro, Fermin, Fermax, Xcmin, Xcmax, W2D, L2D, theta, WM, LM, slo e nnnF, onde nnnF é o número de coeficientes de Fourier usados para representar a projeção de partículas. A quantidade é o ângulo, em graus, que o eixo que define WM e LM faz com o eixo x ⁶⁰. A quantidade slo é apenas a razão entre o seno de e o cosseno de . Nenhuma das quantidades é usada na análise de partículas descrita aqui e é incluída apenas como uma verificação no cálculo. Os dados para cada partícula vêm em conjuntos de três, uma linha para cada uma das três projeções, (1,2,3) = (L,W,T).

7. Processamento de dados geométricos de partículas 3D e 2D para produzir vários gráficos

1. Use qualquer software que o usuário goste para processar os dados de tamanho e forma das partículas. Qualquer que seja o software usado, um determinado procedimento deve ser seguido.
2. Para os dados 3D, combine os dados SH e não SH em listas SnS e NS, usando os valores de corte L/T determinados anteriormente para cada classe de partículas. Distribuições e médias devem ser calculadas para as partículas SnS e NS separadamente, e também para os dados combinados de SnS e NS, para todos os parâmetros geométricos de interesse, como L, W, T, L/T, W/T, L/W, diâmetro esférico equivalente ao volume e outros.
3. Para os dados de projeção 2D, combine os dados SH e não SH. Existem três projeções 2D para cada partícula 3D, tomadas ao longo dos vetores unitários para L, W e T. A combinação de todas essas três projeções deve fornecer resultados semelhantes a uma técnica experimental que gira aleatoriamente as partículas antes de fazer uma projeção. Usando apenas os dados vetoriais da unidade L , por exemplo, simula uma técnica experimental na qual as partículas são aproximadamente alinhadas ao longo de sua direção mais longa, perpendicular à direção de queda e paralela à direção da luz estroboscópica/projeção em um dispositivo típico.

Resultados

A ASTM iniciou um programa de testes de proficiência (AMPM, Additive Manufacturing Powder Metallurgy) para pó metálico usado para fusão em leito de pó a laser, onde os participantes realizam uma bateria de testes padrão de pó metálico e a ASTM compila a distribuição estatística desses resultados em um relatório para os participantes⁶¹. Amostras de pó metálico são distribuídas duas vezes por ano a todos os participantes. O pessoal do NIST atua como ...

Discussão

O método baseado em XCT para caracterizar o tamanho e a forma 3D de partículas metálicas tem mais aplicações possíveis, mas também algumas limitações. As limitações serão abordadas primeiro.

Um epóxi de cura rápida é usado para que a viscosidade do epóxi seja alta o suficiente para evitar que o pó se assente sob a gravidade enquanto o epóxi está curando, ou pelo menos reduzindo o tempo durante o qual a sedimentação pode acontecer e a dispe...

Materiais

Name	Company	Catalog Number	Comments
Epoxy	Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/	Hardman Part # 4001	case of 100