Dreidimensionale Partikelformanalyse mittels Röntgen-Computertomographie: Experimentelles Vorgehen und Analysealgorithmen für Metallpulver

Zusammenfassung

Größe und Form von Pulverpartikeln sind keine unabhängigen Größen. Übliche Messtechniken messen diese miteinander verflochtenen Parameter nicht in drei Dimensionen (3D). Es wird eine 3D-Mess-/Analysetechnik beschrieben, die auf der Röntgen-Computertomographie basiert und Größe und Form messen und Pulverpartikel nach beiden Parametern klassifizieren kann.

Zusammenfassung

Die Messung der Größenverteilung der Partikel in einem Pulver ist eine gängige Tätigkeit in Wissenschaft und Industrie. Die Messung der Formverteilung der Partikel ist deutlich seltener. Die Form und Größe der Pulverpartikel sind jedoch keine unabhängigen Größen. Alle bekannten Größen-/Formmesstechniken gehen entweder von einer kugelförmigen Form aus oder messen die Form nur in zwei Dimensionen. Die hier vorgestellte auf der Röntgen-Computertomographie (XCT) basierende Methode misst sowohl Größe als auch Form in 3D, ohne Annahmen zu treffen. Ausgehend von einem 3D-Bild von Partikeln kann das Verfahren Partikel mathematisch nach ihrer Form klassifizieren, zum Beispiel Partikel, die aus mehreren kleineren Partikeln bestehen, die miteinander verschweißt sind, im Gegensatz zu einzelnen Partikeln, die nicht unbedingt kugelförmig sind. Natürlich ist es prinzipiell nicht möglich, eine einzelne Zahl als "Größe" oder "Form" eines zufälligen nicht-sphärischen Partikels zu definieren, was zu vielen Möglichkeiten führt, die Partikelgröße und -form über verschiedene miteinander verknüpfte Parameter zu schätzen, die alle aus dieser vollständigen 3D-Charakterisierung in Form von Mittelwerten und Verteilungen generiert werden können. Es werden die notwendigen experimentellen Verfahren, die mathematische Analyse und die Computeranalyse beschrieben und ein Beispiel für ein Metallpulver gegeben. Die Technik ist auf Partikel beschränkt, die mit XCT mit einem Minimum von etwa 1000 Voxeln pro Partikelvolumen abgebildet werden können.

Einleitung

Die Messung der Größenverteilung der Partikel in einem Pulver ist eine gängige Tätigkeit in Wissenschaft und Industrie ^1,2.  Die Messung der Formverteilung der Partikel ist weniger üblich, aber sowohl Größe als auch Form bestimmen zusammen mit dem Material, aus dem die Partikel hergestellt sind, ihre Eigenschaften, entweder allein oder in einer Art Matrixmaterial 3,4,5,6,7. Zu den Materialien, deren Partikelgröße und -form von Interesse sind, gehören Portlandzement, Sand und Kies 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22^{, 23}, Metallpulver für die Pulvermetallurgie und additive Fertigung 24,25,26, Mondboden 27,28,29, geschredderte Autoreifen³⁰, zerkleinertes Altglas ³¹, Stammzellen³² sowie Kohlenstoffnanoröhren und Graphen 33,34,35,36,37. Die Form und Größe der Pulverpartikel sind jedoch keine unabhängigen Größen²⁶. Nehmen wir zum Beispiel an, man hat ein geometrisch regelmäßiges Teilchen, dessen "Größe" d sein soll. Ohne zu sagen, ob es sich bei diesem Teilchen um eine Kugel, einen Würfel oder einen dünnen Stab der Länge d handelt, weiß man nicht wirklich, wie sich die Größe auf dieses Teilchen bezieht. Wenn man sagt, dass das Partikel eine Kugel, ein Würfel oder ein Stab ist, gibt man in Wirklichkeit die Form des Partikels an, und ohne diese zusätzliche Information ist die Größeninformation bedeutungslos.

Für diese drei Beispiele, eine Kugel, einen Würfel oder einen dünnen Stab, kann die Partikelgröße durch eine einzelne Zahl angegeben werden. Aber selbst wenn der Stab einen kreisförmigen Querschnitt hätte, müsste man auch den Durchmesser dieses Querschnitts messen, so dass für das dünne Stabkorn wirklich zwei Größenparameter benötigt würden. Was ist mit Partikeln in Form von Ellipsoiden oder rechteckigen Kästen? Für jeden dieser Werte werden drei Zahlen benötigt, um die Größe anzugeben, und dennoch muss die Form entweder als Ellipsoid oder als rechteckiges Feld angegeben werden, damit die drei Größenparameter eine Bedeutung haben. Für ein zufällig geformtes Teilchen wäre eine unendliche Anzahl von Größenparametern (z. B. die Länge der Sehnen über das Teilchen) erforderlich, um die "Größe" des Teilchens vollständig zu charakterisieren, und doch wären diese ohne eine "Formcharakterisierung" bedeutungslos, da man weiß, in welchen Winkeln relativ zum Schwerpunkt des Teilchens diese Sehnen gezeichnet wurden.

Es gibt viele Techniken, um die Größenverteilung der Partikel in einem Pulver zu messen, wobei unterschiedliche physikalische Prinzipien angewendet^{werden 1,2}. Was jedoch in der Regel nicht erkannt wird, ist, dass zur Extraktion der Partikelgröße Informationen über die Partikelform, ob angenommen oder gemessen, verwendet werden müssen. Derzeitige Techniken können klassifiziert werden als: (I) Messungen der dreidimensionalen (3D) Partikelgröße unter Annahme einer 3D-Form und (II) Messungen von Größe und Form, jedoch nur von zweidimensionalen (2D) Projektionen unter Verwendung von 2D-Bildanalysetechniken. Bei sphärischen Partikeln handelt es sich bei allen 2D-Projektionen um Kreise mit dem gleichen Durchmesser wie die ursprünglichen Partikel, und alle diese Messtechniken, sowohl die Klasse I als auch die Klasse II, liefern innerhalb der Messunsicherheit die gleichen Ergebnisse für perfekte Kugeln. Bei nicht-sphärischen Partikeln sind die 2D-Projektionen viel weniger eng mit den ursprünglichen Partikeln verwandt. Wenn ein Partikel eine innere Porosität aufweist, die die Partikeloberfläche nicht durchbricht, werden diese Poren mit keiner dieser 3D- oder 2D-Messtechniken gemessen. Klasse I umfasst Laserbeugung, elektrisches Messvolumen (ESV)³⁸, Siebanalyse und Sedimentation; und Klasse II umfasst die Transmissions- und Rasterelektronenmikroskopie, die Rasterkraftmikroskopie sowie die dynamische und statische Bildanalyse mit optischen Techniken. Keine der beiden Klassen misst die Größe und Form von nicht-sphärischen Partikeln in 3D genau.

Seit etwa 2002³⁹ wurde eine neue Methode der Partikelanalyse entwickelt 40,41,42,43,44,45, die ein 3D-Teilchen in 3D abbildet und dann verschiedene Formen der mathematischen Analyse verwendet, um jedes Teilchen darzustellen und zu klassifizieren. Für jedes einzelne Partikel wird ein 3D-Bild gespeichert, das mit den geometrischen und mathematischen Informationen verglichen werden kann, die ebenfalls für jedes Partikel gespeichert sind. Diese mathematische Information kann verwendet werden, um das Teilchen in jeder Art von 3D-Modell 46,47,48,49 an jedem Ort und in jeder Ausrichtung neu zu erzeugen, oder um virtuelle Teilchen zu erzeugen, die gezwungen sind, die gleiche Statistik ^50,51 zu haben. Diese Partikelanalysemethode basiert auf XCT-Scans von Partikeln, die in Epoxidharz oder einem anderen derartigen Medium dispergiert sind. Die XCT-Scans werden von einer speziellen Software bearbeitet, die den Brennalgorithmus 52,53,54,55,56 verwendet, um Partikel zu identifizieren, und dann entweder eine sphärische harmonische Reihenanpassung oder eine Voxelzählung, um Partikelform und -größe, 3D-Bilder der Partikel und in einem zweiten Schritt geometrische Informationen für jedes Partikel zu erzeugen und zu speichern. Jedes analysierte Partikel verfügt über eine eindeutige alphanumerische Beschriftung, die verwendet wird, um jedes Partikel zu verfolgen, die Informationen über jedes Partikel zu erhalten und jedes Partikel mit seinem 3D-Bild zu verknüpfen. Während dieses Analyseprozesses werden die Poren, die sich in einem Partikel befinden, analysiert und die Gesamtporosität in diesem bestimmten Partikel gespeichert, da die XCT-Rekonstruktion eine vollständige 3D-Ansicht einer Probe liefert.

Drei (von vielen) geometrischen Größen-/Formparametern haben sich bei der Analyse und Klassifizierung von Partikeln in 3D als besonders nützlich erwiesen: die Länge, L, die Breite, W und die Dicke, T. L ist definiert als der längste Punkt-zu-Fläche-Punkt-Abstand über ein Partikel, W ist ähnlich wie L definiert, mit der zusätzlichen Einschränkung, dass der Einheitsvektor entlang W senkrecht zum Einheitsvektor entlang L sein muss, und T ist auch ähnlich wie L definiert, mit der zusätzlichen Einschränkung, dass der Einheitsvektor entlang T senkrecht sowohl zum Einheitsvektor entlang L als auch zum Einheitsvektor entlang W¹² stehen muss. Diese drei Parameter definieren den minimalen rechteckigen oder Begrenzungsrahmen, der nur das Partikel enthält, und die Verhältnisse dieser drei Parameter liefern wertvolle, aber ungefähre Forminformationen über jedes Partikel. Von jedem dieser können Verteilungen vorgenommen werden. Es ist möglich, dass W gut mit den mit der Siebanalyse⁵⁷ gemessenen "Größen" korreliert, während die mit Laserbeugung gemessenen "Größen" mit einem Gemisch aus L, W und T³¹ korrelieren.

Schließlich werden die 3D-Bilder einer Testprobe von 100-200 der Partikel visuell überprüft, um zu bestimmen, wo die Grenzwerte in L/T liegen, die es der Methode ermöglichen, zwischen einzelnen, nahezu kugelförmigen (SnS) Partikeln und nicht-sphärischen (NS) Partikeln zu unterscheiden, bei denen es sich um mehrere miteinander verschweißte Partikel handeln kann, oder bei denen es sich eindeutig um einzelne Partikel handelt, die jedoch eine seltsame Form haben.

Protokoll

HINWEIS: Das folgende Protokoll wurde für Metallpulverpartikel mit einer Größe zwischen 10 μm und 100 μm geschrieben, die einem volumenäquivalenten Kugeldurchmesser (VESD, Durchmesser der Kugel mit dem gleichen Volumen wie das Partikel) entspricht. Nehmen wir an, dass das Metall eine Dichte in der Einheit g/cm³ hat. Während der Probenvorbereitung sollten Handschuhe und ein Augenschutz getragen werden. Es ist wichtig, alle Schritte in Protokoll 1 durchzulesen, da einige Geräte bereit sein müssen, bevor das Protokoll gestartet wird.

1. Vorbereitung der Epoxid-Pulver-Mischung

1. Bereiten Sie ca. 25 g eines schnell aushärtenden (5 min) Epoxidharzes in einer kleinen Einwegschale vor. Boote aus Aluminiumfolie eignen sich gut für diesen Zweck. Ein gutes Epoxidharz ist in einer Luftpolsterfolie erhältlich, bei der das Harz vom Härter getrennt ist, dessen ausgehärtete Dichte ρ_e g/cm³ beträgt.
2. Verwenden Sie M Gramm des Pulvers aus einer gut geschüttelten größeren Pulverprobe, wobei M so konzipiert ist, dass es einen Volumenanteil von etwa 10 % ergibt, sobald die M Gramm in das Epoxidharz gemischt werden. Dadurch soll vermieden werden, dass sich Partikel so nahe beieinander befinden, dass der XCT-Scan sie fälschlicherweise als echte Multipartikel identifiziert, die fest verbunden sind. Die Gleichung, die M definiert, lautet:
   
   
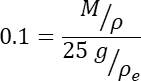
3. Mischen Sie das Metallpulver mit einem Einweg-Rührstab - ein einfacher Bastelstab aus Holz funktioniert gut - etwa 30 s lang kräftig in das Epoxidharz, lange genug, um das Pulver ausreichend zu verteilen. Dieser Prozess macht, wenn er gut gemacht wird, die Bildanalyse der einzelnen Partikel viel einfacher.
   1. Kratzen Sie die viskoplastische Mischung nach dem Mischen zu einem kompakten Klumpen mit möglichst viel vertikaler Ausdehnung, um für den nächsten Schritt bereit zu sein. Es ist wichtig, die folgenden Schritte im Voraus vorzubereiten, da nicht mehr viel Zeit verbleibt, bis das Epoxidharz aushärtet.
4. Verwenden Sie eine kleine Vakuumpumpe, die an einen 0,5 m langen Kunststoffschlauch angeschlossen ist, mit einer Düse am offenen Ende des Schlauchs, die genau in einen Polymerstrohhalm mit einem Innendurchmesser von etwa 3 mm passt.
   HINWEIS: Cocktail-Strohhalme, die im Lebensmittelgeschäft leicht erhältlich sind, eignen sich gut für den Polymerstrohhalm mit einem Durchmesser von 3 mm und haben eine Länge von ca. 150 mm. Bei einer Düse ist in der Regel das abgeschnittene Ende einer Einweg-Kunststoffpipette von 1 ml bis 2 ml wirksam. An der Stelle, an der die Düse in den Kunststoffschlauch passt, sollte etwas Isolierband fest um die Fuge gespannt werden, um eine luftdichte Abdichtung zu gewährleisten. Die 25 g Epoxy plus Pulver sollten mehr als genug sein, um zwei komplette Strohhalme zu füllen.
5. Führen Sie die Düse in den Strohhalm ein und halten Sie die Düse und das Strohhalmende fest zusammengedrückt. Führen Sie das freie Ende des Strohhalms in den kompakten Epoxidpulverklumpen ein und schalten Sie die Vakuumpumpe ein.
   HINWEIS: Halten Sie das freie Ende des Strohhalms in das Epoxid-Pulver-Gemisch getaucht, um zu vermeiden, dass Luftblasen in den Strohhalm gelangen - einige Luftblasen werden immer vorhanden sein, aber dieses Verfahren minimiert deren Vorhandensein. Die Strohhalme sollten bis auf 10 mm von oben gefüllt sein - die Fülllinie ist durch den durchscheinenden Strohhalm zu sehen. Wenn der erste Strohhalm gefüllt ist, schalten Sie die Vakuumpumpe aus und nehmen Sie den Strohhalm aus der Düse.
6. Wischen Sie die Epoxidmischung von der Füllung des Strohhalms ab und drücken Sie beide Enden des Strohhalms in einen kleinen Klumpen Ton, um beide Enden des Strohhalms zu füllen, damit beim Aushärten kein Epoxid-Pulver-Gemisch austritt. Legen Sie den 2^. Strohhalm auf die Düse und wiederholen Sie den Vorgang, wobei Sie bei Bedarf zuerst mit dem Mischstab die Epoxid-Pulver-Mischung zusammenfangen.
7. Nachdem das Epoxidharz in den beiden Strohhalmen ausgehärtet ist, schneiden Sie die Strohenden, an denen sich die Tonversiegelung befand, mit einem Rasiermesser ab und schneiden Sie dann jeden Strohhalm in zwei Hälften, um vier Proben abzugeben. Verwenden Sie einen Strohhalm als Probe #1 für den XCT, der vertikal montiert ist, so dass die Röntgenstrahlen über den kreisförmigen Querschnitt des Strohhalms eindringen.

2. Das XCT-Instrument

HINWEIS: Diese Schritte setzen voraus, dass Sie mit dem vom Benutzer ausgewählten XCT-Instrument vertraut sind.

1. Verwenden Sie eine hohe Spannung, in der Regel 100 kV oder höher, da ein guter Kontrast zwischen der Epoxidmatrix und den Metallpulverpartikeln besteht und nichts in der Epoxidmatrix aufgelöst werden muss, was normalerweise niedrige Spannungen um 40 kV erfordern würde. Verwenden Sie einen vollständigen 360^° -Scan mit einer Voxelgröße von etwa 1 μm. Das Verhältnis zwischen der kleinsten berücksichtigten Partikelgröße und der verwendeten Voxelgröße sollte mindestens 8-10³⁹ betragen.
2. Nehmen Sie genügend FOVs über mehr als eine Probe, um genügend Partikel für die Analyse zu erhalten. Wenn die Richtlinien für die Probenvorbereitung befolgt werden, sind 2 bis 8 FOVs ausreichend. In der Regel reichen mindestens 1000 Partikel für eine gültige Form-/Größenanalyse aus, aber mehr Partikel führen zu glatteren Verteilungskurven und besseren Statistiken. Die rekonstruierten Schichten werden von 0 bis nz-1 nummeriert, vom unteren zum oberen Rand des Sichtfelds, wobei nz die Gesamtzahl der rekonstruierten Schichten ist.
   1. Speichern Sie die Slices mit vertikalem Querschnitt für jedes FOV einzeln im 8-Bit-Format (z. B. tiff) und notieren Sie sich die Pixelgröße jedes Bildsatzes (nx x ny), die Anzahl dieser Slices (nz) und die Voxelgröße in Mikrometern (v). Das 8-Bit-Format ist für diese Art von einfachen Metallpartikel-Epoxid-Matrix-Graustufenbildern geeignet, die sich leicht segmentieren lassen.

3. Zusammenfügen der zu jedem FOV gehörenden Schichten zu einer 3D-ASCII-Mikrostruktur

HINWEIS: Das C-Programm, das am NIST verwendet wird, heißt tiff2array.c und wird am häufigsten mit TIFF-Dateien verwendet, kann aber auch mit anderen 8-Bit-Formaten umgehen. Es kann so kompiliert werden, wie es ist, mit der ausführbaren Datei namens tiff2array. Dieses Programm liest jedes Bild von unten nach oben ein, konvertiert es in das ASCII-Format (0 bis 255 Graustufen) und stapelt sie dann am Ende einer Masterdatei.

1. Wenn die rekonstruierten Bilder z. B. im tiff-Format vorliegen und von unten nach oben fortlaufend nummeriert sind, verwenden Sie die folgende Syntax in einem Zeilenterminalbefehl: tiff2array *.tiff. Diese Masterdatei oder Mikrostrukturdatei ist eine 3D-Darstellung des Sichtfelds. Wenn die Variable a(i,j,k) die Grauskala an der Position (i,j,k) ist, wobei k die Nummer der Scheibe ist, k = 1 bis nz und (i,j) das Pixel in der k-ten Scheibe ist, wobei i von links nach rechts und j von oben nach unten gemessen wird.
   HINWEIS: Die gesamte Software, die für das Protokoll benötigt wird, ist im Abschnitt "Ergänzende Informationen" dieses Dokuments über einen Link zu einer NIST-Datenbank verfügbar, die sich unter https://doi.org/10.18434/M32265 befindet.
2. Erstellen Sie für P-FOVs eine kleine Datei namens particle-class-sysconfig.dat mit P-Zeilen, wobei jede Zeile für das p-te (p=1,P) FOV gelesen wird:
   Dateiname nx ny nz v b c
   Dabei ist Dateiname = eine 12-stellige Kennung für ein bestimmtes Sichtfeld, b = 1 für einen Innenscan und 0 für einen Außenscan und c = die Anzahl der in den Bildern vorhandenen Phasen. Wenn ein Innenscan durchgeführt wird, sind in der Regel drei (c = 3) Phasen vorhanden: 1) das Epoxidharz, 2) die schwarzen Bereiche, die die Außenseite des kreisförmigen Scans und der Luftblasen anzeigen, und 3) die helleren Partikel. Manchmal scheinen vier Phasen für das Auge eine vernünftigere Annahme zu sein, und so ist c = 4. Werte für c von 3 oder 4 sind die einzigen beiden Optionen. Der Wert von c teilt der Partikelanalysesoftware mit, welcher automatische Segmentierungsalgorithmus von Otsu, der ursprünglich für Zweiphasenbilder geschrieben wurde, aber leicht auf eine beliebige Anzahl von Phasen erweitert werden kann, zur automatischen Segmentierung der Bilder in einem bestimmten FOV^26,58 verwendet werden soll. Die Mikrostrukturdateien, die im nächsten Softwareprogramm verwendet werden, müssen 12-stellige Namen haben, die genau mit dem Dateinamen übereinstimmen, der in der FOV-name-sysconfig.dat Datei aufgeführt ist, gefolgt von der Erweiterung .mic.
3. Führen Sie die Partikelanalyse-Software pp-Otsu.f aus, wobei Sie als Eingabe die particle-class-sysconfig.dat-Datei und die verschiedenen Mikrostrukturdateien, Dateiname.mic, verwenden. Nehmen Sie für ein neues System nur zwei Änderungen an diesem Programm vor, die alle mit dem Kommentar "USER" in der Fortran-Quelle gekennzeichnet sind: die Dateinamen für die allgemeinen Ausgabedateien (ändern Sie den Namen der allgemeinen Partikelklasse) und die Anzahl der in particle-class-sysconfig.dat aufgeführten FOVs. Das Programm pp-Otsu.f ist in Fortran, ist skalar und wird normalerweise in Fortran 77 kompiliert, obwohl Fortran 90 gut funktionieren sollte. Es und alle anderen unten beschriebenen Fortran-Programme sollten mit doppelter Genauigkeit (-r8) kompiliert werden, um genaue Ergebnisse zu erzielen.
   1. Da pp-Otsu.f mit großen Dateien arbeitet, fügen Sie der Kompilierung immer die Parameter (oder deren Äquivalent) -mcmodel=medium und -Mlarge_arrays hinzu. Eine Hilfsdatei (gauss120.dat) enthält die Gewichtungen und Punkte für eine 120-Punkt-Gaußsche Quadratur, die in pp-Otsu.f häufig verwendet wird, und muss sich im selben Verzeichnis wie pp-Otsu.f befinden. Alle unten beschriebenen Programme sind in Fortran 77 geschrieben, mit Ausnahme der MPI-Programme, die in Fortran 90 geschrieben sind.
4. Zeigen Sie die Partikeldateien an, die die Hauptausgaben von pp-Otsu.f darstellen, deren Ausführung auf einem einzelnen Prozessor mehrere Stunden dauern kann, wenn Tausende von Partikeln analysiert werden müssen. Dazu gehören Dateien mit Namen wie Particle-class-name-anm-particle-number.dat, die die Liste der komplexen Koeffizienten (n = 0,26) mit Einheiten von Mikrometern oder in welcher Einheit v auch immer enthalten, für die Teilchen, die als ausreichend sternförmig³⁹ beurteilt werden und daher in sphärischen harmonischen Funktionen erweitert werden können (sogenannte SH-Teilchen). Zu den Partikeldateien gehören auch Dateien wie Particle-class-name-part-particle- number.dat, die die Anzahl der Voxel im Partikel und alle Voxelpositionen (in Voxelkoordinaten) für Partikel enthalten, die nicht durch sphärische harmonische Erweiterungen beschrieben werden können (sogenannte Nicht-SH-Partikel).
5. Zeigen Sie die beiden Dateien an, eine für die SH- und eine für die Nicht-SH-Partikel, die die Porositäten aller gefundenen Partikel angeben, auch wenn die Porosität Null ist, mit dem Ausdruck Porosität in den Dateinamen. Ein zusätzliches Programm, porosity-analyze.f, sollte die Anzahl der Zeilen in jeder Porositätsdatei und deren Dateinamen erhalten - die zu ändernden Dateinamen stehen am Anfang des Quellcodes. Die Ausgabe dieses Programms sind die beiden Dateien Particle-class-intern-poros-analysis.txt und Particle-class-intern-poros-list.txt. Die Analysedatei generiert die in Tabelle 2 im Abschnitt "Repräsentative Ergebnisse" gezeigten Informationen, und die Listendatei enthält die Informationen, die zum Generieren von Abbildung 5 im Abschnitt "Repräsentative Ergebnisse" erforderlich sind.
6. Sehen Sie sich die drei Tiff-Bilddateien an, die einen Ausschnitt des ersten berücksichtigten FOV zeigen. Die erste Scheibe (OriA-0500.tiff) zeigt die k = 500 Scheibe des ersten FOV in der particle-class-sysconfig.dat Datei, ohne jegliche Bildverarbeitung, und die zweite Bilddatei zeigt das gleiche Bild, aber jetzt segmentiert und mit Schwellenwerten (PixA-0500.tiff). Wenn eine begrenzte Aufteilung der Wasserscheide angewendet wird, zeigt die dritte Bilddatei die Ergebnisse dieses Algorithmus an (LWSA-0500.tiff). In der Regel wird dieser Bildverarbeitungsschritt nicht angewendet, so dass die dritte Bilddatei mit der zweiten identisch ist. Diese Bilder werden als Fehlerprüfungsschritt bei der ursprünglichen Montage der 3D-Mikrostruktur und der automatischen Otsu-Bildsegmentierung generiert. Es wird eine allgemeine Ausgabedatei (particle-class-name-particles-data.dat) erstellt, in der alle Hilfsinformationen für die Verarbeitung der einzelnen Partikel aufgeführt sind. Diese Datei wird nur als Referenz verwendet, aber die Voxelvolumina und Nummernbeschriftungen aller verarbeiteten Partikel werden an das Ende dieser Datei geschrieben.
7. Zeigen Sie für jedes verarbeitete Partikel, ob SH oder nicht-SH, die 3D-VRML-Bilddatei mit der Namenskonvention particle-name-particle-number.wrl an. Für SH-Partikel enthält diese VRML-Bilddatei zwei nebeneinander liegende Bilder, ein Voxelbild des ursprünglichen Partikels und ein glatteres gerendertes Bild unter Verwendung der SH-Koeffizienten. Für die Nicht-SH-Partikel wird nur das Voxelbild gespeichert.

4. Generieren Sie geometrische Informationen für alle SH- und Nicht-SH-Partikel

1. Erstellen Sie vor der weiteren Verarbeitung eine Liste der Particle-class-name-anm-particle-number.dat Dateinamen mit dem Namen anm.lis und eine Liste der nonSH Particle-class-name-part-particle-number.dat-Partikel mit dem Namen nonSH.lis. Führen Sie das kleine Programm number.f aus, das zuvor bearbeitet wurde, um die korrekte Anzahl von Dateien in anm.lis zu haben. Dadurch wird die Datei anm.lis so geändert, dass die Nummer des Partikels in jeder Zeile der Listendatei sowie der Dateiname die vorherige Datei ersetzen.
2. Verwenden Sie das Programm part-lwt-listnum-unitvector.f, um geometrische Informationen für die SH-Partikel zu generieren und auszuwerten. Dies ist ein paralleles MPI-Programm, da Tausende von SH-Teilchen ausgewertet werden müssen und es Tage dauern kann, jeweils nur ein Teilchen zu bearbeiten. Die einzigen Änderungen, die in diesem Programm vorgenommen werden müssen, wenn eine neue Partikelklasse verarbeitet wird, sind die Ntot-Nummer der Partikelklassenname-anm-Partikel number.dat Dateien und die Informationen zur Benennung der Partikelklasse für die Ausgabedatei (Particle-class-name-un-geom-len.dat). Das Programm hat Kommentare (USER) an den wenigen Stellen, die für einen neuen Partikeltyp geändert werden müssen. Die Ausgabedatei vereint Particle-type-info-un-SH-geom-len.dat Partikel aus jedem FOV, und jede Zeile hat die folgende Struktur.
   
   SH-Koeffizienten Dateiname, x1, x2, y1, y2, z1, z2, Volumen, Oberfläche, SA-Verhältnis, Krümmung, Verhältnis, nnn, Gauss, Platzhalter, L, W, T, L/T, W/T, T/T, Trägheitsmoment-Tensorkomponenten, L-Einheitsvektor, Theta, Phi-Winkel, W-Einheitsvektor, Theta, Phi-Winkel, T-Einheitsvektor, Theta, Phi-Winkel
   
   x1 ist der minimale x-Wert auf der Oberfläche des Partikels und x2 ist der Höchstwert, und ähnlich verhält es sich mit y und z. Diese definieren eine "Ausdehnungsbox", die das Partikel nur in seiner gemessenen Ausrichtung⁴² umschließt. Das Ausdehnungsfeld wird in anderen Anwendungen^verwendet 46,47,48,49. Das SA-Verhältnis ist die Oberfläche des Partikels geteilt durch die Oberfläche der volumenäquivalenten Kugel. Curv ist die integrierte mittlere Krümmung, die invertiert und normalisiert wird, so dass sie gleich dem Durchmesser ist, wenn das Partikel eine perfekte Kugel ist. Das Verhältnis ist die Spur des Trägheitsmoment-Tensors dividiert durch die Spur des Trägheitsmoment-Tensors für die volumenäquivalente Kugel. nnn ist die maximale Anzahl von SH-Koeffizienten (n=0, nnn), die bei der Arbeit mit dem gegebenen Teilchen verwendet werden sollten. Gauß ist die integrierte Gaußsche Krümmung, geteilt durch 4π, was für ein geschlossenes Objekt gleich 1 sein sollte. Der Punkt, an dem Gauß um mehr als 5 % von Eins abweicht, definiert die maximale Anzahl von SH-Koeffizienten (n= nnn), die bei der Neuerstellung des Teilchens verwendet werden sollten. L, W, T sind die Länge, Breite und Dicke des Partikels und wurden im Abschnitt Einführung definiert. Die unabhängigen Komponenten des Trägheitsmoment-Tensors sind als I₁₁, I₂₂, I₃₃, I₁₃, I₂₃, I₁₂ aufgeführt. Schließlich wird der Einheitsvektor für L in der Reihenfolge der x-, y- und z-Koordinaten aufgelistet, gefolgt von den sphärischen Polarwinkeln θ (Winkel von der positiven z-Achse) und Φ (Drehwinkel um die z-Achse, definiert als Null auf der positiven x-Achse, definiert als Null und gegen den Uhrzeigersinn positiv). Es folgen die Parameter für W und T, die auf die gleiche Weise aufgelistet sind.
3. Verwenden Sie das Programm nonSH-lwt-un-scalar.f , um die L- , W- und T-Parameter für die nonSH-Partikel zu berechnen, wobei Sie mit der Liste der Dateinamen nonSH.lis arbeiten, und um die zugehörigen Einheitsvektoren aufzuzeichnen. Die einzigen Änderungen, die in dieser Datei für eine neue Partikelklasse vorgenommen werden müssen, sind die Anzahl der Dateinamen in nonSH.lis und die Ausgabedateinamen. Die Hauptausgabe dieses Programms mit dem Namen Particle-name-info-nonSH-len.dat hat jede Zeile im folgenden Format:
   
   Dateiname: Volumen, L, W, T, a1, a2, a3 (LWT-Einheit, Vektoren und Winkel)
   
   Dabei sind a1, a2 und a3 die endgültigen Winkel (in Grad - 90^O) zwischen den Einheitsvektoren für L und W, W und T sowie L und T, die als Fehlerprüfung für den Berechnungsalgorithmus L, W und T enthalten sind, da diese Winkel für eine perfekte Berechnung alle Null sein sollten. Die Vektoren und Winkel der Einheiten L, W und T haben das gleiche Format wie für die SH-Partikel.

5. Wählen Sie eine Teilmenge von SH- und Nicht-SH-Partikeln aus, um die SnS- und NS-L/T-Grenzwerte visuell zu bestimmen

HINWEIS: Die SH-Partikel bestehen im Allgemeinen aus einzelnen kugelförmigen Partikeln, einzelnen nicht-sphärischen (ellipsoiden oder in irgendeiner Weise gebrochenen oder zufällig geformten) Partikeln, Doppelpartikeln und mehreren (mehr als zwei miteinander verbundenen Partikeln) Partikeln. Die Partikel, aus denen sich die mehreren Partikel zusammensetzen, können kugelförmig oder nicht kugelförmig sein. Die nicht-SH-Partikel weisen im Allgemeinen einige wenige einzelne kugelförmige Partikel auf, wenn auch hauptsächlich mit großen Poren, die zur Oberfläche durchgebrochen sind, und der Rest besteht meist aus Doppel- und Mehrfachpartikeln²⁶. Dies wird durch die Betrachtung einer Zufallsstichprobe beider Arten von Partikeln mit Werten von L/T von 1 bis 2 bestimmt. Eine solche visuelle Inspektion wird zu einem wichtigen Schritt, um die SnS- und NS-Klassifizierung zu ermöglichen.

1. Führen Sie das Programm (VRML-select-multi-single.f) aus, das die Particle-type-info-SH-geom-len.dat und Particle-name-info-nonSH-len.dat Dateien liest und 10 Partikel in jedem L/T-Intervall der Größe 0,1 auswählt, d.h. (1,1,1), (1,1,1,2) usw. Dieser speichert bis zu 100 SH-Partikel mit einem L/T-Bereich von 1 bis 2 und bis zu 100 Nicht-SH-Partikel mit demselben L/T-Bereich . Es werden zwei Textdateien (*SH-VRML-list.txt und *nonSH-VRML-list.txt) generiert, in denen die L/T-Werte und die Stammnamen der gefundenen VRML-Bilddateien aufgeführt sind. Diese sollten in eine Art Tabelle eingetragen und nach dem L/T-Wert sortiert werden.
2. Untersuchen Sie die 3D-Bilder jedes dieser Partikel visuell, um den Gesamtbereich der Morphologien zu bestimmen, beginnend mit den Partikeln mit dem niedrigsten L /T-Wert . Die Teilchen werden dahingehend bewertet, ob es sich um gebrochene Teilchen, Doppelteilchen, Mehrfachteilchen, unregelmäßig (z. B. nicht sehr kugelförmig) handelt und ob sie Satelliten haben, die viel kleinere Teilchen sind, die an das Hauptteilchen gebunden sind. Ein Satellit wird so beurteilt, dass das Hauptteilchen ein Doppel- oder Mehrfachteilchen ist, wenn die Satelliten mehr als 1/5 des Durchmessers des Hauptteilchens haben. Es wird der ungefähre Wert von L/T gefunden, der einzelne, nahezu sphärische (SnS) Partikel von mehreren und sehr nicht-sphärischen Partikeln (NS) trennt, was für die SH- und Nicht-SH-Partikel etwas unterschiedlich sein kann. Das erste gefundene Doppel- oder Mehrfachpartikel bestimmt den Grenzwert sowohl für SH- als auch für Nicht-SH-Partikel.
   HINWEIS: Das Zusatzmaterial, das sich unter https://doi.org/10.18434/M32265 befindet, enthält eine Tabellenkalkulationsdatei für die untersuchten Partikel, um zu sehen, wie diese Grenzwerte bestimmt wurden. Diese Zahlen sind mit einer gewissen Unsicherheit und einem gewissen Grad an Subjektivität behaftet, die beurteilt werden kann, indem ein anderer Satz von 100 SH- und 100 nicht-SH-Partikeln mit L/T zwischen 1 und 2 gewählt wird, um die Cutoff-Werte zu bewerten. Neuere Arbeiten ergaben, dass diese Unsicherheit gering war²⁶ und die Ergebnisse nicht signifikant beeinflusste.

6. Generieren Sie 2D-Projektionsdaten aus den 3D-Partikeln

HINWEIS: Die einzigen aktuellen kommerziellen Partikelanalysatoren, die die Partikelform überhaupt messen, tun dies mit 2D-Projektionen. Die XCT-Daten können analysiert werden, um beliebige 2D-Prognosen zu erstellen und Daten zu generieren, die quantitativ mit den Ergebnissen dieser kommerziellen Instrumente abgeglichen werden können. Die 2D-Projektionen bestehen sowohl aus den SH- als auch aus den Nicht-SH-Partikeln und werden kombiniert, ohne dass versucht wird, sie in die 2D-Kategorien SnS und NS zu klassifizieren, da derzeit nicht bekannt ist, wie diese Klassen für 2D-Projektionen definiert werden sollen.

1. Verwenden Sie die beiden Programme (proj-mpi-SH-LWT.f) für die SH-Partikel und (proj2D-nonSH-LWT.f) für die Nicht-SH-Partikel, um für jedes Teilchen drei orthogonale Projektionen entlang der Richtung der drei LWT-Einheitsvektoren zu erzeugen, und generieren Sie dann Fourier-Koeffizienten für den Umriss der Projektion. Diese Koeffizienten werden verwendet, um verschiedene 2D-Größen wie Fläche, Umfang und verschiedene Längen und Seitenverhältnisse zu berechnen.
2. Für jede Projektion wird eine Reihe von (XY)-Punkten generiert und gespeichert, die mit dem Namen der Partikeldatei und 1 für die Projektion entlang des Vektors der L-Einheit, 2 für die Projektion entlang des Vektors der Einheit W und 3 für die Projektion entlang des Vektors der Einheit T gekennzeichnet sind. Geben Sie diese in ein beliebiges Grafikprogramm ein, das diese Eingabe akzeptiert, und stellen Sie sicher, dass die Achsengrenzen von x und y gleich sind und jede Achse die gleiche physikalische Länge hat.
3. Speichern Sie die Fourier-Koeffizienten mit einer ähnlichen Dateibenennungskonvention, aber diese Funktion ist standardmäßig mit Kommentaren deaktiviert. Die einzigen Änderungen, die in einem dieser Programme vorgenommen werden (Programmposition mit "USER" gekennzeichnet), sind die Gesamtzahl der zu berücksichtigenden Partikel (Ntot) und die Ein- und Ausgabedateinamen, die die zu analysierende Partikelklasse widerspiegeln sollten.
4. Die Hauptausgabe von running (proj-mpi-SH-LWT.f) und (proj2D-nonSH-LWT.f) sind Projektionsdatendateien, bei denen die Namenskonvention Particle-class-info-SH-proj.dat und Particle-class-info-nonSH-proj.dat ist. Es kann eine Vielzahl von 2D-Größen berechnet werden, darunter einige, die von zwei verschiedenen kommerziellen Instrumenten (Horiba Camsizer⁵⁹ und Malvern MORPHOLOGI G3⁶⁰) verwendet werden. In beiden Fällen berechnen die Programme eine 2D-Version von L und W, die als L2D und W2D bezeichnet wird.
5. Die Struktur der Ausgabedatei listet für jedes Teilchen, jede Fläche, jeden Umfang Xcmax, Xcmin, Fermax, Fermin, W2D, L2D, WM und LM auf, wobei Fermax und Fermin die maximalen und minimalen Feret-Durchmesser sind und Xcmax und Xcmin aus den Sehnendurchmessern definiert werden, die in verschiedenen Richtungen genommen werden⁵⁹. Es kann theoretisch gezeigt werden, dass L2D die gleiche Größe wie Xcmax ist, was auch in den Datendateien zu sehen ist. Die Parameter LM und WM sind Versionen von L2D und W2D, die im Malvern MORPHOLOGI G3 Handbuch⁶⁰ leicht unterschiedlich definiert sind. Das Dateiformat lautet: Partikelname/-nummer, Fläche, Umfang, Fermin, Fermax, Xcmin, Xcmax, W2D, L2D, Theta, WM, LM, slo und nnnF, wobei nnnF die Anzahl der Fourier-Koeffizienten ist, die zur Darstellung der Partikelprojektion verwendet werden. Die Größe Theta ist der Winkel in Grad, den die Achse, die WM und LM definiert, mit der x-Achse ⁶⁰ bildet. Die Quantität slo ist genau das Verhältnis des Sinus von Theta zum Kosinus von Theta. Beide Größen werden in der hier beschriebenen Partikelanalyse nicht verwendet und dienen nur als Überprüfung in der Berechnung. Die Daten für jedes Teilchen werden in Dreiersätzen geliefert, eine Linie für jede der drei Projektionen, (1,2,3) = (L,W,T).

7. Verarbeitung von geometrischen 3D- und 2D-Partikeldaten zur Erstellung verschiedener Diagramme

1. Verwenden Sie eine beliebige Software, um die Partikelgrößen- und Formdaten zu verarbeiten. Unabhängig davon, welche Software verwendet wird, muss ein bestimmtes Verfahren eingehalten werden.
2. Kombinieren Sie für die 3D-Daten die SH- und Nicht-SH-Daten in SnS- und NS-Listen, wobei Sie die zuvor ermittelten L/T-Grenzwerte für jede Partikelklasse verwenden. Verteilungen und Mittelwerte sollten für die SnS- und NS-Partikel separat und auch für die kombinierten SnS- und NS-Daten für alle interessierenden geometrischen Parameter wie L, W, T, L/T, W/T, L/W, volumenäquivalenter Kugeldurchmesser und andere berechnet werden.
3. Kombinieren Sie für die 2D-Projektionsdaten die SH- und Nicht-SH-Daten. Für jedes 3D-Teilchen gibt es drei 2D-Projektionen, die entlang der Einheitsvektoren für L, W und T erstellt werden. Die Kombination aller drei Projektionen sollte zu Ergebnissen führen, die einer experimentellen Technik ähneln, bei der die Teilchen vor einer Projektion nach dem Zufallsprinzip gedreht werden. Die ausschließliche Verwendung der Vektordaten der L-Einheit simuliert beispielsweise eine experimentelle Technik, bei der die Partikel in einem typischen Gerät grob entlang ihrer längsten Richtung, senkrecht zur Tropfrichtung und parallel zur Stroboskoplicht-/Projektionsrichtung ausgerichtet werden.

Ergebnisse

ASTM hat ein Eignungsprüfungsprogramm (AMPM, Additive Manufacturing Powder Metallurgy) für Metallpulver initiiert, das für das Laser-Pulverbettschmelzen verwendet wird, bei dem die Teilnehmer eine Reihe von Standard-Metallpulvertests durchführen und ASTM die statistische Verteilung dieser Ergebnisse in einem Bericht an die Teilnehmer zusammenstellt⁶¹. Zweimal im Jahr werden Proben von Metallpulver an alle Teilnehmer verteilt. NIST-Mitarbeiter fungieren als ein...

Diskussion

Die XCT-basierte Methode zur Charakterisierung der 3D-Größe und -Form von Metallpartikeln hat mehr Anwendungsmöglichkeiten, aber auch einige Einschränkungen. Die Einschränkungen werden zuerst angesprochen.

Ein schnell aushärtendes Epoxidharz wird verwendet, so dass die Viskosität des Epoxidharzes hoch genug ist, um zu verhindern, dass sich das Pulver während der Aushärtung des Epoxidharzes unter der Schwerkraft absetzt, oder zumindest die Zeit zu verk...

Materialien

Name	Company	Catalog Number	Comments
Epoxy	Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/	Hardman Part # 4001	case of 100