A subscription to JoVE is required to view this content. Sign in or start your free trial.
Method Article
ניתוח צורת חלקיקים תלת מימדית באמצעות טומוגרפיה ממוחשבת של קרני רנטגן: הליך ניסיוני ואלגוריתמי ניתוח לאבקות מתכת
In This Article
Summary
הגודל והצורה של חלקיקי האבקה אינם כמויות עצמאיות. טכניקות מדידה רגילות אינן מודדות את הפרמטרים השזורים זה בזה בתלת מימד (תלת מימד). מתוארת טכניקת מדידה/ניתוח תלת מימדית, המבוססת על טומוגרפיה ממוחשבת של קרני רנטגן, שיכולה למדוד גודל וצורה ולסווג חלקיקי אבקה לפי שני הפרמטרים.
Abstract
מדידת התפלגות הגודל של החלקיקים באבקה היא פעילות נפוצה במדע ובתעשייה. מדידת התפלגות הצורה של החלקיקים היא הרבה פחות נפוצה. עם זאת, הצורה והגודל של חלקיקי האבקה אינם כמויות עצמאיות. כל טכניקות מדידת הגודל/צורה הידועות מניחות צורה כדורית או מודדות את הצורה בשני ממדים בלבד. השיטה המבוססת על טומוגרפיה ממוחשבת של קרני רנטגן (XCT) המוצגת כאן מודדת הן את הגודל והן את הצורה בתלת מימד מבלי להניח הנחות. החל מתמונה תלת מימדית של חלקיקים, השיטה יכולה לסווג מתמטית חלקיקים לפי צורה, למשל חלקיקים המורכבים מכמה חלקיקים קטנים יותר המרותכים יחד בניגוד לחלקיקים בודדים שאינם בהכרח כדוריים. כמובן, הגדרת מספר בודד כ"גודל" או "צורה" של חלקיק אקראי לא כדורי אינה אפשרית באופן עקרוני, מה שמוביל לדרכים רבות להעריך את גודל החלקיקים וצורתם באמצעות פרמטרים שונים המקושרים זה לזה, שכולם יכולים להיווצר מאפיון תלת-ממדי שלם זה בצורה של ממוצעים והתפלגויות. מתוארים הליכי הניסוי הדרושים, ניתוח מתמטי וניתוח ממוחשב וניתנת דוגמה לאבקת מתכת. הטכניקה מוגבלת לחלקיקים הניתנים להדמיה על ידי XCT עם מינימום של כ-1000 ווקסלים לנפח חלקיקים.
Introduction
מדידת התפלגות הגודל של החלקיקים באבקה היא פעילות נפוצה במדע ובתעשייה 1,2. מדידת התפלגות הצורה של החלקיקים פחות נפוצה, אך גם הגודל וגם הצורה, יחד עם החומר ממנו עשויים החלקיקים, קובעים את תכונותיהם, לבד או בחומר מטריצה כלשהו 3,4,5,6,7. חומרים שגודל החלקיקים וצורתם מעניינים כוללים מלט פורטלנד, חול וחצץ 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22, 23, אבקות מתכת לייצור מתכות אבקה ותוספים 24,25,26, אדמת ירח 27,28,29, צמיגי רכב מגוררים30, פסולת זכוכית כתושה 31, תאי גזע32, וננו-צינורות פחמן וגרפן33,34,35,36,37. עם זאת, הצורה והגודל של חלקיקי האבקה אינם כמויות עצמאיות26. לדוגמה, נניח שיש לאדם חלקיק רגיל מבחינה גיאומטרית ש"גודלו" נאמר שהוא d. מבלי לומר אם חלקיק זה הוא כדור, קובייה או מוט דק באורך d, לא באמת יודעים כיצד הגודל חל על חלקיק זה. כשאומרים שהחלקיק הוא כדור, קובייה או מוט, אנחנו למעשה מציינים את צורת החלקיק, וללא המידע הנוסף הזה, מידע הגודל הוא חסר משמעות.
עבור שלוש הדוגמאות הללו, כדור, קובייה או מוט דק, ניתן לציין את גודל החלקיקים במספר יחיד. אבל גם אם למוט היה חתך עגול, היה צריך למדוד גם את הקוטר של חתך זה, כך שבאמת יהיה צורך בשני פרמטרי גודל עבור חלקיק המוט הדק. מה לגבי חלקיקים בצורת אליפסואידים, או קופסאות מלבניות? עבור כל אחד מאלה, יש צורך בשלושה מספרים כדי לציין את הגודל, ועדיין יש לתת את הצורה כאליפסואיד או כתיבה מלבנית על מנת שלשלושת פרמטרי הגודל תהיה משמעות. עבור חלקיק בעל צורה אקראית, יהיה צורך במספר אינסופי של פרמטרי גודל (למשל, אורך האקורדים על פני החלקיק) כדי לאפיין לחלוטין את "גודל" החלקיק, ועם זאת הם יהיו חסרי משמעות ללא "אפיון צורה", לדעת באילו זוויות ביחס למרכז המסה של החלקיק צוירו האקורדים הללו.
ישנן טכניקות רבות המשמשות למדידת התפלגות הגודל של החלקיקים באבקה, תוך שימוש בעקרונות פיזיקליים שונים 1,2. מה שלא מוכר בדרך כלל הוא שכדי לחלץ את גודל החלקיקים, יש להשתמש במידע על צורת החלקיק, בין אם משוער או נמדד. ניתן לסווג את הטכניקות הנוכחיות כ: (I) מדידות של גודל חלקיקים תלת מימדיים (3D) תוך הנחת צורה תלת מימדית, ו-(II) מדידות של גודל וצורה אך רק של הקרנות דו-ממדיות (2D), תוך שימוש בטכניקות ניתוח תמונה דו-ממדיות. עבור חלקיקים כדוריים, כל ההקרנות הדו-ממדיות הן מעגלים, בקוטר זהה לחלקיקים המקוריים, וכל טכניקות המדידה הללו, הן Class I והן Class II, בתוך אי ודאות המדידה, נותנות את אותן תוצאות עבור כדורים מושלמים. עבור חלקיקים לא כדוריים, ההקרנות הדו-ממדיות קשורות הרבה פחות לחלקיקים המקוריים. אם לחלקיק יש נקבוביות פנימית שאינה שוברת את פני החלקיק, נקבוביות אלו לא יימדדו כלל על ידי אף אחת מטכניקות המדידה התלת-ממדיות או הדו-ממדיות הללו. Class I כולל עקיפה של לייזר, נפח חישה חשמלית (ESV)38, ניתוח מסננת ושקיעה; ו-Class II מכסה מיקרוסקופ אלקטרונים שידור וסריקה, מיקרוסקופ כוח אטומי וניתוח תמונה דינמית וסטטית בטכניקות אופטיות. אף אחת מהמחלקות לא מודדת במדויק את הגודל והצורה של חלקיקים לא כדוריים בתלת מימד.
מאז 2002בערך, פותחה שיטה חדשה לניתוח חלקיקים 40,41,42,43,44,45 המדמה חלקיק תלת-ממדי בתלת-ממד, ולאחר מכן משתמשת במספר צורות של ניתוח מתמטי כדי לייצג ולסווג כל חלקיק. נשמרת תמונה תלת-ממדית לכל חלקיק בנפרד, וניתן להשוות אותה למידע הגיאומטרי והמתמטי שנשמר גם עבור כל חלקיק. ניתן להשתמש במידע מתמטי זה כדי ליצור מחדש את החלקיק כרצונך בכל סוג של מודל תלת מימד 46,47,48,49, בכל מיקום וכיוון, או כדי ליצור חלקיקים וירטואליים שנאלצים לקבל את אותה סטטיסטיקה 50,51. שיטת ניתוח חלקיקים זו מבוססת על סריקות XCT של חלקיקים המפוזרים באפוקסי או במדיום אחר כזה. סריקות ה-XCT מופעלות על ידי תוכנה מיוחדת המשתמשת באלגוריתם הצריבה 52,53,54,55,56 כדי לזהות חלקיקים, ולאחר מכן התאמת סדרות הרמוניות כדוריות או ספירת ווקסל כדי ליצור ולאחסן את צורת החלקיקים וגודלם, תמונות תלת מימד של החלקיקים, ובשלב שני, מידע גיאומטרי עבור כל חלקיק. לכל חלקיק שנותח יש תווית אלפאנומרית ייחודית, המשמשת למעקב אחר כל חלקיק, המידע על כל חלקיק ולקישור כל חלקיק לתמונה התלת-ממדית שלו. במהלך תהליך ניתוח זה, נקבוביות שנמצאות בתוך חלקיק מנותחות ומאוחסנת הנקבוביות הכוללת בחלקיק המסוים הזה, מכיוון ששחזור XCT נותן תצוגה תלת מימדית מלאה של דגימה.
שלושה (מתוך רבים) פרמטרים גיאומטריים של גודל/צורה נמצאו שימושיים במיוחד בניתוח וסיווג חלקיקים בתלת מימד: האורך, L, הרוחב, W והעובי, T. L מוגדר כמרחק הארוך ביותר מנקודת המשטח לנקודת השטח על פני חלקיק, W מוגדר באופן דומה כ-L עם האילוץ הנוסף וקטור היחידה לאורך W חייב להיות מאונך לווקטור היחידה לאורך L, ו-T מוגדר גם באופן דומה כ-L עם האילוץ הנוסף שווקטור היחידה לאורך T חייב להיות מאונך הן לווקטור היחידה לאורך L והן לווקטור היחידה לאורך W12. שלושת הפרמטרים הללו מגדירים את התיבה המלבנית או התוחמת המינימלית שמכילה רק את החלקיק, והיחסים בין שלושת הפרמטרים הללו נותנים מידע צורה בעל ערך אך משוער על כל חלקיק. ניתן לבצע הפצות של כל אחד מאלה. ייתכן ש-W מתאם היטב עם ה"גדלים" שנמדדו בניתוח מסננת57, בעוד שה"גדלים" שנמדדו עם עקיפה של לייזר מתאמים לתערובת של L, W ו-T31.
לבסוף, התמונות התלת-ממדיות של דגימת בדיקה של 100-200 מהחלקיקים נבדקות ויזואלית כדי לקבוע היכן נמצאים החתכים ב-L/T המאפשרים לשיטה להבחין בין חלקיקים בודדים, כמעט כדוריים (SnS), לבין חלקיקים לא כדוריים (NS), שיכולים להיות חלקיקים מרובים המרותכים יחד, או מה שהם בבירור חלקיקים בודדים אך בעלי צורה מוזרה.
Access restricted. Please log in or start a trial to view this content.
Protocol
הערה: הפרוטוקול הבא נכתב עבור חלקיקי אבקת מתכת בגודל, על פי קירוב קוטר כדורי שווה נפח (VESD, קוטר כדור בנפח זהה לחלקיק), בין 10 מיקרומטר ל-100 מיקרומטר. נניח שלמתכת יש צפיפות ביחידות של גרם/ס"מ3. יש ללבוש כפפות במהלך שלבי הכנת הדגימה, יחד עם הגנה על העיניים. חשוב לקרוא את כל השלבים בפרוטוקול 1, מכיוון שחלק מהציוד צריך להיות מוכן לפני תחילת הפרוטוקול.
1. הכנת תערובת אבקת אפוקסי
- מכינים כ -25 גרם אפוקסי מהיר (5 דקות) בכלי חד פעמי קטן. סירות נייר אלומיניום עובדות היטב למטרה זו. אפוקסי טוב לשימוש מגיע בניילון בועות, כאשר השרף מופרד מהמקשה, שצפיפות הריפוי שלו היא ρe g/cm3.
- השתמש ב-M גרם של האבקה, מדגימה גדולה יותר של אבקה מנוערת היטב, כאשר M נועד לתת חלק נפח של כ-10% לאחר ערבוב ה-M גרם לאפוקסי. זה נועד למנוע מצב שבו חלקיקים כל כך קרובים זה לזה עד שסריקת ה-XCT מזהה אותם בטעות כרב-חלקיקים אמיתיים המחוברים היטב. המשוואה המגדירה את M היא:
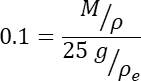
- מערבבים את אבקת המתכת במרץ לתוך האפוקסי, ידנית, באמצעות מוט ערבוב חד פעמי - מקל מלאכה פשוט מעץ עובד מצוין - למשך כ -30 שניות, מספיק זמן כדי לפזר את האבקה כראוי. תהליך זה, שנעשה היטב, הופך את ניתוח התמונה של החלקיקים הבודדים להרבה יותר פשוט.
- לאחר הערבוב, מגרדים את תערובת הויסקופלסטיק לגוש קומפקטי עם מידה אנכית רבה ככל האפשר, כדי להיות מוכנים לשלב הבא. חשוב להכין את השלבים הבאים מבעוד מועד, מכיוון שלא יישאר הרבה זמן עד שהאפוקסי יתקשה.
- השתמש במשאבת ואקום קטנה המחוברת לצינור פלסטיק באורך 0.5 מ ', עם זרבובית המוכנסת בקצה הפתוח של הצינור שתתאים היטב לקש פולימרי בקוטר פנימי של כ -3 מ"מ.
הערה: קשיות קוקטייל, הזמינות בקלות בחנויות מכולת, עובדות היטב עבור קש פולימרי בקוטר 3 מ"מ ואורכן כ-150 מ"מ. עבור זרבובית, הקצה החתוך של פיפטת פלסטיק חד פעמית של 1 מ"ל עד 2 מ"ל יעיל בדרך כלל. כאשר הזרבובית נכנסת לצינור הפלסטיק, יש למתוח סרט חשמלי בחוזקה סביב המפרק כדי להבטיח אטימה אטומה. 25 גרם אבקת אפוקסי פלוס אמורות להיות די והותר בכדי למלא שתי קשיות שלמות. - הכנס את הזרבובית לקש, החזק את הזרבובית ואת קצה הקש צבוטים היטב זה לזה. הכנס את הקצה החופשי של הקשית לתוך גוש אבקת האפוקסי הקומפקטי והפעל את משאבת הוואקום.
הערה: שמור את הקצה החופשי של הקש שקוע בתערובת אבקת האפוקסי כדי למנוע הכנסת בועות אוויר לקשית - כמה בועות אוויר תמיד יהיו קיימות, אך הליך זה ממזער את נוכחותן. יש למלא את הקשיות עד 10 מ"מ מלמעלה - ניתן לראות את קו המילוי דרך הקש השקוף. כאשר הקש הראשון מתמלא, כבה את משאבת הוואקום והסר את הקש מהזרבובית. - נגב את תערובת האפוקסי מקצה המילוי של הקשית ודחף את שני קצוות הקשית לגוש חימר קטן על מנת למלא את שני קצוות הקש כך שלא תדלוף תערובת אבקת אפוקסי במהלך הריפוי. הניחואת הקשית השנייה על הזרבובית וחזרו על הפעולה, תחילה בעזרת מוט הערבוב כדי לאסוף את תערובת אבקת האפוקסי יחד במידת הצורך.
- לאחר ריפוי האפוקסי בשתי הקשיות, חותכים את קצוות הקש, היכן שהיה אוטם החימר, בעזרת סכין גילוח ואז חותכים כל קשית לשניים כדי לתת ארבע דגימות. השתמש בקשית אחת כדוגמה #1 עבור ה-XCT, המותקנת אנכית כך שקרני הרנטגן יחדרו על פני החתך העגול של הקשית.
2. מכשיר XCT
הערה: שלבים אלה מניחים היכרות עם מכשיר ה-XCT שנבחר על ידי המשתמש.
- השתמש במתח גבוה, בדרך כלל 100 קילו וולט ומעלה, מכיוון שיש ניגודיות טובה בין מטריצת האפוקסי לחלקיקי אבקת המתכת ואין צורך לפתור שום דבר בתוך מטריצת האפוקסי, מה שבדרך כלל ידרוש מתחים נמוכים סביב 40 קילו וולט. השתמש בסריקת 360o מלאה, עם גודל ווקסל של כ-1 מיקרומטר. היחס בין גודל החלקיקים הקטן ביותר שנחשב לגודל הווקסל בשימוש צריך להיות מינימום של 8-1039.
- קח מספיק FOVs, על פני יותר מדגימה אחת, כדי לתת מספיק חלקיקים לניתוח. אם מקפידים על הנחיות ההכנות לדוגמא, 2 עד 8 FOVs יספיקו. בדרך כלל, מינימום של 1000 חלקיקים מספיק לניתוח צורה/גודל תקף, אך יותר חלקיקים מביאים לעקומות התפלגות חלקות יותר ולסטטיסטיקה טובה יותר. הפרוסות המשוחזרות ממוספרות מ-0 עד nz-1, מלמטה למעלה של ה-FOV, כאשר nz הוא המספר הכולל של הפרוסות המשוחזרות.
- שמור את פרוסות החתך האנכיות עבור כל FOV בנפרד, בפורמט 8 סיביות (למשל, tiff) תוך ציון גודל הפיקסלים של כל ערכת תמונות (nx x ny), מספר הפרוסות הללו (nz) וגודל הווקסל במיקרומטר (v). פורמט 8 סיביות מתאים לסוגים אלה של תמונות פשוטות בקנה מידה אפור של חלקיקי מתכת-אפוקסי, שקל לפלח.
3. הרכבת הפרוסות השייכות לכל FOV למיקרו-מבנה ASCII תלת מימדי
הערה: תוכנית C המשמשת ב-NIST נקראת tiff2array.c והיא משמשת לרוב עם קבצי tiff אך יכולה להתמודד עם פורמטים אחרים של 8 סיביות. ניתן להדר אותו כפי שהוא, כאשר קובץ ההפעלה נקרא tiff2array. תוכנית זו קוראת בכל תמונה, מלמטה למעלה, ממירה אותם לפורמט ascii (סולם אפור של 0 עד 255) ולאחר מכן עורמת אותם בסוף קובץ מאסטר.
- לדוגמה, אם התמונות המשוחזרות הן בתבנית tiff וממוספרות ברצף מלמטה למעלה, השתמש בתחביר הבא בפקודת מסוף שורה: tiff2array *.tiff. קובץ אב זה, או קובץ מיקרו-מבנה, הוא ייצוג תלת מימדי של ה-FOV. אם המשתנה a(i,j,k) הוא הסקאלה האפורה במיקום (i,j,k), כאשר k הוא מספר הפרוסה, k = 1 עד nz, ו-(i,j) הוא הפיקסל בפרוסה kth, כאשר i נמדד משמאל לימין ו-j נמדד מלמעלה למטה.
הערה: כל התוכנות הדרושות בפרוטוקול זמינות בסעיף מידע משלים במאמר זה באמצעות קישור למסד נתונים של NIST הממוקם בכתובת https://doi.org/10.18434/M32265. - עבור P FOVs, צור קובץ קטן בשם particle-class-sysconfig.dat, עם קווי P, שבו כל שורה קוראת, עבור ה-pth (p=1,P) FOV:
שם הקובץ nx ny nz v b c
כאשר Filename = זיהוי בן 12 תווים עבור FOV מסוים, b = 1 עבור סריקה פנימית ו-0 עבור סריקה חיצונית, ו-c = מספר השלבים הקיימים בתמונות. כאשר מתבצעת סריקה פנימית, בדרך כלל קיימים שלושה שלבים (c=3): 1) האפוקסי, 2) האזורים השחורים המציינים את החלק החיצוני של הסריקה המעגלית ובועות האוויר, ו-3) החלקיקים הבהירים יותר. לפעמים ארבעה שלבים עשויים להיראות לעין כהנחה סבירה יותר ולכן c = 4. ערכים עבור c של 3 או 4 הם שתי האפשרויות היחידות. הערך של c אומר לתוכנת ניתוח החלקיקים שבה אלגוריתם הפילוח האוטומטי של Otsu, שנכתב במקור עבור תמונות דו-פאזיות אך מורחב בקלות לכל מספר שלבים, להשתמש בו כדי לפלח אוטומטית את התמונות ב-FOVמסוים 26,58. קבצי המיקרו-מבנה שישמשו בתוכנה הבאה חייבים להיות בעלי שמות בני 12 תווים זהים לחלוטין לשם הקובץ הרשום בקובץ FOV-name-sysconfig.dat, ואחריו הסיומת .mic. - הפעל את תוכנת ניתוח החלקיקים pp-Otsu.f, תוך שימוש כקלט בקובץ particle-class-sysconfig.dat ובקבצי המיקרו-מבנה השונים, Filename.mic. בצע רק שני שינויים בתוכנית זו עבור מערכת חדשה, שכולם מסומנים בהערה "USER" במקור Fortran: שמות הקבצים עבור קבצי הפלט הכלליים (שנה את שם מחלקת החלקיקים הכללית) ומספר ה-FOVs הרשומים ב-particle-class-sysconfig.dat. התוכנית pp-Otsu.f נמצאת ב-Fortran, היא סקלרית, ובדרך כלל מורכבת ב-Fortran 77, אם כי Fortran 90 אמור לעבוד מצוין. זה, וכל שאר תוכנות Fortran המתוארות להלן, צריכות להיות מהודרות בדיוק כפול (-r8) לקבלת תוצאות מדויקות.
- בנוסף, מכיוון ש-pp-Otsu.f עובד עם קבצים גדולים, הוסף תמיד את הפרמטרים (או המקבילה שלהם) -mcmodel=medium ו-Mlarge_arrays לתרכובת. קובץ עזר, gauss120.dat, מכיל את המשקולות והנקודות עבור ריבוע גאוס בן 120 נקודות הנמצא בשימוש נרחב ב-pp-Otsu.f, וחייב להיות באותה ספרייה כמו pp-Otsu.f. כל התוכניות המתוארות להלן כתובות ב-Fortran 77 למעט תוכניות MPI, הכתובות ב-Fortran 90.
- הצג את קבצי החלקיקים שהם הפלטים העיקריים מ-pp-Otsu.f, שיכולים לקחת מספר שעות לפעול על מעבד יחיד אם יש אלפי חלקיקים לניתוח. אלה כוללים קבצים עם שמות כמו Particle-class-name-anm-particle-number.dat, המכילים את רשימת המקדמים המרוכבים (n = 0,26), עם יחידות של מיקרומטר או בכל יחידה v שהיא, עבור החלקיקים שנתפסו כבעלי צורת כוכב39 ובכך מסוגלים להתרחב בפונקציות הרמוניות כדוריות (הנקראות חלקיקי SH). קבצי חלקיקים כוללים גם קבצים כמו Particle-class-name-part-particle- number.dat, המכילים את מספר הווקסלים בחלקיק ואת כל מיקומי הווקסל (בקואורדינטות ווקסל) עבור חלקיקים שאינם מסוגלים להיות מתוארים על ידי הרחבות הרמוניות כדוריות (הנקראות חלקיקים nonSH).
- הצג את שני הקבצים, אחד עבור ה-SH ואחד עבור החלקיקים שאינם SH, הנותנים את הנקבוביות של כל החלקיקים שנמצאו, גם אם הנקבוביות היא אפס, עם הביטוי נקבוביות בשמות הקבצים. יש לתת לתוכנה נוספת, porosity-analyze.f, את מספר השורות בכל קובץ נקבוביות ואת שמות הקבצים שלהם - שמות הקבצים שיש לשנות נמצאים בתחילת קוד המקור. הפלט מתוכנית זו הוא שני הקבצים Particle-class-intern-poros-analysis.txt ו-Particle-class-intern-poros-list.txt. קובץ הניתוח יוצר את המידע המוצג בטבלה 2 במקטע תוצאות מייצגות, וקובץ הרשימה מספק את המידע הדרוש ליצירת איור 5 בסעיף תוצאות מייצגות.
- הצג את שלושת קבצי התמונות tiff המציגים פרוסה אחת של ה-FOV הראשון שנבחן. הפרוסה הראשונה (OriA-0500.tiff) מציגה את פרוסת k = 500 של ה-FOV הראשון בקובץ particle-class-sysconfig.dat , ללא כל עיבוד תמונה, וקובץ התמונה השני מציג את אותה תמונה אך כעת מפולח וסף (PixA-0500.tiff). אם מוחל פיצול פרשת מים מוגבל, קובץ התמונה השלישי מציג את התוצאות של אלגוריתם זה (LWSA-0500.tiff). בדרך כלל שלב עיבוד תמונה זה אינו מוחל, ולכן קובץ התמונה השלישי זהה לשני. תמונות אלו נוצרות כשלב בדיקת שגיאות בהרכבה המקורית של המיקרו-מבנה התלת-ממדי ופילוח תמונת האוטסו האוטומטי. נוצר קובץ פלט כללי (particle-class-name-particles-data.dat) המפרט את כל מידע העזר לעיבוד כל חלקיק. קובץ זה משמש רק כסימוכין, אך נפחי הווקסל ותוויות המספרים של כל החלקיקים המעובדים כתובים בסוף קובץ זה.
- עבור כל חלקיק מעובד, בין אם SH או nonSH, הצג את קובץ התמונה התלת-ממדי VRML, עם מוסכמת השמות particle-name-particle-number.wrl. עבור חלקיקי SH, קובץ תמונה VRML זה מכיל שתי תמונות זו לצד זו, תמונת ווקסל של החלקיק המקורי ותמונה מעובדת חלקה יותר באמצעות מקדמי SH. עבור החלקיקים שאינם SH, רק תמונת הווקסל מאוחסנת.
4. צור מידע גיאומטרי עבור כל חלקיקי SH ו-nonSH
- לפני עיבוד נוסף, ערכו רשימה של שמות הקבצים Particle-class-name-anm-particle-number.dat, הנקראים anm.lis, ורשימה של חלקיקי nonSH Particle-class-name-part-particle-number.dat , הנקראים nonSH.lis. הפעל את התוכנית הקטנה number.f, לאחר שנערך תחילה כדי לקבל את המספר הנכון של קבצים ב-anm.lis. פעולה זו משנה את הקובץ anm.lis כך שמספר החלקיק בכל שורה בקובץ הרשימה, כמו גם שם הקובץ, יחליף את הקובץ הקודם.
- השתמש בתוכנית part-lwt-listnum-unitvector.f כדי ליצור ולהעריך מידע גיאומטרי עבור חלקיקי SH. זוהי תוכנית מקבילה של MPI, מכיוון שיכולים להיות אלפי חלקיקי SH להערכה, וביצוע רק חלקיק אחד בכל פעם יכול לקחת ימים. השינויים היחידים בתוכנית זו שצריכים להתבצע בעת עיבוד מחלקת חלקיקים חדשה הם מספר ה-Ntot של קבצי number.dat Particle-class-name-anm-particle , ומידע שמות מחלקת החלקיקים עבור קובץ הפלט (Particle-class-name-un-geom-len.dat). לתוכנה יש הערות (USER) במקומות המעטים שצריך לשנות עבור סוג חלקיק חדש. קובץ הפלט Particle-type-info-un-SH-geom-len.dat מאחד חלקיקים מכל FOV, ולכל שורה יש את המבנה הבא.
מקדמי SH שם קובץ, x1, x2, y1, y2, z1, z2, נפח, שטח פנים, יחס SA, עקום, יחס, nnn, גאוס, מציין מיקום, L, W, T, L/T, W/T, T/T, מומנט של רכיבי טנזור אינרציה, וקטור יחידת L, תטא, זוויות פי, וקטור יחידת W, תטא, זוויות פי, וקטור יחידת T, תטא, זוויות פי
x1 הוא ערך ה-x המינימלי על פני החלקיק ו-x2 הוא המקסימום ובאופן דומה עבור y ו-z. אלה מגדירים "קופסת היקף" שפשוט סוגרת את החלקיק בכיוון הנמדדשלו 42. תיבת ההיקף משמשת ביישומים אחרים 46,47,48,49. יחס SA הוא שטח הפנים של החלקיק חלקי שטח הפנים של הכדור שווה הנפח. Curv הוא העקמומיות הממוצעת המשולבת הפוכה ומנורמלת כך שהיא שווה לקוטר כאשר החלקיק הוא כדור מושלם. יחס הוא העקבות של מומנט טנזור האינרציה חלקי העקבות של רגע טנזור האינרציה עבור הכדור המקביל לנפח. nnn הוא המספר המקסימלי של מקדמי SH (n=0, nnn) שיש להשתמש בהם בעת עבודה עם החלקיק הנתון. גאוס היא העקמומיות הגאוסית המשולבת, חלקי 4π, שאמורה להיות שווה ל-1 עבור אובייקט סגור. הנקודה שבה גאוס משתנה מאחדות ביותר מ-5% מגדירה את המספר המקסימלי של מקדמי SH (n= nnn) שיש להשתמש בהם בעת יצירה מחדש של החלקיק. L, W, T הם האורך, הרוחב והעובי של החלקיק, והוגדרו בסעיף המבוא. המרכיבים הבלתי תלויים של טנזור מומנט האינרציה רשומים כ-I11, I22, I33, I13, I23, I12. לבסוף, וקטור היחידה עבור L רשום, בסדר הקואורדינטות x,y ו-z, ואחריו הזוויות הקוטביות הכדוריות θ (זווית מציר ה-z החיובי) ו-Φ (זווית הסיבוב סביב ציר z, המוגדרת כאפס בציר ה-x החיובי והיא חיובית נגד כיוון השעון). הפרמטרים עבור W ו-T עוקבים, מפורטים באותו אופן. - השתמש בתוכנית nonSH-lwt-un-scalar.f כדי לחשב את הפרמטרים L, W ו-T עבור החלקיקים nonSH, הפועלים על רשימת שמות הקבצים nonSH.lis , וגם לתעד את וקטורי היחידות המשויכים. השינויים היחידים שצריכים להתבצע בקובץ זה עבור מחלקת חלקיקים חדשה הם מספר שמות הקבצים ב-nonSH.lis, ושמות קבצי הפלט. הפלט העיקרי מתוכנית זו, בשם Particle-name-info-nonSH-len.dat, כולל כל שורה בתבנית:
שם קובץ: נפח: L, W, T, a1, a2, a3 (יחידת LWT, וקטור וזוויות)
כאשר a1, a2 ו-a3 הן הזוויות הסופיות (במעלות - 90o) בין וקטורי היחידה עבור L ו-W, W ו-T, ו-L ו-T, הכלולים כבדיקת שגיאות עבור אלגוריתם החישוב L, W ו-T , מכיוון שכל הזוויות הללו צריכות להיות אפס לחישוב מושלם. וקטורי היחידות והזוויות L, W ו-T הם באותה תבנית כמו עבור חלקיקי SH.
5. בחר תת-קבוצה של חלקיקי SH ו-nonSH כדי לקבוע חזותית חתכי SnS ו-NS L/T
הערה: חלקיקי SH, באופן כללי, מורכבים מחלקיקים כדוריים בודדים, חלקיקים בודדים שאינם כדוריים (אליפסואידים או שבורים בדרך כלשהי או צורה אקראית), חלקיקים כפולים וחלקיקים מרובים (יותר משני חלקיקים המחוברים יחד). החלקיקים המרכיבים את החלקיקים המרובים יכולים להיות כדוריים או לא כדוריים. לחלקיקים שאינם SH יש בדרך כלל כמה חלקיקים כדוריים בודדים, אם כי בעיקר עם נקבוביות גדולות שפרצו אל פני השטח, והשאר הם בעיקר חלקיקים כפולים ומרובים26. זה נקבע על ידי צפייה במדגם אקראי של שני סוגי החלקיקים עם ערכים של L/T מ-1 עד 2. בדיקה ויזואלית כזו הופכת לצעד חשוב כדי לאפשר את סיווג SnS ו-NS.
- הפעל תוכנית (VRML-select-multi-single.f) שקוראת את קבצי Particle-type-info-SH-geom-len.dat ו-Particle-name-info-nonSH-len.dat , ובוחרת 10 חלקיקים בכל מרווח L/T בגודל 0.1, כלומר (1,1.1), (1.1,1.2) וכו'. זה מאחסן עד 100 חלקיקי SH עם L/T בטווח שבין 1 ל-2, ועד 100 חלקיקים nonSH עם אותו טווח L/T . נוצרים שני קובצי טקסט (*SH-VRML-list.txt ו-*nonSH-VRML-list.txt) המפרטים את ערכי ה-L/T ואת שמות השורש של קובצי התמונה של VRML שנמצאו. יש להכניס אותם לגיליון אלקטרוני כלשהו ולהזמין אותם לפי ערך L/T.
- בחן את התמונות התלת-ממדיות של כל אחד מהחלקיקים הללו באופן חזותי כדי לקבוע את הטווח הכולל של מורפולוגיות, החל מחלקיקי ערך ה-L/T הנמוכים ביותר. החלקיקים מוערכים במונחים של האם הם חלקיקים שבורים, חלקיקים כפולים, חלקיקים מרובים, לא סדירים (למשל, לא כדוריים במיוחד), והאם יש להם לוויינים, שהם חלקיקים קטנים בהרבה, המחוברים לחלקיק הראשי. לוויין נשפט כמי שהופך את החלקיק הראשי לחלקיק כפול או מרובה אם הלוויין/ים הם יותר מ-1/5 מקוטר החלקיק הראשי. נמצא הערך המשוער של L/T המפריד בין חלקיקים בודדים, כמעט כדוריים (SnS) לבין חלקיקים מרובים ומאוד לא כדוריים (NS), שיכולים להיות מעט שונים עבור חלקיקי SH ו-nonSH. החלקיק הכפול או המרובה הראשון שנמצא קובע את ערך החיתוך הן עבור חלקיקי SH והן עבור חלקיקים שאינם SH.
הערה: החומר המשלים, הממוקם ב-https://doi.org/10.18434/M32265, כולל קובץ גיליון אלקטרוני עבור החלקיקים שנבדקו, כדי לראות כיצד נקבעו ערכי חיתוך אלה. יש אי ודאות מסוימת ומידה מסוימת של סובייקטיביות במספרים אלה, שניתן להעריך על ידי בחירת קבוצה שונה של 100 חלקיקי SH ו-100 חלקיקים nonSH, עם L/T בין 1 ל-2, כדי להעריך את ערכי החיתוך. עבודה אחרונה מצאה כי אי ודאות זו הייתה קטנה26 ולא השפיעה באופן משמעותי על התוצאות.
6. צור נתוני הקרנה דו-ממדיים מהחלקיקים התלת מימדיים
הערה: מנתחי החלקיקים המסחריים היחידים הנוכחיים המודדים את צורת החלקיקים בכלל עושים זאת באמצעות הקרנות דו-ממדיות. ניתן לנתח את נתוני ה-XCT כדי לתת תחזיות דו-ממדיות שרירותיות, וליצור נתונים שניתן להתאים כמותית לתוצאות של מכשירים מסחריים אלה. ההקרנות הדו-ממדיות עשויות הן מחלקיקי SH והן מחלקיקים שאינם SH ומשולבות, ללא ניסיון לסווג לקטגוריות SnS ו-NS דו-ממדיות, מכיוון שלא ידוע כיום כיצד להגדיר מחלקות אלה עבור הקרנות דו-ממדיות.
- השתמש בשתי התוכניות, (proj-mpi-SH-LWT.f) עבור חלקיקי SH ו-(proj2D-nonSH-LWT.f) עבור חלקיקי nonSH, כדי ליצור שלוש הטלות אורתוגונליות עבור כל חלקיק, לאורך הכיוון של שלושת וקטורי יחידת LWT , ולאחר מכן ליצור מקדמי פורייה עבור קווי המתאר של ההטלה. מקדמים אלה משמשים לחישוב כמויות דו-ממדיות שונות כגון שטח, היקף ואורכים ויחסי גובה-רוחב שונים.
- סדרה של נקודות (x,y) נוצרות ומאוחסנות עבור כל הקרנה, המסומנות בשם קובץ החלקיקים ו-1 עבור ההקרנה לאורך וקטור היחידה L , 2 עבור ההקרנה לאורך וקטור יחידת W ו-3 עבור ההקרנה לאורך וקטור יחידת T . הזן אותם לכל תוכנת גרפים שמקבלת קלט זה, וודא שגבולות הציר של x ו-y צריכים להיות זהים, וכל ציר הוא באותו אורך פיזי.
- אחסן את מקדמי פורייה עם מוסכמה דומה למתן שמות לקבצים, אך תכונה זו מבוטלת, כברירת מחדל, באמצעות הערות. השינויים היחידים שבוצעו בכל אחת מהתוכניות הללו (מיקום התוכנית המסומן ב-"USER") הם המספר הכולל של החלקיקים שיש לקחת בחשבון (Ntot), ושמות קבצי הקלט והפלט, שאמורים לשקף את מחלקת החלקיקים המנותחת.
- הפלט העיקרי מהרצת (proj-mpi-SH-LWT.f) ו-(proj2D-nonSH-LWT.f) הם קבצי נתוני הקרנה, עם מוסכמות שמות Particle-class-info-SH-proj.dat ו-Particle-class-info-nonSH-proj.dat. ניתן לחשב מגוון כמויות דו-ממדיות, כולל כאלה המשמשות שני מכשירים מסחריים שונים (Horiba Camsizer59 ו-Malvern MORPHOLOGI G360). בשני המקרים, התוכנות מחשבות גרסה דו-ממדית של L ו-W, הנקראת L2D ו-W2D.
- מבנה קובץ הפלט מפרט, עבור כל חלקיק, שטח, היקף, Xcmax, Xcmin, Fermax, Fermin, W2D, L2D, WM ו-LM, כאשר Fermax ו-Fermin הם קוטר ה-Feret המקסימלי והמינימלי ו-Xcmax ו-Xcmin מוגדרים מקוטר האקורדים שנלקחו לכיוונים שונים59. ניתן להראות באופן תיאורטי כי L2D זהה לכמות Xcmax, אותה ניתן לראות גם בקבצי הנתונים. הפרמטרים LM ו-WM הם גרסאות של L2D ו-W2D המוגדרות בצורה מעט שונה במדריך Malvern MORPHOLOGI G360. פורמט הקובץ הוא: שם/מספר חלקיקים, שטח, היקף, פרמין, פרמקס, Xcmin, Xcmax, W2D, L2D, תטא, WM, LM, slo ו-nnnF, כאשר nnnF הוא מספר מקדמי פורייה המשמשים לייצוג הקרנת החלקיקים. כמות התטא היא הזווית, במעלות, שהציר שמגדיר את WM ו-LM יוצר עם ציר ה-x 60. הכמות slo היא רק היחס בין הסינוס של תטה לקוסינוס של תטה. אף אחת מהכמויות אינה משמשת בניתוח החלקיקים המתואר כאן וכלולה רק כבדיקה של החישוב. הנתונים עבור כל חלקיק מגיעים בקבוצות של שלוש, קו אחד לכל אחת משלוש ההטלות, (1,2,3) = (L,W,T).
7. עיבוד נתונים גיאומטריים של חלקיקים תלת מימדיים ודו-ממדיים להפקת גרפים שונים
- השתמש בכל תוכנה שמוצאת חן בעיני המשתמש כדי לעבד את נתוני גודל החלקיקים וצורתם. לא משנה באיזו תוכנה משתמשים, יש לבצע הליך מסוים.
- עבור הנתונים התלת-ממדיים, שלב את נתוני SH ו-nonSH לרשימות SnS ו-NS, תוך שימוש בערכי החיתוך L/T שנקבעו בעבר עבור כל מחלקת חלקיקים. יש לחשב התפלגויות וממוצעים עבור חלקיקי SnS ו-NS בנפרד, וגם עבור נתוני SnS ו-NS המשולבים, עבור כל הפרמטרים הגיאומטריים המעניינים, כגון L, W, T, L/T, W/T, L/W, קוטר כדורי שווה נפח ואחרים.
- עבור נתוני ההקרנה הדו-ממדית, שלב את נתוני SH ו-nonSH. ישנן שלוש הטלות דו-ממדיות עבור כל חלקיק תלת-ממדי, שנלקחו לאורך וקטורי היחידה עבור L, W ו-T. שילוב כל שלושת ההקרנות הללו אמור לתת תוצאות דומות לטכניקה ניסויית שמסובבת את החלקיקים באופן אקראי לפני ביצוע הקרנה. שימוש רק בנתונים וקטוריים של יחידת L , למשל, מדמה טכניקה ניסיונית שבה החלקיקים מיושרים בערך לאורך הכיוון הארוך ביותר שלהם, בניצב לכיוון הנפילה ובמקביל לכיוון האור/הקרנה במכשיר טיפוסי.
Access restricted. Please log in or start a trial to view this content.
תוצאות
ASTM יזמה תוכנית בדיקת מיומנות (AMPM, מטלורגיית אבקת ייצור תוספים) לאבקת מתכת המשמשת לאיחוי מיטת אבקת לייזר, שבה המשתתפים מבצעים סוללה של בדיקות אבקת מתכת סטנדרטיות ו- ASTM אוסף את ההתפלגות הסטטיסטית של תוצאות אלה בדוח למשתתפים61. דגימות של אבקת מתכת מחולקות פעמיים...
Access restricted. Please log in or start a trial to view this content.
Discussion
לשיטה מבוססת XCT לאפיון הגודל והצורה התלת-ממדיים של חלקיקי מתכת יש יישומים אפשריים יותר אך גם כמה מגבלות. המגבלות יטופלו תחילה.
נעשה שימוש באפוקסי מהיר ריפוי כך שצמיגות האפוקסי גבוהה מספיק כדי למנוע מהאבקה להתיישב תחת כוח הכבידה בזמן שהאפוקסי מתרפא, או לפח?...
Access restricted. Please log in or start a trial to view this content.
Disclosures
למחברים אין מה לחשוף.
Acknowledgements
המחברים רוצים להכיר בתמיכה ארוכת הטווח של NIST לניתוח אבקה תלת מימדית.
Access restricted. Please log in or start a trial to view this content.
Materials
| Name | Company | Catalog Number | Comments |
| Epoxy | Ellsworth Adhesives https://www.ellsworth.com/products/adhesives/epoxy/hardman-doublebubble-extra-fast-set-epoxy-red-package-3.5-g-packet/ | Hardman Part # 4001 | case of 100 |
References
- Allen, T. Powder Sampling and Particle Size Determination, 1st edition. , Elsevier Science. (2003).
- Rodriguez, J., Edeskär, T., Knutsson, S. Particle shape quantities and measurement techniques: a review. Electron Journal of Geotechnical Engineering. , 18(2013).
- Garboczi, E. J., Douglas, J. F. Intrinsic conductivity of objects having arbitrary shape and conductivity. Physical Review E. 53, 6169-6180 (1996).
- Mansfield, M. L., Douglas, J. F., Garboczi, E. J. Intrinsic viscosity and the electrical polarizability of arbitrarily shaped objects. Physical Review E. 64, 61401-61416 (2001).
- Garboczi, E. J., Douglas, J. F., Bohn, R. B. A hybrid finite element-analytical method for determining the intrinsic elastic moduli of particles having moderately extended shapes and a wide range of elastic properties. Mechanics of Materials. 38, 786-800 (2006).
- Garboczi, E. J., Douglas, J. F. Elastic Moduli of Composites Containing a Low Concentration of Complex-Shaped Particles Having a General Property Contrast with the Matrix. Mechanics of Materials. 5, 53-65 (2012).
- Audus, D. J., Hassan, A. M., Garboczi, E. J., Hudson, S. D., Douglas, J. F. Interplay of particle shape and suspension properties: A study of cube-like particles. Soft Matter. 11, 3360-3366 (2015).
- Garboczi, E. J., Bullard, J. W. Shape analysis of a reference cement. Cement and Concrete Research. 34, 1933-1937 (2004).
- Masad, E., Saadeh, S., Al-Rousan, T., Garboczi, E. J., Little, D. Computations of particle surface characteristics using optical and x-ray CT images. Computational Materials Science. 34, 406-424 (2005).
- Cheok, G. S., Stone, W. C., Garboczi, E. J. Using LADAR to characterize the 3-D shape of aggregates: Preliminary results. Cement and Concrete Research. 36, 1072-1075 (2006).
- Mahmoud, E., Gates, L., Masad, E., Garboczi, E. J. Comprehensive Evaluation of AIMS Texture, Angularity, and Dimensions Measurements. Journal of Materials in Civil Engineering. 22, 369-379 (2010).
- Erdoğan, S. T., Nie, X., Stutzman, P. E., Garboczi, E. J. Micrometer-scale 3-D imaging of eight cements: Particle shape, cement chemistry, and the effect of particle shape on laser diffraction size analysis. Cement and Concrete Research. 40, 731-739 (2010).
- Holzer, L., Flatt, R., Erdoğan, S. T., Nie, X., Garboczi, E. J. Shape comparison between 0.4 µm to 2.0 µm and 20 µm to 60 µm cement particles. Journal of the American Ceramic Society. 93, 1626-1633 (2010).
- Erdoğan, S. T., Fowler, D. W., Garboczi, E. J. Shape and size of microfine aggregates: X-ray microcomputed tomography vs. laser diffraction. Powder Technology. 177, 53-63 (2007).
- Garboczi, E. J., Liu, X., Taylor, M. A. The Shape of a Blasted and Crushed Rock Material over More than Three Orders of Magnitude: 20 µm to 60 mm. Powder Technology. 229, 84-89 (2012).
- Cepuritis, R., Wigum, B. J., Garboczi, E. J., Mørtsell, E., Jacobsen, S. Filler from crushed aggregate for concrete: Pore structure, specific surface, particle shape and size distribution. Cement and Concrete Composites. 54, 2-16 (2014).
- Cepuritis, R., Garboczi, E. J., Jacobsen, S., Snyder, K. A. Comparison of 2-D and 3-D shape analysis of concrete aggregate fines from VSI crushing. Powder Technology. 309, 110-125 (2017).
- Cepuritis, R., Garboczi, E. J., Jacobsen, S. Three-dimensional shape analysis of concrete aggregate fines produced by VSI crushing. Powder Technology. 308, 410-421 (2017).
- Cepuritis, R., Garboczi, E. J., Ferraris, C. F., Jacobsen, S., Sørensen, B. E. Measurement of particle size distribution and specific surface area for crushed concrete aggregate fines. Advanced Powder Technology. 28, 7065(2017).
- Erdogan, S. T., Forster, A. M., Stutzman, P. E., Garboczi, E. J. Particle-based characterization of Ottawa sand: Shape, size, mineralogy, and elastic moduli. Cement and Concrete Composites. 83, 36-44 (2017).
- Olivas, A., et al. Certification of SRM 2493: Standard Reference Mortar for Rheological Measurements. NIST Special Publication. , 260(2017).
- Martys, N., Peltz, W., George, W., Toman, B., Garboczi, E. J. Certification of SRM 2497: Standard Reference Concrete for Rheological Measurement, NIST SP1237. , (2019).
- Estephane, P., Garboczi, E. J., Bullard, J. W., Wallevik, O. H. Three-dimensional shape characterization of fine sands and the influence of particle shape on the packing and workability of mortars. Cement and Concrete Composites. 97, 125-142 (2019).
- Slotwinski, J. A., et al. Characterization of Metal Powders Used for Additive Manufacturing. Journal of Research of the National Institute of Standards and Technology. 119, (2014).
- Grell, W. A., et al. Effect of powder oxidation on the impact toughness of electron beam melting Ti-6Al-4V. Additive Manufacturing. 17, 123-134 (2017).
- Garboczi, E. J., Hrabe, N. Particle shape and size analysis for metal powders used for additive manufacturing: Technique description and application to a gas-atomized Ti64 powder and a plasma-atomized Ti64 powder. Additive Manufacturing. 31, 100965(2020).
- Garboczi, E. J. Three-Dimensional Shape Analysis of JSC-1A Simulated Lunar Regolith Particles. Powder Technology. 207, 96-103 (2011).
- Chiaramonti, A. N., Goguen, J. D., Garboczi, E. J. Quantifying the 3-Dimensional Shape of Lunar Regolith Particles Using X-Ray Computed Tomography and Scanning Electron Microscopy at Sub-λ Resolution. Microscopy and Microanalysis. 23, Suppl 1 (2017).
- Escobar-Cerezo, J., et al. An Experimental Scattering Matrix for Lunar Regolith Simulant JSC-1A at Visible Wavelengths. The Astrophysical Journal Supplement Series. 235, 19(2018).
- Hu, M., Zhang, T., Stansbury, J., Neal, J., Garboczi, E. J. Determination of Porosity and Thickness of Biofilm Attached on Irregular-Shaped Media. Journal of Environmental Engineering. 139 (7), 923-931 (2013).
- Garboczi, E. J., Riding, K. A., Mirzahosseini, M. Particle shape effects on particle size measurement for crushed waste glass. Advanced Powder Technology. 28, 648-657 (2017).
- Baidya, S., et al. Analysis of Different Computational Techniques for Calculating the Polarizability Tensors of Stem Cells with Realistic Three-Dimensional Morphologies. IEEE Transactions on Biomedical Engineering. , (2018).
- Vargas-Lara, F., Hassan, A. M., Garboczi, E. J., Douglas, J. F. Intrinsic Conductivity of Carbon Nanotubes and Graphene Sheets Having a Realistic Geometry. Journal of Chemical Physics. 143, 204902(2015).
- Hassan, A. M., Vargas-Lara, F., Douglas, J. F., Garboczi, E. J. Electromagnetic Resonances of Individual Single-Walled Carbon Nanotubes with Realistic Shapes: A Characteristic Modes Approach. IEEE Transactions on Antennas and Propagation. 64, 2743(2016).
- Durbhakula, K. C., et al. Electromagnetic Scattering From Individual Crumpled Graphene Flakes: A Characteristic Modes Approach. IEEE Transactions on Antennas and Propagation. 65, 6035(2017).
- Hassan, A. M., et al. Electromagnetic Scattering from Multiple Single-Walled Carbon Nanotubes Having Tumbleweed Configurations. IEEE Transactions on Antennas and Propagation. 65, (2017).
- Malavé, V., Killgore, J. P., Garboczi, E. J., Berger, J. R. Decoupling the effects of surface topography and material heterogeneity on indentation modulus: A simple numerical linear-elastic model. International Journal of Solids and Structures. 124, 235-243 (2017).
- Garboczi, E. J. The influence of particle shape on the results of the electrical sensing zone method as explained by the particle intrinsic conductivity. Powder Technology. 322, 32-40 (2017).
- Garboczi, E. J. Three-dimensional mathematical analysis of particle shape using x-ray tomography and spherical harmonics: Application to aggregates used in concrete. Cement and Concrete Research. 32, 1621-1638 (2002).
- Erdoğan, S. T., et al. Three-dimensional shape analysis of coarse aggregates: New techniques for and preliminary results on several different coarse aggregates and reference rocks. Cement and Concrete Research. 36, 1619-1627 (2006).
- Taylor, M. A., Garboczi, E. J., Erdoğan, S. T., Fowler, D. W. Some properties of irregular particles in 3-D. Powder Technology. 162, 1-15 (2006).
- Garboczi, E. J., Bullard, J. W. Contact function, uniform-thickness shell volume, and convexity measure for 3D star-shaped random particles. Powder Technology. 237, 191-201 (2013).
- Bullard, J. W., Garboczi, E. J. Defining shape measures for 3D star-shaped particles: Sphericity, roundness, and dimensions. Powder Technology. 249, 241-252 (2013).
- Jia, X., Garboczi, E. J. Advances in shape measurement in the digital world. Particuology. 26, 19-31 (2016).
- Garboczi, E. J., Bullard, J. W. 3D analytical mathematical models of random star-shape particles via a combination of X-ray computed microtomography and spherical harmonic analysis. Advanced Powder Technology. 28, 325-339 (2017).
- Qian, Z., Garboczi, E. J., Ye, G., Schlangen, E. Anm: A geometrical model for the composite structure of mortar and concrete using real-shape particles. Materials and Structures. 49 (1), 149-158 (2015).
- Thomas, S., Lu, Y., Garboczi, E. J. Improved model for 3-D virtual concrete: Anm model. Journal of Computing in Civil Engineering. , (2015).
- Zuo, Y., Qian, Z., Garboczi, E. J., Ye, G. Numerical simulation of the initial particle parking structure of cement/geopolymer paste and the dissolution of amorphous silica using real-shape particles. Construction and Building Materials. 185, 206-219 (2018).
- Lu, Y., Islam, A., Thomas, S., Garboczi, E. J. Three-dimensional mortar models using real-shaped sand particles and uniform thickness interfacial transition zones: Artifacts seen in 2D slices. Construction and Building Materials. 236, 117590(2020).
- Grigoriu, M., Garboczi, E. J., Kafali, C. Spherical harmonic-based random fields for aggregates used in concrete. Powder Technology. 166, 123-138 (2006).
- Liu, X., Garboczi, E. J., Grigoriu, M., Lu, Y., Erdoğan, S. T. Spherical harmonic-based random fields based on real particle 3D data: Improved numerical algorithm and quantitative comparison to real particles. Powder Technology. 207, 78-86 (2011).
- Stauffer, D., Aharony, A. Introduction To Percolation Theory: Revised, second edition. , Taylor & Francis. London. (1994).
- Bentz, D. P., Garboczi, E. J. Percolation of phases in a three-dimensional cement paste microstructural model. Cement and Concrete Research. 21, 325-344 (1991).
- Garboczi, E. J., Snyder, K. A., Douglas, J. F., Thorpe, M. F. Geometrical percolation threshold of overlapping ellipsoids. Physical Review E. 52, 819-828 (1995).
- Garboczi, E. J., Bentz, D. P. Computer simulation and percolation theory applied to concrete, in. Annual Reviews of Computational Physics VII. Stauffer, D. , World Scientic. Singapore. 85-123 (2000).
- Garboczi, E. J. Percolation phase diagrams for multi-phase models built on the overlapping sphere model. Physica A: Statistical Mechanics and its Applications. 442, 156-168 (2016).
- Fernlund, J. M. R. The effect of particle form on sieve analysis: a test by image analysis. Engineering Geology. 50 (1), 111-124 (1998).
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Transactions on Systems, Man, and Cybernetics. 9, 62-66 (1979).
- Horiba. , Available from: https://www.horiba.com/fileadmin/uploads/Scientific/Documents/PSA/Manuals/CAMSIZER_Characteristics_Nov2009.pdf (2020).
- Malvern MORPHOLOGI G3. , Available from: https://www.malvernpanalytical.com/en/support/product-support/morphologi-range/morphologi-g3 (2020).
- ASTM. , Available from: https://www.astm.org/STATQA/Additive_Manufacturinng_Powder_Metallurgy.htm (2020).
- Bain, E., Garboczi, E. J., Seppala, J., Parker, T., Migler, K. AMB2018-04: Benchmark Physical Property Measurements for Powder Bed Fusion Additive Manufacturing of Polyamide 12. Integrating Materials and Manufacturing Innovation. , (2019).
- du Plessis, A., Sperling, P., Beerlink, A., du Preez, W., le Roux, S. G. Standard method for microCT-based additive manufacturing quality control 4: Metal powder analysis. MethodsX. 5, 1336-1345 (2018).
- DeCost, B. L., Jain, J., Rollett, A. D., Holm, E. A. Computer vision and machine learning for autonomous characterization for AM powder feedstocks. JOM. 69, 456-465 (2017).
- DeCost, B. L., Holm, E. A. Characterizing powder materials using keypoint-based computer vision methods. Computational Materials Science. 126, 438-445 (2017).
Access restricted. Please log in or start a trial to view this content.
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionExplore More Articles
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved