Induktion von Mikroströmungen durch nichtsphärische Blasenschwingungen in einem akustischen Levitationssystem

Zusammenfassung

Es wird eine schnelle und zuverlässige Technik vorgeschlagen, um die Formschwingungen einer einzelnen, gefangenen akustischen Blase zu kontrollieren, die auf der Koaleszenztechnik zwischen zwei Blasen basiert. Die stationären, symmetriegesteuerten Blasenformoszillationen ermöglichen die Analyse der Fluidströmung, die in der Nähe der Blasengrenzfläche erzeugt wird.

Zusammenfassung

Wenn sie sich in der Nähe biologischer Barrieren befinden, können oszillierende Mikrobläschen die Durchlässigkeit der Zellmembran erhöhen und so die Internalisierung von Medikamenten und Genen ermöglichen. Experimentelle Beobachtungen deuten darauf hin, dass die vorübergehende Permeabilisierung dieser Barrieren auf Scherbeanspruchung zurückzuführen sein könnte, die durch Kavitations-Mikrostreaming auf das Zellgewebe ausgeübt wird. Kavitations-Mikrostreaming ist die Erzeugung von Wirbelströmungen, die um oszillierende Ultraschall-Mikrobläschen entstehen. Um solche Flüssigkeitsströmungen zu erzeugen, müssen Blasenschwingungen von rein sphärischen Schwingungen abweichen und entweder eine Translationsinstabilität oder Formmoden enthalten. Experimentelle Untersuchungen von blaseninduzierten Strömungen und Scherspannungen auf benachbarten Oberflächen sind oft in ihrem Umfang eingeschränkt, da es schwierig ist, Formverformungen von Mikrobläschen stabil und kontrollierbar zu erfassen. Wir beschreiben den Aufbau einer akustischen Schwebekammer zur Untersuchung symmetriegesteuerter nichtsphärischer Schwingungen. Eine solche Kontrolle erfolgt durch die Verwendung einer Koaleszenztechnik zwischen zwei sich nähernden Blasen in einem ausreichend intensiven Ultraschallfeld. Die Kontrolle nichtsphärischer Schwingungen eröffnet den Weg zu einer kontrollierten Kavitations-Mikroströmung einer freien oberflächenoszillierenden Mikroblase. Kameras mit hoher Bildrate ermöglichen es, quasi gleichzeitig die nicht-sphärische Blasendynamik auf der akustischen Zeitskala und die Flüssigkeitsströmung auf einer niedrigeren Zeitskala zu untersuchen. Es wird gezeigt, dass eine große Vielfalt von Fluidmustern erhalten werden kann und dass diese mit dem modalen Inhalt der Blasengrenzfläche korreliert sind. Wir zeigen, dass selbst die Formmoden hoher Ordnung Fluidmuster über große Entfernungen erzeugen können, wenn die Grenzflächendynamik mehrere Moden enthält, was das Potenzial von nicht-sphärischen Oszillationen für eine gezielte und lokalisierte Wirkstoffabgabe unterstreicht.

Einleitung

In der Medizin muss ein verabreichtes Medikament viele Hindernisse im lebenden System durchdringen, bevor es die gewünschten Ziele erreicht. Die meisten Medikamente werden jedoch schnell aus dem Blutkreislauf entfernt. Die Targeting-Effizienz ist gering und sie können die Zellmembranen nicht leicht durchdringen, was zu einer unwirksamen Wirkstoffabgabe führt. Derzeit wird die Verwendung von Mikrobläschen in Kombination mit Ultraschall als innovative Methode für die nicht-invasive, präzise und gezielte Verabreichung von Medikamenten und Genen an pathologische Gewebe und Zellen vorgeschlagen¹. Bei diesem Ansatz können Mikrobläschen als Träger eine Rolle spielen, bei denen freie Medikamente entweder mit einer Gasblasensuspension co-injiziert oder auf deren Oberfläche geladen werden. Mikrobläschen können auch als lokaler Vektor für die Neufokussierung der Ultraschallenergie fungieren, um mit den Zellen zu interagieren. Grundsätzlich komprimieren und dehnen sich Blasen unter Ultraschallbestrahlung stabil aus, ein Bereich, der als stabile Kavitation bezeichnet wird und Flüssigkeitsströme und damit Scherspannungen auf nahe gelegene Objekte erzeugt. Mikrobläschen können auch nichtlinear schwingen und sich im Bereich der Trägheitskavitation bis zum Kollaps ausdehnen, wobei Stoßwellen erzeugt werden, die sich radial von der Kollapsstelle² ausbreiten. Es hat sich gezeigt, dass Kavitation, ob stabil oder träge, die Permeabilisierung von Zellmembranen und damit die Internalisierung von Medikamenten in die Zelle verbessert³.

In therapeutischen Anwendungen ist es sehr wichtig, den Mechanismus der Blasen-Zell-Interaktion zu verstehen, aber es gibt mehrere Hindernisse, sowohl von wissenschaftlicher als auch von technischer Seite, die unseren Wissensfortschritt verhindern. Erstens ist es sehr schwierig, die Dynamik von Zellen als Reaktion auf blaseninduzierte mechanische Reize zu erfassen⁴. Auf der akustischen Zeitskala können die Mikroblasenoszillationen erster Ordnung zu einer Aktivierung von Membrankanälen führen, was die molekulare Passage über biologische Grenzflächen erleichtert. Dies geschieht durch die direkte Schwingung der Zellmembran, auch "Zellmassage" ^genannt5. Die Kanalaktivierung nach direkter mechanischer Belastung wurde mit Hilfe von Patch-Clamp-Techniken nachgewiesen, die die elektrophysiologischen Eigenschaften der Zellmembranen während und nach der Ultraschallexposition messen⁶. Die Messung der blaseninduzierten Zelldynamik (d.h. des gesamten Verformungsfeldes der Zellmembran) auf der akustischen Zeitskala würde auch Einblicke in den Schwellenwert der Membranflächenausdehnung Δ A/A liefern, der erforderlich ist, um Poren in die Zellmembran zu induzieren⁷. Die zweite Barriere besteht darin, das kollabierende Blasenregime zu kontrollieren, um eine durch Mikrobläschen induzierte Zelllyse zu vermeiden. Blasenkollapse und induzierte Mikrojets wurden als ein Mechanismus identifiziert, durch den die Perforation der Membran erfolgt ^8,9. Nach der Permeabilisierung repariert sich die Zellmembran durch Kalziumselbstabdichtung der Lipiddoppelschichten und Fusion intrazellulärer Vesikel⁹. Das Auftreten von Blasenkollapsen kann auch tödliche Schäden an der Zelle verursachen und unnötige Nebenwirkungen in der Umgebung hervorrufen. Bei sensiblen Anwendungen, wie z. B. der ultraschallvermittelten Öffnung der Blut-Hirn-Schranke, ist es allgemein anerkannt, dass Trägheitsblasenkollapse vermieden werden sollten¹⁰.

Daher werden derzeit große Anstrengungen in die Entwicklung von Ultraschall-Emissionssequenzen in Verbindung mit passiver Kavitationsüberwachung und -steuerung gesteckt, um stabile Schwingungen von Mikrobläschen^{zu gewährleisten 11}. In diesem stabilen Regime wurde die Hypothese aufgestellt, dass stabil oszillierende Blasen eine wichtige Rolle bei der Auslösung der Membranpermeabilisierung spielen, indem sie eine räumlich gezielte Scherspannung auf die Zellmembran^{fördern 7}. Die Scherspannung ergibt sich aus den Flüssigkeitsströmen, die in der Nähe der oszillierenden Blasen entstehen. Diese Flüssigkeitsströmungen werden als Kavitations-Mikrostreaming bezeichnet und sind, wie oben erwähnt, einer von mehreren möglichen Mechanismen, die für eine verstärkte Aufnahme extrazellulärer Moleküle verantwortlich sind. Bei der Suspension von Blasen oder Zellen, wie z. B. bei biologischen In-vitro-Transfektionsassays¹², könnte die Permeabilisierung durch Mikrostreaming viel effizienter sein als die Permeabilisierung durch Blasenkollaps. Dies kann durch eine einfache geometrische Betrachtung gezeigt werden. Bei Zellsuspensionen ist die Sonoporation effizient, wenn der Großteil der suspendierten Zellen ausreichend großen mechanischen Effekten ausgesetzt ist (was zu einer Membranpermeabilisierung führt). Es ist bekannt, dass Blasenkollapse entlang der Richtung der isotropen Symmetriebrechung gerichtet sind, wie z. B. die Blasenwandachse¹³ oder die Blasen-Blase- und Blasenzellenlinie, die ihren Massenschwerpunkt¹⁴ verbinden. Der erzeugte Mikrojet ist also ein räumlich lokalisiertes Phänomen entlang einer endlichen Anzahl von Linien, die die Zell- und Blasenzentren verbinden. Abhängig von der Zell- und Blasenkonzentration sowie dem Abstand zwischen Blase und Zelle ist dieser Effekt möglicherweise nicht der effizienteste, um die gesamte Anzahl der suspendierten Zellen zu permeabilisieren. Im Gegensatz dazu ist Kavitations-Microstreaming ein Phänomen, das auf einer langsamen Zeitskala auftritt und im Vergleich zum Blasenradius eine große räumliche Ausdehnung aufweist. Außerdem ist der Flüssigkeitsstrom um die Blase herum verteilt und kann daher eine größere Anzahl von Zellen in einer sehr großen Entfernung beeinflussen. Daher ist das Verständnis der erzeugten Kavitations-Mikroströmung um eine oszillierende Blase eine Voraussetzung für die Kontrolle und Quantifizierung der blaseninduzierten Scherspannung, die auf Zellen ausgeübt wird.

Zu diesem Zweck besteht ein vorbereitender Schritt darin, die sphärischen und nichtsphärischen Schwingungen einer ultraschallgetriebenen Blase zu steuern, da die erzeugten Flüssigkeitsströme durch die Bewegung der Blasengrenzfläche^{15, 16} induziert werden. Insbesondere müssen Formschwingungen von Mikrobläschen ausgelöst und stabil gehalten werden. Darüber hinaus muss die Orientierung der blasenförmigen Oszillationen kontrolliert werden, um die Korrelation zwischen der Dynamik der Blasengrenzfläche und dem induzierten Mikroströmungsmuster zu analysieren. Fasst man die vorhandene Literatur zusammen, so fällt auf, dass detaillierte experimentelle Ergebnisse des kavitationsinduzierten Mikrostreamings nur für Blasen vorliegen, die an einer Oberfläche haften. An der Wand befestigte Mikrobläschen werden häufig verwendet, um die genaue Grenzflächendynamik und Zellinteraktionen auf der Mikrometerskala unter einem ultraschnellen Mikroskopiesystem zu beurteilen. Diese Konfiguration ist therapeutisch relevant, wenn vibrierende Mikrobläschen auf der Zellmembran^17,18,19 betrachtet werden. Die Untersuchung von substratgebundenen Blasen kann jedoch die Analyse der Blasendynamik komplizierter machen, was zum Teil auf die komplexe Natur der Kontaktliniendynamik²⁰ und das Auslösen asymmetrischer Formmoden²¹ zurückzuführen ist. In medizinischen und biologischen Anwendungen finden sich Blasen, die nicht an einer Wand befestigt sind, häufig in begrenzten Geometrien wie kleinen Gefäßen. Dies wirkt sich erheblich auf die Blasendynamik und Forminstabilitäten aus. Insbesondere verschiebt das Vorhandensein einer Wand in der Nähe die Druckschwelle für das Auslösen des Formmodus auf niedrigere Druckwerte in Abhängigkeit von der Anzahl der Formformen und der Blasengröße²². Die Wand wirkt sich auch auf die blaseninduzierte Mikroströmung mit möglicherweise höherer Intensität für die erzeugte Strömung²³ aus.

Unter all den möglichen Szenarien, die Mikrobläschen erleben können (frei oder anhaftend, in der Nähe einer Wand, kollabierend oder stabil oszillierend), schlagen wir vor, die nichtsphärische Dynamik einer einzelnen Blase weit weg von jeder Grenze zu untersuchen. Der Versuchsaufbau basiert auf einem akustischen Levitationssystem²⁴, bei dem eine stehende Ultraschallwelle verwendet wird, um die Blase einzufangen. Dieses Szenario steht im Einklang mit medizinischen Anwendungen, bei denen beispielsweise eine Ansammlung von Schwebeblasen und Zellen in einer Sonotransfektionskammer koexistieren. Soweit Blasen und Zellen nicht zu nahe beieinander liegen, wird angenommen, dass das Vorhandensein einer Zelle keinen Einfluss auf die Dynamik der Blasengrenzfläche hat. Wenn Zellen den schleifenartigen Trajektorien der kavitationsinduzierten Mikroströmung folgen, nähern sie sich zyklisch der Blasenposition und stoßen sich von ihr ab, und wir können davon ausgehen, dass die Anwesenheit der Zelle weder das Strömungsmuster noch ihre mittlere Geschwindigkeit beeinflusst. Darüber hinaus sind aus theoretischer Sicht nichtsphärische Dynamik und induzierte Mikroströmungen aus einzelnen Blasen, die weit von der Grenze entfernt sind, bekannt. Um die blaseninduzierte Flüssigkeitsströmung mit der Dynamik der Blasenkontur zu verknüpfen, ist es erforderlich, die Dynamik der Blasengrenzfläche genau zu charakterisieren. Um dies zu erreichen, ist es vorzuziehen, die räumlich-zeitliche Skala in experimentellen Studien so anzupassen, dass die Aufnahme mit herkömmlichen Hochgeschwindigkeitskameras (unter 1 Million Bildern/Sekunde) durch die Verwendung großer Blasen, die bei niedrigeren Frequenzen angeregt werden, möglich ist. Bei der Betrachtung von unbeschichteten Blasen wird die Eigenfrequenz ω n einer gegebenen Mode _n mit der Blasengröße 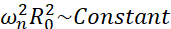als ²⁵ in Beziehung gesetzt. Diese Radius-Eigenfrequenz-Beziehung wird bei der Betrachtung von geschälten Blasen²⁶ leicht modifiziert, aber die Größenordnung der Eigenfrequenz ω_n bleibt gleich. Daher ist die Untersuchung von Blasen mit Gleichgewichtsradien ~50 μm in einem 30-kHz-Ultraschallfeld vergleichbar mit der Untersuchung von beschichteten Blasen mit Radien ~3 μm in einem 1,7-MHz-Feld, wie von Dollet et ^al.27 vorgeschlagen. Es werden daher ähnliche Shape-Mode-Nummern und damit Microstreaming-Muster erwartet.

Um nicht-sphärische Schwingungen der Blasengrenzfläche auszulösen, ist es notwendig, eine bestimmte Druckschwelle zu überschreiten, die radiusabhängig ist, wie in Abbildung 1 dargestellt. Bestehende experimentelle Techniken beruhen auf der Erhöhung des Schalldrucks, um Oberflächenmoden auszulösen (dargestellt durch Pfad (1) in 1), entweder durch eine schrittweise Druckerhöhung²⁸ oder durch eine Anregung mit modulierter Amplitude, die für das periodische Einsetzen und Erlöschen von Oberflächenmoden²⁹ verantwortlich ist. Die Hauptnachteile dieser Techniken sind (i) eine zufällige Ausrichtung der Symmetrieachse der Oberflächenschwingungen, die nicht kontrolliert werden kann, um sich in der Abbildungsebene zu befinden, (ii) eine kurze Lebensdauer der blasenförmigen Oszillationen, die die Analyse der induzierten Flüssigkeitsströmungen auf größeren Zeitskalen erschwert, und (iii) das häufige Auslösen instabiler Formmoden. Wir schlagen eine alternative Technik vor, um die Druckschwelle bei konstantem Schalldruck in der Radius-/Druckkarte zu überschreiten, wie durch den Pfad (2) in Abbildung 1 dargestellt. Dazu ist es erforderlich, die Blasengröße so zu erhöhen, dass sie sich in der Instabilitätszone befindet. Eine solche Erhöhung wird durch eine Blasenkoaleszenztechnik durchgeführt. Die Verschmelzung zweier, zunächst kugelförmig oszillierender Mikrobläschen wird ausgenutzt, um eine einzige deformierte Blase zu erzeugen. Wenn der Schalldruck und die Blasengröße der koaleszierten Blase in der Instabilitätszone liegen, werden Oberflächenmoden ausgelöst. Wir konnten auch zeigen, dass die Koaleszenztechnik stabile Formoszillationen in einem stationären Zustand induziert, sowie eine kontrollierte Symmetrieachse, die durch die geradlinige Bewegung der beiden sich nähernden Blasen definiert wird. Da eine stabile Formoszillation über Minuten gewährleistet ist, ist die Analyse der blaseninduzierten Flüssigkeitsströmung möglich, indem das flüssige Medium mit fluoreszierenden Mikropartikeln bestückt wird, die von einer dünnen Laserschicht beleuchtet werden. Die Aufzeichnung der Bewegung der festen Mikropartikel in der Nähe der Blasengrenzfläche ermöglicht die Identifizierung des Musters der induzierten Fluidströmung³⁰. Das Gesamtprinzip der Auslösung blasenförmiger Oszillationen, die zu einer zeitstabilen Fluidströmung führen, ist in Abbildung 2 dargestellt.

Im folgenden Protokoll skizzieren wir die Schritte, die erforderlich sind, um stabile blasenförmige Oszillationen mit der Koaleszenztechnik zu erzeugen, und beschreiben die Messungen des Flüssigkeitsflusses. Dazu gehören das Design des akustischen Levitationssystems, die akustische Kalibrierung, die Blasennukleation und die Koaleszenztechnik, die Messung der Blasengrenzflächendynamik und der umgebenden Flüssigkeitsströmung sowie die Bildverarbeitung.

Protokoll

1. Aufbau der akustischen Schwebekammer

1. Entwerfen Sie einen optisch transparenten (PMMA-ähnlichen) kubischen Tank (8 cm Kante und 2,8 mm Dicke pro Fläche) mit dem Geometriemodul einer multiphysikalischen Simulationssoftware (Table of Materials).
2. Setzen Sie eine zylindrische Fläche (Ø = 35 mm) mittig am Boden des Tanks ein, um den Ultraschallwandler zu modellieren.
3. Stellen Sie die Randbedingungen an jeder Wand mit einer normalen Verschiebung von 1 μm an der Wandleroberfläche auf Druck Null ein.
4. Simulieren Sie mit einem Frequenzbereichsmodul die Frequenzgangfunktion (FRF) des Tanks im Frequenzbereich [10 - 40] kHz an den drei beliebigen Positionen loc1 = (0,01375, 0,01375, 0,04125), loc2 = (0, 0, 0,0088) und loc3 = (0,021725, 0,023375, 0,00935).
5. Passen Sie die Tankgröße so an, dass eine der akustischen Moden des Hohlraums der Nennfrequenz des Wandlers (hier 31,2 kHz) entspricht. Der FRF enthält daher eine Resonanzspitze in der Nähe dieser Frequenz, wie in Abbildung 3 dargestellt.
6. Zeichnen Sie das Druckfeld im Inneren des Tanks auf, wie in Abbildung 4 dargestellt. Der gewählte Resonanzmodus muss mindestens einen Druckknoten im Inneren des Behälters enthalten, an dem die akustische Blase eingeschlossen wird.
7. Entwerfen Sie bei der Konstruktion des Tanks eine bewegliche Oberseite mit einer Führungsnut an jeder Kante, um die Tankflächen fest zu schließen. Bohren Sie ein winziges Loch in die Oberseite, um den Tank mit dem flüssigen Medium zu füllen.
8. Stellen Sie den Wassertank auf einen selbstgebauten Rahmen, in dem sich der Ultraschallwandler (Langevin-Typ, 31,2 kHz Nennfrequenz) befindet. Verwenden Sie echographisches Gel, um den Wandler an die Bodenwand des Tanks anzukoppeln.
9. Platzieren Sie den Tank und das Rahmensystem auf einem Drei-Richtungs-Verdrängungstisch mit mikrometrischen Schrauben.
10. Füllen Sie den Tank mit mikrofiltristem, demineralisiertem und nicht entgastem Wasser (Volumen ~500 ml, Sauerstoffsättigung von ca. 8 mg· ^L-1).
    HINWEIS: Die Verwendung von nicht entgastem Wasser anstelle von entgastem Wasser ermöglicht es, stabile Blasen für die Dauer der Experimente aufrechtzuerhalten. Die Verwendung von entgastem Wasser beschleunigt das Schrumpfen der Blase aufgrund der Gasdiffusion, auch wenn es durch eine gleichgerichtete (ultraschallvermittelte) Diffusion leicht ausgeglichen wird.

2. Blasenerzeugung und akustische Kalibrierung

1. Bereiten Sie den Versuchsaufbau vor, der für die laserinduzierte Blasennukleation, die akustische Anregung und die Hochgeschwindigkeitsaufzeichnung verwendet wird (Abbildung 5a,b,c). Der Versuchsaufbau besteht aus (A) dem akustischen Schwebesystem, (B) der Laserstromversorgung und (C) dem Laserkopf, (D) einer sphärischen konkaven Linse, (E) einer plankonkaven Linse und einer asphärischen Linse, (F) der Hochgeschwindigkeitskamera, (G) der kontinuierlichen Leuchtdiode. Später wird für Messungen von Flüssigkeitsströmungen (Abbildung 5d) (H) eine Dauerstrich-Laserquelle, (I) eine zylindrische plankonkave Linse, gefolgt von einer zylindrischen plankonkaven Linse, die hinter der ersten Linse eingesetzt und auf der orthogonalen Achse ausgerichtet ist, hinzugefügt.
2. Schließen Sie den Ultraschallwandler an einen Funktionsgenerator an. Stellen Sie das Erregersignal wie folgt ein: sinusförmige Wellenform, Dauerstrich, Frequenz 31,2 kHz. Die Amplitude ist der einzige variable Parameter.
3. Platzieren Sie die Linse (D) in einem Abstand von ca. 6 cm vor dem Laserkopf (C).
4. Platzieren Sie die Linse (E) in einem Abstand von ca. 12 cm vor der Linse (D).
5. Platzieren Sie den Wassertank (A) so, dass sich ein Fokuspunkt des Lasers im Wassertank befindet, was zu einer Funkenbildung bei jedem Laserpuls (5 -10 mJ) führt. Der Laserfunke sollte sich ca. 3 cm unterhalb des anvisierten Druckknotens befinden.
   HINWEIS: Ohne Ultraschall (US) steigt die lasernukleierte Blase aufgrund des Auftriebs auf die Oberseite.
6. Schalten Sie den Ultraschallwandler ein. Erhöhen Sie die angelegte Spannung, bis die Blase nicht mehr senkrecht aufsteigt, sondern in Richtung des Druckknotens abgelenkt und für einen ausreichend hohen Druck eingeschlossen wird.
7. Stellen Sie die Hintergrundbeleuchtung (Dauerleuchtdiode) und die Hochgeschwindigkeitskamera so ein, dass die eingeschlossene Blase beobachtet wird.
   HINWEIS: Beim Nukleieren einer neuen Blase mit einem Laserfunken ist es einfach, die Flugbahn der Blase zu erfassen, die sich ihrem Einfangort nähert.
8. Verschieben Sie die Position des Laserfunkens im Wassertank so, dass die Blasenbahn innerhalb der Fokusebene der Kamera bleibt.
9. Fangen Sie eine Blase ein und erfassen Sie ihre radialen Schwingungen mit den folgenden Parametern: Bildgröße 128 x 128 Pixel, Erfassungsrate 180 kHz. Ein Beispiel für radiale Schwingungen mit großer Amplitude über zwei akustische Perioden ist in Abbildung 6 dargestellt. Typische Gasblasengrößen liegen zwischen 30 und 80 μm.
10. Zeichnen Sie die radialen Blasenschwingungen während 3 bis 30 Millisekunden auf, um Hunderte bis Tausende von Blasenschwingungen zu erfassen. Wiederholen Sie diese Aufzeichnung, um die angelegten Spannungen des Wandlers zu erhöhen. Typische angelegte Spannungen liegen im Bereich von 0 - 8 V.
    Anmerkungen: Wenn Sie die angelegte Spannung ändern, verschiebt sich die Gleichgewichtsposition der eingeschlossenen Blase leicht vertikal. Um den Schwingungen zu folgen, ohne die Hintergrundbeleuchtung und die Kamera zu bewegen, stellen Sie das System (Wandler und Wassertank) mikrometrisch genau auf einen in drei Richtungen beweglichen Tisch.
11. Schalten Sie den Ultraschallwandler ein und nehmen Sie ein Bild des Hintergrunds für die Nachanalyse auf.
12. Bearbeiten Sie die Videoserie wie folgt nach:
    1. Führen Sie die ausführbare Datei VoltagePressure.exe aus. Die in Abbildung 7 gezeigte Schnittstelle sollte geöffnet werden.
       HINWEIS: Das Skript ist als ergänzendes Dokument verfügbar.
    2. Geben Sie die physikalischen und experimentellen Parameter in der linken Spalte an (Abbildung 7A).
    3. Geben Sie die Werte der angelegten Spannung für die Aufzeichnungsreihe in der Tabelle unten rechts an (Abbildung 7B).
    4. Klicken Sie im Bereich " Blasenradiusanalyse " auf " Parameter laden" (Abbildung 7C) und wählen Sie den Ordner aus, der alle Dateien Ihrer Videoserie enthält, und wählen Sie dann das Hintergrundbild (obligatorisch) aus.
    5. Sie haben die Wahl zwischen der Analyse aller Videos auf einmal, indem Sie auf Auto klicken, oder einzeln, indem Sie auf Schritt für Schritt klicken.
    6. Für jede Videodatei wird die Entwicklung des Blasenradius über eine akustische Periode aufgetragen und eine numerische Anpassung überlagert. Die rote Kurve entspricht einer linearisierten Rayleigh-Plesset-Modellierung. Der Radius der Gleichgewichtsblase wird dargestellt (Abbildung 7D).
    7. Gemäß der numerischen Anpassung wird der angelegte Druck für diese Spannung im Diagrammfeld Druck (Spannung) angezeigt (Abbildung 7E). Der Wert des ausgeübten Drucks wird auch in der Tabelle unten rechts angezeigt (Abbildung 7B). Typische angelegte Drücke, die der Spannungsdynamik von 0 - 8 V entsprechen, betragen 0 - 25 kPa.
    8. Sobald alle Videos verarbeitet sind, klicken Sie auf die Schaltfläche Lineare Regression , um eine lineare Anpassung der Druck-/Spannungskurve durchzuführen. Die Daten (Spannungs- und Druckwerte) werden in einer .txt Datei gespeichert, die sich im aktuellen Verzeichnis befindet. Die Neigung der Passform wird angegeben.

3. Koaleszenz-Technik

1. Schalten Sie den Ultraschallwandler ein. Stellen Sie die angelegte Spannung so hoch ein, dass der entsprechende Schalldruck zur Auslösung einer Oberflächeninstabilität gemäß dem numerischen Druck-/Radiusdiagramm der Instabilitätszonen führen kann, wie in Abbildung 8 gezeigt.
2. Bilden Sie eine Blase, die dann zu ihrem Einfangort wandert. Wenn die gefangene Blase nur sphärische Schwingungen aufweist, fahren Sie mit dem nächsten Schritt fort. Wenn nichtsphärische Schwingungen auftreten:
   1. Schalten Sie die Ultraschallleistung aus, damit die Blase an die Oberfläche aufsteigen kann.
   2. Modifizieren Sie die Laserenergie (durch Feinabstimmung über einige mJ) oder reduzieren Sie die Wandlerspannung.
   3. Schalten Sie die Ultraschallleistung ein.
   4. Bilden Sie eine neue Blase.
   5. Wiederholen Sie diesen Vorgang, bis die Blasengröße zu rein sphärischen Schwingungen führt.
3. Wenn eine eingeschlossene Blase nur sphärische Schwingungen aufweist, erzeugen Sie einen neuen Laserfunken. Wenn die neue Blase den Einfangort erreicht, kommt es zur Koaleszenz.
4. Wenn die verschmolzene Blase nur sphärische Schwingungen aufweist, erzeugen Sie eine neue Blase. Es können mehrere Verschmelzungen erforderlich sein, um den Blasenradius zu erreichen, bei dem nichtsphärische Verformungen auftreten. Ein Beispiel für eine Blasenverschmelzung, die zu nichtsphärischen Schwingungen führt, ist in Abbildung 9 dargestellt.
5. Sobald die zusammengewachsene Blase nicht-sphärische Schwingungen aufweist, zeichnen Sie die Blasenschwingungen für eine Dauer von ca. 3 bis 30 Millisekunden auf.
6. Identifizieren Sie die Modenzahl von Formschwingungen anhand von Abbildung 10.

4. Durchflussmessungen

1. Bei Kavitations-Microstreaming-Messungen müssen dem Wasser vor der Blasenkeimbildung fluoreszierende Tracerpartikel zugesetzt werden. In dieser Studie werden 0,71 μm Partikel verwendet (Materialtabelle). Sie sind klein genug, um akustisch transparent zu sein (unbeeinflusst von der akustischen Abstrahlkraft) und der Strömung genau zu folgen, sowie groß genug, um Laserlicht zu streuen. Verwenden Sie drei Tropfen für das Volumen des Wassertanks, was ungefähr 2,10⁴ Partikeln/mm³ entspricht.
2. Stellen Sie vor der Durchführung von Messungen die folgenden Parameter ein, um sowohl die Blasendynamik (schnelle Zeitskala) als auch die Flüssigkeitsströmung (niedrige Zeitskala) zu erfassen:
   1. Erstellen Sie eine Partitionierung des Kamera-Aufzeichnungsdatenträgers.
   2. Alternativ können Sie die Aufnahmeparameter wie folgt definieren:
      1. Bildrate 180 kHz, Bildgröße 128 x 128 Pixel und Belichtungszeit 1 μs für eine Aufnahme der Dynamik der Blasenschnittstelle
      2. Bildrate 600 Hz, Bildgröße 1024 x 768 Pixel und Belichtungszeit 1 ms für eine Aufnahme der Bewegung von Farbstofftracern.
3. Verwenden Sie einen kontinuierlichen Laser.
4. Erstellen Sie eine dünne Laserschicht, indem Sie den Laserstrahl nacheinander durch eine zylindrische plankonkave Linse und eine zylindrische plankonvexe Linse laufen lassen, die auf einer orthogonalen Achse ausgerichtet sind. Es kann eine Strahlbreite von ca. 160 μm erreicht werden.
5. Richten Sie die Laserfolie so ein, dass sie der Abbildungsebene entspricht:
   1. Stellen Sie den Laser auf ein bewegliches Gerät ein, so dass das Laserblatt parallel zur Abbildungsebene bewegt werden kann.
   2. Passen Sie die Position so an, dass die beleuchteten Partikel von der Kamera sichtbar sind.
   3. Keime und fange eine Blase ein.
   4. Passen Sie die Position der Laserfolie weiter an, so dass ein Schatten hinter der Blase sichtbar wird. Die Blase befindet sich nun in der Laserfolie, wie in Abbildung 11 dargestellt.
6. Induzieren Sie die Blasenkoaleszenz, bis ein stabil oszillierender Formmodus sichtbar ist.
7. Machen Sie mehrere Aufnahmen, indem Sie zwischen Blasendynamik und Microstreaming hin- und herwechseln.
   Anmerkungen: Schalten Sie den kontinuierlichen Laser aus, wenn er nicht benötigt wird. Durch Erhitzen können unerwünschte konvektive Strömungen entstehen. Schalten Sie auch die Leuchtdiode aus, wenn Sie die Messungen des Strömungsflusses durchführen.

5. Bildverarbeitung zur Visualisierung der Kavitations-Microstreaming-Muster

1. Installieren Sie die Visualisierungssoftware ImageJ für die Bildverarbeitung und -analyse in Java. Installieren Sie auch das Plugin CINE File Reader, um die Dateien der Hochgeschwindigkeitskamera zu öffnen.
2. Klicken Sie auf Datei | Importieren | CineFile und wählen Sie das Video *.cine aus, das die Aufnahme der Partikelbewegung enthält.
3. Wählen Sie im neuen Fenster Virtuellen Stack verwenden aus, das Video ist jetzt geladen.
4. Um die Partikelbewegung zu beobachten, ohne das Strömungsmuster anzuzeigen, klicken Sie auf Bild | Anpassen | Helligkeit/Kontrast | Automatisch. Der dunkle Hintergrund wird nun durch ein automatisch optimiertes Bild ersetzt.
5. Um das resultierende Muster anzuzeigen, klicken Sie auf Bild | Stapel | Z Projizieren und wählen Sie die Option Max. Intensität für die Bildprojektion. Es wird ein Ausgabebild mit Pixeln angezeigt, die den Maximalwert für alle Bilder im Stapel enthalten. Passen Sie ggf. den Bildkontrast wie in Schritt 5.4 beschrieben an.
   HINWEIS: Es wird ein Streaming-Muster wie in Abbildung 12b und Abbildung 12d angezeigt.

Ergebnisse

Eine vollständige Abfolge der Blasenkoaleszenz, die zu zeitstabilen, symmetriegesteuerten nicht-sphärischen Oszillationen führt, ist in Abbildung 9 dargestellt. Die Annäherungsphase zweier kugelschwingender Blasen endet, wenn der dünne Flüssigkeitsfilm zwischen den beiden Blasen aufgerissen ist. Es ist erwähnenswert, dass in der letzten Phase vor der Verschmelzung die Blasengrenzflächen von der Sphärizität abweichen. Beide Blasen dehnen sich ellipso...

Diskussion

Das vorgestellte Verfahren besteht darin, die Blasenkoaleszenz zu verwenden, um stationäre, symmetriegesteuerte Blasenformoszillationen auszulösen, die es ermöglichen, die durch diese Oszillationen induzierte langfristige Fluidströmung zu untersuchen. Die größte Herausforderung bei der Technik ist die Kontrolle von nicht-sphärischen Schwingungen für eine Blase, die weit weg von jeglichen Grenzen gefangen wird.

Die meisten der in der Literatur vorgeschlagenen Techniken konzentrierten si...

Materialien

Name	Company	Catalog Number	Comments
Aspherical lens	Thorlabs	AL4050	Lens of focus 40 mm
Continuous wave laser source	CNI	MLL6FN	DPSS laser of wavelength 532nm, energy 400 mW
Cylindrical plano-concave lens	Thorlabs	LJ1277L1-A	lens of focus -25?4mm
Cylindrical plano-concave lens	Thorlabs	LK1900L1	lens of focus 250 mm
Fluorescent particles	Duke Scientific	R700	Red polymer fluorescent microspheres
Function generator	Agilent	HP33120	Generator of function feeding the ultrasound transducer
High-speed camera	Vision Research	Phantom v12.0	High-speed recording up to 1 Mfps
Liquid medium	Carlo Erba	Water for analysis	Demineralized, undegassed water
Multiphysics software	Comsol	None	Softwate for simulating the acoustic field of the levitation chamber
Nd:Yag pulsed laser	New Wave Research	Solo III-15	5 ns pulse duration, λ=532 nm, 3.5 mm beam diameter, up to 50 mJ
Plano-concave lens	Thorlabs	N-BK7	lens of focus 125 mm
Spherical concave lens	Thorlabs	N-SF11	Bi-concave lens of focus -25mm
Ultrasound transducer	SinapTec	Custom-made	Nominal frequency 31kHz, active area 35mm diameter
Visualization software	NIH	ImageJ	Software for image processing and analysis in Java
XY Linear stage	Newport	M-406	Displacement stage with micrometric screw
Z-axis linear stage	Edmund Optics	62-299	Vertical displacement stage with micrometric screw