Induction of Microstreaming by Nonspherical Bubble Oscillations in an Acoustic Levitation System

Summary

A fast and reliable technique is proposed to control the shape oscillations of a single, trapped acoustic bubble that is based on coalescence technique between two bubbles. The steady-state, symmetry-controlled bubble shape oscillations allow analysis of the fluid flow generated in the vicinity of the bubble interface.

Abstract

When located near biological barriers, oscillating microbubbles may increase cell membrane permeability, allowing for drug and gene internalization. Experimental observations suggest that the temporary permeabilization of these barriers may be due to shear stress that is exerted on cell tissues by cavitation microstreaming. Cavitation microstreaming is the generation of vortex flows which arise around oscillating ultrasound microbubbles. To produce such liquid flows, bubble oscillations must deviate from purely spherical oscillations and include either a translational instability or shape modes. Experimental studies of bubble-induced flows and shear stress on nearby surfaces are often restricted in their scope due to the difficulty of capturing shape deformations of microbubbles in a stable and controllable manner. We describe the design of an acoustic levitation chamber for the study of symmetry-controlled nonspherical oscillations. Such control is performed by using a coalescence technique between two approaching bubbles in a sufficiently intense ultrasound field. The control of nonspherical oscillations opens the way to a controlled cavitation microstreaming of a free surface-oscillating microbubble. High-frame rate cameras allow investigating quasi-simultaneously the nonspherical bubble dynamics at the acoustic timescale and the liquid flow at a lower timescale. It is shown that a large variety of fluid patterns may be obtained and that they are correlated to the modal content of the bubble interface. We demonstrate that even the high-order shape modes can create large-distance fluid patterns if the interface dynamics contain several modes, highlighting the potential of nonspherical oscillations for targeted and localized drug delivery.

Introduction

In medicine, an administered drug must penetrate many obstacles in the living system before reaching the desired targets. However, most drugs are rapidly cleaned away from the blood stream. The targeting efficiency is low and they cannot easily cross cell membranes, leading to ineffective drug delivery. Currently, the use of microbubbles in combination with ultrasound has been proposed as an innovative method for noninvasive, precise and targeted delivery of drugs and genes to pathological tissues and cells¹. In this approach, microbubbles can play a role as carriers where free drugs are either co-injected with a gas bubble suspension or loaded on its surface. Microbubbles can also act as a local vector for refocusing the ultrasound energy in order to interact with the cells. Basically, under ultrasound exposure, bubbles stably compress and expand, a regime called stable cavitation that generates liquid flows and hence shear stress on nearby objects. Microbubbles may also oscillate non-linearly and expand until collapse, in the regime of inertial cavitation, producing shock waves that propagate radially from the collapse site². It has been shown that cavitation, either stable or inertial, enhances the permeabilization of cell membranes, and thus enhances the internalization of drugs into the cell³.

In therapeutic applications, understanding the mechanism of the bubble-cell interaction is very important, but there are several barriers, both from scientific and technical sides, that prevent our knowledge from advancing. First, capturing the dynamics of cells in response to bubble-induced mechanical stimuli is very difficult⁴. At the acoustic timescale, the first-order microbubble oscillations can lead to activation of membrane channels, facilitating molecular passage across biological interfaces. This occurs through the direct oscillation of the cell membrane, also called "cellular massage"⁵. Channel activation following direct mechanical stress was evidenced using patch-clamp techniques that measured electrophysiological properties of cell membranes during and after ultrasound exposure⁶. Measuring bubble-induced cell dynamics (meaning the complete field of deformation of the cell membrane) at the acoustic timescale, would also provide insights in the threshold of membrane area expansion ΔA/A required to induce pores into the cell membrane⁷. The second barrier is controlling the collapsing bubble regime to avoid microbubble-induced cell lysis. Bubble collapses and induced microjets have been identified as a mechanism through which membrane perforation occurs^8,9. Once permeabilized, the cell membrane repairs through calcium self-sealing of the lipid bilayers and fusion of intracellular vesicles⁹. The occurrence of bubble collapses may also cause lethal damages to the cell and induce unnecessary side effects in the surrounding ones. In sensitive applications such as ultrasound-mediated blood-brain barrier opening, it is generally accepted that inertial bubble collapses should be avoided¹⁰.

Therefore, huge efforts are currently devoted to the design of ultrasound emission sequences, coupled with passive cavitation monitoring and control, in order to ensure stable oscillations of microbubbles¹¹. In this stable regime, it has been hypothesized that stably oscillating bubbles play a strong role in the triggering of membrane permeabilization by promoting spatially-targeted shear stress on the cell membrane⁷. The shear stress results from the liquid flows created in the vicinity of the oscillating bubbles. These liquid flows are called cavitation microstreaming, and, as mentioned above, they are one of the several possible mechanisms which are responsible for enhanced uptake of extracellular molecules. When dealing with suspension of bubbles or cells such as in-vitro biological transfections assays¹², permeabilization by microstreaming might be much more efficient than permeabilization by bubble collapse. This can be shown by a simple geometrical consideration. In cell suspensions, sonoporation will be efficient if the majority of the suspended cells is submitted to sufficiently large mechanical effects (leading to membrane permeabilization). It is known that bubble collapses are directed along the direction of isotropic symmetry breaking, such as the bubble-wall axis¹³ or the bubble-bubble and bubble-cell line joining their center of mass¹⁴. The produced microjet is therefore a spatially-localized phenomenon along a finite number of lines joining the cell and bubble centers. Depending on the cell and bubble concentration, as well as the bubble-cell distance, this effect may not be the most efficient to permeabilize the whole number of suspended cells. In contrast, cavitation microstreaming is a phenomenon occurring at a slow timescale, with a large spatial expansion in comparison to the bubble radius. Also, the liquid flow is distributed all around the bubble, and may therefore impacts a larger number of cells, at a very long range. Therefore, understanding the generated cavitation microstreaming around an oscillating bubble is a prerequisite for controlling and quantifying the bubble-induced shear stress that is applied to cells.

To do so, a preliminary step consists in controlling the spherical and nonspherical oscillations of an ultrasound-driven bubble, as the generated liquid flows are induced by the motion of the bubble interface^15,16. In particular, shape oscillations of microbubbles have to be triggered and kept stable. Furthermore, the orientation of the bubble shape oscillations has to be controlled to properly analyze the correlation between the bubble interface dynamics and the induced microstreaming pattern. When summarizing the existing literature, it is obvious that detailed experimental results of cavitation-induced microstreaming are only available for bubbles attached to a surface. Wall-attached microbubbles are commonly-used for assessing accurate interface dynamics and cell interactions at the micrometer scale under an ultrafast microscopy system. This configuration is therapeutically relevant when considering vibrating microbubbles located on the cell membrane^17,18,19. The study of substrate-attached bubble may however make the analysis of bubble dynamics more complicated, partly due to the complex nature of contact line dynamics²⁰, and the triggering of asymmetric shape modes²¹. In medical and biological applications, bubbles that are not attached to a wall are commonly found in confined geometries such as small vessels. This impacts significantly bubble dynamics and shape instabilities. Particularly, the presence of a nearby wall shifts the pressure threshold for shape mode triggering to lower pressure values depending on the shape mode number and bubble size²². The wall also affects the bubble-induced microstreaming with possibly higher intensity for the produced flow²³.

Amongst all the possible scenario that microbubbles may experience (free or attached, close to a wall, collapsing or stably-oscillating), we propose to investigate the nonspherical dynamics of a single bubble far from any boundary. The experimental setup is based on an acoustic levitation system²⁴ in which a standing ultrasound wave is used to trap the bubble. This scenario is consistent with medical applications in which a collection of suspended bubbles and cells coexist in a sonotransfection chamber, for instance. As far as bubbles and cells are not too close, it is assumed that the presence of a cell does not impact the bubble interface dynamics. When cells follow the loop-like trajectories of the cavitation-induced microstreaming, they are cyclically approaching and repelling from the bubble location and we can assume that the cell presence impacts neither the streaming pattern nor its mean velocity. In addition, nonspherical dynamics and induced microstreaming from single bubbles far from boundary are well known from a theoretical point of view. In order to link the bubble-induced liquid flow to the bubble contour dynamics, it is required to accurately characterize the bubble interface dynamics. To do so, it is preferable to adapt the spatiotemporal scale in experimental studies with respect to those used in therapeutics so that acquisition with common high-speed cameras (below 1 million frame/second) is possible by using large bubbles excited at lower frequencies. When considering uncoated bubbles, the eigenfrequency ω_n of a given mode n is related to the bubble size as 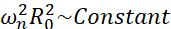²⁵. This radius-eigenfrequency relationship is slightly modified when considering shelled bubbles²⁶, but the order of magnitude of the eigenfrequency ω_n remains the same. Thus, investigating bubbles with equilibrium radii ~50μm in a 30 kHz ultrasound field is similar to studying coated bubbles of radii ~3μm in a 1.7 MHz field, as proposed by Dollet et al.²⁷. Similar shape mode numbers and hence microstreaming patterns are therefore expected.

In order to trigger nonspherical oscillations of the bubble interface, it is necessary to exceed a certain pressure threshold that is radius-dependent, as shown in Figure 1. Existing experimental techniques rely on the increase of the acoustic pressure to trigger surface modes (illustrated by path (1) in Figure 1), either by step-by-step pressure increase²⁸ or by modulated-amplitude excitation responsible of periodic onset and extinction of surface modes²⁹. The main drawbacks of these techniques are (i) a random orientation of the symmetry axis of the surface oscillations that cannot be controlled to be in the imaging plane, (ii) a short lifetime of the bubble shape oscillations that makes the analysis of the induced liquid flows difficult at larger timescales, and (iii) the frequent triggering of unstable shape modes. We propose an alternative technique to cross the pressure threshold at a constant acoustic pressure in the radius/pressure map, as illustrated by the path (2) in Figure 1. To do so, it is required to increase the bubble size such that it will be in the instability zone. Such an increase is performed by a bubble coalescence technique. The coalescence of two, initially spherically-oscillating, microbubbles is exploited to create one single deformed bubble. If the acoustic pressure and bubble size of the coalesced bubble are in the instability zone, surface modes are triggered. We also evidenced that the coalescence technique induces stable shape oscillations in a steady-state regime, as well as a controlled symmetry axis defined by the rectilinear motion of the two approaching bubbles. Because a stable shape oscillation is ensured over minutes, the analysis of bubble-induced fluid flow is possible by seeding the liquid medium with fluorescent microparticles, lighted by a thin laser sheet. Recording the motion of the solid microparticles in the vicinity of the bubble interface allows identifying the pattern of the induced fluid flow³⁰. The overall principle of the triggering of bubble shape oscillations, leading to a time-stable fluid flow, is illustrated in Figure 2.

In the following protocol, we outline the steps required to create stable bubble shape oscillations via the coalescence technique and describe the measurements of fluid flow. This includes the design of the acoustic levitation system, the acoustic calibration, bubble nucleation and the coalescence technique, the measurement of bubble interface dynamics and surrounding fluid flow, and the image processing.

Protocol

1. Design of the acoustic levitation chamber

1. Design an optically transparent (PMMA-like) cubic tank (8 cm edge and 2.8 mm thickness per face) with the geometry module of a multiphysics simulation software (Table of Materials).
2. Insert a cylindrical surface (Ø = 35 mm) centered at the bottom of the tank, to model the ultrasonic transducer.
3. Set the boundary conditions to zero pressure on each wall with a normal displacement of amplitude 1 µm at the transducer surface.
4. Using a Frequency domain module, simulate the Frequency Response Function (FRF) of the tank in the frequency range [10 - 40] kHz, at the three arbitrary locations loc1 = (0.01375, 0.01375, 0.04125), loc2 = (0, 0, 0.0088), and loc3 = (0.021725, 0.023375, 0.00935).
5. Adapt the tank size such that one of the acoustic modes of the cavity corresponds to the nominal frequency of the transducer (here 31.2 kHz). The FRF therefore contains one resonance peak close to this frequency, as illustrated in Figure 3.
6. Plot the pressure field inside the tank, as shown in Figure 4. The chosen resonance mode must contain at least one pressure antinode in the inner of the container, on which the acoustic bubble will be trapped.
7. When designing the tank, design a movable top face with a guiding groove on each edge to tightly close the tank faces. Drill a tiny hole at the top face in order to fill the tank with the liquid medium.
8. Place the water tank atop a homemade frame that contains the ultrasound transducer (Langevin-type, 31.2 kHz nominal frequency). Use echographic gel to couple the transducer to the tank bottom wall.
9. Place the tank and frame system atop a three-directions displacement table with micrometric screws.
10. Fill the tank with microfiltered, demineralized and water (not degassed, volume ~500mL, oxygen saturation of approximatively 8 mg·L^-1).
    ​NOTE: Using not degassed water instead of degassed makes it possible to maintaining stable bubbles for the duration of experiments. Using degassed water will accelerate bubble shrinking due to gas diffusion, even if slightly counterbalanced by rectified (ultrasound-mediated) diffusion.

2. Bubble generation and acoustic calibration

1. Prepare the experimental setup used for laser-induced bubble nucleation, acoustic excitation and high-speed recording (Figure 5a,b,c). The experimental setup consists of (A) the acoustic levitation system, (B) the laser power supply and (C) the laser head, (D) one spherical concave lens, (E) one plano-concave lens and one aspherical lens, (F) the high-speed camera, (G) the continuous light-emitting diode. Later, for measurements of liquid flows (Figure 5d) (H) one continuous wave laser source, (I) a cylindrical plano-concave lens followed by a cylindrical plano-concave lens inserted behind the first lens and oriented on the orthogonal axis will be added.
2. Plug the ultrasound transducer to a function generator. Set the excitation signal as: sinusoidal waveform, continuous wave, frequency 31.2 kHz. The amplitude is the only variable parameter.
3. Place the lens (D) at a distance of approximatively 6 cm in front of the laser head (C).
4. Place the lens (E) at a distance of approximatively 12 cm in front of the lens (D).
5. Place the water tank (A) such that a focusing point of the laser is located inside the water tank, leading to spark generation for every laser pulse (5 -10 mJ). The laser spark should be located approximately 3 cm below the targeted pressure antinode.
   NOTE: Without ultrasound (US), laser-nucleated bubble will rise to the top face due to buoyancy.
6. Switch on the ultrasound transducer. Increase the applied voltage until the bubble no longer rises vertically but is deviated towards the pressure antinode and, for a sufficient high pressure, trapped.
7. Set the backlit illumination (continuous light-emitting diode) and the high-speed camera in order to observe the trapped bubble.
   NOTE: When nucleating a new bubble with a laser spark, it is easy to capture the trajectory of the bubble approaching its trapping location.
8. Move the location of the laser spark within the water tank such that the bubble trajectory remains inside the focal plane of the camera.
9. Trap one bubble and capture its radial oscillations with the following parameters: frame size 128 x 128 pixels, acquisition rate 180 kHz. An example of large-amplitude radial oscillations over two acoustic periods is provided in Figure 6. Typical gas bubbles size ranges from 30 to 80 µm.
10. Record the bubble radial oscillations during 3 to 30 milliseconds in order to capture hundreds to thousands of bubble oscillations. Repeat this recording for increasing applied voltages of the transducer. Typical applied voltages are in the range of 0 - 8 V.
    NOTE: When modifying the applied voltage, the equilibrium location of the trapped bubble slightly moves vertically. To follow the oscillations without moving the backlit illumination and camera, place the system (transducer and water tank) onto a three-directions movable table with micrometric accuracy.
11. Switch on the ultrasound transducer and capture one image of the background for post-analysis.
12. Post-process the video series following this procedure:
    1. Run the executable file VoltagePressure.exe. The interface shown in Figure 7 should open.
       NOTE: The script is available as a supplementary document.
    2. Specify the physical and experimental parameters in the left column (Figure 7A).
    3. Specify the values of applied voltage for the series of recordings in the bottom-right table (Figure 7B).
    4. In the Bubble radius analysis panel, click on Load parameters (Figure 7C) and select the folder containing all the files of your video series, and then the background image (mandatory).
    5. The choice is allowed between analyzing all the videos at once, by clicking on Auto, or one-by-one by clicking on Step by step.
    6. For each video file, the evolution of the bubble radius is plotted over one acoustic period, and a numerical fit is superimposed. The red curve corresponds to a linearized Rayleigh-Plesset modeling. The equilibrium bubble radius is displayed (Figure 7D).
    7. According to the numerical fitting, the applied pressure for this voltage is displayed in the Pressure (Voltage) graph panel (Figure 7E). The value of the applied pressure is also displayed in the bottom-right table (Figure 7B). Typical applied pressures corresponding to the 0 - 8 V voltage dynamics are 0 - 25 kPa.
    8. Once all videos are processed, click on the Linear regression button to perform a linear fit of the pressure/voltage curve. The data (voltage and pressure values) are saved into a .txt file located in the current directory. The slope of the fit is provided.

3. Coalescence technique

1. Switch on the ultrasound transducer. Set the applied voltage high enough such that the corresponding acoustic pressure may lead to the triggering of surface instability, according to the numerical pressure/radius diagram of instability zones, as shown in Figure 8.
2. Nucleate a bubble, which will then migrate to its trapping location. If the trapped bubble only exhibits spherical oscillations, move on to the next step. If nonspherical oscillations appear:
   1. Switch off the ultrasound power to let the bubble rise to the top surface.
   2. Modify the laser energy (by finely tuning over a few mJ) or reduce the transducer voltage.
   3. Switch on the ultrasound power.
   4. Nucleate a new bubble.
   5. Repeat this procedure until the bubble size leads to purely spherical oscillations.
3. When a trapped bubble exhibits only spherical oscillations, generate a new laser spark. When the new bubble reaches the trapping location, coalescence occurs.
4. If the coalesced bubble exhibits only spherical oscillations, generate a new bubble. Multiple coalescences may be necessary to reach the bubble radius at which nonspherical deformations occur. An example of bubble coalescence leading to nonspherical oscillations is shown in Figure 9.
5. Once the coalesced bubble exhibits nonspherical oscillations, record the bubble oscillations for a duration of approximatively 3 to 30 milliseconds.
6. Identify the mode number of shape oscillations by referring to Figure 10.

4. Fluid flow measurements

1. In the case of cavitation microstreaming measurements, fluorescent tracer particles must be added to the water prior to bubble nucleation. In this study, 0.71 µm particles are used (Table of Materials). They are sufficiently small to be acoustically transparent (not influenced by the acoustic radiation force) and to accurately follow the flow as well as sufficiently large to scatter laser light. Use three drops for the volume of the water tank, corresponding to approximatively 2.10⁴ particles/mm³.
2. Prior to taking measurements, set the following parameters for capturing both the (fast timescale) bubble dynamics and (low timescale) fluid flow:
   1. Create a partitioning of the camera recording disk.
   2. Alternatively define the recording parameters as:
      1. Frame rate 180 kHz, frame size 128 x 128 pixels, and exposure time 1 µs for one recording of the dynamics of the bubble interface
      2. Frame rate 600 Hz, frame size 1024 x 768 pixels, and exposure time 1 ms for one recording of the motion of dye tracers.
3. Use a continuous laser.
4. Create a thin laser sheet by successively letting the laser beam pass through cylindrical plano-concave lens and cylindrical plano-convex lens oriented on an orthogonal axis. A beam width of about 160 µm can be obtained.
5. Set up the laser sheet to correspond to the imaging plane:
   1. Set the laser on a movable device so that the laser sheet can be moved parallel to the imaging plane.
   2. Adjust the position so that the illuminated particles are visible by the camera.
   3. Nucleate and trap a bubble.
   4. Adjust the position of the laser sheet further, so that a shadow becomes visible behind the bubble. The bubble is now inside the laser sheet, as shown in Figure 11.
6. Induce bubble coalescence until a stably oscillating shape mode is apparent.
7. Do several recordings switching back and forth between bubble dynamics and microstreaming.
   ​NOTE: Switch off the continuous laser when not needed. Heating can create unwanted convective flows. Also, turn off the light-emitting diode when performing the measurements of streaming flow.

5. Image processing to visualize the cavitation microstreaming patterns

1. Install the visualization software ImageJ for image processing and analysis in Java. Also install the plugin CINE File Reader in order to open the high-speed camera files.
2. Click on File | Import | CineFile and select the video *.cine containing the capture of the particle motion.
3. Select Use virtual stack in the new window, the video is now loaded.
4. In order to observe the particle motion without displaying the streaming pattern, click on Image | Adjust | Brightness/Contrast | Auto. The dark background is now replaced by an automatically optimized image.
5. In order to display the resulting pattern, click on Image | Stacks | Z Project and choose the Max Intensity option for the image projection. An output image with pixels containing the maximum value over all images in the stack is displayed. Adjust the image contrast as described in step 5.4, if necessary.
   NOTE: A streaming pattern such as the ones shown in Figure 12b and Figure 12d is obtained.

Results

A complete sequence of bubble coalescence leading to time-stable, symmetry-controlled nonspherical oscillations is presented in Figure 9. The approaching phase of two spherically-oscillating bubbles ends when the thin liquid film between the two bubbles is ruptured. It is worth noting that, at the last stage prior to the coalescence, the bubble interfaces deviate from sphericity. Both bubbles elongate on an ellipsoidal shape along the path of the rectilinear ...

Discussion

The presented procedure consists of using bubble coalescence in order to trigger steady-state, symmetry-controlled bubble shape oscillations, allowing the study of the long-term fluid flow induced by these oscillations. The main challenge in the technique is the control of nonspherical oscillations for a bubble being trapped, far from any boundaries.

Most of the existing techniques proposed in the literature focused on substrate-attached bubbles^7,

Materials

Name	Company	Catalog Number	Comments
Aspherical lens	Thorlabs	AL4050	Lens of focus 40 mm
Continuous wave laser source	CNI	MLL6FN	DPSS laser of wavelength 532nm, energy 400 mW
Cylindrical plano-concave lens	Thorlabs	LJ1277L1-A	lens of focus -25?4mm
Cylindrical plano-concave lens	Thorlabs	LK1900L1	lens of focus 250 mm
Fluorescent particles	Duke Scientific	R700	Red polymer fluorescent microspheres
Function generator	Agilent	HP33120	Generator of function feeding the ultrasound transducer
High-speed camera	Vision Research	Phantom v12.0	High-speed recording up to 1 Mfps
Liquid medium	Carlo Erba	Water for analysis	Demineralized, undegassed water
Multiphysics software	Comsol	None	Softwate for simulating the acoustic field of the levitation chamber
Nd:Yag pulsed laser	New Wave Research	Solo III-15	5 ns pulse duration, λ=532 nm, 3.5 mm beam diameter, up to 50 mJ
Plano-concave lens	Thorlabs	N-BK7	lens of focus 125 mm
Spherical concave lens	Thorlabs	N-SF11	Bi-concave lens of focus -25mm
Ultrasound transducer	SinapTec	Custom-made	Nominal frequency 31kHz, active area 35mm diameter
Visualization software	NIH	ImageJ	Software for image processing and analysis in Java
XY Linear stage	Newport	M-406	Displacement stage with micrometric screw
Z-axis linear stage	Edmund Optics	62-299	Vertical displacement stage with micrometric screw