Indução de Microstreaming por Oscilações de Bolhas Não Esféricas em um Sistema de Levitação Acústica

Resumo

Uma técnica rápida e confiável é proposta para controlar as oscilações de forma de uma única bolha acústica aprisionada que é baseada na técnica de coalescência entre duas bolhas. As oscilações em forma de bolhas controladas por simetria em estado estacionário permitem a análise do fluxo de fluido gerado nas proximidades da interface de bolhas.

Resumo

Quando localizadas próximas a barreiras biológicas, microbolhas oscilantes podem aumentar a permeabilidade da membrana celular, permitindo a internalização de fármacos e genes. Observações experimentais sugerem que a permeabilização temporária dessas barreiras pode ser devida ao estresse de cisalhamento que é exercido sobre os tecidos celulares por cavitação microstreaming. Microstreaming de cavitação é a geração de fluxos de vórtice que surgem em torno de microbolhas de ultrassom oscilantes. Para produzir tais fluxos de líquidos, as oscilações de bolhas devem desviar-se de oscilações puramente esféricas e incluir uma instabilidade translacional ou modos de forma. Estudos experimentais de escoamentos induzidos por bolhas e tensões de cisalhamento em superfícies próximas são frequentemente restritos em seu escopo devido à dificuldade de capturar deformações de forma de microbolhas de forma estável e controlável. Descrevemos o projeto de uma câmara de levitação acústica para o estudo de oscilações não esféricas controladas por simetria. Esse controle é realizado utilizando-se a técnica de coalescência entre duas bolhas que se aproximam em um campo de ultrassom suficientemente intenso. O controle de oscilações não esféricas abre caminho para um microfluxo de cavitação controlado de uma microbolha livre de superfície oscilante. Câmeras de alta taxa de quadros permitem investigar quase simultaneamente a dinâmica de bolhas não esféricas na escala de tempo acústica e o fluxo de líquido em uma escala de tempo mais baixa. Mostra-se que uma grande variedade de padrões de fluidos pode ser obtida e que eles estão correlacionados com o conteúdo modal da interface de bolhas. Demonstramos que mesmo os modos de forma de alta ordem podem criar padrões de fluidos de grande distância se a dinâmica da interface contiver vários modos, destacando o potencial de oscilações não esféricas para liberação de fármacos direcionados e localizados.

Introdução

Na medicina, um medicamento administrado deve penetrar em muitos obstáculos no sistema vivo antes de atingir os alvos desejados. No entanto, a maioria das drogas são rapidamente limpas longe da corrente sanguínea. A eficiência do direcionamento é baixa e eles não podem atravessar facilmente as membranas celulares, levando à entrega ineficaz de drogas. Atualmente, o uso de microbolhas em combinação com o ultrassom tem sido proposto como um método inovador para a liberação não invasiva, precisa e direcionada de fármacos e genes para tecidos e células^{patológicas1}. Nesta abordagem, as microbolhas podem desempenhar um papel como transportadores onde as drogas livres são co-injetadas com uma suspensão de bolha de gás ou carregadas em sua superfície. As microbolhas também podem atuar como um vetor local para redirecionar a energia do ultrassom, a fim de interagir com as células. Basicamente, sob exposição ao ultrassom, as bolhas se comprimem e se expandem de forma estável, um regime chamado cavitação estável que gera fluxos de líquido e, portanto, estresse de cisalhamento em objetos próximos. As microbolhas também podem oscilar de forma não linear e expandir-se até o colapso, em regime de cavitação inercial, produzindo ondas de choque que se propagam radialmente a partir do local do colapso². Tem sido demonstrado que a cavitação, estável ou inercial, aumenta a permeabilização das membranas celulares e, assim, aumenta a internalização de fármacos na célula³.

Em aplicações terapêuticas, entender o mecanismo da interação célula-bolha é muito importante, mas existem várias barreiras, tanto do lado científico quanto técnico, que impedem que nosso conhecimento avance. Primeiro, capturar a dinâmica das células em resposta a estímulos mecânicos induzidos por bolhas é muito^difícil4. Na escala de tempo acústica, as oscilações de microbolhas de primeira ordem podem levar à ativação de canais de membrana, facilitando a passagem molecular através de interfaces biológicas. Isso ocorre por meio da oscilação direta da membrana celular, também chamada de "massagem celular"⁵. A ativação do canal após estresse mecânico direto foi evidenciada usando técnicas de patch-clamp que mediram as propriedades eletrofisiológicas das membranas celulares durante e após a exposição ao ultrassom⁶. A medição da dinâmica celular induzida por bolhas (ou seja, o campo completo de deformação da membrana celular) na escala de tempo acústica também forneceria informações sobre o limiar de expansão da área da membrana Δ A/A necessário para induzir poros na membrana celular⁷. A segunda barreira é controlar o regime de bolhas em colapso para evitar a lise celular induzida por microbolhas. Colapsos de bolhas e microjatos induzidos têm sido identificados como mecanismo pelo qual ocorre perfuração da membrana ^8,9. Uma vez permeabilizada, a membrana celular se repara através do auto-selamento das bicamadas lipídicas com cálcio e fusão das vesículas intracelulares⁹. A ocorrência de colapsos de bolhas também pode causar danos letais à célula e induzir efeitos colaterais desnecessários nas vizinhas. Em aplicações sensíveis, como a abertura da barreira hematoencefálica mediada por ultrassom, é geralmente aceito que colapsos de bolhas inerciais devem ser evitados¹⁰.

Portanto, grandes esforços são atualmente dedicados ao projeto de sequências de emissão de ultrassom, juntamente com o monitoramento e controle passivo da cavitação, a fim de garantir oscilações estáveis das^{microbolhas11}. Nesse regime estável, foi levantada a hipótese de que bolhas oscilantes estáveis desempenham um forte papel no desencadeamento da permeabilização da membrana, promovendo tensões de cisalhamento espacialmente direcionadas na membrana celular⁷. A tensão de cisalhamento resulta dos fluxos de líquidos criados nas proximidades das bolhas oscilantes. Esses fluxos líquidos são chamados de cavitation microstreaming, e, como mencionado acima, são um dos vários mecanismos possíveis responsáveis pelo aumento da captação de moléculas extracelulares. Quando se trata de suspensão de bolhas ou células, como ensaios de transfecção biológica in vitro¹², a permeabilização por microstreaming pode ser muito mais eficiente do que a permeabilização por colapso de bolhas. Isso pode ser demonstrado por uma simples consideração geométrica. Em suspensões celulares, a sonoporação será eficiente se a maioria das células em suspensão for submetida a efeitos mecânicos suficientemente grandes (levando à permeabilização da membrana). Sabe-se que os colapsos de bolhas são direcionados na direção da quebra de simetria isotrópica, como o eixo parede-bolhas¹³ ou a linhagem bolha-bolha e célula-bolha unindo seu centro de massa¹⁴. O microjato produzido é, portanto, um fenômeno espacialmente localizado ao longo de um número finito de linhas que unem os centros celulares e de bolhas. Dependendo da concentração celular e de bolhas, bem como da distância célula-bolha, esse efeito pode não ser o mais eficiente para permeabilizar todo o número de células em suspensão. Em contraste, o microfluxo de cavitação é um fenômeno que ocorre em uma escala de tempo lenta, com uma grande expansão espacial em comparação com o raio da bolha. Além disso, o fluxo de líquido é distribuído por toda a bolha, podendo, portanto, impactar um número maior de células, em um intervalo muito longo. Portanto, entender o microfluxo de cavitação gerado em torno de uma bolha oscilante é um pré-requisito para controlar e quantificar a tensão de cisalhamento induzida por bolhas que é aplicada às células.

Para tanto, uma etapa preliminar consiste em controlar as oscilações esféricas e não esféricas de uma bolha impulsionada por ultrassom, uma vez que os fluxos líquidos gerados são induzidos pelo movimento da interface da bolha^15,16. Em particular, as oscilações de forma das microbolhas devem ser acionadas e mantidas estáveis. Além disso, a orientação das oscilações da forma da bolha deve ser controlada para analisar adequadamente a correlação entre a dinâmica da interface da bolha e o padrão de microstreaming induzido. Ao resumir a literatura existente, é óbvio que resultados experimentais detalhados de microfluxo induzido por cavitação estão disponíveis apenas para bolhas presas a uma superfície. Microbolhas acopladas à parede são comumente usadas para avaliar a dinâmica precisa da interface e interações celulares na escala micrométrica sob um sistema de microscopia ultrarrápida. Essa configuração é terapeuticamente relevante quando se considera microbolhas vibratórias localizadas na membrana celular^17,18,19. O estudo da bolha acoplada ao substrato pode, no entanto, tornar a análise da dinâmica das bolhas mais complicada, em parte devido à natureza complexa da dinâmica das linhas de contato²⁰ e ao desencadeamento de modos de forma assimétricos²¹. Em aplicações médicas e biológicas, bolhas que não estão presas a uma parede são comumente encontradas em geometrias confinadas, como pequenos vasos. Isso afeta significativamente a dinâmica das bolhas e as instabilidades de forma. Particularmente, a presença de uma parede próxima desloca o limiar de pressão para o acionamento do modo de forma para valores de pressão mais baixos, dependendo do número do modo de forma e do tamanho da bolha²². A parede também afeta o microfluxo induzido por bolhas com possivelmente maior intensidade para o fluxo produzido²³.

Entre todos os cenários possíveis que as microbolhas podem experimentar (livres ou presas, próximas a uma parede, colapsando ou oscilando de forma estável), propomos investigar a dinâmica não esférica de uma única bolha longe de qualquer fronteira. O arranjo experimental é baseado em um sistema de levitação acústica²⁴ no qual uma onda de ultrassom estacionária é usada para aprisionar a bolha. Esse cenário é consistente com aplicações médicas em que uma coleção de bolhas e células suspensas coexistem em uma câmara de sonotransfecção, por exemplo. Na medida em que bolhas e células não estão muito próximas, supõe-se que a presença de uma célula não afeta a dinâmica da interface de bolhas. Quando as células seguem as trajetórias em loop do microfluxo induzido por cavitação, elas estão ciclicamente se aproximando e repelindo do local da bolha e podemos supor que a presença celular não impacta nem o padrão de fluxo nem sua velocidade média. Além disso, a dinâmica não esférica e o microfluxo induzido a partir de bolhas únicas longe da fronteira são bem conhecidos do ponto de vista teórico. Para ligar o fluxo de líquido induzido por bolhas à dinâmica do contorno de bolhas, é necessário caracterizar com precisão a dinâmica da interface de bolhas. Para tanto, é preferível adaptar a escala espaço-temporal em estudos experimentais em relação àquelas utilizadas na terapêutica para que a aquisição com câmeras comuns de alta velocidade (abaixo de 1 milhão de frames/segundo) seja possível utilizando grandes bolhas excitadas em frequências mais baixas. Ao considerar bolhas não revestidas, a autofrequência ω n de um dado modo _n está relacionada ao tamanho da bolha como 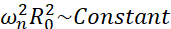²⁵. Essa relação rádio-autofreqüência é ligeiramente modificada quando se consideram bolhas descascadas²⁶, mas a ordem de grandeza da autofreqüência ω_n permanece a mesma. Assim, investigar bolhas com raios de equilíbrio ~50μm em um campo de ultrassom de 30 kHz é semelhante ao estudo de bolhas revestidas de raios ~3μm em um campo de 1,7 MHz, como proposto por Dollet et ^al.27. Números de modo de forma semelhantes e, portanto, padrões de microstreaming são, portanto, esperados.

Para desencadear oscilações não esféricas da interface de bolhas, é necessário exceder um determinado limiar de pressão que é dependente do raio, como mostrado na Figura 1. As técnicas experimentais existentes baseiam-se no aumento da pressão acústica para desencadear modos de superfície (ilustrado pelo caminho (1) na Figura 1), seja pelo aumento passo a passo da pressão²⁸ ou pela excitação de amplitude modulada responsável pelo início periódico e extinção dos modos de superfície²⁹. As principais desvantagens dessas técnicas são (i) uma orientação aleatória do eixo de simetria das oscilações da superfície que não pode ser controlada para estar no plano da imagem, (ii) uma curta vida útil das oscilações da forma da bolha que dificulta a análise dos fluxos de líquido induzidos em escalas de tempo maiores, e (iii) o desencadeamento frequente de modos de forma instáveis. Propomos uma técnica alternativa para cruzar o limiar de pressão a uma pressão acústica constante no mapa de raio/pressão, como ilustrado pelo caminho (2) na Figura 1. Para isso, é necessário aumentar o tamanho da bolha de forma que ela fique na zona de instabilidade. Tal aumento é realizado por uma técnica de coalescência de bolhas. A coalescência de duas microbolhas, inicialmente oscilantes esfericamente, é explorada para criar uma única bolha deformada. Se a pressão acústica e o tamanho da bolha coalescida estiverem na zona de instabilidade, os modos de superfície serão acionados. Também evidenciamos que a técnica de coalescência induz oscilações de forma estáveis em regime de estado estacionário, bem como um eixo de simetria controlado definido pelo movimento retilíneo das duas bolhas que se aproximam. Como uma oscilação de forma estável é garantida ao longo de minutos, a análise do fluxo de fluido induzido por bolhas é possível semeando o meio líquido com micropartículas fluorescentes, iluminadas por uma fina folha de laser. O registro do movimento das micropartículas sólidas nas proximidades da interface de bolhas permite identificar o padrão do fluxo de fluido induzido³⁰. O princípio geral do desencadeamento de oscilações em forma de bolha, levando a um fluxo de fluido estável no tempo, é ilustrado na Figura 2.

No protocolo a seguir, descrevemos os passos necessários para criar oscilações estáveis em forma de bolhas através da técnica de coalescência e descrevemos as medidas de fluxo de fluido. Isso inclui o projeto do sistema de levitação acústica, a calibração acústica, a nucleação de bolhas e a técnica de coalescência, a medição da dinâmica da interface de bolhas e do fluxo de fluido circundante e o processamento de imagens.

Protocolo

1. Projeto da câmara de levitação acústica

1. Projetar um tanque cúbico opticamente transparente (semelhante ao PMMA) (8 cm de borda e 2,8 mm de espessura por face) com o módulo de geometria de um software de simulação multifísica (Tabela de Materiais).
2. Inserir uma superfície cilíndrica (Ø = 35 mm) centrada no fundo do tanque, para modelar o transdutor ultrassônico.
3. Ajuste as condições de contorno para pressão zero em cada parede com um deslocamento normal de amplitude de 1 μm na superfície do transdutor.
4. Usando um módulo no domínio da frequência, simule a Função de Resposta de Frequência (FRF) do tanque na faixa de frequência [10 - 40] kHz, nos três locais arbitrários loc1 = (0,01375, 0,01375, 0,04125), loc2 = (0, 0, 0,0088) e loc3 = (0,021725, 0,023375, 0,00935).
5. Adaptar o tamanho do tanque de forma que um dos modos acústicos da cavidade corresponda à frequência nominal do transdutor (aqui 31,2 kHz). O FRF contém, portanto, um pico de ressonância próximo a essa frequência, conforme ilustrado na Figura 3.
6. Plote o campo de pressão dentro do tanque, como mostrado na Figura 4. O modo de ressonância escolhido deve conter pelo menos um antinó de pressão no interior do recipiente, no qual a bolha acústica será aprisionada.
7. Ao projetar o tanque, projete uma face superior móvel com um sulco de guia em cada borda para fechar firmemente as faces do tanque. Faça um pequeno furo na face superior para encher o tanque com o meio líquido.
8. Coloque a caixa d'água em cima de uma estrutura caseira que contenha o transdutor de ultrassom (tipo Langevin, frequência nominal de 31,2 kHz). Use gel ecográfico para acoplar o transdutor à parede inferior do tanque.
9. Coloque o tanque e o sistema de quadro sobre uma mesa de deslocamento de três direções com parafusos micrométricos.
10. Encha o tanque com água microfiltrada, desmineralizada e (não desgaseificada, volume ~500mL, saturação de oxigênio de aproximadamente 8 mg· ^L-1).
    NOTA: O uso de água não desgaseificada em vez de desgaseificado torna possível a manutenção de bolhas estáveis durante os experimentos. O uso de água desgaseificada acelerará o encolhimento de bolhas devido à difusão de gás, mesmo que ligeiramente contrabalançado pela difusão retificada (mediada por ultrassom).

2. Geração de bolhas e calibração acústica

1. Preparar o arranjo experimental usado para nucleação de bolhas induzida por laser, excitação acústica e gravação em alta velocidade (Figura 5a,b,c). O arranjo experimental consiste em (A) o sistema de levitação acústica, (B) a fonte de alimentação do laser e (C) a cabeça do laser, (D) uma lente côncava esférica, (E) uma lente plano-côncava e uma lente asférica, (F) a câmera de alta velocidade, (G) o diodo emissor contínuo de luz. Posteriormente, para as medidas dos fluxos líquidos (Figura 5d) (H) será adicionada uma fonte de laser de onda contínua, (I) uma lente cilíndrica plano-côncava seguida de uma lente cilíndrica plano-côncava inserida atrás da primeira lente e orientada no eixo ortogonal.
2. Conecte o transdutor de ultrassom a um gerador de funções. Defina o sinal de excitação como: forma de onda senoidal, onda contínua, frequência 31,2 kHz. A amplitude é o único parâmetro variável.
3. Coloque a lente (D) a uma distância de aproximadamente 6 cm à frente da cabeça do laser (C).
4. Coloque a lente (E) a uma distância de aproximadamente 12 cm à frente da lente (D).
5. Coloque o tanque de água (A) de tal forma que um ponto de foco do laser esteja localizado dentro do tanque de água, levando à geração de faísca para cada pulso de laser (5 -10 mJ). A faísca do laser deve estar localizada aproximadamente 3 cm abaixo do antinó de pressão alvo.
   NOTA: Sem ultrassom (US), a bolha nucleada por laser subirá para a face superior devido à flutuabilidade.
6. Ligue o transdutor de ultrassom. Aumente a tensão aplicada até que a bolha não sobe mais verticalmente, mas seja desviada em direção ao antinó de pressão e, para uma pressão alta suficiente, presa.
7. Ajuste a iluminação retroiluminada (diodo emissor de luz contínua) e a câmera de alta velocidade para observar a bolha presa.
   NOTA: Ao nuclear uma nova bolha com uma faísca de laser, é fácil capturar a trajetória da bolha se aproximando de seu local de aprisionamento.
8. Mova a localização da faísca laser dentro do tanque de água de modo que a trajetória da bolha permaneça dentro do plano focal da câmera.
9. Aprisione uma bolha e capture suas oscilações radiais com os seguintes parâmetros: tamanho do quadro 128 x 128 pixels, taxa de aquisição 180 kHz. Um exemplo de oscilações radiais de grande amplitude ao longo de dois períodos acústicos é apresentado na Figura 6. O tamanho típico das bolhas de gás varia de 30 a 80 μm.
10. Registre as oscilações radiais da bolha durante 3 a 30 milissegundos para capturar centenas a milhares de oscilações de bolhas. Repita esta gravação para aumentar as tensões aplicadas do transdutor. As tensões aplicadas típicas estão na faixa de 0 - 8 V.
    NOTA: Ao modificar a tensão aplicada, o local de equilíbrio da bolha aprisionada move-se ligeiramente verticalmente. Para acompanhar as oscilações sem mover a iluminação retroiluminada e a câmera, coloque o sistema (transdutor e caixa d'água) em uma mesa móvel de três direções com precisão micrométrica.
11. Ligue o transdutor de ultrassom e capture uma imagem do fundo para pós-análise.
12. Pós-processar a série de vídeos seguindo este procedimento:
    1. Execute o arquivo executável VoltagePressure.exe. A interface mostrada na Figura 7 deve abrir.
       Observação : o script está disponível como um documento suplementar.
    2. Especificar os parâmetros físicos e experimentais na coluna da esquerda (Figura 7A).
    3. Especifique os valores de tensão aplicada para a série de gravações na tabela inferior direita (Figura 7B).
    4. No painel Análise do raio de bolhas , clique em Parâmetros de carregamento (Figura 7C) e selecione a pasta que contém todos os arquivos da sua série de vídeos e, em seguida, a imagem de fundo (obrigatória).
    5. A escolha é permitida entre analisar todos os vídeos de uma só vez, clicando em Automático, ou um a um, clicando em Passo a passo.
    6. Para cada arquivo de vídeo, a evolução do raio da bolha é plotada ao longo de um período acústico, e um ajuste numérico é sobreposto. A curva vermelha corresponde a uma modelagem linearizada de Rayleigh-Plesset. O raio da bolha de equilíbrio é exibido (Figura 7D).
    7. De acordo com o ajuste numérico, a pressão aplicada para esta tensão é exibida no painel do gráfico Pressão (Tensão) (Figura 7E). O valor da pressão aplicada também é exibido na tabela inferior direita (Figura 7B). As pressões aplicadas típicas correspondentes à dinâmica de tensão de 0 - 8 V são de 0 - 25 kPa.
    8. Depois que todos os vídeos forem processados, clique no botão Regressão linear para realizar um ajuste linear da curva de pressão/tensão. Os dados (valores de tensão e pressão) são salvos em um arquivo .txt localizado no diretório atual. A inclinação do encaixe é fornecida.

3. Técnica de coalescência

1. Ligue o transdutor de ultrassom. Ajuste a tensão aplicada suficientemente alta para que a pressão acústica correspondente possa levar ao desencadeamento da instabilidade superficial, de acordo com o diagrama numérico pressão/raio das zonas de instabilidade, como mostra a Figura 8.
2. Nuclear uma bolha, que então migrará para seu local de captura. Se a bolha presa exibir apenas oscilações esféricas, passe para a próxima etapa. Se aparecerem oscilações não esféricas:
   1. Desligue a alimentação do ultrassom para deixar a bolha subir até a superfície superior.
   2. Modifique a energia do laser (ajustando finamente em alguns mJ) ou reduza a tensão do transdutor.
   3. Ligue a alimentação do ultrassom.
   4. Nuclear uma nova bolha.
   5. Repita este procedimento até que o tamanho da bolha leve a oscilações puramente esféricas.
3. Quando uma bolha presa exibe apenas oscilações esféricas, gere uma nova faísca de laser. Quando a nova bolha atinge o local de aprisionamento, ocorre coalescência.
4. Se a bolha coalescida exibir apenas oscilações esféricas, gere uma nova bolha. Coalescências múltiplas podem ser necessárias para atingir o raio da bolha no qual ocorrem deformações não esféricas. Um exemplo de coalescência de bolhas levando a oscilações não esféricas é mostrado na Figura 9.
5. Uma vez que a bolha coalescida exibe oscilações não esféricas, registre as oscilações da bolha por uma duração de aproximadamente 3 a 30 milissegundos.
6. Identifique o número de modo das oscilações da forma consultando a Figura 10.

4. Medições de fluxo de fluido

1. No caso de medições de microfluxo de cavitação, partículas traçadoras fluorescentes devem ser adicionadas à água antes da nucleação de bolhas. Neste estudo, são utilizadas partículas de 0,71 μm (Tabela de Materiais). Eles são suficientemente pequenos para serem acusticamente transparentes (não influenciados pela força de radiação acústica) e para acompanhar com precisão o fluxo, bem como suficientemente grandes para espalhar a luz laser. Utilizar três gotas para o volume da caixa d'água, correspondendo a aproximadamente 2,10⁴ partículas/mm³.
2. Antes de fazer as medições, defina os seguintes parâmetros para capturar a dinâmica da bolha (escala de tempo rápida) e o fluxo de fluido (escala de tempo baixa):
   1. Crie um particionamento do disco de gravação da câmera.
   2. Alternativamente, defina os parâmetros de gravação como:
      1. Taxa de quadros 180 kHz, tamanho do quadro 128 x 128 pixels e tempo de exposição 1 μs para uma gravação da dinâmica da interface de bolhas
      2. Taxa de quadros de 600 Hz, tamanho de quadro de 1024 x 768 pixels e tempo de exposição de 1 ms para uma gravação do movimento dos traçadores de corante.
3. Use um laser contínuo.
4. Crie uma folha de laser fina deixando sucessivamente o feixe de laser passar através de lente cilíndrica plano-côncava e lente cilíndrica plano-convexa orientada em um eixo ortogonal. Uma largura de feixe de cerca de 160 μm pode ser obtida.
5. Configure a folha de laser para corresponder ao plano de imagem:
   1. Coloque o laser em um dispositivo móvel para que a folha de laser possa ser movida paralelamente ao plano de imagem.
   2. Ajuste a posição para que as partículas iluminadas sejam visíveis pela câmera.
   3. Nuclear e prender uma bolha.
   4. Ajuste ainda mais a posição da folha de laser, para que uma sombra se torne visível atrás da bolha. A bolha está agora dentro da folha de laser, como mostrado na Figura 11.
6. Induza a coalescência de bolhas até que um modo de forma oscilante estável seja aparente.
7. Faça várias gravações alternando entre dinâmica de bolhas e microstreaming.
   NOTA: Desligue o laser contínuo quando não for necessário. O aquecimento pode criar fluxos convectivos indesejados. Além disso, desligue o diodo emissor de luz ao realizar as medições de fluxo de fluxo.

5. Processamento de imagens para visualização dos padrões de microstreaming de cavitação

1. Instale o software de visualização ImageJ para processamento e análise de imagens em Java. Instale também o plugin CINE File Reader para abrir os arquivos da câmera de alta velocidade.
2. Clique em Arquivo | Importação | CineFile e selecione o vídeo *.cine contendo a captura do movimento das partículas.
3. Selecione Usar pilha virtual na nova janela, o vídeo agora é carregado.
4. Para observar o movimento das partículas sem exibir o padrão de streaming, clique em Imagem | Ajustar | Brilho/Contraste | Auto. O fundo escuro agora é substituído por uma imagem otimizada automaticamente.
5. Para exibir o padrão resultante, clique em Imagem | Pilhas | Projeto Z e escolha a opção Intensidade máxima para a projeção da imagem. Uma imagem de saída com pixels contendo o valor máximo sobre todas as imagens na pilha é exibida. Ajuste o contraste da imagem conforme descrito na etapa 5.4, se necessário.
   NOTA: Um padrão de streaming como os mostrados na Figura 12b e na Figura 12d é obtido.

Resultados

Uma sequência completa de coalescência de bolhas levando a oscilações não esféricas estáveis no tempo, controladas por simetria, é apresentada na Figura 9. A fase de aproximação de duas bolhas oscilantes esfericamente termina quando o fino filme líquido entre as duas bolhas é rompido. Vale notar que, no último estágio anterior à coalescência, as interfaces de bolhas se desviam da esfericidade. Ambas as bolhas se alongam em uma forma elipsoidal...

Discussão

O procedimento apresentado consiste em utilizar coalescência de bolhas para desencadear oscilações em forma de bolhas em estado estacionário, controladas por simetria, permitindo o estudo do fluxo de fluido de longa duração induzido por essas oscilações. O principal desafio da técnica é o controle de oscilações não esféricas para uma bolha ser aprisionada, longe de quaisquer limites.

A maioria das técnicas existentes propostas na literatura enfocou bolhas acopladas ao

Materiais

Name	Company	Catalog Number	Comments
Aspherical lens	Thorlabs	AL4050	Lens of focus 40 mm
Continuous wave laser source	CNI	MLL6FN	DPSS laser of wavelength 532nm, energy 400 mW
Cylindrical plano-concave lens	Thorlabs	LJ1277L1-A	lens of focus -25?4mm
Cylindrical plano-concave lens	Thorlabs	LK1900L1	lens of focus 250 mm
Fluorescent particles	Duke Scientific	R700	Red polymer fluorescent microspheres
Function generator	Agilent	HP33120	Generator of function feeding the ultrasound transducer
High-speed camera	Vision Research	Phantom v12.0	High-speed recording up to 1 Mfps
Liquid medium	Carlo Erba	Water for analysis	Demineralized, undegassed water
Multiphysics software	Comsol	None	Softwate for simulating the acoustic field of the levitation chamber
Nd:Yag pulsed laser	New Wave Research	Solo III-15	5 ns pulse duration, λ=532 nm, 3.5 mm beam diameter, up to 50 mJ
Plano-concave lens	Thorlabs	N-BK7	lens of focus 125 mm
Spherical concave lens	Thorlabs	N-SF11	Bi-concave lens of focus -25mm
Ultrasound transducer	SinapTec	Custom-made	Nominal frequency 31kHz, active area 35mm diameter
Visualization software	NIH	ImageJ	Software for image processing and analysis in Java
XY Linear stage	Newport	M-406	Displacement stage with micrometric screw
Z-axis linear stage	Edmund Optics	62-299	Vertical displacement stage with micrometric screw