Induction de microflux par des oscillations de bulles non sphériques dans un système de lévitation acoustique

Résumé

Une technique rapide et fiable est proposée pour contrôler les oscillations de forme d’une seule bulle acoustique piégée basée sur la technique de coalescence entre deux bulles. Les oscillations de forme de bulle à l’état stationnaire, contrôlées par symétrie, permettent d’analyser l’écoulement du fluide généré au voisinage de l’interface de bulle.

Résumé

Lorsqu’elles sont situées près de barrières biologiques, les microbulles oscillantes peuvent augmenter la perméabilité de la membrane cellulaire, permettant l’internalisation des médicaments et des gènes. Les observations expérimentales suggèrent que la perméabilisation temporaire de ces barrières peut être due à la contrainte de cisaillement exercée sur les tissus cellulaires par la microdiffusion en cavitation. Le microstreaming de cavitation est la génération de flux de vortex qui se produisent autour de microbulles d’ultrasons oscillantes. Pour produire de tels écoulements liquides, les oscillations à bulles doivent s’écarter des oscillations purement sphériques et inclure soit une instabilité translationnelle, soit des modes de forme. Les études expérimentales des écoulements induits par les bulles et des contraintes de cisaillement sur les surfaces voisines ont souvent une portée limitée en raison de la difficulté de capturer les déformations de forme des microbulles de manière stable et contrôlable. Nous décrivons la conception d’une chambre de lévitation acoustique pour l’étude des oscillations non sphériques contrôlées par symétrie. Un tel contrôle est effectué en utilisant une technique de coalescence entre deux bulles approchantes dans un champ ultrasonore suffisamment intense. Le contrôle des oscillations non sphériques ouvre la voie à un microflux de cavitation contrôlée d’une microbulle libre oscillant en surface. Les caméras à fréquence d’images élevée permettent d’étudier presque simultanément la dynamique des bulles non sphériques à l’échelle de temps acoustique et l’écoulement du liquide à une échelle de temps inférieure. Il est montré qu’une grande variété de motifs de fluide peut être obtenue et qu’ils sont corrélés au contenu modal de l’interface à bulles. Nous démontrons que même les modes de forme d’ordre élevé peuvent créer des motifs fluides à grande distance si la dynamique de l’interface contient plusieurs modes, soulignant le potentiel des oscillations non sphériques pour l’administration ciblée et localisée de médicaments.

Introduction

En médecine, un médicament administré doit franchir de nombreux obstacles dans le système vivant avant d’atteindre les cibles souhaitées. Cependant, la plupart des médicaments sont rapidement nettoyés de la circulation sanguine. L’efficacité du ciblage est faible et ils ne peuvent pas facilement traverser les membranes cellulaires, ce qui entraîne une administration inefficace des médicaments. Actuellement, l’utilisation de microbulles en combinaison avec les ultrasons a été proposée comme une méthode innovante pour l’administration non invasive, précise et ciblée de médicaments et de gènes aux tissus et cellules pathologiques¹. Dans cette approche, les microbulles peuvent jouer un rôle de support lorsque les médicaments libres sont soit co-injectés avec une suspension de bulles de gaz, soit chargés à sa surface. Les microbulles peuvent également agir comme un vecteur local pour recentrer l’énergie ultrasonore afin d’interagir avec les cellules. Fondamentalement, sous exposition aux ultrasons, les bulles se compriment et se dilatent de manière stable, un régime appelé cavitation stable qui génère des écoulements liquides et donc une contrainte de cisaillement sur les objets proches. Les microbulles peuvent également osciller de manière non linéaire et se dilater jusqu’à l’effondrement, dans le régime de cavitation inertielle, produisant des ondes de choc qui se propagent radialement à partir du site d’effondrement². Il a été démontré que la cavitation, stable ou inertielle, améliore la perméabilisation des membranes cellulaires, et améliore ainsi l’internalisation des médicaments dans la cellule³.

Dans les applications thérapeutiques, la compréhension du mécanisme de l’interaction bulle-cellule est très importante, mais il existe plusieurs obstacles, tant du point de vue scientifique que technique, qui empêchent nos connaissances de progresser. Premièrement, capturer la dynamique des cellules en réponse à des stimuli mécaniques induits par des bulles est très difficile⁴. À l’échelle de temps acoustique, les oscillations de microbulles de premier ordre peuvent conduire à l’activation des canaux membranaires, facilitant le passage moléculaire à travers les interfaces biologiques. Cela se produit par l’oscillation directe de la membrane cellulaire, également appelée « massage cellulaire »⁵. L’activation des canaux à la suite d’un stress mécanique direct a été mise en évidence à l’aide de techniques de pince patch-clamp qui mesuraient les propriétés électrophysiologiques des membranes cellulaires pendant et après l’exposition aux ultrasons⁶. La mesure de la dynamique cellulaire induite par les bulles (c’est-à-dire le champ complet de déformation de la membrane cellulaire) à l’échelle de temps acoustique permettrait également de mieux comprendre le seuil d’expansion de la zone membranaire Δ A/A nécessaire pour induire les pores dans la membrane cellulaire⁷. La deuxième barrière consiste à contrôler le régime d’effondrement des bulles pour éviter la lyse cellulaire induite par les microbulles. Les effondrements de bulles et les microjets induits ont été identifiés comme un mécanisme par lequel la perforation de la membrane se produit ^8,9. Une fois perméabilisée, la membrane cellulaire se répare par auto-obturation calcique des bicouches lipidiques et fusion des vésicules intracellulaires⁹. L’apparition d’effondrements de bulles peut également causer des dommages mortels à la cellule et induire des effets secondaires inutiles dans les environs. Dans les applications sensibles telles que l’ouverture de la barrière hémato-encéphalique médiée par les ultrasons, il est généralement admis que les effondrements de bulles inertielles doivent être évités¹⁰.

Par conséquent, d’énormes efforts sont actuellement consacrés à la conception de séquences d’émission d’ultrasons, couplées à la surveillance et au contrôle passifs de la cavitation, afin d’assurer des oscillations stables des microbulles¹¹. Dans ce régime stable, on a émis l’hypothèse que les bulles oscillantes de manière stable jouent un rôle important dans le déclenchement de la perméabilisation membranaire en favorisant une contrainte de cisaillement spatialement ciblée sur la membrane cellulaire⁷. La contrainte de cisaillement résulte des écoulements de liquide créés au voisinage des bulles oscillantes. Ces flux liquides sont appelés microflux de cavitation et, comme mentionné ci-dessus, ils sont l’un des nombreux mécanismes possibles responsables de l’absorption accrue des molécules extracellulaires. Lorsqu’il s’agit de suspensions de bulles ou de cellules telles que les tests de transfections biologiques in vitro¹², la perméabilisation par microdiffusion pourrait être beaucoup plus efficace que la perméabilisation par effondrement de bulles. Cela peut être démontré par une simple considération géométrique. Dans les suspensions cellulaires, la sonoporation sera efficace si la majorité des cellules en suspension est soumise à des effets mécaniques suffisamment importants (conduisant à une perméabilisation membranaire). On sait que les effondrements de bulles sont dirigés le long de la direction de rupture de symétrie isotrope, comme l’axe bulle-paroi¹³ ou la bulle-bulle et la lignée bulle-cellule joignant leur centre de masse¹⁴. Le microjet produit est donc un phénomène spatialement localisé le long d’un nombre fini de raies joignant les centres de cellules et de bulles. Selon la concentration de la cellule et de la bulle, ainsi que la distance cellule-bulle, cet effet peut ne pas être le plus efficace pour perméabiliser le nombre total de cellules en suspension. En revanche, le microstreaming par cavitation est un phénomène qui se produit à une échelle de temps lente, avec une grande expansion spatiale par rapport au rayon de la bulle. De plus, le flux de liquide est réparti tout autour de la bulle, et peut donc impacter un plus grand nombre de cellules, à très longue distance. Par conséquent, la compréhension du microflux de cavitation généré autour d’une bulle oscillante est une condition préalable au contrôle et à la quantification de la contrainte de cisaillement induite par les bulles appliquée aux cellules.

Pour ce faire, une étape préliminaire consiste à contrôler les oscillations sphériques et non sphériques d’une bulle pilotée par ultrasons, car les écoulements liquides générés sont induits par le mouvement de l’interface bulle^15,16. En particulier, les oscillations de forme des microbulles doivent être déclenchées et maintenues stables. De plus, l’orientation des oscillations en forme de bulle doit être contrôlée pour analyser correctement la corrélation entre la dynamique de l’interface de bulle et le motif de microdiffusion induit. En résumant la littérature existante, il est évident que les résultats expérimentaux détaillés du microflux induit par cavitation ne sont disponibles que pour les bulles attachées à une surface. Les microbulles murales sont couramment utilisées pour évaluer la dynamique précise de l’interface et les interactions cellulaires à l’échelle micrométrique dans le cadre d’un système de microscopie ultrarapide. Cette configuration est thérapeutiquement pertinente lorsque l’on considère des microbulles vibrantes situées sur la membrane cellulaire^17,18,19. L’étude de la bulle attachée au substrat peut cependant rendre plus compliquée l’analyse de la dynamique des bulles, en partie en raison de la nature complexe de la dynamique des lignes de contact²⁰ et du déclenchement de modes de forme asymétriques²¹. Dans les applications médicales et biologiques, les bulles qui ne sont pas attachées à un mur se trouvent couramment dans des géométries confinées telles que de petits vaisseaux. Cela a un impact significatif sur la dynamique des bulles et les instabilités de forme. En particulier, la présence d’un mur à proximité déplace le seuil de pression pour le déclenchement du mode de forme vers des valeurs de pression inférieures en fonction du numéro de mode de forme et de la taille de la bulle²². La paroi affecte également le microflux induit par les bulles avec une intensité peut-être plus élevée pour le flux produit²³.

Parmi tous les scénarios possibles que les microbulles peuvent connaître (libres ou attachées, proches d’un mur, s’effondrant ou oscillant de manière stable), nous proposons d’étudier la dynamique non sphérique d’une seule bulle loin de toute frontière. La configuration expérimentale est basée sur un système de lévitation acoustique²⁴ dans lequel une onde ultrasonore stationnaire est utilisée pour piéger la bulle. Ce scénario est cohérent avec les applications médicales dans lesquelles une collection de bulles et de cellules en suspension coexiste dans une chambre de sonotransfection, par exemple. Dans la mesure où les bulles et les cellules ne sont pas trop proches, on suppose que la présence d’une cellule n’a pas d’impact sur la dynamique de l’interface des bulles. Lorsque les cellules suivent les trajectoires en boucle du microflux induit par la cavitation, elles s’approchent cycliquement et se repoussent de l’emplacement de la bulle et nous pouvons supposer que la présence de cellules n’affecte ni le modèle d’écoulement ni sa vitesse moyenne. De plus, la dynamique non sphérique et le microflux induit à partir de bulles simples loin de la frontière sont bien connus d’un point de vue théorique. Afin de relier l’écoulement de liquide induit par les bulles à la dynamique du contour de la bulle, il est nécessaire de caractériser avec précision la dynamique de l’interface de la bulle. Pour ce faire, il est préférable d’adapter l’échelle spatio-temporelle dans les études expérimentales par rapport à celles utilisées en thérapeutique afin que l’acquisition avec des caméras à grande vitesse communes (inférieure à 1 million d’images/seconde) soit possible en utilisant de grosses bulles excitées à des fréquences plus basses. Lorsque l’on considère les bulles non revêtues, la fréquence propre ω_n d’un mode n donné est liée à la taille de la bulle comme 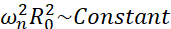²⁵. Cette relation rayon-fréquence propre est légèrement modifiée lorsque l’on considère les bulles décortiquées²⁶, mais l’ordre de grandeur de la fréquence propre ω_n reste le même. Ainsi, l’étude de bulles avec des rayons d’équilibre ~50μm dans un champ ultrasonore de 30 kHz est similaire à l’étude de bulles enrobées de rayons ~3μm dans un champ de 1,7 MHz, comme proposé par Dollet et ^al.27. Des numéros de mode de forme similaires et donc des modèles de microdiffusion sont donc attendus.

Afin de déclencher des oscillations non sphériques de l’interface à bulles, il est nécessaire de dépasser un certain seuil de pression dépendant du rayon, comme le montre la figure 1. Les techniques expérimentales existantes reposent sur l’augmentation de la pression acoustique pour déclencher des modes de surface (illustrés par le chemin (1) de la figure 1), soit par augmentation progressive de la pression²⁸ , soit par excitation d’amplitude modulée responsable de l’apparition périodique et de l’extinction des modes de surface²⁹. Les principaux inconvénients de ces techniques sont (i) une orientation aléatoire de l’axe de symétrie des oscillations de surface qui ne peut pas être contrôlée pour être dans le plan d’imagerie, (ii) une courte durée de vie des oscillations en forme de bulle qui rend l’analyse des écoulements de liquide induits difficile à des échelles de temps plus grandes, et (iii) le déclenchement fréquent de modes de forme instables. Nous proposons une technique alternative pour franchir le seuil de pression à pression acoustique constante dans la carte rayon/pression, comme illustré par le chemin (2) de la figure 1. Pour ce faire, il est nécessaire d’augmenter la taille de la bulle de sorte qu’elle se trouve dans la zone d’instabilité. Une telle augmentation est réalisée par une technique de coalescence de bulles. La coalescence de deux microbulles, initialement oscillantes sphériquement, est exploitée pour créer une seule bulle déformée. Si la pression acoustique et la taille de la bulle coalescée se trouvent dans la zone d’instabilité, les modes de surface sont déclenchés. Nous avons également mis en évidence que la technique de coalescence induit des oscillations de forme stable dans un régime d’état stationnaire, ainsi qu’un axe de symétrie contrôlé défini par le mouvement rectiligne des deux bulles qui s’approchent. Parce qu’une oscillation de forme stable est assurée sur quelques minutes, l’analyse de l’écoulement de fluide induit par des bulles est possible en ensemençant le milieu liquide avec des microparticules fluorescentes, éclairées par une fine feuille laser. L’enregistrement du mouvement des microparticules solides au voisinage de l’interface bulle permet d’identifier le schéma de l’écoulement du fluide induit³⁰. Le principe général du déclenchement des oscillations en forme de bulle, conduisant à un écoulement de fluide stable dans le temps, est illustré à la figure 2.

Dans le protocole suivant, nous décrivons les étapes nécessaires pour créer des oscillations stables en forme de bulle via la technique de coalescence et décrivons les mesures de l’écoulement des fluides. Cela comprend la conception du système de lévitation acoustique, l’étalonnage acoustique, la nucléation des bulles et la technique de coalescence, la mesure de la dynamique de l’interface des bulles et de l’écoulement du fluide environnant, ainsi que le traitement de l’image.

Protocole

1. Conception de la chambre de lévitation acoustique

1. Concevoir un réservoir cubique optiquement transparent (de type PMMA) (8 cm de bord et 2,8 mm d’épaisseur par face) avec le module géométrique d’un logiciel de simulation multiphysique (Table of Materials).
2. Insérez une surface cylindrique (Ø = 35 mm) centrée au fond du réservoir, pour modéliser le transducteur à ultrasons.
3. Réglez les conditions aux limites à zéro pression sur chaque paroi avec un déplacement normal d’amplitude 1 μm à la surface du transducteur.
4. À l’aide d’un module de domaine fréquentiel, simuler la fonction de réponse en fréquence (FRF) du réservoir dans la gamme de fréquences [10 - 40] kHz, aux trois emplacements arbitraires loc1 = (0,01375, 0,01375, 0,04125), loc2 = (0, 0, 0,0088) et loc3 = (0,021725, 0,023375, 0,00935).
5. Adapter la taille du réservoir de telle sorte que l’un des modes acoustiques de la cavité corresponde à la fréquence nominale du transducteur (ici 31,2 kHz). Le FRF contient donc un pic de résonance proche de cette fréquence, comme l’illustre la figure 3.
6. Tracez le champ de pression à l’intérieur du réservoir, comme illustré à la figure 4. Le mode de résonance choisi doit contenir au moins un antinoeud de pression à l’intérieur du récipient, sur lequel la bulle acoustique sera piégée.
7. Lors de la conception du réservoir, concevez une face supérieure mobile avec une rainure de guidage sur chaque bord pour fermer étroitement les faces du réservoir. Percez un petit trou sur la face supérieure afin de remplir le réservoir avec le milieu liquide.
8. Placez le réservoir d’eau sur un cadre fait maison contenant le transducteur à ultrasons (type Langevin, fréquence nominale de 31,2 kHz). Utilisez du gel échographique pour coupler le transducteur à la paroi inférieure du réservoir.
9. Placez le réservoir et le système de cadre sur une table de déplacement à trois directions avec des vis micrométriques.
10. Remplir le réservoir avec de l’eau microfiltrée, déminéralisée et (non dégazée, volume ~ 500 mL, saturation en oxygène d’environ 8 mg· ^L-1).
    NOTE: L’utilisation d’eau non dégazée au lieu d’eau dégazée permet de maintenir des bulles stables pendant toute la durée des expériences. L’utilisation d’eau dégazée accélérera le rétrécissement des bulles dû à la diffusion de gaz, même s’il est légèrement contrebalancé par une diffusion rectifiée (par ultrasons).

2. Génération de bulles et étalonnage acoustique

1. Préparer la configuration expérimentale utilisée pour la nucléation de bulles induite par laser, l’excitation acoustique et l’enregistrement à grande vitesse (Figure 5a,b,c). La configuration expérimentale comprend (A) le système de lévitation acoustique, (B) l’alimentation laser et (C) la tête laser, (D) une lentille concave sphérique, (E) une lentille plano-concave et une lentille asphérique, (F) la caméra haute vitesse, (G) la diode électroluminescente continue. Plus tard, pour les mesures des écoulements de liquides (Figure 5d) (H) une source laser à ondes continues, (I) une lentille plano-concave cylindrique suivie d’une lentille plano-concave cylindrique insérée derrière la première lentille et orientée sur l’axe orthogonal sera ajoutée.
2. Branchez le transducteur à ultrasons à un générateur de fonctions. Réglez le signal d’excitation comme suit : forme d’onde sinusoïdale, onde continue, fréquence 31,2 kHz. L’amplitude est le seul paramètre variable.
3. Placez la lentille (D) à une distance d’environ 6 cm devant la tête laser (C).
4. Placez la lentille (E) à une distance d’environ 12 cm devant la lentille (D).
5. Placez le réservoir d’eau (A) de telle sorte qu’un point de focalisation du laser soit situé à l’intérieur du réservoir d’eau, ce qui entraîne la génération d’étincelles pour chaque impulsion laser (5 -10 mJ). L’étincelle laser doit être située à environ 3 cm sous l’antinoeud de pression ciblé.
   REMARQUE: Sans ultrasons (US), la bulle nucléée au laser montera jusqu’à la face supérieure en raison de la flottabilité.
6. Allumez le transducteur à ultrasons. Augmentez la tension appliquée jusqu’à ce que la bulle ne monte plus verticalement mais soit déviée vers l’antinœud de pression et, pour une pression suffisamment élevée, piégée.
7. Réglez l’éclairage rétroéclairé (diode électroluminescente continue) et la caméra haute vitesse afin d’observer la bulle piégée.
   REMARQUE: Lors de la nucléation d’une nouvelle bulle avec une étincelle laser, il est facile de capturer la trajectoire de la bulle approchant de son emplacement de piégeage.
8. Déplacez l’emplacement de l’étincelle laser dans le réservoir d’eau de sorte que la trajectoire de la bulle reste à l’intérieur du plan focal de la caméra.
9. Trap une bulle et capturer ses oscillations radiales avec les paramètres suivants: taille d’image 128 x 128 pixels, taux d’acquisition 180 kHz. Un exemple d’oscillations radiales de grande amplitude sur deux périodes acoustiques est fourni à la figure 6. La taille typique des bulles de gaz varie de 30 à 80 μm.
10. Enregistrez les oscillations radiales des bulles pendant 3 à 30 millisecondes afin de capturer des centaines à des milliers d’oscillations de bulles. Répétez cet enregistrement pour augmenter les tensions appliquées du transducteur. Les tensions appliquées typiques sont comprises entre 0 et 8 V.
    REMARQUE: Lors de la modification de la tension appliquée, l’emplacement d’équilibre de la bulle piégée se déplace légèrement verticalement. Pour suivre les oscillations sans déplacer l’éclairage rétroéclairé et la caméra, placez le système (transducteur et réservoir d’eau) sur une table mobile à trois directions avec une précision micrométrique.
11. Allumez le transducteur à ultrasons et capturez une image de l’arrière-plan pour la post-analyse.
12. Post-traiter la série de vidéos en suivant cette procédure :
    1. Exécutez le fichier exécutable VoltagePressure.exe. L’interface illustrée à la figure 7 doit s’ouvrir.
       Remarque : Le script est disponible en tant que document supplémentaire.
    2. Précisez les paramètres physiques et expérimentaux dans la colonne de gauche (figure 7A).
    3. Spécifiez les valeurs de tension appliquée pour la série d’enregistrements dans le tableau inférieur droit (figure 7B).
    4. Dans le panneau Analyse du rayon de bulle , cliquez sur Paramètres de chargement (Figure 7C) et sélectionnez le dossier contenant tous les fichiers de votre série vidéo, puis l’image de fond (obligatoire).
    5. Le choix est autorisé entre analyser toutes les vidéos à la fois, en cliquant sur Auto, ou une par une en cliquant sur Étape par étape.
    6. Pour chaque fichier vidéo, l’évolution du rayon de bulle est tracée sur une période acoustique, et un ajustement numérique est superposé. La courbe rouge correspond à une modélisation linéarisée de Rayleigh-Plesset. Le rayon de bulle d’équilibre est affiché (Figure 7D).
    7. Selon le raccord numérique, la pression appliquée pour cette tension est affichée dans le panneau graphique Pression (tension) (Figure 7E). La valeur de la pression appliquée est également affichée dans le tableau inférieur droit (figure 7B). Les pressions appliquées typiques correspondant à la dynamique de tension de 0 à 8 V sont de 0 à 25 kPa.
    8. Une fois toutes les vidéos traitées, cliquez sur le bouton Régression linéaire pour effectuer un ajustement linéaire de la courbe pression/tension. Les données (valeurs de tension et de pression) sont enregistrées dans un fichier .txt situé dans le répertoire courant. La pente de l’ajustement est fournie.

3. Technique de coalescence

1. Allumez le transducteur à ultrasons. Réglez la tension appliquée suffisamment haut pour que la pression acoustique correspondante puisse entraîner le déclenchement d’une instabilité de surface, selon le diagramme numérique pression/rayon des zones d’instabilité, comme illustré à la figure 8.
2. Nucléez une bulle, qui migrera ensuite vers son emplacement de piégeage. Si la bulle piégée ne présente que des oscillations sphériques, passez à l’étape suivante. Si des oscillations non sphériques apparaissent :
   1. Éteignez l’alimentation ultrasonore pour laisser la bulle monter à la surface supérieure.
   2. Modifier l’énergie laser (en réglant finement sur quelques mJ) ou réduire la tension du transducteur.
   3. Allumez l’alimentation par ultrasons.
   4. Nucléez une nouvelle bulle.
   5. Répétez cette procédure jusqu’à ce que la taille de la bulle entraîne des oscillations purement sphériques.
3. Lorsqu’une bulle piégée ne présente que des oscillations sphériques, générez une nouvelle étincelle laser. Lorsque la nouvelle bulle atteint le lieu de piégeage, la coalescence se produit.
4. Si la bulle coalescente ne présente que des oscillations sphériques, générez une nouvelle bulle. Plusieurs coalescences peuvent être nécessaires pour atteindre le rayon de bulle auquel se produisent les déformations non sphériques. Un exemple de coalescence de bulles conduisant à des oscillations non sphériques est présenté à la figure 9.
5. Une fois que la bulle coalescée présente des oscillations non sphériques, enregistrez les oscillations de la bulle pendant une durée d’environ 3 à 30 millisecondes.
6. Identifiez le nombre de modes d’oscillations de forme en vous référant à la figure 10.

4. Mesures du débit des fluides

1. Dans le cas des mesures de microflux de cavitation, des particules traceurs fluorescentes doivent être ajoutées à l’eau avant la nucléation des bulles. Dans cette étude, des particules de 0,71 μm sont utilisées (Tableau des matériaux). Ils sont suffisamment petits pour être acoustiquement transparents (non influencés par la force de rayonnement acoustique) et pour suivre avec précision le flux ainsi que suffisamment grands pour diffuser la lumière laser. Utiliser trois gouttes pour le volume du réservoir d’eau, correspondant à environ 2,10⁴ particules/mm³.
2. Avant de prendre des mesures, définissez les paramètres suivants pour capturer à la fois la dynamique des bulles (échelle de temps rapide) et l’écoulement du fluide (échelle de temps basse) :
   1. Créez un partitionnement du disque d’enregistrement de la caméra.
   2. Vous pouvez également définir les paramètres d’enregistrement comme suit :
      1. Fréquence d’images 180 kHz, taille d’image 128 x 128 pixels et temps d’exposition 1 μs pour un enregistrement de la dynamique de l’interface à bulles
      2. Fréquence d’images 600 Hz, taille d’image 1024 x 768 pixels et temps d’exposition 1 ms pour un enregistrement du mouvement des traceurs de colorant.
3. Utilisez un laser continu.
4. Créez une fine feuille laser en laissant passer successivement le faisceau laser à travers une lentille plano-concave cylindrique et une lentille plano-convexe cylindrique orientée sur un axe orthogonal. Une largeur de faisceau d’environ 160 μm peut être obtenue.
5. Configurez la feuille laser pour qu’elle corresponde au plan d’imagerie :
   1. Réglez le laser sur un dispositif mobile de sorte que la feuille laser puisse être déplacée parallèlement au plan d’imagerie.
   2. Ajustez la position de sorte que les particules éclairées soient visibles par la caméra.
   3. Nucléer et piéger une bulle.
   4. Ajustez davantage la position de la feuille laser afin qu’une ombre devienne visible derrière la bulle. La bulle est maintenant à l’intérieur de la feuille laser, comme le montre la figure 11.
6. Induire la coalescence des bulles jusqu’à ce qu’un mode de forme oscillant de manière stable soit apparent.
7. Faites plusieurs enregistrements en alternant entre la dynamique des bulles et le microstreaming.
   REMARQUE: Éteignez le laser continu lorsque vous n’en avez pas besoin. Le chauffage peut créer des flux convectifs indésirables. Éteignez également la diode électroluminescente lorsque vous effectuez les mesures du débit de flux.

5. Traitement d’images pour visualiser les modèles de microstreaming de cavitation

1. Installez le logiciel de visualisation ImageJ pour le traitement et l’analyse d’images en Java. Installez également le plugin CINE File Reader afin d’ouvrir les fichiers de la caméra haute vitesse.
2. Cliquez sur Fichier | Importation | CineFile et sélectionnez la vidéo *.cine contenant la capture du mouvement de la particule.
3. Sélectionnez Utiliser la pile virtuelle dans la nouvelle fenêtre, la vidéo est maintenant chargée.
4. Afin d’observer le mouvement de la particule sans afficher le motif de streaming, cliquez sur Image | Ajuster | Luminosité/Contraste | Automatique. L’arrière-plan sombre est maintenant remplacé par une image optimisée automatiquement.
5. Pour afficher le motif résultant, cliquez sur Image | Piles | Projet Z et choisissez l’option Intensité maximale pour la projection d’image. Une image de sortie avec des pixels contenant la valeur maximale sur toutes les images de la pile s’affiche. Ajustez le contraste de l’image comme décrit à l’étape 5.4, si nécessaire.
   REMARQUE : Un modèle de diffusion en continu tel que ceux illustrés à la figure 12b et à la figure 12d est obtenu.

Résultats

Une séquence complète de coalescence de bulles conduisant à des oscillations non sphériques stables dans le temps et contrôlées par symétrie est présentée à la figure 9. La phase d’approche de deux bulles oscillantes sphériques se termine lorsque le mince film liquide entre les deux bulles est rompu. Il convient de noter qu’au dernier stade précédant la coalescence, les interfaces à bulles s’écartent de la sphéricité. Les deux bulles s?...

Discussion

La procédure présentée consiste à utiliser la coalescence des bulles afin de déclencher des oscillations en forme de bulle à l’état stationnaire, contrôlées par symétrie, permettant l’étude de l’écoulement de fluide à long terme induit par ces oscillations. Le principal défi de la technique est le contrôle des oscillations non sphériques pour une bulle piégée, loin de toute frontière.

La plupart des techniques existantes proposées dans la littérature se sont concentr...

matériels

Name	Company	Catalog Number	Comments
Aspherical lens	Thorlabs	AL4050	Lens of focus 40 mm
Continuous wave laser source	CNI	MLL6FN	DPSS laser of wavelength 532nm, energy 400 mW
Cylindrical plano-concave lens	Thorlabs	LJ1277L1-A	lens of focus -25?4mm
Cylindrical plano-concave lens	Thorlabs	LK1900L1	lens of focus 250 mm
Fluorescent particles	Duke Scientific	R700	Red polymer fluorescent microspheres
Function generator	Agilent	HP33120	Generator of function feeding the ultrasound transducer
High-speed camera	Vision Research	Phantom v12.0	High-speed recording up to 1 Mfps
Liquid medium	Carlo Erba	Water for analysis	Demineralized, undegassed water
Multiphysics software	Comsol	None	Softwate for simulating the acoustic field of the levitation chamber
Nd:Yag pulsed laser	New Wave Research	Solo III-15	5 ns pulse duration, λ=532 nm, 3.5 mm beam diameter, up to 50 mJ
Plano-concave lens	Thorlabs	N-BK7	lens of focus 125 mm
Spherical concave lens	Thorlabs	N-SF11	Bi-concave lens of focus -25mm
Ultrasound transducer	SinapTec	Custom-made	Nominal frequency 31kHz, active area 35mm diameter
Visualization software	NIH	ImageJ	Software for image processing and analysis in Java
XY Linear stage	Newport	M-406	Displacement stage with micrometric screw
Z-axis linear stage	Edmund Optics	62-299	Vertical displacement stage with micrometric screw