Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.
Method Article
Intravaskulärer Ultraschall Bildbasierter Finite-Elemente-Modellierungsansatz zur Quantifizierung der mechanischen Eigenschaften der menschlichen Koronararterie in vivo
* Diese Autoren haben gleichermaßen beigetragen
In diesem Artikel
Zusammenfassung
In vivo cine intravaskuläre Ultraschallbilder zeigen die koronare Querschnittsbewegung entsprechend unterschiedlichen Druckbelastungsbedingungen. Basierend auf einem Finite-Elemente-Modell wurde ein iteratives Schema verwendet, um die patientenspezifischen mechanischen Eigenschaften der Herzkranzgefäße in vivo zu bestimmen, indem die Koronarbewegung aus dem Computermodell mit medizinischen Bildern abgeglichen wurde.
Zusammenfassung
Die Quantifizierung der mechanischen Eigenschaften der koronaren Arterienwände könnte aussagekräftige Informationen für die Diagnose, das Management und die Behandlung von Erkrankungen der Herzkranzgefäße liefern. Da für Patienten, die eine kontinuierliche Überwachung benötigen, keine patientenspezifischen Koronarproben zur Verfügung stehen, wird eine direkte experimentelle Prüfung der Materialeigenschaften der Gefäße unmöglich. Aktuelle Koronarmodelle verwenden in der Regel Materialparameter aus der verfügbaren Literatur, was zu erheblichen Fehlern bei der Berechnung mechanischer Spannungen/Dehnungen führt. Hier würden wir einen Finite-Elemente-Modell-basierten Aktualisierungsansatz (FEMBUA) einführen, um patientenspezifische in vivo Materialeigenschaften von Koronararterien auf der Grundlage medizinischer Bilder zu quantifizieren. In-vivo-Bilder des intravaskulären Ultraschalls (IVUS) und der virtuellen Histologie (VH)-IVUS von Koronararterien wurden von einem Patienten mit koronarer Herzkrankheit aufgenommen. Cine IVUS-Bilder, die die Gefäßbewegung über einen Herzzyklus zeigten, wurden segmentiert, und es wurden zwei IVUS-Rahmen mit maximalem und minimalem Lumenumfang ausgewählt, um die koronare Geometrie unter systolischen bzw. diastolischen Druckbedingungen darzustellen. Das VH-IVUS-Bild wurde ebenfalls segmentiert, um die Gefäßkonturen zu erhalten, und den VH-IVUS-Konturen wurde eine Schichtdicke von 0,05 cm hinzugefügt, um die koronare Geometrie zu rekonstruieren. Es wurde ein rechnerisches Finite-Elemente-Modell mit einem anisotropen Mooney-Rivlin-Materialmodell erstellt, das verwendet wurde, um die mechanischen Eigenschaften des Gefäßes und die pulsierenden Blutdruckbedingungen zu beschreiben, die der koronaren luminalen Oberfläche vorgeschrieben sind, damit sie sich zusammenzieht und ausdehnt. Anschließend wurde ein iterativer Aktualisierungsansatz verwendet, um die Materialparameter des anisotropen Mooney-Rivlin-Modells zu bestimmen, indem die minimalen und maximalen Lumenumfänge aus dem rechnerischen Finite-Elemente-Modell mit denen aus Cine-IVUS-Bildern abgeglichen wurden. Dieser bildbasierte, auf Finite-Elemente-Modellen basierende Aktualisierungsansatz könnte erfolgreich erweitert werden, um die Materialeigenschaften von Arterienwänden in verschiedenen Gefäßbetten zu bestimmen und birgt das Potenzial für die Risikobewertung von Herz-Kreislauf-Erkrankungen.
Einleitung
Die koronare Herzkrankheit (KHK) ist eine der Hauptursachen für Mortalität und Morbidität und war im Jahr 2019 weltweit für mehr als 9,14 Millionen Todesfälle verantwortlich 1,2. Die Entwicklung von Erkrankungen der Herzkranzgefäße, wie Arteriosklerose und Stenose, geht häufig mit Veränderungen der mechanischen Kräfte und Veränderungen der Materialeigenschaften der Gefäßwand einher3. Die Materialeigenschaften der Herzkranzgefäße sind nicht nur der Eckpfeiler für die Bestimmung ihrer mechanischen Reaktion auf die physiologische Belastung, sondern auch für die Simulation des mechanischen Verhaltens von Blutgefäßen, die Vorhersage der Entwicklung atherosklerotischer Läsionen und die Bewertung der therapeutischen Wirkung verschiedener medizinischer Geräte 4,5. Folglich sind ein tiefgreifendes Verständnis und eine genaue Quantifizierung der Eigenschaften von koronarem Material von größter Bedeutung für die frühzeitige Diagnose von Krankheiten, die Präzisionsmedizin und die Prognosebewertung6.
Mechanische Experimente an isolierten Koronargeweben, wie z. B. planare biaxiale Tests, Indentationstests, Inflation-Extension- und uniaxiale Extensionstests, sind gängige Ansätze zur Quantifizierung der mechanischen Eigenschaften von Koronargefäßwänden ex vivo 7,8,9. Bei diesen Ansätzen wurden Koronararterienproben von Patienten oder Versuchstieren gewonnen. Es wurden mechanische Tests durchgeführt, um die Dehnungsreaktionen der Gefäßwand unter verschiedenen Belastungsbedingungen zu bestimmen, und dann wurden die Materialparameter durch Anpassung der experimentellen Daten10 bestimmt. Frühere Studien haben gezeigt, dass die koronaren Eigenschaften hochgradig nichtlinear und anisotrop sind11. Obwohl Ex-vivo-Experimente genaue Daten zu den Materialeigenschaften liefern können, gibt es auch signifikante Einschränkungen, die wie folgt lauten: Erstens unterscheidet sich das mechanische Verhalten der Probe nach der Entnahme von lebenden Probanden von dem unter In-vivo-Bedingungen, was die Genauigkeit der Testergebnisse beeinträchtigen kann. Zweitens ist es aufgrund ethischer und praktischer Zwänge schwierig, eine große Ansammlung von normalem oder pathologischem Gewebe der Koronararterien zu erhalten, um die mechanische Prüfung durchzuführen.
Um diese Einschränkungen zu überwinden, haben Forscher neuartige Techniken für die In-vivo-, Echtzeit- und patientenspezifische Quantifizierung der Eigenschaften von Koronarmaterialien erforscht. Unter ihnen verspricht der auf medizinischen Bildern basierende Finite-Elemente-Modell-basierte Aktualisierungsansatz (FEMBUA), diese herausfordernden Probleme zu lösen. Bei diesem Ansatz werden fortschrittliche bildgebende Verfahren wie intravaskulärer Ultraschall (IVUS) und virtuelle Histologie (VH)-IVUS verwendet, um die detaillierte Koronargeometrie, die Gewebezusammensetzung und ihre Bewegung zu erfassen12. Durch die Konstruktion von 3D-Finite-Elemente-Modellen (FE) und die Einbeziehung patientenspezifischer physiologischer Blutdruckbedingungen konnte das dynamische Gefäßverhalten während der Herzzyklen wiederhergestellt werden, indem Materialparameter so optimiert wurden, dass sie mit den Bilddaten für eine schnelle und genaue Quantifizierung der koronaren Materialeigenschaften übereinstimmten13. Zu den Vorteilen des In-vivo-FE-Aktualisierungsansatzes gegenüber ex vivo-Experimenten gehören die In-vivo-Bewertung ohne Gewebeexzision, die Erleichterung groß angelegter Auswertungen und die Simulation der Gefäßdynamik unter komplexen Bedingungen, um das pathophysiologische Verständnis von Koronarerkrankungen zu unterstützen.
In dieser Arbeit werden die wichtigsten Schritte des auf Finite-Elemente-Modellen basierenden Aktualisierungsansatzes vorgestellt, darunter eine detaillierte Segmentierung und Verarbeitung von cine IVUS- und VH-IVUS-Bildern, die Rekonstruktion eines rechnerischen Dünnschichtstrukturmodells und die Ausführung des iterativen Schemas zur Suche nach optimalen Materialparametern für koronares arterielles Gewebe. Ziel dieses Protokolls ist es, die Materialeigenschaften der Koronararterie aus einem Probenpatienten mit KHK unter Verwendung der FEMBUA-Methode als Demonstration zu quantifizieren, insbesondere die Veranschaulichung von Schritt-für-Schritt-Methoden. Abschließend diskutierten wir die Bedeutung und andere Aspekte dieser in vivo-Methode .
Bei der ausgewählten Teilnehmerin handelt es sich um eine 64-jährige Frau ohne klinische Vorgeschichte einer koronaren Herzkrankheit. Bei diesem Patienten wurde eine koronare Herzkrankheit diagnostiziert, nachdem er Symptome von Brustschmerzen hatte. Das Koronarangiogramm und der IVUS-Scan wurden durchgeführt, um die Diagnose zu bestätigen. Eine Plaqueläsion mit 60% Stenose wurde in der Mitte der linken vorderen absteigenden Arterie gefunden. Nach der Beurteilung wurde eine optimale medikamentöse Therapie zur Behandlung des Patienten angenommen.
Protokoll
Anonymisierte klinische Daten, einschließlich In-vivo-IVUS-Bilder und Blutdruckdaten, wurden von einem Patienten mit KHK im Zhongda Hospital der Southeast University mit Einverständniserklärung aufgenommen. Der Probenpatient wurde aus dem Patientenpool einer klinischen Studie zu intermediären koronaren atherosklerotischen Läsionen ausgewählt, um die Methode zur Quantifizierung der Materialeigenschaften patientenspezifischer Koronargefäßezu demonstrieren 14. Die Studie wurde nach dem Protokoll durchgeführt, das von der Ethikkommission für klinische Forschung des Zhongda Hospital, Southeast University, genehmigt wurde (Zulassungsnummer: 2017ZDSYLL023-p01).
1. Datenerhebung und -verarbeitung
- Cine IVUS und VH-IVUS Bilderfassung
- Platzieren Sie den IVUS-Katheter distal der atherosklerotischen Läsion unter Anleitung eines Koronarangiogramms und ziehen Sie ihn zur proximalen Seite zurück. Generieren Sie nebenbei IVUS-Graustufenbilder, um den Querschnitt des Herzkranzgefäßes zu visualisieren.
- Verwenden Sie das IVUS-Bildgebungssystem, das mit einem leistungsstarken 20 MHz, 2,9F Platinkatheter ausgestattet ist, um IVUS-Bilder des koronaren arteriellen Segments mit atherosklerotischer Plaque von Patienten mit KHK aufzunehmen (Abbildung 1).
- Halten Sie den Katheter während der IVUS-Bildaufnahme an der vorausgewählten Läsionsstelle für ca. 2 s an, um eine Sequenz von IVUS-Bildern zu erhalten, die als cine IVUS bezeichnet wird. Die cine IVUS-Bilder zeigten deutlich die dynamischen Querschnittsveränderungen an der gegebenen Plaquestelle über den Herzzyklus.
- Generieren Sie VH-IVUS-Bilder basierend auf IVUS-Frames, die zum Zeitpunkt des R-Peaks in Elektrokardiogrammen aufgenommen wurden, um Plaquekomponenten in farbcodierter Form mit dem Bildgebungssystem zu visualisieren.
HINWEIS: VH-IVUS-Bilder bieten eine intuitive Farbkarte für vier wichtige Plaquekomponenten in der atherosklerotischen Plaque: lipidreicher nekrotischer Kern (Lipid) in rot, Verkalkung in weiß, fibröses Gewebe in dunkelgrün und fibröses Fettgewebe in hellgrün. - Speichern Sie VH-IVUS- und Cine-IVUS-Bilder im DICOM-Format für die Offline-Analyse.
- Bildsegmentierung und -verarbeitung
- Öffnen Sie DICOM-Dateien mit dem Viewer, doppelklicken Sie auf den entsprechenden Sequenznamen , um das Bild zu öffnen, und klicken Sie auf Exportieren > Bilder exportieren , um jeden Cine-IVUS-Frame oder VH-IVUS-Frame als einzelnes Bild im BMP-Format zu speichern. Jedes BMP-Bild enthält 500 x 500 Pixel, wie in der ursprünglichen DICOM-Datei angegeben.
- Untersuchen Sie das cine IVUS-Bild Bild für Bild, um die aufeinanderfolgenden Bilder zu finden, die während eines Herzzyklus an der vorausgewählten Plaquestelle aufgenommen wurden. Es wurden 26 cine IVUS-Frames während eines Herzzyklus für diese Proben-Plaque-Stelle erzeugt.
- Untersuchen Sie alle generierten VH-IVUS-Bilder, um das VH-IVUS-Bild zu finden, das an der angegebenen Plaquestelle aufgenommen wurde. Die hier verwendeten VH-IVUS-Bilder wurden mit einem IVUS-Frame aus den cine IVUS-Frames in einem Herzzyklus erstellt.
- Segmentieren Sie VH-IVUS- und Cine-IVUS-Bilder mit der ImageJ-Software, um die Konturen von Gefäßgrenzen und Plaquekomponentengrenzen zu erhalten (siehe Abbildung 1C).
- Wählen Sie auf der Registerkarte "Segmentierte Linie" die Option "Gerade > " und zeichnen Sie die Konturen des Lumens, der äußeren Begrenzung des Herzkranzgefäßes und der Plaquekomponenten auf cine IVUS- und VH-IVUS-Bildern manuell ab. Für das Cine-IVUS-Bild segmentieren Sie nur die Konturen des Lumens und der äußeren Gefäßgrenze, während Sie für das VH-IVUS-Bild die Konturen des Lumens, der äußeren Gefäßgrenze und der Plaquekomponentengrenzen segmentieren.
- Der Einfachheit halber sollten Sie nur große Lipidkomponenten für die Erstellung eines Finite-Elemente-Modells aufbewahren und kleine, isolierte Lipidkomponenten ignorieren. In dieser Plaque-Probe war nur ein Lipid vorhanden. Überlagern Sie die abgegrenzten Konturen mit den Originalbildern auf der Registerkarte "Bild> "Überlagern" > "Auswahl hinzufügen ".
- Navigieren Sie zum Menü Zum ROI-Manager , um Konturen zu verwalten, Eigenschaften anzupassen und Farben und Linienbreite für eine bessere Visualisierung auf die richtigen Werte festzulegen. Wählen Sie die Registerkarte Eigenschaften aus, legen Sie die Strichfarbe auf eine andere Farbe fest, und füllen Sie die Linienbreite in der Breite aus. Legen Sie hier die Linienfarben auf Grün, Blau und Rot für Lumen-, Außengrenz- bzw. Lipidkonturen und die Linienbreite auf 3 fest.
- Glätten Sie Konturen mit der Option "Auswahl bearbeiten" >> "Spline anpassen" in der Befehlsleiste, nachdem Sie eine bestimmte Kontur ausgewählt haben, um eine glatte Kontur zu erhalten. Bei diesem Vorgang werden Techniken zur Anpassung von Spline-Kurven verwendet, um die Konturen automatisch zu glätten.
- Klicken Sie auf der Registerkarte XY-Koordinaten > Speichern unter > Datum, um die Punktkoordinaten jeder Kontur wie Lumen, äußere Begrenzung und Plaque-Komponente in einer separaten txt-Datei zu speichern. Diese Datei enthält die X- und Y-Koordinatenwerte der Punkte, aus denen die Konturlinie besteht, mit Pixeln als Einheit.
- Nehmen Sie die tatsächliche physische Größe jedes Pixels in Cine-IVUS- und VH-IVUS-Bildern (als Pixelgröße bezeichnet) aus der DICOM-Datei auf. Der reale Abstand für ein Pixel in den hier verwendeten IVUS-Daten beträgt 0,002 cm. Diese Informationen werden verwendet, um die Punktkoordinaten mit dem Pixel als Einheit in die reale Entfernung mit cm als Einheit umzuwandeln.
- Verarbeitung von Konturdaten
- Cine IVUS Konturdatenverarbeitung
- Lesen Sie txt-Dateien von Lumenkonturen aus allen cine IVUS-Bildern in einem Herzzyklus mit MATLAB.
- Multiplizieren Sie alle Lumenkonturen mit der Pixelgröße, um die tatsächliche Größe der Lumenkonturen zu erhalten.
- Berechnen Sie die Lumenumfänge für alle Lumenkonturen und identifizieren Sie die IVUS-Rahmen mit maximalen (Cmax) und minimalen (Cmin) Lumenumfängen, die diastolische bzw. systolische Bedingungen darstellen.
- VH-IVUS Konturdatenverarbeitung
- Lesen Sie txt-Dateien der Konturen des Lumens, der äußeren Begrenzung und der Plaque-Komponenten aus dem VH-IVUS-Bild mit MATLAB.
- Multiplizieren Sie alle Konturen mit der Pixelgröße, um die tatsächliche Größe aller Konturen zu erhalten.
- Unterteilen Sie jede Kontur in 100 Punkte mit gleichmäßigem Abstand, und führen Sie eine 2D-Glättung durch, um neue VH-IVUS-Konturdaten zu erhalten, die die alten ersetzen.
- Cine IVUS Konturdatenverarbeitung
2. Finite-Elemente-Modell
- Rekonstruktion der Koronargefäßgeometrie
- Erstellen Sie eine Konturschicht im dreidimensionalen Raum, indem Sie den Z-Koordinatenwert für alle Punkte der VH-IVUS-Konturen, einschließlich Lumen, äußerer Begrenzung und Lipid, hinzufügen und z = 0 für alle Punkte festlegen (Abbildung 2).
- Erstellen Sie eine weitere Konturebene, indem Sie den z-Koordinatenwert für alle Punkte der VH-IVUS-Konturen hinzufügen und z = 0,05 cm für alle Punkte zurücksetzen.
HINWEIS: Diese beiden Konturschichten rekonstruieren die 3D-Geometrie der Herzkranzgefäße für das reine Dünnschichtstrukturmodell, indem sie den VH-IVUS-Konturen eine feste Schichtdicke von 0,05 cm hinzufügen (Abbildung 2).
- Generierung von Finite-Elemente-Netzen
- Erstellen Sie zwei Hilfskonturen, indem Sie Lumen und äußere Begrenzungskonturen mit den Gewichtungen 1/3 und 2/3 (Abbildung 3A) für jede Schicht linear interpolieren.
- Unterteilen Sie die Gefäßfläche in 8 umlaufende Teile und 3 radiale Teile (siehe Abbildung 3B), indem Sie das Lumen/die äußere Begrenzung mit dem nächstgelegenen Punkt auf der Lipidkontur verbinden (z. B. die Punkte A und B in Abbildung 3B) oder zwei Hilfskonturen mit radialen Linien.
- Verbinden Sie alle Punkte zwischen den Schichten mit geraden Linien und bilden Sie eine 3D-Struktur mit 3 x 8 Volumen (Abbildung 3B). Teilen Sie jedes Volumen mit hexaedrischen Elementen, um das Finite-Elemente-Netz (Abbildung 3C) und verschiedene Materialgruppen (Abbildung 3D) zu erzeugen.
- Führen Sie eine Netzanalyse durch, indem Sie die Netzdichte um 10 % verfeinern, bis die Änderungen der Lösungen 5 % <.
- Definition der Materialeigenschaft
- Verwenden Sie ein modifiziertes anisotropes Mooney-Rivlin-Materialmodell, um die Materialeigenschaften der koronaren Gefäßwand zu beschreiben. Es wurde angenommen, dass Koronargefäße und Plaquekomponenten hyperelastische, anisotrope, nahezu inkompressible und homogene Materialien sind, und die Dehnungsenergiedichtefunktion des modifizierten anisotropen Mooney-Rivlin-Materialmodells lautet:
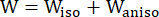 (1)
(1)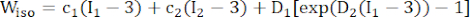 (2)
(2)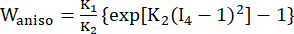 (3)
(3)
wobei I1 und I2 die erste und zweite Invariante des rechten Cauchy-Green-Verformungstensors C sind, definiert als c = [cij] = XTX, X = [Xij] = [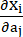 ], (Xi) war die aktuelle Position (aj) war die ursprüngliche Position, I4 = cij(nc)i(nc)j, nc war der Einheitsvektor in Umfangsrichtung des Gefäßes. c1, c2, D1, D2, K1 und K2 waren patientenspezifische Materialparameter.
], (Xi) war die aktuelle Position (aj) war die ursprüngliche Position, I4 = cij(nc)i(nc)j, nc war der Einheitsvektor in Umfangsrichtung des Gefäßes. c1, c2, D1, D2, K1 und K2 waren patientenspezifische Materialparameter. - Ordnen Sie die Anfangswerte der Materialparameter für ein patientenspezifisches Koronargefäß entsprechend den biaxialen ex vivo-Testergebnissen zu, d. h. c1 = -1.312,9 kPa, c2 = 114,7 kPa, D1 = 629,7 kPa, D2 = 2,0, K1 = 35,9 kPa und K2 = 23,5 (Abbildung 4A-B)13,15.
- Weisen Sie die Materialparameter für die Plaque-Komponente zu, falls vorhanden. Genauer gesagt für Lipide: c1 = 0,5 kPa, c2 = 0, D1 = 0,5 kPa und D2 = 1,5; für die Verkalkung verwendeten wir c1=920 kPa, c2=0, D1=360 kPa und D2=2,0 (Abbildung 4B)16.
HINWEIS: Es wurde angenommen, dass die Plaquekomponenten (Lipid und Verkalkung) hyperelastisch, isotrop und nahezu inkompressibel sind, und ihre mechanischen Eigenschaften wurden durch ein isotropes Mooney-Rivlin-Materialmodell mit den in Formel (2) angegebenen Dehnungsenergiedichtefunktionen beschrieben.
- Verwenden Sie ein modifiziertes anisotropes Mooney-Rivlin-Materialmodell, um die Materialeigenschaften der koronaren Gefäßwand zu beschreiben. Es wurde angenommen, dass Koronargefäße und Plaquekomponenten hyperelastische, anisotrope, nahezu inkompressible und homogene Materialien sind, und die Dehnungsenergiedichtefunktion des modifizierten anisotropen Mooney-Rivlin-Materialmodells lautet:
- Festlegen von Gleichungen und Randbedingungen
- Definieren Sie maßgebende Gleichungen für das reine Dünnschichtstrukturmodell, das die Bewegungsgleichung, die nichtlineare Cauchy-Green-Dehnungs-Verschiebungsbeziehung und das Modell des Koronargefäßmaterials11 umfasst.
- Verschreiben Sie patientenspezifische Blutdruckwellenformen auf der Lumenoberfläche, um reale physiologische Bedingungen zu simulieren (Abbildung 4C). Um patientenspezifische Blutdruck-Wellenformen zu erhalten, skalieren Sie eine typische Aortendruck-Wellenform mit systolischen und diastolischen Druckwerten, die mit der Armmanschette gemessen werden (Abbildung 4D).
3. Finite-Elemente-modellbasierter Aktualisierungsansatz für patientenspezifische Materialeigenschaften der Koronararterien
HINWEIS: Der iterative Prozess zur Bestimmung patientenspezifischer Koronarmaterialeigenschaften ist in Abbildung 5 dargestellt.
- Bestimmen Sie die Leerlaufgeometrie, die der Nulldruckbedingung als Anfangsgeometrie für das Berechnungsmodell entspricht, indem Sie die aus dem VH-IVUS-Bild rekonstruierte Koronargeometrie axial mit einer festen Schrumpfungsrate von 95 % und umlaufend mit einer Umfangsschrumpfung (als S bezeichnet) schrumpfen, die ursprünglich auf 98 % festgelegt war.
HINWEIS: Da die aus dem VH-IVUS-Bild rekonstruierte Koronargeometrie unter In-vivo-Bedingungen mit Blutdruck auf dem Lumen und axialer Dehnung aus angebundenen distalen und proximalen Koronararteriensegmenten erfolgte, sollte die In-vivo-Koronargeometrie umfangs- und axial schrumpfen, um die Nulldruckgeometrie zu erhalten. - Fixieren Sie die axiale Schrumpfung auf 95% und aktualisieren Sie die Umfangsschrumpfung in den folgenden Schritten.
- Definieren Sie das Materialverhältnis (bezeichnet als k), um die patientenspezifischen Materialeigenschaften des Koronargefäßes wie folgt zuzuweisen: c1 = k*(−1.312,9) kPa, c2 = k*114,7 kPa, D1 = k*629,7 kPa, K1 = k*35,9 kPa und fix D2 = 2,0 und K2 = 23,5.
HINWEIS: Da nur zwei Datenpunkte (minimale und maximale Lumenumfänge entsprechend dem diastolischen und systolischen Druck) zur Bestimmung der unbekannten Parameter (umlaufende Schrumpfungsrate S und Materialparameter des Mooney-Rivlin-Modells) erhalten wurden, reduzierten wir die Anzahl der unbekannten Parameter, indem wir annahmen, dass die patientenspezifischen Materialeigenschaften des Koronargefäßes in vivo proportional zur anfänglichen Vermutung mit dem Materialverhältnis waren, das als k bezeichnet wurde: das heißt, c1 = k*(−1.312,9) kPa, c2 = k*114,7 kPa, D1 = k*629,7 kPa, K1 = k*35,9 kPa, während D2 = 2,0 und K2 = 23,5 fixiert waren. - Aktualisieren Sie den festgelegten k-Wert auf einen Anfangswert k von 1 zusammen mit der Umfangsschrumpfungsrate S während des folgenden iterativen Verfahrens.
- Führen Sie eine Software aus, um das Rechenmodell zu lösen und die numerischen Ergebnisse zu erhalten.
- Schreiben Sie alle Befehle zum Erstellen des reinen Dünnschichtstrukturmodells mit MATLAB in eine Batch-Datei (Ergänzungsdatei 1).
- Laden Sie diese Batch-Datei über die erweiterte Benutzeroberfläche (AUI), um das Modell zu generieren (Abbildung 6A). Lösen Sie das reine Dünnschichtstrukturmodell, indem Sie auf Datendatei/Lösung klicken, und speichern Sie es als .dat Datei (Abbildung 6C). Simulieren Sie drei Herzzyklen und übernehmen Sie die Lösung im letzten Zyklus, um numerische Ergebnisse zu präsentieren.
- Exportieren Sie die Ergebnisse von Knotenkoordinaten in eine txt-Datei, indem Sie in Liste > Werteliste > Zone navigieren und X-POSITION, Y-POSITION und Z-POSITION in Aufzulistende Variablen unter Koordinate auswählen. Klicken Sie auf Anwenden und exportieren , um die Koordinatenergebnisse zu exportieren.
- Speichern Sie Lumenkonturdaten, die den diastolischen und systolischen Druckbedingungen entsprechen, in .txt Dateien für die Berechnung des Lumenumfangs.
- Vergleichen Sie die Lumenumfänge, die mit dem FE-Modell (Thin-Slice Layer Structure-Only Model) unter diastolischen Druckbedingungen berechnet wurden, mit in vivo cine IVUS-Daten (Cmin) und prüfen Sie, ob der relative Fehler <1% betrug. Wenn die Bedingung erfüllt war, fahren Sie mit dem nächsten Schritt fort, oder aktualisieren Sie das Materialverhältnis k mit der Sekantenmethode und fahren Sie mit Schritt 3.3 fort, um 17,18 erneut auszuführen.
HINWEIS: In der ersten Iteration wurde die Newton-Methode verwendet, um das Materialverhältnis anstelle der Sekantenmethode zu aktualisieren. - Vergleichen Sie die vom FE-Modell berechneten Lumenumfänge bei systolischen Druckbedingungen mit in vivo cine IVUS-Daten (Cmax) und prüfen Sie, ob der relative Fehler <1% betrug. Wenn ja, stoppen Sie die iterative Prozedur, oder aktualisieren Sie andernfalls die Umfangsschrumpfungsrate S und leiten Sie zu Schritt 3.4 weiter, um die Ausführung erneut durchzuführen.
HINWEIS: In der ersten Iteration wurde die Newton-Methode verwendet, um die Umfangsschrumpfungsrate anstelle der Sekantenmethode zu aktualisieren. - Erfassen Sie optimale S- und k-Werte und berechnen Sie die entsprechenden Materialparameter des Mooney-Rivlin-Materialmodells.
- Plotten Sie die umlaufenden und axialen Spannungs-Dehnungs-Verhältnis-Kurven des Koronargefäßes (Abbildung 7), die sich wie folgt ableiten lassen:
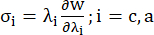 (4)
(4)
wobei σ die Cauchy-Spannung darstellt, λ das Dehnungsverhältnis, i = c, a die Umfangs- und Achsenrichtung darstellt.- Um eine Materialkurve in eine bestimmte Richtung zu zeichnen, fixieren Sie das Dehnungsverhältnis in die andere Richtung auf 1. Berechnen Sie den effektiven Elastizitätsmodul im Umfang und axial (jeweils mit YMc und YMa bezeichnet) als Steigung der Skalenfunktion der Materialkurve im Dehnungsverhältnisintervall [1,0, 1,1], um die allgemeine Materialsteifigkeit der Koronararterien13 widerzuspiegeln:
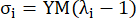 (5)
(5)
- Um eine Materialkurve in eine bestimmte Richtung zu zeichnen, fixieren Sie das Dehnungsverhältnis in die andere Richtung auf 1. Berechnen Sie den effektiven Elastizitätsmodul im Umfang und axial (jeweils mit YMc und YMa bezeichnet) als Steigung der Skalenfunktion der Materialkurve im Dehnungsverhältnisintervall [1,0, 1,1], um die allgemeine Materialsteifigkeit der Koronararterien13 widerzuspiegeln:
- Extrahieren Sie jederzeit Plaque-Spannungs-/Dehnungsverteilungen und erfassen Sie die Knotenverteilung und die maximalen Stresswerte während der systolischen und diastolischen Phase (Abbildung 8).
Ergebnisse
Wir beschreiben ausführlich die FEMBUA-Methode, die eine schnelle Plaquematerial- und Stressanalyse von koronaren Plaques nach Echtzeit-IVUS-Bildgebung ermöglicht und die in vivo Materialeigenschaften und biomechanischen Ergebnisse von Plaques bestimmen kann. Die in vivo Materialparameter des Mooney-Rivlin-Materialmodells für dieses Herzkranzgefäß sind in Tabelle 1 aufgeführt. Die Simulationsergebnisse des Finite-Elemente-Modells, einschließlich ...
Diskussion
Kritische Schritte im Protokoll
Der kritischste Schritt im auf dem Finite-Elemente-Modell basierenden Aktualisierungsansatz liegt im iterativen Vorgehen. Bei diesem Ansatz sollte das Finite-Elemente-Modell die Bewegung der Herzkranzgefäße auf dem Gefäßquerschnitt aus in vivo cine IVUS-Bildern genau rekonstruieren. Zu diesem Zweck wurde in dieser Studie die Minimierung der Lumenumfangsdifferenz zwischen dem Finite-Elemente-Modell und in vivo-Bildern
Offenlegungen
Die Autoren erklären, dass kein Interessenkonflikt besteht.
Danksagungen
Diese Forschung wurde teilweise unterstützt durch das Medical Health Science and Technology Project der Provinz Shandong (Nr. 202425020256 und 202403010254), die National Natural Science Foundation of China mit Zuschüssen 11972117 und 11802060, die Natural Science Foundation der Provinz Jiangsu unter der Fördernummer BK20180352 und die Natural Science Foundation der Provinz Shandong unter der Fördernummer ZR2024QA110.
Materialien
| Name | Company | Catalog Number | Comments |
| Bee DICOM Viewer | SinoUnion Healthcare Inc. | Version 3.5.1 | A DICOM image reader software |
| ADINA | Adina R & D | Version 9.0 | Finite element solver |
| ImageJ | National Institutes of Health | Segmented IVUS contours | |
| MATLAB | MathWorks | Version R2018a | Commercial programming platform |
| Volcano s5 imaging system | Volcano Company | Intravascular ultrasound imaging system |
Referenzen
- Roth, G. A., et al. Global burden of cardiovascular diseases and risk factors, 1990-2019: update from the GBD 2019 study. J Am Coll Cardiol. 76 (25), 2982-3021 (2020).
- Kanwar, S. S., et al. Acute coronary syndromes without coronary plaque rupture. Nat Rev Cardiol. 13 (5), 257-265 (2016).
- Milzi, A., et al. Coronary plaque composition influences biomechanical stress and predicts plaque rupture in a morpho-mechanic OCT analysis. Elife. 10, e64020 (2021).
- Stefanati, M., et al. Effect of variability of mechanical properties on the predictive capabilities of vulnerable coronary plaques. Comput Methods Programs Biomed. 254, 108271 (2024).
- Laurent, S., et al. Expert consensus document on arterial stiffness: methodological issues and clinical applications. Eur Heart J. 27 (21), 2588-2605 (2006).
- Daisuke, K., et al. Coronary plaque phenotype associated with positive remodeling. J Cardiovasc Comput Tomogr. 18 (4), 401-407 (2024).
- Macrae, R. A., Miller, K., Doyle, B. J. Methods in mechanical testing of arterial tissue: A review. Strain. 52, 380-399 (2016).
- Hayashi, K. Experimental approaches on measuring the mechanical properties and constitutive laws of arterial walls. J Biomech Eng. 115 (4B), 481-488 (1993).
- Sacks, M. S., Sun, W. Multiaxial mechanical behavior of biological materials. Annu Rev Biomed Eng. 5, 251-284 (2003).
- Charis, C., et al. Impact of combined plaque structural stress and wall shear stress on coronary plaque progression, regression, and changes in composition. Eur Heart J. 40 (18), 1411-1422 (2019).
- Wang, L., et al. Quantifying patient-specific in vivo coronary plaque material properties for accurate stress/strain calculations: An IVUS-based multi-patient study. Front Physiol. 12, 721195 (2021).
- Guo, X. Y., et al. Quantify patient-specific coronary material property and its impact on stress/strain calculations using in vivo IVUS data and 3D FSI models: a pilot study. Biomech Model Mechanobiol. 16 (1), 333-344 (2017).
- Wang, L., et al. Quantification of patient-specific coronary material properties and their correlations with plaque morphological characteristics: An in vivo IVUS study. Int J Cardiol. 371, 21-27 (2023).
- Lu, W., et al. Accurate identification of potential critical coronary lesions for the reduction of risk of cardiovascular events: study protocol for a randomized, open-label, active-controlled multi-center trial. Clin Trial Degenerat Dis. 3 (3), 106-110 (2018).
- Lv, R., et al. Using optical coherence tomography and intravascular ultrasound imaging to quantify coronary plaque cap stress/strain and progression: A follow-up study using 3D thin-layer models. Front Bioeng Biotechnol. 9, 713525 (2021).
- Camasao, D. B., Mantovani, D. The mechanical characterization of blood vessels and their substitutes in the continuous quest for physiological-relevant performances. A critical review. Mater Today Bio. 10, 100106 (2021).
- Holistic Numerical Methods Institute at University of South Florida. . Secant Method. , (2003).
- Barnes, J. An algorithm for solving nonlinear equations based on the secant method. Comp J. 8 (8), 66-72 (1965).
- Liu, M., Liang, L., Sun, W. A new inverse method for estimation of in vivo mechanical properties of the aortic wall. J Mech Behav Biomed Mater. 72, 148-158 (2017).
- Yu, H., et al. Patient-specific in vivo right ventricle material parameter estimation for patients with tetralogy of Fallot using MRI-based models with different zero-load diastole and systole morphologies. Int J Cardiol. 276, 93-99 (2019).
- Meuwissen, M. H. H., Oomens, C. W. J., Baaijens, F. P. T., Petterson, R., Janssen, J. D. Determination of the elasto-plastic properties of aluminium using a mixed numerical-experimental method. J Mater Process Technol. 75, 204-211 (1998).
- Davis, F. M., Luo, Y., Avril, S., Duprey, A., Lu, J. Local mechanical properties of human ascending thoracic aneurysms. J Mech Behav Biomed Mater. 61, 235-249 (2016).
- Fan, L., Wang, H., Kassab, G. S., Lee, L. C. Review of cardiac-coronary interaction and insights from mathematical modeling. WIREs Mech Dis. 16 (3), e1642 (2024).
- Andreas, W., et al. A finite element updating approach for identification of the anisotropic hyperelastic properties of normal and diseased aortic walls from 4D ultrasound strain imaging. J Mech Behav Biomed Mater. 58, 122-138 (2016).
- Liu, M., et al. Identification of in vivo nonlinear anisotropic mechanical properties of ascending thoracic aortic aneurysm from patient-specific CT scans. Sci Rep. 9, 12983 (2019).
- Trabelsi, O., Duprey, A., Favre, J. P., Avril, S. Predictive models with patient specific material properties for the biomechanical behavior of ascending thoracic aneurysms. Ann Biomed Eng. 44, 84-98 (2016).
- Cosentino, F., et al. On the role of material properties in ascending thoracic aortic aneurysms. Comput Biol Med. 109, 70-78 (2019).
- Krauz, K., et al. The role of epicardial adipose tissue in acute coronary syndromes, post-infarct remodeling and cardiac regeneration. Int J Mol Sci. 25 (7), 3583 (2024).
- McCracken, I. R., Smart, N. Control of coronary vascular cell fate in development and regeneration. Semin Cell Dev Biol. 155 (Pt C), 50-61 (2024).
- Holzapfel, G. A., et al. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol. 289 (5), H2048-H2058 (2005).
- Han, Y., et al. Ventricle stress/strain comparisons between Tertalogy of Fallot patients and healthy using models with different zero-load diastole and systole morphologies. PLoS One. 14 (8), e0220328 (2019).
- Ryo, K., et al. Role of the low-density lipoprotein-cholesterol/high-density lipoprotein-cholesterol ratio in predicting serial changes in the lipid component of coronary plaque. Circ J. 81 (10), 1439-1446 (2017).
- Thomas, T. W., et al. In vivo characterization and quantification of atherosclerotic carotid plaque components with multidetector computed tomography and histopathological correlation. Arterioscler Thromb Vasc Biol. 26 (10), 2366-2372 (2006).
- Masanori, K., et al. In vivo quantitative tissue characterization of human coronary arterial plaques by use of integrated backscatter intravascular ultrasound and comparison with angioscopic findings. Circulation. 105 (21), 2487-2492 (2002).
- Roach, M. R., Burton, A. C. The reason for the shape of the distensibility curves of arteries. Can J Biochem Physiol. 35, 681-690 (1957).
- Fung, Y. C., Liu, S. Q. Strain distribution in small blood vessel with zero-stress state taken into consideration. Am J Physiol. 262, 544-552 (1992).
- Ohayon, J., et al. Influence of residual stress/strain on the biomechanical stability of vulnerable coronary plaques: Potential impact for evaluating the risk of plaque rupture. Am J Physiol Heart Circ Physiol. 293, 1987-1996 (2007).
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten