Mapeo de superficie de exoplanetas similares a la Tierra mediante curvas de luz de un solo punto

Resumen

El protocolo extrae información de curvas de luz de exoplanetas y construye sus mapas de superficie. Utiliza curvas de luz de la Tierra, que sirve como un exoplaneta proxy, para demostrar el enfoque.

Resumen

La resolución espacial de las características del exoplaneta a partir de observaciones de un solo punto es esencial para evaluar la habitabilidad potencial de los exoplanetas. El objetivo final de este protocolo es determinar si estos mundos planetarios albergan características geológicas y/o sistemas climáticos. Presentamos un método para extraer información de curvas de luz de punto único de longitud de onda múltiple y recuperar mapas de superficie. Utiliza la descomposición de valores singulares (SVD) para separar las fuentes que contribuyen a las variaciones de la curva de la luz e infieren la existencia de sistemas climáticos parcialmente nublados. Mediante el análisis de las series temporales obtenidas a partir de SVD, las atribuciones físicas de los componentes principales (PC) podrían deducirse sin suposiciones de ninguna propiedad espectral. Al combinar con la geometría de visualización, es posible reconstruir mapas de superficie si se encuentra que uno de los equipos contiene información de superficie. La degeneración originada a partir de la convolución de la geometría de píxeles y la información del espectro determina la calidad de los mapas de superficie reconstruidos, lo que requiere la introducción de la regularización. Con el propósito de demostrar el protocolo, se analizan las curvas de luz de longitud de onda múltiple de la Tierra, que sirve como un exoplaneta proxy. La comparación entre los resultados y la verdad del terreno se presenta para mostrar el rendimiento y la limitación del protocolo. Este trabajo proporciona un punto de referencia para la generalización futura de aplicaciones de exoplanetas.

Introducción

Identificar mundos habitables es uno de los objetivos finales en astrobiología^1. Desde la primera detección², se han confirmado más de 4000 exoplanetas hasta la fecha³ con una serie de análogos de la Tierra (por ejemplo, TRAPPIST-1e)⁴. Estos planetas tienen propiedades orbitales y planetarias similares a las de la Tierra, y por lo tanto son potencialmente habitables. Evaluar su habitabilidad a partir de observaciones limitadas es esencial en este contexto. Sobre la base del conocimiento de la vida en la Tierra, los sistemas geológicos y climáticos son fundamentales para la habitabilidad, que por lo tanto puede servir como biofirmas. En principio, las características de estos sistemas podrían observarse a distancia incluso cuando un planeta no podía resolverse espacialmente mejor que un solo punto. En este caso, la identificación de características geológicas y sistemas climáticos a partir de curvas de luz de un solo punto es esencial a la hora de evaluar la habitabilidad de los exoplanetas. El mapeo superficial de estos exoplanetas se vuelve urgente.

A pesar de la convolución entre la geometría de visualización y las entidades espectrales, la información de la superficie de un exoplaneta está contenida en sus curvas de luz de un solo punto resueltas en el tiempo, que se pueden obtener a distancia y derivarse con observaciones suficientes. Sin embargo, el mapeo de superficie bidimensional (2D) de exoplanetas potencialmente habitables similares a la Tierra es un desafío debido a la influencia de las nubes. Los métodos de recuperación de mapas 2D han sido desarrollados y probados utilizando curvas de luz simuladas y espectros conocidos^5,6,7,8, pero no se han aplicado a observaciones reales. Además, en los análisis de observaciones de exoplanetas ahora y en un futuro próximo, las suposiciones de espectros característicos pueden ser controvertidas cuando las composiciones de la superficie planetaria no están bien restringidas.

En este artículo, demostramos una técnica de mapeo de superficies para exoplanetas similares a la Tierra. Utilizamos SVD para evaluar y separar información de diferentes fuentes que está contenida en curvas de luz de longitud de onda múltiple sin suposiciones de ningún espectro específico. En combinación con la geometría de visualización, presentamos la reconstrucción de mapas de superficie utilizando información de superficie oportunamente resuelta pero espacialmente enrevesada. Con el fin de demostrar este método, se analizan las observaciones de punto único de longitud de onda multidesámica de dos años de la Tierra obtenidas por el Observatorio del Clima del Espacio Profundo/Cámara de Imágenes Policromáticas de la Tierra (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html). Usamos la Tierra como un exoplaneta proxy para evaluar este método porque las observaciones disponibles actualmente de exoplanetas no son suficientes. Adjuntamos el código con el papel como ejemplo. Se desarrolla bajo python 3.7 con paquetes de anaconda y healpy, pero las matemáticas del protocolo también se pueden hacer en otros entornos de programación (por ejemplo, IDL o MATLAB).

Protocolo

1. Configuración de programación

1. Configure el entorno de programación para el código adjunto. Se requiere un equipo con sistema operativo Linux, ya que el paquete healpy no está disponible en Windows. El código no es costoso desde el punto de vista computacional, por lo que un equipo personal normal puede controlar el protocolo.
2. Siga las instrucciones (https://docs.anaconda.com/anaconda/install/linux/) para instalar Anaconda con Python 3.7 en el sistema y, a continuación, utilice los siguientes comandos en el terminal para configurar el entorno de programación:
   $ conda crear --nombre myenv python 3.7
   $ conda activar myenv
   $ conda instalar anaconda
   $ conda instalar healpy
   NOTA: Estos pasos pueden tardar decenas de minutos dependiendo del hardware y la velocidad de Internet. El nombre del entorno 'myenv' en las dos primeras líneas de comandos se puede cambiar a cualquier otra cadena.

2. Obtención de curvas de luz de varias longitudes de onda y geometría de visualización a partir de observaciones

1. En la geometría de visualización, incluya la longitud y la latitud del sub-estelar y los puntos subcomeguales para cada período de tiempo correspondiente.
   Para utilizar el siguiente código adjunto, asegúrese de que estos dos archivos tienen el mismo formato que LightCurve.csv y Geometry.csv.
2. Ejecute PlotTimeSeries.py para visualizar los datos y comprobar sus cualidades. Se crearán dos figuras LightCurve.png y Geometría.png (Figura complementaria 1-2). Es posible que sea necesario ajustar los parámetros de este y los siguientes códigos de trazado si se aplican a diferentes observaciones.
   $ pitón PlotTimeSeries.py LightCurve
   Geometría PlotTimeSeries.py python

3. Extraer información de la superficie de las curvas de luz

1. Centrar las curvas de luz de albedo de longitud de onda múltiple resueltas en el tiempo de un exoplaneta y normalizarlas por la desviación estándar correspondiente en cada longitud de onda. Esto da como resultado la misma importancia de cada canal.
   
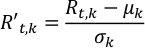
   donde R'_t,k y R_t,k son el albedo escalado y observado en el paso de tiempo t-ésimo y la longitud de onda k-ésima, respectivamente; μ_k y σ_k son la desviación media y estándar de la serie temporal de albedo en la longitud de onda k-ésima.
   1. Ejecute Normalize.py para normalizar las curvas de luz, R_t,k. La salida se guarda en NormalizedLightCurve.csv.
      Normalize.py de pitón de la Normalize.py
2. Ejecute PlotTimeSeries.py para visualizar las curvas de luz normalizadas. Se creará una figura NormalizedLightCurve.png (Figura complementaria 3).
   $ python PlotTimeSeries.py NormalizedLightCurve
3. Aplique SVD en las curvas de luz de albedo a escala para encontrar PCs dominantes y sus series temporales correspondientes.
   
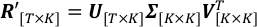
   En el lado izquierdo, T y K son el número total de pasos de tiempo y longitudes de onda de observación; R' es la matriz de observaciones de albedo escaladas, cuyo elemento (t,k)-ésimo es R'_t,k. En el lado derecho, las columnas de V son PC, vectores ortonormales que definen el espacio al que se proyecta SVD; Es una matriz diagonal, cuyo elemento (k,k)-ésimo es la desviación estándar de las curvas de luz escaladas a lo largo del eje k-ésimo definido por la columna k-ésima de V; columnas de U son las series temporales correspondientes de cada PC en V.
   1. Ejecute SingularValueDecomposition.py para descomponer R'. Los archivos de salida U.csv ,SingularValue.csv y V_T.csv , respectivamente, se guardan los archivos de salida U.csv, SingularValue.csv y V_T.csv, respectivamente.
      $ pitón SingularValueDecomposition.py
4. Utilice PlotTimeSeries.py y PlotSVD.py para visualizar el resultado de SVD. Se crearán tres figuras U.png, Sigma.png y V_T.png (Figura complementaria 4-6).
   $ pitón PlotTimeSeries.py U
   PlotSVD.py de pitón de la PlotSVD.py
5. Analice las contribuciones y las series temporales correspondientes de PC para determinar la que contiene información de superficie.
   1. Compare los valores singularesen la diagonal de . Se espera que un exoplaneta parcialmente nublado similar a la Tierra tenga dos valores singulares dominantes comparables.
      NOTA: Puede contener menos o más de dos valores singulares dominantes, que se describen a continuación.
   2. Compare los patrones de series temporales de los dos PC dominantes. El PC que contiene información de superficie tiende a tener una forma más regular que la otra. Debido a la asimetría longitudinal y la reaparición de la superficie con pequeños cambios en dos días consecutivos, la serie temporal correspondiente tiende a tener una variación diaria aproximadamente constante.
   3. Calcular las periodicidades de los dos PC dominantes utilizando el periodograma Lomb-Scargle^9,10 para confirmar la selección de PC. El PC que contiene información de superficie tiende a tener un pico más alto correspondiente al período de rotación en el espectro de densidad de potencia.
   4. Ejecute Periodogram.py para obtener los espectros de potencia de la serie temporal de cada PC. Los espectros de potencia se guardan en Periodogram.csv.
      $ pitón Periodogram.py
   5. Ejecute PlotPeriodogram.py para visualizar estos periodogramas y confirmar la selección de PC. Se creará una figura Periodogram.png (Figura suplementaria 7). El código de trazado actual se añade en líneas discontinuas que representan ciclos anuales, semestrales, diurnos y semi diarios para referencia, que pueden necesitar ser cambiados cuando se aplican a otras observaciones.
      $ pitón PlotPeriodogram.py
   6. Seleccione el PC, v_j, que contiene información de superficie y su serie temporal, u_j.
      
      
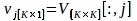
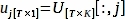
      donde V[:,j] y U[:,j] son las columnas j-ésimas de V y U,respectivamente; j es el índice de PC inferido en el paso 3.3 que contiene información de superficie.

4. Construir mapa de superficie planetaria

1. Utilice el método Hierarchical Equal Area iso-Latitude Pixelization (HEALPix)¹¹ para pixelar el mapa de recuperación. Divide la superficie esférica de un planeta en píxeles con la misma área y distribución uniforme. Denotar el valor desconocido del píxel p-it como x_p.
   1. Ejecute HEALPixRandom.py para visualizar el método de pixelización. Se creará una figura HEALPixRandom.png (Figura suplementaria 8). El parámetro_N lado en la línea 17 se puede cambiar para diferentes resoluciones. Este paso puede tardar unos segundos o minutos dependiendo de la resolución.
      $ pitón HEALPixRandom.py
2. Calcular el peso del píxel p en observaciones en el paso de tiempo t-ésimo, w_t,p, utilizando la geometría de visualización.
   
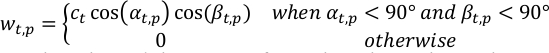
   donde α_t,p, β_t,p son los ángulos solares y la nave espacial cenit en el píxel p-ésimo en el paso de tiempo t-ésimo; c_t es un término de normalización de la observación t-ésima de modo que la suma del peso total en cada paso de tiempo es la unidad.
   NOTA: Se supone que la geometría se conoce en este paso, o puede derivarse de otro análisis, que se describe a continuación.
   1. Ejecute ComputeWeight.py para calcular w_t,p. Cambie el valor del_lado N en la línea 23 para otras resoluciones del mapa recuperado. La salida se guarda como W.npz debido a su tamaño.
      $ pitón ComputeWeight.py
3. Utilice PlotWeight.py para visualizar estos pesos. Se creará una serie de cifras, una en cada paso de tiempo, en una carpeta Peso. La combinación de ellos da como resultado vídeo suplementario 1, que muestra cómo cambia el peso de cada píxel con el tiempo. Este paso puede tardar horas en finalizar debido al gran número de visualizaciones.
   PlotWeight.py de pitón $
4. Combine geometría y observaciones para alcanzar un problema de regresión lineal.
   
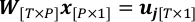
   donde P es el número total de píxeles de recuperación; W es la matriz de peso con w_t,p como el elemento (t,p)-ésimo; x consiste en x_p como el elemento p-ésimo, que es la cantidad a resolver en este problema.
   Resuelva el problema de regresión lineal con una regularización de la norma L-2.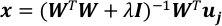
   
   donde I es la matriz de identidad y el parámetro de regularización es el parámetro de regularización.
   NOTA: 10^-3 es un buen valor para el valor de los valores de 10^{a 4} y de 3 a^{10 3}. Deben ajustarse comparando los valores de los dos términos en el error cuadrado regularizado, e, como se muestra a continuación.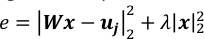
   
   1. Ejecute LinearRegression.py para resolver este problema de regresión lineal. El resultado de x se guarda en el archivo PixelValue.csv. Cambie el valor de la línea 16 para diferentes puntos fuertes de regularización.
      $ pitón LinearRegression.py
5. Convierta x en un mapa de superficie 2D según la regla de asignación de HEALPix.
   1. Ejecute PlotMap.py para construir los mapas recuperados utilizando diferentes parámetros de regularización. Se crearán tres cifras Map_-2.png, Map_-3.png y Map_-4.png con la configuración actual(Figura complementaria 9). La relación entre los índices de píxeles y sus ubicaciones en el mapa se describe en el documento HEALPix¹¹. Este paso toma decenas de segundos.
      PolotMap.py de pitón de la PolotMap.py

5. Estimar la incertidumbre del mapa recuperado

1. Vuelva a escribir el problema de regresión lineal en el paso 4.3 con el "valor verdadero" de x como z y el ruido de observación, ε.
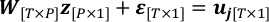
   1. Supongamos ε seguir una distribución gaussiana N (0, σ²I_[T*T]) y estimar su covarianza. T-P es el grado de libertad de u_j de observación cuando se fija el mapa recuperado.
      
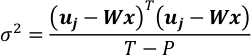
   2. Combine ecuaciones en los pasos 4.4 y 5.1. Resulta en un vector gaussiano de x.
      
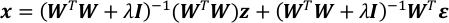
   3. Calcular la expectativa y la matriz de covarianza de x.
      
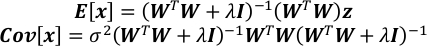
   4. Obtenga la incertidumbre de cada elemento en x como la raíz cuadrada del elemento correspondiente en la diagonal de Cov[x].
      
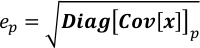
      donde e_p es la incertidumbre de x_p; Diag[Cov[x]]_p es un elemento p-ésimo en la diagonal de Cov[x].
   5. Ejecute Covariance.py para calcular la matriz de covarianza de x. El resultado se guarda en Covariance.npz debido a su tamaño. Este paso tarda decenas de segundos a minutos dependiendo del tamaño de W.
      $ pitón Covariance.py
2. Convierta e_p en el mapa 2D recuperado según la regla de asignación de HEALPix.
   1. Ejecute PlotCovariance.py para visualizar Cov[x] y asigne la incertidumbre p_al mapa recuperado. Se crearán dos cifras Covarianza.png e Incertidumbre.png (Figura complementaria 10-11).
      $ pitón PlotCovariance.py

Resultados

Utilizamos curvas de luz de punto único de longitud de onda múltiple de la Tierra para demostrar el protocolo, y comparamos los resultados con la verdad del suelo para evaluar la calidad de la asignación de superficie. La observación utilizada aquí es obtenida por DSCOVR/EPIC, que es un satélite situado cerca del primer punto lagrangian (L1) entre la Tierra y el Sol tomando imágenes a diez longitudes de onda de la cara iluminada por el sol de la Tierra. Dos años (2016 y 2017) de observaciones se utilizan para est...

Discusión

Un requisito crítico del protocolo es la viabilidad de extraer información de superficie de curvas de luz, que depende de la cobertura de la nube. En el paso 3.5.1, los valores relativos de los PC pueden ser diferentes entre los exoplanetas. En el caso de la Tierra, los dos primeros PC dominan las variaciones de la curva de luz, y corresponden a las nubes y la superficie independientes de la superficie (Fan et al. 2019)¹³. Tienen valores singulares comparables para que la información de la supe...

Materiales

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.