Tek NoktaLı Işık Eğrileri kullanarak Dünya benzeri dış gezegenlerin yüzey haritalaması

Özet

Protokol, dış gezegenlerin ışık eğrilerinden bilgi alır ve yüzey haritalarını inşa eder. Bu yaklaşım göstermek için, bir proxy ötegezegen olarak hizmet veren Dünya'nın ışık eğrileri kullanır.

Özet

Dış gezegenlerin potansiyel yaşanabilirliğini değerlendirmek için tek noktalı gözlemlerden ötegezegen özelliklerini uzamsal olarak çözmek esastır. Bu protokolün nihai amacı, bu gezegen dünyalarının jeolojik özellikler ve/veya iklim sistemlerine sahip olup olmadığını belirlemektir. Çok dalga boyunlu tek noktalı ışık eğrilerinden bilgi çıkarma ve yüzey haritaları alma yöntemi salıyoruz. Işık eğrisi varyasyonlarına katkıda bulunan ve kısmen bulutlu iklim sistemlerinin varlığını ortaya çıkaran kaynakları ayırmak için tekil değer ayrıştırma (SVD) kullanır. SVD'den elde edilen zaman serilerinin analizi sayesinde, ana bileşenlerin (PK'lar) fiziksel atıfları herhangi bir spektral özellik varsayımı olmadan çıkarılabilir. Görüntüleme geometrisi ile birleştirerek, bir mm yüzey bilgileri içerdiği tespit edilirse yüzey haritaları yeniden oluşturmak mümkündür. Piksel geometrisi ve spektrum bilgilerinin kıvrımlaşmasından kaynaklanan degeneracy, yeniden inşa edilmiş yüzey haritalarının kalitesini belirler ve bu da düzenlileştirmenin başlatılmasını gerektirir. Protokolü göstermek amacıyla, vekil bir ötegezegen olarak hizmet veren Dünya'nın çok dalga boyundaki ışık eğrileri analiz edilir. Protokolperformansı ve sınırlamagöstermek için sonuçlar ve zemin gerçeği arasında karşılaştırma sunulur. Bu çalışma, dış gezegen uygulamalarının gelecekteki genellemesi için bir ölçüt sağlar.

Giriş

Yaşanabilir dünyaların belirlenmesi astrobiyoloji^1'innihai hedeflerinden biridir. İlk^tespit2'den bu yana, 4000'den fazla ötegezegen³ bugüne kadar dünya analogları bir dizi (örneğin, TRAPPIST-1e)⁴ile teyit edilmiştir. Bu gezegenlerin yörünge selve gezegensel özellikleri Dünya'nınkine benzerdir ve bu nedenle yaşanabilirdirler. Bu bağlamda, yaşanabilirliklerinin sınırlı gözlemlerle değerlendirilmesi esastır. Jeolojik ve iklim sistemleri, Dünya'daki yaşam bilgisine dayanarak yaşanabilirlik açısından kritik öneme sahiptir ve bu nedenle biyoimza görevi görebilir. Prensip olarak, bir gezegen mekansal olarak tek bir noktadan daha iyi çözülemese bile bu sistemlerin özellikleri uzaktan gözlemlenebilir. Bu durumda, dış gezegenlerin yaşanabilirliğini değerlendirirken jeolojik özelliklerin ve iklim sistemlerinin tek noktalı ışık eğrilerinden belirlenmesi esastır. Bu dış gezegenlerin yüzey haritalaması acil hale geliyor.

Görüntüleme geometrisi ile spektral özellikler arasındaki kıvrıma rağmen, bir dış gezegenin yüzeyinin bilgileri, uzaktan elde edilebilen ve yeterli gözlemlerle elde edilebilen, zaman içinde çözülmüş tek noktalı ışık eğrilerinde bulunur. Ancak, potansiyel olarak yaşanabilir Dünya benzeri dış gezegenlerin iki boyutlu (2D) yüzey haritalaması bulutların etkisi nedeniyle zordur. 2B haritaları alma yöntemleri simüle ışık eğrileri ve bilinen spektrumlar^5,6,7,8kullanılarak geliştirilmiş ve test edilmiştir, ancak gerçek gözlemlere uygulanmamıştır. Dahası, şimdi ve yakın gelecekte dış gezegen gözlemlerinin analizlerinde, gezegen yüzey imallerinin iyi sınırlandırılmaması durumunda karakteristik spektrumvarsayımları tartışmalı olabilir.

Bu yazıda, Dünya benzeri ötegezegenler için bir yüzey haritalama tekniği gösteriyoruz. SVD'yi, belirli bir spektrum varsayımı olmadan çok dalga boyunlu ışık eğrilerinde bulunan farklı kaynaklardan gelen bilgileri değerlendirmek ve ayırmak için kullanırız. Görüntüleme geometrisi ile birlikte, zamanında çözülmüş ancak mekansal olarak karmaşık yüzey bilgilerini kullanarak yüzey haritalarının yeniden yapılandırılmayı sıyoruz. Bu yöntemi göstermek amacıyla, Derin Uzay İklim Gözlemevi/Dünya Polikromatik Görüntüleme Kamerası (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html) tarafından elde edilen iki yıllık çok dalga boyu tek noktalı dünya gözlemleri analiz edilmektedir. Bu yöntemi değerlendirmek için Dünya'yı vekil ötegezegen olarak kullanıyoruz çünkü şu anda mevcut ötegezegenlerin gözlemleri yeterli değil. Biz örnek olarak kağıt ile kod eklemek. Anakonda ve healpy paketleri ile python 3.7 altında geliştirilmiştir, ancak protokolün matematiği diğer programlama ortamlarında da (örneğin, IDL veya MATLAB) yapılabilir.

Protokol

1. Programlama kurulumu

1. Ekli kod için programlama ortamını ayarlayın. Healpy paketi Windows'da kullanılamadığından, Linux işletim sistemine sahip bir bilgisayar gereklidir. Kod hesaplama olarak pahalı değildir, bu nedenle normal bir kişisel bilgisayar protokolü işleyebilir.
2. Anaconda'yı Python 3.7 ile sisteme yüklemek için talimatları (https://docs.anaconda.com/anaconda/install/linux/) izleyin ve programlama ortamını ayarlamak için terminaldeki aşağıdaki komutları kullanın:
   $ conda oluşturmak --isim myenv python=3.7
   $ conda myenv etkinleştirmek
   $ conda anaconda yüklemek
   $ conda healpy yüklemek
   NOT: Bu adımlar, donanım ve Internet hızına bağlı olarak onlarca dakika sürebilir. İlk iki komut satırındaki ortam adı 'myenv' başka bir dize yle değiştirilebilir.

2. Gözlemlerden çok dalga boyu ışık eğrileri ve görüntüleme geometrisi elde edilmesi

1. Görüntüleme geometrisinde, ilgili her zaman dilimi için alt yıldız ve alt gözlemci noktalarının boylamını ve enlemisini içerir.
   Aşağıdaki ekli kodu kullanmak için, bu iki dosyanın LightCurve.csv ve Geometri ile aynı biçime sahip olduğundan emin olun.csv.
2. Verileri görselleştirmek ve niteliklerini kontrol etmek için PlotTimeSeries.py çalıştırın. İki rakam LightCurve.png ve Geometri.png oluşturulacaktır(Ek Şekil 1-2). Farklı gözlemlere uygulandığında, bu ve aşağıdaki çizim kodlarının ayarlanması gerekebilir.
   $ python PlotTimeSeries.py LightCurve
   $ python PlotTimeSeries.py Geometri

3. Işık eğrilerinden yüzey bilgilerini ayıklamak

1. Bir dış gezegenin zaman çözümlü çok dalga boyu albedo ışık eğrilerini merkezi ve her dalga boyunda standart sapma ile normalleştirin. Bu, her kanalın eşit öneme sahip olduğunu.
   
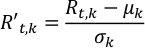
   nerede R'_t,k ve R_t,k t-th zaman basamağı ve k-th dalga boyunda ölçekli ve gözlenen albedo, sırasıyla; μ_k ve σ_k k dalga boyunda albedo zaman serisinin ortalama ve standart sapmasıdır.
   1. Işık eğrilerini normalleştirmek için Normalize.py çalıştırın, R_t,k. Çıktı NormalizeLightCurve.csvkaydedilir.
      $ piton Normalize.py
2. Normalleştirilmiş ışık eğrilerini görselleştirmek için PlotTimeSeries.py çalıştırın. NormalizeLightCurve.png bir rakam oluşturulacaktır (Ek Şekil 3).
   $ python PlotTimeSeries.py NormalizeLightCurve
3. Baskın CD'leri ve bunların karşılık gelen zaman serilerini bulmak için ölçeklenmiş albedo ışık eğrilerine SVD uygulayın.
   
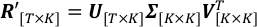
   Sol tarafta, T ve K toplam zaman adımları ve gözlem dalga boyları sayısıdır; R' ölçeklenmiş albedo gözlemlerinin matrisidir, (t,k)-th elemanı R'_t,k' dır. Sağ tarafta, V sütunları, svd projelerinin uzayını tanımlayan pC'ler, ortonormal vektörlerdir; Σ, (k,k)-th elemanı V'nink-th sütunu tarafından tanımlanan k-th ekseni boyunca ölçeklenmiş ışık eğrilerinin standart sapması olan bir diyagonal matristir; U sütunları Vher bilgisayarın karşılık gelen zaman serisidir.
   1. R'ı çürütmek için SingularValueDecomposition.py koş. Elde edilen U, Σ, V^T çıkış dosyaları U.csv, SingularValue.csv ve V_T.csv,sırasıyla kaydedilir.
      $ piton SingularValueDecomposition.py
4. SVD sonucunu görselleştirmek için PlotTimeSeries.py ve PlotSVD.py kullanın. Üç rakamlar U.png, Sigma.png ve V_T.png oluşturulacaktır(Ek Şekil 4-6).
   $ python PlotTimeSeries.py U
   $ piton PlotSVD.py
5. Yüzey bilgilerini içereni belirlemek için katkıları ve ilgili zaman dizilerini analiz edin.
   1. Σdiyagonalindeki tekil değerleri karşılaştırın. Dünya benzeri kısmen bulutlu bir ötegezegenin iki karşılaştırılabilir baskın tekil değere sahip olması beklenmektedir.
      NOT: Σ, aşağıda tartışılan ikiden az veya ikiden fazla baskın tekil değer içerebilir.
   2. İki baskın DC'nin zaman serisi desenlerini karşılaştırın. Yüzey bilgileri içeren bilgisayar, diğerinden daha düzenli bir şekle sahip olma eğilimindedir. Uzunlamasına asimetri ve iki gün üst üste küçük değişiklikler ile yüzeyin yeniden ortaya çıkması nedeniyle, karşılık gelen zaman serisi yaklaşık sabit günlük varyasyon olma eğilimindedir.
   3. Pc seçimini onaylamak için Lomb-Scargle periodogram^9,10 kullanarak iki baskın PC'lerin periyodik hesaplamak. Yüzey bilgileri içeren PC güç yoğunluğu spektrumunda dönme süresine karşılık gelen daha yüksek tepe eğilimindedir.
   4. Her bilgisayarın zaman serisinin güç spektrumlarını elde etmek için Periodogram.py çalıştırın. Güç spektrumları Periodogram.csvkaydedilir.
      $ piton Periodogram.py
   5. Bu periodogramları görselleştirmek ve BILGISAYAR seçimini onaylamak için PlotPeriodogram.py çalıştırın. Bir şekil Periodogram.png oluşturulacaktır (Ek Şekil 7). Geçerli çizim kodu, başvuru için yıllık, yarı yıllık, diurnal ve yarı günlük döngüleri temsil eden kesik çizgiler ekler ve bu satırlar diğer gözlemlere uygulandığında değiştirilmesi gerekebilir.
      $ piton PlotPeriodogram.py
   6. Pc seçin, v_j, yüzey bilgileri ve zaman serisi içeren, u_j.
      
      
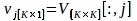
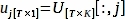
      V [:,j] ve U[:,j] sırasıyla V ve U'nunj-th sütunlarıdır; j, yüzey bilgilerini içeren 3.3.

4. Gezegensel yüzey haritası oluşturma

1. Alan korsanını pikselleştirmek için Hiyerarşik Eşit Alan izo-Latitude Pikselleştirme (HEALPix)¹¹ yöntemini kullanın. Bir gezegenin küresel yüzeyini aynı alana ve tek düze dağılıma sahip piksellere böler. p-th pikselin bilinmeyen değerini x_polarak gösterir.
   1. Pikselleştirme yöntemini görselleştirmek için HEALPixRandom.py çalıştırın. Bir rakam HEALPixRandom.png oluşturulacak(Ek Şekil 8). 17. satırdaki N_yan parametresi farklı çözünürlükler için değiştirilebilir. Bu adım, çözünürlüğe bağlı olarak birkaç saniye ile dakikalar arasında sürebilir.
      $ piton HEALPixRandom.py
2. Görüntüleme geometrisini kullanarak t-th time adımında gözlemlerde p-th pikselin ağırlığını hesapla, w_t,p,görüntüleme geometrisi kullanarak.
   
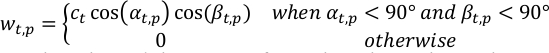
   α_t,p,β_t,p t-th zaman adımında p-th piksel de güneş ve uzay aracı zenith açıları vardır; c_t t-th gözlemnormalleştirme terimidir, böylece her adımda toplam ağırlığın toplamı birliktir.
   NOT: Geometrinin bu adımda bilindiği varsayılır veya aşağıda tartışılan diğer analizlerden türetilebilir.
   1. W_t,p'yihesaplamak için ComputeWeight.py çalıştırın. Alınan haritanın diğer çözünürlükleri için 23. Çıktı boyutu nedeniyle W.npz olarak kaydedilir.
      $ piton ComputeWeight.py
3. Bu ağırlıkları görselleştirmek için PlotWeight.py kullanın. Bir dizi rakam, her adımda bir, bir klasör Ağırlıkoluşturulacaktır. Bunları birleştirmek, her pikselin ağırlığının zamanla nasıl değiştiğini gösteren Tamamlayıcı Video 1ile sonuçlanır. Bu adım, çok sayıda görselleştirme nedeniyle tamamlanması saatler sürebilir.
   $ piton PlotWeight.py
4. Doğrusal bir regresyon sorununa ulaşmak için geometri ve gözlemleri birleştirin.
   
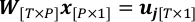
   P'nin toplam alan piksel sayısı olduğu durumlarda; W,w _t,p (t,p)-th elemanı olarak ağırlık matrisidir; x, bu sorunda çözülecek miktar olan p-th elemanı olarak x_p'den oluşur.
   L-2 normunun düzenlileştirilmesi ile doğrusal regresyon problemini çözün.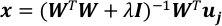
   
   nerede kimlik matrisi ve λ düzenlileştirme parametresi.
   NOT: 10^-3 λ için iyi bir değerdir zaman T ~ 10⁴ ve P ~ 3 *10³. Bunlar, aşağıda gösterildiği gibi, normalleştirilmiş kare hata, e iki terimin değerleri karşılaştırılarak ayarlanmalıdır.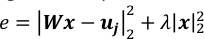
   
   1. Bu doğrusal regresyon sorununu çözmek için LinearRegression.py çalıştırın. X'in sonucu PixelValue.csvdosyasına kaydedilir. Normalleştirmenin farklı güçleri için 16.
      $ piton LinearRegression.py
5. HEALPix'in haritalama kuralına göre x'i 2B yüzey haritasına dönüştürün.
   1. Farklı düzenlilleştirme parametrelerini kullanarak alınan haritaları oluşturmak için PlotMap.py çalıştırın. Map_-2.png, Map_-3.png ve Map_-4.png olmak üzere üç rakam, mevcut ayarı ile oluşturulacaktır(Ek Şekil 9). Piksel endeksleri ve haritadaki konumları arasındaki ilişki HEALPix belge^11'deaçıklanmıştır. Bu adım on saniye sürer.
      $ piton PolotMap.py

5. Alınan haritanın belirsizliğini tahmin edin

1. Doğrusal regresyon problemini 4.3 adımda x'in "gerçek değeri" z ve gözlem gürültüsü ile yeniden yazmak, ε.
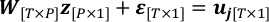
   1. Gauss distribution N (0, σ²I_[T*T]) ε izleyin ve onun covariance tahmin varsayalım. T-P, alınan harita sabitlendiğinde u_j'nin gözlemden serbestlik derecesidir.
      
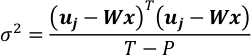
   2. Adım 4.4 ve 5.1 denklemleri birleştirin. Bu xgaussian vektör ü sonuçlanır.
      
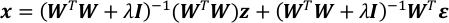
   3. Beklentiyive x'in covariance matrisini hesapla.
      
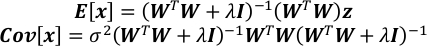
   4. Cov[x] diyagonal üzerinde karşılık gelen öğenin kare kökü olarak x her öğenin belirsizlik elde edin.
      
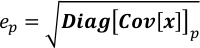
      e_p x_pbelirsizliği nerede ; Diag[Cov[x]]_p Cov[x] diyagonal üzerinde p-th elemanıdır.
   5. x'incovariance matrisini hesaplamak için Covariance.py çalıştırın. Sonuç covariance.npz boyutu nedeniyle kaydedilir. Bu adım Wboyutuna bağlı olarak dakika onlarca saniye sürer.
      $ piton Covariance.py
2. HEALPix'in eşleme kuralına göre e_p'yi alınan 2B haritaya dönüştürün.
   1. Cov[x ]görselleştirmek için PlotCovariance.py çalıştırın ve alınan harita belirsizlik e_p harita. İki rakam Covariance.png ve Belirsizlik.png oluşturulacaktır(Ek Şekil 10-11).
      $ piton PlotCovariance.py

Sonuçlar

Protokolü göstermek için Dünya'nın çok dalga boyunlu tek noktalı ışık eğrilerini kullanıyoruz ve yüzey haritalamakalitesini değerlendirmek için sonuçları zemin gerçeğiyle karşılaştırıyoruz. Burada kullanılan gözlem, Dünya ile Güneş arasındaki ilk Lagrangian noktası (L1) yakınında bulunan ve Dünya'nın güneşli yüzünün on dalga boyunda görüntü alan bir uydu olan DSCOVR/EPIC tarafından elde edilir. Bu gösteri için iki yıl (2016 ve 2017) gözlemler kullanılıyor, bunlar Jiang ve...

Tartışmalar

Protokolün kritik gereksinimlerinden biri, bulut kapsama alanına bağlı olan ışık eğrilerinden yüzey bilgilerinin ayıklanmasının fizibilitesidir. Adım 3.5.1'de, dc'lerin göreli değerleri dış gezegenler arasında farklı olabilir. Dünya söz konusu olduğunda, ilk iki cd ışık eğrisi varyasyonlarına hakimdir ve yüzeyden bağımsız bulutlara ve yüzeye karşılık gelir (Fan ve ark. 2019)¹³. Yüzey bilgilerinin 3.5.2 ve 3.5.3 adımlarını izleyerek ayrılabilmesi için karş?...

Malzemeler

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.