단일 점 라이트 커브를 사용하여 지구와 같은 외계 행성의 표면 매핑

요약

이 프로토콜은 외계 행성의 빛 곡선에서 정보를 추출하고 표면 지도를 구성합니다. 그것은 프록시 외계 행성 역할을 지구의 빛 곡선을 사용하여 접근 방식을 보여줍니다.

초록

외계 행성의 잠재적 거주가능성을 평가하는 데 필수적인 외계 행성의 특징을 단일 점 관측에서 공간적으로 해결하는 것은 필수적입니다. 이 프로토콜의 궁극적인 목표는 이 행성 세계가 지질학적 특징 및/또는 기후 시스템을 수용하는지 여부를 결정하는 것입니다. 다중 파장 단일 점 라이트 커브에서 정보를 추출하고 표면 맵을 검색하는 방법을 제시합니다. 단수 값 분해(SVD)를 사용하여 광 곡선 변화에 기여하고 부분적으로 흐린 기후 시스템의 존재를 추론하는 소스를 분리합니다. SVD에서 얻은 서전분석을 통해 주 성분(PC)의 물리적 인귀속은 스펙트럼 특성에 대한 가정 없이 유추될 수 있습니다. 보기 형상과 결합하면 PC 중 하나가 표면 정보를 포함하는 것으로 밝혀지면 표면 맵을 재구성할 수 있습니다. 픽셀 형상 및 스펙트럼 정보의 컨볼루션에서 비롯된 퇴진은 정규화의 도입이 필요한 재구성된 표면 맵의 품질을 결정합니다. 프로토콜을 시연하기 위해, 대리 외계 행성 역할을 하는 지구의 다파장 광 곡선을 분석한다. 결과와 지상 진실 간의 비교는 프로토콜의 성능과 한계를 나타내기 위해 제시됩니다. 이 작품은 외계 행성 응용 프로그램의 미래 일반화를위한 벤치 마크를 제공합니다.

서문

거주 가능한 세계를 식별하는 것은 천체 생물학^1의궁극적 인 목표 중 하나입니다. 첫 번째 검출²이후, 4000개 이상의 외계 행성이 현재까지 확인되었으며, 지구 유사체(예: TRAPPIST-1e)^4와함께^3개 행성이 확인되었다. 이 행성들은 지구와 유사한 궤도 및 행성 성질을 가지고 있으며, 따라서 잠재적으로 거주할 수 있다. 제한된 관찰에서 거주성을 평가하는 것은 이 맥락에서 필수적입니다. 지구상의 생명에 대한 지식을 바탕으로 지질학적 및 기후 시스템은 거주성에 매우 중요하며, 따라서 생체 서명역할을 할 수 있습니다. 원칙적으로, 행성이 하나의 지점보다 더 잘 해결될 수 없을 때에도 이러한 시스템의 특징을 멀리서 관찰할 수 있다. 이 경우 외계 행성의 거주성을 평가할 때 단일 점 광 곡선에서 지질 학적 특징과 기후 시스템을 식별하는 것이 필수적입니다. 이 외계 행성의 표면 매핑이 시급해진다.

지오메트리와 스펙트럼 피처 사이의 컨볼루션에도 불구하고, 외계 행성의 표면의 정보는 거리에서 얻을 수 있는 시간 해결된 단일 점 광 곡선에 포함되어 있으며 충분한 관측으로 도출됩니다. 그러나, 잠재적으로 거주 가능한 지구와 같은 외계 행성의 2차원 (2D) 표면 매핑은 구름의 영향으로 인해 도전적이다. 2D 맵을 검색하는 방법은 시뮬레이션된 라이트 커브와 알려진 스펙트럼^5,6,7,8을사용하여 개발 및 테스트되었지만 실제 관측에는 적용되지 않았습니다. 더욱이, 현재와 가까운 장래에 외계 행성 관측의 분석에서, 행성 표면 조성이 잘 제한되지 않을 때 특성 스펙트럼의 가정은 논란이 될 수 있습니다.

이 논문에서는 지구와 같은 외계 행성에 대한 표면 매핑 기술을 시연합니다. SVD를 사용하여 특정 스펙트럼의 가정 없이 다파장 광 곡선에 포함된 다른 소스에서 정보를 평가하고 분리합니다. 보기 지오메트리와 결합하여 적시에 해결되었지만 공간적으로 복잡한 표면 정보를 사용하여 표면 맵의 재구성을 제공합니다. 이 방법을 시연하기 위해 심층 우주 기후 천문대/지구 다색 이미징 카메라(DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html)가 획득한 지구의 2년 다중 파장 단일 점 관측을 분석합니다. 현재 외계 행성의 관측이 충분하지 않기 때문에 우리는 지구를 프록시 외계 행성으로 사용하여 이 방법을 평가합니다. 예를 들어 종이와 코드를 첨부합니다. 그것은 아나콘다 및 healpy 패키지와 파이썬 3.7에서 개발, 하지만 프로토콜의 수학은 다른 프로그래밍 환경에서 수행 할 수 있습니다 (예를 들어, IDL 또는 MATLAB).

프로토콜

1. 프로그래밍 설정

1. 연결된 코드에 대한 프로그래밍 환경을 설정합니다. Windows에서는 healpy 패키지를 사용할 수 없습니다. 코드는 계산 비용이 많이 들지 않으므로 일반 개인용 컴퓨터가 프로토콜을 처리할 수 있습니다.
2. 지시(https://docs.anaconda.com/anaconda/install/linux/)를 따라 파이썬 3.7이 있는 아나콘다를 시스템에 설치한 다음 터미널에서 다음 명령을 사용하여 프로그래밍 환경을 설정합니다.
   $ 콘다 만들기 --이름 myenv 파이썬 = 3.7
   $ 콘다 활성화 myenv
   $ 콘다 설치 아나콘다
   $ 콘다 설치 치유
   참고: 이러한 단계는 하드웨어 및 인터넷 속도에 따라 수십 분 정도 걸릴 수 있습니다. 처음 두 명령줄의 환경 이름 'myenv'를 다른 문자열로 변경할 수 있습니다.

2. 다파장 광 곡선 을 획득하고 관찰에서 지오메트리를 보기

1. 보기 형상에서, 각 해당 시간 프레임에 대한 서브 별의 경도 및 위도 및 하위 관찰자 점을 포함한다.
   다음 첨부 코드를 사용하려면 이 두 파일이 LightCurve.csv 및 형상.csv과 동일한 형식을 가지고 있는지 확인합니다.csv.
2. PlotTimeSeries.py 실행하여 데이터를 시각화하고 품질을 확인합니다. 라이트커브.png 및 기하학.png 두 가지 피규어가 생성됩니다(보조도 1-2). 다른 관측전에 적용하면 이 및 다음 플롯 코드의 매개 변수를 조정해야 할 수 있습니다.
   라이트커브를 PlotTimeSeries.py 달러 파이썬
   $ 파이썬 PlotTimeSeries.py 기하학

3. 라이트 커브에서 표면 정보 추출

1. 외계 행성의 중앙 시간 해결 다중 파장 알베도 라이트 커브를 각 파장의 해당 표준 편차로 정상화한다. 이렇게 하면 각 채널의 중요성이 동일합니다.
   
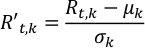
   여기서_R't,k및 R_t,k는 t-th 시간 단계와 k-th 파장에서 각각 스케일및 관찰 된 알베도입니다; μ_k와 σ_k는 k-th 파장에서 알베도 타임 시리즈의 평균 및 표준 편차입니다.
   1. 라이트 커브를 정규화하기 위해 Normalize.py 실행, R_t,k. 출력은 정규화라이트커브.csv에 저장됩니다.
      $ 파이썬 Normalize.py
2. PlotTimeSeries.py 실행하여 정규화된 라이트 곡선을 시각화합니다. 그림정규라이트곡선.png 생성됩니다(보충도 3).
   $ 파이썬 PlotTimeSeries.py 정규화라이트 커브
3. 스케일된 알베도 라이트 커브에 SVD를 적용하여 지배적인 PC와 해당 타임 시리즈를 찾습니다.
   
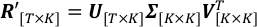
   왼쪽에, T와 K는 총 시간 단계 및 관측 파장의 수; R'은 스케일링된 알베도 관측의 매트릭스로, 그 (t,k)-th 요소는_{R't,k입니다.} 오른쪽에 V의 열은 SVD 프로젝트의 공간을 정의하는 PC, 직교 벡터입니다. Σ는 대각선 매트릭스로, 그 (k,k)-th 요소는 V의k-th 열에 의해 정의된 k-th 축을 따라 스케일링된 라이트 커브의 표준 편차입니다. U의 열은 V의각 PC의 해당 시간 시리즈입니다.
   1. SingularValueDecomposition.py 실행하여 R'을 분해합니다. 결과 U, Σ, V^T는 각각 출력 파일 U.csv, singularValue.csv 및 V_T.csv저장됩니다.
      $ 파이썬 SingularValueDecomposition.py
4. PlotTimeSeries.py 및 PlotSVD.py 사용하여 SVD 결과를 시각화합니다. 세 가지 수치 U.png, 시그마.png 및 V_T.png 생성됩니다(보충 도 4-6).
   $ 파이썬 PlotTimeSeries.py U
   $ 파이썬 PlotSVD.py
5. 기여도 및 해당 시간 시리즈를 분석하여 표면 정보가 포함된 PC를 결정합니다.
   1. Σ의 대각선에서 단수 값을 비교합니다. 지구와 같은 부분적으로 흐린 외계 행성은 두 개의 비슷한 지배적 인 단수 값을 가질 것으로 예상된다.
      참고: Σ는 아래에 설명된 두 개 이상의 지배적인 단수 값을 포함할 수 있습니다.
   2. 두 지배적인 PC의 타임시리즈 패턴을 비교합니다. 표면 정보가 포함된 PC는 다른 PC보다 더 규칙적인 모양을 갖는 경향이 있습니다. 경도 비대칭과 2일 연속으로 작은 변화와 표면의 재등장으로 인해 해당 타임 시리즈는 대략 일정한 일일 변동을 갖는 경향이 있다.
   3. Lomb-Scargle^{주기전도 9,10을} 사용하여 두 개의 지배적인 PC의 주기도를 계산하여 PC의 선택을 확인합니다. 표면 정보를 포함하는 PC는 전력 밀도 스펙트럼의 회전 기간에 해당하는 피크가 높은 경향이 있습니다.
   4. Periodogram.py 실행하여 각 PC의 타임 시리즈의 전력 스펙트럼을 얻습니다. 파워 스펙트럼은 주기적 .csv저장됩니다.
      $ 파이썬 Periodogram.py
   5. 이러한 주기사진을 시각화하고 PC의 선택을 확인하기 위해 PlotPeriodogram.py 실행합니다. 피규어 치수.png 생성됩니다(추가도 7). 현재 플로팅 코드는 참조를 위해 연간, 반기, 주가지 및 반일 주기를 나타내는 파선에 추가되며, 다른 관측전에 적용할 때 변경해야 할 수 있습니다.
      $ 파이썬 PlotPeriodogram.py
   6. 표면 정보와 그 타임 시리즈, U_j를포함하는 PC, v_j를선택합니다.
      
      
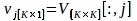
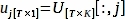
      여기서 V[:,j] 및 U[:,j]는 V와 U의j-th 열입니다. j는 표면 정보를 포함하는 3.3 단계에서 유추된 PC의 인덱스입니다.

4. 행성 표면지도를 구성

1. 계층적 동일 영역 Iso-Latitude 픽셀화(HEALPix)¹¹ 메서드를 사용하여 검색 맵을 픽셀화합니다. 행성의 구형 표면을 동일한 면적과 균일한 분포를 가진 픽셀로 나눕니다. p-th 픽셀의 알 수 없는 값을 x_p로나타냅니다.
   1. HEALPixRandom.py 실행하여 픽셀화 메서드를 시각화합니다. 피규어 HEALPixRandom.png 생성됩니다(보충 도8). 17호선의 매개변수_N측은 다른 해상도에 대해 변경할 수 있습니다. 이 단계는 해상도에 따라 몇 초에서 몇 분 정도 걸릴 수 있습니다.
      $ 파이썬 HEALPixRandom.py
2. 보기 형상을 사용하여 t-th 시간 단계에서 관측에서 p-th 픽셀의_중량을계산합니다.
   
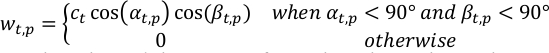
   여기서_{α t,p,}β_t,p는 태양과 t-th 시간 단계에서 p-th 픽셀에서 우주선 정각; c_t는 t-th 관측의 정상화 기간이므로 각 단계의 총 중량합계가 통일됩니다.
   참고: 형상은 이 단계에서 알려지거나 아래에 설명된 다른 분석에서 파생될 수 있습니다.
   1. ComputeWeight.py 실행하여_{t,p를 계산합니다.} 검색된 맵의 다른 해상도에 대해 23번 줄에서 N_측값을 변경합니다. 출력은 크기로 인해 W.npz로 저장됩니다.
      $ 파이썬 ComputeWeight.py
3. 이러한 가중치를 시각화하려면 PlotWeight.py 사용합니다. 각 단계마다 하나씩 폴더 가중치에서여러 그림이 만들어집니다. 병합하면 추가 비디오 1이생성되며, 이는 각 픽셀의 무게가 시간에 따라 어떻게 변하는지 보여줍니다. 이 단계는 많은 수의 시각화로 인해 완료하는 데 몇 시간이 걸릴 수 있습니다.
   $ 파이썬 PlotWeight.py
4. 형상과 관측을 결합하여 선형 회귀 문제에 도달합니다.
   
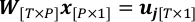
   여기서 P는 검색 픽셀의 총 수입니다; W는 _wt,p를 (t,p)-th 요소로 하는 중량 행렬입니다. x는 p-th 요소로 x_p로 구성되며, 이 요소는 이 문제에서 해결해야 할 수량입니다.
   L-2 규범의 정규화로 선형 회귀 문제를 해결합니다.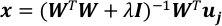
   
   여기서 ID 매트릭스이고 λ는 정규화 매개 변수입니다.
   참고: 10^-3은 T~10⁴ 및 P~3*10^3일때 λ에 좋은 값입니다. 아래와 같이 정규화된 정사각형 오류(e)에서 두 용어의 값을 비교하여 조정해야 합니다.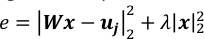
   
   1. 이 선형 회귀 문제를 해결하기 위해 LinearRegression.py 실행합니다. x의 결과는 파일 픽셀값에 저장됩니다.csv. 정규화의 다른 강점에 대해 16호선에서 λ값을 변경합니다.
      $ 파이썬 LinearRegression.py
5. HEALPix의 매핑 규칙에 따라 x를 2D 표면 맵으로 변환합니다.
   1. PlotMap.py 실행하여 다른 정규화 매개 변수를 사용하여 검색된 맵을 구성합니다. Map_-2.png, Map_-3.png 및 Map_-4.png 세 가지 수치는 현재 설정(보충도 9)으로생성됩니다. 픽셀 지수와 맵의 위치 간의 관계는 HEALPix 문서^11에설명되어 있습니다. 이 단계는 수십 초 정도 걸립니다.
      $ 파이썬 PolotMap.py

5. 검색된 맵의 불확실성 추정

1. z와 관측 잡음으로 x의 "실제 값"으로 4.3 단계에서 선형 회귀 문제를 다시 작성하여 ε.
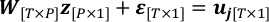
   1. ε 가우시안 분포 N(0, σ²I_[T*T])을따르고 그 공변성을 추정한다고 가정합니다. T-P는 검색된 맵이 고정될 때 관찰에서 U_j의 자유의 정도입니다.
      
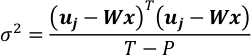
   2. 4.4 및 5.1 단계에서 방정식을 결합합니다. 그것은 x의 가우시안 벡터를 초래한다.
      
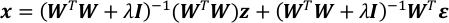
   3. x의기대와 공변 행렬을 계산합니다.
      
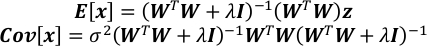
   4. Cov[x]의대각선에 해당 요소의 제곱근으로 x에서 각 요소의 불확실성을 가져옵니다.
      
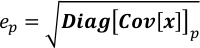
      여기서 e_p는 x_p의불확실성이다; 디아그[Cov[x]]_p는 Cov의대각선에 p-th 원소 【x】입니다.
   5. Covariance.py 실행하여 x의공변 성 행렬을 계산합니다. 그 결과 크기로 인해 Covariance.npz에 저장됩니다. 이 단계는 W의크기에 따라 수십 초에서 몇 분 정도 걸립니다.
      $ 파이썬 Covariance.py
2. HEALPix의 매핑 규칙에 따라 검색된 2D 맵으로 e_p를 변환합니다.
   1. PlotCovariance.py 실행하여 Cov[x]를시각화하고 불확실성 e_p를 검색된 맵에 매핑합니다. 두 가지 수치(.png 및 불확실성.png 생성됩니다(추가수치 10-11).
      $ 파이썬 PlotCovariance.py

결과

우리는 지구의 다중 파장 단일 점 광 곡선을 사용하여 프로토콜을 시연하고 결과를 지면 진실과 비교하여 표면 매핑의 품질을 평가합니다. 여기에 사용되는 관측은 지구와 태양 사이의 첫 번째 라그란지아 지점 (L1) 근처에 위치한 위성인 DSCOVR / EPIC에 의해 얻어지며, 지구의 햇빛이 비추는 얼굴의 10 파장에서 이미지를 촬영합니다. 2년(2016년과 2017년)의 관측은 이 데모에 사용되며, 이는 장 외(2018)

토론

프로토콜의 중요한 요구 사항 중 하나는 구름 커버리지에 따라 달라지는 라이트 커브에서 표면 정보를 추출할 수 있는 타당성입니다. 3.5.1 단계에서 PC의 상대값은 외계 행성마다 다를 수 있다. 지구의 경우, 처음 두 개의 PC가 광 곡선 변화를 지배하고, 표면 독립적 인 구름과 표면 (Fan et al. 2019)^13에대응한다. 3.5.2 및 3.5.3 단계에 따라 표면 정보를 분리할 수 있도록 유사한 단수 값?...

자료

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.