Mapeamento de superfície de exoplanetas semelhantes à Terra usando curvas de luz de ponto único

Resumo

O protocolo extrai informações de curvas de luz de exoplanetas e constrói seus mapas superficiais. Ele usa curvas de luz da Terra, que serve como um exoplaneta proxy, para demonstrar a abordagem.

Resumo

Resolver espacialmente características de exoplanetas a partir de observações de ponto único é essencial para avaliar a potencial habitabilidade de exoplanetas. O objetivo final deste protocolo é determinar se esses mundos planetários abrigam características geológicas e/ou sistemas climáticos. Apresentamos um método de extrair informações de curvas de luz de um ponto único de comprimento de onda e recuperar mapas de superfície. Utiliza decomposição de valor singular (SVD) para separar fontes que contribuem para variações de curvas leves e inferem a existência de sistemas climáticos parcialmente nublados. Através da análise das séries temporais obtidas a partir de SVD, as atribuições físicas dos componentes principais (PCs) poderiam ser inferidas sem suposições de quaisquer propriedades espectrais. Combinando com a geometria de visualização, é viável reconstruir mapas superficiais se um dos PCs for encontrado para conter informações de superfície. A degeneração originada da convolução da geometria dos pixels e das informações de espectro determina a qualidade dos mapas de superfície reconstruídos, o que requer a introdução da regularização. Com o objetivo de demonstrar o protocolo, são analisadas as curvas de luz de vários comprimentos de onda da Terra, que serve como um exoplaneta proxy. A comparação entre os resultados e a verdade fundiária é apresentada para mostrar o desempenho e limitação do protocolo. Este trabalho fornece uma referência para a generalização futura de aplicações de exoplanetas.

Introdução

Identificar mundos habitáveis é um dos objetivos finais da astrobiologia¹. Desde a primeira detecção², mais de 4000 exoplanetas foram confirmados até o momento³ com um número de análogos da Terra (por exemplo, TRAPPIST-1e)⁴. Esses planetas têm propriedades orbitais e planetárias semelhantes às da Terra, e, portanto, são potencialmente habitáveis. Avaliar sua habitabilidade a partir de observações limitadas é essencial nesse contexto. Com base no conhecimento da vida na Terra, os sistemas geológicos e climáticos são críticos para a habitabilidade, que, portanto, pode servir como bioassinaturas. Em princípio, características desses sistemas poderiam ser observadas à distância mesmo quando um planeta não poderia ser resolvido espacialmente melhor do que um único ponto. Neste caso, identificar características geológicas e sistemas climáticos a partir de curvas de luz de ponto único é essencial ao avaliar a habitabilidade dos exoplanetas. O mapeamento superficial desses exoplanetas torna-se urgente.

Apesar da convolução entre a geometria de visualização e as características espectrais, as informações da superfície de um exoplaneta estão contidas em suas curvas de luz de ponto único resolvidas pelo tempo, que podem ser obtidas à distância, e derivadas com observações suficientes. No entanto, o mapeamento de superfície bidimensional (2D) de exoplanetas potencialmente habitáveis semelhantes à Terra é desafiador devido à influência das nuvens. Métodos de recuperação de mapas 2D foram desenvolvidos e testados usando curvas de luz simuladas e espectros conhecidos^5,6,7,8, mas não foram aplicados a observações reais. Além disso, nas análises das observações de exoplanetas agora e em um futuro próximo, suposições de espectros característicos podem ser controversas quando as composições da superfície planetária não são bem constrangidas.

Neste artigo, demonstramos uma técnica de mapeamento de superfície para exoplanetas semelhantes à Terra. Usamos SVD para avaliar e separar informações de diferentes fontes que estão contidas em curvas de luz de vários comprimentos de onda sem suposições de qualquer espectro específico. Combinado com a geometria de visualização, apresentamos a reconstrução de mapas superficiais usando informações de superfície oportunamente resolvidas, mas espacialmente complicadas. Para demonstrar este método, observações de dois anos de comprimento de onda de um ponto único da Terra obtidas pelo Deep Space Climate Observatory/Earth Polychromatic Imaging Camera (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html) são analisadas. Usamos a Terra como um exoplaneta proxy para avaliar esse método porque as observações disponíveis atualmente de exoplanetas não são suficientes. Anexamos o código ao papel como exemplo. É desenvolvido sob python 3.7 com pacotes anaconda e healpy, mas a matemática do protocolo também pode ser feita em outros ambientes de programação (por exemplo, IDL ou MATLAB).

Protocolo

1. Configuração de programação

1. Configure o ambiente de programação para o código anexado. Um computador com sistema operacional Linux é necessário, pois o pacote healpy não está disponível no Windows. O código não é computacionalmente caro, então um computador pessoal normal pode lidar com o protocolo.
2. Siga a instrução (https://docs.anaconda.com/anaconda/install/linux/) para instalar o Anaconda com Python 3.7 no sistema e use os seguintes comandos no terminal para configurar o ambiente de programação:
   $ conda criar --nome myenv python=3.7
   Conda ativa myenv
   $ conda instalar anaconda
   $ conda instalar healpy
   NOTA: Essas etapas podem levar dezenas de minutos dependendo do hardware e da velocidade da Internet. O nome do ambiente 'myenv' nas duas primeiras linhas de comando pode ser alterado para qualquer outra string.

2. Obtenção de curvas de luz de comprimento de onda e geometria de visualização a partir de observações

1. Na geometria de visualização, incluem a longitude e latitude dos pontos sub-estelares e sub-observadores para cada período de tempo correspondente.
   Para usar o seguinte código anexado, certifique-se de que esses dois arquivos tenham o mesmo formato que LightCurve.csv e Geometria.csv.
2. Execute PlotTimeSeries.py para visualizar os dados e verificar suas qualidades. Serão criadas duas figuras LightCurve.png e Geometria.png (Figura Suplementar 1-2). Os parâmetros neste e seguindo códigos de plotagem podem precisar ser ajustados se aplicados a observações diferentes.
   $ python PlotTimeSeries.py LightCurve
   $ píton PlotTimeSeries.py Geometria

3. Extrair informações de superfície de curvas de luz

1. Centro de comprimento de onda de vários comprimentos de onda albedo curvas de luz de um exoplaneta e normalizá-los por desvio padrão correspondente em cada comprimento de onda. Isso resulta na igual importância de cada canal.
   
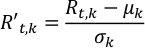
   onde_R't,k e R_t,k são o albedo escalonado e observado na etapa t-th e o comprimento de onda k-th, respectivamente; μ_k e σ_k são o desvio médio e padrão da série de tempo albedo no comprimento de onda k-th.
   1. Corra Normalize.py para normalizar as curvas de luz, R_t,k. A saída é salva em NormalizedLightCurve.csv.
      $ píton Normalize.py
2. Corra PlotTimeSeries.py para visualizar as curvas de luz normalizadas. Uma figura NormalizadaLightCurve.png será criada(Figura Suplementar 3).
   $ píton PlotTimeSeries.py NormalizedLightCurve
3. Aplique SVD nas curvas de luz albedo dimensionadas para encontrar PCs dominantes e suas séries temporáticas correspondentes.
   
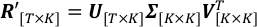
   No lado esquerdo, T e K são o número total de passos de tempo e comprimentos de onda de observação; R' é a matriz de observações de albedo dimensionadas, cujo (t,k)-th elemento é_R't,k. Do lado direito, colunas de V são PCs, vetores ortoonormais que definem os projetos de SVD de espaço; Σ é uma matriz diagonal, cujo (k,k)-th elemento é o desvio padrão das curvas de luz escalonadas ao longo do eixo k-th definido pela coluna k-th de V; colunas de U são a série de tempo correspondente de cada PC em V.
   1. Corra SingularValueDecomposition.py para decompor R'. Os U, Σ, V^T resultantes são salvos nos arquivos de saída U.csv, SingularValue.csv e V_T.csv, respectivamente.
      $ píton SingularValueDecomposition.py
4. Use PlotTimeSeries.py e PlotSVD.py para visualizar o resultado do SVD. Serão criadas três figuras U.png, Sigma.png e V_T.png (Figura Suplementar 4-6).
   $ python PlotTimeSeries.py U
   $ píton PlotSVD.py
5. Analise as contribuições e a série temporal correspondente de PCs para determinar a que contém informações de superfície.
   1. Compare os valores singulares na diagonal de Σ. Espera-se que um exoplaneta parcialmente nublado com a Terra tenha dois valores singulares dominantes comparáveis.
      NOTA: Σ pode conter menos ou mais de dois valores singulares dominantes, que são discutidos abaixo.
   2. Compare os padrões da série temporal dos dois PCs dominantes. O PC que contém informações de superfície tende a ter uma forma mais regular do que o outro. Devido à assimetria longitudinal e ao reaparecimento da superfície com pequenas mudanças em dois dias consecutivos, a série temporal correspondente tende a ter variação diária aproximadamente constante.
   3. Calcular as periodicidades dos dois PCs dominantes usando o períodograma Lomb-Scargle^9,10 para confirmar a seleção do PC. O PC que contém informações de superfície tende a ter picos mais elevados correspondentes ao período de rotação no espectro de densidade de energia.
   4. Execute Periodogram.py para obter o espectro de energia da série de tempo de cada PC. Os espectros de energia são salvos em Periodograma.csv.
      $ píton Periodogram.py
   5. Execute PlotPeriodogram.py para visualizar esses periodogramas e confirmar a seleção do PC. Será criado um periodograma.png (Figura Suplementar 7). O código de plotagem atual adiciona em linhas tracejadas representando ciclos anuais, semianuários, diurnos e meio-diários para referência, que podem precisar ser alterados quando aplicados a outras observações.
      $ píton PlotPeriodogram.py
   6. Selecione o PC, v_j, que contém informações de superfície e sua série de tempo, u_j.
      
      
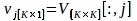
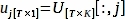
      onde V[:,j] e U[:,j] são as colunas j-th de V e U, respectivamente; j é o índice de PC inferido na etapa 3.3 que contém informações de superfície.

4. Construir mapa de superfície planetária

1. Use o método Hierárquico equal area iso-Latitude Pixelization (HEALPix)¹¹ para pixelar o mapa de recuperação. Ele divide a superfície esférica de um planeta em pixels com a mesma área e distribuição uniforme. Denotar o valor desconhecido do pixel p-th como x_p.
   1. Execute HEALPixRandom.py para visualizar o método de pixelização. Uma figura HEALPixRandom.png será criada (Figura Suplementar 8). O_lado do parâmetro N na linha 17 pode ser alterado para diferentes resoluções. Esta etapa pode levar alguns segundos a minutos, dependendo da resolução.
      $ píton HEALPixRandom.py
2. Calcule o peso do pixel p-th em observações no t-th time step, w_t,p, usando geometria de visualização.
   
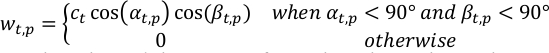
   onde α_t,p, β_t,p são os ângulos solares e a espaçonave zenith no pixel p-th no t-th time step; c_t é um termo de normalização da observação t-th de modo que a soma do peso total em cada passo de cada vez é unidade.
   NOTA: A geometria é considerada conhecida nesta etapa, ou pode ser derivada de outras análises, que são discutidas abaixo.
   1. Executar ComputeWeight.py para calcular w_t,p. Altere o valor do_lado N na linha 23 para outras resoluções do mapa recuperado. A saída é salva como W.npz devido ao seu tamanho.
      $ píton ComputeWeight.py
3. Use PlotWeight.py para visualizar esses pesos. Uma série de números, um em cada etapa de cada vez, será criado em uma pasta Peso. Fundi-los resulta em Vídeo Suplementar 1, que mostra como o peso de cada pixel muda com o tempo. Esta etapa pode levar horas para ser concluída devido ao grande número de visualizações.
   $ píton PlotWeight.py
4. Combine geometria e observações para chegar a um problema de regressão linear.
   
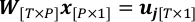
   onde P é o número total de pixels de recuperação; W é a matriz de peso com w_t,p como o elemento (t,p)-th; x consiste em x_p como o elemento p-th, que é a quantidade a ser resolvida neste problema.
   Resolva o problema de regressão linear com uma regularização da norma L-2.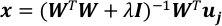
   
   onde eu sou a matriz de identidade e λ é o parâmetro de regularização.
   NOTA: 10^-3 é um bom valor para λ quando T~10⁴ e P~3*10³. Eles devem ser ajustados comparando os valores dos dois termos no erro quadrado regularizado, e, como mostrado abaixo.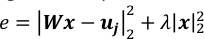
   
   1. Corra LinearRegression.py para resolver este problema de regressão linear. O resultado de x é salvo no arquivo PixelValue.csv. Altere o valor do λ na linha 16 para diferentes pontos fortes da regularização.
      $ píton LinearRegression.py
5. Converta x em um mapa de superfície 2D de acordo com a regra de mapeamento do HEALPix.
   1. Execute PlotMap.py para construir os mapas recuperados usando diferentes parâmetros de regularização. Três números Map_-2.png, Map_-3.png e Map_-4.png serão criados com a configuração atual (Figura Suplementar 9). A relação entre os índices de pixels e suas localizações no mapa está descrita no documento HEALPix¹¹. Este passo leva dezenas de segundos.
      $ píton PolotMap.py

5. Estimar a incerteza do mapa recuperado

1. Reescreva o problema de regressão linear na etapa 4.3 com o "verdadeiro valor" de x como z e o ruído de observação, ε.
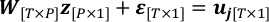
   1. Assuma ε seguir uma Distribuição Gaussiana N (0, σ²I_[T*T]) e estimar sua covariância. T-P é o grau de liberdade de u_j da observação quando o mapa recuperado é fixo.
      
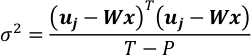
   2. Combine equações na etapa 4.4 e 5.1. Resulta em um vetor gaussiano de x.
      
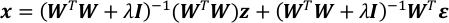
   3. Calcular a expectativa e a matriz de covariância de x.
      
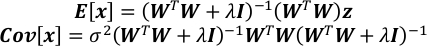
   4. Obtenha a incerteza de cada elemento em x como a raiz quadrada do elemento correspondente na diagonal de Cov[x].
      
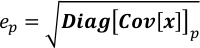
      onde e_p é a incerteza de x_p; Diag[Cov[x]]_p é p-th elemento na diagonal de Cov[x].
   5. Executar Covariance.py para calcular a matriz de covariância de x. O resultado é salvo em Covariance.npz devido ao seu tamanho. Este passo leva dezenas de segundos a minutos, dependendo do tamanho de W.
      $ píton Covariance.py
2. Converta_{e p} para o mapa 2D recuperado de acordo com a regra de mapeamento do HEALPix.
   1. Execute PlotCovariance.py para visualizar Cov[x] e mapear a incerteza e_p para o mapa recuperado. Serão criadas duas figuras Covariância.png e Incerteza.png (Figura Suplementar 10-11).
      $ píton PlotCovariance.py

Resultados

Usamos curvas de luz de um ponto único de comprimento de onda da Terra para demonstrar o protocolo, e comparamos os resultados com a verdade do solo para avaliar a qualidade do mapeamento da superfície. A observação utilizada aqui é obtida pelo DSCOVR/EPIC, que é um satélite localizado perto do primeiro ponto lagrangiano (L1) entre a Terra e o Sol tirando imagens em dez comprimentos de onda da face iluminada pelo sol da Terra. Dois anos (2016 e 2017) de observações são utilizados para esta demonstração, que s...

Discussão

Um requisito crítico do protocolo é a viabilidade de extrair informações superficiais de curvas de luz, o que depende da cobertura da nuvem. Na etapa 3.5.1, os valores relativos dos PCs podem ser diferentes entre exoplanetas. No caso da Terra, os dois primeiros PCs dominam as variações da curva de luz, e correspondem a nuvens e superfícies independentes da superfície (Fan et al. 2019)¹³. Eles têm valores singulares comparáveis para que as informações de superfície possam ser separadas...

Materiais

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.