Surface Mapping of Earth-like Exoplanets using Single Point Light Curves

Summary

The protocol extracts information from light curves of exoplanets and constructs their surface maps. It uses light curves of Earth, which serves as a proxy exoplanet, to demonstrate the approach.

Abstract

Spatially resolving exoplanet features from single-point observations is essential for evaluating the potential habitability of exoplanets. The ultimate goal of this protocol is to determine whether these planetary worlds harbor geological features and/or climate systems. We present a method of extracting information from multi-wavelength single-point light curves and retrieving surface maps. It uses singular value decomposition (SVD) to separate sources that contribute to light curve variations and infer the existence of partially cloudy climate systems. Through analysis of the time series obtained from SVD, physical attributions of principal components (PCs) could be inferred without assumptions of any spectral properties. Combining with viewing geometry, it is feasible to reconstruct surface maps if one of the PCs are found to contain surface information. Degeneracy originated from convolution of the pixel geometry and spectrum information determines the quality of reconstructed surface maps, which requires the introduction of regularization. For the purpose of demonstrating the protocol, multi-wavelength light curves of Earth, which serves as a proxy exoplanet, are analyzed. Comparison between the results and the ground truth is presented to show the performance and limitation of the protocol. This work provides a benchmark for future generalization of exoplanet applications.

Introduction

Identifying habitable worlds is one of the ultimate goals in astrobiology¹. Since the first detection², more than 4000 exoplanets have been confirmed to date³ with a number of Earth analogs (e.g., TRAPPIST-1e)⁴. These planets have orbital and planetary properties similar to those of Earth, and therefore are potentially habitable. Evaluating their habitability from limited observations is essential in this context. Based on the knowledge of life on Earth, geological and climate systems are critical to habitability, which can therefore serve as biosignatures. In principle, features of these systems could be observed from a distance even when a planet could not be spatially resolved better than one single point. In this case, identifying geological features and climate systems from single-point light curves is essential when assessing the habitability of exoplanets. Surface mapping of these exoplanets becomes urgent.

Despite the convolution between viewing geometry and spectral features, information of an exoplanet’s surface is contained in its time-resolved single-point light curves, which can be obtained from a distance, and derived with sufficient observations. However, two-dimensional (2D) surface mapping of potentially habitable Earth-like exoplanets is challenging due to the influence of clouds. Methods of retrieving 2D maps have been developed and tested using simulated light curves and known spectra^5,6,7,8, but they have not been applied to real observations. Moreover, in the analyses of exoplanet observations now and in the near future, assumptions of characteristic spectra may be controversial when the planetary surface compositions are not well-constrained.

In this paper, we demonstrate a surface mapping technique for Earth-like exoplanets. We use SVD to evaluate and separate information from different sources that is contained in multi-wavelength light curves without assumptions of any specific spectra. Combined with viewing geometry, we present the reconstruction of surface maps using timely resolved but spatially convoluted surface information. For the purpose of demonstrating this method, two-year multi-wavelength single-point observations of Earth obtained by the Deep Space Climate Observatory/Earth Polychromatic Imaging Camera (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html) are analyzed. We use Earth as a proxy exoplanet to assess this method because currently available observations of exoplanets are not sufficient. We attach the code with the paper as an example. It is developed under python 3.7 with anaconda and healpy packages, but the mathematics of the protocol can also be done in other programming environments (e.g., IDL or MATLAB).

Protocol

1. Programming setup

1. Set up the programming environment for the attached code. A computer with Linux operating system is required, as the healpy package is not available on Windows. The code is not computationally expensive, so a normal personal computer can handle the protocol.
2. Follow the instruction (https://docs.anaconda.com/anaconda/install/linux/) to install Anaconda with Python 3.7 onto the system, then use the following commands in terminal to set up the programming environment:
   $ conda create --name myenv python=3.7
   $ conda activate myenv
   $ conda install anaconda
   $ conda install healpy
   NOTE: These steps may take tens of minutes depending on the hardware and Internet speed. The environment name ‘myenv’ in the first two command lines can be changed to any other string.

2. Obtaining multi-wavelength light curves and viewing geometry from observations

1. In the viewing geometry, include the longitude and latitude of the sub-stellar and the sub-observer points for each corresponding time frame.
   To use the following attached code, ensure that these two files have the same format as LightCurve.csv and Geometry.csv.
2. Run PlotTimeSeries.py to visualize the data and check their qualities. Two figures LightCurve.png and Geometry.png will be created (Supplemental Figure 1-2). Parameters in this and following plotting codes may need to be adjusted if applied to different observations.
   $ python PlotTimeSeries.py LightCurve
   $ python PlotTimeSeries.py Geometry

3. Extract surface information from light curves

1. Center time-resolved multi-wavelength albedo light curves of an exoplanet and normalize them by corresponding standard deviation at each wavelength. This results in the equal importance of each channel.
   
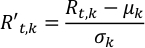
   where R’_t,k and R_t,k are the scaled and observed albedo at the t-th time step and the k-th wavelength, respectively; μ_k and σ_k are the mean and standard deviation of the albedo time series at the k-th wavelength.
   1. Run Normalize.py to normalize the light curves, R_t,k. The output is saved in NormalizedLightCurve.csv.
      $ python Normalize.py
2. Run PlotTimeSeries.py to visualize the normalized light curves. A figure NormalizedLightCurve.png will be created (Supplemental Figure 3).
   $ python PlotTimeSeries.py NormalizedLightCurve
3. Apply SVD on the scaled albedo light curves to find dominant PCs and their corresponding time series.
   
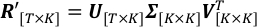
   On the left hand side, T and K are the total number of time steps and observation wavelengths; R’ is the matrix of scaled albedo observations, whose (t,k)-th element is R’_t,k. On the right hand side, columns of V are PCs, orthonormal vectors that define the space SVD projects to; Σ is a diagonal matrix, whose (k,k)-th element is the standard deviation of scaled light curves along the k-th axis defined by the k-th column of V; columns of U are the corresponding time series of each PC in V.
   1. Run SingularValueDecomposition.py to decompose R’. The resulting U, Σ, V^T are saved in the output files U.csv, SingularValue.csv and V_T.csv, respectively.
      $ python SingularValueDecomposition.py
4. Use PlotTimeSeries.py and PlotSVD.py to visualize the SVD result. Three figures U.png, Sigma.png and V_T.png will be created (Supplemental Figure 4-6).
   $ python PlotTimeSeries.py U
   $ python PlotSVD.py
5. Analyze contributions and corresponding time series of PCs to determine the one that contains surface information.
   1. Compare the singular values at the diagonal of Σ. An Earth-like partially cloudy exoplanet is expected to have two comparable dominant singular values.
      NOTE: Σ may contain less or more than two dominant singular values, which is discussed below.
   2. Compare the time series patterns of the two dominant PCs. The PC that contains surface information tends to have more regular shape than the other. Due to the longitudinal asymmetry and the reappearance of surface with small changes in two consecutive days, the corresponding time series tends to have approximately constant daily variation.
   3. Compute the periodicities of the two dominant PCs using Lomb-Scargle periodogram^9,10 to confirm the selection of PC. The PC that contains surface information tends to have higher peak corresponding to rotation period in the power density spectrum.
   4. Run Periodogram.py to obtain the power spectra of the time series of each PC. The power spectra are saved in Periodogram.csv.
      $ python Periodogram.py
   5. Run PlotPeriodogram.py to visualize these periodograms and confirm the selection of PC. A figure Periodogram.png will be created (Supplemental Figure 7). The current plotting code adds in dashed lines representing annual, semi-annual, diurnal and half-daily cycles for reference, which may need to be changed when applied to other observations.
      $ python PlotPeriodogram.py
   6. Select the PC, v_j, that contains surface information and its time series, u_j.
      
      
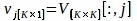
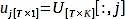
      where V[:,j] and U[:,j] are the j-th columns of V and U, respectively; j is the index of PC inferred at step 3.3 that contains surface information.

4. Construct planetary surface map

1. Use the Hierarchical Equal Area iso-Latitude Pixelization (HEALPix)¹¹ method to pixelate the retrieving map. It divides spherical surface of a planet into pixels with the same area and uniform distribution. Denote the unknown value of the p-th pixel as x_p.
   1. Run HEALPixRandom.py to visualize the pixelization method. A figure HEALPixRandom.png will be created (Supplemental Figure 8). The parameter N_side at line 17 can be changed for different resolutions. This step may take a few seconds to minutes depending on the resolution.
      $ python HEALPixRandom.py
2. Compute the weight of the p-th pixel in observations at the t-th time step, w_t,p, using viewing geometry.
   
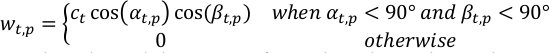
   where α_t,p, β_t,p are the solar and the spacecraft zenith angles at the p-th pixel at the t-th time step; c_t is a normalization term of the t-th observation so that sum of the total weight at each time step is unity.
   NOTE: Geometry is assumed to be known at this step, or can be derived from other analysis, which is discussed below.
   1. Run ComputeWeight.py to compute w_t,p. Change the value of N_side at line 23 for other resolutions of the retrieved map. The output is saved as W.npz due to its size.
      $ python ComputeWeight.py
3. Use PlotWeight.py to visualize these weights. A number of figures, one at each time step, will be created in a folder Weight. Merging them results in Supplemental Video 1, which shows how the weight of each pixel changes with time. This step may take hours to finish due to the large number of visualizations.
   $ python PlotWeight.py
4. Combine geometry and observations to reach a linear regression problem.
   
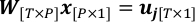
   where P is the total number of retrieving pixels; W is the weight matrix with w_t,p as the (t,p)-th element; x consists of x_p as the p-th element, which is the quantity to be solved in this problem.
   Solve the linear regression problem with a regularization of L-2 norm.
   
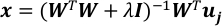
   where I is the identity matrix and λ is the regularization parameter.
   NOTE: 10^-3 is a good value for λ when T~10⁴ and P~3*10³. They should be adjusted by comparing the values of the two terms in the regularized square error, e, as shown below.
   
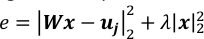
   1. Run LinearRegression.py to solve this linear regression problem. The result of x is saved in the file PixelValue.csv. Change the value of λ at line 16 for different strengths of regularization.
      $ python LinearRegression.py
5. Convert x to a 2D surface map according to the mapping rule of HEALPix.
   1. Run PlotMap.py to construct the retrieved maps using different regularization parameters. Three figures Map_-2.png, Map_-3.png and Map_-4.png will be created with the current setting (Supplemental Figure 9). The relationship between the pixel indices and their locations on map is described in the HEALPix document¹¹. This step takes tens of seconds.
      $ python PolotMap.py

5. Estimate uncertainty of the retrieved map

1. Rewrite the linear regression problem at step 4.3 with the “true value” of x as z and the observation noise, ε.
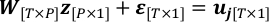
   1. Assume ε to follow a Gaussian Distribution N (0, σ²I_[T*T]) and estimate its covariance. T-P is the degree of freedom of u_j from observation when the retrieved map is fixed.
      
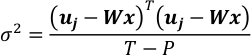
   2. Combine equations in step 4.4 and 5.1. It results in a Gaussian vector of x.
      
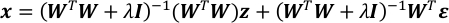
   3. Compute the expectation and the covariance matrix of x.
      
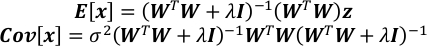
   4. Obtain the uncertainty of each element in x as the square root of the corresponding element on the diagonal of Cov[x].
      
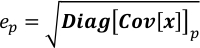
      where e_p is the uncertainty of x_p; Diag[Cov[x]]_p is p-th element on the diagonal of Cov[x].
   5. Run Covariance.py to compute the covariance matrix of x. The result is saved in Covariance.npz due to its size. This step takes tens of seconds to minutes depending on the size of W.
      $ python Covariance.py
2. Convert e_p to the retrieved 2D map according to the mapping rule of HEALPix.
   1. Run PlotCovariance.py to visualize Cov[x] and map the uncertainty e_p to the retrieved map. Two figures Covariance.png and Uncertainty.png will be created (Supplemental Figure 10-11).
      $ python PlotCovariance.py

Results

We use multi-wavelength single-point light curves of Earth to demonstrate the protocol, and compare the results with the ground truth to evaluate the quality of surface mapping. Observation used here is obtained by DSCOVR/EPIC, which is a satellite located near the first Lagrangian point (L1) between Earth and Sun taking images at ten wavelengths of the sunlit face of Earth. Two years (2016 and 2017) of observations are used for this demonstration, which are the same as those in Jiang et al. (2018)¹²

Discussion

One critical requirement of the protocol is the feasibility of extracting surface information from light curves, which depends on the cloud coverage. In step 3.5.1, the relative values of the PCs may be different among exoplanets. In the case of Earth, the first two PCs dominate the light curve variations, and correspond to surface-independent clouds and surface (Fan et al. 2019)¹³. They have comparable singular values so that the surface information can be separated following steps 3.5.2 and 3.5....

Materials

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.