Cartographie de surface des exoplanètes de la Terre à l’aide de courbes lumineuses à point unique

Résumé

Le protocole extrait des informations des courbes lumineuses des exoplanètes et construit leurs cartes de surface. Il utilise des courbes lumineuses de la Terre, qui sert d’exoplanète proxy, pour démontrer l’approche.

Résumé

La résolution spatiale des caractéristiques des exoplanètes à partir d’observations en un seul point est essentielle pour évaluer l’habitabilité potentielle des exoplanètes. Le but ultime de ce protocole est de déterminer si ces mondes planétaires abritent des caractéristiques géologiques et/ou des systèmes climatiques. Nous présentons une méthode d’extraction de l’information à partir de courbes lumineuses à un point à longueur d’onde multiples et de récupération des cartes de surface. Il utilise la décomposition de la valeur singulière (SVD) pour séparer les sources qui contribuent aux variations de la courbe lumineuse et en déduire l’existence de systèmes climatiques partiellement nuageux. Grâce à l’analyse des séries de temps obtenues à partir de la SVD, les attributions physiques des principaux composants (PC) pourraient être déduites sans hypothèses de propriétés spectrales. En combinaison avec la géométrie de visualisation, il est possible de reconstruire des cartes de surface si l’un des PC contient des informations de surface. La dégénérisation provenant de la convolution de la géométrie des pixels et de l’information sur le spectre détermine la qualité des cartes de surface reconstruites, ce qui nécessite l’introduction d’une régularisation. Dans le but de démontrer le protocole, des courbes lumineuses à longueurs d’onde multiples de la Terre, qui sert d’exoplanète proxy, sont analysées. La comparaison entre les résultats et la vérité du sol est présentée pour montrer la performance et la limitation du protocole. Ces travaux fournissent une référence pour la généralisation future des applications d’exoplanètes.

Introduction

Identifier les mondes habitables est l’un des objectifs ultimes de l’astrobiologie¹. Depuis la première détection², plus de 4000 exoplanètes ont été confirmées à ce^{jour 3} avec un certain nombre d’analogues de la Terre (par exemple, TRAPPIST-1e)⁴. Ces planètes ont des propriétés orbitales et planétaires similaires à celles de la Terre, et sont donc potentiellement habitables. L’évaluation de leur habitabilité à partir d’observations limitées est essentielle dans ce contexte. Basés sur la connaissance de la vie sur Terre, les systèmes géologiques et climatiques sont essentiels à l’habitabilité, qui peut donc servir de biosignatures. En principe, les caractéristiques de ces systèmes pouvaient être observées à distance même lorsqu’une planète ne pouvait pas être résolue spatialement mieux qu’un seul point. Dans ce cas, il est essentiel d’identifier les caractéristiques géologiques et les systèmes climatiques à partir de courbes lumineuses à point unique lorsqu’il s’agit d’évaluer l’habitabilité des exoplanètes. La cartographie de surface de ces exoplanètes devient urgente.

Malgré la convolution entre la géométrie de visualisation et les caractéristiques spectrales, l’information de la surface d’une exoplanète est contenue dans ses courbes lumineuses à un point résolues dans le temps, qui peuvent être obtenues à distance et dérivées d’observations suffisantes. Toutefois, la cartographie de surface bidimensionnelle (2D) des exoplanètes potentiellement habitables de la Terre est difficile en raison de l’influence des nuages. Des méthodes de récupération des cartes 2D ont été développées et testées à l’aide de courbes lumineuses simulées et de spectres^{connus 5,6,7,8}, mais elles n’ont pas été appliquées à des observations réelles. En outre, dans les analyses des observations d’exoplanètes aujourd’hui et dans un proche avenir, les hypothèses de spectres caractéristiques peuvent être controversées lorsque les compositions planétaires de surface ne sont pas bien limitées.

Dans cet article, nous démontrons une technique de cartographie de surface pour les exoplanètes de type Terre. Nous utilisons SVD pour évaluer et séparer l’information de différentes sources qui est contenue dans les courbes de lumière à plusieurs longueurs d’onde sans hypothèses de spectres spécifiques. Combiné avec la géométrie de visualisation, nous présentons la reconstruction des cartes de surface en utilisant des informations de surface résolues en temps opportun mais spatialement alambiquées. Dans le but de démontrer cette méthode, des observations à un point multi-longueurs d’onde de deux ans de la Terre obtenues par l’Observatoire du climat spatial profond/Caméra d’imagerie polychromatique de la Terre (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html) sont analysées. Nous utilisons la Terre comme exoplanète proxy pour évaluer cette méthode parce que les observations actuellement disponibles des exoplanètes ne sont pas suffisantes. Nous attachons le code avec le papier à titre d’exemple. Il est développé sous python 3.7 avec des paquets anaconda et healpy, mais les mathématiques du protocole peuvent également être faites dans d’autres environnements de programmation (par exemple, IDL ou MATLAB).

Protocole

1. Configuration de programmation

1. Configurer l’environnement de programmation pour le code ci-joint. Un ordinateur avec système d’exploitation Linux est nécessaire, car le paquet healpy n’est pas disponible sur Windows. Le code n’est pas coûteux sur le plan informatique, de sorte qu’un ordinateur personnel normal peut gérer le protocole.
2. Suivez les instructions (https://docs.anaconda.com/anaconda/install/linux/) pour installer Anaconda avec Python 3.7 sur le système, puis utilisez les commandes suivantes dans le terminal pour configurer l’environnement de programmation :
   $ conda créer - nom python myenv =3,7
   $ conda activer myenv
   $ conda installer anaconda
   $ conda installer healpy
   REMARQUE : Ces étapes peuvent prendre des dizaines de minutes selon le matériel et la vitesse d’Internet. Le nom de l’environnement « myenv » dans les deux premières lignes de commande peut être changé en n’importe quelle autre chaîne.

2. Obtenir des courbes de lumière à longueur d’onde multiples et la géométrie de visualisation à partir d’observations

1. Dans la géométrie de visualisation, inclure la longitude et la latitude du sous-stellaire et les points de sous-observateur pour chaque période correspondante.
   Pour utiliser le code ci-joint suivant, assurez-vous que ces deux fichiers ont le même format que LightCurve.csv et Geometry.csv.
2. Exécutez PlotTimeSeries.py pour visualiser les données et vérifier leurs qualités. Deux figures LightCurve.png et Geometry.png seront créées(Figure supplémentaire 1-2). Les paramètres de ce code et des codes de traçage suivants peuvent devoir être ajustés s’ils sont appliqués à différentes observations.
   $ python PlotTimeSeries.py LightCurve
   $ python PlotTimeSeries.py Géométrie

3. Extraire l’information de surface des courbes lumineuses

1. Courbes de lumière albédées multi-longueurs d’onde multi-longueurs d’onde de centre d’une exoplanète et normalisent-les par déviation standard correspondante à chaque longueur d’onde. Il en résulte la même importance de chaque canal.
   
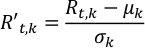
   où R'_t,k et R_{t,k sont} l’albébétie à l’étape t-th temps et la longueur d’onde k-th, respectivement; μ_k et σ_{k sont l’écart} moyen et standard de la série de temps albédéno à la longueur d’onde k-th.
   1. Courez Normalize.py pour normaliser les courbes lumineuses, R_t,k. La sortie est enregistrée dans NormalizedLightCurve.csv.
      $ python Normalize.py
2. Exécutez PlotTimeSeries.py pour visualiser les courbes de lumière normalisées. Un chiffre NormalizedLightCurve.png sera créé(Figure supplémentaire 3).
   $ python PlotTimeSeries.py NormalizedLightCurve
3. Appliquez le SVD sur les courbes de lumière albédéno à l’échelle pour trouver les PC dominants et leurs séries de temps correspondantes.
   
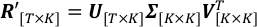
   Sur le côté gauche, T et K sont le nombre total d’étapes de temps et de longueurs d’onde d’observation; R' est la matrice d’observations à l’échelle de l’albédée, dont (t,k)-th élément est R'_t,k. Sur le côté droit, les colonnes de V sont des PC, des vecteurs orthonormaux qui définissent l’espace des projets SVD à; C’est une matrice diagonale, dont l’élément (k,k)-th est l’écart type des courbes de lumière à l’échelle le long de l’axe k-th défini par la colonne k-th de V; colonnes de U sont les séries de temps correspondantes de chaque PC en V.
   1. Courez SingularValueDecomposition.py pour décomposer R'. Le U résultant, Ţ, V T^sont enregistrés dans les fichiers de sortie U.csv, SingularValue.csv et V_T.csv, respectivement.
      $ python SingularValueDecomposition.py
4. Utilisez PlotTimeSeries.py et PlotSVD.py pour visualiser le résultat SVD. Trois chiffres U.png, Sigma.png et V_T.png seront créés (Figure supplémentaire 4-6).
   $ python PlotTimeSeries.py U
   $ python PlotSVD.py
5. Analyser les contributions et les séries de temps correspondantes des PC pour déterminer celle qui contient des informations de surface.
   1. Comparez les valeurs singulières à la diagonale de Ţ. On s’attend à ce qu’une exoplanète partiellement nuageuse de la Terre a deux valeurs singulières dominantes comparables.
      REMARQUE: Ρ peut contenir moins ou plus de deux valeurs singulières dominantes, qui est discuté ci-dessous.
   2. Comparez les modèles de séries de temps des deux PC dominants. Le PC qui contient des informations de surface a tendance à avoir une forme plus régulière que l’autre. En raison de l’asymétrie longitudinale et de la réapparition de la surface avec de petits changements en deux jours consécutifs, la série de temps correspondante tend à avoir la variation quotidienne approximativement constante.
   3. Calculez les périodiques des deux PC dominants à l’aide du parallélogramme Lomb-Scargle^9,10 pour confirmer la sélection du PC. Le PC qui contient des informations de surface a tendance à avoir un pic plus élevé correspondant à la période de rotation dans le spectre de densité de puissance.
   4. Exécutez Periodogram.py pour obtenir les spectres de puissance de la série de temps de chaque PC. Les spectres de puissance sont enregistrés dans Periodogram.csv.
      $ python Periodogram.py
   5. Exécutez PlotPeriodogram.py pour visualiser ces parogrammes et confirmer la sélection du PC. Un .png figure sera créé (Figure supplémentaire 7). Le code de traçage actuel s’ajoute dans les lignes pointillées représentant des cycles annuels, semestriels, diurnes et demi quotidiens de référence, qui peuvent devoir être modifiés lorsqu’ils sont appliqués à d’autres observations.
      $ python PlotPeriodogram.py
   6. Sélectionnez le PC, v_j, qui contient des informations de surface et sa série de temps, u_j.
      
      
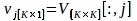
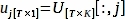
      où V[:,j] et U[:,j] sont les colonnes j-th de V et U, respectivement; j est l’index du PC déduit à l’étape 3.3 qui contient des informations de surface.

4. Construire une carte de surface planétaire

1. Utilisez la méthode hiérarchique de pixelisation iso latitude (HEALPix)^pour pixeliser la carte de récupération. Il divise la surface sphérique d’une planète en pixels avec la même zone et la distribution uniforme. Dénotez la valeur inconnue du pixel p-th comme x_p.
   1. Exécutez HEALPixRandom.py pour visualiser la méthode de pixelisation. Un chiffre HEALPixRandom.png sera créé (Figure supplémentaire 8). Le paramètre N_côté à la ligne 17 peut être modifié pour différentes résolutions. Cette étape peut prendre de quelques secondes à quelques minutes selon la résolution.
      $ python HEALPixRandom.py
2. Calculez le poids du pixel p-th dans les observations à l’étape t-th temps, w_t,p, en utilisant la géométrie de visualisation.
   
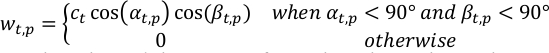
   où α_t,p, β_{t,p sont les} angles solaires et le zénith vaisseau spatial au pixel p-th à l’étape t-th temps; c_{t est} un terme de normalisation de l’observation t-th de sorte que la somme du poids total à chaque étape de temps est l’unité.
   REMARQUE : La géométrie est supposée être connue à cette étape, ou peut être dérivée d’autres analyses, qui sont discutées ci-dessous.
   1. Exécutez ComputeWeight.py pour calculer w_t,p. Modifiez la valeur du_côté N à la ligne 23 pour d’autres résolutions de la carte récupérée. La sortie est enregistrée sous le nom de W.npz en raison de sa taille.
      $ python ComputeWeight.py
3. Utilisez PlotWeight.py pour visualiser ces poids. Un certain nombre de chiffres, un à chaque étape, seront créés dans un dossier Poids. Leur fusion se traduit par la vidéo supplémentaire 1, qui montre comment le poids de chaque pixel change avec le temps. Cette étape peut prendre des heures à se terminer en raison du grand nombre de visualisations.
   $ python PlotWeight.py
4. Combinez la géométrie et les observations pour atteindre un problème de régression linéaire.
   
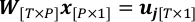
   où P est le nombre total de pixels de récupération; W est la matrice de poids avec w_t,p comme l’élément (t,p)-th; x se compose de x_p comme élément p-th, qui est la quantité à résoudre dans ce problème.
   Résoudre le problème de régression linéaire avec une régularisation de la norme L-2.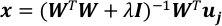
   
   où je suis la matrice d’identité et c’est le paramètre de régularisation.
   NOTE: 10^{-3 est} un bon rapport qualité/prix pour ν lorsque T ~^{10 4} et P ~ 3 * 10³. Ils doivent être ajustés en comparant les valeurs des deux termes dans l’erreur carrée régularisée, e, comme indiqué ci-dessous.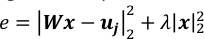
   
   1. Exécutez LinearRegression.py pour résoudre ce problème de régression linéaire. Le résultat de x est enregistré dans le fichier PixelValue.csv. Modifier la valeur de la ligne 16 pour différentes forces de régularisation.
      $ python LinearRegression.py
5. Convertissez x en une carte de surface 2D selon la règle de cartographie de HEALPix.
   1. Exécutez PlotMap.py construire les cartes récupérées à l’aide de différents paramètres de régularisation. Trois figures Map_-2.png, Map_-3.png et Map_-4.png seront créées avec le réglage actuel(Figure supplémentaire 9). La relation entre les indices de pixels et leurs emplacements sur la carte est décrite dans le document HEALPix¹¹. Cette étape prend des dizaines de secondes.
      $ python PolotMap.py

5. Estimer l’incertitude de la carte récupérée

1. Réécrire le problème de régression linéaire à l’étape 4.3 avec la « vraie valeur » de x comme z et le bruit d’observation, ε.
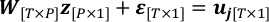
   1. Supposons ε de suivre un Gaussian Distribution N (0, σ²I_[T*T]) et d’estimer sa covariance. T-P est le degré de liberté d’u_{j de} l’observation lorsque la carte récupérée est fixée.
      
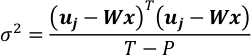
   2. Combinez les équations à l’étape 4.4 et 5.1. Il en résulte un vecteur gaussien de x.
      
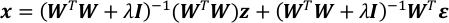
   3. Calculez l’attente et la matrice de covariance de x.
      
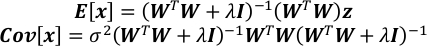
   4. Obtenez l’incertitude de chaque élément en x comme racine carrée de l’élément correspondant sur la diagonale de Cov[x].
      
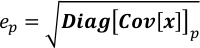
      où e_p est l’incertitude de x_p; Diag[Cov[x]]_p est p-th élément sur la diagonale de Cov[x].
   5. Exécutez Covariance.py pour calculer la matrice de covariance de x. Le résultat est enregistré dans Covariance.npz en raison de sa taille. Cette étape prend des dizaines de secondes à quelques minutes en fonction de la taille de W.
      $ python Covariance.py
2. Convertissez e_p en la carte 2D récupérée selon la règle de cartographie de HEALPix.
   1. Exécutez PlotCovariance.py pour visualiser Cov[x] et cartographier l’incertitude e_p à la carte récupérée. Deux chiffres Covariance.png et Incertitude.png seront créés(Figure supplémentaire 10-11).
      $ python PlotCovariance.py

Résultats

Nous utilisons des courbes de lumière à un point à longueur d’onde multiples de la Terre pour démontrer le protocole, et comparer les résultats avec la vérité du sol pour évaluer la qualité de la cartographie de surface. L’observation utilisée ici est obtenue par DSCOVR/EPIC, un satellite situé près du premier point lagrangien (L1) entre la Terre et le Soleil prenant des images à dix longueurs d’onde de la surface ensoleillée de la Terre. Deux années (2016 et 2017) d’observations sont utilisées po...

Discussion

Une exigence essentielle du protocole est la faisabilité d’extraire des informations de surface des courbes lumineuses, qui dépendent de la couverture nuageuse. À l’étape 3.5.1, les valeurs relatives des PC peuvent être différentes d’une exoplanète à l’autre. Dans le cas de la Terre, les deux premiers PC dominent les variations de la courbe lumineuse et correspondent à des nuages et à une surface indépendants de la surface (Fan et al., 2019)¹³. Ils ont des valeurs singulières c...

matériels

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.