このコンテンツを視聴するには、JoVE 購読が必要です。 サインイン又は無料トライアルを申し込む。
Method Article
単一点光曲線を用いた地球系外惑星の表面マッピング
要約
このプロトコルは、系外惑星の光曲線から情報を抽出し、その表面マップを構築します。これは、プロキシ系外惑星として機能する地球の光曲線を使用して、アプローチを実証します。
要約
単一点観測から系外惑星の特徴を空間的に解決することは、系外惑星の潜在的な居住性を評価するために不可欠です。このプロトコルの最終的な目標は、これらの惑星世界が地質学的特徴および/または気候システムを収容しているかどうかを判断することです。多波長の単一点光曲線から情報を抽出し、サーフェスマップを取得する方法を紹介します。これは、特異値分解(SVD)を使用して、光曲線の変化に寄与する光源を分離し、部分的に曇った気候システムの存在を推測します。SVDから得られた時系列の解析を通じて、主成分(PC)の物理的な帰属は、スペクトル特性を仮定することなく推測することができる。表示ジオメトリと組み合わせることで、いずれかの PC にサーフェス情報が含まれていることが判明した場合に、サーフェス マップを再構築できます。ピクセルジオメトリの畳み込みから生じたデジェネラシーとスペクトル情報は、再構築されたサーフェスマップの品質を決定し、正規化の導入が必要です。プロトコルを実証するために、プロキシ系外惑星として機能する地球の多波長光曲線を分析する。結果とグランドトゥルースの比較は、プロトコルのパフォーマンスと制限を示すために提示されます。この研究は、太陽系外惑星アプリケーションの将来の一般化のためのベンチマークを提供します。
概要
居住可能な世界を特定することは、アストロバイオロジー1の究極の目標の1つです。最初の検出2以来、4000以上の系外惑星が、多数の地球アナログ(例えばTRAPPIST-1e)4で現在までに確認されている。これらの惑星は、地球と同様の軌道および惑星特性を有するため、潜在的に居住可能である。限られた観察から居住性を評価することは、この文脈において不可欠です。地球上の生命の知識に基づいて、地質学的および気候システムは居住性にとって重要であり、したがってバイオシグネチャとして役立つ可能性があります。原理的には、惑星が1つの点よりも空間的にうまく解決できなかった場合でも、これらのシステムの特徴は遠くから観察することができた。この場合、系外惑星の居住性を評価する際には、単一点光曲線から地質学的特徴と気候システムを特定することが不可欠です。これらの系外惑星の表面マッピングが緊急になる。
視差ジオメトリとスペクトル特徴の間の畳み込みにもかかわらず、系外惑星の表面の情報は、距離から得ることができる時間分解された単一点光曲線に含まれており、十分な観測で導き出されます。しかし、雲の影響により、地球に似た外惑星の2次元(2D)表面マッピングは困難です。2Dマップを取得する方法は、シミュレートされた光曲線と既知のスペクトル5、6、7、8を使用して開発され、テストされていますが、実際の観測には適用されていません。さらに、現在および近い将来の系外惑星観測の分析では、惑星表面組成が十分に制約されていない場合、特徴的なスペクトルの仮定が議論の余地がある。
本論文では、地球系外惑星の表面マッピング技術を示す。SVDを使用して、特定のスペクトルを仮定することなく、多波長光曲線に含まれる異なるソースからの情報を評価し、分離します。表示ジオメトリと組み合わせることで、時間的に解決されたが空間的に複雑なサーフェス情報を使用して、サーフェス マップの再構築を提示します。この方法を実証するために、深宇宙気候観測所/地球多色画像カメラ(DSCOVR/EPIC;www.nesdis.noaa.gov/DSCOVR/spacecraft.html)が得た地球の2年間の多波長単一点観測を解析する。現在利用可能な系外惑星の観測では十分ではないので、この方法を評価するために地球を代理系外惑星として使用しています。例として、この紙にコードを添付します。これは、アナコンダとhealpyパッケージを持つpython 3.7の下で開発されていますが、プロトコルの数学は他のプログラミング環境(例えば、IDLまたはMATLAB)でも行うことができます。
プロトコル
1. プログラミングのセットアップ
- 添付コードのプログラミング環境を設定します。Windows では、このシステムの修復パッケージを使用できないので、Linux オペレーティング システムを搭載したコンピュータが必要です。コードは計算負荷が高くないので、通常のパーソナル コンピュータはプロトコルを処理できます。
- 指示に従って(https://docs.anaconda.com/anaconda/install/linux/)、Python 3.7を備えたAnacondaをシステムにインストールし、ターミナルで次のコマンドを使用してプログラミング環境をセットアップします。
$ conda 作成 --name myenv python=3.7
$ コンダ活性化ミエンビト
$ conda インストールアナコンダ
$ conda インストールヒール
注: これらの手順は、ハードウェアとインターネットの速度によっては数十分かかることがあります。最初の 2 つのコマンド ラインの環境名 'myenv' は、他の任意の文字列に変更できます。
2. 多波長光曲線の取得と観測からの幾何学的表示
- 表示ジオメトリには、サブ恒星の経度と緯度、および対応する各時間枠のサブ観測点を含めます。
次の添付コードを使用するには、これら 2 つのファイルの形式が ライト カーブ と ジオメトリ.csvジオメトリ.csvと同じであることを確認します。 - PlotTimeSeries.pyを実行してデータを視覚化し、その品質を確認します。2 つの図ライトカーブ.pngおよびジオメトリ.pngが作成されます (補足図 1-2)。このプロットコードとそれに続くプロットコードのパラメータは、異なる観測値に適用する場合に調整する必要があります。
ライトカーブPlotTimeSeries.py $ パイソン
$ パイソンPlotTimeSeries.py ジオメトリ
3. 光カーブからサーフェス情報を抽出する
- 系外惑星の時間分解された多波長アルベド光曲線を中心とし、各波長で対応する標準偏差によってそれらを正規化する。これにより、各チャネルの重要度が等しくなります。
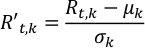
ここでR't,kおよび Rt,kは、それぞれ t-th 時間ステップおよび k-th 波長でスケーリングされ、観測されたアルベドです。kとσ k μは、k番目の波長におけるアルベド時系列の平均および標準偏差である。- Normalize.pyを実行してライトカーブを正規化します。出力は正規化されたライトカーブ.csvに保存されます。
$ パイソンNormalize.py
- Normalize.pyを実行してライトカーブを正規化します。出力は正規化されたライトカーブ.csvに保存されます。
- PlotTimeSeries.pyを実行して、正規化されたライト カーブを視覚化します。図正規化光曲線.pngが作成されます (補足図 3)。
$ パイソンPlotTimeSeries.py正規化されたライトカーブ - SVD をスケールアルベドライトカーブに適用して、支配的なPCとそれに対応する時系列を見つけます。
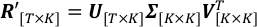
左側の T と K は、時間ステップと観測波長の合計です。 R' は、スケールされたアルベド観測値の行列で、(t,k)番目の要素は R't,kです。右側には 、V の列は、SVDの投影空間を定義するPC、直交正規ベクトルです。 Σ は対角行列であり、(k,k)番目の要素は 、Vの k 番目の列で定義された k 番目の軸に沿ったスケールされた光曲線の標準偏差です。 U の列は V の各 PC の対応する時系列 です。- SingularValueDecomposition.pyを実行して R' を分解します。結果のU、 Σ、 VTは、それぞれ出力ファイルU.csv、SingularValue.csvおよび V_T.csvに保存されます。
$ パイソンSingularValueDecomposition.py
- SingularValueDecomposition.pyを実行して R' を分解します。結果のU、 Σ、 VTは、それぞれ出力ファイルU.csv、SingularValue.csvおよび V_T.csvに保存されます。
- PlotTimeSeries.pyとPlotSVD.pyを使用して、SVD 結果を視覚化します。U.png、シグマ.png、V_T.pngの3つの図が作成されます (補足図 4-6)。
$ パイソン PlotTimeSeries.py U
$ パイソンPlotSVD.py - 貢献度と対応する一連の PC を分析して、サーフェス情報を含む PC を特定します。
- Σの対角線での単数形値を比較します。地球のような部分的に曇った系外惑星は、2つの同等の支配的な特異値を有すると予想される。
注: Σ は、以下で説明する、2 つ以下または 2 つ以上の優勢な単数形値を含む場合があります。 - 2 つの主要 PC の時系列パターンを比較します。表面情報を含む PC は、他の PC よりも規則的な形状を持つ傾向があります。2日連続で、縦方向非対称性と小さな変化を伴う表面の再出現により、対応する時系列は毎日の変動がほぼ一定である傾向があります。
- LOMB-スカーグルのピリオドグラム9、10を使用して、2つの支配的なPCの周期性を計算し、PCの選択を確認します。表面情報を含むPCは、パワー密度スペクトルの回転周期に対応するピークが高くなる傾向があります。
- Periodogram.pyを実行して、各PCの時系列の電力スペクトルを取得します。パワースペクトルはピリオドグラム.csvに保存されます。
$ パイソンPeriodogram.py - PlotPeriodogram.py実行して、これらのピリオドグラムを視覚化し、PCの選択を確認します。図のピリオドグラム.pngが作成されます (補足図 7)。現在のプロット コードは、参照のために年間、半年、日単位、および半日のサイクルを表す破線で追加され、他の観測値に適用する場合に変更する必要があります。
$ パイソンPlotPeriodogram.py - サーフェス情報とその時系列を含むPC、vjを選択します。
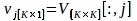
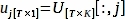
ここで 、V[:,j] と U[:,j] はそれぞれ V と Uの j 番目の列です。j は、サーフェス情報を含むステップ 3.3 で推論された PC のインデックスです。
- Σの対角線での単数形値を比較します。地球のような部分的に曇った系外惑星は、2つの同等の支配的な特異値を有すると予想される。
4. 惑星表面マップの構築
- 取得マップをピクセル化するには、階層均等領域等度ピクセル化 (HEALPix)11 メソッドを使用します。惑星の球面を同じ面積と均一な分布を持つピクセルに分割します。p 番目のピクセルの不明な値を xpとして示します。
- HEALPixRandom.pyを実行して、ピクセル化方法を視覚化します。図HEALPixRandom.pngが作成されます (補足図 8)。17 行目のパラメータ N側は、解像度ごとに変更できます。この手順は、解像度によっては数秒から数分かかります。
$ パイソンHEALPixRandom.py
- HEALPixRandom.pyを実行して、ピクセル化方法を視覚化します。図HEALPixRandom.pngが作成されます (補足図 8)。17 行目のパラメータ N側は、解像度ごとに変更できます。この手順は、解像度によっては数秒から数分かかります。
- ビュージオメトリを使用して、観測値の p 番目のピクセルの重みを計算します(tt,p) を使用します。
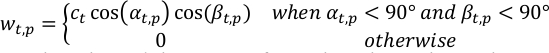
ここでαt,p,βt,p は、t-th 時間ステップの p 番目のピクセルにおける太陽と宇宙船の天頂角です。ct はt-th観測の正規化項であり、各時間ステップにおける総重量の合計が統一となる。
注: ジオメトリは、この手順で既知であると想定されるか、または後で説明する他の解析から派生することができます。- ComputeWeight.pyを実行して、wt,pを計算します。取得したマップの他の解像度の場合は、行 23 の N側の値を変更します。出力は、サイズのためW.npzとして保存されます。
$ パイソンComputeWeight.py
- ComputeWeight.pyを実行して、wt,pを計算します。取得したマップの他の解像度の場合は、行 23 の N側の値を変更します。出力は、サイズのためW.npzとして保存されます。
- これらの重みを視覚化するには 、PlotWeight.py を使用します。複数の図形が、時間ステップごとに 1 つずつ作成 されます。それらをマージすると、各ピクセルのウェイトが時間とともに変化する方法を示す 補足ビデオ 1が表示されます。ビジュアライゼーションの数が多いため、この手順が完了するまでに数時間かかる場合があります。
$ パイソンPlotWeight.py - 幾何学と観測値を組み合わせて、線形回帰の問題に到達します。
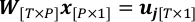
P は取得するピクセルの総数です。 W は wt,p を持つ重み行列で、(t,p)番目の要素です。 x は、この 問題で解決される量である p 番目の要素として x p で構成されます。
L-2ノルムの正規化で線形回帰の問題を解決します。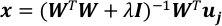
ここで I は単位行列で、λ は正規化パラメータです。
注意: T〜104とP〜3*10 3の場合、10-3はλに適した値です。以下に示すように、正規化された二乗誤差eの2つの項の値を比較して調整する必要があります。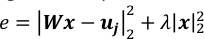
- この線形回帰の問題を解決するには 、LinearRegression.py を実行します。 x の結果は 、.csv ファイルに保存されます。正則化の強度を変える場合は、ライン16のλの値を変更します。
$ パイソンLinearRegression.py
- この線形回帰の問題を解決するには 、LinearRegression.py を実行します。 x の結果は 、.csv ファイルに保存されます。正則化の強度を変える場合は、ライン16のλの値を変更します。
- HEALPix のマッピング ルールに従って 、x を 2D サーフェス マップに変換します。
- PlotMap.py実行して、異なる正規化パラメーターを使用して取得したマップを構築します。現在の設定Map_Map_2.png、Map_-3.png、Map_-4.pngの3つの図が作成されます(図 9 を補足します)。 ピクセルインデックスと地図上の位置との関係については、HEALPix ドキュメント11に記載されています。このステップには数十秒かかります。
$ パイソンPolotMap.py
- PlotMap.py実行して、異なる正規化パラメーターを使用して取得したマップを構築します。現在の設定Map_Map_2.png、Map_-3.png、Map_-4.pngの3つの図が作成されます(図 9 を補足します)。 ピクセルインデックスと地図上の位置との関係については、HEALPix ドキュメント11に記載されています。このステップには数十秒かかります。
5. 取得したマップの不確実性を見積もる
- ステップ 4.3 の線形回帰問題を、zと観測ノイズの 「真値」 をεして書き換えます。
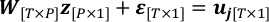
- εガウス分布 N (0, σ 2I[T*T])に従って共分散を推定するとします。T-Pは、取得したマップが固定されている場合の観測からのujの自由度です。
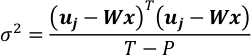
- ステップ 4.4 と 5.1 の方程式を組み合わせます。この結果、ガウスベクトル x が 得られます。
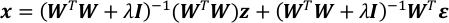
- xの期待値と共分散行列を計算します。
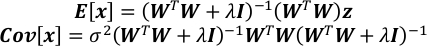
- Cov[x]の対角線上の対応する要素の平方根としてxの各要素の不確実性を求める。
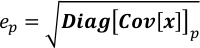
ここで epは xpの不確実性です。Diag[Cov] x]pは、Cov[x]の対角線上のp番目の要素である。 - Covariance.pyを実行して x の共分散行列を計算します。結果は、そのサイズのためにCovariance.npzに保存されます。この手順は、Wのサイズに応じて数十秒から数分かかります。
$ パイソン Covariance.py
- εガウス分布 N (0, σ 2I[T*T])に従って共分散を推定するとします。T-Pは、取得したマップが固定されている場合の観測からのujの自由度です。
- HEALPix のマッピングルールに従って ep を取得した 2D マップに変換します。
- PlotCovariance.py実行してCov[x] を視覚化し、不確定性epを取得したマップにマップします。共分散.pngと不確実性.pngの2つの数値が作成されます (補足図 10-11)。
$ パイソンPlotCovariance.py
- PlotCovariance.py実行してCov[x] を視覚化し、不確定性epを取得したマップにマップします。共分散.pngと不確実性.pngの2つの数値が作成されます (補足図 10-11)。
結果
私たちは、地球の多波長単一点光曲線を使用してプロトコルを実証し、その結果を地上の真理と比較して、表面マッピングの品質を評価します。ここで使用される観測は、地球と太陽の間の最初のラグランジ点(L1)の近くに位置する衛星であるDSCOVR/EPICが、地球の日当たりの良い顔の10波長で画像を撮ることによって得られます。このデモンストレーションには2年間(2016年と2017年)の観測が使用...
ディスカッション
プロトコルの重要な要件の 1 つは、クラウドのカバレッジに依存する光カーブからサーフェス情報を抽出する可能性です。ステップ3.5.1では、PCの相対値が系外惑星によって異なる場合があります。地球の場合、最初の2台のPCは、光曲線の変動を支配し、表面に依存しない雲と表面に対応する(Fan et al. 2019)13。これらの値は、手順 3.5.2 と 3.5.3 に従ってサーフェス情報を分離で...
開示事項
著者らは開示するものは何もない。
謝辞
この研究の一部は、NASAとの契約の下、カリフォルニア工科大学ジェット推進研究所によって支えられていました。YLYは、ワシントン大学のバーチャルプラネタリー研究所の支援を認めています。
資料
| Name | Company | Catalog Number | Comments |
| Python 3.7 with anaconda and healpy packages | Other programming environments (e.g., IDL or MATLAB) also work. |
参考文献
- Schwieterman, E. W., et al. Exoplanet Biosignatures: A Review of Remotely Detectable Signs of Life. Astrobiology. 18 (6), 663-708 (2018).
- Campbell, B., Walker, G. A. H., Yang, S. A Search for Substellar Companions to Solar-type Stars. The Astrophysical Journal. 331, 902 (1988).
- NASA. . NASA Exoplanet Archive (2019) Confirmed Planets Table. , (2019).
- Gillon, M., et al. Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1. Nature. 542 (7642), 456-460 (2017).
- Kawahara, H., Fujii, Y. Global Mapping of Earth-like Exoplanets from Scattered Light Curves. The Astrophysical Journal. 720 (2), 1333 (2010).
- Fujii, Y., Kawahara, H. Mapping Earth Analogs from Photometric Variability: Spin-Orbit Tomography for Planets in Inclined Orbits. The Astrophysical Journal. 755 (2), 101 (2012).
- Cowan, N. B., Fujii, Y. Mapping Exoplanets. Handbook of Exoplanets. , (2018).
- Farr, B., Farr, W. M., Cowan, N. B., Haggard, H. M., Robinson, T. exocartographer: A Bayesian Framework for Mapping Exoplanets in Reflected Light. The Astronomical Journal. 156 (4), 146 (2018).
- Lomb, N. R. Least-Squares Frequency Analysis of Unequally Spaced Data. Astrophysics and Space Science. 39 (2), 447 (1976).
- Scargle, J. D. Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. The Astrophysical Journal. 263, 835 (1982).
- Górski, K. M., et al. HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere. The Astrophysical Journal. 622 (2), 759 (2005).
- Jiang, J. H., et al. Using Deep Space Climate Observatory Measurements to Study the Earth as an Exoplanet. The Astronomical Journal. 156 (1), 26 (2018).
- Fan, S., et al. Earth as an Exoplanet: A Two-dimensional Alien Map. The Astrophysical Journal Letters. 882 (1), 1 (2019).
- Cowan, N. B., Strait, T. E. Determining Reflectance Spectra of Surfaces and Clouds on Exoplanets. The Astrophysical Journal Letters. 765 (1), 17 (2013).
- Fujii, Y., Lustig-Yaeger, J., Cowan, N. B. Rotational Spectral Unmixing of Exoplanets: Degeneracies between Surface Colors and Geography. The Astronomical Journal. 154 (5), 189 (2017).
- Kawahara, H., Fujii, Y. Mapping Clouds and Terrain of Earth-like Planets from Photomertic Variability: Demonstration with Planets in Face-on Orbits. The Astrophysical Journal Letters. 739 (2), 62 (2011).
- Kawahara, H. Frequency Modulation of Directly Imaged Exoplanets: Geometric Effect as a Probe of Planetary Obliquity. The Astrophysical Journal. 822 (2), 112 (2016).
- Schwartz, J. C., Sekowski, C., Haggard, H. M., Pall ́e, E., Cowan, N. B. Inferring planetary obliquity using rotational and orbital photometry. Monthly Notices of the Royal Astronomical Society. 457 (1), 926-938 (2016).
転載および許可
このJoVE論文のテキスト又は図を再利用するための許可を申請します
許可を申請さらに記事を探す
This article has been published
Video Coming Soon
Copyright © 2023 MyJoVE Corporation. All rights reserved