Mappatura superficiale di esopianeti simili alla Terra utilizzando curve di luce a punto singolo

Riepilogo

Il protocollo estrae informazioni dalle curve di luce degli esopianeti e costruisce le loro mappe di superficie. Usa curve di luce della Terra, che funge da esopianeta proxy, per dimostrare l'approccio.

Abstract

La risoluzione spaziale delle caratteristiche degli esopianeti dalle osservazioni a punto singolo è essenziale per valutare la potenziale abitabilità degli esopianeti. L'obiettivo finale di questo protocollo è determinare se questi mondi planetari ospitano caratteristiche geologiche e /o sistemi climatici. Presentiamo un metodo per estrarre informazioni da curve di luce a punto singolo multi-lunghezza d'onda e recuperare mappe di superficie. Utilizza la decomposizione del valore singolare (SVD) per separare le fonti che contribuiscono alle variazioni della curva di luce e dedurre l'esistenza di sistemi climatici parzialmente nuvolosi. Attraverso l'analisi delle serie temporali ottenute dall'SVD, le attribuzioni fisiche dei componenti principali (PC) potrebbero essere dedotte senza ipotesi di proprietà spettrali. Combinandosi con la geometria di visualizzazione, è possibile ricostruire le mappe di superficie se si riscontra che uno dei PC contiene informazioni sulla superficie. La degenerazione originata dalla convoluzione della geometria dei pixel e delle informazioni sullo spettro determina la qualità delle mappe superficiali ricostruite, il che richiede l'introduzione della regolarizzazione. Allo scopo di dimostrare il protocollo, vengono analizzate le curve di luce a più lunghezze d'onda della Terra, che funge da esopianeta proxy. Viene presentato il confronto tra i risultati e la verità fondamentale per mostrare le prestazioni e la limitazione del protocollo. Questo lavoro fornisce un punto di riferimento per la futura generalizzazione delle applicazioni degli esopianeti.

Introduzione

Identificare mondi abitabili è uno degli obiettivi finali dell'astrobiologia^1. Dal primo rilevamento^2,più di 4000 esopianeti sono stati confermati fino ad^{oggi 3} con un certo numero di analoghi terrestri (ad esempio, TRAPPIST-1e)⁴. Questi pianeti hanno proprietà orbitali e planetarie simili a quelle della Terra, e quindi sono potenzialmente abitabili. Valutare la loro abitabilità da osservazioni limitate è essenziale in questo contesto. Sulla base della conoscenza della vita sulla Terra, i sistemi geologici e climatici sono fondamentali per l'abitabilità, che può quindi servire come biofirme. In linea di principio, le caratteristiche di questi sistemi potevano essere osservate da lontano anche quando un pianeta non poteva essere risolto spazialmente meglio di un singolo punto. In questo caso, identificare le caratteristiche geologiche e i sistemi climatici dalle curve di luce a punto singolo è essenziale quando si valuta l'abitabilità degli esopianeti. La mappatura superficiale di questi esopianeti diventa urgente.

Nonostante la convoluzione tra la geometria di visualizzazione e le caratteristiche spettrali, le informazioni sulla superficie di un esopianeta sono contenute nelle sue curve di luce a punto singolo risolte nel tempo, che possono essere ottenute da una distanza e derivate con osservazioni sufficienti. Tuttavia, la mappatura superficiale bidimensionale (2D) di esopianeti potenzialmente abitabili simili alla Terra è impegnativa a causa dell'influenza delle nuvole. I metodi di recupero delle mappe 2D sono stati sviluppati e testati utilizzando curve di luce simulate e^{spettri noti 5,6,7,8}, ma non sono stati applicati a osservazioni reali. Inoltre, nelle analisi delle osservazioni degli esopianeti ora e nel prossimo futuro, le ipotesi degli spettri caratteristici possono essere controverse quando le composizioni superficiali planetarie non sono ben vincolate.

In questo articolo, dimostriamo una tecnica di mappatura delle superfici per esopianeti simili alla Terra. Utilizziamo SVD per valutare e separare le informazioni da diverse fonti contenute in curve di luce multi-lunghezza d'onda senza ipotesi di spettri specifici. In combinazione con la geometria di visualizzazione, presentiamo la ricostruzione delle mappe di superficie utilizzando informazioni superficiali tempestivamente risolte ma contorte spazialmente. Allo scopo di dimostrare questo metodo, vengono analizzate le osservazioni a punto singolo a più lunghezze d'onda di due anni della Terra ottenute dal Deep Space Climate Observatory/Earth Polychromatic Imaging Camera (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html). Usiamo la Terra come esopianeta proxy per valutare questo metodo perché le osservazioni attualmente disponibili degli esopianeti non sono sufficienti. Alleghiamo il codice con la carta come esempio. È sviluppato sotto python 3.7 con pacchetti anaconda e healpy, ma la matematica del protocollo può essere fatta anche in altri ambienti di programmazione (ad esempio, IDL o MATLAB).

Protocollo

1. Configurazione della programmazione

1. Impostare l'ambiente di programmazione per il codice allegato. È necessario un computer con sistema operativo Linux, poiché il pacchetto healpy non è disponibile su Windows. Il codice non è computazalmente costoso, quindi un normale personal computer può gestire il protocollo.
2. Seguire le istruzioni (https://docs.anaconda.com/anaconda/install/linux/) per installare Anaconda con Python 3.7 nel sistema, quindi utilizzare i seguenti comandi nel terminale per configurare l'ambiente di programmazione:
   $ conda create --name myenv python=3.7
   $ conda attivare myenv
   $ conda installare anaconda
   $ conda installare healpy
   NOTA: questi passaggi possono richiedere decine di minuti a seconda dell'hardware e della velocità di Internet. Il nome dell'ambiente 'myenv' nelle prime due righe di comando può essere modificato in qualsiasi altra stringa.

2. Ottenere curve di luce a più lunghezze d'onda e visualizzare la geometria dalle osservazioni

1. Nella geometria di visualizzazione, includere la longitudine e la latitudine del sub-stellare e i punti sub-osservatori per ogni periodo di tempo corrispondente.
   Per utilizzare il codice allegato riportato di seguito, assicurarsi che questi due file abbiano lo stesso formato di LightCurve.csv e Geometry.csv.
2. Eseguire PlotTimeSeries.py per visualizzare i dati e verificarne le qualità. Verranno create due figure LightCurve.png e Geometry.png (Figura supplementare 1-2). I parametri in questo e seguendo i codici di plottaggio potrebbero dover essere regolati se applicati a osservazioni diverse.
   $ PlotTimeSeries.py LightCurve
   $ geometria PlotTimeSeries.py pitone

3. Estrarre le informazioni sulla superficie dalle curve di luce

1. Centra le curve di luce albedo multi-lunghezza d'onda risolte nel tempo di un esopianeta e normalizzale con la corrispondente deviazione standard ad ogni lunghezza d'onda. Ciò si traduce nell'uguale importanza di ogni canale.
   
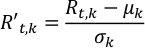
   dove_{R't,k e} R_{t,k sono} l'albedo scalato e osservato rispettivamente al passo del tempo t-esimo e la lunghezza d'onda k-esima; μ k_e σ_{k sono} la deviazione media e standard della serie di tempo di albedo alla lunghezza d'onda k-esima.
   1. Eseguire Normalize.py per normalizzare le curve di luce, R_t,k. L'output viene salvato in NormalizedLightCurve.csv.
      $ Normalize.py
2. Eseguire PlotTimeSeries.py per visualizzare le curve di luce normalizzate. Verrà creata una figura NormalizedLightCurve.png (Figura supplementare 3).
   $ python PlotTimeSeries.py NormalizedLightCurve
3. Applicare SVD sulle curve di luce albedo in scala per trovare PC dominanti e le relative serie temporali.
   
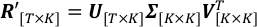
   Sul lato sinistro, T e K sono il numero totale di passi di tempo e lunghezze d'onda di osservazione; R' è la matrice delle osservazioni di albedo scalate, il cui (t,k)-esimo elemento è R'_t,k. Sul lato destro, le colonne di V sono PC, vettori ortonormali che definiscono i progetti SVD spaziali a; Σ è una matrice diagonale, il cui elemento (k,k)-esimo è la deviazione standard delle curve di luce scalata lungo l'asse k-esimo definito dalla colonna k-esima di V; colonne di U sono le corrispondenti serie temporali di ogni PC in V.
   1. Corri SingularValueDecomposition.py per decomporre R'. Gli U, Σ, V T^{risultanti vengono} salvati rispettivamente nei file di output U.csv, SingularValue.csv V_T.csv.
      $ SingularValueDecomposition.py
4. Utilizzare PlotTimeSeries.py e PlotSVD.py per visualizzare il risultato SVD. Verranno create .pngcifre U.png , Sigma.png e V_T.png (Figura supplementare 4-6).
   $ PlotTimeSeries.py U
   $ PlotSVD.py
5. Analizzare i contributi e le corrispondenti serie temporali di PC per determinare quello che contiene informazioni sulla superficie.
   1. Confrontare i valori singolari nella diagonale di Σ. Si prevede che un esopianeta parzialmente torbido simile alla Terra abbia due valori singolari dominanti comparabili.
      NOTA: Σ può contenere meno o più di due valori singolari dominanti, che sono discussi di seguito.
   2. Confrontare i modelli delle serie temporali dei due PC dominanti. Il PC che contiene informazioni sulla superficie tende ad avere una forma più regolare rispetto all'altro. A causa dell'asimmetria longitudinale e della ricomparsa della superficie con piccoli cambiamenti in due giorni consecutivi, le corrispondenti serie temporali tendono ad avere variazioni giornaliere approssimativamente costanti.
   3. Calcolare le periodicità dei due PC dominanti utilizzando il periodogramma Lomb-Scargle^9,10 per confermare la selezione del PC. Il PC che contiene informazioni sulla superficie tende ad avere un picco più elevato corrispondente al periodo di rotazione nello spettro di densità di potenza.
   4. Eseguire Periodogram.py per ottenere gli spettri di potenza delle serie temporali di ciascun PC. Gli spettri di potenza vengono salvati in Periodogram.csv.
      $ Periodogram.py
   5. Eseguire PlotPeriodogram.py per visualizzare questi parogrammi e confermare la selezione del PC. Verrà creata una .png periodogramma ( Figurasupplementare 7). L'attuale codice di plottaggio si aggiunge in linee tratteggiate che rappresentano cicli annuali, semestrali, diurni e semigiornali di riferimento, che potrebbero dover essere modificati se applicati ad altre osservazioni.
      $ PlotPeriodogram.py
   6. Selezionare il PC v_j, che contiene le informazioni sulla superficie e le relative serie temporali, u_j.
      
      
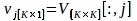
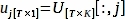
      dove V[:,j] e U[:,j] sono rispettivamente le colonne j-esima di V e U; j è l'indice del PC dedotto al passaggio 3.3 che contiene informazioni sulla superficie.

4. Costruisci una mappa di superficie planetaria

1. Utilizzate il metodo HEALPix (Hierarchical Equal Area iso-Latitude Pixelization)¹¹ per pixelare la mappa di recupero. Divide la superficie sferica di un pianeta in pixel con la stessa area e distribuzione uniforme. Indicare il valore sconosciuto del pixel p-esimo come x_p.
   1. Eseguire HEALPixRandom.py per visualizzare il metodo di pixelizzazione. Verrà creata una .png HEALPixRandom (Figura supplementare 8). Il parametro N_lato alla riga 17 può essere modificato per diverse risoluzioni. Questo passaggio può richiedere alcuni secondi o minuti a seconda della risoluzione.
      $ HEALPixRandom.py
2. Calcolare il peso del pixel p-esimo nelle osservazioni al passo del tempo t-esimo, w_t,p, utilizzando la geometria di visualizzazione.
   
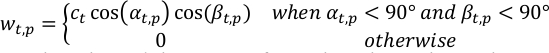
   dove α_t,p, β_{t,p sono} gli angoli solari e zenit della sonda al p-esimo pixel al passo del tempo t-esimo; c_t è un termine di normalizzazione dell'osservazione t-esima in modo che la somma del peso totale in ogni fase del tempo sia unità.
   NOTA: Si presume che la geometria sia nota in questo passaggio o possa essere derivata da altre analisi, che sono discusse di seguito.
   1. Eseguire ComputeWeight.py per calcolare w_t,p. Modificare il valore di N_lato alla riga 23 per altre risoluzioni della mappa recuperata. L'output viene salvato come W.npz a causa delle sue dimensioni.
      $ ComputeWeight.py
3. Utilizzare PlotWeight.py per visualizzare questi pesi. Un certo numero di figure, una alla volta, verranno create in una cartella Weight. Unendoli si traduce in Video supplementare 1, che mostra come cambia il peso di ogni pixel con il tempo. Il termine di questo passaggio potrebbe richiedere ore a causa dell'elevato numero di visualizzazioni.
   $ PlotWeight.py
4. Combina geometria e osservazioni per raggiungere un problema di regressione lineare.
   
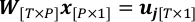
   dove P è il numero totale di pixel di recupero; W è la matrice di peso con w_t,p come elemento (t,p)-esimo; x è costituito da x_p come elemento p-esimo, che è la quantità da risolvere in questo problema.
   Risolvi il problema della regressione lineare con una regolarizzazione della norma L-2.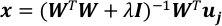
   
   dove I è la matrice identità e λ è il parametro di regolarizzazione.
   NOTA: 10^-3 è un buon valore per λ quando T~10⁴ e P~3*10³. Dovrebbero essere regolati confrontando i valori dei due termini nell'errore quadrato regolarizzato, e, come mostrato di seguito.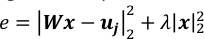
   
   1. Eseguire LinearRegression.py per risolvere questo problema di regressione lineare. Il risultato di x viene salvato nel file PixelValue.csv. Modificare il valore di λ alla riga 16 per diversi punti di forza della regolarizzazione.
      $ LinearRegression.py
5. Converti x in una mappa di superficie 2D in base alla regola di mappatura di HEALPix.
   1. Eseguire PlotMap.py per costruire le mappe recuperate utilizzando diversi parametri di regolarizzazione. Con l'impostazione corrente verranno create tre figure Map_-2.png , Map_-3.png e Map_-4.png conl'impostazionecorrente ( Figura supplementare 9 ). La relazione tra gli indici di pixel e le loro posizioni sulla mappa è descritta nel documento^{HEALPix 11}. Questo passaggio richiede decine di secondi.
      $ PolotMap.py

5. Stimare l'incertezza della mappa recuperata

1. Riscrivere il problema della regressione lineare al passaggio 4.3 con il "valore reale" di x come z e il rumore di osservazione, ε.
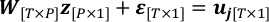
   1. Si ε di seguire una distribuzione gaussiana N (0, σ²I_[T*T]) e stimarne la covarianza. T-P è il grado di libertà di u_{j dall'osservazione} quando la mappa recuperata è fissa.
      
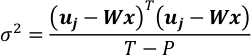
   2. Combinare le equazioni nei passaggio 4.4 e 5.1. Si traduce in un vettore gaussiano di x.
      
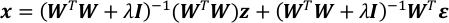
   3. Calcolare l'aspettativa e la matrice di covarianza di x.
      
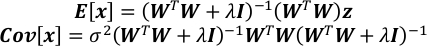
   4. Ottenere l'incertezza di ogni elemento in x come radice quadrata dell'elemento corrispondente sulla diagonale di Cov[x].
      
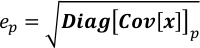
      dove e_{p è} l'incertezza di x_p; Diag[Cov[x]]_{p è} l'elemento p-esimo sulla diagonale di Cov[x].
   5. Eseguire Covariance.py per calcolare la matrice di covarianza di x. Il risultato viene salvato in Covariance.npz a causa delle sue dimensioni. Questo passaggio richiede da decine di secondi a minuti a seconda delle dimensioni di W.
      $ Covariance.py
2. Converti e_p nella mappa 2D recuperata in base alla regola di mappatura di HEALPix.
   1. Eseguire PlotCovariance.py per visualizzare Cov[ x ]emappare l'incertezza e_p alla mappa recuperata. Saranno create due cifre .png e incertezza.png (Figura supplementare 10-11).
      $ PlotCovariance.py

Risultati

Usiamo curve di luce a punto singolo multi-lunghezza d'onda della Terra per dimostrare il protocollo e confrontiamo i risultati con la verità del suolo per valutare la qualità della mappatura della superficie. L'osservazione qui usata è ottenuta da DSCOVR/EPIC, che è un satellite situato vicino al primo punto lagrangiano (L1) tra la Terra e il Sole che scatta immagini a dieci lunghezze d'onda della faccia illuminata dal sole della Terra. Due anni (2016 e 2017) di osservazioni sono utilizzati per questa dimostrazione,...

Discussione

Un requisito critico del protocollo è la fattibilità di estrarre informazioni sulla superficie dalle curve di luce, che dipende dalla copertura del cloud. Nel passaggio 3.5.1, i valori relativi dei PC possono essere diversi tra gli esopianeti. Nel caso della Terra, i primi due PC dominano le variazioni della curva di luce e corrispondono a nubi e superfici indipendenti dalla superficie (Fan et al. 2019)¹³. Hanno valori singolari comparabili in modo che le informazioni sulla superficie possano es...

Materiali

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.