Oberflächenkartierung erdähnlicher Exoplaneten mit Single-Point-Lichtkurven

Zusammenfassung

Das Protokoll extrahiert Informationen aus Lichtkurven von Exoplaneten und erstellt deren Oberflächenkarten. Es verwendet Lichtkurven der Erde, die als Proxy-Exoplanet dient, um den Ansatz zu demonstrieren.

Zusammenfassung

Die räumliche Auflösung von Exoplaneten-Features aus Einzelpunktbeobachtungen ist für die Bewertung der potenziellen Bewohnbarkeit von Exoplaneten von entscheidender Bedeutung. Das ultimative Ziel dieses Protokolls ist es, festzustellen, ob diese Planetenwelten geologische Merkmale und/oder Klimasysteme aufweisen. Wir stellen eine Methode zum Extrahieren von Informationen aus Mehrwellenlängen-Einpunktlichtkurven und zum Abrufen von Oberflächenkarten vor. Es verwendet Singular Value Decomposition (SVD), um Quellen zu trennen, die zu Lichtkurvenschwankungen beitragen und die Existenz von teilweise trüben Klimasystemen ableiten. Durch die Analyse der von SVD erhaltenen Zeitreihen konnten physikalische Zuschreibungen von Hauptkomponenten (PCs) ohne Annahmen von Spektraleigenschaften abgeleitet werden. In Kombination mit der Anzeigegeometrie ist es möglich, Oberflächenkarten zu rekonstruieren, wenn einer der PCs Oberflächeninformationen enthält. Die Degenerität entstand aus der Faltung der Pixelgeometrie und Spektruminformationen bestimmt die Qualität rekonstruierter Oberflächenkarten, was die Einführung einer Regularisierung erfordert. Zur Demonstration des Protokolls werden mehrwellige Lichtkurven der Erde, die als Proxy-Exoplanet dient, analysiert. Ein Vergleich zwischen den Ergebnissen und der Bodenwahrheit wird präsentiert, um die Leistung und Einschränkung des Protokolls zu zeigen. Diese Arbeit bietet einen Maßstab für die zukünftige Verallgemeinerung von Exoplanetenanwendungen.

Einleitung

Das Identifizieren bewohnbarer Welten ist eines der ultimativen Ziele in der Astrobiologie¹. Seit der ersten Detektion²wurden bisher mehr als 4000 Exoplaneten³ mit einer Reihe von Erdanalogen (z.B. TRAPPIST-1e)⁴bestätigt. Diese Planeten haben orbitale und planetare Eigenschaften, die denen der Erde ähneln, und sind daher potenziell bewohnbar. Die Bewertung ihrer Bewohnbarkeit anhand begrenzter Beobachtungen ist in diesem Zusammenhang von wesentlicher Bedeutung. Basierend auf dem Wissen über das Leben auf der Erde sind geologische und Klimasysteme entscheidend für die Bewohnbarkeit, die daher als Biosignaturen dienen können. Prinzipiell könnten Merkmale dieser Systeme aus der Ferne beobachtet werden, selbst wenn ein Planet nicht räumlich besser gelöst werden könnte als ein einziger Punkt. In diesem Fall ist die Identifizierung geologischer Merkmale und Klimasysteme aus Einpunktlichtkurven bei der Beurteilung der Bewohnbarkeit von Exoplaneten von entscheidender Bedeutung. Die Oberflächenkartierung dieser Exoplaneten wird dringend.

Trotz der Faltung zwischen Betrachtungsgeometrie und spektralen Merkmalen sind Informationen über die Oberfläche eines Exoplaneten in seinen zeitaufgelösten Einpunktlichtkurven enthalten, die aus einer Entfernung erhalten und mit ausreichenden Beobachtungen abgeleitet werden können. Die zweidimensionale (2D) Oberflächenkartierung potenziell bewohnbarer erdähnlicher Exoplaneten ist jedoch aufgrund des Einflusses von Wolken eine Herausforderung. Methoden zum Abrufen von 2D-Karten wurden mit simulierten Lichtkurven und bekannten Spektren^5,6,7,8, getestet, aber sie wurden nicht auf reale Beobachtungen angewendet. Darüber hinaus können bei den Analysen von Exoplanetenbeobachtungen jetzt und in naher Zukunft Annahmen von charakteristischen Spektren kontrovers sein, wenn die planetarischen Oberflächenzusammensetzungen nicht gut eingeschränkt sind.

In diesem Beitrag zeigen wir eine Oberflächenkartierungstechnik für erdähnliche Exoplaneten. Wir verwenden SVD, um Informationen aus verschiedenen Quellen auszuwerten und zu trennen, die in Lichtkurven mit mehreren Wellenlängen enthalten sind, ohne dass bestimmte Spektren angenommen werden. In Kombination mit der Betrachtungsgeometrie präsentieren wir die Rekonstruktion von Oberflächenkarten mit zeitnah aufgelösten, aber räumlich verworrenen Oberflächeninformationen. Zum Nachweis dieser Methode werden zweijährige mehrwellige Einpunktbeobachtungen der Erde analysiert, die von der Deep Space Climate Observatory/Earth Polychromatic Imaging Camera (DSCOVR/EPIC; www.nesdis.noaa.gov/DSCOVR/spacecraft.html) erhalten wurden. Wir verwenden die Erde als Proxy-Exoplaneten, um diese Methode zu bewerten, da derzeit verfügbare Beobachtungen von Exoplaneten nicht ausreichen. Als Beispiel fügen wir den Code dem Papier bei. Es wird unter Python 3.7 mit Anaconda- und Healpy-Paketen entwickelt, aber die Mathematik des Protokolls kann auch in anderen Programmierumgebungen (z.B. IDL oder MATLAB) durchgeführt werden.

Protokoll

1. Programmier-Setup

1. Richten Sie die Programmierumgebung für den angefügten Code ein. Ein Computer mit Linux-Betriebssystem ist erforderlich, da das healpy-Paket unter Windows nicht verfügbar ist. Der Code ist nicht rechnerisch teuer, so dass ein normaler PC das Protokoll verarbeiten kann.
2. Befolgen Sie die Anweisung (https://docs.anaconda.com/anaconda/install/linux/), an Anaconda mit Python 3.7 auf dem System zu installieren, und verwenden Sie dann die folgenden Befehle im Terminal, um die Programmierumgebung einzurichten:
   - conda erstellen --name myenv python=3.7
   • conda aktivieren myenv
   • conda install anaconda
   • conda install healpy
   HINWEIS: Diese Schritte können je nach Hardware und Internetgeschwindigkeit zig Minuten dauern. Der Umgebungsname 'myenv' in den ersten beiden Befehlszeilen kann in eine andere Zeichenfolge geändert werden.

2. Abrufen von Mehrwellenlängen-Lichtkurven und Betrachtungsgeometrie aus Beobachtungen

1. Fügen Sie in die Betrachtungsgeometrie den Längen- und Breitengrad des Substellars und die Unterbeobachterpunkte für jeden entsprechenden Zeitrahmen ein.
   Um den folgenden angefügten Code zu verwenden, stellen Sie sicher, dass diese beiden Dateien das gleiche Format wie LightCurve.csv und Geometry.csvhaben.
2. Führen Sie PlotTimeSeries.py aus, um die Daten zu visualisieren und ihre Qualitäten zu überprüfen. Es werden zwei Figuren LightCurve.png und Geometry.png erstellt (Ergänzungsfigur 1-2). Parameter in diesem und folgenden Plotcodes müssen möglicherweise angepasst werden, wenn sie auf verschiedene Beobachtungen angewendet werden.
   • Python PlotTimeSeries.py LightCurve
   • Python-PlotTimeSeries.py Geometrie

3. Oberflächeninformationen aus Lichtkurven extrahieren

1. Zentrieren Sie zeitaufgelöste Albedo-Lichtkurven mit mehreren Wellenlängen eines Exoplaneten und normalisieren sie durch entsprechende Standardabweichung bei jeder Wellenlänge. Dies führt zu der gleichen Bedeutung jedes Kanals.
   
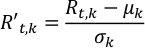
   wobei R'_t,k und R_t,k die skalierte und beobachtete Albedo beim t-ten Zeitschritt bzw. der k-ten Wellenlänge sind; μ_k und σ_k sind die Mittelwert- und Standardabweichung der Albedo-Zeitreihen bei der k-ten Wellenlänge.
   1. Führen Sie Normalize.py aus, um die Lichtkurven zu normalisieren, R_t,k. Der Ausgang wird in NormalizedLightCurvegespeichert.csvgespeichert.
      • Python-Normalize.py
2. Führen Sie PlotTimeSeries.py aus, um die normalisierten Lichtkurven zu visualisieren. Eine Figur NormalizedLightCurve.png wird erstellt (Ergänzungsabbildung 3).
   Python PlotTimeSeries.py NormalizedLightCurve
3. Tragen Sie SVD auf die skalierten Albedo-Lichtkurven auf, um dominante PCs und deren entsprechende Zeitreihen zu finden.
   
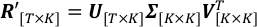
   Auf der linken Seite sind T und K die Gesamtzahl der Zeitschritte und Beobachtungswellenlängen; R' ist die Matrix der skalierten Albedo-Beobachtungen, deren (t,k)-d.M. Element R'_t,kist. Auf der rechten Seite sind Spalten von V PCs, orthonormale Vektoren, die den Raum definieren, auf den SVD-Projekte angewendet werden. - ist eine diagonale Matrix, deren (k,k)-stes Element die Standardabweichung von skalierten Lichtkurven entlang der k-ten Achse ist, die durch die k-te Spalte von Vdefiniert wird; Spalten von U sind die entsprechenden Zeitreihen jedes PCs in V.
   1. Führen Sie SingularValueDecomposition.py aus, um R' zu zersetzen. Die resultierenden U, , , V^T werden in den Ausgabedateien U.csv, SingularValue.csv bzw. V_T.csvgespeichert.
      • Python-SingularValueDecomposition.py
4. Verwenden Sie PlotTimeSeries.py und PlotSVD.py, um das SVD-Ergebnis zu visualisieren. Es werden die drei Figuren U.png, Sigma.png und V_T.png erstellt (Zusatzfigur 4-6).
   $ Python PlotTimeSeries.py U
   • Python-PlotSVD.py
5. Analysieren Sie Beiträge und entsprechende Zeitreihen von PCs, um diejenige zu ermitteln, die Oberflächeninformationen enthält.
   1. Vergleichen Sie die Singularwerte in der Diagonale von . Es wird erwartet, dass ein erdähnlicher, teils bewölkter Exoplanet zwei vergleichbare dominante Singularwerte hat.
      ANMERKUNG: Die Werte können weniger oder mehr als zwei dominante Singularwerte enthalten, die im Folgenden erläutert werden.
   2. Vergleichen Sie die Zeitreihenmuster der beiden dominanten PCs. Der PC, der Oberflächeninformationen enthält, hat tendenziell eine normalere Form als der andere. Aufgrund der Längsasymmetrie und des Wiedererscheinens der Oberfläche mit kleinen Veränderungen an zwei aufeinanderfolgenden Tagen neigt die entsprechende Zeitreihe dazu, ungefähr konstante tägliche Schwankungen zu aufweisen.
   3. Berechnen Sie die Periodizitäten der beiden dominanten PCs mit Lomb-Scargle Periodogramm^9,10, um die Auswahl des PCs zu bestätigen. Der PC, der Oberflächeninformationen enthält, neigt dazu, einen höheren Spitzenwert zu haben, der der Rotationsperiode im Leistungsdichtespektrum entspricht.
   4. Führen Sie Periodogram.py aus, um die Leistungsspektren der Zeitreihen jedes PCs zu erhalten. Die Leistungsspektren werden in Periodogrammgespeichert.csvgespeichert.
      • Python-Periodogram.py
   5. Führen Sie PlotPeriodogram.py aus, um diese Parodogramme zu visualisieren und die PC-Auswahl zu bestätigen. Eine Figur Periodogramm.png wird erstellt (Ergänzungsfigur 7). Der aktuelle Plotcode fügt gestrichelte Zeilen hinzu, die jährliche, halbjährliche, tagestägliche und halbtägliche Zyklen als Referenz darstellen, die möglicherweise geändert werden müssen, wenn sie auf andere Beobachtungen angewendet werden.
      • Python-PlotPeriodogram.py
   6. Wählen Sie den PC, v_j, der Oberflächeninformationen und seine Zeitreihen enthält, u_j.
      
      
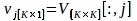
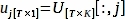
      wobei V[:,j] und U[:,j] die j-ten Spalten von V bzw. Usind; j ist der INDEX des PCs, der in Schritt 3.3 abgeleitet wird und Oberflächeninformationen enthält.

4. Konstruieren Sie eine planetare Oberflächenkarte

1. Verwenden Sie die Hierarchical Equal Area iso-Latitude Pixelization (HEALPix)^11-Methode, um die Abrufkarte zu verpixeln. Es teilt die kugelförmige Oberfläche eines Planeten in Pixel mit der gleichen Fläche und gleichmäßiger Verteilung. Bezeichnen Sie den unbekannten Wert des p-ten Pixels als x_p.
   1. Führen Sie HEALPixRandom.py aus, um die Pixelisierungsmethode zu visualisieren. Eine Figur HEALPixRandom.png wird erstellt (Ergänzungsfigur 8). Der Parameter_N-Seite an Zeile 17 kann für unterschiedliche Auflösungen geändert werden. Dieser Schritt kann je nach Auflösung einige Sekunden bis Minuten dauern.
      • Python-HEALPixRandom.py
2. Berechnen Sie die Gewichtung des p-ten Pixels in Beobachtungen beim t-ten Zeitschritt, w_t,p, mithilfe der Anzeigegeometrie.
   
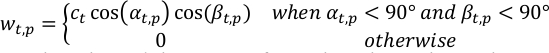
   wobei α_t,p, β_t,p sind die Solar und die Raumsonde ZenitWinkel am p-ten Pixel bei der t-ten Zeit Schritt; c_t ist ein Normalisierungsbegriff der t-ten Beobachtung, so dass die Summe des Gesamtgewichts bei jedem Zeitschritt Einheit ist.
   HINWEIS: Es wird angenommen, dass Geometrie in diesem Schritt bekannt ist oder aus anderen Analysen abgeleitet werden kann, die im Folgenden erläutert werden.
   1. Führen Sie ComputeWeight.py aus, um w_t,pzu berechnen. Ändern Sie den Wert von_N-Seite in Zeile 23 für andere Auflösungen der abgerufenen Karte. Die Ausgabe wird aufgrund ihrer Größe als W.npz gespeichert.
      • Python-ComputeWeight.py
3. Verwenden Sie PlotWeight.py, um diese Gewichtungen zu visualisieren. Eine Reihe von Zahlen, eine zu jedem Zeitschritt, wird in einem Ordner Weighterstellt. Durch das Zusammenführen führt das Ergebnis in Supplemental Video 1, das zeigt, wie sich das Gewicht jedes Pixels mit der Zeit ändert. Dieser Schritt kann aufgrund der großen Anzahl von Visualisierungen Stunden dauern.
   • Python-PlotWeight.py
4. Kombinieren Sie Geometrie und Beobachtungen, um ein lineares Regressionsproblem zu erreichen.
   
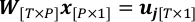
   wobei P die Gesamtzahl der abzurufenden Pixel ist; W ist die Gewichtsmatrix mit w_t,p als (t,p)-th-Element; x besteht aus x_p als p-th-Element, das die Menge ist, die in diesem Problem gelöst werden soll.
   Lösen Sie das problem der linearen Regression mit einer Regularisierung der L-2-Norm.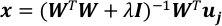
   
   wobei ich die Identitätsmatrix und der Regularisierungsparameter ist.
   ANMERKUNG: 10^-3 ist ein guter Wert für , wenn T-10⁴ und P 3 * 10³. Sie sollten durch einen Vergleich der Werte der beiden Begriffe im regularisierten Quadratischefehler e, wie unten gezeigt, angepasst werden.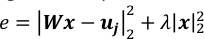
   
   1. Führen Sie LinearRegression.py aus, um dieses problem der linearen Regression zu lösen. Das Ergebnis von x wird in der Datei PixelValue.csvgespeichert. Ändern Sie den Wert von - in Zeile 16 für verschiedene Stärken der Regularisierung.
      • Python-LinearRegression.py
5. Konvertieren Sie x in eine 2D-Oberflächenkarte gemäß der Mapping-Regel von HEALPix.
   1. Führen Sie PlotMap.py aus, um die abgerufenen Karten mit verschiedenen Regularisierungsparametern zu erstellen. Mit der aktuellen Einstellungwerdendrei Zahlen Map_-2.png, Map_-3.png und Map_-4erstellt.png erstellt. Die Beziehung zwischen den Pixelindizes und ihren Positionen auf der Karte wird im HEALPix-Dokument¹¹beschrieben. Dieser Schritt dauert zig Sekunden.
      • Python-PolotMap.py

5. Schätzung der Unsicherheit der abgerufenen Karte

1. Schreiben Sie das lineare Regressionsproblem in Schritt 4.3 mit dem "wahren Wert" von x als z und dem Beobachtungsrauschen εum.
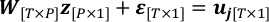
   1. Nehmen wir an ε einer Gaußschen Verteilung N (0, σ²I_[T*T]) zu folgen und deren Kovarianz zu schätzen. T-P ist der Grad der Freiheit von u_j von der Beobachtung, wenn die abgerufene Karte fixiert ist.
      
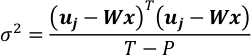
   2. Kombinieren Sie Gleichungen in Schritt 4.4 und 5.1. Es ergibt sich ein Gauß-Vektor von x.
      
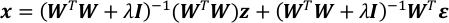
   3. Berechnen Sie die Erwartung und die Kovarianzmatrix von x.
      
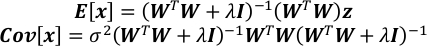
   4. Erhalten Sie die Unsicherheit jedes Elements in x als Quadratwurzel des entsprechenden Elements auf der Diagonale von Cov[x].
      
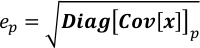
      wobei e_p die Ungewissheit von x_pist; Diag[Cov[x]]_p ist p-th Element auf der Diagonale von Cov[x].
   5. Führen Sie Covariance.py aus, um die Kovarianzmatrix von xzu berechnen. Das Ergebnis wird aufgrund seiner Größe in Covariance.npz gespeichert. Dieser Schritt dauert je nach Größe von Wzig Sekunden bis Minuten.
      $ Python-Covariance.py
2. Konvertieren Sie e_p in die abgerufene 2D-Karte gemäß der Mapping-Regel von HEALPix.
   1. Führen Sie PlotCovariance.py aus, um Cov[x] zu visualisieren und die Unsicherheit e_p der abgerufenen Karte zuzuordnen. Es werden zwei Zahlen Kovarianz.png und Ungewissheit.png erstellt (Zusatzfigur 10-11).
      • Python-PlotCovariance.py

Ergebnisse

Wir verwenden mehrwellige Einpunktlichtkurven der Erde, um das Protokoll zu demonstrieren, und vergleichen die Ergebnisse mit der Bodenwahrheit, um die Qualität der Oberflächenkartierung zu bewerten. Die hier verwendete Beobachtung wird von DSCOVR/EPIC erhalten, einem Satelliten, der sich in der Nähe des ersten lagrangischen Punktes (L1) zwischen Erde und Sonne befindet und Bilder mit zehn Wellenlängen der sonnenbeschienenen Erdoberfläche macht. Zwei Jahre (2016 und 2017) von Beobachtungen werden für diese Demonstr...

Diskussion

Eine wichtige Anforderung des Protokolls ist die Machbarkeit der Extraktion von Oberflächeninformationen aus Lichtkurven, die von der Wolkenabdeckung abhängen. In Schritt 3.5.1 können die relativen Werte der PCs zwischen Exoplaneten unterschiedlich sein. Im Falle der Erde dominieren die ersten beiden PCs die Lichtkurvenvariationen und entsprechen oberflächenunabhängigen Wolken und Oberfläche (Fan et al. 2019)¹³. Sie haben vergleichbare Singularwerte, so dass die Oberflächeninformationen nac...

Materialien

Name	Company	Catalog Number	Comments
Python 3.7 with anaconda and healpy packages			Other programming environments (e.g., IDL or MATLAB) also work.