La méthode Evans

Source : Tamara M. Powers, département de chimie, Texas A & M University

Alors que les molécules organiques plus sont diamagnétiques, dans lequel tous leurs électrons sont jumelés dans des obligations, plusieurs complexes de métaux de transition sont paramagnétiques, qui a haché déclare avec des électrons non appariés. Rappelons la règle de Hund, qui stipule que pour les orbitales des énergies similaires, électrons comblera les orbitales pour maximiser le nombre d’électrons non appariés avant appariement vers le haut. Métaux de transition ont rempli partiellement d-orbitales dont les énergies sont perturbées à des degrés divers par la coordination des ligands au métal. Ainsi, le d-orbitales sont similaires en énergie à un autre, mais ne sont pas tous les dégénérés. Cela permet des complexes pour être diamagnétique, avec tous les électrons jumelés ou paramagnétique, avec des électrons non appariés.

Connaître le nombre d’électrons non appariés dans un complexe métallique peut fournir des indices dans l’état d’oxydation et la géométrie du métal complexe, ainsi que dans l’intensité des ligands de ligand champ (champ cristallin). Ces propriétés grandement influer la spectroscopie et la réactivité des complexes de métaux de transition et sont donc importantes de comprendre.

Compter le nombre d’électrons non appariés consiste à mesurer la susceptibilité magnétique χ, le composé de coordination. Susceptibilité magnétique est la mesure de l’aimantation d’un matériau (ou composé) quand placé dans un champ magnétique appliqué. Les électrons appariés sont légèrement repoussés par un champ magnétique appliqué, et cette répulsion augmente linéairement comme étant l’intensité du champ magnétique augmente. En revanche, sont attirés par les électrons non appariés (dans une mesure plus grande) à un champ magnétique, et l’attraction augmente linéairement avec l’intensité du champ magnétique. Par conséquent, tout composé avec des électrons non appariés est attirés par un champ magnétique. ¹

Quand nous mesurons la susceptibilité magnétique, nous obtenons des renseignements sur le nombre d’électrons non appariés du moment magnétique, µ. La susceptibilité magnétique est liée au moment magnétique, µ par équation 1²:

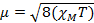(1)

La constante 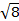= [(3k_B) / Nβ²)], où β = magnéton de Bohr de l’électron (0,93 x 10^-20 erg gauss^-1), N = nombre d’Avogadro et k_B = constante de Boltzmann
X_M = molaire susceptibilité magnétique (cm3/mole/sec)
T = température (K)
µ = moment magnétique, mesuré en unités de magnéton de Bohr, µ_B = 9,27 x 10^-24 JT^-1

Le moment magnétique des complexes est donné par l’équation 2¹:

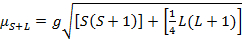(2)

g = facteur de Landé = µ 2.00023_B
S = nombre quantique de spin = ∑m_s = [nombre d’électrons non appariés, n] / 2
L = nombre quantique orbital = ∑m_l

Cette équation a des contributions orbitale et de spin. Des complexes de métaux de transition de première ligne, la contribution orbitale est petite et donc peut être omise, alors le moment magnétique de spin seule est donné par équation 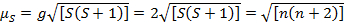3 :

(3)

Le moment magnétique de spin seule peut donner ainsi directement le nombre d’électrons non appariés. Cette approximation est également pour les métaux lourds, bien que les contributions orbitales peuvent être importantes pour les métaux de transition de deuxième et troisième rangées. Cette contribution peut être tellement importante qu’il gonfle le moment magnétique assez que le composé semble ont impair plus d’électrons qu’il fait. Par conséquent, une caractérisation plus poussée peut être nécessaire pour ces complexes.

Dans cette expérience, la solution du moment magnétique de tris(acetylacetonato)iron(III) (Fe(acac)₃) est déterminé expérimentalement en utilisant la méthode Evans dans le chloroforme.

Il existe de nombreuses méthodes pour mesurer la susceptibilité magnétique. À la fin du 19^ème siècle, Louis Georges Gouy a développé le solde de Gouy, qui est une méthode très précise pour mesurer la susceptibilité magnétique. Dans cette approche, une balance analytique est utilisée pour masse un aimant et le changement dans la masse observée à placer un échantillon paramagnétique entre les pôles de l’aimant est lié à la susceptibilité magnétique. Cette méthode n’est pas pratique, en suspendant l’échantillon entre les pôles de l’aimant n’est pas négligeable. Cela nécessite quatre mesures de masse entre qui l’aimant ne peut pas bouger et des échantillons d’air sensible, cette mesure doit être réalisée dans une boîte à gants. Les soldes de susceptibilité magnétique plus modernes sont disponibles, mais cela nécessite l’achat d’un tel équilibre.

Une autre méthode consiste à utiliser un magnétomètre SQUID (supraconducteurs Quantum Interference Device). Cela nécessite plusieurs mg d’échantillon solide et à moins que les autres mesures magnétiques sont à effectuer sur l’échantillon, n’est pas pratique ni rentable pour les complexes paramagnétiques qui peuvent être transformés en solutions.

Enfin, et ce qui sera démontré ici, est l’utilisation d’un spectromètre RMN pour mesurer la susceptibilité magnétique. Cette approche a été développée par Dennis Evans en 1959. Il est simple et repose sur l’effet une existence en solution sur le déplacement chimique d’un composé de référence, généralement le solvant. Collecte des données peut se faire sur un spectromètre RMN, les données sont faciles à interpréter, et préparation des échantillons est simple et nécessite peu de matériel. Il est devenu la méthode standard pour obtenir des données de susceptibilité magnétique des complexes inorganiques.

La mesure de la susceptibilité magnétique par la méthode Evans s’appuie sur le fait que les électrons non appariés de l’existence en solution seront traduira par un changement du déplacement chimique de toutes les espèces en solution (Figure 1). Ainsi, en notant la différence de déplacement chimique d’une molécule de solvant en présence et en absence d’une espèce paramagnétique, la susceptibilité magnétique peut être obtenue via l' équation 4 (pour un spectromètre RMN de champ élevé)³

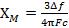(4)

Δf = différence de fréquence en Hz entre la résonance décalée et la résonance de solvant pure
F = spectromètre radiofréquence en Hz
c = concentration des espèces paramagnétiques (mol/mL)

Données sont facilement obtenues en recueillant un spectre de RMN H ¹d’un échantillon qui contient un capillaire du solvant pur, avec une solution de l’existence qui entourent le capillaire dans le tube de NMR (Figure 2).

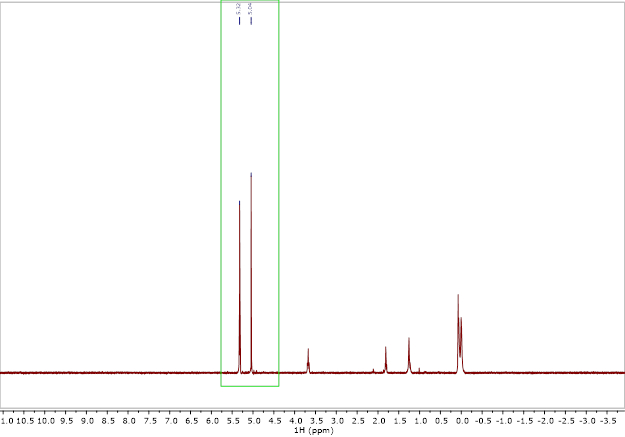
Figure 1. Exemple ¹H RMN spectre de l’expérience

Figure 2. Image d’un capillaire dans la configuration du tube NMR

1. préparation de l’Insert capillaire

1. À l’aide d’une flamme de briquet ou d’autres gaz, faire fondre l’embout de la pipette Pasteur longue. Tourner délicatement l’embout de la pipette dans la flamme jusqu'à une petite ampoule. Laissez le verre refroidir.
2. Dans un flacon à scintillation, préparer une solution de 50 : 1 (volume) de deutéré : proteo chloroforme. Pipette de 2 mL de solvant deutéré et à cela ajouter 40 µL de solvant proteo. Boucher le flacon.
3. Ajouter avec précaution quelques gouttes du mélange solvant à la pipette de verre scellé. Doucement effleurer l’embout de la pipette scellée afin que le liquide pénètre dans le tube capillaire. Répétez jusqu'à ce que la solution a une profondeur de ~ 2 pouces du fond du capillaire. Assurez-vous qu’il n’y a pas de bulles d’air.
4. Cap de la pipette avec un septum en caoutchouc 14/20. À l’aide d’une seringue de 3 mL, coiffée d’une aiguille, introduire l’aiguille dans la pipette et retirer 3 mL d’air. Cela crée un vide partiel, faciliter l’étape suivante.
5. Sceller la partie supérieure du capillaire. Horizontalement, pince la pipette à un support de bague. Utilisez un briquet pour ramollir le verre au-dessus de la solution dans le fond de la pipette. Une fois que le verre se ramollit, commencent à tourner l’embout de la pipette et tirez sur l’extrémité de la pipette de la base fixée. Laissez le refroidir capillaire scellé.

2. préparation de la Solution paramagnétique

1. À l’aide d’une balance analytique, la masse un flacon à scintillation et le couvercle. Noter la masse.
2. Masse sortir 5-10 mg du Fe(acac)₃ dans le flacon à scintillation et noter la masse. Fe(acac)₃ a un moment magnétique de solution très élevé. 5-10 mg génère donc un grand changement du déplacement chimique. En règle générale, 10-15 mg est une masse plus appropriée à utiliser pour les échantillons de méthode Evans.
3. Pipetter ~ 600 µL du mélange solvant préparé dans le flacon contenant les espèces paramagnétiques. Boucher le flacon et notez la masse. Assurez-vous que le solide se dissout complètement.

3. préparation de l’échantillon de la RMN

1. Dans un tube standard de NMR, soigneusement déposer l’insert capillaire à un angle, pour s’en assurer qu'il ne rompt pas il.
2. Pipetter dans la solution contenant l’espèce paramagnétique.
3. Capuchon du tube de NMR. Pour les échantillons d’air sensible, envelopper Parafilm autour du bouchon.

4. collecte des données

1. Acquérir et conserver un spectre de RMN H standard ¹.
2. Noter la température de la sonde.
3. Notez la radiofréquence.

5. résultats et analyse de données

1. À l’aide de la masse et la densité du solvant, calculer le volume du solvant utilisé pour préparer la solution paramagnétique.
2. Calculer la concentration (M) de la solution paramagnétique.
3. Calculer la séparation de la crête de la résonance du solvant entre celui du solvant pur (dans le capillaire) et celui décalé de l’existence (en dehors du capillaire) (Δ_ppm). Si cela est fait en ppm, convertissez-la en Hz par équation 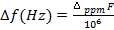5:
   (5)
   F = spectromètre radiofréquence en Hz
4. Calculer la susceptibilité magnétique utilisant l’équation 4.
5. Calculer le moment magnétique à l’aide de l’équation 1.
6. Comparer le moment magnétique obtenu avec celle prédite pour n électrons non appariés de l’équation 3. La susceptibilité magnétique sera légèrement supérieure à la valeur prévue de spin seulement indiquée dans le tableau, mais doit être inférieure à celle qui correspond à n + 1 électrons non appariés.
7. Donner le nombre d’électrons non appariés pour les espèces paramagnétiques.

6. problèmes et solutions

1. Si deux pics de solvants bien résolues ne s’observent pas, essayez ce qui suit :
   1. Utiliser un spectromètre avec une intensité de champ supérieure pour augmenter la différence de déplacement chimique (en ppm) des deux sommets.
   2. Faire l’échantillon plus concentré, afin que le changement est plus grand.
2. Parfois la valeur n’a aucun sens. Si on obtient une valeur qui est trop faible, essayez ce qui suit :
   1. Répéter, prendre un plus grand soin dans sa masse sur l’espèce de solvant et paramagnétique.
   2. S’assurer que l’espèce paramagnétique utilisé est pur. Même solvants impuretés dans les cristaux aura une incidence sur la masse et donc concentration.
   3. Pour les grosses molécules, le diamagnétisme peut être tellement important qu’il faut une correction diamagnétique. Ce terme est soustraite aux équation 4 :
      
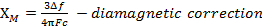
3. Parfois la valeur n’a aucun sens. Si on obtient une valeur qui est trop élevée, essayez ce qui suit :
   1. Suivez les mêmes étapes comme 6.2.1-6.2.3.
   2. Pour les métaux lourds, des contributions orbitales peut être nécessaire.

7. air-sensible des échantillons

1. Air échantillons peuvent facilement être analysés en utilisant cette technique. Mesures 1.2 à 1.4, étapes 2 et 3 sont simplement effectuées à l’intérieur d’une boîte à gants.

E xperimental résultats

	Fe(acac)3	Chloroforme
m (g)	0.0051	0,874
MW (g/mol)	353.17	n/a
n (mol)	1.44⋅10-5	n/a
Densité (g/mL)	n/a	1.49*
Volume (mL)	n/a	0,587
c (mol/mL)	2.45⋅10-5
Déplacements en RMN	PIC 1	PIC 2
Δ (ppm)	7.26	5,85
Δppm	1.41
Instrument de la RMN
Température (K)	296,3
Champ, F (Hz)	500⋅106

* la densité du solvant peut être approchée de la densité du solvant utilisé

Calculs :

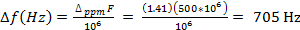
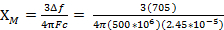= 0,0137 cm3/mole/sec
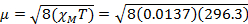₌ 5.70 µ _B

Donne des résultats théoriques pour S et valeurs de n :

S	n	Μ S
1/2	1	1,73
1	2	2,83
3/2	3	3,87
2	4	4.90
5/2	5	5.92

Pour 4,5 mg de Fe(acac)₃ dissous dans un solvant 0,58 mL, avec un instrument de 300 MHz, on observe une séparation maximale de 1,41 ppm, qui donne X_M= 1,37 x 10^-2 et µ_eff = 5.70. Cette valeur de_FEP µ est compatible avec un S = 5/2 complex, qui possède 5 électrons non appariés.

La méthode Evans est une méthode simple et pratique pour l’obtention de la susceptibilité magnétique des complexes métalliques solubles. Ceci fournit le nombre d’électrons non appariés dans un métal complex, qui est pertinent à la spectroscopie, propriétés magnétiques et la réactivité du complexe.

Mesurer la susceptibilité magnétique des espèces paramagnétiques donne le nombre d’électrons non appariés, qui est une propriété de clé de complexes métalliques. Comme la réactivité des complexes de métaux est influencée par sa structure électronique - autrement dit, comment les orbitales d sont remplies - il est important d’établir le nombre d’électrons non appariés. La susceptibilité magnétique peut être utilisée pour déterminer la géométrie du métal complexe en solution, donner un aperçu de l’intensité de champ de ligand et peut fournir des preuves pour l’affectation formelle correcte d’état d’oxydation du métal complexe. Dans les modules sur la « Théorie des groupes » et « Théorie MO de Complexes de métaux de Transition », nous allons introduire comment prévoir les orbitales d Division diagrammes ainsi que la façon d’utiliser les données de la méthode Evans pour aider à déterminer la géométrie d’une complexe de métal et de fournir des preuves pour le État d’oxydation du centre métallique.

Il existe plusieurs instruments qui peuvent être utilisés pour mesurer la susceptibilité magnétique d’une espèce paramagnétique, y compris un équilibre de Gouy, calmar, ou instrument de NMR. La méthode Evans est une technique simple et pratique qui utilise NMR pour déterminer le moment magnétique de solution d’une existence. Alors que la méthode Evans est un outil puissant dans le domaine du magnétisme, il y a plusieurs inconvénients à la technique. Tout d’abord, la molécule doit être soluble dans le solvant utilisé dans l’expérience. Si l’échantillon paramagnétique n’est pas entièrement dissous, la concentration de la solution sera incorrecte, qui aboutiront à des erreurs dans le moment magnétique de solution déterminée expérimentalement. Autres erreurs de concentration peuvent survenir si l’échantillon paramagnétique est diamagnétique (solvant) ou impuretés paramagnétiques.