Source : Faisal Alamgir, School of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA

La diffraction des rayons X (XRD) est une technique utilisée dans la science des matériaux pour déterminer la structure atomique et moléculaire d'un matériau. Pour ce faire, on irradie un échantillon du matériau avec des rayons X incident, puis en mesurant les intensités et les angles de diffusion des rayons X qui sont dispersés par le matériau. L'intensité des rayons X dispersés est tracée en fonction de l'angle de diffusion, et la structure du matériau est déterminée à partir de l'analyse de l'emplacement, en angle, et les intensités des pics d'intensité dispersés. Au-delà de la mesure des positions moyennes des atomes dans le cristal, des informations sur la façon dont la structure réelle s'écarte de l'idéal, résultant par exemple d'un stress interne ou de défauts, peuvent être déterminées.

La diffraction des rayons X, qui est au cœur de la méthode XRD, est un sous-ensemble des phénomènes généraux de diffusion des rayons X. XRD, qui est généralement utilisé pour signifier peut grand angle diffraction des rayons X (WAXD), tombe sous plusieurs méthodes qui utilisent les ondes élastiquement dispersés rayons X. D'autres techniques de diffusion élastique basées sur la radiographie comprennent la diffusion à faible angle des rayons X (SAXS), où les rayons X sont des incidents sur l'échantillon sur la petite plage angulaire de 0,1-10⁰ généralement). SAXS mesure les corrélations structurelles de l'échelle de plusieurs nanomètres ou plus (comme les superstructures de cristaux), et la réflectivité des rayons X qui mesure l'épaisseur, la rugosité et la densité des couches minces. WAXD couvre une gamme angulaire au-delà de 10⁰.

Relation entre les positions de pointe diffractées et la structure cristalline :

Lorsque des ondes lumineuses de longueur d'onde suffisamment petite sont accidentelles sur un treillis de cristal, elles diffractent à partir des points de treillis. À certains angles d'incidence, les ondes parallèles diffractées interfèrent de manière constructive et créent des pics d'intensité détectables. W.H. Bragg a identifié la relation illustrée à la figure 1 et a dérivé une équation correspondante :

n '2d_hkl sin '[1]

Voici la longueur d'onde des rayons X utilisés, d_hkl est l'espacement entre un ensemble particulier d'avions avec (hkl) indices Miller, et est l'angle d'incidence auquel un pic de diffraction est mesuré. Enfin, n est un entier qui représente l'ordre harmonique de la diffraction. À n'1, par exemple, nous avons la première harmonique, ce qui signifie que le chemin des rayons X diffracté à travers le cristal (équivalent à 2d_{péché hkl} ) est exactement 1,tandis qu'à n '2, le chemin diffracted est de 2. Nous pouvons généralement supposer n '1, et, en général, n '1 pour 'lt; péché^-1(2 '/d_h'k'l'), où h'k'l' sont les indices Miller des avions qui montrent le premier pic (à la valeur la plus basse de 2 ') dans une expérience de diffraction. Les indices Miller sont un ensemble de trois entiers qui constituent un système de notation pour identifier les directions et les plans à l'intérieur des cristaux. Pour les directions, les indices [h k l] Miller représentent la différence normalisée dans les coordonnées respectives de x, y et z (dans un système de coordonnées cartésiennes) de deux points le long de la direction. Pour les avions, les indices Miller (h k l) d'un avion sont simplement les valeurs h k l de la direction perpendiculaire à l'avion.

Dans une expérience XRD typique en mode de réflexion, la source de rayons X est fixée en position et l'échantillon est tourné en fonction du faisceau de rayons X au-dessus de l'écran. Un détecteur capte le faisceau diffracté et doit suivre la rotation de l'échantillon en tournant à deux fois la vitesse (c.-à-d. pour un angle d'échantillon donné de - l'angle du détecteur est de 2 ). La géométrie de l'expérience est illustrée schématiquement dans la figure 1.

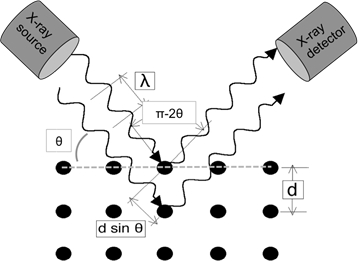
Figure 1 : Illustration de la loi de Bragg.

Lorsqu'un pic d'intensité est observé, l'équation 1 est nécessairement satisfaite. Par conséquent, nous pouvons calculer les espacements d en fonction des angles où ces pics sont observés. En calculant les espacements d de plusieurs pics, la classe de cristal et l'échantillon de matériaux de paramètres de structure cristalline peuvent être identifiés à l'aide d'une base de données comme le manuel de recherche Hanawalt ou les bibliothèques de base de données disponibles avec le logiciel XRD utilisé.

Nous supposerons que l'échantillon à l'étude n'est pas un seul cristal. Si l'échantillon était un seul cristal avec un plan particulier (hôkl) parallèle à la surface de l'échantillon, il faudrait qu'il soit tourné jusqu'à ce que l'état de Bragg pour le (hôklô) soit satisfait afin de voir un pic d'intensité diffractée (pour n '1) avec des pics harmoniques potentiellement plus élevés (hôkl) (par exemple pour n '2) également détectables à des angles plus élevés. À tous les autres angles, il n'y aurait pas de pics dans un seul échantillon de cristal. Supposons plutôt que l'échantillon soit polycrystalline ou qu'il s'agit d'une poudre, avec un nombre statistiquement significatif de grains cristallins ou de particules de poudre éclairées par le faisceau de rayons X incident. Selon cette hypothèse, l'échantillon se compose de grains orientés au hasard, avec une probabilité statistique similaire pour tous les plans de treillis possibles à diffract.

Les relations entre le d_hkl et les paramètres cellulaires unitaires sont indiquées ci-dessous dans les équations 2-7 pour les 7 classes de cristal, cubique, tétine, hexagonale, rhombohedral, orthorhombe, monoclinique et triclinique. Les paramètres des cellules unitairesse composent de longueurs de(a,b,c) et les angles entre les bords des cellules unitaires pour les 7 classes de cristaux (Figure 1x montre l'exemple de l'une des classes de cristaux : la structure tetragonale où a'b 'c, et '90⁰). À l'aide de plusieurs positions de pointe diffractées (c.-à-d. plusieurs valeurs _dhkl distinctes), les valeurs des paramètres cellulaires unitaires peuvent être résolues de façon unique.

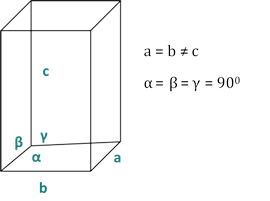
Figure 2 : La structure tetragonale comme l'une des sept classes de cristal.

Cubic (a b 'c'à c; ''90^0'):

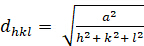[2]

Tetragonal (a 'b 'c'; '' ''90^0'):

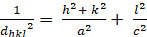[3]

Hexagonal (a b 'c; '90^0;' 120⁰⁾:

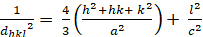[4]

Orthorhombic (a 'b 'c; ''' ''90^0'):

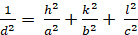[5]

Rhombohedral (a 'b 'c'; ''90^0'):

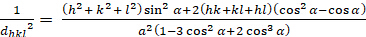[6]

Monoclinique (a 'b 'c; '90^{0 '}) :

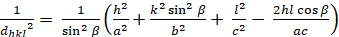[7]

Triclinique (a 'b 'c; '90⁰⁾:

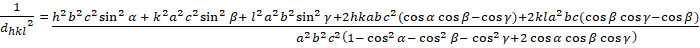      [8]

Relation entre les intensités maximales diffractées et la structure cristalline :

Ensuite, nous examinons les facteurs qui contribuent à l'intensité dans un modèle XRD. Les facteurs peuvent être ventilés en 1) la contribution à la dispersion qui résulte directement des aspects structurels uniques du matériau (les types et les emplacements spécifiques des atomes de diffusion dans la structure) et 2) ceux qui ne sont pas spécifiques au matériau. Dans le premier cas, il y a deux facteurs : le « facteur d'absorption » et le « facteur structurel ». Le facteur d'absorption dépend principalement de la capacité du matériau à absorber les rayons X sur leur chemin à l'intérieur et à l'extérieur. Ce facteur n'a pas de dépendance tant que les échantillons ne sont pas minces (l'échantillon doit être 3 fois plus épais que la longueur d'atténuation des rayons X). En d'autres termes, la contribution par le facteur d'absorption à l'intensité des différents pics est constante. Le « facteur de structure » affecte directement l'intensité de pics spécifiques en conséquence directe de la structure. Les autres facteurs, la «multiplicité», qui explique tous les plans qui appartiennent à la même famille parce qu'ils sont symétriquement liés, et le facteur «Lorentz-Polarisation», qui provient de la géométrie de l'expérience XRD, affectent également le l'intensité relative des pics, mais ils ne sont pas spécifiques à un matériau et peuvent facilement être expliqués avec des expressions analytiques (c.-à-d. le logiciel d'analyse XRD peut les supprimer avec des fonctions analytiques).

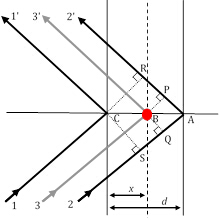
Figure 3 : Trois chemins de rayons de diffraction, dont les rayons 11' et 22' satisfont à l'état de Bragg, tandis que le rayon 33' résulte de la dispersion par un atome (cercle rouge) à une position arbitraire.

En tant que seul facteur qui porte la contribution structurelle unique d'un matériau aux intensités relatives des pics XRD, le facteur de structure est très important et nécessite un examen plus attentif. Dans la figure 2, supposons que la condition de diffraction bragg du^1er ordre (rappelez-vous, que cela correspond à n '1) est satisfaite entre le rayon_11' et le rayon_22' qui sont dispersés sur deux plans atomiques dans la direction h00 (en utilisant la notation des indices Miller décrit précédemment) séparés par une distance d. Dans ces conditions, la différence de longueur de chemin entre le rayon_11' et le rayon_22' est de_22'-11') et de SA et AR. Le décalage de phase entre les rayons diffractés 1 et 2 est, par conséquent, de_{22'-11' (22'-11')}/ ') 2 '2 '(en supposant une symétrie cubique et, par conséquent, d 'a/h dans la direction h00].

Avec quelques étapes dans la géométrie analytique, il peut être démontré que le changement de phase,_'33'-11'), avec le rayon 3 diffracté par un plan arbitraire d'atomes qui sont espacés d'une distance arbitraire x, est donné par:_(33'-11') ' 2'hu, où u 'x/a (a est le paramètre de cellule unitaire dans la direction (h00). Prenant les deux autres directions orthogonales, (0k0) et (00l), et v'y/a et w'z/a comme coordonnées fractionnaires dans les directions y- et z, l'expression pour le décalage de phase s'étend à 2 '(hu'kv'lw). Maintenant, l'onde de rayon X dispersée par l'atome j-thdans une cellule d'unité aura une amplitude 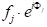de diffusion de f_j et une phase de_j,de telle sorte que la fonction la décrivant est. Le facteur de structure que nous recherchons, par conséquent, est la somme de toutes les fonctions de diffusion dues à tous les atomes uniques dans une cellule unitaire. Ce facteur de structure, F, est donné comme:

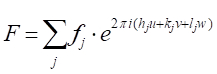[9]

et le facteur d'intensité contribué par le facteur de structure est I F².

Sur la base des positions (u,v,w) des atomes sur des plans particuliers (h,k,l), il y a la possibilité d'interférence entre les vagues éparses qui est constructive, destructrice, ou entre les deux, et cette interférence affecte directement l'amplitude des pics XRD représentant les avions (hkl).

Maintenant, une parcelle d'intensité, je, contre 2 est ce qui est mesuré dans une expérience XRD. La détermination du type de cristal et des paramètres des cellules unitaires associées(a, b, c, ' ' ' ' ' ' ' ' ' ' '' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' Aujourd'hui, c'est processus est assez automatisé par une variété de logiciels liés à des bases de données de structure cristalline.

La procédure suivante s'applique à un instrument XRD spécifique et à son logiciel associé, et il peut y avoir quelques variations lorsque d'autres instruments sont utilisés.

1. Nous examinerons un échantillon de poudre de Ni sur un instrument Panalytical Alpha-1 XRD.
2. Tout d'abord, choisissez le masque pour fixer la taille du faisceau en fonction de votre diamètre d'échantillon. Le faisceau ne doit pas avoir une empreinte plus grande que l'échantillon à la plus petite valeur de la valeur (généralement 7⁰-10⁰). Pour un échantillon de largeur, la taille du faisceau doit être 'lt; 'sin'.
3. Chargez l'échantillon à l'étape de spinner de l'échantillon et verrouillez l'échantillon en position. Le spinner d'échantillon aide à randomiser spatialement l'exposition de l'échantillon à la source de rayon X.
4. Choisissez la plage d'angle pour votre scan XRD. Par exemple 15-90 degrés est une gamme typique.
5. Choisissez une taille d'étape, c'est-à-d. l'augmentation en 2, et l'intégration (compte) le temps. En général, une taille d'étape de 0,05 degré et une intégration de 4 secondes est la valeur par défaut pour un balayage grand angle.
6. Une fois que toutes les positions de pointe sont déterminées à travers cette analyse initiale, les scans ultérieurs peuvent se concentrer sur une plage d'analyse plus étroite autour de pics spécifiques en utilisant une taille d'étape plus petite dans l'angle si des données de résolution plus élevée de ces pics sont souhaitées.

Dans la figure 4, nous voyons les pics XRD pour l'échantillon de poudre Ni. Notez que les pics observés (p. ex. {111}, {200}) sont pour ceux qui ont soit toutes les combinaisons égales ou toutes les combinaisons étranges de h, k, et l. Ni est centré sur le visage cubique (FCC), et dans toutes les structures fcc, les pics correspondant à des planshkloù h, k, et l sont des mélanges d'intégristes uniformes et impairs, sont absents en raison de l'interférence destructrice des rayons X dispersés. Les pics correspondant aux avions, tels que les {210} et les {211} sont manquants. Ce phénomène est appelé les règles systématiques de présence et d'absence, et ils fournissent un outil d'analyse pour évaluer la structure cristalline de l'échantillon.

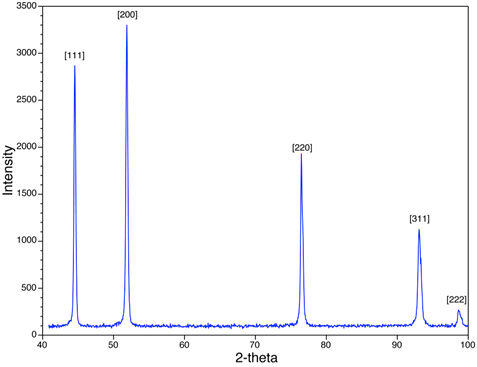
Figure 4: Un balayage XRD de Ni avec une structure cubique centrée sur le visage est montré.

Il s'agit d'une démonstration d'une expérience XRD standard. Le matériau examiné dans cette expérience était sous forme de poudre, mais XRD fonctionne aussi bien avec le morceau solide de matériel tant que l'échantillon a une surface plane qui peut être mise parallèlement au plan de l'étape de l'échantillon.

XRD est une méthode assez omniprésente pour déterminer la présence (ou l'absence) de l'ordre cristallographique dans les matériaux. Au-delà de l'application standard de la détermination de la structure cristalline, XRD est souvent utilisé pour obtenir une variété d'autres informations structurelles telles que:

1. Que la structure d'un matériau soit amorphe ou non (caractérisée par une large bosse dans l'intensité de diffraction et un manque de pics cristallologiques discernables),
2. Que l'échantillon soit un matériau composite composé de plusieurs phases cristallographiques et, dans l'affirmative, déterminer la fraction de chaque phase,
3. Déterminer si un matériau est un composite amorphe/cristallin
4. Déterminer la taille du grain/particule du matériau,
5. Déterminer le degré de texture (orientation préférée des grains) dans le matériau.