פיזור וקליטת האור בריגולסים פלנטרית

Summary

שיטות מספריים ונסיוניות מוצגות לפיזור מספר רב של אור במדיה אקראית דיסקרטית של חלקיקים צפופים. השיטות מנוצלים כדי לפרש את התצפיות של האסטרואיד (4) וסטה ו שביט 67 p/צ'יומוב-Gerasimenko.

Abstract

שיטות תאורליות, מספריות ונסיוניות מוצגות לפיזור מספר רב של אור במדיה אקראית מאקרוסקופית ומיקרוסקופית של חלקיקים מיקרוסקופיים הארוזים בצפיפות. השיטות התאורטי והמספרי מהוות מסגרת של העברה רדיטיבית עם עסקאות הדדיות (R²T²). מסגרת R²T² מצריכה מונטה קרלו מעקב אחר פיזור של האינטראקציות במרחב התדר, בהנחה כי המסטרים ובולמי היסוד הם רכיבי נפח בקנה מידה של אורך הגל המורכב ממספר גדול של באופן אקראי חלקיקים מבוזרים. המדיה האקראית הדיסקרטית מלאה ברכיבי אמצעי האחסון. עבור חלקיקים כדוריים ושאינם כדוריים, האינטראקציות בתוך רכיבי אמצעי האחסון מחושבות בדיוק באמצעות שיטת ה-מטריצה הסופרפוזיציה (stmm) ושיטת המשוואה האינטגרלית של אמצעי האחסון (viem), בהתאמה. עבור שני סוגי החלקיקים, האינטראקציות בין רכיבי אמצעי אחסון שונים מחושבות בדיוק באמצעות הפונקציה STMM. כאשר העקיבה מתרחשת בתוך המדיה האקראית הדיסקרטית, משתמשים בשדות אלקטרומגנטיים לא מסוימים, כלומר, השדה העקבי של רכיבי אמצעי האחסון מוסר מהאינטראקציות. השיטות הנסיוניות מבוססות על ריחוף אקוסטי של הדגימות עבור מדידות ללא מגע, פיזור לא הרסני. הריחוף כרוך בשליטה מלאה של אולטרה סאונד של התנוחה וכיוון המדגם, כלומר, שש דרגות חופש. מקור האור הוא מקור אור לבן מונחה לייזר עם monochromator ו מקטצר. הגלאי הוא צינור מיני פוטופולייר על גלגל מסתובב, מצויד במקטליטורים. ה-R²T² מאומת באמצעות מדידות למדגם כדורי בקנה מידה מ"מ של חלקיקי סיליקה כדוריים צפופים. לאחר האימות, השיטות מוחלות על פענוח תצפיות אסטרונומיות עבור האסטרואיד (4) וסטה ו שביט 67 p/צ'יומוב-Gerasimenko (איור 1) ביקר לאחרונה על ידי משימת השחר של נאס א ואת המשימה רוזטה לרדוף, בהתאמה.

Introduction

אסטרואידים, גרעיני מימיים, ואובייקטים מערכת השמש ללא אוויר בגודל גדול מכוסים על ידי regoliths פלנטרית, שכבות רופף של חלקיקים בגדלים שונים, צורה, וקומפוזיציה. עבור אובייקטים אלה, שתי תופעות אסטרונומיות בכל מקום נצפו בזוויות שלב קטן של השמש (זווית השמש-המתבונן). ראשון, הבהירות של האור הפזורים בקנה המידה האסטרונומי הוא נצפתה כדי להגדיל בצורה לא לינארית לקראת זווית אפס שלב, הנקרא בדרך כלל אפקט האופוזיציה^1,2. שנית, האור הפזורים מקוטב ליניארי באופן חלקי מקביל למישור הפיזור (מישור השמש-משקיף), שנקרא בדרך כלל קיטוב שלילי³. התופעות היו חסרות פרשנות כמותית מאז סוף המאה^ה -19 לאפקט האופוזיציה ומאז תחילת המאה^ה -20 לקיטוב השלילי. הפרשנות הראויה שלהם היא תנאי מוקדם לפרשנות הכמותית של הפוטומטרי, הקיטוב ותצפיות הספקטרומטריים של עצמים נטולי אוויר, כמו גם פיזור מכ ם משטחי השטח שלהם.

זה הוצע^4,5,6,7 כי מנגנון פיזור הרקע קוהרנטי (cbm) בפיזור מרובים הוא לפחות בחלקו אחראי על התופעות האסטרונומיות. ב-CBM, גלים חלקיים, האינטראקציה עם אותם מפזרים בסדר הפוך, תמיד מפריעים לקונסטרוקטיבית בכיוון המדויק של פיזור הרקע. זה נובע הנתיבים האופטיים בד בבד של גלים הדדיים. בכיוונים אחרים, ההפרעות משתנה מהרס לקונסטרוקטיבי. מבצעות בממוצע בתוך מדיום אקראי בנפרד של חלקיקים תוצאות משופרות לפיזור הרקע. באשר לקיטוב הליניארי, ה-CBM סלקטיבי והתוצאה היא פולריזציה שלילית במקרה של הקטפולנים באופן חיובי, מאפיין נפוץ בפיזור יחיד (cf. פיזור ריילי, השתקפות פרנל).

פיזור וקליטת גלים אלקטרומגנטיים (אור) במדיום אקראי מקרוסקופי של חלקיקים מיקרוסקופיים היווה בעיה חישובית פתוחה באסטרופיסיקה פלנטרית^8,9. כפי שמודגם לעיל, הדבר גרם להעדר שיטות הופכי כמותית לפענוח תצפיות מבוססות-שטח ומבוססות-חלל של אובייקטי מערכת השמש. בכתב היד הנוכחי מוצגים שיטות הרומן לגישור הפער בין התצפיות לבין המידול שלהם.

מדידות ניסויית של פיזור על ידי מדגם קטן-חלקיק בתנוחה מבוקרת וכיוון (שש דרגות חופש) נשארה פתוחה. מאפייני פיזור עבור חלקיקים בודדים נמדדו מוקדם יותר כמו ההרכב ממוצעים על גודל, צורה, התפלגות כיוון¹⁰ על ידי החדרת זרימת חלקיקים דרך עוצמת המדידה. פיזור מאפייני חלקיקים בודדים בריחוף בוצעו באמצעות, למשל, ריחוף אלקטרודינמי¹¹ ו מלקחיים אופטיים^12,13,14. בכתב היד הנוכחי, שיטה ניסיונית הרומן המבוסס על ריחוף אולטרה סאונד עם שליטה מלאה של המיקום לדוגמה ואוריינטציה מוצעת¹⁵.

כתב היד הנוכחי מסכם את ממצאי הפרויקט במימון חמש שנים בשנת 2013-2018 על ידי מועצת המחקר האירופית (ERC): פיזור וקליטת גלים אלקטרומגנטיים במדיה חלקיקים (SAEMPL, ERC מתקדם מענק). Saempl הצליח לפגוש את שלוש המטרות העיקריות שלה: ראשית, הספר הרומן מונטה קרלו שיטות נגזר על פיזור מרובים על ידי מדיה אקראית בדידה של חלקיקים צפוף בצפיפות^16,17,18; שנית, מכשור ניסיוני הרומן פותח ונבנה עבור מדידות מעבדה מבוקרת של דגימות אימות בריחוף¹⁵; שלישית, השיטות המספריים והנסיוניות הוחלו על פענוח תצפיות אסטרונומיות בגיל^19,20.

באופן הבא, פרוטוקולים לניצול צינור הפיזור הניסיוני עבור מדידות, צינור החישוב המקביל, כמו גם צינורות היישום מתוארים בפרוטרוט. קו הצינור החישובית מורכב מתוכנה לחישובים מדויקים במקרה של מערכות של חלקיקים סופיים (מיקום מערכת T-מטריקס שיטת stmm²¹ ושלמות היקף שיטת המשוואה viem²²) ומשוער חישובי מדיה אקראית בדידה אינסופית אינסופי של חלקיקים באמצעות שיטות פיזור מרובות (siris^23,24, העברה רדיוטיבית עם מעבר קוהרנטי לפיזור RT-CB^8,9, ו העברה רדיוטיבית עם תנועות הדדיות R²T^216,17,18). קו הצינור הניסיוני כולל את ההכנה, האחסון והניצול של הדגימות, הריחוף שלהם בנפח המדידה, וביצוע מדידת פיזור בפועל על פני מגוון זוויות פיזור עם מקטצר שונים תצורות. קו הצנרת של האפליקציה נוגע לניצול קווי הצנרת החישוביים והניסיוניים כדי לפרש תצפיות אסטרונומיות או מדידות נסיוניות.

Protocol

1. מדידת פיזור אור

1. התקנת המטר למדידה (איור 2)
   1. כדי להתחיל, להגדיר את מדידת הארץ על ידי הפעלת מקור האור, מכפיל את התמונה צינורות (PMTs), מגברים. הניחו למערכת להתייצב במשך 30 דקות.
   2. ליישר ולמרכז את קרן האירוע עם חורים. שני חורים מחוברים בנקודות שנמדדו מראש על קרש הלחם המסתובב, 180 ° ובאותו רדיוס. מרכז את הקרן על החור הראשון ולהתאים את הזווית שלה כך האור נכנס גם דרך החור השני.
2. הגדרת לויטור המדגם האקוסטי
   1. לאחר מכן, הגדר את לויטור המדגם האקוסטי על-ידי הוספת המיקרופון במרכז הויטור והפעלת סקריפט הכיול.
   2. כיול לויטור האקוסטי של מערך השלבים באמצעות מדידת הלחץ האקוסטי עבור כל רכיב מערך בנקודת הריחוף המיועדת כפונקציה של מתח הנהיגה. השתמש בכיול זה כדי לפצות על הבדלים בין ערוצי המערך. הצב את מיקרופון הכיול על-ידי מרכוז הצל שלו הן בקרן והן בקרן מאונך שנוצרה עם שתי מראות.
   3. חשב את פרמטרי הנהיגה עבור המערך היוצר מלכודת אקוסטית אסימטרית וספק אותם למוצרי האלקטרוניקה של יצירת האותות. הדבר מתבצע על ידי מזעור הפוטנציאל של גורקוב²⁵ ויישור מעברי הלחץ בנקודת הריחוף.
   4. לאחר מכן, בצע ניקוי מדידה עם לויטור ריק. הסריקה מגלה את כל האותות שנוצרו על ידי אור הסביבה, השתקפויות מן הסביבה, או רעשים חשמליים.
3. טיפול בדוגמאות, הוספה ומדידה
   1. לאחר ההגדרה, השתמש בכף רשת שקופה השקופה כדי להזריק את המדגם לתוך לויטור אקוסטי.
   2. באמצעות מצלמת וידאו ואופטיקה בעלת הגדלה גבוהה, בדוק את הכיוון ואת יציבות המדגם לפני ואחרי מדידות הפיזור.
   3. החוזק והסימטריה של המלכודת האקוסטית ממוטבים ליציבות דגימה מקסימלית. כתוצאה מכך, העוצמה האקוסטית מוגדרת כנמוכה ככל האפשר.
   4. אם המדגם הוא אסימטרי, סובב אותו סביב הציר האנכי כדי לקבל מידע אודות צורתו. בצע את הסיבוב על-ידי שינוי איטי של יישור המלכודת האקוסטית. במהלך הדמיה, להחיל תאורה נוספת כדי לשפר את איכות התמונה.
   5. לאחר מכן, סגור את תא המדידה כדי לחסום את האור החיצוני.
   6. באמצעות ממשק המחשב, בחרו בכיוון המדגם, כמו גם ברזולוציה הזוויתית ובטווח המדידה. האור הנכנס ומפוזר מסוננים על ידי מקטפי ליניארי, שהם ממונעים.
   7. הפעל את ניקוי המדידה האוטומטית. זה יהיה למדוד ארבע נקודות עבור כל זווית עם הכיוונים מקטמד של (אופקי, אופקי), (אופקי, אנכי), (אנכי, אנכי), ו (אנכי, אופקי).
   8. חזור על כל סריקה שלוש פעמים כדי לחסל את הערים. עבור דוגמאות אסימטריים, חזור על המדידה בכיוונים שונים לדוגמה.
   9. שחזר את הדגימה לאחר המדידה על-ידי החלפת השדה האקוסטי והצגת הדגימה על הבד השקוף ההוליסטי. לאחר מכן, לבצע לטאטא מדידה נוספת עם לויטור ריק כדי לזהות כל האפשרות נסחף עקב תנאי תאורה הסביבה.
   10. כשתסיים, שמור את הנתונים. לנתח את הנתונים כדי לחשב אלמנטים מטריקס מולר עבור כל זווית באמצעות שילוב ליניארי של עוצמות בקיטוב שונים¹

2. דוגמנות התקשורת הכדורית בגודל mm המורכב מחלקיקים כדוריים

1. כדי להתחיל דוגמנות, להשתמש בגישה SSH כדי להתחבר לתוך מרכז CSC – IT של המדע מוגבלת של האשכול, טאיto.  להוריד ולקמפל את כל התוכניות הדרושות אשר מוגדרות מראש עבור Taito על ידי הפעלת bash compile.sh.
2. עבור לספריית העבודה על-ידי ביצוע $WRKDIR תקליטורים.
3. מקורות להוריד קבצים עם לזוז (לgit@bitbucket.org לשכפול: הplanetarysystemresearch חקר/protocol2. לך protocol2).
4. להעביר לתוך הprotocol2 התקליטורהחדש שנוצר.
5. להוריד ולקמפל תוכניות נדרשות על ידי הפעלת bash compile.sh, אשר מוגדרות מוגדר עבור taito.
6. הבא, לפתוח את עורך הטקסט ננו ולהגדיר את הפרמטרים עבור בודד, אלמנט אמצעי אחסון, ואת המדגם למד כדי להתאים את המדגם למד על ידי שינוי הקובץ Params.
7. לאחר מכן, הפעל צינור על-ידי ביצוע bash הפקודה run.sh. כאשר סיים, לכתוב את מטריצה מלאה מילר של המדגם לתוך התיקייה temp כמו סופי. out.

3. פענוח ספקטרום ההשתקפות של האסטרואיד (4) וסטה

1. הנובעות ממדד השבירה המרוכב.
   1. הורד SIRIS4 (להוריד שיבוט git@bitbucket.org: הplanetarysystemresearch חקר/siris 4.2. לך).
   2. בצע קומפילציה על-ידי ביצוע הפוך בתיקיה src. שנה את שם קובץ ההפעלה siris42 ל- siris4.
   3. ב Maingo. f90, לשנות את הקו 395 כדי r0 = 0.05 * rmax * sqrt (ran2). בצעקומפילציה על-ידי ביצוע הביצוע.
   4. הורד את MATLAB סקריפטים הדרושים על ידי ביצוע "להוריד שיבוט git@bitbucket.org: כפלקיקיsystemמחקר/protocol4a. לך".
   5. העתק את קבצי ההפעלה שנוצרו בשלבים 3.1.2. ו3.1.3. כדי JoVEOptimize-תיקיה.
   6. עבור אל התיקיה JoVEOptimize.
   7. בקובץ input1.in , להגדיר את הרדיוס 30 יקרומטר עבור גודל החלקיקים האוארדיט, ולתקן את החלק האמיתי של השבירה המדד כדי 1.8. בקובץ input2.in , הגדר את הרדיוס עד 15,000 μm.
   8. העריכו את הגבולות העליונים והתחתונים של החלק הדמיוני של מדדי השבירה ושמרו אותם לשני קבצים נפרדים. הקוד מנצל את השיטה הביקטנה ומשתמש בערכים אלה כנקודת ההתחלה.
   9. בקובץ אופטימיזציה. m , להגדיר את שמות הקבצים של הגבולות העליונים והתחתונים של החלק הדמיוני של מדדי השבירה ואת שם הקובץ של הספקטרום השתקפות נמדד של אבקת האוארדיט. הגדר את טווח אורך הגל ל-0.4 – 2.5 יקרומטר עם שלבים 0.05-יקרומטר.
   10. הפעל אופטימיזציה. m ב MATLAB על מנת לקבל את מדדי השבירה המורכבים של הוביטה (ראה איור 3). ראשית, הקוד מחשב פיזור מאפיינים עבור 30-μm בגודל (רדיוס) חלקיקים המכונה, ולאחר מכן משתמש חלקיקים אלה כמו מתפזר מפוזר בתוך 15,000-μm בגודל (רדיוס) אמצעי אחסון. שלבים אלה חוזרים על כל אורך גל עד שההשתקפות המחושבת מתאימה להשתקפות שנמדדה.
2. מידול הספקטרום השתקפות של וסטה.
   1. חישוב תכונות הפיזור של חלקיקי הSIRIS4 באמצעות שימוש ב
      1. לנצל SIRIS4 כדי לחשב את המאפיינים פיזור של חלקיקי הוביטה על ידי הזזת הקובץ ההפעלה SIRIS4 לתוך אותה תיקיה עם קובץ הקלט ו-p-מטריקס קובץ.  לאחר מכן, העתק את ה -input_1. in ו- pmatrix_1 מתוך תיקיית המבחן.
      2. ב -input_1, הגדר את מספר הקרניים ל-2,000,000, את מספר החלקיקים ל-1000, את סטיית התקן של רדיוס ל0.17, ואת מדד חוק הכוח של פונקציית המתאם ל-3. ואז, לקבוע את החלק האמיתי של השבירה המדד כדי 1.8 ולהשתמש בחלק הדמיוני של מדד השבירה n כמתואר בפרוטוקול טקסט.
      3. הבא, להפעיל SIRIS4 על ידי ביצוע הפקודה המוצגת כאן עבור כל אורך גל מ 0.4 כדי 2.5 מיקרון באמצעות טווח גודל של 10 כדי 200 מיקרון בקוטר עם צעד דגימה של 10 מיקרון.
      4. לאחר מכן, שמור כל שלב פיזור מחושב מטריצה P לתוך pmatrix_x. in קובץ.  ה-x בשם הקובץ מתאר את מספר אורך הגל והטווחים מ-1 עד 43 עבור כל גודל חלקיק. הקובץ יכיל את זוויות פיזור, כמו גם את האלמנטים פיזור מטריקס P₁₁, p₁₂, p₂₂, p₃₃, p₃₄, ו p₄₄ עבור אורך גל אחד וגודל החלקיקים.
   2. ממוצע מטריצות פיזור שהושג, פיזור יחיד albedos, ממוצע שבילים חינם על התפלגות גודל חוק כוח עם מדד של 3.2 מיכל ^{בן 19 ,} . ^{עשרים וארבע}
      1. העבר את קובצי ה -pmatrixלתיקיות כך שכל תיקיה מייצגת גודל חלקיק אחד ומכילה את מטריצות ה-p המחושבת עבור כל אורכי הגל. ציין את שם התיקיות fold1, fold2,..., foldN, כאשר N הוא מספר גדלי החלקיקים.
      2. כתוב את הפיזור ואת יעילות ההכחדה q_סקה ו-q שלוחה, כמו גם את ערכי רדיוס שווה-שטח-כדור r להיט מן outputq-קבצים לקובץ אחד, qscas. dat.
      3. עבור אל התיקיה JoVEAverage שהורד בשלב 3.1.4.
      4. העבר את התיקיות ואת Qscas. dat לתוך אותה תיקיה עם Avgpowerlaw. m.
      5. הפעל את Avgpowerlaw. m ב MATLAB. הקוד מחשב מטריצות פיזור ממוצע, פיזור יחיד albedos, ומתכוון אורך הנתיב חופשי על התפלגות גודל כוח החוק עם מדד 3.2.
   3. חישוב הספקטרום הסופי של וסטה על ידי ניצול SIRIS4
      1. השתמש מפוזר לפזר בתוך וסטה בגודל נפח עם מדד השבירה של 1. בקובץ הקלט, השתמש בממוצע פיזור יחיד של ממוצע בודד ומתכוון לאורך הנתיב החופשי עבור מפזרים פנימיים.
      2. הבא, לרוץ SIRIS4 בכל אורך הגל על ידי ביצוע הפקודה המוצגת כאן, כאשר X הוא אורך הגל. הקוד קורא את מטריצות פיזור הממוצע כקלט שלה עבור מפוזר הפנימי לפזר.
      3. למדו את ההשתקפות המוחלטת. בזוית שלב 17.4 מעלות
      4. להשיג את וסטה הנצפים של ספקטרום ב 17.4-שלב מדרגה זווית ממערכת הנתונים פלנטרית של נאס א²⁶.
      5. קנה מידה של וסטה הנצפים ספקטרום של ערך אלבדו גיאומטרי של 0.42327 ב 0.55 מיקרון²⁷. כדי להגיע ל 17.4 מעלות, החל פקטור של 0.491 בספקטרום הקנה מידה²⁸. להשוות הן את המודל ואת ספקטרום נצפה לרוחב אורך הגל כולו.

4. מידול הפומטרי והקיטוב של (4) וסטה

1. מחשוב פיזור תכונות עבור רכיבי נפח המכילים וורוונרוי חלקיקים בצורת הוביטה
   1. התחבר לתוך האשכול CSC – IT למדע בע מ של מרכז טאיאל באמצעות גישה SSH.
   2. עבור לספריית העבודה על-ידי ביצוע $WRKDIR תקליטורים.
   3. הורד את קבצי המקור (להוריד שיבוט git@bitbucket.org: הפלקיקיsystemמחקר/jvie_t_matrix. לך).
   4. בצע קומפילציה על-ידי ביצוע הפוך בתיקיה.
   5. צור רכיבי אמצעי אחסון המכילים חלקיקים בצורת Voronoi בצורה מMATLAB באמצעות קוד voronoi_element. m. בשנת voronoi_element. m, להגדיר את אורך הגל כדי 0.45 μm, N_elems כדי 128, את הפרמטר גודל (elem_ka) עד 10, כוח חוק המדד ל 3, מינימום חלקיקים רדיוס כדי 0.143 μm, רדיוס חלקיקים מירבי כדי 0.35 μm, אריזה צפיפות 30%, ולהשתמש במדד השבירה מורכבים נגזר על הכמה.
   6. הפעל voronoi_element. m ב-MATLAB. הקוד יוצר 128 שינוי קבצים עבור רכיבי נפח עם היבטים שונים של הוראורוי-חלקיקים באמצעות התפלגות גודל חוק הכוח.
   7. חשב T-מטריצות עבור רכיבי עוצמת הקול שנוצרו באמצעות jvie. ב runarray_JVIE_T. sh, הגדר מערך = 1-128. הפרטרים הם k = 13.962634, רשת שינוי = שם של רשת השינוי הנוצרת ב-4.1.6, T_out = שם הפלט T-matrix, T_matrix = 1 ו-elem_ka = 10.
   8. הפעל JVIE על ידי ביצוע sbatch runarray_JVIE_T. sh.
   9. חישוב מאפייני פיזור ממוצעים מהטריצות Tשחושבו באמצעות קוד jvie. ביצוע ./Multi_t-N_Tin 128 באותה תיקיה שבה מטריצות ה- Tהמחושבים הן. הקוד כותב את מטריצה מולר בממוצע לא בסדר לתוך והחוצה סעיפים אלבדו לתוך פלט. txt.
2. מדי מעשה
   1. התחל על-ידי הורדת קבצי מקורות עם לזוז (לgit@bitbucket.org לשכפל: הפלקיקיsystemמחקר/protocol4b. לך protocol4b) ולהעביר את הקבצים לתוך protocol4bספריה שהורדת.
   2. הבא, להוריד ולקמפל את כל התוכניות הדרושות על ידי הפעלת bash compile.sh.
   3. כאשר מוכן, העתק את מטריצה פיזור הקלט הממוצע (שלב 3.2.2.5), כמו גם את המטריצה פיזור משרעת (שלב 4.1.9) לתוך ספריית העבודה הנוכחית.
   4. לאחר מכן, פתח את עורך הטקסט, ננו ושנה את הקובץ Params כדי להגדיר את הפרמטרים הרצויים.
   5. הפעל את הצינור על-ידי ביצוע bash run.sh. אז, לכתוב את מטריקס מולר מלא לתוך התיקיה temp כמו rtcb. החוצה.

5. פענוח התצפיות של שביט 67 p/צ'יומוב-גראסימנקו.

1. מחשב רכיבי נפח במצב לא בהיר עם התנוחה המהירה שיטת T-מטריקס (fastmm) עבור גרגרי החלקיקים האורגניים
   1. . הפעל את הקובץ /הקלט – למדא 0.649-m_r 2.0-m_i 0.2-צפיפות 0.3-lowb 0.075-upb 0.125-npower 3-S_out pmatrix_org. dat.
   2. . הפעל את הקובץ /הקלט – למדא 0.649-m_r 1.6-m_i 0.0001-צפיפות 0.0375-lowb 0.6-upb 1.3-npower 3-S_out pmatrix_sil. dat.
2. מחשב את הממוצע הממוצעים מטריקס מולר (pmatrix.in), אלבדו (אלבדו), מתכוון שביל חופשי (mfp), ואינדקס השבירה יעיל העקבי (m_eff)
   1. . הפעל matlab פקודות כתב:
      Sorg = לטעון (' pmatrix_org. dat ');
      Ssil = load (' pmatrix_sil. dat ');
      S = (Sorg + Ssil)/2; שמור (' pmatrix. in ', ' s ', '-ascii ');
      מיכל = (Csca_sil + Csca_org)/2;
      Cext = (Cext_sil + Cext_org)/2;
      אלבדו = Csca/Csca;
      m fp = Vol/Cext;
      כאשר Csca_org ו-Cext_org הם פיזור בסדר והכחדה מקטעים מתוך השלב 5.1.2, ו Csca_sil ו Cext_sil הם פיזור בסדר והכחדה מקטעים מתוך השלב 5.1.3.
   2. . בסדר. בשורת הפקודה כדי להשיג m_eff היכן נמצא הרדיוס של רכיב אמצעי האחסון.
3. מחשוב פיזור מאפיינים עבור חלקיקי התרדמת.
   1. הגדר את הערכים מהשלב 5.2.1 ו-5.2.2 (כלומר, albedo, mfp, m_eff בקובץ input.in ).
   2. הגדר אינדקס חוק-כוח עבור אורך המתאם ל-3.5 בקובץ input.in .
   3. הפעל SIRIS4 solver (./siris4 input.in pmatrix.in) עבור גודלי חלקיקים מ-5 יקרומטר עד 100 יקרומטר באמצעות שלב של 5.
   4. הפלט של פונקציות שלב התרדמת מ-SIRIS4 solver.
4. מאפייני פיזור המחשוב של הגרעין
   1. התחל ב-MATLAB והפעל את ה- powerlaw_ave. m השגרתי כדי לחשב את התוצאות באמצעות התפלגות גודל חוק הכוח של מדד-3 לאחר חישוב פונקציות שלב התרדמת (שלב 5.3.4) מ-SIRIS4 solver. פלטי השגרה הצפויים הם pmatrix2.in, אלבדו והשביל החופשי הממוצע.
   2. לאחר מכן, הגדר את התוצאות מהתפוקות, אלבדו והנתיב החופשי הממוצע, לתוך קובץ input.in .
   3. הגדר את הגודל ל-1,000,000,000, ואת מדד חוק הכוח של פונקציית המתאם עבור הצורה ל-2.5. לאחר מכן, הפעל את SIRIS4 באמצעות שורת הפקודה המוצגת כאן כדי לקבל את הפונקציה של השלב הגרעין.

תוצאות

עבור הניסוי שלנו, צבירה המורכבת של צפוף בצפיפות Ø = 0.5 יקרומטר כדורי SiO₂ חלקיקים נבחר^29,30 ו מלוטש נוסף, כדי לקירוב צורה כדורית, לאחר שהוא התאפיין על ידי שקילה ומדידת מימדים (איור 4). צבירה כדורית כמעט היה קוטר של 1.16 מ"מ וצפיפות נפח של 0.47. פיזור אור נמדד לפי שלב 1. הקרן סונן ל-488 ± 5 ננומטר, בספקטרום גאוסיאני. המדידה הייתה ממוצעים משלוש מטאטא והאות לויטור הריק התרוקן מהתוצאה.

מתוך העוצמות של ארבע תצורות הפולריזציה השונות, אנו מחשבים את פונקציית הפאזה, מידת הקיטוב הליניארי של המקרה הבלתי מקוטב-M₁₂/m₁₁, והדפולריזציה M מיכל בן ₂₂ /מ ₁₁, כפונקציה של זווית הפאזה (איור 5, איור 6, איור 7). אחד מקור השגיאה הסיסטמטית הידוע של המדידה שלנו הוא יחס ההכחדה של מקטלי ליניארי, שהוא 300:1. לדוגמה זו, הוא, עם זאת, הולם כך שהאור הקוטב הדלף נמצא מתחת לסף האיתור.

המידול המספרי מורכב מתוכנות מרובות המקושרות על-ידי סקריפטים המטפלים בזרימת המידע בהתאם לפרמטרים הניתנים על ידי המשתמש. סקריפטים ותוכנות מוגדרות מוגדר לעבוד על מרכז CSC-IT של האשכול של מדעי המחשב בע מ, ואת המשתמש צריך לשנות את קבצי ה-script ואת Makefiles עצמם כדי לקבל את כלי הדוגמנות לעבוד על פלטפורמות אחרות. הכלי מתחיל בהפעלת ה-STMM solver²⁰, אשר מחשב מאפיינים של אלמנט הנפח, כפי שמתואר על ידי וללא¹⁸. לאחר מכן, מאפייני הפיזור והספיגה של רכיב אמצעי האחסון משמשים כקלט עבור שתי תוכנות שונות. פותר פיזור של מ. י. משמש כדי למצוא את מדד השבירה האפקטיבית על ידי התאמת חתך הפיזור קוהרנטי של אלמנט הנפח לספירה של מ. י. בגודל שווה²⁰. לאחר מכן הצבירה היא במודל על ידי הפעלת התוכנה SIRIS4 עם אלמנט נפח כמו מפוזרת מפוזר עם מדד השבירה יעיל על פני השטח של צבירה. רכיב פיזור הרקע העקבי מתווסף בנפרד משום שאין תוכנה שיכולה לטפל בפיזור ממוצע ועקבי של השבירה בו. כיום, RT-CB אינו מסוגל החשבונאות עבור בינוני השבירה יעיל, בעוד SIRIS4 אינו מסוגל החשבונאות לפיזור מאחור קוהרנטית. הרקע העקבי הוא, עם זאת, הוסיף SIRIS4^23,24 תוצאות בקירוב על ידי הפעלת מאפייני פיזור אלמנט הנפח דרך הפירוק פיזור מטריצה השלב תוכנה pmdec אשר נובע מטריצות ומילר טהור של ג'ונס נדרש עבור ה-RT-CB⁹. רכיב פיזור הרקע העקבי מופק לאחר מכן על-ידי חיסור רכיב ההעברה הרדיוטיבי מהתוצאות של RT-CB. לאחר מכן, רכיב פיזור הרקע העקבי שחולץ מתווסף לתוצאות שהתקבלו מ-SIRIS4.

אנו מדומה מספרית את המאפיינים של mm בגודל (רדיוס 580 μm) SiO₂ צבירה על-ידי לאחר שלב 2. השתמשנו בשני סוגים של רכיבי נפח, אחד המורכב חלקיקים משקל נומינלי (0.25 μm) והשני המורכב בדרך כלל מופץ (ממוצע 0.25 μm, תקן סטייה 0.1 μm) חלקיקים מעוגלים לטווח של 0.1-0.2525 μm. היכרות עם האחרון התפלגות של חלקיקים מבוססת על העובדה כי ביסודו של כל SiO₂ דגימות עם גודל החלקיק נתון יש גם התפלגות חייזרית משמעותית של חלקיקים קטנים³¹. בסך הכל, 128 רכיבי נפח של גודל kR₀= 10 נמשכו מ 128 תיבות תקופתיות המכילות על החלקיקים 10,000 ארוז על צפיפות עוצמת הקול v= 47% כל. מתוך המפרט של החומר, יש לנו n= 1.463 + i0 באורך הגל של 0.488 μm, אשר הוא אורך הגל המשמש את המידות.

עם SIRIS4, את המאפיינים פיזור של 100,000 אגרגטים, עם רדיוס של 580 μm, סטיית תקן של 5.8 μm, ועם אינדקס חוק הכוח של הפונקציה מתאם 2, נפתרו הממוצע. תוצאות אלה מותוות (ראה איור 5, איור 6, איור 7) עם המידות הנסיוניות, וסימולציה נוספת ללא המדיום האפקטיבי. שתי האפשרויות עבור התפלגות החלקיקים יוצרות התאמה לפונקציית הפאזה הנמדדת (ראה איור 5), למרות שהן מייצרות מאפיינים שונים של הקיטוב כפי שהוא נראה באיור 6. ניתן להשתמש בהבדלים אלה כדי לזהות את ההתפלגות הבסיסית של החלקיקים במדגם. הבחירה הטובה ביותר היא להשתמש בהתפלגות הרגילה הקטומה במקום בחלקיקים הבינוניים (ראה איור 6). אם נעשה שימוש בפונקציות מנורמלות בלבד, ההפצות המשמשות כבסיס לא ניתן להבחין בהן (השוואת איור 5, איור 6, איור 7). באיור 7 עבור depolarization, התוצאות מספריים יש תכונות דומות לעקומה נמדד, אבל הפונקציות מוזדות על ידי 10 ° לכיוון כיוון לאחור. מדד השבירה האפקטיבי מתקן באופן חיובי את התוצאות כפי שנראה מן הסימולציות שהושגו עם ובלי המדיום האפקטיבי (ראה איור 5, איור 6, איור 7). ההבדלים בקיטוב (איור 6) מצביעים על כך שלמדגם יש ככל הנראה מבנה מורכב יותר (למשל, מעיל וליבה נפרדים) מאשר המודל הומוגנית שלנו. עם זאת, מעבר לשיטות המיקרוסקופית הקיימות לאפיון מדגם כדי לאחזר את המבנה האמיתי של הצבירה. פיזור הרקע העקבי התווסף בנפרד לתוצאות. המידות חסרות בעוצמה מסוימת בזווית שנצפתה בזוויות פיזור הרקע, אבל מידת הקיטוב הליניארית שלילית יותר בין 0-30 ° שאין אפשרות להפיק ללא פיזור החזרה קוהרנטי (השוואת "הפצה" באמצעות "no cb", ראו איור 5, איור 6 ).

עבור יישומים מערכת השמש, השוואנו את וסטה ספקטרום נצפתה ואת הספקטרום המודל המתקבל על ידי ביצוע הפרוטוקול 3. התוצאות מוצגות באיור 3 ובאיור 8 והם מציעים כי חלקיקים howte, עם יותר מ 75% מהם בעל גודל החלקיקים קטן יותר 25 μm, לשלוט re, וסטה של החדש. למרות ההתאמה הכוללת הוא די משביע רצון, ספקטרום המודל נצפתה שונים מעט: מרכזי הלהקה הקליטה של הספקטרום המודל הם העביר לאורכי גל ארוכים יותר, ואת קיצון ספקטרלי מקסימה נוטים להיות רדוד לעומת הנצפים ספקטרום. ההבדלים קיצון ומקסימה יכול להיות מוסבר על ידי העובדה כי השפעות צל הדדית בין החלקיקים re, לא נספרו: אפקטי הוספת צל חזקים יותר עבור השתקפות נמוכות וחלשים יותר עבור השתקפות גבוהה, ב המובן היחסי, להקטין את מינימה ספקטרלי ולהגדיל את מקסימה ספקטרלית כאשר מדווח בדוגמנות. יתר על כן, החלק הדמיוני של המורכב השבירה המדדים של האוארדיט נגזר מבלי לקחת בחשבון בקנה מידה של אורך הגל, ולכן הערכים הנגזרים הם קטנים מדי כדי להסביר את מהפך ספקטרלי. כאשר משתמשים בערכים אלה במודל שלנו על ידי ניצול אופטיקה גאומטרית, עומק הלהקה בספקטרום המודל יכול להיות רדוד מדי. אלה אפקטים בקנה מידה של אורך הגל יכול גם לשחק חלק באורכי גל ארוכים יחד עם תרומה קטנה של הזנב נמוכה של ספקטרום פליטה תרמית. ההבדלים יכולים גם להיגרם על ידי חוסר התאמה של משתנה של המדגם שלנו הובידיט מינרלים וסטה ועל ידי הפצה בגודל חלקיקים שונים הדרושים עבור המודל. בסופו של דבר, ספקטרום ההשתקפות של וסטה נצפו ב 180-200 K, והדוגמית שלנו ההארדיטה נמדד בטמפרטורת החדר. רדי ואח '³² הראו כי פס הקליטה מרכזי משמרת לאורכי גל ארוכים יותר עם הגדלת הטמפרטורה.

בשלב הפומטרי והפולקטמטרי עקומת התצפיות של האסטרואיד (4) וסטה הם מ Gehrels³³ ואת נאס א של מערכת הנתונים הפלנטרית של מערכות המידע של הגופים הקטנים (http://pdssbn.astro. umd.edu/sbnhtml), בהתאמה. המידול שלהם עוקב אחר שלב 4 ומתחיל השבירה החלקיקים מדד התפלגות גודל זמין ממידול ספקטרומטרי באורך הגל של 0.45 μm. חלקיקים אלה יש גדלים גדולים יותר 5 μm, כלומר, הרבה יותר גדול מאורך הגל והם ולכן במשטר אופטיקה גיאומטרי, הנקרא אוכלוסיית חלקיקים גדולים. עבור מידול עקומת הפאזה, אוכלוסיית חלקיקים קטנים נוספים של חלקיקים בקנה מידה צפוף בצפיפות תת-גל משולבים גם, עם תשומת לב משולמת כדי למנוע התנגשויות עם הדוגמנות הספקטרומטרית לעיל.

מדד השבירה המורכבת הוגדרה כדי 1.8 + i 0.000168. גודל החלקיקים האפקטיבי והפיזור היחיד באוכלוסייה הגדולה-חלקיק והחלקיקים הקטנים השווים (9.385 μm, 0.791) ו-(0.716 μm, 0.8935), בהתאמה. אורך הנתיב החופשי הממוצע במדיה הגדולה-חלקיק והחלקיקים הקטנים הם 16.39 יקרומטר ו-0.56 יקרומטר. המדיום הגדול חלקיקים יש צפיפות נפח של 0.4, ואילו בינונית-חלקיק קטן יש צפיפות העוצמה של 0.3. השברים של גדול-חלקיק ומדיה קטנה-חלקיק בתוך וסטה רגולית הם הניחו 99% ו 1%, בהתאמה, מתן הכולל בודד פיזור אלבדו של 0.815 ואורך נתיב חופשי ממוצע כולל של 12.78 μm. לאחר שלב 4, וסטה גיאומטריים אלבדו ב 0.45 יקרומטר מתברר להיות 0.32 בהסכם הוגן עם התצפיות (cf. איור 8 כאשר מתברר לזווית אפס שלב).

איור 9, איור 10, איור 11 מתארים את מידול בשלב הפוקטמטרי והקיטוב של עקומת מודלים עבור וסטה. עבור עקומת השלב הפוטומטרי (איור 10, שמאל), עקומת מודל שלב מ RT-CB כבר מלווה עם תלות ליניארית בסולם הגודל (מקדם מדרון-0.0179 mag/°), מחקה את האפקט של הצללה בצפיפות צפופה, . היי. לא הופעל שום שינוי לדרגת הקיטוב (איור 10, נכון; איור 11). המודל מסביר בהצלחה את הפוקטטריק הנצפה והקוטביות בשלב הקיטוב ומציעה חיזוי ריאליסטי עבור הקיטוב המקסימלי ליד זווית השלב של 100 °, כמו גם עבור המאפיינים בזוויות שלב קטן < 3 °.

זה מרשים כיצד בדקה חלק של אוכלוסיית החלקיקים הקטנים מסוגל להשלים את ההסבר של עקומות שלב (איור 10, איור 11). יש היבטים מודלים מסקרנים מעורבים. ראשית, כפי שמוצג באיור 9 (משמאל), השלב היחיד של פיזור החלקיקים עבור האוכלוסיות הגדולות והחלקיקים הקטנים הם דומים למדי, ואילו האלמנטים הפולריזציה הליניארים שונים באופן משמעותי. שנית, בחישובי RT-CB, שתי אוכלוסיות החלקיקים תורמות להשפעות העקביות של פיזור הרקע. שלישית, על מנת להשיג פולריזציה ריאליסטית מקסימה, יש להיות אוכלוסייה גדולה חלקיקים משמעותיים של רגולית (בהסכמה עם הדוגמנות ספקטרלי). עם ערבוב עצמאי הנוכחי של מדיה קטנה חלקיקים וחלקיקים גדולים, זה נשאר אפשרי להקצות חלק מתרומת חלקיקים קטנים אל משטחי החלקיקים הגדולים. עם זאת, כדי שאפקטי הרקע הקוהרנטיים מתקיימים ומסבירים את התצפיות, חובה לשלב אוכלוסיית חלקיקים קטנים.

סוכנות החלל האירופית (ESA) המשימה רוזטה של שביט 67 p/הצ-Gerasimenko סיפק הזדמנות למדוד את תפקוד השלב הפוטומטרי של התרדמת ואת הגרעין על טווח רחב זווית השלב בתוך כמה שעות³⁴. הפונקציות בשלב התרדמת הנמדד מראות וריאציה חזקה עם הזמן והמיקום המקומי של החללית. הפונקציה של שלב התרדמת בוצע בהצלחה²⁰ עם מודל חלקיקים המורכב חלקיקים אורגניים בגודל submicrometer וסיליקטיים באמצעות שיטות מספריות (שלבים 5 ו 2) כמוצג באיור 12. התוצאות מרמזות על כך שפיזור המידות של האבק משתנה בתרדמת עקב פעילות השביט והאבולוציה הדינמית של האבק. על ידי מידול פיזור על ידי אובייקט בגודל של 1 ק מ אשר המשטח שלו מכוסה חלקיקי אבק, הראינו כי פיזור על ידי גרעין השביט נשלט באותו סוג של חלקיקים ששולטים גם על הפיזור בתרדמת (איור 13).

איור 1: האסטרואיד (4) וסטה (שמאל) ו שביט 67 p/צ'יוומוב-Gerasimenko (מימין) ביקר על ידי משימת השחר של נאס א ועל ידי המשימה רוזטה ESA, בהתאמה. תמונה קרדיטים: נאס א/JPL/MPS/DLR/אידה/ביורק Jpl (משמאל), ESA/רוזטה/NAVCAM (מימין). אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

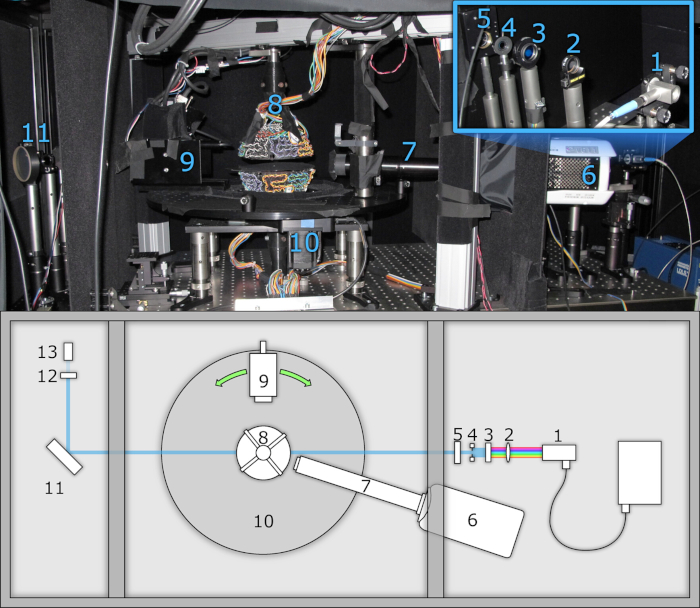
איור 2: פיזור אור מכשיר מדידה. תמונה (לעיל) ואת התצוגה העליונה סכמטית (להלן) מראה: (1) סיבים מצמידים מקור אור עם מפוצץ, (2) מיקוד העדשה (אופציונלי), (3) מסנן bandpass עבור בחירת אורך הגל, (4) הצמצם מתכווננת לעיצוב הקורה, (5) ממונע ליניארי מקטזר, ( מצלמה במהירות גבוהה, (7) מטרה בעלת הגדלה גבוהה, (8) לויטור אקוסטי להשמנה לדוגמה, (9) ראש מדידה, המורכב מסנן IR, תריס ממונע, מקטריר ליניארי ממונע, ושפופרת פוטוטוטיפייר (PMT), (10) השלב סיבוב מוטורי עבור התאמת זווית ראש המדידה, (11) שטוח אופטי עבור השתקפות פרנל, (12) דחיסות נייטרלית מסנן, ו (13) הפניה PMT, עבור ניטור עוצמת הקרן. המערכת מחולקת לשלושה תאים סגורים כדי למנוע אור תועה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

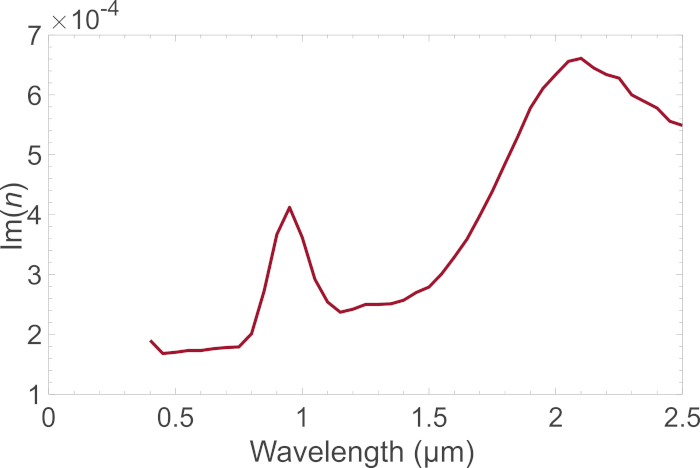
איור 3: החלק הדמיוני של מדד השבירה עבור המין הטוב ביותר כפונקציה של אורך הגל. החלק הדמיוני של השבירה Im (n) התקבל עבור מינרל האוארדיט על ידי ביצוע הפרוטוקול 3.1. מדד השבירה מנוצל במידול מאפייני פיזור של אסטרואיד (4) וסטה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

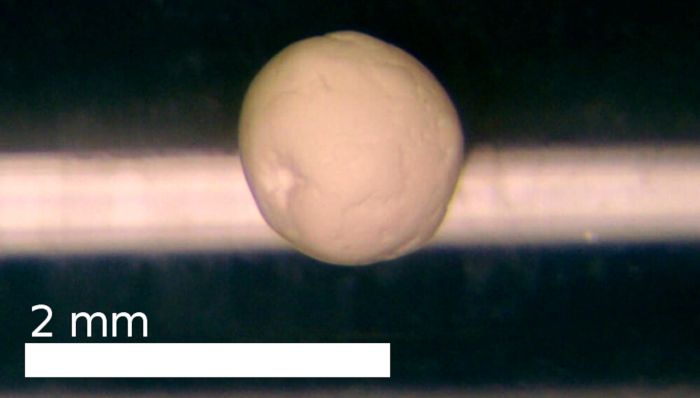
איור 4: דגימת המדידה המורכבת מחלקיקים מלאים בצפיפות של SiO₂ . המדגם כבר מלוטש בקפידה על מנת להשיג צורה כדורית כמעט המאפשרת גם ניסויים פיזור יעיל ומידול מספרי. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

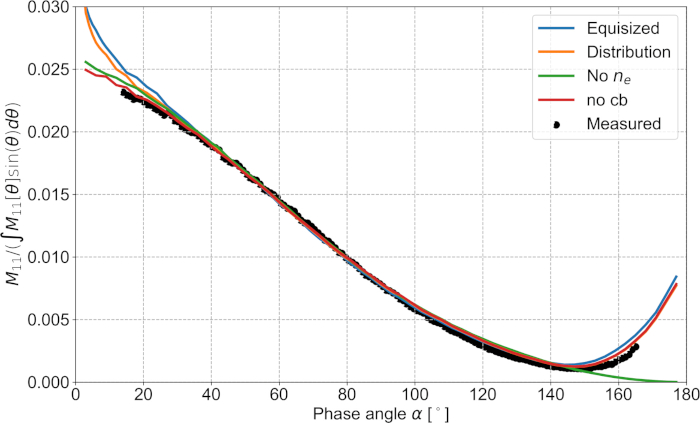
איור 5: פונקציה פאזה. פונקציות השלב של מצבור המדגם שהתקבלו על-ידי ביצוע הפרוטוקולים הניסיוניים 1 ואת שלב המידול המספרי 2. פונקציות הפאזה מנורמלות להעניק אחדות כאשר הם משולבים מ 15.1 ° עד 165.04 °. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

איור 6: מידת הקיטוב הליניארי. כמו באיור 5 לדרגת הקיטוב הליניארי של אור התקרית הבלתי מקוטב-M₁₂/M₁₁ (ב-%). אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

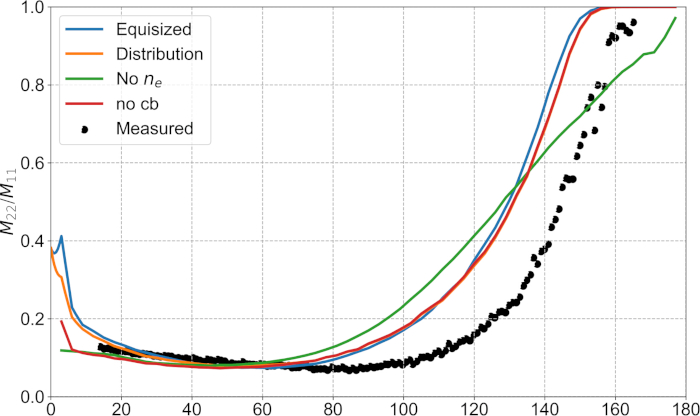
איור 7: דפולריזציה. כמו באיור 5 לגבי הדפולריזציה משנת ₂₂/m₁₁. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

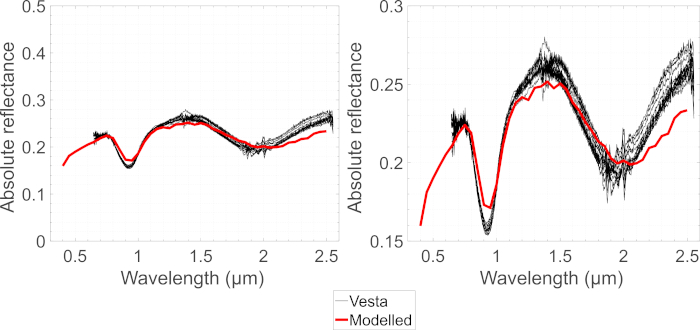
איור 8: ספקטרום השתקפות מוחלט. אסטרואיד (4) וסטה של המודל והתבונן השתקפות מוחלטת ספקטרום ב 17.4-מעלות שלב זווית. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

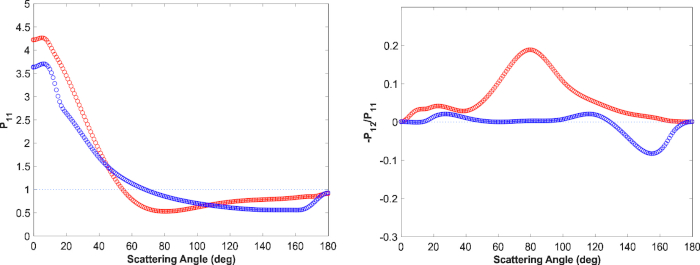
איור 9: פיזור שלב פונקציה P₁₁ ומידת הקיטוב הליניארי לאור התקרית הבלתי מקוטב -P₂₁/p₁₁ כפונקציה של זווית הפיזור עבור רכיבי נפח של חלקיקים גדולים (אדום) וחלקיקים קטנים (כחול) בריגולה של אסטרואיד (4) וסטה. הקו המנוקד מציין פונקציית שלב היפוטרופית (משמאל) ורמת אפס של קיטוב (מימין). אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

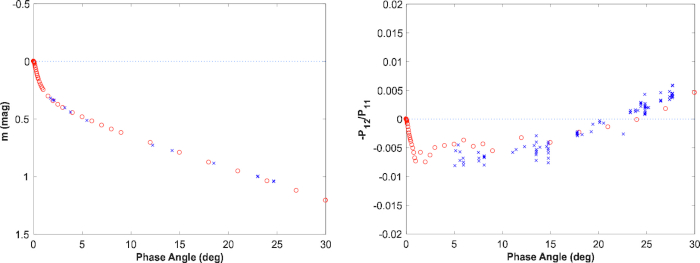
איור 10: נצפה (כחול) ו המודל (אדום) בהירות משולבת דיסק בקנה המידה, כמו גם את מידת הקיטוב הליניארי לאור האירוע מקוטב כפונקציה של השלב זווית האסטרואיד (4) וסטה. התצפיות הפוקטריות והקיטוב הן מGehrels (1967) וצומת הגופים הקטנים של מערכת הנתונים הפלנטרית (http://pdssbn.astro.umd.edu/sbnhtml), בהתאמה. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

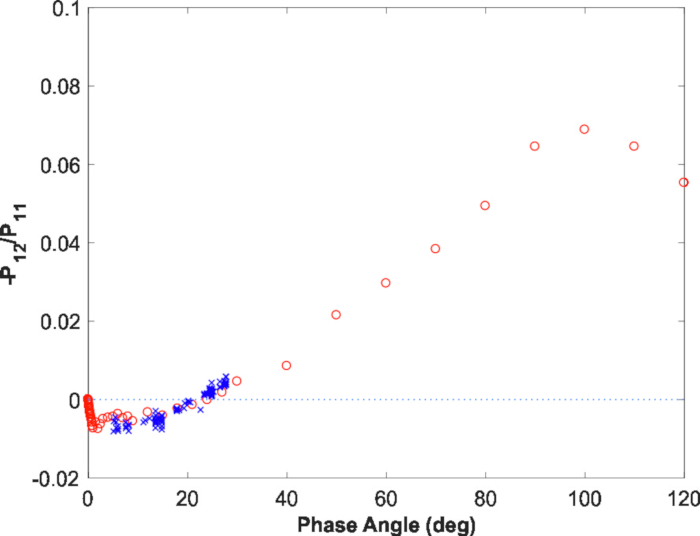
איור 11: מידת הקיטוב הליניארי. מידת הקיטוב הליניארי של האסטרואיד (4) וסטה החזוי לזוויות פאזה גדולות המבוססות על מידול מספרי פיזור מספריים. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

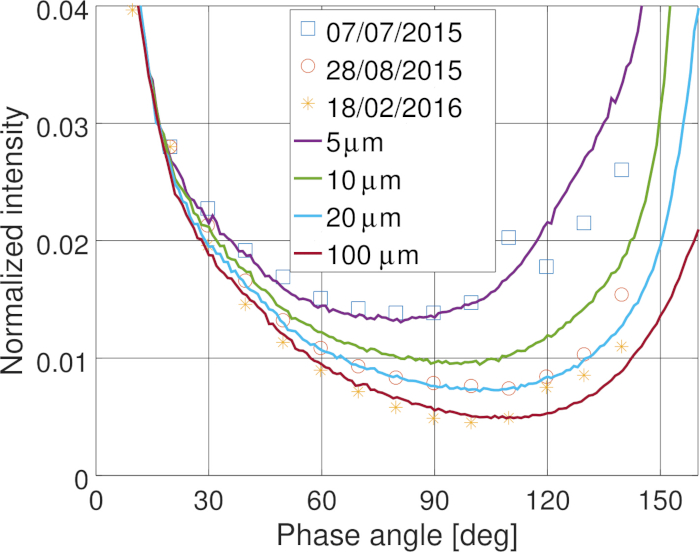
איור 12: המודל של השלב הפומטרי והנמדד בתרדמת . של שביט-גאסימוב-גרסימיקו הווריאציות של השלב הנמדד פונקציות בזמן יכול להיות מוסבר על ידי התפלגות בגודל אבק שונים בתרדמת. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

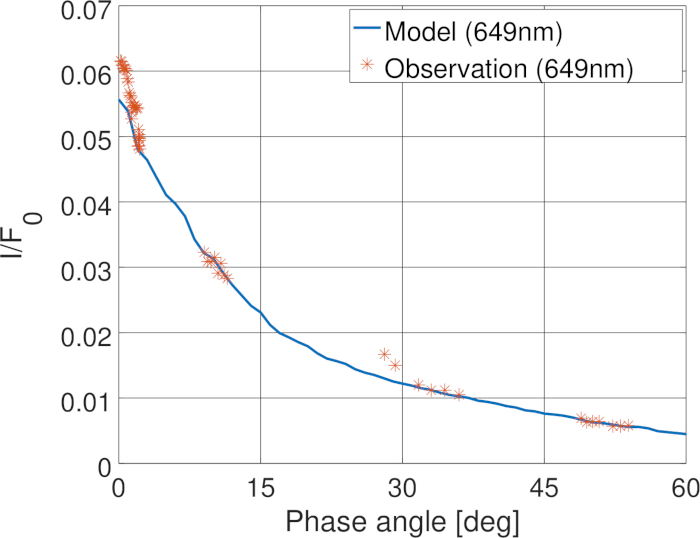
איור 13: פונקציות פאזה. פונקציות הפאזה ומדד של הגרעין של שביט 67 p. אנא לחץ כאן כדי להציג גירסה גדולה יותר של איור זה.

Discussion

שיטות נסיוניות, תאורטי וחישוביות הוצגו לפיזור אור על ידי תקשורת אקראית בדידה של חלקיקים. השיטות הנסיוניות השתמשו כדי לאמת את המושגים הבסיסיים בשיטה התיאורטית והחישובית. השיטות האחרונות הוחלו לאחר מכן בהצלחה בפרשנות של תצפיות אסטרונומיות של אסטרואיד (4) וסטה ושביט 67 p/צ'יוומוב-גראסימיקו.

הלומטר הנסיוני מסתמך על ריחוף בדגימה מבוקרת באולטרסאונד המאפשר מדידות מולר-מטריקס לצבור מדגם בכיוון הרצוי. הצבירה יכולה להיות מנוצל שוב ושוב במידות, כפי שניתן לשמר את הצבירה לאחר כל ערכת מדידה. זוהי הפעם הראשונה שאין ליצור קשר, מדידות פיזור שאינן הרסניות, מתבצעות במדגם תחת שליטה מלאה.

השיטות התאורטי והחישוביות מסתמכות על תהליכי הפיזור, הספיגה וההשמדה הלא בסדר בתקשורת אקראית. הואיל והאינטראקציות האלקטרומגנטיות המדויקות תמיד מתרחשות בצורה מדויקת, בתוך מדיום אקראית אינסופי לאחר מבצעות בממוצע, רק אינטראקציות בלתי מדויקות נשארות בין רכיבי נפח של חלקיקים. בעבודה הנוכחית, האינטראקציות האינן מדויקות בקרב המרכיבים הללו מעובדות בדיוק על-ידי שימוש במשוואות של מקסוול: לאחר הפחתת השדות הקוהרנטיים מהשדות בחלל החופשי, זהו התחום החסר היגיון בתוך המדיום האקראי שנשאר. הטיפול הועבר כיום לקשיחות המוחלטת שלה בכך שאינטראקציות, כמו גם הכחדה, פיזור ומקדמי הקליטה של המדיום, נגזרות מתוך מסגרת של אינטראקציות בחוסר היגיון. יתר על כן, זה הוכח כי החשבונאות עבור השפעות השדה קוהרנטי על הממשק בין החלל החופשי התוצאות בינונית אקראית בטיפול הכולל מוצלח עבור מדיום אקראית מוגבל.

היישום של שיטות תיאורטי וחישובית כבר מומחש עבור מדידות ניסיוני של מדגם כדורי מ"מ בקנה מידה של מילימטר מורכב משני חלקיקים בקנה מידה של כדורי מיקרו-מיקרון. היישום מציג, חד-משמעית, כי צבירה לדוגמה חייב להיות מורכב התפלגות של חלקיקים עם גדלים שונים, במקום להיות מורכב חלקיקים כדוריים בינוניים. ייתכנו השלכות מרחיקות לכת על תוצאה זו לאפיון מדיה אקראית: סביר שהתקשורת מורכבת באופן משמעותי יותר ממה שהסיק קודם לכן באמצעות שיטות אפיון משוכלל.

פרשנות מפה סינופטית של הספקטרום של האסטרואיד (4) וסטה לרוחב אורכי גל הגלויים והכמעט אינפרא-אדום, כמו גם וסטה של הדרך הפוטומטרית ומטריקה בשלב עקומות באורך הגל של 0.45 יקרומטר מראה כי הוא מעשי כדי לנצל את השיטות מספריים לאלץ את קומפוזיציות המינרלים, הפצות גודל החלקיקים, כמו גם צפיפות העוצמה החוזרת מתצפיות אסטרונומיות מרוחקות. אחזורים מסוג זה משופרים עוד יותר על-ידי הפרשנות הסימולטנית של השלב הפומטרי של שביט 67 p/צ'יוומוב-גראסימנקו בנוגע לתרדמת ולגרעין. לבסוף, מידול ריאליסטי של עקומת השלב הקיטוב של 67 p הושגה²⁰. ישנם הסיכויים העיקריים בעתיד ביישום שיטות הנוכחי בפרשנות של תצפיות של אובייקטים מערכת השמש בגדול.

יש סיכויים עתידיים לגישה הניסיונית והתיאורטית המשולבת הנוכחית. כפי שקשה מאוד לאפיין במדויק מדיה אקראית המורכבת של מדידות תת-גל בקנה מידה, בפיקוח מולר מטריקס המדידות יכול להציע כלי לאחזור מידע על צפיפות נפח התפלגות גודל החלקיקים ב המדיום. היפוך כמותי של פרמטרים פיזיים אלה הוא הקלה על ידי השיטות המספרי הספר.

Materials

Name	Company	Catalog Number	Comments
10GL08	Newport		Calcite polarizer
12X Zoom Body Tube 1-50487AD	Navitar		Microscope objective
43-412-000	Edmund optics		Optical flat
8MPR16-1	Standa		Motorized Polarizer Rotator
8MRB240-152-59D	Standa		Rotation stage
8SMC5-ETHERNET	Standa		Motor controller
Digi-pas DWL3500XY	Digi-pas		Digital 2-axis level
DMT 65-D25-HiDS	Owis		Optics rotation stage
EQ-99 LDLS	Energetiq		Light source
FL488-10	Thorlabs		Laser line filter
IBM 65-D0-35-HiDS	Owis		Motorized iris shutter
LPVISE100-A	Thorlabs		Film polarizer
microPMT H12403-01	Hamamatsu		Photomultiplier tube
NI PXIe-5171R	National Instruments		Digital oscilloscope
NI PXIe-8880	National Instruments		PXIe chassis
Phantom v611	Vision Research		High speed camera
PS 10-32-DC	Owis		Motor controller
RC08FC-P01	Thorlabs		Fiber collimator
SET-NDF-D22-G25	Owis		Neutral density filter
TIA60	Thorlabs		PMT amplifier