Streuung und Absorption des Lichts in planetarischen Regolithen

Zusammenfassung

Numerische und experimentelle Methoden werden für die mehrfache Streuung von Licht in diskreten Zufallsmedien dicht gepackter Teilchen vorgestellt. Die Methoden werden verwendet, um die Beobachtungen des Asteroiden (4) Vesta und des Kometen 67P/Tschurjumow-Gerasimenko zu interpretieren.

Zusammenfassung

Theoretische, numerische und experimentelle Methoden werden für die mehrfache Streuung von Licht in makroskopischen diskreten Zufallsmedien dicht gepackter mikroskopischer Partikel vorgestellt. Die theoretischen und numerischen Methoden bilden einen Rahmen der Radiativen Übertragung mit wechselseitigen Transaktionen (R²T²). Das R²T2-Framework beinhaltet die Streureihenfolge von Taktungen im Frequenzraum in Monte Carlo, wobei davon ausgegangen wird, dass die fundamentalen Streuer und Absorber Wellenlängen-Volumenelemente sind, die aus einer großen Anzahl zufälliger verteilten Partikeln. Die diskreten Zufallsmedien sind vollgepackt mit den Volumenelementen. Für sphärische und nichtsphärische Partikel werden die Wechselwirkungen innerhalb der Volumenelemente exakt mit der Superposition T-Matrix-Methode (STMM) bzw. der Volume Integral Equation Method (VIEM) berechnet. Für beide Partikeltypen werden die Wechselwirkungen zwischen verschiedenen Volumenelementen exakt mit dem STMM berechnet. Da die Rückverfolgung innerhalb der diskreten Zufallsmedien stattfindet, werden inkohärente elektromagnetische Felder genutzt, d.h. das zusammenhängende Feld der Volumenelemente wird aus den Wechselwirkungen entfernt. Die experimentellen Methoden basieren auf der akustischen Schwebung der Proben für berührungslose, zerstörungsfreie Streumessungen. Die Schwebeung beinhaltet eine vollständige Ultraschallkontrolle der Probenposition und -ausrichtung, d.h. sechs Freiheitsgrade. Die Lichtquelle ist eine lasergesteuerte Weißlichtquelle mit Monochromator und Polarisator. Der Detektor ist ein Mini-Photomultiplier-Rohr auf einem rotierenden Rad, ausgestattet mit Polarisatoren. Die R²T2 wird anhand von Messungen für eine kugelförmige Probe von dicht gepackten sphärischen Kieselsäurepartikeln im mm-Maßstab validiert. Nach der Validierung werden die Methoden angewendet, um astronomische Beobachtungen für den Asteroiden (4) Vesta und den Kometen 67P/Tschurjumow-Gerasimenko (Abbildung1) zu interpretieren, die kürzlich von der NASA-Dawn-Mission bzw. der ESA-Mission Rosetta besucht wurden.

Einleitung

Asteroiden, Kometenkerne und Objekte des luftlosen Sonnensystems im Großen und Ganzen werden von planetarischen Regolithen, losen Schichten von Teilchen unterschiedlicher Größe, Form und Zusammensetzung bedeckt. Für diese Objekte werden zwei allgegenwärtige astronomische Phänomene in kleinen Sonnenphasenwinkeln beobachtet (sonnenobjekt-Beobachterwinkel). Zunächst wird die Helligkeit des streunenden Lichts in der astronomischen Magnitudenskala beobachtet, um nichtlinear in Richtung des Nullphasenwinkels zu zunehmen, der gemeinhin als Oppositionseffekt^1,2bezeichnet wird. Zweitens wird das gestreute Licht teilweise linear parallel zur Streuebene (der Sonnenobjekt-Beobachterebene) polarisiert, die gemeinhin als negative Polarisation³bezeichnet wird. Die Phänomene haben seit Ende des 19. Jahrhunderts keine quantitative Interpretation für den Oppositionseffekt und seit Anfang des 20. Jahrhunderts für die negative Polarisierung. Ihre richtige Interpretation ist Eine Voraussetzung für die quantitative Interpretation der photometrischen, polarimetrischen und spektrometrischen Beobachtungen von airless-Objekten sowie für die Radarstreuung von ihren Oberflächen.

Es wurdevorgeschlagen 4^,5,6,7, dass der kohärente Rückstreumechanismus (CBM) bei der Mehrfachstreuung zumindest teilweise für die astronomischen Phänomene verantwortlich ist. Im CBM stören Partizipatorwellen, die mit den gleichen Streuern in entgegengesetzter Reihenfolge interagieren, immer konstruktiv in die exakte Rückstreurichtung. Dies ist auf die gleichzeitigen optischen Pfade der wechselseitigen Wellen zurückzuführen. In anderen Richtungen variiert die Interferenz von destruktiv bis konstruktiv. Die Konfigurationsmittelung innerhalb eines diskreten zuzufälligen Partikelmediums führt zu einer verbesserten Rückstreuung. Was die lineare Polarisation betrifft, so ist das CBM selektiv und führt zu einer negativen Polarisation bei positiv polarisierenden Einzelstreuern, ein gemeinsames Merkmal bei der Einzelstreuung (vgl. Rayleigh-Streuung, Fresnel-Reflexion).

Die Streuung und Absorption elektromagnetischer Wellen (Licht) in einem makroskopischen Zufallsmedium mikroskopischer Teilchen stellt ein offenes Rechenproblem in der planetarischen Astrophysik^8,9dar. Wie oben dargestellt, hat dies dazu geführt, dass es keine quantitativen inversen Methoden zur Interpretation bodenbasierter und raumbasierter Beobachtungen von Objekten des Sonnensystems gibt. Im vorliegenden Manuskript werden neuartige Methoden vorgestellt, um die Kluft zwischen den Beobachtungen und ihrer Modellierung zu überbrücken.

Experimentelle Messungen der Streuung durch eine Kleinpartikelprobe in kontrollierter Position und Ausrichtung (sechs Freiheitsgrade) blieben offen. Streueigenschaften für einzelne Partikel wurden früher als Ensembledurchschnitte über größe, Form und Ausrichtungsverteilung¹⁰ gemessen, indem ein Partikelfluss durch das Messvolumen eingeführt wurde. Streueigenschaften für Einzelne Partikel in der Schwebe wurden z.B. mit elektrodynamischer Schwebebahn¹¹ und optischer Pinzette^12,13,14durchgeführt. Im vorliegenden Manuskript wird eine neuartige experimentelle Methode angeboten, die auf Ultraschallschwebeung mit voller Kontrolle der Probenposition und -ausrichtung basiert.

Das vorliegende Manuskript fasst die Ergebnisse eines Projekts zusammen, das 2013-2018 vom Europäischen Forschungsrat (ERC) für fünf Jahre gefördert wurde: Streuung und Absorption elektromagnetischer Wellen in particuLate Medien (SAEMPL, ERC Advanced Grant). SAEMPL gelang es, seine drei Hauptziele zu erreichen: Erstens wurden neuartige numerische Monte-Carlo-Methoden für die mehrfache Streuung durch diskrete zufällige Medien von dicht gepackten Teilchen^16,17,18abgeleitet; zweitens wurde eine neuartige experimentelle Instrumentierung für kontrollierte Labormessungen vonValidierungsproben in der Schwebe 15 entwickelt und konstruiert; drittens wurden die numerischen und experimentellen Methoden angewandt, um astronomische Beobachtungen zu interpretieren^19,20.

Im Folgenden werden Protokolle zur Nutzung der experimentellen Streupipeline für Messungen, der entsprechenden Rechenpipeline sowie der Anwendungspipelines ausführlich beschrieben. Die Rechenpipeline besteht aus Software für asymptotisch exakte Berechnungen bei endlichen Teilchensystemen (Superposition T-Matrix-Methode STMM²¹ und Volume Integral Equation Method VIEM²²) und ungefähre Berechnungen für asymptotisch unendliche diskrete Zufallsmedien von Teilchen mit mehreren Streumethoden (SIRIS^23,24, Radiativtransfer mit coherent Backscattering RT-CB^8,9und Strahlungstransfer mit wechselseitigen Transaktionen R²T^216,17,18). Die experimentelle Pipeline umfasst die Vorbereitung, Lagerung und Nutzung der Proben, deren Schwebung im Messvolumen und die Durchführung der tatsächlichen Streumessung über den Bereich der Streuwinkel mit unterschiedlichem Polarisator. Konfigurationen. Die Anwendungspipeline betrifft die Nutzung der rechnerischen und experimentellen Pipelines zur Interpretation astronomischer Beobachtungen oder experimenteller Messungen.

Protokoll

1. Lichtstreuung

1. Einrichten des Streumessers für die Messung (Abbildung2)
   1. Richten Sie zunächst das Streumesser ein, indem Sie die Lichtquelle, die Photomultiplikatorröhren (PMTs) und die Verstärker einschalten. Lassen Sie das System für 30 min stabilisieren.
   2. Richten Sie den Einfallsbalken mit Lochlöchern aus und zentrieren Sie sie. Zwei Lochlöcher werden an vorgemessenen Punkten auf der rotierenden Brotplatte befestigt, 180° auseinander und im gleichen Radius. Zentrieren Sie den Strahl auf das erste Loch und stellen Sie seinen Winkel so ein, dass das Licht auch durch das zweite Loch eindringt.
2. Einrichten des akustischen Sample-Levitators
   1. Richten Sie als Nächstes den akustischen Sample-Levitator ein, indem Sie das Mikrofon in der Mitte des Levitators einsetzen und das Kalibrierskript ausführen.
   2. Kalibrieren Sie den phasenweisen akustischen Levitator, indem Sie den Schalldruck für jedes Arrayelement im vorgesehenen Schwebepunkt in Abhängigkeit von der Antriebsspannung messen. Verwenden Sie diese Kalibrierung, um Unterschiede zwischen den Arraykanälen auszugleichen. Positionieren Sie das Kalibriermikrofon, indem Sie seinen Schatten sowohl im Strahl als auch in einem senkrechten Strahl zentrieren, der mit zwei Spiegeln erstellt wurde.
   3. Berechnen Sie die Fahrparameter für das Array, das eine asymmetrische Akustische Falle erzeugt, und versorgen Sie sie mit der Signalgenerierungselektronik. Dies wird erreicht, indem das Gor'kov-Potential²⁵ minimiert und die Druckgradienten im Schwebepunkt ausgerichtet werden.
   4. Dann machen Sie einen Messfeger mit einem leeren Levitator. Der Sweep zeigt alle Signale, die durch Umgebungslicht, Reflexionen aus der Umgebung oder elektrische Geräusche erzeugt werden.
3. Probenhandhabung, Einfügung und Messung
   1. Verwenden Sie nach dem Einrichten einen akustisch transparenten Mesh-Löffel, um die Probe in den akustischen Levitator zu injizieren.
   2. Mit einer Videokamera und einer Hochvergrößerungsoptik können Sie die Ausrichtung und Stabilität der Probe vor und nach den Streumessungen überprüfen.
   3. Die Festigkeit und Asymmetrie der Akustikfalle ist für maximale Probenstabilität optimiert. Dadurch wird die Schallenergie so gering wie möglich eingestellt.
   4. Wenn die Probe asymmetrisch ist, drehen Sie sie um die vertikale Achse, um Informationen über ihre Form zu erhalten. Führen Sie die Drehung durch langsames Ändern der Ausrichtung der akustischen Falle. Wenden Sie während der Bildgebung zusätzliche Beleuchtung an, um die Bildqualität zu verbessern.
   5. Schließen Sie anschließend die Messkammer, um externes Licht zu blockieren.
   6. Wählen Sie über die Computerschnittstelle die Ausrichtung der Probe sowie die Winkelauflösung und den Bereich der Messung aus. Das eintreffende und das Streulicht werden durch lineare Polarisatoren gefiltert, die motorisiert sind.
   7. Führen Sie den automatisierten Mess-Sweep aus. Dadurch werden vier Punkte für jeden Winkel mit Polarisatorausrichtungen von (horizontal, horizontal), (horizontal, vertikal), (vertikal, vertikal) und (vertikal, horizontal) gemessen.
   8. Wiederholen Sie jeden Sweep dreimal, um Ausreißer zu eliminieren. Wiederholen Sie bei asymmetrischen Proben die Messung in verschiedenen Probenausrichtungen.
   9. Stellen Sie die Probe nach der Messung wieder her, indem Sie das akustische Feld abschalten und die Probe auf das akustisch transparente Gewebe fallen lassen. Führen Sie dann einen weiteren Mess-Sweep mit leerem Levitator aus, um mögliche Drifts aufgrund der Umgebungslichtbedingungen zu erkennen.
   10. Wenn Sie fertig sind, speichern Sie die Daten. Analysieren Sie die Daten, um Mueller-Matrixelemente für jeden Winkel durch lineare Kombination von Intensitäten bei verschiedenen Polarisationen zu berechnen¹

2. Modellierung der mm-großen, dicht gepackten Kugelmedien, bestehend aus kugelförmigen Partikeln

1. Verwenden Sie zum Starten der Modellierung den SSH-Zugriff, um eine Verbindung zum Cluster Taito des CSC – IT Center for Science Limited herzustellen.  Laden Sie alle erforderlichen Programme herunter und kompilieren Sie sie, die für Taito vorkonfiguriert sind, indem Sie bash compile.shausführen.
2. Wechseln Sie in das Arbeitsverzeichnis, indem Sie cd $WRKDIRausführen.
3. Laden Sie Quellendateien mit git herunter (git clone git-bitbucket.org:planetarysystemresearch/protocol2.git protocol2).
4. Wechseln Sie in das neu erstellte Verzeichnis cd protocol2.
5. Laden Sie erforderliche Programme herunter und kompilieren Sie die erforderlichen Programme, indem Sie bash compile.shausführen, die für Taito vorkonfiguriert sind.
6. Öffnen Sie anschließend den Texteditor nano, und richten Sie die Parameter für einen einzelnen Streuer, ein Volumenelement und das untersuchte Beispiel so ein, dass sie mit der untersuchten Stichprobe übereinstimmen, indem Sie die Datei PARAMSändern.
7. Führen Sie dann die Pipeline aus, indem Sie einen Befehls-Bashrun.sh ausführen. Wenn Sie fertig sind, schreiben Sie die vollständige Mueller-Matrix des Samples als final.outin den temporären Ordner .

3. Interpretation der Reflexionsspektren für Asteroid (4) Vesta

1. Ableitung der komplexen Brechungsindizes für Howardit.
   1. Laden Sie SIRIS4 (git clone git-bitbucket.org:planetarysystemresearch/siris4.2.git) herunter.
   2. Kompilieren, indem Sie make im src-folder ausführen. Benennen Sie die ausführbare dateiierbasierter Datei siris42 in siris4um.
   3. In mainGo.f90,ändern Sie Zeile 395 zu r0=0.05*rmax*sqrt(ran2). Kompilieren, indem Sie makeausführen.
   4. Laden Sie die benötigten MATLAB-Skripte herunter, indem Sie "git clone git-bitbucket.org:planetarysystemresearch/protocol4a.git" ausführen.
   5. Kopieren Sie die ausführbaren Dateien, die in den Schritten 3.1.2 erstellt wurden. und 3.1.3. joVEOptimize-folder.
   6. Wechseln Sie zum Ordner JoVEOptimize.
   7. Legen Sie in input1.in Datei den Radius für die Größe des Howarditpartikels auf 30 m fest, und fixieren Sie den realen Teil des Brechungsindexes auf 1,8. Legen Sie in input2.in Datei den Radius auf 15.000 m fest.
   8. Schätzen Sie die oberen und unteren Grenzen für den imaginären Teil der Brechungsindizes und speichern Sie sie in zwei separaten Dateien. Der Code verwendet die Bisektionsmethode und diese Werte als Ausgangspunkt.
   9. Legen Sie in der Datei optimizek.m die Dateinamen der oberen und unteren Grenzen des imaginären Teils der Brechungsindizes und den Dateinamen des gemessenen Reflexionsspektrums des Howarditpulvers fest. Stellen Sie den Wellenlängenbereich mit 0,05-m-Schritten auf 0,4–2,5 m ein.
   10. Führen Sie optimizek.m in MATLAB aus, um die komplexen Brechungsindizes für Howardit zu erhalten (siehe Abbildung 3). Zunächst berechnet der Code Streueigenschaften für Howarditpartikel mit einer Größe von 30 m (Radius) und verwendet diese Partikel dann als diffuse Streuer innerhalb eines Volumens mit einer Größe von 15.000 m (Radius). Diese Schritte werden für jede Wellenlänge wiederholt, bis die berechnete Reflexion mit der gemessenen Reflexion übereinstimmt.
2. Modellierung des Reflexionsspektrums von Vesta.
   1. Berechnen der Streueigenschaften von Howarditpartikeln durch Verwendung von SIRIS4
      1. Verwenden Sie SIRIS4, um die Streueigenschaften von Howarditpartikeln zu berechnen, indem Sie zuerst die ausführbare Datei siris4 in denselben Ordner mit der Eingabedatei und der p-Matrix-Datei verschieben.  Kopieren Sie dann die eingabe_1.in und pmatrix_1.in aus dem Testordner.
      2. In input_1.inlegen Sie die Anzahl der Strahlen auf 2 Millionen, die Anzahl der Probenteilchen auf 1000, die Standardabweichung des Radius auf 0,17 und den Kraftrechtsindex der Korrelationsfunktion auf 3 fest. Legen Sie dann den realen Teil des Brechungsindex auf 1,8 fest, und verwenden Sie den imaginären Teil des Brechungsindex n, wie im Textprotokoll beschrieben.
      3. Führen Sie als Nächstes SIRIS4 aus, indem Sie den hier gezeigten Befehl für jede Wellenlänge von 0,4 bis 2,5 Mikrometer mit einem Größenbereich von 10 bis 200 Mikrometern Durchmesser mit einem Abtastschritt von 10 Mikrometern ausführen.
      4. Speichern Sie als Nächstes jede berechnete Streuphasenmatrix P in einer Datei pmatrix_x.in.  Das x im Dateinamen beschreibt die Wellenlängenzahl und reicht von 1 bis 43 für jede Partikelgröße. Die Datei enthält die Streuwinkel sowie die Streumatrixelemente P₁₁, P₁₂, P₂₂, P₃₃, P₃₄ und P₄₄ für eine Wellenlänge und Partikelgröße.
   2. Durchschnitt der erhaltenen Streumatrizen, Einzelstreualbedos und mittelfreien Pfade über eine Größenverteilung des Machtgesetzes mit einem Index wert von 3,2 ^{19 , 24}.
      1. Verschieben Sie die pmatrix-Dateienin Ordner, sodass jeder Ordner eine Partikelgröße darstellt und die berechneten p-Matrizen für alle Wellenlängen enthält. Benennen Sie die Ordner fold1, fold2,..., foldN, wobei N die Anzahl der Partikelgrößen ist.
      2. Schreiben Sie die Streuungs- und Auslöschungseffizienzen q_sca und q_extsowie die Gleich-projizierten Flächen-Kugel-Radiuswerte r aus den outputQ-Dateienin eine Datei, Qscas.dat.
      3. Wechseln Sie zum Ordner JoVEAverage, der in Schritt 3.1.4 heruntergeladen wurde.
      4. Verschieben Sie die Ordner und Qscas.dat in denselben Ordner mit AvgPowerLaw.m.
      5. Führen Sie AvgPowerLaw.m in MATLAB aus. Der Code berechnet gemittelte Streuungsmatrizen, Einstreualbedos und mittlere Freie-Pfad-Längen über eine Power-Law-Größenverteilung mit Index 3.2.
   3. Berechnung des Endspektrums von Vesta durch Verwendung von SIRIS4
      1. Verwenden Sie diffuse Streuer innerhalb eines Vesta-großen Volumens mit einem Brechungsindex von 1. Verwenden Sie in der Eingabedatei die gemittelten Albedos mit nur einer Streuung und die mittleren freien Pfadlängen für interne Streuer.
      2. Führen Sie als Nächstes SIRIS4 bei jeder Wellenlänge aus, indem Sie den hier gezeigten Befehl ausführen, wobei X die Wellenlänge ist. Der Code liest die gemittelten Streuungsmatrizen als Eingabe für die internen diffusen Streuer.
      3. Untersuchen Sie die absolute Reflexion in einem Phasenwinkel von 17,4 Grad.
      4. Besorgen Sie sich Vestas beobachtete Spektren im Phasenwinkel von 17,4 Grad aus dem NASA Planetary Data System²⁶.
      5. Skala Vestas beobachtete Spektren auf einen geometrischen Albedowert von 0,42327 bei 0,55 Mikrometern²⁷. Um auf 17,4 Grad zu kommen, wenden Sie einen Faktor von 0,491 auf die skalierten Spektren²⁸an. Vergleichen Sie sowohl die modellierten als auch die beobachteten Spektren über den gesamten Wellenlängenbereich hinweg.

4. Photometrische und polarimetrische Modellierung von (4) Vesta

1. Berechnung der Streueigenschaften für Volumenelemente, die Voronoi-förmige Howarditpartikel enthalten
   1. Verbinden Sie sich über SSH-Zugriff mit dem Cluster Taito des CSC – IT Center for Science Ltd.
   2. Wechseln Sie in das Arbeitsverzeichnis, indem Sie cd $WRKDIRausführen.
   3. Laden Sie die Quelldateien herunter (git clone git-bitbucket.org:planetarysystemresearch/jvie_t_matrix.git).
   4. Kompilieren, indem Sie make im -folder ausführen.
   5. Generieren Sie Volumenelemente, die Voronoi-förmige Howarditpartikel enthalten, mithilfe eines MATLAB-Codes voronoi_element.m. In voronoi_element.m die Wellenlänge auf 0,45 'm, N_elems auf 128, den Größenparameter (elem_ka) auf 10, den Power-Law-Index auf 3, den minimalen Partikelradius auf 0,143 'm, den maximalen Partikelradius auf 0,35 'm, die Packungsdichte auf 30% einstellen und den abgeleiteten komplexen Brechungsindex verwenden für Howardit.
   6. Führen Sie voronoi_element.m in MATLAB aus. Der Code erzeugt 128 Netzdateien für Volumenelemente mit unterschiedlichen Voronoi-Partikel-Realisierungen unter Verwendung der Power-Law-Größenverteilung.
   7. Berechnen Sie T-Matrizen für die generierten Volumenelemente mit JVIE. Legen Sie in runarray_JVIE_T.sharray=1-128 fest. Die Paramater sind k = 13.962634, mesh = Name des erzeugten Netzes in 4.1.6, T_out = Name der Ausgabe T-Matrix, T_matrix = 1 und elem_ka = 10.
   8. Führen Sie JVIE aus, indem Sie sbatch runarray_JVIE_T.shausführen.
   9. Berechnen Sie die durchschnittlichen Streueigenschaften aus den T-Matrizen, die mit dem JVIE-Code berechnet werden. Führen Sie ./multi_T -N_Tin 128 in demselben Ordner aus, in dem sich die berechneten T-Matrizen befinden. Der Code schreibt die gemittelte inkohärente Mueller-Matrix in und die Querschnitte und Albedo in output.txt.
2. RT-CB Berechnungen
   1. Laden Sie zunächst die Quellendateien mit git herunter (git clone git-bitbucket.org:planetarysystemresearch/protocol4b.git protocol4b) und verschieben Sie die Dateien in das heruntergeladene Verzeichnis protocol4b.
   2. Als Nächstes laden Sie alle erforderlichen Programme herunter und kompilieren Sie sie, indem Sie bash compile.shausführen.
   3. Wenn Sie bereit sind, kopieren Sie die gemittelte Eingabestreumatrix (Schritt 3.2.2.5) sowie die Amplitudenstreuungsmatrix (Schritt 4.1.9) in das aktuelle Arbeitsverzeichnis.
   4. Öffnen Sie anschließend den Texteditor, nano, und ändern Sie die Datei PARAMS, um die gewünschten Parameter festzulegen.
   5. Führen Sie die Pipeline aus, indem Sie bash run.shausführen. Schreiben Sie dann die vollständige Mueller-Matrix als rtcb.outin den temporären Ordner .

5. Interpretation der Beobachtungen für den Kometen 67P/Tschurjumow-Gerasimenko.

1. Berechnen inkohärenter Volumenelemente mit der schnellen Überlagerung T-Matrix-Methode (FaSTMM) für organische und Partikelkörner
   1. Ausführen ./incoherent_input -lambda 0.649 -m_r 2.0 -m_i 0.2 -density 0.3 -lowB 0.075 -upB 0.125 -npower 3 -S_out pmatrix_org.dat.
   2. Ausführen ./incoherent_input -lambda 0.649 -m_r 1.6 -m_i 0.0001 -density 0.0375 -lowB 0.6 -upB 1.3 -npower 3 -S_out pmatrix_sil.dat.
2. Berechnung der durchschnittlichen inkohärenten Mueller-Matrix (pmatrix.in), Albedo (Albedo), mittlerer freier Pfad (mfp) und kohärenter effektiver Brechungsindex (m_eff)
   1. Führen Sie matlab aus. Typbefehle:
      Sorg=load('pmatrix_org.dat');
      Ssil=load('pmatrix_sil.dat');
      S = (Sorg+Ssil)/2; save('pmatrix.in','S','--ascii');
      Csca = (Csca_sil + Csca_org)/2;
      Cext = (Cext_sil + Cext_org)/2;
      albedo = Csca/Cext;
      mfp = Vol/Cext;
      wobei Csca_org und Cext_org die inkohärenten Streuungs- und Auslöschungsquerschnitte aus dem Schritt 5.1.2 und Csca_sil und Cext_sil die inkohärenten Streuungs- und Auslöschungsquerschnitte aus schritt 5.1.3 sind.
   2. Führen Sie ./m_eff(Csca, r) in der Befehlszeile aus, um m_eff zu erhalten, wobei der Radius des Volume-Elements liegt.
3. Berechnen von Streueigenschaften für die Komapartikel.
   1. Legen Sie die Werte aus den Schritten 5.2.1 und 5.2.2 fest (d. h. albedo, mfp, m_eff in der input.in Datei).
   2. Legen Sie den Power-Law-Index für die Korrelationslänge in der input.in-Datei auf 3,5 fest.
   3. Führen Sie den SIRIS4-Solver (./siris4 input.in pmatrix.in) für Partikelgrößen von 5 bis 100 m mit einem Schritt von 5 aus.
   4. Ausgabe der Komaphasenfunktionen aus dem SIRIS4-Solver.
4. Berechnen der Streueigenschaften des Kerns
   1. Beginnen Sie in MATLAB und führen Sie die Mittelungsroutine powerlaw_ave.m aus, um die Ergebnisse über die Power-Law-Größenverteilung des Index -3 nach der Berechnung der Komaphasenfunktionen (Schritt 5.3.4) aus dem SIRIS4-Solver zu durchschnittlich. Die erwarteten Routineausgänge sind pmatrix2.in, Albedo und der mittlere freie Pfad.
   2. Als Nächstes legen Sie die Ergebnisse der Ausgaben, Albedo und den mittleren freien Pfad, in die input.in-Datei fest.
   3. Legen Sie die Größe auf 1 Milliarde und den Power-Law-Index der Korrelationsfunktion für die Form auf 2,5 fest. Führen Sie dann SIRIS4 mit der hier gezeigten Befehlszeile aus, um die Kernphasenfunktion zu erhalten.

Ergebnisse

Für unser Experiment wurde ein Aggregat, das nominell aus dicht gepackten siO2-Partikeln besteht,^29,30 ausgewählt und weiter poliert, um eine kugelförmige Form anzunähern, nach der es durch Wiegen und Messen seiner Abmessungen (Abbildung 4). Das fast kugelförmige Aggregat hatte einen Durchmesser von 1,16 mm und eine Volumendichte von 0,47. Die Lichtstreuung wurde gemäß Schritt 1 gemessen. Der Strahl wurde auf 488 x 5 nm gefiltert, mit einem Gaußschen Spektrum. Die Messung wurde von drei Sweeps gemittelt und das leere Levitatorsignal vom Ergebnis abgezogen.

Aus den Intensitäten der vier verschiedenen Polarisationskonfigurationen berechneten wir die Phasenfunktion, den Grad der linearen Polarisation für unpolarisiertes einfallendes Licht -M₁₂/M₁₁und die Depolarisation M ₂₂ /M ₁₁, in Abhängigkeit vom Phasenwinkel (Abbildung 5, Abbildung 6, Abbildung 7). Eine bekannte systematische Fehlerquelle unserer Messung ist das Aussterbeverhältnis der linearen Polarisatoren, das 300:1 beträgt. Für diese Probe ist sie jedoch ausreichend, so dass das ausgelaufene polarisierte Licht unter der Nachweisschwelle liegt.

Die numerische Modellierung besteht aus mehreren Software, die durch Skripte miteinander verbunden ist, die den Informationsfluss entsprechend den vom Benutzer angegebenen Parametern verarbeiten. Die Skripte und die Software sind für die Arbeit am Taito-Cluster von CSC - IT Center for Science Ltd. vorkonfiguriert, und der Benutzer muss die Skripts und Makefiles selbst ändern, damit das Modellierungstool auf anderen Plattformen funktioniert. Das Werkzeug beginnt mit dem StMM-Solver²⁰, der Volumenelementeigenschaften berechnet, wie von Väisänen et al.¹⁸beschrieben. Danach werden die Streu- und Absorptionseigenschaften des Volumenelements als Eingabe für zwei verschiedene Software verwendet. Ein Mie-Streu-Solver wird verwendet, um den effektiven Brechungsindex zu finden, indem der kohärente Streuquerschnitt des Volumenelements mit einer Mie-Kugel gleicher Größe²⁰übereinstimmt. Anschließend wird das Aggregat modelliert, indem die SIRIS4-Software mit dem Volumenelement als diffusem Streuer und mit dem effektiven Brechungsindex auf der Oberfläche des Aggregats ausgeführt wird. Die kohärente Rückstreukomponente wird separat hinzugefügt, da es keine Software gibt, die effektivebreaktive simultane und kohärente Rückstreuung gleichzeitig behandeln kann. Derzeit ist der RT-CB nicht in der Lage, das effektive Brechungsmedium zu verbuchen, während der SIRIS4 nicht in der Lage ist, eine kohärente Rückstreuung zu berücksichtigen. Die kohärente Rückstreuung wird jedoch dem SIRIS4²³hinzugefügt,²⁴ Ergebnisse ungefähr durch Ausführen der Volumenelementstreuungseigenschaften durch die Streuphasenmatrixzersetzungssoftware PMDEC, die reine Mueller- und Jones-Matrizen für den RT-CB⁹erforderlich. Die kohärente Rückstreukomponente wird dann extrahiert, indem die Strahlungstransferkomponente von den Ergebnissen des RT-CB subtrahiert wird. Anschließend wird die extrahierte kohärente Rückstreukomponente zu den Ergebnissen des SIRIS4 hinzugefügt.

Wir simulierten numerisch die Eigenschaften des mm-großen (Radius 580 m) SiO 2-Aggregats, indem wir Schritt 2 folgten. Wir verwendeten zwei Arten von Volumenelementen, eines aus nominellen Äquisutpartikeln (0,25 m) und das andere bestehend aus normal verteilten (Mittelwert 0,25 m, Standardabweichung 0,1 m) Partikeln, die auf den Bereich von 0,1-0,2525 m abgeschnitten wurden. Die Verteilung der Partikel beruht auf der Tatsache, dass im Wesentlichen alle SiO 2-Proben mit einer bestimmten nominalen Partikelgröße auch eine signifikante Alienverteilung kleinerer Teilchen haben³¹. Insgesamt wurden 128 Volumenelemente der Größe kR₀=10 aus 128 periodischen Boxen mit etwa 10.000 Partikeln entnommen, die mit der Volumendichte v=47 % verpackt sind. Aus den Spezifikationen des Materials haben wir n=1.463+i0 bei der Wellenlänge von 0,488 'm, was die Wellenlänge ist, die in den Messungen verwendet wird.

Mit SIRIS4 wurden die Streueigenschaften von 100.000 Aggregaten mit einem Radius von 580 m, einer Standardabweichung von 5,8 m und mit dem Kraftrechtsindex der Korrelationsfunktion 2 gelöst und gemittelt. Diese Ergebnisse werden dargestellt (siehe Abbildung 5, Abbildung 6, Abbildung 7) mit den experimentellen Messungen und einer zusätzlichen Simulation ohne das effektive Medium. Beide Optionen für die Partikelverteilung ergeben eine Übereinstimmung mit der gemessenen Phasenfunktion (siehe Abbildung 5), obwohl sie zu unterschiedlichen Polarisationseigenschaften führen, wie in Abbildung 6zu sehen ist. Diese Unterschiede können verwendet werden, um die zugrunde liegende Verteilung der Partikel in der Probe zu identifizieren. Die beste Wahl ist, die abgeschnittene Normalverteilung anstelle der Äquisepartikel zu verwenden (siehe Abbildung 6). Wenn nur normalisierte Phasenfunktionen verwendet werden, sind die zugrunde liegenden Verteilungen nicht zu unterscheiden (siehe Abbildung 5, Abbildung 6, Abbildung 7). In Abbildung 7 für die Depolarisation weisen die numerischen Ergebnisse ähnliche Merkmale wie die gemessene Kurve auf, aber die Funktionen werden um 10° in die Rückstreurichtung verschoben. Der effektive Brechungsindex korrigiert die Ergebnisse positiv, wie aus den Simulationen hervorgeht, die mit und ohne das effektive Medium erzielt wurden (siehe Abbildung 5, Abbildung 6, Abbildung 7). Die Unterschiede in der Polarisation (Abbildung 6) deuten darauf hin, dass die Probe vermutlich eine komplexere Struktur (z. B. einen separaten Mantel und Kern) aufweist als unser homogenes Modell. Es ist jedoch jenseits der vorhandenen mikroskopischen Methoden für die Probencharakterisierung, um die wahre Struktur des Aggregats abzurufen. Die kohärente Rückstreuung wurde separat zu den Ergebnissen hinzugefügt. Den Messungen fehlt es an sichtbarer Intensitätsspitze, die an den Rückstreuwinkeln beobachtet wird, aber der Grad der linearen Polarisation ist zwischen 0-30° negativer, der nicht ohne kohärente Rückstreuung erzeugt werden kann (vergleiche "Verteilung" mit "no cb", siehe Abbildung 5, Abbildung 6, Abbildung 7).

Für Anwendungen des Sonnensystems verglichen wir die beobachteten Vesta-Spektren und das modellierte Spektrum, das durch das folgende Protokoll 3 erreicht wurde. Die Ergebnisse sind in Abbildung 3 und Abbildung 8 dargestellt und sie deuten darauf hin, dass Howarditpartikel, von denen mehr als 75 % eine Partikelgröße von weniger als 25 m aufweisen, den Regolith von Vesta dominieren. Obwohl die Gesamtübereinstimmung recht zufriedenstellend ist, unterscheiden sich die modellierten und beobachteten Spektren leicht: Die Absorptionsbandzentren des Modellspektrums werden auf längere Wellenlängen verschoben, und die spektralen Minima und Maxima sind im Vergleich zu den beobachteten Spectra. Die Unterschiede in den Minima- und Maxima-Werten lassen sich damit erklären, dass die gegenseitigen Schatteneffekte unter den Regolithpartikeln nicht berücksichtigt wurden: Die Schatteneffekte sind stärker für niedrige Reflexionen und schwächer für hohe Reflexionen und in der relativer Sinn, würde die spektrale Minima verringern und erhöhen die spektrale Maxima, wenn in der Modellierung berücksichtigt. Darüber hinaus wurde der imaginäre Teil der komplexen Brechungsindizes für Howardit ohne Berücksichtigung der Wellenlängenskala Oberflächenrauheit abgeleitet, so dass die abgeleiteten Werte zu klein sein können, um die spektralen Minima zu erklären. Wenn diese Werte in unserem Modell weiter verwendet werden, indem geometrische Optiken verwendet werden, können die Bandtiefen im modellierten Spektrum zu flach werden. Diese Wellenlängen-Effekte könnten auch bei längeren Wellenlängen zusammen mit einem kleinen Beitrag aus dem Low-End-Schwanz des thermischen Emissionsspektrums eine Rolle spielen. Die Unterschiede können auch durch eine kompositorische Diskrepanz zwischen unserer Howarditprobe und Vesta-Mineralien und durch eine andere Partikelgrößenverteilung verursacht werden, die für das Modell benötigt wird. Schließlich wurden die Reflexionsspektren von Vesta bei 180-200 K beobachtet und unsere Howarditprobe bei Raumtemperatur gemessen. Reddy et al.³² haben gezeigt, dass sich die Absorptionsbandzentren auf längere Wellenlängen mit steigender Temperatur verschieben.

Die photometrischen und polarimetrischen Phasenkurvenbeobachtungen für den Asteroiden (4) Vesta stammen aus Gehrels³³ und dem Small Bodies Node (http://pdssbn.astro. umd.edu/sbnhtml) des NASA Planetary Data Systems. Ihre Modellierung folgt Schritt 4 und beginnt mit dem Partikel-Brechungsindex und der Größenverteilung, die bei der spektrometrischen Modellierung bei einer Wellenlänge von 0,45 m verfügbar sind. Diese Teilchen haben Größen größer als 5 m, d.h. viel größer als die Wellenlänge und befinden sich daher im geometrischen Optikregime, der als Großpartikelpopulation bezeichnet wird. Für die Phasenkurvenmodellierung wird auch eine zusätzliche Kleinpartikelpopulation dicht gepackter Teilchen im Subwellenlängenmaßstab integriert, wobei gebührende Aufmerksamkeit darauf zu verwenden ist, Konflikte mit der obigen spektrometrischen Modellierung zu vermeiden.

Der komplexe Brechungsindex wurde auf 1.8+i0.000168 festgelegt. Die effektiven Partikelgrößen und Einzelstreualbedos in den Groß- und Kleinpartikelpopulationen entsprechen (9,385 m, 0,791) bzw. (0,716 m, 0,8935). Die mittleren freien Pfadlängen in den Groß- und Kleinpartikelmedien betragen 16,39 m und 0,56 m. Das Großpartikelmedium hat eine Volumendichte von 0,4, während das Kleinpartikelmedium eine Volumendichte von 0,3 aufweist. Die Fraktionen von Groß- und Kleinpartikelmedien im Vesta-Regolith werden mit 99 % bzw. 1 % angenommen, was eine Gesamt-Einzelstreualbedo von 0,815 und eine gesamtmittelförmige freie Bahnlänge von 12,78 m ergibt. Nach Schritt 4 erweist sich die geometrische Vesta-Albedo bei 0,45 m in fairer Übereinstimmung mit den Beobachtungen als 0,32 (vgl. Abbildung 8, wenn sie auf null Phasenwinkel extrapoliert wird).

Abbildung 9, Abbildung 10, Abbildung 11 zeigt die photometrische und polarimetrische Phasenkurvenmodellierung für Vesta. Für die photometrische Phasenkurve (Abbildung10, links) wurde die Modellphasenkurve von RT-CB mit einer linearen Abhängigkeit von der Magnitudenskala (Neigungskoeffizient -0,0179 mag/°) begleitet, die den Effekt der Schattenung in einem dicht gepackten, Hochalbedo-Regolith. Für den Polarisationsgrad wurde keine Änderung herangezogen (Abbildung10, rechts; Abbildung 11). Das Modell erklärt erfolgreich die beobachteten photometrischen und polarimetrischen Phasenkurven und bietet eine realistische Vorhersage für die maximale Polarisation nahe dem Phasenwinkel von 100° sowie für die Eigenschaften bei kleinen Phasenwinkeln <3°.

Auffallend ist, wie der winzige Anteil der Kleinteilchenpopulation in der Lage ist, die Erklärung der Phasenkurven zu vervollständigen (Abbildung 10, Abbildung 11). Es geht um faszinierende Modellierungsaspekte. Erstens sind die Einzelstreuphasenfunktionen für die Groß- und Kleinteilchenpopulationen, wie in Abbildung 9 (links) dargestellt, recht ähnlich, während die linearen Polarisationselemente sich deutlich unterscheiden. Zweitens tragen beide Teilchenpopulationen bei den RT-CB-Berechnungen zu den kohärenten Rückstreueffekten bei. Drittens muss es, um eine realistische Polarisationsmaxima zu erhalten, eine signifikante Großpartikelpopulation im Regolith geben (in Übereinstimmung mit der Spektralmodellierung). Durch die aktuelle unabhängige Vermischung der Klein- und Großpartikelmedien bleibt es möglich, einen Teil des Kleinpartikelbeitrags den Großpartikeloberflächen zuzuordnen. Damit jedoch kohärente Rückstreueffekte auftreten und die Beobachtungen erläutert werden können, ist es obligatorisch, eine Kleinpartikelpopulation einzubeziehen.

Die Rosetta-Mission der Europäischen Weltraumorganisation (ESA) zum Kometen 67P/Tschurjumow-Gerasimenko bot die Möglichkeit, die photometrische Phasenfunktion des Komas und des Kerns innerhalb weniger Stunden über einen weiten Phasenwinkelbereich zu messen³⁴. Die gemessenen Komaphasenfunktionen zeigen eine starke Variation mit der Zeit und eine lokale Position des Raumschiffs. Die Komaphasenfunktion wurde erfolgreich²⁰ mit einem Partikelmodell modelliert, das aus organischen und silikatgroßen Partikeln in Submikrometergröße besteht, wobei die numerischen Methoden (Schritte 5 und 2) verwendet wurden, wie in Abbildung 12dargestellt. Die Ergebnisse deuten darauf hin, dass die Größenverteilung des Staubes im Koma aufgrund der Aktivität des Kometen und der dynamischen Entwicklung des Staubes variiert. Durch die Modellierung der Streuung durch ein 1 km großes Objekt, dessen Oberfläche mit den Staubpartikeln bedeckt ist, haben wir gezeigt, dass die Streuung durch den Kern des Kometen mit der gleichen Art von Partikeln dominiert wird, die auch die Streuung im Koma dominieren (Abbildung 13).

Abbildung 1: Asteroid (4) Vesta (links) und Komet 67P/Tschurjumow-Gerasimenko (rechts), besucht von der NASA Dawn Mission bzw. von der ESA Rosetta Mission. Bildnachweis: NASA/JPL/MPS/DLR/IDA/Björn Jénsson (links), ESA/Rosetta/NAVCAM (rechts). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

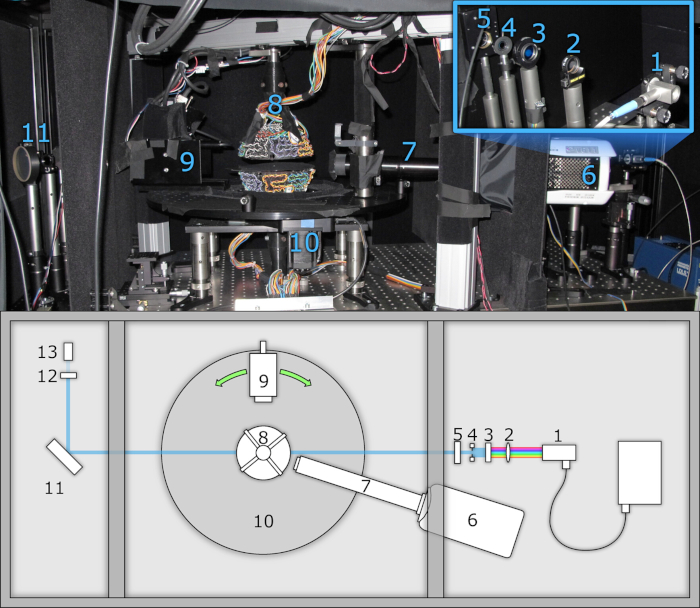
Abbildung 2: Lichtstreuung Messgerät. Foto (oben) und Top-View-Schema (unten) zeigt: (1) fasergekoppelte Lichtquelle mit Kollimator, (2) Fokussierlinse (optional), (3) Bandpassfilter zur Wellenlängenauswahl, (4) einstellbare Blende für Strahlformung, (5) motorisierter linearer Polarisator, (6) Hochgeschwindigkeitskamera, (7) Hochvergrößerungsobjektiv, (8) akustischer Schwebegeber zum Probenfang, (9) Messkopf, bestehend aus IR-Filter, motorisiertem Verschluss, motorisiertem Linearpolarisator und Photomultiplierrohr (PMT), (10) motorisierter Drehstufe zur Einstellung des Messkopfwinkels, (11) optisch flach für Fresnel-Reflexion, (12) Neutraldichtefilter und (13) Referenz-PMT, zur Überwachung der Strahlintensität. Das System ist in drei geschlossene Fächer unterteilt, um Streulicht zu eliminieren. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

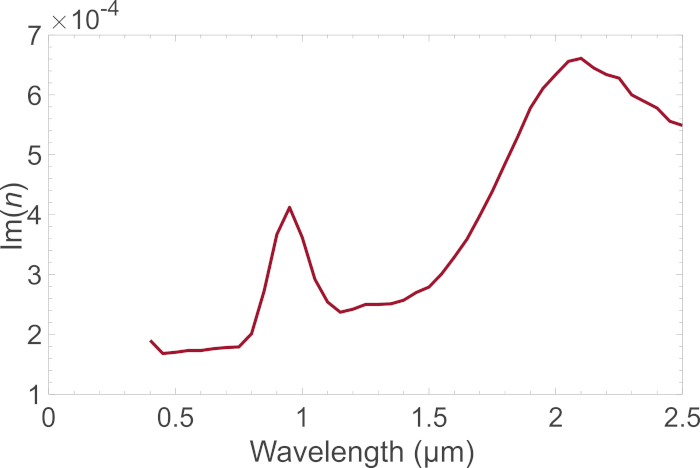
Abbildung 3: Der imaginäre Teil des Brechungsindexes für Howardit als Funktion der Wellenlänge. Der imaginäre Teil des refraktiven Im(n) für das Howarditmineral durch das folgende Protokoll 3.1 erhalten. Der Brechungsindex wird bei der Modellierung der Streueigenschaften des Asteroiden (4) Vesta verwendet. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

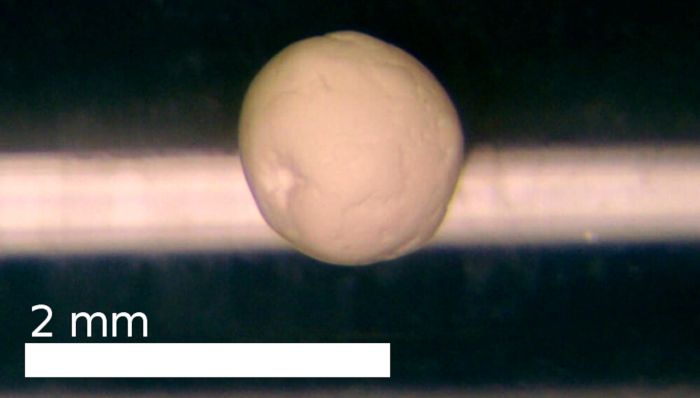
Abbildung 4: Die Messprobe besteht aus dicht gepackten sphärischen SiO₂ Partikeln. Die Probe wurde sorgfältig poliert, um eine nahezu kugelförmige Form zu erhalten, die sowohl effiziente Streuexperimente als auch numerische Modellierungermöglicht. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

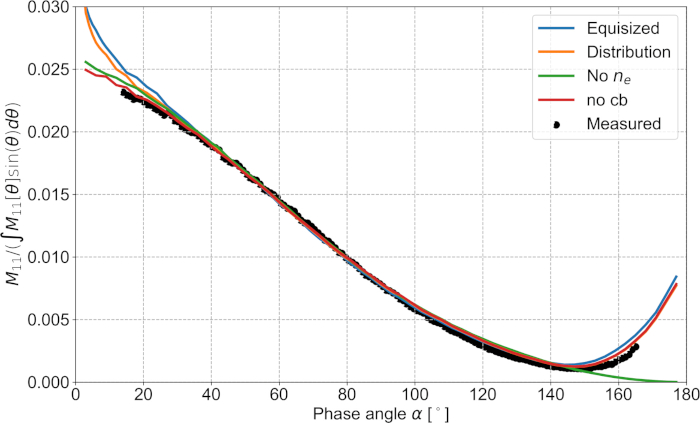
Abbildung 5: Phasenfunktion. Die Phasenfunktionen des Probenaggregats erhalten durch Befolgung der experimentellen Protokolle 1 und des numerischen Modellierungsschritts 2. Die Phasenfunktionen werden normalisiert, um einheitlichkeit zu geben, wenn sie von 15,1° bis 165,04° integriert sind. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Abbildung 6: Grad der linearen Polarisation. Wie in Abbildung 5 für den Grad der linearen Polarisation für unpolarisiertes einfallendes Licht -M₁₂/M₁₁ (in %). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

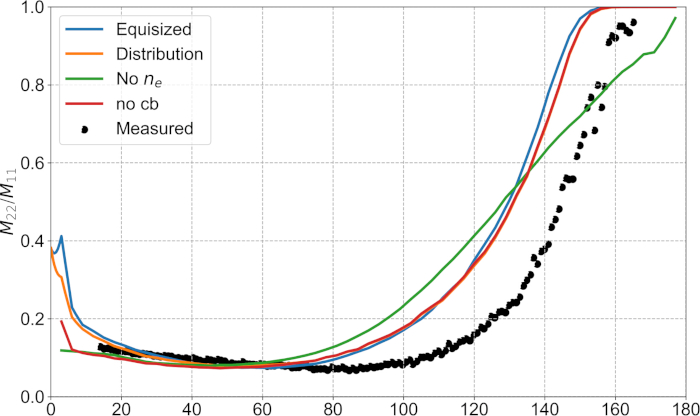
Abbildung 7: Depolarisation. Wie in Abbildung 5 für die Depolarisation M₂₂/M₁₁. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

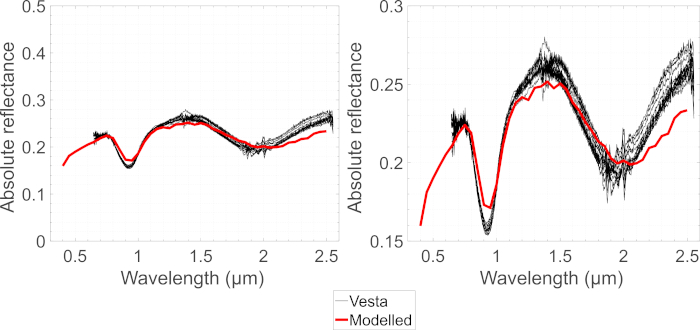
Abbildung 8: Absolute Reflexionsspektren. Asteroid (4) Vestas modellierte und beobachtete absolute Reflexionsspektren bei 17,4-Grad-Phasenwinkel. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

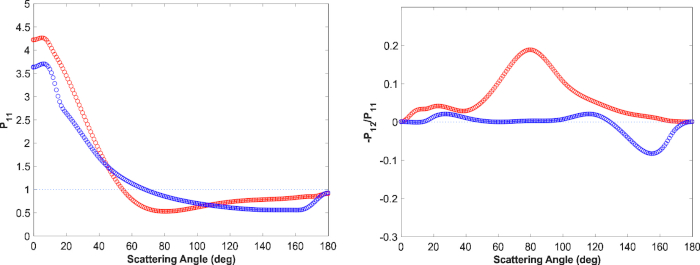
Abbildung 9: Streuphasenfunktion P₁₁ und Grad der linearen Polarisation für unpolarisiertes einfallendes Licht -P₂₁/P₁₁ in Abhängigkeit vom Streuwinkel für Volumenelemente großer (roter) und kleiner Teilchen (blau) im Regolith des Asteroiden (4) Vesta. Die gepunktete Linie zeigt eine hypothetische isotrope Phasenfunktion (links) und eine Polarisationsstufe Null (rechts). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

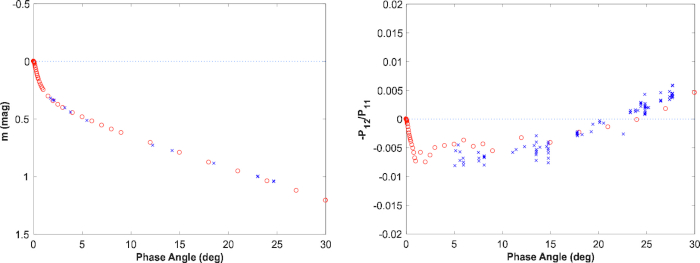
Abbildung 10: Beobachtete (blaue) und modellierte (rote) scheibenintegrierte Helligkeit in der Magnitudenskala sowie der Grad der linearen Polarisation für unpolarisiertes einfallendes Licht als Funktion des Phasenwinkels für Asteroid (4) Vesta. Die photometrischen und polarimetrischen Beobachtungen stammen von Gehrels (1967) bzw. dem Small Bodies Node of the Planetary Data System (http://pdssbn.astro.umd.edu/sbnhtml). Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

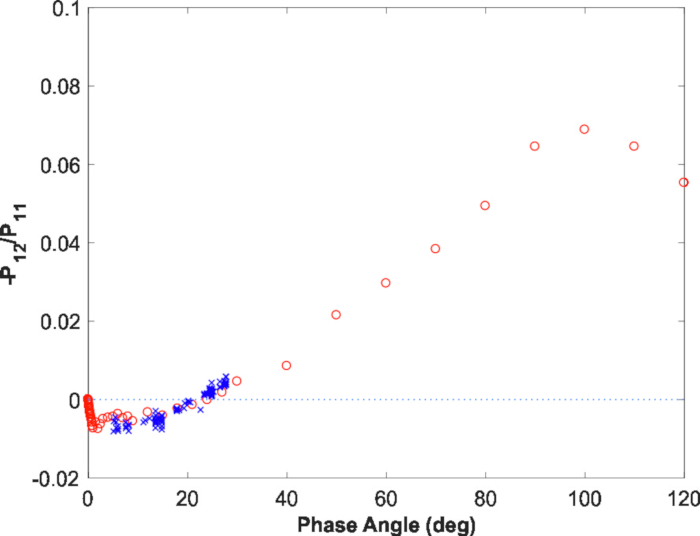
Abbildung 11: Grad der linearen Polarisation. Der Grad der linearen Polarisation für Asteroid (4) Vesta für große Phasenwinkel basierend auf der numerischen Multistreuungsmodellierung vorhergesagt. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

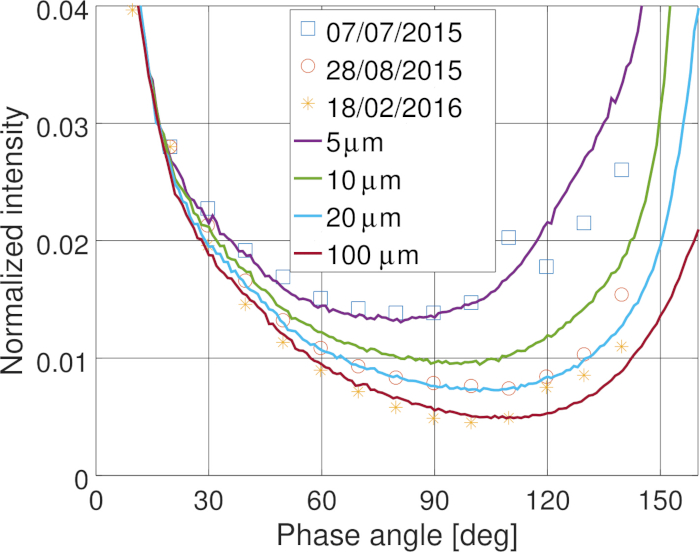
Abbildung 12: Modellierte und gemessene fotometrische Phasenfunktionen im Koma des Kometen 67P/Tschurjumow-Gerasimenko. Die zeitlich endenden Schwankungen der gemessenen Phasenfunktionen lassen sich durch unterschiedliche Staubgrößenverteilung im Koma erklären. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

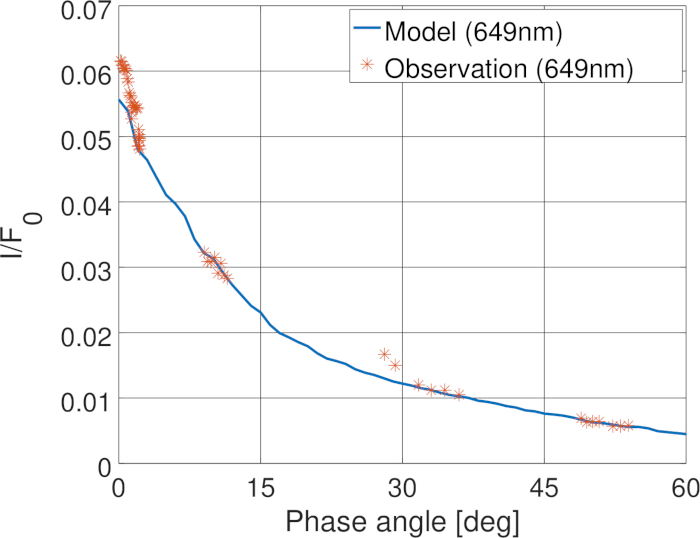
Abbildung 13: Phasenfunktionen. Modellierte und gemessene Phasenfunktionen des Kometenkerns 67P. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Diskussion

Experimentelle, theoretische und rechnerische Methoden wurden für die Lichtstreuung durch diskrete zufällige Teilchenmedien vorgestellt. Die experimentellen Methoden wurden verwendet, um die grundlegenden Konzepte in den theoretischen und rechnerischen Methoden zu validieren. Die letztgenannten Methoden wurden dann erfolgreich bei der Interpretation astronomischer Beobachtungen des Asteroiden (4) Vesta und des Kometen 67P/Tschurjumow-Gerasimenko angewandt.

Das experimentelle Streumesser basiert auf einer ultraschallgesteuerten Probenschwebe, die Mueller-Matrixmessungen für ein Probenaggregat in gewünschter Ausrichtung ermöglicht. Das Aggregat kann in den Messungen wiederholt verwendet werden, da es möglich ist, das Aggregat nach jedem Messsatz zu konservieren. Dies ist das erste Mal, dass solche berührungslosen, zerstörungsfreien Streumessungen an einer Probe unter voller Kontrolle durchgeführt werden.

Die theoretischen und rechnerischen Methoden basieren auf den sogenannten inkohärenten Streu-, Absorptions- und Aussterbeprozessen in zufälligen Medien. Während die genauen elektromagnetischen Wechselwirkungen nach der konfigurationsischen Mittelung immer kohärent innerhalb eines unendlichen Zufallsmediums auftreten, bleiben nur inkohärente Wechselwirkungen zwischen Volumenelementen von Teilchen. In der vorliegenden Arbeit werden die inkohärenten Wechselwirkungen zwischen diesen Elementen genau durch die Verwendung der Maxwell-Gleichungen berücksichtigt: Nachdem die kohärenten Felder von den Feldern im freien Raum subtrahiert wurden, bleiben die inkohärenten Felder innerhalb des zuzufälligen Mediums übrig. Die Behandlung wurde derzeit insofern in vollem Umfang durchgeführt, als die Wechselwirkungen sowie die Aussterbe-, Streuungs- und Absorptionskoeffizienten des Mediums im Rahmen inkohärenter Wechselwirkungen abgeleitet werden. Darüber hinaus hat sich gezeigt, dass die Berücksichtigung der kohärenten Feldeffekte auf die Schnittstelle zwischen freiem Raum und dem zufälligen Medium zu einer erfolgreichen Gesamtbehandlung für ein eingeschränktes Zufallsmedium führt.

Die Anwendung der theoretischen und rechnerischen Methoden wurde für experimentelle Messungen eines kugelförmigen Kugelprobenaggregats im mm-Maßstab veranschaulicht, das aus kugelförmigen SiO 2-Partikeln im Submikron-Skala besteht. Die Anmeldung zeigt eindeutig, dass das Probenaggregat aus einer Verteilung von Partikeln mit unterschiedlichen Größen bestehen muss, anstatt aus äquisitierten kugelförmigen Partikeln bestehen zu müssen. Für die Charakterisierung zufälliger Medien kann dieses Ergebnis weitreichende Folgen haben: Es ist plausibel, dass die Medien wesentlich komplexer sind als das, was früher mit modernsten Charakterisierungsmethoden abgeleitet wurde.

Die synoptische Interpretation des Spektrums für Asteroid (4) Vesta über die sichtbaren und nahinfraroten Wellenlängen sowie vestas photometrische und polarimetrische Phasenkurven bei einer Wellenlänge von 0,45 m zeigt, dass es praktisch ist, die numerischen Methoden zu nutzen. bei der Beschränkung der Mineralzusammensetzungen, der Partikelgrößenverteilung sowie der Regolithvolumendichte aus entfernten astronomischen Beobachtungen. Diese Abrufe werden durch die Simultaninterpretation der photometrischen Phasenkurven für den Kometen 67P/Tschurjumow-Gerasimenko hinsichtlich komaierter und zellscharfer. Schließlich wurde eine realistische Modellierung der polarimetrischen Phasenkurve von 67P erhalten²⁰. Es gibt große Zukunftsperspektiven bei der Anwendung der gegenwärtigen Methoden bei der Interpretation von Beobachtungen von Objekten des Sonnensystems im Allgemeinen.

Es gibt Zukunftsperspektiven für den gegenwärtigen kombinierten experimentellen und theoretischen Ansatz. Da es äußerst schwierig ist, zufällige Medien, die aus Inhomogenitäten im Subwellenlängenmaßstab bestehen, genau zu charakterisieren, können kontrollierte Mueller-Matrix-Messungen ein Werkzeug zum Abrufen von Informationen über die Volumendichte und Partikelgrößenverteilung in das Medium. Die quantitative Umkehrung dieser physikalischen Parameter wird durch die neuartigen numerischen Methoden erleichtert.

Materialien

Name	Company	Catalog Number	Comments
10GL08	Newport		Calcite polarizer
12X Zoom Body Tube 1-50487AD	Navitar		Microscope objective
43-412-000	Edmund optics		Optical flat
8MPR16-1	Standa		Motorized Polarizer Rotator
8MRB240-152-59D	Standa		Rotation stage
8SMC5-ETHERNET	Standa		Motor controller
Digi-pas DWL3500XY	Digi-pas		Digital 2-axis level
DMT 65-D25-HiDS	Owis		Optics rotation stage
EQ-99 LDLS	Energetiq		Light source
FL488-10	Thorlabs		Laser line filter
IBM 65-D0-35-HiDS	Owis		Motorized iris shutter
LPVISE100-A	Thorlabs		Film polarizer
microPMT H12403-01	Hamamatsu		Photomultiplier tube
NI PXIe-5171R	National Instruments		Digital oscilloscope
NI PXIe-8880	National Instruments		PXIe chassis
Phantom v611	Vision Research		High speed camera
PS 10-32-DC	Owis		Motor controller
RC08FC-P01	Thorlabs		Fiber collimator
SET-NDF-D22-G25	Owis		Neutral density filter
TIA60	Thorlabs		PMT amplifier