Espalhamento e absorção da luz em Regoliths planetários

Resumo

Os métodos numéricos e experimentais são apresentados para o espalhamento múltiplo da luz em meios aleatórios discretos de partículas densamente-embaladas. Os métodos são utilizados para interpretar as observações do asteróide (4) Vesta e cometa 67P/Churyumov-Gerasimenko.

Resumo

Os métodos teóricos, numéricos, e experimentais são apresentados para o espalhamento múltiplo da luz em meios aleatórios discretos macroscópicos de partículas microscópicas densamente-embaladas. Os métodos teóricos e numéricos constituem uma estrutura de transferência radiativa com transações recíprocas (R²T²). A estrutura de R²T² implica o traçado de ordem de espalhamento de Monte Carlo de interações no espaço de frequência, assumindo que os disseminadores e absorventes fundamentais são elementos de volume de comprimento de onda compostos por um grande número de aleatoriamente partículas distribuídas. A mídia aleatória discreta é totalmente embalada com os elementos de volume. Para partículas esféricas e não esféricas, as interações dentro dos elementos de volume são computadas exatamente usando o método de matriz Tde superposição (stmm) e o método de equação integral de volume (viem), respectivamente. Para ambos os tipos de partícula, as interações entre diferentes elementos de volume são computadas exatamente usando o STMM. Como o traçado ocorre dentro da mídia aleatória discreta, campos eletromagnéticos incoerentes são utilizados, ou seja, o campo coerente dos elementos de volume é removido das interações. Os métodos experimentais baseiam-se na levitação acústica das amostras para medições de espalhamento não-contato, não destrutiva. A levitação implica controle Ultrassônico completo da posição e orientação da amostra, ou seja, seis graus de liberdade. A fonte luminosa é uma fonte de luz branca laser-conduzida com um monocromador e um polarizador. O detector é um tubo do mini-photomultiplicador em uma roda de giro, equipado com os polarizadores. O R²T² é validado usando medidas para uma amostra esférica da milímetro-escala de partículas esféricas densamente-embaladas do silicone. Após a validação, os métodos são aplicados para interpretar as observações astronômicas para o asteróide (4) Vesta e o cometa 67P/Churyumov-Gerasimenko (Figura 1) recentemente visitados pela missão Dawn da NASA e pela missão de Rosetta da ESA, respectivamente.

Introdução

Asteróides, núcleos cometários e objetos de sistema solar sem ar em geral são cobertos por regolitos planetários, camadas soltas de partículas de tamanho, forma e composição variados. Para esses objetos, dois fenômenos astronômicos onipresentes são observados em pequenos ângulos de fase solar (o ângulo sol-objeto-observador). Em primeiro lugar, observa-se o brilho da luz dispersa na escala de magnitude astronômica para aumentar não linearmente em direção ao ângulo de fase zero, comumente chamado de efeito de oposição^1,2. Em segundo lugar, a luz dispersa é parcialmente polarizada em paralelo ao plano de espalhamento (o plano sol-objeto-observador), comumente chamado de polarização negativa³. Os fenômenos têm faltado a interpretação quantitativa desde o 19o século atrasado para o efeito da oposição e desde o início do século 20 para a polarização negativa. Sua interpretação adequada é um pré-requisito para a interpretação quantitativa das observações fotométricas, polarimétricas e espectrométricas de objetos airless, bem como o espalhamento de radar de suas superfícies.

Sugeriu-se^4,5,6,7 que o mecanismo coerente do Retrodispersão (CBM) no espalhamento múltiplo seja pelo menos em parte responsável para os fenômenos astronômicos. No CBM, as ondas parciais, interagindo com os mesmos disseminadores na ordem oposta, interferem sempre construtivamente na direção de retroespalhamento exata. Isto é devido aos trajetos óticos coincidindo das ondas recíprocas. Em outras direções, a interferência varia de destrutiva a construtiva. A média de configurational dentro de um meio aleatório discreto de partículas resulta em retroespalhamento aprimorado. Quanto à polarização linear, a CBM é seletiva e resulta em polarização negativa no caso de dispersantes de polarização única, uma característica comum em dispersão única (cf. espalhamento de Rayleigh, reflexão de Fresnel).

Dispersão e absorção de ondas eletromagnéticas (luz) em um meio aleatório macroscópico de partículas microscópicas constituiu um problema computacional aberto na astrofísica planetária^8,9. Como ilustrado acima, isso resultou na ausência de métodos quantitativos inversos para interpretar observações baseadas em terra e espaciais de objetos do sistema solar. No presente manuscrito, são apresentados novos métodos para colmatar a lacuna entre as observações e sua modelagem.

As medições experimentais de espalhamento por uma amostra de pequenas partículas em posição controlada e orientação (seis graus de liberdade) permaneceram abertas. As características de dispersão de partículas únicas foram medidas anteriormente como médias de Ensemble sobre o tamanho, a forma e a distribuição de orientação¹⁰ introduzindo um fluxo de partículas através do volume de medição. As características de espalhamento de partículas únicas em levitação foram realizadas utilizando, por exemplo, a levitação eletrodinâmica¹¹ e as pinças ópticas^12,13,14. No presente manuscrito, um novo método experimental baseado na levitação ultra-sônica com controle total da posição e orientação da amostra é oferecido¹⁵.

O presente manuscrito resume os achados de um projeto financiado por cinco anos em 2013-2018 pelo Conselho Europeu de pesquisa (ERC): espalhamento e absorção de ondas eletromagnéticas em meios particulados (SAEMPL, ERC Advanced Grant). Saempl sucedeu em cumprir seus três objetivos principais: primeiramente, os métodos numéricos novos do Monte Carlo foram derivados para o espalhamento múltiplo por meios aleatórios discretos de partículas densa-embaladas^16,17,18; em segundo, a instrumentação experimental nova foi desenvolvida e construída para medidas controladas do laboratório de amostras da validação na levitação¹⁵; em terceiro lugar, os métodos numéricos e experimentais foram aplicados para interpretar as observações astronômicas^19,20.

No que se segue, protocolos para a utilização do pipeline de espalhamento experimental para medições, o pipeline computacional correspondente, bem como os pipelines de aplicação são descritos em detalhe. O pipeline computacional consiste em software para computações assintoticamente exatas no caso de sistemas finitos de partículas (superposição T-Matrix método stmm²¹ e volume integral equação método viem²²) e aproximado cálculos para mídia aleatória discreta e assintoticamente infinita de partículas usando vários métodos de espalhamento (Siris^23,24, transferência radiativa com retroespalhamento coerente RT-CB^8,9e Transferência radiativa com operações recíprocas R²T^216,17,18). O pipeline experimental engloba a preparação, o armazenamento e a utilização das amostras, a sua levitação no volume de medição e a realização da medição de espalhamento real em toda a gama de ângulos de espalhamento com polarizador variável Configurações. O pipeline de aplicação diz respeito à utilização dos pipelines computacionais e experimentais para interpretar observações astronômicas ou medições experimentais.

Protocolo

1. medição de espalhamento de luz

1. Configurar o Scatterometer para medição (Figura 2)
   1. Para começar, configure o scatterômetro ativando a fonte de luz, os tubos com multiplicador de foto (PMTs) e os amplificadores. Permita que o sistema se estabilize por 30 min.
   2. Alinhe e centrem o feixe de incidentes com furos. Dois pinholes são Unidos em pontos pre-medidos na tábua de pão de giro, 180 ° distante e no mesmo raio. Centrar o feixe no primeiro furo de pino e ajustar seu ângulo tal que a luz igualmente entra através do segundo furo de pino.
2. Configurando o levitador de amostra acústica
   1. Em seguida, configure o levitador de amostra acústica inserindo o microfone no centro do levitador e executando o script de calibração.
   2. Calibre o Sirenídeo acústico da disposição faseada medindo a pressão acústica para cada elemento da disposição no ponto pretendido da levitação em função da tensão de condução. Use esta calibração para compensar as diferenças entre os canais de matriz. Posicione o microfone de calibração centrando sua sombra na viga e em um feixe perpendicular criado com dois espelhos.
   3. Calcule os parâmetros de condução para a matriz que criam uma armadilha acústica assimétrica e fornecê-los para a eletrônica de geração de sinal. Isto é conseguido minimizando o potencial de Gor'kov²⁵ e alinhando os gradientes de pressão no ponto de levitação.
   4. Em seguida, faça uma varredura de medição com um levitator vazio. A varredura revela quaisquer sinais gerados pela luz ambiente, reflexões a partir do entorno, ou ruídos elétricos.
3. Manuseio, inserção e medição de amostras
   1. Uma vez que ajustado acima, use uma colher acusstically transparente da malha para injetar a amostra no levitator acústico.
   2. Usando uma câmera de vídeo e óptica de alta ampliação, inspecione a orientação e a estabilidade da amostra antes e depois das medições de espalhamento.
   3. A força e a assimetria da armadilha acústica são otimizadas para a estabilidade máxima da amostra. Consequentemente, o poder acústico é ajustado tão baixo como possível.
   4. Se a amostra for assimétrica, gire-a ao redor do eixo vertical para obter informações sobre sua forma. Realize a rotação mudando lentamente o alinhamento da armadilha acústica. Durante a imagem, aplique iluminação adicional para melhorar a qualidade da imagem.
   5. Em seguida, feche a câmara de medição para bloquear a luz externa.
   6. Usando a interface do computador, selecione a orientação da amostra, bem como a resolução angular e o alcance da medição. A entrada e a luz dispersa são filtradas por polarizadores lineares, que são motorizados.
   7. Execute a varredura de medição automatizada. Isso irá medir quatro pontos para cada ângulo com orientações polarizador de (horizontal, horizontal), (horizontal, vertical), (vertical, vertical), e (vertical, horizontal).
   8. Repita cada varredura três vezes para eliminar outliers. Para amostras assimétricas, repita a medição em diferentes orientações de amostra.
   9. Recupere a amostra após a medição, desligando o campo acústico e deixando a amostra cair sobre o tecido acusticamente transparente. Em seguida, execute outra varredura de medição com levitador vazio para detectar qualquer possível deriva devido às condições de luz ambiente.
   10. Quando terminar, salve os dados. Analise os dados para calcular os elementos da matriz de Mueller para cada ângulo através da combinação linear de intensidades em polarizações diferentes¹

2. modelando os meios esféricos densamente-embalados milímetro-feitos medida que consistem em partículas esféricas

1. Para começar a modelar, use o acesso SSH para conectar-se ao CSC – centro de ti para o cluster do Science Limited, Taito.  Faça o download e compilar todos os programas necessários que são pré-configurados para Taito executando bash compile.sh.
2. Mova-se para o diretório de trabalho executando $WRKDIR de CD.
3. Baixe arquivos de fontes com git (git clone git@bitbucket.org: planetarysystemresearch/protocol2. git protocol2).
4. Mover para o diretório recém-criado CD protocol2.
5. Baixe e compile os programas necessários executando o bash compile.sh, que são pré-configurados para o Taito.
6. Em seguida, abra o editor de texto nano e configure os parâmetros para um único scatterer, um elemento de volume e a amostra estudada para corresponder à amostra estudada modificando o arquivo params.
7. Em seguida, execute pipeline executando um comando bash run.sh. Quando terminar, escreva a matriz Mueller completa da amostra na pasta Temp como final. out.

3. interpretar os espectros de reflectância para o asteróide (4) Vesta

1. Derivando os índices refrativos complexos para howardite.
   1. Baixar SIRIS4 (git clone git@bitbucket.org: planetarysystemresearch/Siris 4.2. git).
   2. Compile executando Make na pasta src. Renomeie o executável siris42 para siris4.
   3. Em Maingo. f90, altere a linha 395 para R0 = 0.05 * RMAX * sqrt (ran2). Compilar executando Make.
   4. Faça o download dos scripts MATLAB necessários executando "git clone git@bitbucket.org: planetarysystemresearch/protocol4a. git".
   5. Copie os arquivos executáveis criados nas etapas 3.1.2. e 3.1.3. para JoVEOptimize-pasta.
   6. Vá para a pasta JoVEOptimize.
   7. No arquivo input1.in , defina o raio para 30 μm para o tamanho de partícula e e corrija a parte real do índice de refração para 1,8. No arquivo INPUT2.in , defina o raio para 15.000 μm.
   8. Estimar os limites superiores e inferiores para a parte imaginária dos índices refrativos e salvá-los em dois arquivos separados. O código utiliza o método bisectioning e usa esses valores como o ponto de partida.
   9. No arquivo optimizek. m , defina os nomes dos arquivos dos limites superior e inferior da parte imaginária dos índices de refração e o nome do arquivo do espectro de reflectância medido do pó e. Defina a faixa de comprimento de onda para 0,4 – 2,5 μm com etapas de 0, 5 μm.
   10. Execute optimizek. m em MATLAB para obter os índices refrativos complexos para e (ver Figura 3). Primeiro, o código calcula as propriedades de dispersão para partículas e de tamanho de 30 μm (raio) e, em seguida, usa essas partículas como espalhadores difusos dentro de um volume de tamanho (raio) de 15.000 μm. Estas etapas são repetidas para cada comprimento de onda até que a reflectância computada combine com a reflectância medida.
2. Modelagem do espectro de reflectância de Vesta.
   1. Computando as propriedades de espalhamento de partículas e utilizando SIRIS4
      1. Utilize SIRIS4 para calcular as propriedades de dispersão de partículas e movendo primeiro o arquivo executável SIRIS4 para a mesma pasta com o arquivo de entrada e p-Matrix-File.  Em seguida, copie o input_1. in e pmatrix_1. in da pasta de teste.
      2. Em input_1. in, defina o número de raios para 2 milhões, o número de partículas de amostra para 1000, o desvio padrão do raio para 0,17 e o índice de poder-lei da função de correlação para 3. Em seguida, defina a parte real do índice de refração para 1,8 e use a parte imaginária do índice de refração n conforme descrito no protocolo de texto.
      3. Em seguida, execute SIRIS4 executando o comando mostrado aqui para cada comprimento de onda de 0,4 a 2,5 mícrons usando uma escala do tamanho de 10 a 200 mícrons no diâmetro com uma etapa de amostragem de 10 mícrons.
      4. Em seguida, salve cada matriz de fase de espalhamento computada P em um arquivo pmatrix_x. in .  O x no nome do arquivo descreve o número de comprimento de onda e varia de 1 a 43 para cada tamanho de partícula. O arquivo conterá os ângulos de espalhamento, bem como os elementos da matriz de dispersão p₁₁, p₁₂, p₂₂, p₃₃, p₃₄ e p₄₄ para um comprimento de onda e tamanho de partícula.
   2. A média das matrizes de espalhamento obtidas, albedos de dispersão única e caminhos livres de média sobre uma distribuição de tamanho de força-lei com um índice de 3,2 ¹⁹ anos de ^, a ²⁴.
      1. Mova os arquivos pmatrixem pastas para que cada pasta represente um tamanho de partícula e contenha as matrizes p computadas para todos os comprimentos de onda. Nomeie as pastas fold1, fold2,..., foldN, onde N é o número de tamanhos de partícula.
      2. Escreva as eficiências de espalhamento e extinção q_SCA e q_ext, bem como os valores de raio de área de superfície projetada igual a r_atingidos a partir dos arquivos Outputqem um arquivo, qscas. dat.
      3. Vá para a pasta JoVEAverage que foi baixada na etapa 3.1.4.
      4. Mova as pastas e Qscas. dat para a mesma pasta com Avgpowerlaw. m.
      5. Execute Avgpowerlaw. m em MATLAB. O código calcula matrizes de dispersão médias, albedos de dispersão única e comprimentos de caminho livre médios sobre uma distribuição de tamanho de força-lei com o índice 3,2.
   3. Computando o espectro final de Vesta utilizando SIRIS4
      1. Use disseminadores difusos dentro de um volume Vesta-feito medida com um índice de refração de 1. No arquivo de entrada, use os albedos de dispersão única média e comprimentos de caminho livres médios para scatterers internos.
      2. Em seguida, execute SIRIS4 em cada comprimento de onda executando o comando mostrado aqui, onde X é o comprimento de onda. O código lê as matrizes de dispersão médias como sua entrada para os scatterers difusos internos.
      3. Estude a reflectância absoluta em um ângulo de fase de 17,4 graus.
      4. Obtenha os espectros observados de Vesta em ângulo de fase de 17,4 graus do sistema de dados planetário da NASA²⁶.
      5. Dimensione os espectros observados de Vesta para um valor de Albedo geométrico de 0,42327 a 0,55 mícrons²⁷. Para chegar a 17,4 graus, aplique um fator de 0,491 nos espectros escalados²⁸. Compare os espectros modelados e observados em toda a faixa de comprimento de onda.

4. modelagem fotométrica e polariométrica de (4) Vesta

1. Computando Propriedades de espalhamento para elementos de volume contendo partículas e em forma de Voronoi
   1. Conecte-se ao CSC – centro de ti para o cluster Taito da Science Ltd. via acesso SSH.
   2. Mova-se para o diretório de trabalho executando $WRKDIR de CD.
   3. Baixe os arquivos de origem (git clone git@bitbucket.org: planetarysystemresearch/jvie_t_matrix. git).
   4. Compile executando Make na pasta-.
   5. Gere elementos de volume que contenham partículas e em forma de Voronoi usando um código MATLAB voronoi_element. m. Em voronoi_element m, defina o comprimento de onda para 0,45 μm, N_elems para 128, o parâmetro de tamanho (elem_ka) para 10, índice de força-lei para 3, raio de partícula mínimo para 0,143 μm, raio máximo de partícula para 0,35 μm, densidade de embalagem para 30%, e use o índice de refração complexo derivado para howardite.
   6. Execute voronoi_element. m em MATLAB. O código gera 128 mesh-Files para volume-elementos com diferentes realizations de Voronoi-partícula usando a distribuição do tamanho da poder-lei.
   7. Calcule as matrizes Tpara os elementos de volume gerados usando o jvie. Em runarray_JVIE_T. sh, defina array = 1-128. Os paramaters são k = 13,962634, mesh = nome da malha gerada em 4.1.6, T_out = nome da matriz de saída T, T_matrix = 1 e elem_ka = 10.
   8. Execute o JVIE executando o sbatch runarray_JVIE_T. sh.
   9. Calcule as propriedades de dispersão médias das matrizes Tcomputadas com o código jvie. Execute ./Multi_t-N_Tin 128 na mesma pasta onde as matrizes Tcomputadas são. O código grava a matriz incoerente média de Mueller em e os Cross-Sections e o albedo no output. txt.
2. Computações RT-CB
   1. Comece baixando os arquivos de fontes com git (git clone git@bitbucket.org: planetarysystemresearch/protocol4b. git protocol4b) e mova os arquivos para o diretório baixado protocol4b.
   2. Em seguida, baixe e compile todos os programas necessários executando o bash compile.sh.
   3. Quando estiver pronto, copie a matriz de dispersão de entrada média (etapa 3.2.2.5), bem como a matriz de dispersão de amplitude (etapa 4.1.9) no diretório de trabalho atual.
   4. Em seguida, abra o editor de texto, nano e modifique o arquivo params para definir os parâmetros desejados.
   5. Execute o pipeline executando bash Run.sh. Em seguida, escreva a matriz Mueller completa na pasta Temp como rtcb. out.

5. interpretar as observações para o cometa 67P/Churyumov-Gerasimenko.

1. Computando elementos de volume incoerentes com a superposição rápida Método da T-matriz (FastMM) para os grãos orgânicos e de partícula
   1. Execute ./incoherent_input – lambda 0,649-m_r 2,0-m_i 0,2-densidade 0,3-lowB 0, 75-upB 0,125-npower 3-S_out pmatrix_org. dat.
   2. Execute ./incoherent_input – lambda 0,649-m_r 1,6-m_i 0, 1-densidade 0, 375-lowB 0,6-upB 1,3-npower 3-S_out pmatrix_sil. dat.
2. Computando a matriz incoerente média de Mueller (pmatrix.in), albedo (albedo), trajeto livre médio (MFP), e índice de refração eficaz coerente (m_eff)
   1. Execute o MATLAB. Comandos de tipo:
      SORG = Load (' pmatrix_org. dat ');
      Ssil = Load (' pmatrix_sil. dat ');
      S = (SORG + ssil)/2; Save (' pmatrix. in ', ' ', '-ASCII ');
      CSCA = (Csca_sil + Csca_org)/2;
      Cext = (Cext_sil + Cext_org)/2;
      albedo = CSCA/Cext;
      MFP = Vol/Cext;
      onde Csca_org e Cext_org são as seções transversais de espalhamento e extinção incoerentes da etapa 5.1.2, e Csca_sil e Cext_sil são as seções transversais de dispersão e extinção incoerentes do passo 5.1.3.
   2. Execute ./m_eff (CSCA, r) na linha de comando para obter m_eff onde está o raio do elemento de volume.
3. Computando Propriedades de espalhamento para as partículas de coma.
   1. Defina os valores da etapa 5.2.1 e 5.2.2 (ou seja, albedo, MFP, m_eff no arquivo Input.in ).
   2. Defina o índice de força-lei para o comprimento de correlação para 3,5 no arquivo Input.in .
   3. Execute SIRIS4 Solver (./siris4 input.in pmatrix.in) para tamanhos de partícula de 5 μm a 100 μm usando uma etapa de 5.
   4. Output as funções da fase do coma do Solver SIRIS4.
4. Computando Propriedades de espalhamento do núcleo
   1. Comece no MATLAB e execute a média de rotina powerlaw_ave. m para calcular os resultados da distribuição de tamanho do índice-3 após o cálculo das funções de fase de coma (etapa 5.3.4) do SOLUCIONADOR de SIRIS4. As saídas de rotina esperadas são pmatrix2.in, albedo e o caminho livre médio.
   2. Em seguida, defina os resultados das saídas, albedo e o caminho livre médio, para o arquivo Input.in .
   3. Defina o tamanho como 1.000.000.000 e o índice de força-lei da função de correlação para a forma como 2,5. Em seguida, execute SIRIS4 usando a linha de comando mostrada aqui para obter a função de fase do núcleo.

Resultados

Para nosso experimento, um agregado nominalmente constituído de partículas de sio₂ esféricas densamente embaladas de Ø = 0,5 μm foi selecionado^29,30 e polido mais, para aproximar uma forma esférica, após a qual foi caracterizada por pesando e medindo suas dimensões (Figura 4). O agregado quase esférico tinha um diâmetro de 1,16 mm e uma densidade de volume de 0,47. O espalhamento de luz foi medido de acordo com a etapa 1. O feixe foi filtrado para 488 ± 5 nm, com espectro gaussiano. A medida foi calculada em média a partir de três varreduras e o sinal do Sirenídeo vazio foi subtraído do resultado.

A partir das intensidades das quatro diferentes configurações de polarização, calculamos a função de fase, o grau de polarização linear para a luz incidente não polarizada-m₁₂/m₁₁, e a despolarização m ₂₂ anos de /M ₁₁, em função do ângulo de fase (figura5, figura 6, Figura 7). Uma fonte sistemática conhecida do erro de nossa medida é a relação da extinção dos polarizadores lineares, que é 300:1. Para esta amostra, é, entretanto, adequada para que a luz polarizada vazada esteja abaixo do limiar de detecção.

A modelagem numérica consiste em vários softwares interligados por scripts que lidam com o fluxo de informações de acordo com os parâmetros fornecidos pelo usuário. Os scripts e o software são pré-configurados para trabalhar no cluster de Taito do CSC-IT Center for Science Ltd., e o usuário precisa modificar os scripts e os próprios makefiles para obter a ferramenta de modelagem para trabalhar em outras plataformas. A ferramenta começa executando o Solver²⁰do stmm, que calcula as características do elemento de volume, conforme descrito por Väisänen et al.¹⁸. Depois disso, as características de espalhamento e absorção do elemento de volume são usadas como entrada para dois softwares diferentes. Um solver de dispersão de Mie é usado para encontrar o índice de refração eficaz combinando a seção transversal de espalhamento coerente do elemento de volume a uma esfera de Mie do tamanho igual²⁰. Em seguida, o agregado é modelado executando o software SIRIS4 com o elemento de volume como um espalhador difuso e com o índice de refração eficaz na superfície do agregado. O componente de retroespalhamento coerente é adicionado separadamente porque não há nenhum software que possa tratar o meio de refração eficaz e a retroespalhamento coerente simultaneamente. Atualmente, o RT-CB é incapaz de contabilizar para o meio refração eficaz, visto que o SIRIS4 é incapaz da contabilidade para o backscattering coerente. O Retrodispersão coerente é, entretanto, adicionado ao SIRIS4^23,24 resultados aproximadamente executando as características do espalhamento do volume-elemento com o software da decomposição da matriz da fase de espalhamento pmdec que deriva matrizes puras de Mueller e de Jones exigidas para o RT-CB⁹. O componente de retroespalhamento coerente é então extraído subtraindo-se o componente de transferência radiativa dos resultados do RT-CB. Em seguida, o componente de retroespalhamento coerente extraído é adicionado aos resultados obtidos a partir do SIRIS4.

Nós simulamos numericamente as propriedades do mm-sized (raio 580 μm) SiO₂ agregado seguindo a etapa 2. Foram utilizados dois tipos de elementos de volume, um constituído por partículas equidimensionadas nominais (0,25 μm) e o outro constituído por partículas normalmente distribuídas (média de 0,25 μm, desvio padrão 0,1 μm) truncados para a faixa de 0,1-0.2525 μm. apresentando o último distribuição de partículas baseia-se no fato de que, essencialmente, todas as amostras de SiO₂ com um determinado tamanho de partícula nominal também têm uma distribuição alienígena significativa de partículas menores³¹. No total, 128 elementos de volume do tamanho Kr₀= 10 foram extraídos de 128 caixas periódicas contendo cerca de 10.000 partículas embaladas para a densidade de volume v= 47% cada. A partir das especificações do material, temos n= 1.463 + i0 no comprimento de onda de 0,488 μm, que é o comprimento de onda utilizado nas medições.

Com SIRIS4, as propriedades de espalhamento de 100.000 agregados, com raio de 580 μm, desvio padrão de 5,8 μm, e com o índice de poder-lei da função de correlação 2, foram resolvidas e médias. Esses resultados são plotados (ver Figura 5, figura 6, Figura 7) com as medidas experimentais, e uma simulação adicional sem o meio efetivo. Ambas as escolhas para a distribuição de partículas produzem uma partida para a função de fase medida (ver Figura 5), embora resultem em diferentes características de polarização como é visto na Figura 6. Essas diferenças podem ser usadas para identificar a distribuição subjacente das partículas na amostra. A melhor opção é usar a distribuição normal truncada em vez das partículas equidimensionadas (veja a Figura 6). Se apenas as funções de fase normalizadas forem usadas, as distribuições subjacentes são indistinguíveis (compare a Figura 5, figura 6, Figura 7). Na Figura 7 para a despolarização, os resultados numéricos têm características semelhantes à curva medida, mas as funções são deslocadas em 10 ° para a direção de retroespalhamento. O índice de refração efetivo corrige positivamente os resultados, como é visto a partir das simulações obtidas com e sem o meio efetivo (ver Figura 5, figura 6, Figura 7). As diferenças na polarização (Figura 6) indicam que a amostra tem, presumivelmente, uma estrutura mais complexa (por exemplo, um manto e um núcleo separados) do que nosso modelo homogêneo. É, entretanto, além dos métodos microscópicos existentes para a caracterização da amostra para recuperar a estrutura verdadeira do agregado. O retroespalhamento coerente foi adicionado separadamente aos resultados. As medições não têm pico de intensidade visível observada nos ângulos de retroespalhamento, mas o grau de polarização linear é mais negativo entre 0-30 ° que não pode ser produzido sem retroespalhamento coerente (compare "distribuição" com "não CB", ver Figura 5, figura 6, Figura 7).

Para aplicações do sistema solar, comparamos os espectros Vesta observados e o espectro modelado obtido pelo seguinte protocolo 3. Os resultados são mostrados na Figura 3 e na Figura 8 e sugerem que as partículas de e, com mais de 75% delas com tamanho de partícula menor que 25 μm, dominam o regolito de Vesta. Embora o fósforo total seja completamente satisfatório, os espectros modelados e observados diferem ligeiramente: os centros da faixa da absorção do espectro modelo são deslocados aos comprimentos de onda mais longos, e o minima espectral e o Maxima tendem a ser rasos em comparação ao observado Espectros. As diferenças nos mínimos e máximos poderiam ser explicadas pelo fato de que os efeitos de sombreamento mútuo entre as partículas de regolito não foram contabilizados: os efeitos de sombreamento são mais fortes para baixas reflectais e mais fracos para refletâncias elevadas e, no sentido relativo, diminuiria a minima espectral e aumentaria o Maxima espectral quando contabilizado na modelagem. Além disso, a parte imaginária dos complexos índices de refração para o e foi derivada sem levar em conta a rugosidade superficial da escala de comprimento de onda e, portanto, os valores derivados podem ser muito pequenos para explicar os mínimos espectrais. Ao usar esses valores em nosso modelo utilizando óptica geométrica, as profundidades da banda no espectro modelado podem se tornar muito superficiais. Estes efeitos da escala de onda podiam igualmente jogar uma parte em comprimentos de onda mais longos junto com uma contribuição pequena da cauda low-end do espectro de emissão térmica. As diferenças também podem ser causadas por uma incompatibilidade composicional de nossa amostra e e minerais Vesta e por uma distribuição de tamanho de partícula diferente necessária para o modelo. Finalmente, os espectros da reflectância de Vesta foram observados em 180-200 K, e nossa amostra e foi medida na temperatura ambiente. Reddy et al.³² mostraram que os centros de banda de absorção mudam para comprimentos de onda mais longos com aumento da temperatura.

As observações da curva de fase fotométrica e polariométrica para o asteróide (4) Vesta são de Gehrels³³ e o nó de corpos pequenos do sistema de dados PLANETÁRIOS da NASA (http://pdssbn.astro. UMD.edu/sbnhtml), respectivamente. Sua modelagem segue a etapa 4 e começa a partir do índice de refração de partículas e distribuição de tamanho disponível a partir da modelagem espectrométrica no comprimento de onda de 0,45 μm. Estas partículas têm tamanhos maiores do que 5 μm, isto é, muito maior do que o comprimento de onda e estão assim no regime ótico geométrico, denominado população da grande-partícula. Para a modelagem da curva de fase, uma população de pequenas partículas adicional de partículas de subcomprimento de onda densamente embaladas também é incorporada, com a devida atenção para evitar conflitos com a modelagem espectrométrica acima.

O índice refração complexo foi ajustado a 1.8 + i 0.000168. Os tamanhos de partícula efetivos e albedos de espalhamento único nas populações de partículas grandes e pequenas partículas iguais (9,385 μm, 0,791) e (0,716 μm, 0,8935), respectivamente. Os comprimentos de trajeto livre médios nos meios da grande-partícula e da pequeno-partícula são 16,39 μm e 0,56 μm. O meio da grande-partícula tem uma densidade do volume de 0,4, visto que o meio da pequeno-partícula tem uma densidade do volume de 0,3. As frações dos meios de partículas grandes e de pequenas partículas no regolito de Vesta são assumidas como sendo 99% e 1%, respectivamente, dando um albedo de espalhamento único total de 0,815 e um comprimento de trajeto livre médio total de 12,78 μm. A seguir ao passo 4, o Albedo geométrico Vesta a 0,45 μm acaba por ser 0,32 em concordância justa com as observações (cf. Figura 8 quando extrapolada para ângulo de fase zero).

A figura 9, figura 10, Figura 11 , retrata a modelagem da curva de fase fotométrica e polariométrica para Vesta. Para a curva de fase fotométrica (Figura 10, esquerda), a curva de fase do modelo de RT-CB foi acompanhada de uma dependência linear na escala de magnitude (coeficiente de inclinação-0, 179 MAG/°), imitando o efeito de sombreamento em um densamente embalado, alto albedo regolito. Nenhuma alteração foi invocada para o grau de polarização (Figura 10, direita; Figura 11). O modelo explica com sucesso as curvas de fase fotométrica e polariométrica observadas e oferece uma predição realista para a polarização máxima perto do ângulo de fase de 100 °, bem como para as características em ângulos de fase pequenos < 3 °.

É impressionante como a fração minuto da população de pequenas partículas é capaz de completar a explicação das curvas de fase (Figura 10, Figura 11). Há aspectos de modelagem intrigante envolvidos. Primeiro, como mostrado na Figura 9 (à esquerda), as funções de fase de espalhamento único para as populações de partículas grandes e de partículas pequenas são bastante semelhantes, enquanto os elementos de polarização linear são significativamente diferentes. Em segundo lugar, nas computações RT-CB, ambas as populações de partículas contribuem para os efeitos de retroespalhamento coerentes. Em terceiro lugar, a fim de obter Maxima de polarização realista, tem de haver uma população significativa de grandes partículas no regolito (de acordo com a modelagem espectral). Com a mistura independente atual dos meios da pequeno-partícula e da grande-partícula, remanesce possível atribuir uma parte da contribuição da pequeno-partícula às superfícies da grande-partícula. No entanto, para que os efeitos de retroespalhamento coerentes tenham lugar e para explicar as observações, é obrigatório incorporar uma população de pequenas partículas.

A missão de Rosetta da Agência Espacial Européia (ESA) ao cometa 67P/Churyumov-Gerasimenko proporcionou uma oportunidade para medir a função de fase fotométrica do coma e do núcleo sobre uma escala larga do ângulo de fase dentro de apenas algumas horas³⁴. As funções de fase de coma medido mostram uma forte variação com o tempo e uma posição local da espaçonave. A função de fase de coma foi modelada com sucesso²⁰ com um modelo de partícula composto de partículas orgânicas e silicato de tamanho submicrômetro usando os métodos numéricos (etapas 5 e 2), como mostrado na Figura 12. Os resultados sugerem que a distribuição do tamanho da poeira varia no coma devido à atividade do cometa e à evolução dinâmica da poeira. Por modelagem de dispersão por um objeto de 1 km de tamanho cuja superfície é coberta com as partículas de poeira, mostramos que a dispersão pelo núcleo do cometa é dominada com o mesmo tipo de partículas que também dominam o espalhamento no coma (Figura 13).

Figura 1: Asteróide (4) Vesta (esquerda) e cometa 67P/Churyumov-Gerasimenko (à direita) visitados pela missão Dawn da NASA e pela missão ESA Rosetta, respectivamente. Créditos da imagem: NASA/JPL/MPS/DLR/IDA/Björn Jónsson (esquerda), ESA/Rosetta/NAVCAM (direita). Por favor clique aqui para ver uma versão maior desta figura.

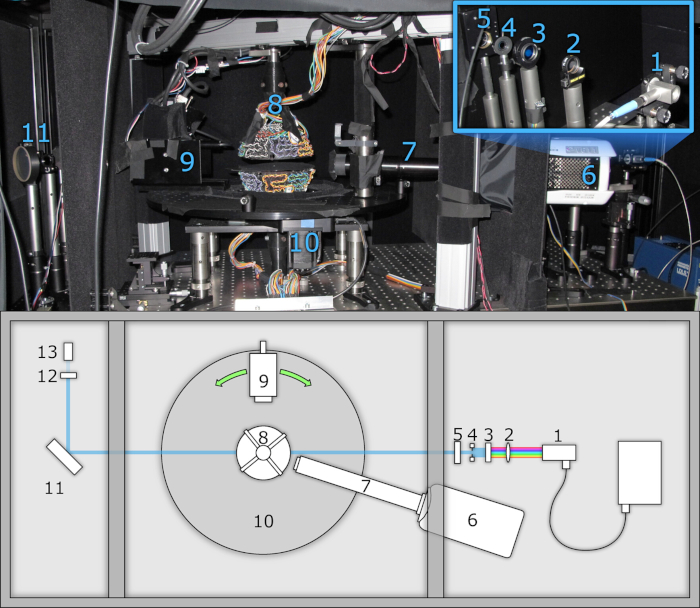
Figura 2: Instrumento de medição de espalhamento de luz. Foto (acima) e vista superior esquemática (abaixo) mostrando: (1) fibra-acoplado fonte de luz com colimador, (2) lente de focagem (opcional), (3) bandpass filtro para seleção de comprimento de onda, (4) abertura ajustável para feixe de modelagem, (5) motorizado linear polarizador, (6) câmera de alta velocidade, (7) objetivo da elevado-ampliação, (8) Sirenídeo acústico para a armadilha da amostra, (9) cabeça da medida, compreendendo um filtro do ir, obturador motorizado, polarizador linear motorizado, e um tubo photomultiplicador (PMT), (10) estágio motorizado da rotação para ajustar o ângulo da cabeça da medida, (11) plano ótico para a reflexão de Fresnel, (12) filtro neutro da densidade, e (13) referência PMT, para a intensidade do feixe da monitoração. O sistema é dividido em três compartimentos fechados para eliminar a luz perdida. Por favor clique aqui para ver uma versão maior desta figura.

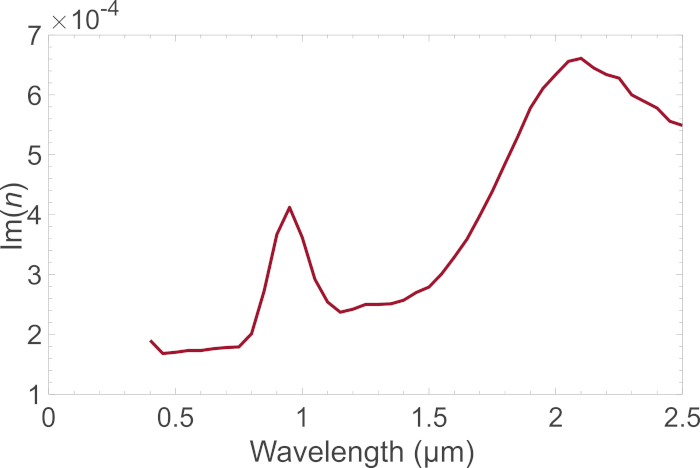
Figura 3: a parte imaginária do índice de refração para e como uma função de comprimento de onda. A parte imaginária do im refração (n) obteve para o mineral e seguindo o protocolo 3,1. O índice de refração é utilizado na modelagem das características de espalhamento do asteróide (4) Vesta. Por favor clique aqui para ver uma versão maior desta figura.

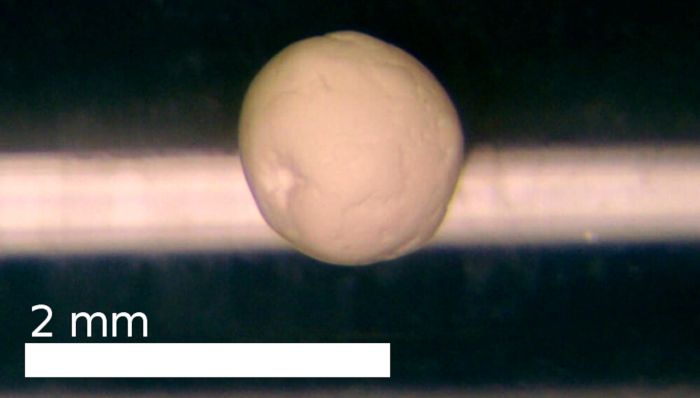
Figura 4: A amostra da medida compor de partículas esféricas densamente-embaladas do sio₂ . A amostra foi cuidadosamente polida, a fim de obter uma forma quase esférica que permite tanto experimentos de espalhamento eficiente e modelagem numérica. Por favor clique aqui para ver uma versão maior desta figura.

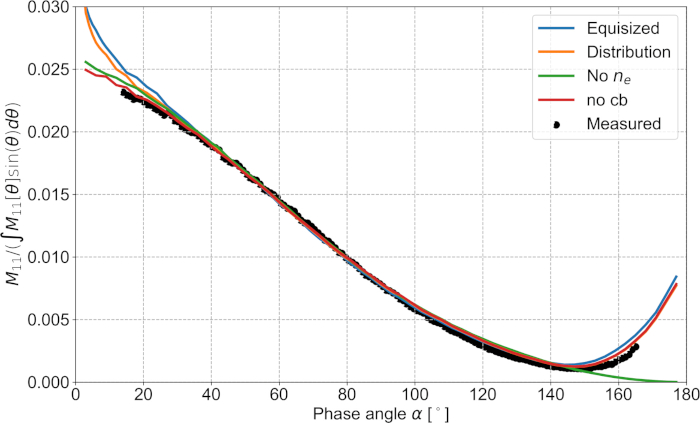
Figura 5: função de fase. As funções de fase do agregado amostral obtiveram-se seguindo os protocolos experimentais 1 e a etapa de modelagem numérica 2. As funções da fase são normalizadas para dar a unidade quando integrado de 15,1 ° a 165, 4 °. Por favor clique aqui para ver uma versão maior desta figura.

Figura 6: grau de polarização linear. Como na Figura 5 para o grau de polarização linear para a luz incidente não polarizada-m₁₂/m₁₁ (em%). Por favor clique aqui para ver uma versão maior desta figura.

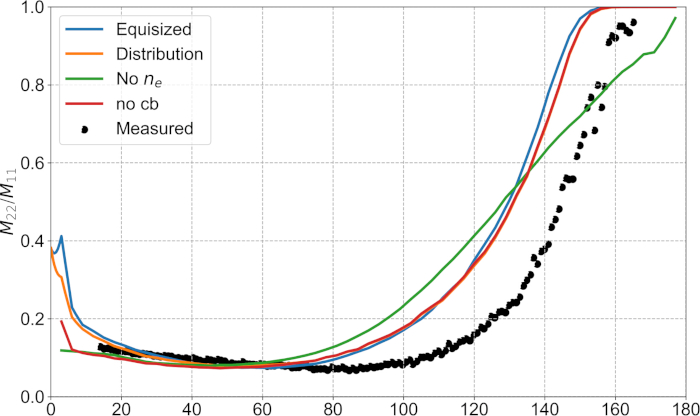
Figura 7: despolarização. Como na Figura 5 para a despolarização m₂₂/m₁₁. Por favor clique aqui para ver uma versão maior desta figura.

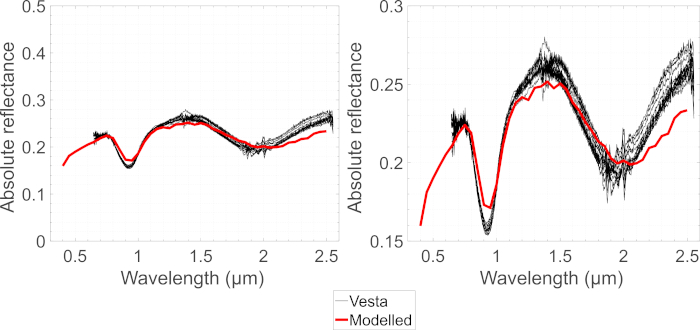
Figura 8: Espectros de reflectância absoluta. Asteróide (4) Vesta modelado e observado espectros de reflectância absoluta em ângulo de fase de 17,4 graus. Por favor clique aqui para ver uma versão maior desta figura.

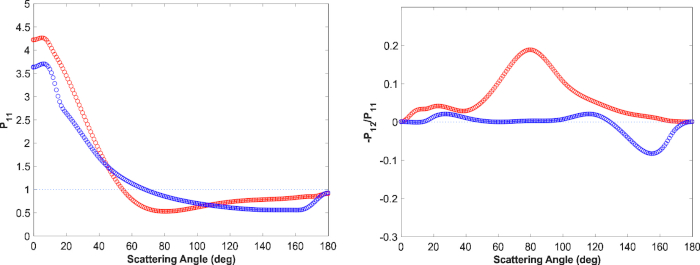
Figura 9: Função de dispersão de fase p₁₁ e grau de polarização linear para luz incidente não polarizada -p₂₁/p₁₁ em função do ângulo de espalhamento para elementos de volume de partículas grandes (vermelhas) e pequenas partículas (azul) no regolito do asteróide (4) Vesta. A linha pontilhada indica uma hipotética função de fase isotrópica (esquerda) e um nível zero de polarização (direita). Por favor clique aqui para ver uma versão maior desta figura.

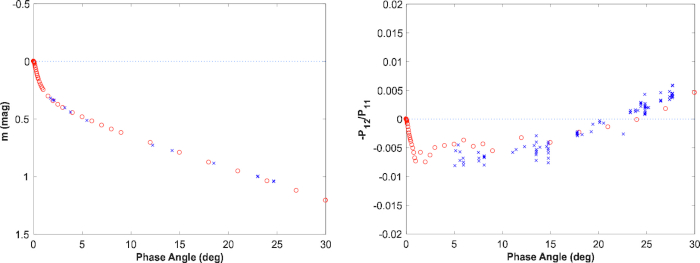
Figura 10: observou (azul) e modelado (vermelho) o brilho disco-integrado na escala da magnitude assim como o grau de polarização linear para a luz incidente unpolarizada em função do ângulo de fase para o asteróide (4) Vesta. As observações fotométricas e polarimétricas são de Gehrels (1967) e o nó de corpos pequenos do sistema de dados planetários (http://pdssbn.astro.umd.edu/sbnhtml), respectivamente. Por favor clique aqui para ver uma versão maior desta figura.

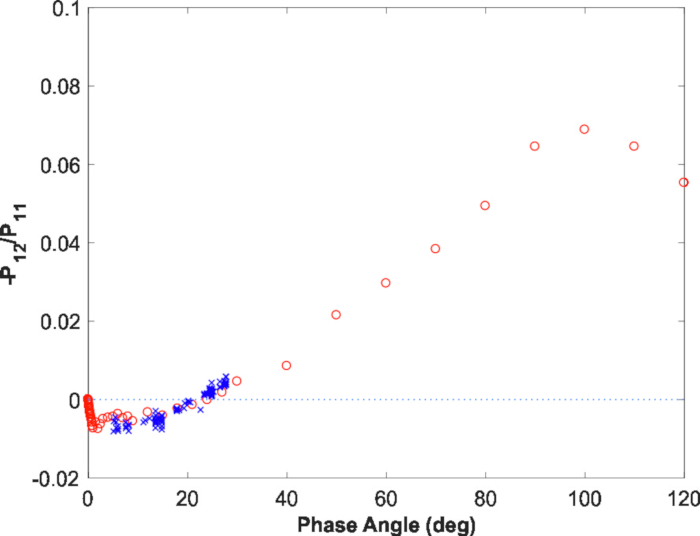
Figura 11: grau de polarização linear. O grau de polarização linear para o asteróide (4) Vesta previu para os ângulos grandes da fase baseados na modelagem numérica da múltiplo-espalhamento. Por favor clique aqui para ver uma versão maior desta figura.

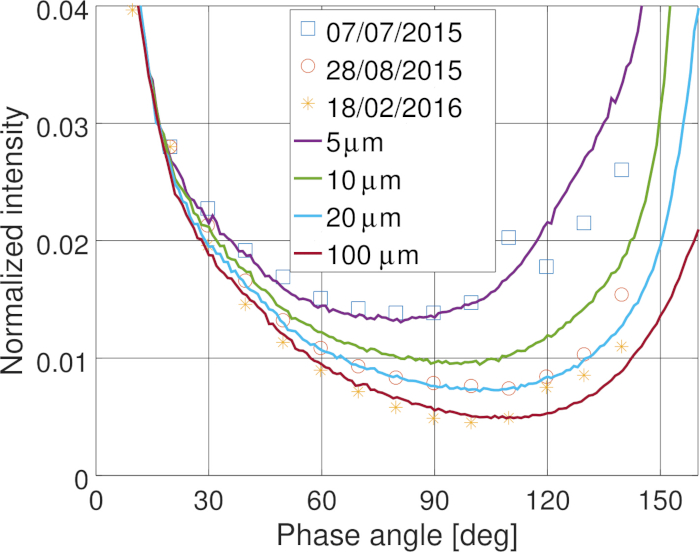
Figura 12: funções de fase fotométrica modeladas e medidas em coma do cometa 67P/Churyumov-Gerasimenko. As variações nas funções da fase medida no tempo podem ser explicadas pela distribuição variando do tamanho da poeira no coma. Por favor clique aqui para ver uma versão maior desta figura.

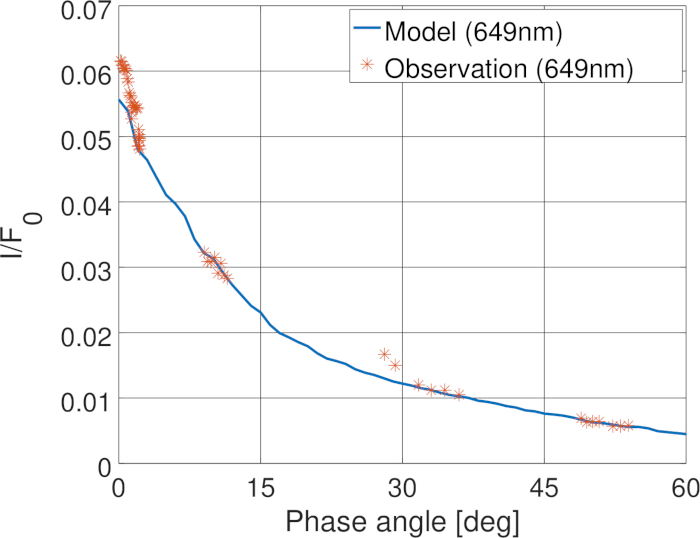
Figura 13: funções de fase. Funções de fase modeladas e medidas do núcleo do cometa 67P. Por favor clique aqui para ver uma versão maior desta figura.

Discussão

Métodos experimentais, teóricos e computacionais foram apresentados para dispersão de luz por meios aleatórios discretos de partículas. Os métodos experimentais têm sido utilizados para validar os conceitos básicos nos métodos teórico-computacionais. Os últimos métodos foram aplicados com sucesso na interpretação de observações astronômicas do asteróide (4) Vesta e cometa 67P/Churyumov-Gerasimenko.

O Scatterometer experimental confia na levitação ultrassonicamente controlada da amostra que permite medidas da Mueller-matriz para um agregado da amostra em uma orientação desejada. O agregado pode ser utilizado repetidamente nas medições, pois é possível conservar o agregado após cada conjunto de medição. Esta é a primeira vez que tais medições de dispersão não-contato, não-destrutiva são realizadas em uma amostra controle total.

Os métodos teóricos e computacionais dependem dos chamados processos de espalhamento, absorção e extinção incoerentes em meios aleatórios. Considerando que as interações eletromagnéticas exatas sempre ocorrem de forma coerente, dentro de um meio aleatório infinito após a média configuracional, apenas interações incoerentes permanecem entre os elementos de volume das partículas. No presente trabalho, as interações incoerentes entre esses elementos são exatamente contabilizadas usando as equações de Maxwell: depois de subtrair os campos coerentes dos campos no espaço livre, são os campos incoerentes dentro do meio aleatório que permanecem. O tratamento foi tomado presentemente a seu rigor completo que as interações, assim como os coeficientes da extinção, do espalhamento, e da absorção do meio, são derivadas dentro da estrutura de interações incoerentes. Além disso, foi demonstrado que a contabilização dos efeitos de campo coerentes na interface entre o espaço livre e o meio aleatório resulta em um tratamento global bem-sucedido para um meio aleatório restrito.

A aplicação dos métodos teóricos e computacionais foi ilustrada para medições experimentais de um agregado amostral esférico em escala de mm composto por partículas de SiO₂ esféricas em escala submícron. A aplicação mostra, inequivocamente, que o agregado amostral deve ser composto de uma distribuição de partículas com tamanhos variados, em vez de serem compostas por partículas esféricas equidimensionadas. Pode haver conseqüências de longo alcance desse resultado para a caracterização de meios aleatórios: é plausível que os meios de comunicação sejam significativamente mais complexos do que o que foi deduzado anteriormente usando métodos de caracterização de ponta.

A interpretação sinótica do espectro para o asteróide (4) Vesta através dos comprimentos de onda visíveis e near-infrared assim como as curvas fotométricas e polarimétricas da fase de Vesta no comprimento de onda de 0,45 μm mostra que é prático utilizar os métodos numéricos em restringir as composições minerais, as distribuições do tamanho de partícula, assim como a densidade do volume do regolito das observações astronômicas remotas. Tais recuperações são reforçadas ainda mais pela interpretação simultânea das curvas da fase fotométrica para o cometa 67P/Churyumov-Gerasimenko a respeito de seu coma e núcleo. Finalmente, a modelagem realística da curva de fase polariométrica de 67P foi obtida²⁰. Há umas perspectivas futuras principais em aplicar os métodos atuais na interpretação das observações de objetos do sistema solar no grande.

Há perspectivas futuras para a presente abordagem experimental e teórica combinada. Como é extremamente difícil caracterizar com precisão a mídia aleatória composta por inhomogenidades em escala de comprimento de onda, as medições controladas da matriz Mueller podem oferecer uma ferramenta para recuperar informações sobre a densidade do volume e a distribuição do tamanho das partículas em o meio. A inversão quantitativa destes parâmetros físicos é facilitada pelos métodos numéricos novos.

Materiais

Name	Company	Catalog Number	Comments
10GL08	Newport		Calcite polarizer
12X Zoom Body Tube 1-50487AD	Navitar		Microscope objective
43-412-000	Edmund optics		Optical flat
8MPR16-1	Standa		Motorized Polarizer Rotator
8MRB240-152-59D	Standa		Rotation stage
8SMC5-ETHERNET	Standa		Motor controller
Digi-pas DWL3500XY	Digi-pas		Digital 2-axis level
DMT 65-D25-HiDS	Owis		Optics rotation stage
EQ-99 LDLS	Energetiq		Light source
FL488-10	Thorlabs		Laser line filter
IBM 65-D0-35-HiDS	Owis		Motorized iris shutter
LPVISE100-A	Thorlabs		Film polarizer
microPMT H12403-01	Hamamatsu		Photomultiplier tube
NI PXIe-5171R	National Instruments		Digital oscilloscope
NI PXIe-8880	National Instruments		PXIe chassis
Phantom v611	Vision Research		High speed camera
PS 10-32-DC	Owis		Motor controller
RC08FC-P01	Thorlabs		Fiber collimator
SET-NDF-D22-G25	Owis		Neutral density filter
TIA60	Thorlabs		PMT amplifier