Fonte: Faisal Alamgir, School of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA

La diffrazione a raggi X (XRD) è una tecnica utilizzata nella scienza dei materiali per determinare la struttura atomica e molecolare di un materiale. Questo viene fatto irradiando un campione del materiale con raggi X incidenti e quindi misurando le intensità e gli angoli di diffusione dei raggi X che vengono dispersi dal materiale. L'intensità dei raggi X sparsi viene tracciata in funzione dell'angolo di diffusione e la struttura del materiale è determinata dall'analisi della posizione, dell'angolo e delle intensità dei picchi di intensità sparsi. Oltre a poter misurare le posizioni medie degli atomi nel cristallo, si possono determinare informazioni su come la struttura effettiva si discosti da quella ideale, derivante ad esempio da stress interni o da difetti.

La diffrazione dei raggi X, che è centrale nel metodo XRD, è un sottoinsieme dei fenomeni generali di diffusione dei raggi X. XRD, che è generalmente usato per indicare la diffrazione a raggi X grandangolare (WAXD), rientra in diversi metodi che utilizzano le onde a raggi X elasticamente disperse. Altre tecniche a raggi X basate sullo scattering elastico includono lo scattering a raggi X ad angolo piccolo (SAXS), in cui i raggi X sono incidenti sul campione oltre il piccolo intervallo angolare di 0,1-10⁰ in genere). SAXS misura le correlazioni strutturali della scala di diversi nanometri o più grandi (come le sovrastrutture cristalline) e la riflettività a raggi X che misura lo spessore, la rugosità e la densità dei film sottili. WAXD copre un intervallo angolare superiore a 10⁰.

Relazione tra posizioni di picco diffratte e struttura cristallina:

Quando onde luminose di lunghezza d'onda sufficientemente piccola sono incidenti su un reticolo cristallino, si dissolvono dai punti reticolari. A determinati angoli di incidenza, le onde parallele diffratte interferiscono in modo costruttivo e creano picchi rilevabili di intensità. W.H. Bragg identificò la relazione illustrata nella Figura 1 e derivò un'equazione corrispondente:

nλ = 2d_hkl sin θ [1]

Qui λ è la lunghezza d'onda dei raggi X utilizzati, d_hkl è la spaziatura tra un particolare insieme di piani con indici di Miller (hkl)* e θ è l'angolo di incidenza a cui viene misurato un picco di diffrazione. Infine, n è un intero che rappresenta l'"ordine armonico" della diffrazione. A n=1, ad esempio, abbiamo la prima armonica, il che significa che il percorso dei raggi X diffratti attraverso il cristallo (equivalente a 2d_hkl sin ) è esattamente 1λ, mentre a n = 2, il percorso diffratto è 2λ. Possiamo tipicamente assumere n=1, e, in generale, n=1 per θ < sin^-1(2λ/d_h'k'l',dove h'k'l' sono gli indici di Miller dei piani che mostrano il primo picco (al valore 2θ più basso) in un esperimento di diffrazione. Gli indici di Miller sono un insieme di tre interi che costituiscono un sistema di notazione per identificare direzioni e piani all'interno dei cristalli. Per le direzioni, gli indici [h k l] di Miller rappresentano la differenza normalizzata nelle rispettive coordinate x, y e z (in un sistema di coordinate cartesiane) di due punti lungo la direzione. Per i piani, gli indici di Miller (h k l) di un piano sono semplicemente i valori h k l della direzione perpendicolare al piano.

In un tipico esperimento XRD in modalità di riflessione, la sorgente di raggi X è fissata in posizione e il campione viene ruotato rispetto al fascio di raggi X su θ. Un rivelatore raccoglie il fascio diffratto e deve tenere il passo con la rotazione del campione ruotando al doppio della velocità (cioè per un dato angolo di campionamento di θ, l'angolo del rivelatore è 2θ). La geometria dell'esperimento è schematicamente mostrata nella Figura 1.

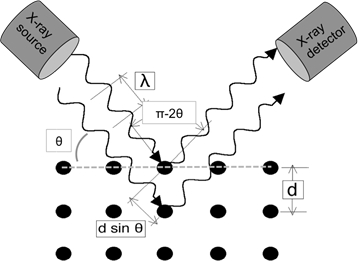
Figura 1: Illustrazione della legge di Bragg.

Quando si osserva un picco di intensità, l'equazione 1 è necessariamente soddisfatta. Di conseguenza, possiamo calcolare le d-spaziature in base agli angoli in cui questi picchi vengono osservati. Calcolando le d-spaziature di più picchi, è possibile identificare il campione di materiale della classe cristallina e dei parametri della struttura cristallina utilizzando un database come il manuale di ricerca Hanawalt o le librerie di database disponibili con il software XRD utilizzato.

Supponiamo che il campione oggetto di indagine non sia un singolo cristallo. Se il campione fosse un singolo cristallo con un particolare piano (h*k*l*) parallelo alla superficie del campione, dovrebbe essere ruotato fino a quando la condizione di Bragg per il (h*k*l*) è soddisfatta al fine di vedere un picco di intensità diffratta (per n=1) con picchi armonici potenzialmente più alti (h*k*l*) (ad esempio per n=2) rilevabili anche ad angoli più alti. In tutti gli altri angoli non ci sarebbero picchi in un singolo campione di cristallo. Supponiamo invece che il campione sia policristallino o che sia una polvere, con un numero statisticamente significativo di grani cristallini o particelle di polvere illuminate dal fascio di raggi X incidente. In base a questa ipotesi, il campione è costituito da grani orientati casualmente, con una probabilità statistica simile per tutti i possibili piani reticolari a diffratta.

Le relazioni tra il d_hkl e i parametri delle cellule unitarie sono mostrate di seguito nelle equazioni 2-7 per le 7 classi di cristalli, cubica, tetragonale, esagonale, romboedrica, ortorombica, monoclinica e tricclinica. I parametri delle celle unitarie sono costituiti dalle lunghezze di (a,b,c) e dagli angoli tra (α, β, γ) i bordi delle celle unitarie per le 7 classi di cristalli (la Figura 1x mostra l'esempio di una delle classi di cristalli: la struttura tetragonale dove a=b≠c, e α=β=γ=90⁰). Utilizzando più posizioni di picco diffratte (cioè diversi valori d_hkl distinti), i valori dei parametri della cella unitaria possono essere risolti in modo univoco.

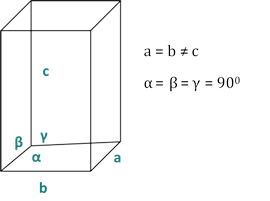
Figura 2: La struttura tetragonale come una delle sette classi di cristalli.

Cubico (a = b = c; α = β = γ = 90⁰):

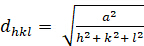[2]

Tetragonale (a = b ≠ c; α = β = γ = 90⁰):

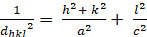[3]

Esagonale (a = b ≠ c; α = β = 90⁰; γ = 120⁰):

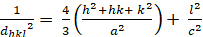[4]

Ortorombico (a ≠ b ≠ c; α = β = γ = 90⁰):

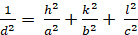[5]

Romboedrico (a = b ≠ c; α = β = γ = 90⁰):

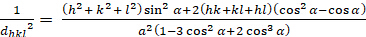[6]

Monoclino (a ≠ b ≠ c; α = γ = 90⁰ ≠ β):

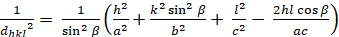[7]

Triclinic (a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90⁰):

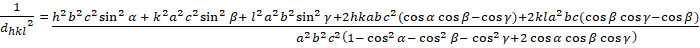      [8]

Relazione tra intensità di picco diffratte e struttura cristallina:

Successivamente esaminiamo i fattori che contribuiscono all'intensità in un modello XRD. I fattori possono essere scomposti come 1) il contributo allo scattering che deriva direttamente dagli aspetti strutturali unici del materiale (i tipi e le posizioni specifiche degli atomi di scattering nella struttura) e 2) quelli che non sono specifici del materiale. Nel primo, ci sono due fattori: il "fattore di assorbimento" e il "fattore di struttura". Il fattore di assorbimento dipende principalmente dalla capacità del materiale di assorbire i raggi X durante l'uscita e l'uscita. Questo fattore non ha una dipendenza θ finché i campioni non sono sottili (il campione deve essere > 3 volte più spesso della lunghezza di attenuazione dei raggi X). In altre parole, il contributo del fattore di assorbimento all'intensità dei diversi picchi è costante. Il "fattore struttura" influenza direttamente l'intensità di picchi specifici come risultato diretto della struttura. I fattori rimanenti, la 'molteplicità', che rappresenta tutti i piani che appartengono alla stessa famiglia perché sono simmetricamente correlati, e il fattore 'Lorentz-Polarization', che deriva dalla geometria dell'esperimento XRD, influenzano anche l'intensità relativa dei picchi ma non sono specifici di un materiale e possono essere facilmente spiegati con espressioni analitiche (cioè il software di analisi XRD può rimuoverli con funzioni analitiche).

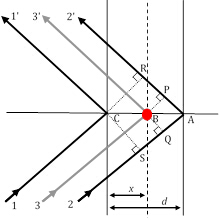
Figura 3: Tre percorsi di raggi di diffrazione, di cui i raggi 11' e 22' soddisfano la condizione di Bragg, mentre il raggio 33' deriva dallo scattering di un atomo (cerchio rosso) in posizione arbitraria.

Essendo l'unico fattore che porta il contributo strutturale unico di un materiale alle intensità relative dei picchi XRD, il fattore di struttura è molto importante e richiede uno sguardo più attento. Nella Figura 2, supponiamo che la condizione di diffrazione di Bragg di^1° ordine (ricordate, che questo corrisponde a n=1) sia soddisfatta tra il raggio_11' e il raggio_22' che sono sparsi su due piani atomici nella direzione h00 (usando la notazione degli indici di Miller descritta in precedenza) separati da una distanza d. In questa condizione, la differenza nella lunghezza del percorso tra il raggio_11' e il raggio_22' è δ_(22'-11') = SA + AR = λ. Lo sfasamento tra i raggi diffratti 1 e 2 è, quindi, Φ_22'-11' = (δ_(22'-11')/λ) 2π = 2π (assumendo una simmetria cubica e, quindi, d = a/h nella direzione h00).

Con pochi passi in geometria analitica, si può dimostrare che lo sfasamento, Φ_(33'-11'), con raggio 3 diffratto da un piano arbitrario di atomi che sono distanziati una distanza arbitraria x, è dato da: Φ_(33'-11') = 2πhu, dove u = x / a (a è il parametro della cella unitaria nella direzione (h00).) Prendendo le altre due direzioni ortogonali, (0k0) e (00l), e v=y/a e w=z/a come coordinate frazionarie nelle direzioni y e z, l'espressione per lo sfasamento si estende a Φ = 2π(hu+kv+lw). Ora, l'onda a raggi X dispersa dall'atomo j-esimoin una cella unitaria avrà un'ampiezza di scattering di f _j e una fase di Φ_j, tale che la funzione che la descrive è 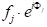. Il fattore di struttura che cerchiamo, quindi, è la somma di tutte le funzioni di scattering dovute a tutti gli atomi unici in una cella unitaria. Questo fattore di struttura, F, è dato come:

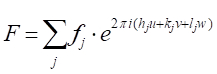[9]

e il fattore di intensità contribuito dal fattore di struttura è I = F².

Sulla base delle posizioni (u,v,w) degli atomi su particolari piani (h,k,l), esiste la possibilità di interferenza tra onde sparse che sia costruttiva, distruttiva o intermedia, e questa interferenza influenza direttamente l'ampiezza dei picchi XRD che rappresentano i piani (hkl).

Ora, un grafico di intensità, I, contro 2θ è ciò che viene misurato in un esperimento XRD. La determinazione del tipo di cristallo e dei parametri delle celle unitarie associate (a, b, c, α, β e γ) può essere raggiunta analiticamente osservando la presenza sistematica/ assenza di picchi, utilizzando le equazioni 2-9, confrontando i valori con i database, utilizzando la deduzione e un processo di eliminazione. Al giorno d'oggi, questo processo è abbastanza automatizzato da una varietà di software collegati a database di strutture cristalline.

La procedura seguente si applica a uno specifico strumento XRD e al software associato e potrebbero esserci alcune variazioni quando vengono utilizzati altri strumenti.

1. Esamineremo un campione di polvere di Ni su uno strumento Panalytical Alpha-1 XRD.
2. Innanzitutto, scegli la maschera per fissare la dimensione del fascio in base al diametro del campione. Il fascio non deve avere un ingombro maggiore del campione al più piccolo valore θ (tipicamente ~ 7⁰-10⁰). Per un campione di larghezza ε, la dimensione del fascio deve essere < ε sinθ.
3. Caricare il campione nella fase di spinner del campione e bloccare il campione in posizione. Lo spinner del campione aiuta a randomizzare spazialmente l'esposizione del campione alla sorgente di raggi X.
4. Scegli l'intervallo di angolazione per la scansione XRD. Ad esempio, 15-90 gradi è un intervallo tipico.
5. Scegli una dimensione del passo, cioè l'incremento in 2θe il tempo di integrazione (conteggio). Generalmente una dimensione del passo di 0,05 gradi e l'integrazione di 4 secondi è l'impostazione predefinita per una scansione grandangolare.
6. Una volta determinate tutte le posizioni di picco attraverso questa scansione iniziale, le scansioni successive possono concentrarsi su un intervallo di scansione più ristretto attorno a picchi specifici utilizzando una dimensione del passo più piccola in angolo se si desiderano dati a risoluzione più elevata da tali picchi.

Nella Figura 4 vediamo i picchi XRD per il campione di polvere ni. Si noti che i picchi osservati (ad esempio {111}, {200}) sono per quelli che hanno tutte le combinazioni pari o tutte le combinazioni dispari di h, ke l. Ni è cubico centrato sulla faccia (FCC), e in tutte le strutture FCC, i picchi corrispondenti ai piani {hkl} dove h, ke l sono miscele di interi pari e dispari, sono assenti a causa dell'interferenza distruttiva dei raggi X sparsi. Mancano picchi corrispondenti agli aerei, come {210} e {211}. Questo fenomeno è chiamato regole sistematiche di presenza e assenza e forniscono uno strumento analitico per valutare la struttura cristallina del campione.

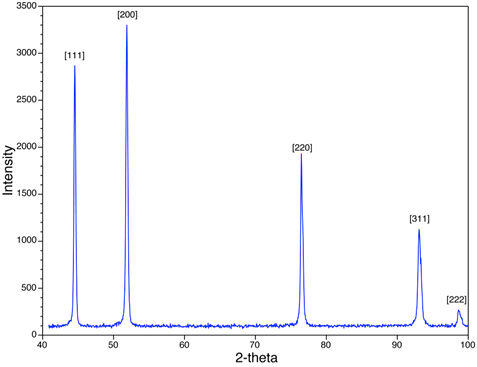
Figura 4: Viene mostrata una scansione XRD di Ni con una struttura cubica centrata sulla faccia.

Questa è una dimostrazione di un esperimento XRD standard. Il materiale esaminato in questo esperimento era in polvere, ma XRD funziona altrettanto bene con un pezzo solido di materiale purché il campione abbia una superficie piana che può essere impostata parallelamente al piano dello stadio del campione.

XRD è un metodo abbastanza onnipresente per determinare la presenza (o l'assenza) di ordine cristallografico nei materiali. Oltre all'applicazione standard di determinazione della struttura cristallina, XRD viene spesso utilizzato per ottenere una varietà di altre informazioni strutturali come:

1. Indipendentemente dal fatto che la struttura di un materiale sia amorfa (caratterizzata da un'ampia gobba nell'intensità della diffrazione e dalla mancanza di picchi cristallografici distinguibili),
2. Se il campione è un materiale composito costituito da più fasi cristallografiche e, in caso affermativo, determinare la frazione di ciascuna fase,
3. Determinare se un materiale è un composito amorfo/cristallino
4. Determinazione della granulometria/granulometria del materiale,
5. Determinazione del grado di consistenza (orientamento preferito dei grani) nel materiale.