A subscription to JoVE is required to view this content. Sign in or start your free trial.
Method Article
تطوير نموذج زيادة منطقة القاعدية الفردية -شجرة باستخدام نهج مختلط الخطي
In This Article
Summary
11 - والنماذج ذات الآثار المختلطة أدوات مرنة ومفيدة لتحليل البيانات ذات الهيكل العشوائي الهرمي في مجال الحراجة ويمكن استخدامها أيضا لتحسين أداء نماذج نمو الغابات بشكل كبير. هنا، يتم تقديم بروتوكول يجمع المعلومات المتعلقة بنماذج التأثيرات المختلطة الخطية.
Abstract
هنا ، وضعنا نموذج الفردية شجرة من 5 سنوات من زيادات المنطقة القاعدية على أساس مجموعة بيانات بما في ذلك 21898 أشجار اسبيراتا Picea من 779 قطعة أرض عينة تقع في مقاطعة شينجيانغ ، شمال غرب الصين. لمنع الارتباطات العالية بين الملاحظات من وحدة أخذ العينات نفسها ، قمنا بتطوير النموذج باستخدام نهج خطي مختلط التأثيرات مع تأثير مؤامرة عشوائية لحساب التغير العشوائي. وقد أدرجت متغيرات مختلفة على مستوى الأشجار والوقوف، مثل الأرقام القياسية لحجم الشجرة والمنافسة وحالة الموقع، كآثار ثابتة لتفسير التغير المتبقي. وبالإضافة إلى ذلك، تم وصف التغايرية والوثوث عن طريق إدخال وظائف التباين وهياكل العلاقات التلقائية. تم تحديد نموذج التأثيرات المختلطة الخطية الأمثل بواسطة العديد من الإحصاءات المناسبة: معيار المعلومات في أكايكي، ومعيار المعلومات باييزي، واحتمال اللوغاريتم، واختبار نسبة الاحتمال. وأشارت النتائج إلى أن المتغيرات الهامة للزيادة في المساحة القاعدية الفردية - الأشجار هي التحول العكسي لقطر عند ارتفاع الثدي، والمساحة القاعدية للأشجار التي أكبر من الشجرة موضوعها، وعدد الأشجار في الهكتار، والارتفاع. علاوة على ذلك، تم تصميم الأخطاء في بنية التباين بنجاح بواسطة الدالة الأسية، وتم تصحيح العلاقات التلقائية بشكل كبير بواسطة بنية التسجيل التلقائي من الدرجة الأولى (AR(1)). وتحسن أداء نموذج التأثيرات المختلطة الخطي تحسناً كبيراً بالنسبة للنموذج باستخدام الانحدار العادي الأقل المربعات.
Introduction
وبالمقارنة مع ثقافة أحادية العمر، فإن إدارة الغابات المختلطة الأنواع غير المتكافئة العمر ذات الأهداف المتعددة قد حظيت باهتمام متزايد مؤخراً1،2،3. والتنبؤ ببدائل مختلفة للإدارة ضروري لصياغة استراتيجيات قوية لإدارة الغابات، ولا سيما بالنسبة للغابات المختلطة المختلطة ذات الأنواع المختلطة المعقدة ذات الأعمار غير المتساوية4. وقد استخدمت نماذج نمو الغابات والغلة على نطاق واسع للتنبؤ شجرة أو الوقوف التنمية والحصاد في إطار مختلف مخططات الإدارة5,6,7. وتصنف نماذج نمو الغابات وغلة في نماذج الفردية شجرة، نماذج من فئة الحجم، ونماذج النمو الوقوف الكامل6،7،8. ومن المؤسف أن النماذج ذات الرتبة الحجمية ونماذج الاستعدادات الكاملة ليست مناسبة للغابات المختلطة الأنواع غير المتفاوتة العمر، مما يتطلب وصفا أكثر تفصيلا لدعم عملية صنع القرار في إدارة الغابات. لهذا السبب، تلقى نمو شجرة الفردية ونماذج الغلة اهتماما متزايدا على مدى العقود القليلة الماضية بسبب قدرتها على جعل التنبؤات للغابات تقف مع مجموعة متنوعة من تكوينات الأنواع، والهياكل، واستراتيجيات الإدارة9،10،11.
تراجع المربعات الأقل العادية (OLS) هو الأسلوب الأكثر استخداما لتطوير نماذج نمو شجرة الفردية12،13،14،15. مجموعات البيانات لنماذج نمو الأشجار الفردية التي تم جمعها مرارا وتكرارا على مدى فترة زمنية محددة على نفس وحدة أخذ العينات (أي، عينة مؤامرة أو شجرة) لها بنية عشوائية هرمية، مع عدم وجود استقلالية والارتباط المكاني والزماني العالي بين الملاحظات10،16. ينتهك الهيكل العشوائي الهرمي الافتراضات الأساسية لتراجع عملية شريان الحياة للسودان: أي المخلفات المستقلة والبيانات الموزعة عادة مع تباينات متساوية. ولذلك، فإن استخدام تراجع عملية شريان الحياة البرية ينتج حتماً تقديرات متحيزة للخطأ القياسي لتقديرات المعلمات لهذه البيانات13و14.
توفر نماذج التأثيرات المختلطة أداة قوية لتحليل البيانات ذات الهياكل المعقدة، مثل بيانات القياسات المتكررة والبيانات الطولية والبيانات متعددة المستويات. تتكون نماذج التأثيرات المختلطة من مكونات ثابتة، مشتركة بين السكان الكاملين، ومكونات عشوائية، والتي هي محددة لكل مستوى أخذ العينات. وبالإضافة إلى ذلك، نماذج الآثار المختلطة تأخذ في الاعتبار عدم القدرة على القياس والعلاقات الذاتية في المكان والزمان من خلال تحديد غير قطري التباين- مصفوفات هيكل التباين17،18،19. لهذا السبب، وقد استخدمت نماذج الآثار المختلطة على نطاق واسع في الغابات، مثل في نماذج قطر الارتفاع20،21، تاج نماذج22،23، ونماذج رقيقة الذاتي24،25، ونماذج النمو26،27.
وكان الهدف الرئيسي هنا هو وضع نموذج لزيادة المساحة القاعدية لشجرة فردية باستخدام نهج خطي مختلط الآثار. ونأمل أن يطبق نهج الآثار المختلطة على نطاق واسع.
Access restricted. Please log in or start a trial to view this content.
Protocol
1 - إعداد البيانات
- إعداد بيانات النمذجة، والتي تشمل معلومات شجرة فردية (الأنواع وقطرها عند ارتفاع الثدي في 1.3 م) ومعلومات مؤامرة (المنحدر، الجانب، والارتفاع). في هذه الدراسة، تم الحصول على البيانات من 8 (2009) و9 (2014) جرد الغابات الوطنية الصينية في مقاطعة شينجيانغ، شمال غرب الصين، والتي تشمل 21،898 ملاحظات من 779 قطعة العينة. وهذه العينات على شكل مربع بحجم 1 مو (وحدة صينية من المساحة تعادل 0.067 هكتار) ويتم ترتيبها بشكل منهجي على شبكة من 4 كم x 8 كم.
ملاحظة: تتطلب البيانات لزيادة النمذجة (المنطقة القاعدية) فترة نمو واحدة على الأقل (أي، ملاحظتان). - تقسيم البيانات عشوائياً إلى مجموعتي بيانات، مع 80٪ من البيانات من عينات المؤامرات المستخدمة لتركيب النموذج (مجموعة بيانات تطوير النموذج)، والتي تتكون من 17145 ملاحظات من 623 قطعة عينة و20٪ للتحقق من صحة النموذج (مجموعة بيانات النموذج) الذي يتكون من 4753 ملاحظات من 156 قطعة عينة. وترد إحصاءات وصفية للمتغيرات الرئيسية المستخدمة في الجدول 1.
ملاحظة: يمكن حذف هذه الخطوة من إجراء النمذجة، ويتم استخدام كافة البيانات لتطوير النموذج.
| المتغيرات | بيانات التركيب | بيانات التحقق من الصحة | |||||||
| دقيقه | ماكس | يعني | س. د. | دقيقه | ماكس | يعني | س. د. | ||
| DBH1 (سم) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD (سم) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| معرف (سم) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (م3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (أشجار / هكتار) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (م2/ هكتار) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| EL (m) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
الجدول 1- الانبعاثات 1000 الإحصاءات الموجزة لبيانات التركيب والتحقق من الصحة DBH1: القطر الأولي عند ارتفاع الثدي عند 1.3 متر (DBH)، DBH2: DBH قياس بعد 5 سنوات من النمو، QMD: متوسط القطر التربيعي، معرف: زيادة قطر لمدة 5 سنوات (DBH2 – DBH1)، BAL: المنطقة القاعدية من الأشجار أكبر من شجرة الموضوع (شجرة الموضوع: الشجرة التي تم حسابها مؤشرات المنافسة)، NT: عدد الأشجار في الهكتار، BA: منطقة القاعدية لكل هكتار، EL: الارتفاع، S.D.: الانحراف المعياري.
2- تطوير النموذج الأساسي
- راجع مراجع لتعريف المتغيرات التي تؤثر على زيادات منطقة القاعدة شجرة فردية.
- حدد و حساب المتغيرات استناداً إلى البيانات. بشكل عام، تتأثر زيادة المنطقة القاعدية الفردية-الشجرة بثلاث مجموعات من المتغيرات: حجم الشجرة، والمنافسة، وحالة الموقع27،28،29،30.
- النظر في آثار حجم شجرة مثل DBH1، مربع من DBH1 (
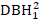 ، والتحول العكسي للDBH1 (1 / DBH1)، واللوغاريتم المشترك للDBH1 (logDBH1) أو تركيبات منها.
، والتحول العكسي للDBH1 (1 / DBH1)، واللوغاريتم المشترك للDBH1 (logDBH1) أو تركيبات منها. - النظر في الآثار التنافسية مثل مؤشرات المنافسة من جانب واحد واثنين على حد سواء لتحديد حجم أكثر شمولا مستوى المنافسة التي تعاني منها شجرة، فضلا عن وضعها الاجتماعي داخل الموقف. وتشمل المنافسة من جانب واحد BAL ومؤشر الكثافة النسبية (RD = DBH1/ QMD)؛ وتشمل المنافسة على الوجهين NT، وBA.
ملاحظة: ينبغي النظر في مؤشرات المنافسة التي تعتمد على المسافة إذا كانت البيانات متاحة. - خذ بعين الاعتبار تأثيرات الموقع مثل المظهر (ASP) ، المنحدر (SL) و EL. يجب تضمين SL و ASP باستخدام تحويل المرحلة31.
- النظر في آثار حجم شجرة مثل DBH1، مربع من DBH1 (
- حدد السجل
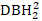 (-
(- 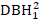 +1)
+1) 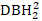 (يشير إلى مربع DBH2) كمتغير تابع.
(يشير إلى مربع DBH2) كمتغير تابع. - تطوير النموذج الأساسي باستخدام أسلوب الانحدار التدريجي. ضمان أن النموذج معقول بيولوجيا ويظهر اختلافات كبيرة بين المتغيرات المستقلة. استخدام عامل التضخم الفرق (VIF) للتحقق من تعدد المستويات.
- اترك المتغيرات المستقلة مع p < 0.05 و VIF < 5 في النموذج الأساسي.
- إخراج نتائج النموذج الأساسي والمؤامرة المتبقية. ويشكل النموذج الأساسي الذي تم إنتاجه هنا أساساً لمواصلة تطوير نموذج الآثار المختلطة.
3. خطي مختلط الآثار نموذج التنمية مع حزمة "nlme" في R البرمجيات
- قراءة مجموعة بيانات تطوير النموذج وتحميل حزمة "nlme".
> model.development.dataset = قراءة.csv ("E:/DATA/JoVE/modelingdata.csv"
رأس = TRUE)
>مكتبة (nlme) - حدد عينات من المؤامرات كمؤثرات عشوائية لتطوير نموذج التأثيرات المختلطة.
- تناسب جميع تركيبات ممكن من الآثار العشوائية مع أقصى احتمال (ML) طريقة وإخراج النتائج.
> نموذج < -lme (Y ~ 1 / DBH1+BAL + NT + EL، البيانات = model.development.dataset،
الأسلوب ="ML" ، عشوائية = ~ 1| مؤامرة)
>الملخص(الطراز)- تعيين عشوائي =~1 هو اعتراض لمعلمات عشوائية. تغيير عبارات عشوائية حتى يتم تركيب كافة المجموعات. على سبيل المثال، لتعيين 1/DBH1 و BAL كمعلمات عشوائية، فإن الرمز هو كما يلي: عشوائي =~1/DBH1+BAL-1. وبالإضافة إلى ذلك، وفي عملية التركيب، قد تبلغ الرموز عن أخطاء بسبب عدم وجود نموذج مجهز.
- حدد أفضل نموذج حسب معيار المعلومات في Akaike (AIC) ومعيار المعلومات بايز (BIC) واحتمال اللوغاريتم (Loglik) واختبار نسبة الاحتمال (LRT).
>anova(Model.1, Model.6)
>anova(Model.6, Model.23)
>anova(Model.23, Model.30) - تحديد بنية Ri. معالجة اللاتراينيستراستيكية والعلاقات الذاتية من Rط32. ط Rهو مكتوب على النحو التالي:
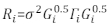 (1)
(1)
حيث σ2 هو عامل قياس غير معروف الذي يساوي التباين المتبقية نموذج، Gط هو مصفوفة قطرية تصف اللاترايكسيستيك، Γأنا هو مصفوفة تصف autocorrelation.- مراقبة ما إذا كانت البقايا لها عدمية من المؤامرة المتبقية. إذا كان هناك عدم القدرة على الوضوح (البقايا لها نمط واضح أو اتجاه واضح)، أدخل ثلاث وظائف تباين مستخدمة بشكل متكرر - وظيفة القوة الثابتة بالإضافة إلى وظيفة الطاقة والوظيفة الأسية - لـ نموذج بنية التباين للأخطاء.
>Model.30.1 < -lme(Y ~ 1/ DBH1+BAL +NT + EL، البيانات = model.development.dataset، الأسلوب ="ML"، عشوائي =~1/DBH1+BAL +NT| الارض
الأوزان = varConstPower (نموذج = ~ المجهزة (.)))
>ملخص(Model.30.1)
>Model.30.2 <-lme(Y ~ 1/DBH1+BAL +NT +EL، البيانات = model.development.dataset، الأسلوب="ML"، عشوائي =~1/DBH1+BAL +NT| الارض
الأوزان = varPower (نموذج = ~ المجهزة (.)))
>ملخص(Model.30.2)
>Model.30.3 < -lme (Y ~ 1/ DBH1+BAL + NT + EL ، البيانات = model.development.dataset ، الأسلوب = "ML" ، random =~ 1 / DBH1+ BAL + NT| الارض
الأوزان = varExp (نموذج = ~ المجهزة (.)))
>ملخص (Model.30.3) - تحديد أفضل وظيفة التباين للنموذج وفقا ل AIC، BIC، Loglik، و LRT.
>anova(Model.30, Model.30.1)
>anova(Model.30, Model.30.2)
>ANOVA(Model.30, Model.30.3) - تقديم ثلاثة هياكل تبعية شائعة الاستخدام - بنية التماثل المركب (CS)، وبنية التسجيل التلقائي من الدرجة الأولى [AR(1)] ، ومزيج من الهياكل المتوسطة التلقائية والمتحركة من الدرجة الأولى [ARMA(1,1)]— لحساب العلاقات التلقائية.
> Model.30.3.1 < -lme (Y ~ 1 / DBH1+BAL + NT + EL ، البيانات = model.development.dataset ، الأسلوب = "ML" ،
عشوائي =~1/DBH1+BAL +NT| PLOT، الأوزان = varExp(نموذج = ~ المجهزة (.))، كور = corCompSymm())
> ملخص (Model.30.3.1)
> Model.30.3.2 < -lme (Y ~ 1 / DBH1+BAL + NT + EL ، البيانات = model.development.dataset ، الأسلوب = "ML" ،
عشوائي =~1/DBH1+BAL +NT| PLOT، الأوزان = varExp(نموذج = ~ المجهزة (.))، كور = corAR1 ())
> ملخص (Model.30.3.2)
> Model.30.3.3 < -lme (Y ~ 1 / DBH1+BAL + NT + EL ، البيانات = model.development.dataset ، الأسلوب = "ML" ،
عشوائي =~1/DBH1+BAL +NT| PLOT، الأوزان = varExp(نموذج = ~ المجهزة (.))، كور = corARMA (q = 1، ف = 1))
> ملخص (Model.30.3.3) - تحديد أفضل بنية autocorrelation وفقا لAIC، BIC، Loglik، وLRT.
>ANOVA (Model.30.3, Model.30.3.2)
ملاحظة: لا يمكن تعريف G i و Γi إذا لم يكن هناك عدم وجود غير عقلانية و وثنائية. - إخراج النتائج النهائية لنموذج التأثيرات المختلطة باستخدام أسلوب الحد الأقصى المحتمل المقيد (REML).
> Mixed.model<-lme(Y ~1/DBH1+BAL+NT+EL, data=model.development.dataset, method="REML",random=~1/DBH1+BAL+NT| الارض
الأوزان = varExp (نموذج = ~ المجهزة (.))، كور = corAR1 ())
> ملخص (Mixed.model)
- مراقبة ما إذا كانت البقايا لها عدمية من المؤامرة المتبقية. إذا كان هناك عدم القدرة على الوضوح (البقايا لها نمط واضح أو اتجاه واضح)، أدخل ثلاث وظائف تباين مستخدمة بشكل متكرر - وظيفة القوة الثابتة بالإضافة إلى وظيفة الطاقة والوظيفة الأسية - لـ نموذج بنية التباين للأخطاء.
4- تصحيح التحيز
- تحويل القيم المتوقعة لزيادة المساحة القاعدية باستخدام النموذج النهائي على مقياس لوغاريتمي إلى المقياس الأصلي. ومع ذلك، فإن مثل هذا التحويل الخلفي الخطي للقيمة المتوقعة من نموذج تحويل السجل ينتج تحيزاً مرتبطاً بتحويل السجل. لمعالجة تحيز اللوغاريتم، تم اشتقاق عامل تصحيح ودمجه في معادلة التنبؤ، التي تقدر الزيادة الفعلية المتوقعة في المنطقة القاعدية لشجرة معينة [المعادلة (2)]:
 (2)
(2)
حيث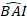 يتوقع قيمة لوغاريتمية من زيادة المنطقة القاعدية من النموذج، في حين
يتوقع قيمة لوغاريتمية من زيادة المنطقة القاعدية من النموذج، في حين 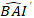 هو من المتوقع مرة أخرى قيمة من الزيادة في منطقة القاعدية لمدة 5 سنوات بعد تصحيح للانحياز تحويل
هو من المتوقع مرة أخرى قيمة من الزيادة في منطقة القاعدية لمدة 5 سنوات بعد تصحيح للانحياز تحويل 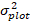 السجل. هو التباين من الآثار العشوائية في مؤامرة و2 σ هو التباين المتبقية.
السجل. هو التباين من الآثار العشوائية في مؤامرة و2 σ هو التباين المتبقية. - قم بتحويل زيادة المساحة القاعدية (
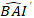 ) إلى زيادة القطر.
) إلى زيادة القطر.
5- التنبؤ والتقييم النموذجيان
- إعداد مجموعة بيانات التحقق من صحة النموذج التي تم إنتاجها في القسم 1-2 للتنبؤ.
- استخدم نموذج التأثيرات المختلطة الخطية للتنبؤ بزيادة المساحة القاعدية لشجرة فردية. تم حساب المكونات العشوائية باستخدام أفضل تنبؤ خطي غير متحيز:
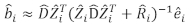 (3)
(3)
حيث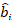 هو متجه للمكونات العشوائية؛
هو متجه للمكونات العشوائية؛ 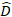 هو مصفوفة التباين التباين لتغيّر بين
هو مصفوفة التباين التباين لتغيّر بين 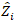 الأراضي؛ هو مصفوفة التصميم للمكونات العشوائية التي تعمل في الملاحظات التكميلية؛
الأراضي؛ هو مصفوفة التصميم للمكونات العشوائية التي تعمل في الملاحظات التكميلية؛ 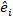 هو المتجه المتبقي الذي تعطى مكوناته بالفرق بين زيادات المنطقة القاعدية والزيادات المتوقعة باستخدام نموذج التأثيرات الثابتة.
هو المتجه المتبقي الذي تعطى مكوناته بالفرق بين زيادات المنطقة القاعدية والزيادات المتوقعة باستخدام نموذج التأثيرات الثابتة. - تقييم ومقارنة القدرة التنبؤية للنموذج الأساسي ونموذج التأثيرات المختلطة الخطي باستخدام المؤشرات الإحصائية الثلاثة التالية23،33.
 (4)
(4)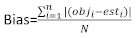 (5)
(5)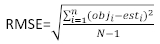 (6)
(6)
حيث أوجi هو الزيادات المنطقة القاعدية، est i هو الزيادات المنطقة القاعدية المتوقعة، هو متوسط من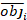 الملاحظات، وN هو عدد من الملاحظات.
الملاحظات، وN هو عدد من الملاحظات.
Access restricted. Please log in or start a trial to view this content.
النتائج
تم التعبير عن نموذج زيادة المنطقة القاعدية الأساسي لـ P. asperata على أنه معادلة (7). يتم عرض تقديرات المعلمة والأخطاء القياسية المقابلة لها وإحصائيات عدم ملائمة في الجدول 2. يتم عرض المؤامرة المتبقية في الشكل 1. لوحظ عدم الوضوح الواضح للمخلفات.
Access restricted. Please log in or start a trial to view this content.
Discussion
مسألة حاسمة لتطوير نماذج الآثار المختلطة هو تحديد المعلمات التي يمكن التعامل معها على أنها تأثيرات عشوائية والتي ينبغي النظر في الآثار الثابتة34،35. وقد اقتُرحت طريقتان. النهج الأكثر شيوعا هو التعامل مع جميع المعلمات كمؤثرات عشوائية ومن ثم الحصول على أفضل ن...
Access restricted. Please log in or start a trial to view this content.
Disclosures
ليس لدى أصحاب البلاغ ما يكشفون عنه.
Acknowledgements
تم تمويل هذا البحث من قبل صناديق البحوث الأساسية للجامعات المركزية، منحة رقم 2019GJZL04. ونشكر البروفيسور ويشينغ تسنغ في أكاديمية جرد وتخطيط الغابات، والإدارة الوطنية للغابات والمراعي، في الصين، على إتاحة الوصول إلى البيانات.
Access restricted. Please log in or start a trial to view this content.
Materials
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
References
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. Modeling Forest Trees and Stands. , Springer. Netherlands. (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , Springer. Boston, MA. (2007).
- Calama, R., Montero, G. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257(2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Access restricted. Please log in or start a trial to view this content.
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionExplore More Articles
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved