Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.
Method Article
Entwicklung eines Individual-Tree Basal Area Increment Modells mit einem linearen Mixed-Effects-Ansatz
In diesem Artikel
Zusammenfassung
Modelle mit gemischten Effekten sind flexible und nützliche Werkzeuge zur Analyse von Daten mit einer hierarchischen stochastischen Struktur in der Forstwirtschaft und könnten auch verwendet werden, um die Leistung von Waldwachstumsmodellen deutlich zu verbessern. Hier wird ein Protokoll vorgestellt, das Informationen zu linearen Mixed-Effekt-Modellen synthetisiert.
Zusammenfassung
Hier haben wir ein individuelles Baummodell von 5-Jahres-Basalflächenschritten entwickelt, das auf einem Datensatz basiert, einschließlich 21898 Picea Asperata-Bäumen aus 779 Musterparzellen in der Provinz Xinjiang, Nordwestchina. Um hohe Korrelationen zwischen Beobachtungen derselben Stichprobeneinheit zu verhindern, haben wir das Modell mit einem linearen Mixed-Effekt-Ansatz mit zufälligem Ploteffekt entwickelt, um die stochastische Variabilität zu berücksichtigen. Verschiedene Variablen auf Baum- und Standebene, wie Z. B. Indizes für Baumgröße, Wettbewerb und Standortbedingung, wurden als feste Effekte zur Erklärung der Restvariabilität einbezogen. Darüber hinaus wurden Heteroskedastizität und Autokorrelation durch die Einführung von Varianzfunktionen und Autokorrelationsstrukturen beschrieben. Das optimale modellte lineare Mixed-Effekte wurde durch mehrere Anpassungsstatistiken bestimmt: das Informationskriterium von Akaike, das Bayessche Informationskriterium, die Logarithmuswahrscheinlichkeit und ein Wahrscheinlichkeitsverhältnistest. Die Ergebnisse zeigten, dass signifikante Variablen der Einzelbaum-Basalflächenzunahme die inverse Transformation des Durchmessers in Brusthöhe, die Basalfläche von Bäumen größer als der Themenbaum, die Anzahl der Bäume pro Hektar und die Höhe waren. Darüber hinaus wurden Fehler in der Varianzstruktur am erfolgreichsten durch die exponentielle Funktion modelliert, und die Autokorrelation wurde durch die autoregressive Struktur erster Ordnung (AR(1)) signifikant korrigiert. Die Leistung des linearen Mixed-Effekt-Modells wurde im Vergleich zum Modell mit der Regression der gewöhnlichen kleinsten Quadrate deutlich verbessert.
Einleitung
Im Vergleich zur monogetagten Monokultur hat die walduneinheitliche Waldbewirtschaftung mit mehreren Zielen in jüngster Zeit erhöhte Aufmerksamkeit erhalten1,2,3. Die Vorhersage verschiedener Bewirtschaftungsalternativen ist für die Formulierung robuster Waldbewirtschaftungsstrategienerforderlich, insbesondere für komplexe, ungleich gealterte Mischarten4 . Waldwachstums- und Ertragsmodelle wurden ausgiebig zur Vorhersage der Baum- oder Standentwicklung und -ernte im Rahmen verschiedener Bewirtschaftungsschemata5,6,7verwendet. Waldwachstums- und Ertragsmodelle werden in Einzelbaummodelle, Größenklassenmodelle und Vollwertmodell6,7,8klassifiziert. Leider eignen sich Modelle der Größenklasse und Ganzstandsmodelle nicht für ungleich gealterte Mischartenwälder, die eine detailliertere Beschreibung erfordern, um den Entscheidungsprozess der Waldbewirtschaftung zu unterstützen. Aus diesem Grund haben individuelle Baumwachstum und Ertragsmodelle in den letzten Jahrzehnten erhöhte Aufmerksamkeit erhalten, weil sie in der Lage sind, Vorhersagen für Waldbestände mit einer Vielzahl von Artenzusammensetzungen, Strukturen und Managementstrategien9,10,11zu machen.
Die Regression der gewöhnlichen kleinsten Quadrate (OLS) ist die am häufigsten verwendete Methode für die Entwicklung von Einzelbaumwachstumsmodellen12,13,14,15. Die Datensätze für einzelne Baumwachstumsmodelle, die wiederholt über einen festen Zeitraum auf derselben Stichprobeneinheit (d. h. Stichprobendiagramm oder Baum) gesammelt wurden, weisen eine hierarchische stochastische Struktur auf, mit einem Mangel an Unabhängigkeit und hoher räumlicher und zeitlicher Korrelation zwischen den Beobachtungen10,16. Die hierarchische stochastische Struktur verstößt gegen die grundannahmen der OLS-Regression: nämlich unabhängige Residuen und normal verteilte Daten mit gleichen Varianzen. Daher führt die Verwendung der OLS-Regression unweigerlich zu verzerrten Schätzungen des Standardfehlers von Parameterschätzungen für diese Daten13,14.
Modelle mit gemischten Effekten bieten ein leistungsstarkes Werkzeug für die Analyse von Daten mit komplexen Strukturen, z. B. Daten mit wiederholten Messeinheiten, Längsschnittdaten und mehrstufigen Daten. Modelle mit gemischten Effekten bestehen aus festen Komponenten, die der gesamten Grundgesamtheit gemeinsam sind, und zufälligen Komponenten, die für jede Stichprobenstufe spezifisch sind. Darüber hinaus berücksichtigen Modelle mit gemischten Effekten Heteroskedastizität und Autokorrelation in Raum und Zeit, indem nicht diagonale Varianz-Kovarianzstrukturmatrizen17,18,19definiert werden. Aus diesem Grund wurden Mixed-Effekt-Modelle in der Forstwirtschaft ausgiebig eingesetzt, wie z.B. in den Durchmesser-Höhen-Modellen20,21, Kronenmodelle22,23, selbstverdünnende Modelle24,25und Wachstumsmodelle26,27.
Dabei ging es vor allem darum, ein individuelles Grundflächen-Inkrementmodell mit einem linearen Mixed-Effekt-Ansatz zu entwickeln. Wir hoffen, dass der Ansatz der gemischten Auswirkungen umfassend angewandt werden kann.
Access restricted. Please log in or start a trial to view this content.
Protokoll
1. Datenaufbereitung
- Vorbereiten von Modellierungsdaten, die Einzelbauminformationen (Art und Durchmesser bei Brusthöhe bei 1,3 m) und Diagramminformationen (Neigung, Aspekt und Höhe) enthalten. In dieser Studie wurden die Daten aus dem 8. (2009) und 9. (2014) Chinesischen National Forest Inventory in der Provinz Xinjiang, Nordwestchina, gewonnen, das 21.898 Beobachtungen von 779 Stichprobenparzellen enthält. Diese Stichprobenparzellen sind quadratisch mit einer Größe von 1 Mu (chinesische Einheit mit einer Fläche von 0,067 ha) und systematisch über ein Raster von 4 km x 8 km angeordnet.
ANMERKUNG: Die Daten für die Modellierung (Basalfläche) erfordern mindestens eine Wachstumsperiode (d. h. zwei Beobachtungen). - Teilen Sie die Daten zufällig in zwei Datasets auf, wobei 80 % der Daten aus den Stichprobendiagrammen für die Modellanpassung verwendet werden (Modellentwicklungsdatensatz), der aus 17.145 Beobachtungen aus 623 Stichprobendiagrammen und 20 % für die Modellvalidierung (Modellvalidierungs-Dataset) besteht, die aus 4.753 Beobachtungen aus 156 Stichprobendiagrammen besteht. Beschreibende Statistiken für die verwendeten Schlüsselvariablen sind in Tabelle 1enthalten.
HINWEIS: Dieser Schritt der Modellierungsprozedur kann weggelassen werden, und alle Daten werden für die Modellentwicklung verwendet.
| Variablen | Anpassen von Daten | Validierungsdaten | |||||||
| Min | Max | Bedeuten | Sd. | Min | Max | Bedeuten | Sd. | ||
| DBH1 (cm) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD (cm) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| ID (cm) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (m3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (Bäume/ha) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (m2/ha) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| EL (m) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
Tabelle 1. Zusammenfassungsstatistiken für Anpassungs- und Validierungsdaten. DBH1: Anfangsdurchmesser bei Brusthöhe bei 1,3 m (DBH), DBH2: DBH gemessen nach 5 Jahren Wachstum, QMD: quadratischer Mittlerer Durchmesser, ID: Durchmesserzuwachs für 5 Jahre (DBH2 – DBH1), BAL: die Grundfläche von Bäumen größer als der Themenbaum (der Subjektbaum: der Baum, der die Wettbewerbsindizes berechnet wurde), NT: die Anzahl der Bäume pro Hektar, BA: Basalfläche pro Hektar, EL: Höhe, S.D.: Standardabweichung.
2. Grundlegende Modellentwicklung
- Konsultieren Sie Verweise, um Variablen zu identifizieren, die sich auf die Einzelnenbaum-Basalflächeninkremente auswirken.
- Wählen Sie Variablen basierend auf den Daten aus und berechnen Sie diese. Im Allgemeinen wird das Einzelbaum-Basalflächeninkrement durch drei Variablengruppen beeinflusst: Baumgröße, Wettbewerb und Standortbedingung27,28,29,30.
- Betrachten Sie Baumgrößeneffekte wie DBH1, Quadrat von DBH1 (
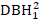 ), die inverse Transformation von DBH1 (1/DBH1), und den gemeinsamen Logarithmus von DBH1 (logDBH1) oder Kombinationen von ihnen.
), die inverse Transformation von DBH1 (1/DBH1), und den gemeinsamen Logarithmus von DBH1 (logDBH1) oder Kombinationen von ihnen. - Betrachten Sie Wettbewerbseffekte wie ein- und zweiseitige Wettbewerbsindizes, um das Wettbewerbsniveau eines Baumes sowie seine soziale Position innerhalb des Standes umfassender zu quantifizieren. Zu den einseitigen Wettbewerben gehören BAL und der relative Dichteindex (RD=DBH1/QMD); Zu den beidseitigen Wettbewerben gehören NT und BA.
HINWEIS: Die entfernungsabhängigen Wettbewerbsindizes sollten berücksichtigt werden, wenn Daten verfügbar sind. - Betrachten Sie Standorteffekte wie Aspekt (ASP), Neigung (SL) und EL. SL und ASP sollten mithilfe der Stage-Transformation31einbezogen werden.
- Betrachten Sie Baumgrößeneffekte wie DBH1, Quadrat von DBH1 (
- Wählen Sie log(
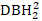 -
- 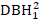 +1) (
+1) ( 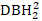 bezeichnet Quadrat von DBH2) als abhängige Variable.
bezeichnet Quadrat von DBH2) als abhängige Variable. - Entwickeln Sie das Basismodell mit der schrittweisen Regressionsmethode. Stellen Sie sicher, dass das Modell biologisch vertretbar ist und erhebliche Unterschiede zwischen unabhängigen Variablen aufweist. Verwenden Sie den Varianzinflationsfaktor (VIF), um die Multikollinearität zu überprüfen.
- Lassen Sie die unabhängigen Variablen mit p < 0.05 und VIF < 5 im Basismodell.
- Geben Sie die Basismodellergebnisse und das Restdiagramm aus. Das hier produzierte Basismodell dient als Grundlage für die Weiterentwicklung eines Mixed-Effekt-Modells.
3. Lineare Mixed-Effekt-Modellentwicklung mit dem Paket "nlme" in R-Software
- Lesen Sie das Modellentwicklungs-Dataset, und laden Sie das Paket "nlme".
>model.development.dataset=read.csv("E:/DATA/JoVE/modelingdata.csv",
header=TRUE)
>Bibliothek(nlme) - Wählen Sie Stichprobendiagramme als Zufallseffekte aus, um das Modell für gemischte Effekte zu entwickeln.
- Passen Sie alle möglichen Kombinationen von Zufallseffekten mit der Methode der maximalen Wahrscheinlichkeit (ML) an und geben Sie die Ergebnisse aus.
>Modell<-lme(Y1/DBH1+BAL+NT+EL,data=model.development.dataset,
method="ML", zufällig = 1| PLOT)
>Zusammenfassung(Modell)- Set zufällig = 1 ist der Abfang zu zufälligen Parametern. Ändern Sie die zufälligen Anweisungen, bis alle Kombinationen angepasst sind. Um beispielsweise 1/DBH1 und BAL als zufällige Parameter festzulegen, lautet der Code wie folgt: zufällig = 1/DBH1+BAL-1. Darüber hinaus können die Codes bei der Anpassung Fehler melden, die auf die Nichtkonvergenz des angepassten Modells zurückzuführen sind.
- Wählen Sie das beste Modell nach dem Informationskriterium (AIC) von Akaike, dem Bayesschen Informationskriterium (BIC), der Logarithmuswahrscheinlichkeit (Loglik) und dem Wahrscheinlichkeitsverhältnistest (LRT).
>anova(Modell.1, Modell.6)
>anova(Modell.6, Modell.23)
>anova(Modell.23, Modell.30) - Bestimmen Sie die Struktur von Ri. Adressieren Sie die Heteroskedastizität und Autokorrelation von Ri32. Das Ri ist wie folgt geschrieben:
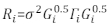 (1)
(1)
wobei σ2 ein unbekannter Skalierungsfaktor ist, der der Modell-Restvarianz entspricht, ist Gi eine diagonale Matrix, die Heteroskedastizität beschreibt, und Γi ist eine Matrix, die die Autokorrelation beschreibt.- Beobachten Sie, ob die Residuen heteroskedasitizität aus dem Restdiagramm haben. Wenn heteroskedastistizistiz ist (die Residuen haben ein klares Muster oder einen klaren Trend), führen Sie drei häufig verwendete Varianzfunktionen ein – die Konstante-Plus-Leistungsfunktion, die Leistungsfunktion und die exponentielle Funktion –, um die Fehlervarianzstruktur zu modellieren.
>Modell.30.1<-lme(Y'1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random='1/DBH1+BAL+NT| Plot
weights=varConstPower(form='angepasst(.)))
>Zusammenfassung(Modell.30.1)
>Modell.30.2<-lme(Y'1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random='1/DBH1+BAL+NT| Plot
gewichte=varPower(form='angepasst(.)))
>Zusammenfassung(Modell.30.2)
>Modell.30.3<-lme(Y'1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random='1/DBH1+BAL+NT| Plot
weights=varExp(form='angepasst(.)))
>Zusammenfassung(Modell.30.3) - Bestimmen Sie die beste Varianzfunktion für das Modell gemäß AIC, BIC, Loglik und LRT.
>anova(Modell.30, Modell.30.1)
>anova (Modell.30, Modell.30.2)
>anova(Modell.30, Modell.30.3) - Führen Sie drei häufig verwendete Autokorrelationsstrukturen ein – die zusammengesetzte Symmetriestruktur (CS), die autoregressive Struktur erster Ordnung [AR(1)] und eine Kombination aus autoregressiven und gleitenden Durchschnittsstrukturen erster Ordnung [ARMA(1,1)]–, um die Autokorrelation zu berücksichtigen.
>Modell.30.3.1<-lme(Y'1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
zufällig = 1 /DBH1+BAL+NT| PLOT, weights=varExp(form='fitted(.)), corr= corCompSymm())
>Zusammenfassung(Modell.30.3.1)
>Modell.30.3.2<-lme(Y'1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
zufällig = 1 /DBH1+BAL+NT| PLOT,weights=varExp(form='angepasst(.)), corr=corAR1())
>Zusammenfassung(Modell.30.3.2)
>Modell.30.3.3<-lme(Y1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
zufällig = 1 /DBH1+BAL+NT| PLOT,weights=varExp(form='angepasst(.)), corr=corARMA(q=1,p=1))
>Zusammenfassung(Modell.30.3.3) - Bestimmen Sie die beste Autokorrelationsstruktur gemäß AIC, BIC, Loglik und LRT.
>anova(Modell.30.3, Modell.30.3.2)
ANMERKUNG: Die Gi und i können nicht definiert werden, wenn es keine Heteroskedastizität und Autokorrelation gibt. - Geben Sie die Endergebnisse des Mixed-Effekt-Modells mit der REML-Methode (Restricted Maximum Likelihood) aus.
>Mixed.model<-lme(Y'1/DBH1+BAL+NT+EL,data=model.development.dataset, method="REML",random='1/DBH1+BAL+NT| Plot
weights=varExp(form=' fitted(.)), corr=corAR1()))
>Zusammenfassung(Mixed.model)
- Beobachten Sie, ob die Residuen heteroskedasitizität aus dem Restdiagramm haben. Wenn heteroskedastistizistiz ist (die Residuen haben ein klares Muster oder einen klaren Trend), führen Sie drei häufig verwendete Varianzfunktionen ein – die Konstante-Plus-Leistungsfunktion, die Leistungsfunktion und die exponentielle Funktion –, um die Fehlervarianzstruktur zu modellieren.
4. Bias-Korrektur
- Transformieren Sie die vorhergesagten Werte des Basalflächeninkrements mithilfe des endgültigen Modells auf einer logarithmischen Skala in den ursprünglichen Maßstab. Eine solche lineare Rücktransformation des vorhergesagten Wertes aus einem logtransformierten Modell erzeugt jedoch eine zugeordnete Log-Transformationsverzerrung. Um die Log-Bias zu behandeln, wurde ein Korrekturfaktor abgeleitet und in die Vorhersagegleichung integriert, die das tatsächliche vorhergesagte Grundflächeninkrement für einen bestimmten Baum schätzt [Gleichung (2)]:
 (2)
(2)
wobei der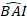 prognostizierte logarithmische Wert des Basalflächeninkrements aus dem Modell vorhergesagt wird, während
prognostizierte logarithmische Wert des Basalflächeninkrements aus dem Modell vorhergesagt wird, während 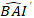 der vorhergesagte rücktransformierte Wert des Basalflächeninkrements für 5 Jahre nach Korrektur für Log-Transformations-Bias ist.
der vorhergesagte rücktransformierte Wert des Basalflächeninkrements für 5 Jahre nach Korrektur für Log-Transformations-Bias ist. 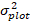 ist die Varianz von Zufälligeffekten im Diagramm und σ2 ist Restvarianz.
ist die Varianz von Zufälligeffekten im Diagramm und σ2 ist Restvarianz. - Konvertieren Sie das Grundflächeninkrement (
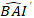 ) in das Durchmesserinkrement.
) in das Durchmesserinkrement.
5. Modellvorhersage und -auswertung
- Bereiten Sie das in Abschnitt 1.2 erstellte Modellvalidierungs-Dataset für die Vorhersage vor.
- Verwenden Sie das lineare Modell für gemischte Effekte, um das Inkrement der einzelnen Baumbasalflächen vorherzusagen. Die zufälligen Komponenten wurden mit dem folgenden besten linearen unvoreingenommenen Prädiktor berechnet:
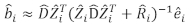 (3)
(3)
wobei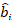 ein Vektor für die zufälligen Komponenten ist; ist die
ein Vektor für die zufälligen Komponenten ist; ist die 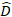 Varianz-Kovarianz-Matrix für die Variabilität zwischen den Plots;
Varianz-Kovarianz-Matrix für die Variabilität zwischen den Plots; 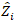 ist die Konstruktionsmatrix für die zufälligen Komponenten, die auf die komplementären Beobachtungen wirken;
ist die Konstruktionsmatrix für die zufälligen Komponenten, die auf die komplementären Beobachtungen wirken; 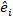 ist der Restvektor, dessen Komponenten durch die Differenz zwischen den Basalflächenschritten und den vorhergesagten Inkrementen mit dem Modell der festen Effekte angegeben werden.
ist der Restvektor, dessen Komponenten durch die Differenz zwischen den Basalflächenschritten und den vorhergesagten Inkrementen mit dem Modell der festen Effekte angegeben werden. - Bewerten und vergleichen Sie die Vorhersagefähigkeit des Basismodells und des linearen Mixed-Effekt-Modells anhand der folgenden drei statistischen Indikatoren23,33.
 (4)
(4)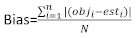 (5)
(5)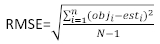 (6)
(6)
wobei obji die Basalflächeninkremente ist, esti die vorhergesagten Basalflächenschritte,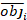 das Mittel der Beobachtungen und N die Anzahl der Beobachtungen.
das Mittel der Beobachtungen und N die Anzahl der Beobachtungen.
Access restricted. Please log in or start a trial to view this content.
Ergebnisse
Das grundlegende Grundflächeninkrementmodell für P. asperata wurde als Gleichung (7) ausgedrückt. Die Parameterschätzungen, die entsprechenden Standardfehler und die Nichtanpassungsstatistiken sind in Tabelle 2dargestellt. Das Restdiagramm ist in Abbildung 1dargestellt. Es wurde eine ausgeprägte Heteroskedastizität der Residuen beobachtet.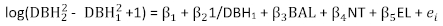 (7)
(7)
Access restricted. Please log in or start a trial to view this content.
Diskussion
Eine entscheidende Frage für die Entwicklung von Modellen mit gemischten Effekten ist die Bestimmung, welche Parameter als Zufallseffekte behandelt werden können und welche als feste Effekte34,35betrachtet werden sollten. Es wurden zwei Methoden vorgeschlagen. Der häufigste Ansatz besteht darin, alle Parameter als Zufallseffekte zu behandeln und dann das beste Modell von AIC, BIC, Loglik und LRT auswählen zu lassen. Dies war die Methode unserer Studie
Access restricted. Please log in or start a trial to view this content.
Offenlegungen
Die Autoren haben nichts zu verraten.
Danksagungen
Diese Forschung wurde aus den Grundlagenforschungsfonds für die Zentraluniversitäten, Fördernummer 2019GJZL04, gefördert. Wir danken Professor Weisheng Zeng von der Academy of Forest Inventory and Planning, National Forestry and Grassland Administration, China für den Zugang zu Daten.
Access restricted. Please log in or start a trial to view this content.
Materialien
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
Referenzen
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. Modeling Forest Trees and Stands. , Springer. Netherlands. (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , Springer. Boston, MA. (2007).
- Calama, R., Montero, G. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257(2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Access restricted. Please log in or start a trial to view this content.
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten