JoVE 비디오를 활용하시려면 도서관을 통한 기관 구독이 필요합니다. 전체 비디오를 보시려면 로그인하거나 무료 트라이얼을 시작하세요.
Method Article
선형 혼합 효과 접근 방식을 사용하여 개별 트리 기초 영역 증분 모델 개발
요약
혼합 효과 모델은 임업의 계층적 스토세스 구조로 데이터를 분석하기 위한 유연하고 유용한 도구이며 산림 성장 모델의 성능을 크게 향상시키는 데 사용할 수도 있습니다. 여기서선형 혼합 효과 모델과 관련된 정보를 합성하는 프로토콜이 제시됩니다.
초록
여기서 중국 북서부 신장성에 위치한 779개의 샘플 플롯에서 21898 피케아 아스페라타 나무를 포함한 데이터 세트를 기반으로 5년 기저면적 증분의 개별 트리 모델을 개발했습니다. 동일한 샘플링 단위의 관측 값 간의 높은 상관관계를 방지하기 위해 난사 적 가변성을 고려하여 임의의 플롯 효과가 있는 선형 혼합 효과 접근 방식을 사용하여 모델을 개발했습니다. 나무 크기, 경쟁 및 사이트 조건에 대한 인덱스와 같은 다양한 트리 및 스탠드 레벨 변수가 잔여 가변성을 설명하기 위한 고정 효과로 포함되었습니다. 또한, 이종분증 및 자기상관성은 분산 기능 및 자기 상관 구조를 도입하여 기술되었다. 최적의 선형 혼합 효과 모델은 아카이케의 정보 기준, 베이지안 정보 기준, 로가릿암 가능성 및 가능성 비율 테스트와 같은 여러 가지 적합성 통계에 의해 결정되었습니다. 그 결과 개별 나무 기저 면적 증분의 중요한 변수는 유방 높이에서 직경의 역 변환, 피사체 트리보다 큰 나무의 기저 면적, 헥타르당 나무 수 및 고도가 있음을 나타냈다. 또한 분산 구조의 오차는 지수 함수에 의해 가장 성공적으로 모델링되었으며, 1차 자동 회귀 구조(AR(1)에 의해 자가 상관관계가 현저히 수정되었다. 리니어 혼합 효과 모델의 성능은 일반 최소 제곱 회귀를 사용하여 모델에 비해 크게 향상되었습니다.
서문
짝수 숙성 된 단일 문화와 비교하여, 여러 목표를 가진 고르지 못한 숙성 혼합 종 산림 관리는 최근1,2,3의관심을 증가시켰습니다. 특히 복잡한 고르지 못한 혼합종 숲4에대해 강력한 산림 관리 전략을 수립하기 위해서는 다양한 관리 대안이 필요하다. 산림 의 성장과 수율 모델은 다양한 관리 계획에 따라 나무 또는 서 개발 및 수확을 예측하기 위해 광범위하게 사용되어왔다 5,6,7. 숲의 성장과 수율 모델은 개별 트리 모델, 크기 클래스 모델 및 전스탠드 성장 모델6,7,8로분류됩니다. 안타깝게도 크기 급 모델과 전스탠드 모델은 고르지 못한 숙성 된 혼합 종 숲에 적합하지 않으며, 산림 관리 의사 결정 과정을 지원하기 위해 보다 자세한 설명이 필요합니다. 이러한 이유로, 개별 나무 의 성장 및 수율 모델은 다양한 종 조성, 구조 및 관리 전략9,10,11로산림 스탠드에 대한 예측을 할 수있는 능력으로 인해 지난 수십 년 동안 증가 된 관심을 받고 있습니다.
일반 최소 제곱(OLS)회귀는 개별 트리 성장모델(12,13,14,15)의개발을 위해 가장 일반적으로 사용되는 방법입니다. 동일한 샘플링 단위(즉, 샘플 플롯 또는 트리)에서 고정된 시간 동안 반복적으로 수집된 개별 트리 성장 모델에 대한 데이터 집합은관측수(10,16)의독립성 및 높은 공간 적 및 시간적 상관관계가 없는 계층적 적재 구조를 갖는다. 계층적 적 재계 구조는 OLS 회귀의 기본 가정을 위반합니다: 즉 독립적 인 잔류물 및 일반적으로 동일한 분산 데이터를 분산합니다. 따라서 OLS 회귀의 사용은 필연적으로 이러한데이터(13,14)에대한 파라미터 추정치의 표준 오차에 대한 편향된추정치를생성한다.
혼합 효과 모델은 반복측정 데이터, 세로 데이터 및 다단계 데이터와 같은 복잡한 구조로 데이터를 분석할 수 있는 강력한 도구를 제공합니다. 혼합 효과 모델은 고정 된 구성 요소, 전체 채우기에 공통, 그리고 각 샘플링 수준에 특정 하는 임의구성 요소로 구성 됩니다. 또한, 혼합효과 모델은 비대각선 분산-공변구조행렬(17,18,19)을정의함으로써 공간과 시간의 이종성 및 자기상관성을 고려한다. 이러한 이유로, 혼합 효과 모델은 직경 높이모델(20, 21,크라운 모델22,23,자가 감산 모델24,25,및 성장 모델26,27)과같은 임업에 광범위하게 사용되어 왔다.
여기서 주요 목적은 선형 혼합 효과 접근 방식을 사용하여 개별 트리 기저 영역 증분 모델을 개발하는 것이었습니다. 우리는 혼합 효과 접근 방식이 광범위하게 적용될 수 있기를 바랍니다.
프로토콜
1. 데이터 준비
- 개별 트리 정보(1.3m의 유방 높이의 종 및 직경)와 플롯 정보(경사, 측면 및 고도)를 포함하는 모델링 데이터를 준비합니다. 이 연구에서는 중국 북서부 신장성에서 8일(2009년)과 9일(2014년) 중국 국유림 인벤토리에서 779개의 표본플롯을 관측한 21,898건의 관측을 통해 입수했다. 이 샘플 플롯은 1 Mu (0.067 ha에 해당하는 면적의 중국 단위)의 크기로 사각형 모양이며 4km x 8km의 격자 위에 체계적으로 배치됩니다.
참고: 모델링(기초 영역) 증분에 대한 데이터는 적어도 하나의 성장 기간(즉, 두 가지 관찰)이 필요합니다. - 623개의 샘플 플롯에서 17,145개의 관측값과 156개의 샘플 플롯에서 4,753개의 관측으로 구성된 모델 유효성 검사(모델 유효성 검사 데이터 집합)의 20%로 구성된 모델 피팅(모델 개발 데이터 집합)에 사용되는 샘플 플롯의 데이터의 80%와 데이터를 무작위로 두 개의 데이터 집합으로 나눕니다. 사용되는 주요 변수에 대한 설명 통계는 표 1에제공됩니다.
참고: 모델링 절차의 이 단계를 생략할 수 있으며 모든 데이터는 모델 개발에 사용됩니다.
| 변수 | 데이터 피팅 | 유효성 검사 데이터 | |||||||
| 분 | 최대 | 의미 | Sd. | 분 | 최대 | 의미 | Sd. | ||
| DBH 1(cm) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD(cm) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| 신분증(cm) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (m3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT(나무/하) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (m2/ha) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| EL (m) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
표 1. 피팅 및 유효성 검사 데이터에 대한 요약 통계입니다. DBH1: 유방 높이에서 초기 직경 1.3 m (DBH), DBH2: DBH는 5 년 의 성장 후 측정, QMD: 이차 평균 직경, ID: 5년 동안 직경 증분(DBH2 - DBH1),BAL: 피사체 트리보다 큰 나무의 기저면적(주제트리: 경쟁 지수를 계산한 나무), NT: 헥타르당 나무 수, BA: 헥타르당 나무 수, EL: 고도, S.D.: 표준 기량
2. 기본 모델 개발
- 개별 트리 기초 영역 증분에 영향을 주는 변수를 식별하려면 참조를 참조하십시오.
- 데이터를 기반으로 변수를 선택하고 계산합니다. 일반적으로, 개별 나무 기저면적 증분은 트리 크기, 경쟁 및 사이트조건(27,28,29,30)의세 가지 변수 그룹에 의해 영향을 받습니다.
- DBH1,DBH 1(1/DBH1)의
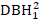 역변환, DBH1(logDBH 1)또는 조합의 일반적인 로고릿헴과같은 나무 크기 효과를 고려한다.
역변환, DBH1(logDBH 1)또는 조합의 일반적인 로고릿헴과같은 나무 크기 효과를 고려한다. - 경쟁의 1면 지수와 같은 경쟁 효과를 고려하여 나무가 경험한 경쟁 수준을 보다 포괄적으로 정량화하고 스탠드 내의 사회적 위치를 보다 포괄적으로 정량화하십시오. 일방적 경쟁으로는 BAL 및 상대 밀도 지수(RD=DBH 1/QMD)가 포함됩니다. 양면 경쟁으로는 NT와 BA가 포함됩니다.
참고: 데이터를 사용할 수 있는 경우 거리 종속 경쟁 지수를 고려해야 합니다. - 위상(ASP), 경사(SL), EL. SL 및 ASP와 같은 사이트 효과를 스테이지 변환31을사용하여 포함해야 합니다.
- DBH1,DBH 1(1/DBH1)의
- 로그를
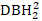 선택(-
선택(- 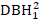 +1)
+1) 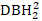 (DBH2의정사각형)을 종속 변수로 나타낸다.
(DBH2의정사각형)을 종속 변수로 나타낸다. - 단계별 회귀 방법을 사용하여 기본 모델을 개발합니다. 모델이 생물학적으로 합리적이고 독립적인 변수 간에 상당한 차이를 보이는지 확인합니다. 분산 인플레이션 계수(VIF)를 활용하여 다중 collinearity를 확인합니다.
- 기본 모델에 는 독립적인 변수를 p<, 0.05 및 VIF & lt; 5로 둡니다.
- 기본 모델 결과와 잔여 플롯을 출력합니다. 여기서 생산되는 기본 모델은 혼합 효과 모델의 추가 개발을 위한 토대가 됩니다.
3. R 소프트웨어의 패키지 "nlme"와 선형 혼합 효과 모델 개발
- 모델 개발 데이터 집합을 읽고 패키지 "nlme"를 로드합니다.
>model.development.dataset=read.csv("E:/DATA/JoVE/모델링 데이터.csv.csv
헤더=TRUE)
>라이브러리(nlme) - 샘플 플롯을 임의 효과로 선택하여 혼합 효과 모델을 개발합니다.
- 최대 가능성(ML) 메서드와 임의 효과의 가능한 모든 조합을 맞추고 결과를 출력합니다.
>모델&lme(Y~1/DBH1+BAL+NT+EL, 데이터=model.development.dataset,
방법 ="ML", 무작위 =~1| 플롯)
>요약(모델)- 랜덤 =~1을 설정하는 것은 임의의 매개 변수에 대한 가로채기입니다. 모든 조합이 장착될 때까지 임의문을 변경합니다. 예를 들어 1/DBH1 및 BAL을 임의 매개 변수로 설정하려면 코드는 다음과 같습니다: 임의 =~1/DBH1+BAL-1. 또한 피팅 과정에서 코드는 장착된 모델의 수렴되지 않아 오류를 보고할 수 있습니다.
- 아카이케의 정보 기준(AIC), 베이지안 정보 기준(BIC), 로가릿가능성(Loglik), 가능성 비율 테스트(LRT)로 최고의 모델을 선택합니다.
>아노바 (모델.1, 모델.6)
>아노바 (모델.6, 모델.23)
>아노바 (모델.23, 모델.30) - R i의 구조를 결정합니다. Ri32의이종과 자기 상관 관계를 해결하십시오. Ri는 다음과 같이 작성됩니다.
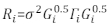 (1)
(1)
σ2가 모델 잔여 분산과 동일한 알 수 없는 스케일링 계수인 경우 Gi는 이종성을 설명하는 대각선 행렬이며 Γ나는 자기 상관 관계를 설명하는 매트릭스입니다.- 잔류물잔류가 잔류 음모로부터 이종성이 있는지 관찰한다. 이종성(잔류에는 명확한 패턴 또는 추세가 있음)이 있는 경우, 오류 분산 구조를 모델링하기 위해 상수 플러스 전원 기능, 전원 함수 및 지수 함수와 같은 자주 사용되는 세 가지 분산 함수를 소개합니다.
>Model.30.1&lme(Y~1/DBH1+BAL+NT+EL, 데이터=모델.개발.데이터셋, 메서드="ML", 랜덤=~1/DBH1+BAL+NT| 플롯
가중치=varConstPower(폼=~ 장착(.))
>요약(모델.30.1)
>Model.30.2&lme(Y~1/DBH1+BAL+NT+EL, 데이터=모델.개발.데이터셋, 메서드="ML", 랜덤=~1/DBH1+BAL+NT| 플롯
가중치=varPower(폼=~ 장착(.))
>요약(모델.30.2)
>Model.30.3&lme(Y~1/DBH1+BAL+NT+EL, 데이터=모델.개발.데이터셋, 메서드="ML", 랜덤=~1/DBH1+BAL+NT| 플롯
가중치=varExp(폼=~ 장착(.))
>요약(모델.30.3) - AIC, BIC, Loglik 및 LRT에 따라 모델에 가장 적합한 분산 함수를 결정합니다.
>아노바(모델.30, 모델.30.1)
>아노바(모델.30, 모델.30.2)
>아노바 (모델.30, 모델.30.3) - 일반적으로 사용되는 세 가지 자동 상관 구조(CS), 일차 자동 회귀 구조 [AR(1)], 선차 자동 회귀 및 이동 평균 구조 [ARMA(1,1]]의 조합 --자기 상관 관계를 고려합니다.
>Model.30.3.1&lme(Y~1/DBH1+BAL+NT+EL, 데이터=모델.development.dataset, 메서드="ML",
랜덤=~1/DBH1+BAL+NT| 플롯, 가중치=varExp(폼=~장착(.)), 코르= 코르콤심())
>요약(모델.30.3.1)
>Model.30.3.2&lme(Y~1/DBH1+BAL+NT+EL, 데이터=모델.development.dataset, 메서드="ML",
랜덤=~1/DBH1+BAL+NT| 플롯, 가중치=바렉스(폼=~ 장착(.)), 코르=코라1())
>요약(모델.30.3.2)
>Model.30.3.3&lme(Y~1/DBH1+BAL+NT+EL, 데이터=모델.development.dataset, 메서드="ML",
랜덤=~1/DBH1+BAL+NT| 플롯, 가중치=varExp(폼=~ 장착(.)), 코르=코르아르마(q=1,p=1))
>요약(모델.30.3.3) - AIC, BIC, Loglik 및 LRT에 따라 최고의 자기 상관 구조를 결정합니다.
>아노바 (모델.30.3, 모델.30.3.2)
참고: 이종성 및 자기 상관관계가 없는 경우 Gi와 Γi를 정의할 수 없습니다. - 제한된 최대 가능성(REML) 방법을 사용하여 혼합 효과 모델의 최종 결과를 출력합니다.
>Mixed.model1+BAL+NT+EL, 데이터=모델.개발.데이터셋, 메서드="REML", 랜덤=~1/DBH1+BAL+NT| 플롯
가중치=varExp(폼=~ 장착(.)), 코르=코르아1())
>요약(혼합.모델)
- 잔류물잔류가 잔류 음모로부터 이종성이 있는지 관찰한다. 이종성(잔류에는 명확한 패턴 또는 추세가 있음)이 있는 경우, 오류 분산 구조를 모델링하기 위해 상수 플러스 전원 기능, 전원 함수 및 지수 함수와 같은 자주 사용되는 세 가지 분산 함수를 소개합니다.
4. 바이어스 수정
- 로그리스믹 스케일의 최종 모델을 사용하여 기초 영역 증분의 예측값을 원래 축척으로 변환합니다. 그러나 로그 변환 모델에서 예측값의 선형 백 변환은 연결된 로그 변환 편향을 생성합니다. 로그 바이어스를 처리하기 위해 보정 계수가 파생되고 예측 방정식에 통합되어 지정된 트리 [방정식(2)]에 대한 실제 예측 기저 영역 증분을 추정합니다.
 (2)
(2)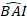 여기서 모델으로부터 기저면적증의 로그와스믹값이 예측되는 반면,
여기서 모델으로부터 기저면적증의 로그와스믹값이 예측되는 반면, 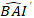 로그 변환 편향을 보정한 후 5년 동안 기저면적증의 예측된 역변화값은
로그 변환 편향을 보정한 후 5년 동안 기저면적증의 예측된 역변화값은 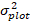 플롯및 σ2의 무작위 효과로부터의 분산이다.
플롯및 σ2의 무작위 효과로부터의 분산이다. - 기저 면적
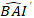 증분()을 직경 증분으로 변환합니다.
증분()을 직경 증분으로 변환합니다.
5. 모델 예측 및 평가
- 예측을 위해 섹션 1.2에서 생성된 모델 유효성 검사 데이터 집합을 준비합니다.
- 선형 혼합 효과 모델을 사용하여 개별 트리 기저 영역 증분을 예측합니다. 임의 구성 요소는 다음과 같은 최고의 선형 편향되지 않은 예측 변수를 사용하여 계산되었습니다.
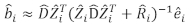 (3)
(3)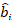 임의 구성 요소에 대한 벡터는 어디; 플롯 간
임의 구성 요소에 대한 벡터는 어디; 플롯 간 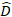 가변성에 대한 분산-코바변
가변성에 대한 분산-코바변 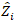 매트릭스; 상호 보완적인 관측에서 작용하는 임의구성요소에 대한 설계 매트릭스;
매트릭스; 상호 보완적인 관측에서 작용하는 임의구성요소에 대한 설계 매트릭스; 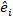 고정효과 모델을 이용한 기저 면적 증분과 예측된 증분의 차이에 의해 구성요소가 주어지는 잔류 벡터이다.
고정효과 모델을 이용한 기저 면적 증분과 예측된 증분의 차이에 의해 구성요소가 주어지는 잔류 벡터이다. - 다음 세 가지 통계지표(23,33)를사용하여 기본 모델 및 선형 혼합 효과 모델의 예측 능력을 평가하고 비교한다.
 (4)
(4)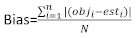 (5)
(5)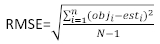 (6)
(6)
obji가 기저 면적 증분인 경우, esti는 예측된 기저 면적 증분이며,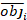 관측의 평균이며, N은 관측수의 수입니다.
관측의 평균이며, N은 관측수의 수입니다.
결과
P. 아스페라타에 대한 기본 기저영역 증분 모델은 방정식(7)으로 표현되었다. 매개 변수 추정, 해당 표준 오류 및 적합성 부족 통계가 표 2에표시됩니다. 잔여 플롯은 그림 1에표시됩니다. 잔류물의 발음이 관찰되었다.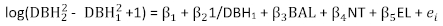 (7)
(7)
| 견적 |
토론
혼합 효과 모델의 개발에 대 한 중요 한 문제는 어떤 매개 변수 임의 효과로 처리 될 수 있습니다 결정 하 고 고정 효과 간주 되어야 한다34,35. 두 가지 방법이 제안되었습니다. 가장 일반적인 방법은 모든 매개 변수를 임의의 효과로 처리한 다음 AIC, BIC, Loglik 및 LRT에서 선택한 최상의 모델을 사용하는 것입니다. 이것은 우리의 연구35에?...
공개
저자는 공개 할 것이 없습니다.
감사의 말
이 연구는 중앙 대학에 대한 기본 연구 기금에 의해 투자되었다, 부여 번호 2019GJZL04. 우리는 산림 재고 및 계획 아카데미에서 교수 Weisheng Zeng 교수 에게 감사, 국립 임업 및 초원 행정, 중국에 대한 액세스를 제공에 대한.
자료
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
참고문헌
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. . Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. . Modeling Forest Trees and Stands. , (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. . Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , (2007).
- Calama, R., Montero, G. . Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257 (2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
재인쇄 및 허가
JoVE'article의 텍스트 или 그림을 다시 사용하시려면 허가 살펴보기
허가 살펴보기This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. 판권 소유