Un abonnement à JoVE est nécessaire pour voir ce contenu. Connectez-vous ou commencez votre essai gratuit.
Method Article
Développement d’un modèle d’incrément de zone basale d’arbre individuel utilisant une approche linéaire à effets mixtes
Dans cet article
Résumé
Les modèles à effets mixtes sont des outils flexibles et utiles pour analyser les données avec une structure hiérarchique stochastique en foresterie et pourraient également être utilisés pour améliorer considérablement les performances des modèles de croissance forestière. Ici, un protocole est présenté qui synthétise l’information relative aux modèles linéaires à effets mixtes.
Résumé
Ici, nous avons développé un modèle d’arbre individuel d’incréments de superficie basale de 5 ans basé sur un ensemble de données comprenant 21898 arbres Picea asperata à partir de 779 parcelles d’échantillons situées dans la province du Xinjiang, au nord-ouest de la Chine. Afin d’éviter des corrélations élevées entre les observations de la même unité d’échantillonnage, nous avons mis au point le modèle à l’aide d’une approche linéaire à effets mixtes avec effet de parcelle aléatoire pour tenir compte de la variabilité stochastique. Diverses variables au niveau des arbres et des montants, telles que les indices de taille des arbres, de concurrence et d’état du site, ont été incluses comme effets fixes pour expliquer la variabilité résiduelle. En outre, l’hétéroscasticité et l’autocorrérelation ont été décrites en introduisant des fonctions de variance et des structures d’autocorrépendance. Le modèle d’effets mixtes linéaires optimaux a été déterminé par plusieurs statistiques d’ajustement : critère d’information d’Akaike, critère d’information bayésien, probabilité de logarithm, et un essai de rapport de probabilité. Les résultats ont indiqué que des variables significatives de l’incrément de zone basale d’arbre individuel étaient la transformation inverse du diamètre à la hauteur de sein, la zone basale des arbres plus grand que l’arbre en question, le nombre d’arbres par hectare, et l’élévation. En outre, les erreurs dans la structure de variance ont été modélisées avec le plus de succès par la fonction exponentielle, et l’autocorrérelation a été sensiblement corrigée par la structure autorégressive de premier ordre (AR(1)). La performance du modèle linéaire à effets mixtes a été considérablement améliorée par rapport au modèle en utilisant la régression ordinaire des moins carrés.
Introduction
Par rapport à la monoculture d’âges communs, la gestion forestière mixte d’âge inégal avec de multiples objectifs a reçu une attentionaccrue récemment 1,2,3. La prévision des différentes solutions de gestion est nécessaire pour formuler des stratégies robustes de gestion forestière, en particulier pour les forêts complexes d’espèces mixtes d’âgeinégal 4. Les modèles de croissance et de rendement forestiers ont été largement utilisés pour prévoir le développement et la récolte des arbres ou des supports dans le cadre de divers schémas de gestion5,6,7. Les modèles de croissance et de rendement forestiers sont classés dans les modèles d’arbres individuels, les modèles de classe taille et les modèles de croissance à supportentier 6,7,8. Malheureusement, les modèles de classe taille et les modèles de stand entier ne conviennent pas aux forêts mixtes d’âge inégal, qui nécessitent une description plus détaillée pour appuyer le processus décisionnel en gestion forestière. Pour cette raison, les modèles de croissance et de rendement des arbres individuels ont reçu une attention accrue au cours des dernières décennies en raison de leur capacité à faire des prédictions pour les peuplements forestiers avec une variété de compositions d’espèces, de structures et de stratégiesde gestion 9,10,11.
La régression ordinaire des moins carrés (OLS) est la méthode la plus couramment utilisée pour le développement de modèles de croissanced’arbres individuels 12,13,14,15. Les ensembles de données pour les modèles de croissance des arbres individuels recueillis à plusieurs reprises sur une durée fixe sur la même unité d’échantillonnage (c.-à-d. parcelle d’échantillon ou arbre) ont une structure hiérarchique stochastique, avec un manque d’indépendance et une forte corrélation spatiale et temporelle entre les observations10,16. La structure hiérarchique stochastique viole les hypothèses fondamentales de régression ols: à savoir les résidus indépendants et normalement distribué des données avec des écarts égaux. Par conséquent, l’utilisation de la régression ols produit inévitablement des estimations biaisées de l’erreur standard des estimations des paramètrespour ces données 13,14.
Les modèles à effets mixtes fournissent un outil puissant pour analyser les données avec des structures complexes, telles que des données de mesures répétées, des données longitudinales et des données à plusieurs niveaux. Les modèles à effets mixtes se composent à la fois de composants fixes, communs à l’ensemble de la population, et de composants aléatoires, qui sont spécifiques à chaque niveau d’échantillonnage. En outre, les modèles à effets mixtes prennent en compte l’hétéroscasticité et l’autocorrépendance dans l’espace et le temps en définissant la structure de variance-covariance non diagonale matrices17,18,19. Pour cette raison, les modèles à effets mixtes ont été largement utilisés dans la foresterie, tels que dans les modèles de hauteurde diamètre 20,21, couronne modèles22,23, auto-amincissement modèles24,25, et les modèles de croissance26,27.
Ici, l’objectif principal était de développer un modèle d’incrément de zone basale d’arbre individuel utilisant une approche linéaire d’effets mélangés. Nous espérons que l’approche des effets mixtes pourrait être largement appliquée.
Protocole
1. Préparation des données
- Préparer des données de modélisation, qui comprennent des renseignements sur les arbres individuels (espèces et diamètre à la hauteur des seins à 1,3 m) et des renseignements sur les parcelles (pente, aspect et élévation). Dans cette étude, les données ont été obtenues à partir du 8e (2009) et du 9e (2014) Inventaire national des forêts chinoises dans la province du Xinjiang, au nord-ouest de la Chine, qui comprend 21 898 observations de 779 parcelles échantillonnées. Ces parcelles échantillonnées sont de forme carrée avec une taille de 1 Mu (unité chinoise de superficie équivalente à 0,067 ha) et sont systématiquement disposées sur une grille de 4 km x 8 km.
REMARQUE : L’incrément de modélisation (zone basale) nécessite au moins une période de croissance (c.-à-d. deux observations). - Divisez aléatoirement les données en deux ensembles de données, avec 80 % des données des parcelles d’échantillons utilisées pour l’ajustement du modèle (ensemble de données de développement de modèles), qui se compose de 17 145 observations provenant de 623 parcelles d’échantillons et de 20 % pour la validation de modèles (ensemble de données de validation de modèle) qui se compose de 4 753 observations provenant de 156 parcelles d’échantillons. Des statistiques descriptives pour les variables clés utilisées sont fournies dans le tableau 1.
REMARQUE : Cette étape de la procédure de modélisation peut être omise, et toutes les données sont utilisées pour le développement de modèles.
| Variables | Données d’ajustement | Données de validation | |||||||
| Min | Max | Veux dire | S.d. | Min | Max | Veux dire | S.d. | ||
| DBH1 (cm) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| DMQ (cm) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| ID (cm) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (m3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (arbres/ha) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (m2/ha) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| EL (m) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
Tableau 1. Statistiques sommaires pour l’ajustement et la validation des données. DBH1: diamètre initial à la hauteur du sein à 1,3 m (DBH), DBH2: DBH mesuré après 5 ans de croissance, QMD: diamètre moyen quadratique, ID: augmentation de diamètre pendant 5 ans (DBH2 - DBH1), BAL: la zone basale des arbres plus grands que l’arbre en question (l’arbre en question: l’arbre qui a été calculé les indices de compétition), NT: le nombre d’arbres par hectare, BA: superficie basale par hectare, EL: élévation, S.D.: écart type.
2. Développement de modèle de base
- Consultez les références pour identifier les variables qui affectent les incréments de la zone basale des arbres individuels.
- Sélectionnez et calculez les variables en fonction des données. En général, l’incrément de la zone basale des arbres individuels est affecté par trois groupes de variables : la taille des arbres, la concurrence et l’état du site27,28,29,30.
- Considérez les effets de la taille des arbres tels que DBH1, carré de DBH1 (
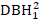 ), la transformation inverse de DBH1 (1/DBH1), et le logarithme commun de DBH1 (logDBH1) ou des combinaisons d’entre eux.
), la transformation inverse de DBH1 (1/DBH1), et le logarithme commun de DBH1 (logDBH1) ou des combinaisons d’entre eux. - Tenir compte des effets concurrentiels tels que les indices uni et à deux côtés de la concurrence pour quantifier plus en détail le niveau de concurrence d’un arbre, ainsi que sa position sociale au sein du stand. La concurrence à un côté comprend le BAL et l’indice de densité relative (RD=DBH1/QMD); la concurrence à deux côtés incluent NT, et BA.
REMARQUE : Les indices de concurrence dépendant de la distance doivent être pris en considération si des données sont disponibles. - Considérez les effets du site tels que l’aspect (ASP), la pente (SL), et EL. SL et ASP devraient être inclus en utilisant la transformation de stage31.
- Considérez les effets de la taille des arbres tels que DBH1, carré de DBH1 (
- Sélectionnez journal
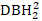 ( +
( + 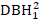 1) (
1) ( 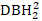 désigne carré de DBH2) comme variable dépendante.
désigne carré de DBH2) comme variable dépendante. - Développez le modèle de base en utilisant la méthode de régression stepwise. Assurez-vous que le modèle est biologiquement raisonnable et présente des différences significatives entre les variables indépendantes. Utilisez le facteur d’inflation de variance (VIF) pour vérifier la multicollinarité.
- Laissez les variables indépendantes avec p < 0,05 et VIF < 5 dans le modèle de base.
- Extrayant les résultats du modèle de base et la parcelle résiduelle. Le modèle de base produit ici sert de base à la poursuite du développement d’un modèle à effets mixtes.
3. Développement linéaire de modèles à effets mixtes avec le paquet « nlme » dans le logiciel R
- Lisez l’ensemble de données de développement du modèle et chargez le paquet « nlme ».
>model.development.dataset=read.csv(« E:/DATA/JoVE/modelingdata.csv »,
en-tête=TRUE)
>library(nlme) - Sélectionnez des parcelles d’échantillons comme effets aléatoires pour développer le modèle à effets mixtes.
- Adapter toutes les combinaisons possibles d’effets aléatoires avec la méthode de probabilité maximale (ML) et la sortie des résultats.
>Model<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset,
méthode="ML », aléatoire =~1| PARCELLE)
>résumé (Modèle)- Ensemble aléatoire =~1 est l’interception de paramètres aléatoires. Modifiez les instructions aléatoires jusqu’à ce que toutes les combinaisons soient équipées. Par exemple, pour définir 1/DBH1 et BAL comme paramètres aléatoires, le code est le suivant : aléatoire =~1/DBH1+BAL-1. En outre, dans le processus d’ajustement, les codes peuvent signaler des erreurs dues à la non-conformité du modèle équipé.
- Sélectionnez le meilleur modèle selon le critère d’information d’Akaike (AIC), le critère d’information bayésien (BIC), la probabilité de logarithme (Loglik) et le test de ratio de probabilité (TLR).
>anova (Model.1, Model.6)
>anova (Model.6, Model.23)
>anova (Model.23, Model.30) - Déterminer la structure de Ri. Adressez-vous à l’hétéroscasticité et à l’autocorrépendation de Ri32. Le Ri est écrit comme suit:
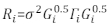 (1)
(1)
où σ2 est un facteur d’échelle inconnu qui est égal à la variance résiduelle du modèle, Gi est une matrice diagonale décrivant l’hétéroscasticité, et Γ i est une matrice décrivant l’autocorrépendance.- Observez si les résidus sont hétéroscasticité de la parcelle résiduelle. S’il y a hétéroscasticité (les résidus ont un modèle ou une tendance clair), introduisez trois fonctions de variance fréquemment utilisées — la fonction constante plus puissance, la fonction de puissance et la fonction exponentielle — pour modéliser la structure de variance des erreurs.
>Model.30.1<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML »,random=~1/DBH1+BAL+NT| Intrigue
poids=varConstPower (form=~ fitted(.)))
>résumé (Modèle.30.1)
>Model.30.2<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML »,random=~1/DBH1+BAL+NT| Intrigue
poids=varPower (form=~ fitted(.)))
>résumé (Modèle.30.2)
>Model.30.3<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML », random=~1/DBH1+BAL+NT| Intrigue
poids=varExp(form=~ fitted(.)))
>résumé (Model.30.3) - Déterminez la meilleure fonction de variance pour le modèle selon l’AIC, le BIC, loglik et le TLR.
>anova (Model.30, Modèle.30.1)
>anova (Modèle.30, Modèle.30.2)
>anova (Model.30, Model.30.3) - Introduire trois structures d’autocorréfération couramment utilisées — la structure de symétrie composée (CS), la structure autorégressive de premier ordre [AR(1)], et une combinaison de structures moyennes autorégressives et mobiles de premier ordre [ARMA(1,1)]— pour tenir compte de l’autocorrépendation.
>Model.30.3.1<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML »,
aléatoire=~1/DBH1+BAL+NT| PARCELLE, poids=varExp (form=~fitted(.)), corr= corCompSymm())
>résumé (Model.30.3.1)
>Model.30.3.2<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML »,
aléatoire=~1/DBH1+BAL+NT| PLOT,weights=varExp(form=~ fitted(.)), corr=corAR1())
>résumé (Model.30.3.2)
>Model.30.3.3<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML »,
aléatoire=~1/DBH1+BAL+NT| PLOT,weights=varExp(form=~ fitted(.)), corr=corARMA(q=1,p=1))
>résumé (Model.30.3.3) - Déterminez la meilleure structure d’autocorrépendation selon l’AIC, le BIC, loglik et le TLR.
>anova (Model.30.3, Model.30.3.2)
REMARQUE : Le Gi et le Γi ne peuvent pas être définis s’il n’y a pas d’hétéroscasticité et d’autocorrépendance. - Extrayant les résultats finaux du modèle à effets mixtes en utilisant la méthode de la probabilité maximale restreinte (REML).
>Mixed.model<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="REML », random=~1/DBH1+BAL+NT| Intrigue
poids=varExp(form=~ fitted(.)), corr=corAR1())
>résumé (Mixed.model)
- Observez si les résidus sont hétéroscasticité de la parcelle résiduelle. S’il y a hétéroscasticité (les résidus ont un modèle ou une tendance clair), introduisez trois fonctions de variance fréquemment utilisées — la fonction constante plus puissance, la fonction de puissance et la fonction exponentielle — pour modéliser la structure de variance des erreurs.
4. Correction des biais
- Transformez les valeurs prévues de l’incrément de surface basale à l’aide du modèle final à l’échelle logarithmique à l’échelle d’origine. Toutefois, une telle transformation linéaire du dos de la valeur prévue à partir d’un modèle transformé en journal produit un biais de transformation de journal associé. Pour faire face au biais de journal, un facteur de correction a été dérivé et intégré dans l’équation de prédiction, qui estime l’augmentation réelle prévue de la superficie basale pour un arbre donné [Équation (2)]:
 (2)
(2)
où est prévue la valeur logarithmique de l’incrément de la zone basale par rapport au modèle, tandis que la valeur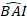 transformée en arrière prévue de l’incrément de la zone basale pendant 5 ans après correction du biais de transformation des
transformée en arrière prévue de l’incrément de la zone basale pendant 5 ans après correction du biais de transformation des 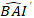
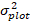 grumes. est la variance par rapport aux effets aléatoires à la parcelle et la σ2 est la variance résiduelle.
grumes. est la variance par rapport aux effets aléatoires à la parcelle et la σ2 est la variance résiduelle. - Convertir l’incrément de la zone basale
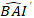 () en l’incrément de diamètre.
() en l’incrément de diamètre.
5. Prévision et évaluation des modèles
- Préparez l’ensemble de données de validation du modèle produit à la section 1.2 pour la prédiction.
- Utilisez le modèle linéaire à effets mixtes pour prédire l’augmentation de la superficie basale des arbres individuels. Les composants aléatoires ont été calculés à l’aide du meilleur prédicteur linéaire impartial suivant :
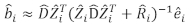 (3)
(3)
où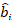 est un vecteur pour les composants
est un vecteur pour les composants 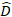 aléatoires; est la matrice de variance-covariance pour la variabilité entre les parcelles; est la matrice de conception pour les composants aléatoires agissant aux observations complémentaires; est le vecteur résiduel dont les composants sont donnés par
aléatoires; est la matrice de variance-covariance pour la variabilité entre les parcelles; est la matrice de conception pour les composants aléatoires agissant aux observations complémentaires; est le vecteur résiduel dont les composants sont donnés par 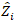 la différence entre les
la différence entre les 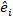 incréments de zone basale et les incréments prévus utilisant le modèle à effets fixes.
incréments de zone basale et les incréments prévus utilisant le modèle à effets fixes. - Évaluer et comparer la capacité prédictive du modèle de base et du modèle linéaire à effets mixtes à l’aide des trois indicateursstatistiques suivants 23,33.
 (4)
(4)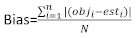 (5)
(5)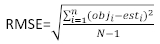 (6)
(6)
où obji est les incréments de la zone basale, est iest la zone basale prévue incréments,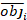 est le moyen d’observations, et N est le nombre d’observations.
est le moyen d’observations, et N est le nombre d’observations.
Résultats
Le modèle d’incrément basal de base pour P. asperata a été exprimé en équation (7). Les estimations des paramètres, leurs erreurs standard correspondantes et les statistiques sur le manque d’ajustement sont indiquées dans le tableau 2. La parcelle résiduelle est indiquée dans la figure 1. L’hétéroscasticité prononcée des résidus a été observée.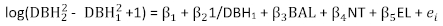 (7)
(7)
Discussion
Une question cruciale pour le développement de modèles à effets mixtes est de déterminer quels paramètres peuvent être traités comme des effets aléatoires et qui devraient être considérés comme des effetsfixes 34,35. Deux méthodes ont été proposées. L’approche la plus courante consiste à traiter tous les paramètres comme des effets aléatoires, puis à avoir le meilleur modèle sélectionné par AIC, BIC, Loglik et LRT. C’était la méthode e...
Déclarations de divulgation
Les auteurs n’ont rien à divulguer.
Remerciements
Cette recherche a été financée par les Fonds de recherche fondamentale pour les universités centrales, numéro de subvention 2019GJZL04. Nous remercions le professeur Weisheng Zeng de l’Academy of Forest Inventory and Planning, National Forestry and Grassland Administration, Chine, d’avoir fourni l’accès aux données.
matériels
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
Références
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. . Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. . Modeling Forest Trees and Stands. , (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. . Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , (2007).
- Calama, R., Montero, G. . Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257 (2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Réimpressions et Autorisations
Demande d’autorisation pour utiliser le texte ou les figures de cet article JoVE
Demande d’autorisationThis article has been published
Video Coming Soon