需要订阅 JoVE 才能查看此. 登录或开始免费试用。
Method Article
使用线性混合效应方法开发单树基数增量模型
摘要
混合效应模型是分析林业中分层随机结构数据的灵活而有用的工具,也可用于显著提高森林生长模型的性能。在这里,提出了一个协议,合成与线性混合效应模型相关的信息。
摘要
在这里,我们根据一个数据集开发了一个5年基底面积增量的单树模型,其中包括来自中国西北部新疆省779个样本地块的21898 棵皮卡阿斯佩拉塔 树。为了防止来自同一采样单元的观测结果之间的高相关性,我们使用具有随机绘图效果的线性混合效应方法开发了该模型,以考虑随机变异性。各种树和立级变量,如树的大小、竞争和场地条件的指数,都作为固定效应包括在内,以解释残余变异性。此外,通过引入方差函数和自动相关结构来描述异构性和自动相关性。最佳线性混合效应模型由几个合适的统计数据决定:Akaike 的信息标准、贝叶斯信息标准、对数可能性和可能性比率测试。结果表明,单树基底面积增量的重要变量为胸高直径的反向转化、大于主体树的树木基底面积、每公顷树木数量和海拔高度。此外,方差结构中的错误最成功地通过指数函数建模,并且通过一阶自动反向结构 (AR(1)显著纠正了自动反差。与使用普通最小正方形回归的模型相比,线性混合效应模型的性能显著提高。
引言
与均匀的单一栽培、不均匀年龄的混合种林管理相比,具有多重目标的混合物种森林管理最近受到越来越多的关注。预测不同的管理备选方案是制定强有力的森林管理战略的必要条件,特别是对于复杂的不均匀年龄的混合物种森林4。森林生长和产量模型已被广泛使用,以预测树木或站在发展和收获下的各种管理计划5,6,7。森林生长和产量模型分为个体树模型、大小级模型和全站生长模型6、7、8。不幸的是,大小类模型和全站模型不适合年龄不均匀的混合物种森林,这需要更详细的描述来支持森林管理决策过程。因此,单树生长和产量模型在过去几十年中受到越来越多的关注,因为它们能够预测森林站与各种物种组成,结构和管理策略9,10,11。
普通最小正方形 (OLS) 回归是开发单树生长模型 12、13、14、15 的最常用方法。在同一采样单元(即样本图或树)上,在同一采样单元(即样本图或树)上反复收集的单树生长模型数据集具有层次结构,在观测点 10、16之间缺乏独立性和高空间和时间相关性。分层随机结构违反了 OLS 回归的基本假设:即独立残余和通常分布的数据具有相等的方差。因此,OLS回归的使用不可避免地会产生对这些数据13、14参数估计标准误差的偏颇估计。
混合效应模型为分析结构复杂的数据提供了强大的工具,例如重复测量数据、纵向数据和多级数据。混合效应模型由固定组件和随机组件组成,这些组件是每个采样水平所特有的。此外,混合效应模型通过定义非对角方差-共变结构矩阵17、18、19来考虑空间和时间的异构性和自动校际性。为此,混合效应模型已广泛应用于林业,如直径高度模型20,21,冠模型22,23,自瘦模型24,25,生长模型26,27。
在这里,主要目标是使用线性混合效应方法开发单树基底区域增量模型。我们希望混合效应方法能够得到广泛应用。
研究方案
1. 数据准备
- 准备建模数据,包括单树信息(1.3米乳房高度的物种和直径)和绘图信息(坡度、侧面和海拔)。在这项研究中,数据取自中国西北新疆省第8次(2009年)和第9次(2014年)中国国家森林清查,其中包括对779个样本地块的21,898次观测。这些样本地块为方形,面积为1亩(面积相当于0.067公顷),系统地排列在4公里×8公里的网格上。
注:建模(基础区域)增量的数据至少需要一个增长期(即两个观测点)。 - 随机将数据分成两个数据集,其中 80% 的数据来自用于模型拟合的样本图(模型开发数据集),其中包括来自 623 个样本图的 17,145 个观测结果和 20% 的模型验证(模型验证数据集),其中包括来自 156 个样本图的 4,753 个观测结果。 表 1中提供了关键变量的描述性统计数据。
注:可以省略建模过程的这一步骤,所有数据都用于模型开发。
| 变量 | 拟合数据 | 验证数据 | |||||||
| 最小 | 麦克斯 | 意味 着 | S.D. | 最小 | 麦克斯 | 意味 着 | S.D. | ||
| DBH1 (厘米) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD(厘米) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| ID(厘米) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| 巴尔 (米3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT(树木/公顷) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA(米2/公顷) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| 埃尔 (米) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
表 1.拟合和验证数据的摘要统计。DBH1: 乳房高度在 1.3 米 (DBH) 的初始直径, DBH2:DBH 在生长 5 年后测量, QMD: 二次平均直径, ID: 直径增量 5 年 (DBH2 - DBH1),BAL: 大于主题树的树木的基底面积 (主题树: 计算竞争指数的树), NT: 每公顷的树木数量, BA: 每公顷的基底面积, EL: 海拔, S.D.: 标准偏差.
2. 基本模型开发
- 请查阅引用,以确定影响单树基底区域增量的变量。
- 根据数据选择和计算变量。一般来说,单树基底面积增量受三组变量的影响:树的大小、竞争和场地条件27、28、29、30。
- 考虑树大小的效果,如 DBH1的方形
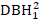 ()、DBH1 (1/DBH 1)的逆向转换,以及 DBH 1 (logDBH1)的常见对数或它们的组合。
()、DBH1 (1/DBH 1)的逆向转换,以及 DBH 1 (logDBH1)的常见对数或它们的组合。 - 考虑竞争效应,如单边和双面竞争指数,以更全面地量化树木所经历的竞争水平,以及其在展台内的社会地位。片面竞争包括BAL和相对密度指数(RD+DBH 1/QMD):双面竞争包括NT和英航。
注:如果有数据,应考虑距离依赖竞争指数。 - 考虑现场效果,如方面 (ASP), 斜坡 (SL), 和 EL. SL 和 ASP 应该包括使用阶段的转换31.
- 考虑树大小的效果,如 DBH1的方形
- 选择日志
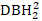
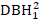 (-+1)(
(-+1)( 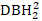 表示DBH2的正方形)作为附属变量。
表示DBH2的正方形)作为附属变量。 - 使用渐进回归法开发基本模型。确保模型在生物学上合理,并显示独立变量之间的显著差异。利用方差通货膨胀系数 (VIF) 来检查多共性。
- 在基本模型中保留 p < 0.05 和 VIF +lt 的独立变量。
- 输出基本模型结果和剩余图。这里生产的基本模型是进一步发展混合效应模型的基础。
3. 与R软件中的包"nlme"一起开发线性混合效应模型
- 阅读模型开发数据集并加载包"nlme"。
•模型.开发.数据集=读取.csv("电子数据/JoVE/建模数据.csv"
标题=真实)
•库(内姆) - 选择样本图作为随机效果,以开发混合效应模型。
- 将所有可能的随机效果组合与最大可能性 (ML) 方法配合并输出结果。
•模型+lt;-lme(Y~1/DBH1=BAL+NT+EL,数据=模型.开发.数据集,
方法="ML",随机=~1|图)
•摘要(模型)- 随机设置=~1是拦截到随机参数。更改随机语句,直到安装所有组合。例如,将 1/DBH1 和 BAL 设置为随机参数,代码如下:随机 +1/DBH1=BAL-1。此外,在拟合过程中,代码可能会报告由于安装模型不融合而出现的错误。
- 通过 Akaike 的信息标准 (AIC)、贝叶斯信息标准 (BIC)、对数可能性 (Loglik) 和可能性比率测试 (LRT) 选择最佳模型。
•新星(型号.1,型号。6)
•新星(型号.6,型号.23)
•新星(型号.23,型号.30) - 确定 R i.的结构。解决Ri32的异质性和自动相关性。Ri的编写如下:
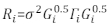 (1)
(1)
其中σ2 是一个未知的缩放因子,等于模型残差方差 ,Gi 是描述异构性的对角矩阵 ,Γi 是描述自相关性的矩阵。- 观察残余物是否具有残余情节的异构性。如果存在异构性(残余物具有清晰的模式或趋势),则引入三个常用的方差函数-常数加功率函数、功率函数和指数函数-以模拟误差方差结构。
>型号.30.1=lme(Y~1/DBH 1=BAL+NT+EL,数据+模型.开发.数据集,方法="ML",随机=1/DBH1=BAL+NT|情节
重量=瓦尔康斯特电源(形式=*安装)
>摘要(模型.30.1)
>型号.30.2+lme(Y~1/DBH1=BAL+NT+EL,数据+模型.开发.数据集,方法="ML",随机=1/DBH1=BAL+NT|情节
重量=功率(形式=*安装)
>摘要(模型.30.2)
>型号.30.3+lme(Y~1/DBH1=BAL+NT+EL,数据+模型.开发.数据集,方法="ML",随机=1/DBH1=BAL+NT|情节
重量=变量(形式=*安装)
>摘要(型号.30.3) - 根据 AIC、BIC、洛格利克和轻轨确定模型的最佳方差函数。
>新星(型号.30,型号.30.1)
>新星(型号.30,型号.30.2)
•新星(型号.30,型号。30.3) - 引入三种常用的自动对关系结构(复合对称结构 (CS)、一阶自动反向结构 [AR(1)],以及一阶自动反向结构和移动平均结构 [ARMA(1,1))的组合 -以解释自动反向结构。
•型号.30.3.1=lme(Y~1/DBH1+BAL+NT+EL,数据=模型.开发.数据集,方法="ML",
随机=~1/DBH1=巴尔+NT|情节,重量=变量(形式=*安装),科雷科姆(
•摘要(型号.30.3.1)
•型号.30.3.2=lme(Y~1/DBH1+BAL+NT+EL,数据=模型.开发.数据集,方法="ML",
随机=~1/DBH1=巴尔+NT|情节,重量=变量(形式=*安装),科雷科拉尔1(
•摘要(型号.30.3.2)
•型号.30.3.3=lme(Y~1/DBH1+BAL+NT+EL,数据=模型.开发.数据集,方法="ML",
随机=~1/DBH1=巴尔+NT|情节,重量=瓦勒普(形式=*安装(),科拉玛(q=1,p=1))
•摘要(型号.30.3.3) - 根据 AIC、BIC、洛格利克和轻轨确定最佳的自动相关结构。
•新星(型号.30.3,型号。30.3.2)
注:如果没有异质性和自动关联性,则无法定义Gi和Γi。 - 使用受限的最大可能性 (REML) 方法输出混合效应模型的最终结果。
•混合.模型(Y~1/DBH1=BAL+NT+EL,数据+模型.开发.数据集,方法="REML",随机=1/DBH 1=BAL+NT|情节
重量=变量(形式=*安装),科雷科拉尔1(
•摘要(混合模型)
- 观察残余物是否具有残余情节的异构性。如果存在异构性(残余物具有清晰的模式或趋势),则引入三个常用的方差函数-常数加功率函数、功率函数和指数函数-以模拟误差方差结构。
4. 偏差校正
- 使用对数刻度上的最终模型将基底区域增量的预测值转换为原始刻度。但是,从日志转换模型中对预测值的这种线性反向转换会产生相关的日志转换偏差。为了处理日志偏差,生成了一个修正因子并集成到预测方程中,该方程估计了给定树的实际预测基数面积增量 [方程 (2)]:
 (2)
(2)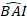 从模型中预测基底区域增量的对数值在哪里,而
从模型中预测基底区域增量的对数值在哪里,而 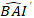 基底区域增量在修正日志转换偏差后5年的预测回转值
基底区域增量在修正日志转换偏差后5年的预测回转值 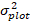 σ。
σ。 - 将基底区域增量
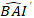 () 转换为直径增量。
() 转换为直径增量。
5. 模型预测和评估
- 准备第 1.2 节中生成的模型验证数据集以供预测。
- 使用线性混合效应模型预测单树基底面积增量。随机组件使用以下最佳线性公正预测器计算:
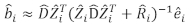 (3)
(3)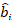 随机组件的载体在哪里:
随机组件的载体在哪里: 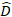 是图之间变异的方差-共变矩阵:
是图之间变异的方差-共变矩阵: 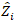 是随机组件在补充观测中作用的设计矩阵:
是随机组件在补充观测中作用的设计矩阵: 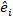 是残余载体,其成分是由基底区域增量与使用固定效应模型预测增量之间的差异给出的。
是残余载体,其成分是由基底区域增量与使用固定效应模型预测增量之间的差异给出的。 - 使用以下三个统计指标23、33来评估和比较基础模型和线性混合效应模型的预测能力。
 (4)
(4)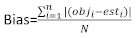 (5)
(5)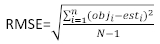 (6)
(6)
其中obji是基底区域增量,esti是预测的基底区域增量,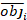 是观测的平均值,N是观测次数。
是观测的平均值,N是观测次数。
结果
P. asperata的基本基底区域增量模型表示为方程 (7)。参数估计值、相应的标准误差和不合适的统计数据显示在表 2中。残余情节显示在图 1中。观察到残留物的明显异构性。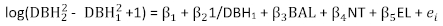 (7)
(7)
| 估计 | 标准错误 | t 测试 |
讨论
发展混合效应模型的一个关键问题是确定哪些参数可以被视为随机效应,哪些参数应被视为固定效应34,35。提出了两种方法。最常见的方法是将所有参数视为随机效应,然后由 AIC、BIC、Loglik 和 LRT 选择最佳模型。这是我们研究35所采用的方法。另一种选择是为 OLS 回归的每个示例图安装基底区域增量模型。在这些模型的样本图中具有?...
披露声明
作者没有什么可透露的。
致谢
这项研究由中央大学基础研究基金资助,资助编号为2019GJZL04。我们感谢中国国家林业和草原管理局森林盘点与规划学院的曾伟生教授提供数据。
材料
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
参考文献
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. . Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. . Modeling Forest Trees and Stands. , (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. . Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , (2007).
- Calama, R., Montero, G. . Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257 (2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
转载和许可
请求许可使用此 JoVE 文章的文本或图形
请求许可探索更多文章
This article has been published
Video Coming Soon
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。