É necessária uma assinatura da JoVE para visualizar este conteúdo. Faça login ou comece sua avaliação gratuita.
Method Article
Desenvolvimento de um modelo de incremento de área basal de árvore individual usando uma abordagem linear de efeitos mistos
Neste Artigo
Resumo
Modelos de efeitos mistos são ferramentas flexíveis e úteis para analisar dados com uma estrutura estocástica hierárquica na silvicultura e também poderiam ser usados para melhorar significativamente o desempenho dos modelos de crescimento florestal. Aqui, é apresentado um protocolo que sintetiza informações relativas a modelos lineares de efeitos mistos.
Resumo
Aqui, desenvolvemos um modelo de árvore individual de incrementos de área basal de 5 anos com base em um conjunto de dados incluindo 21898 Picea asperata de 779 parcelas de amostras localizadas na província de Xinjiang, noroeste da China. Para evitar altas correlações entre observações da mesma unidade amostral, desenvolvemos o modelo utilizando uma abordagem linear de efeitos mistos com efeito de parcela aleatória para explicar a variabilidade estocástica. Várias variáveis de nível de árvore e suporte, como índices de tamanho de árvore, concorrência e condição do local, foram incluídas como efeitos fixos para explicar a variabilidade residual. Além disso, heteroscedasticidade e autocorrelação foram descritas pela introdução de funções de variância e estruturas de autocorrelação. O modelo de efeitos mistos lineares ideais foi determinado por várias estatísticas de ajuste: critério de informação de Akaike, critério de informação bayesiana, probabilidade de logaritmo e teste de razão de probabilidade. Os resultados indicaram que variáveis significativas do incremento da área basal de árvores individuais foram a transformação inversa do diâmetro na altura da mama, a área basal das árvores maior que a árvore objeto, o número de árvores por hectare e a elevação. Além disso, os erros na estrutura de variância foram modelados com mais sucesso pela função exponencial, e a correção automática foi significativamente corrigida pela estrutura autoregressiva de primeira ordem (AR(1)). O desempenho do modelo linear de efeitos mistos foi significativamente melhorado em relação ao modelo utilizando regressão ordinário de quadrados.
Introdução
Em comparação com a monocultura envelhecida, o manejo florestal de espécies mistas de idade desigual com múltiplos objetivos tem recebido maior atenção recentemente1,2,3. A previsão de diferentes alternativas de manejo é necessária para a formulação de estratégias robustas de manejo florestal, especialmente para a complexa floresta de espécies mistas de idade irregular4. Modelos de crescimento e rendimento florestal têm sido amplamente utilizados para prever o desenvolvimento e a colheita de árvores ou suportes sob vários regimes de manejo5,6,7. Os modelos de crescimento e rendimento florestal são classificados em modelos de árvores individuais, modelos de classe de tamanho e modelos de crescimento de suporte inteiro6,7,8. Infelizmente, modelos de classe de tamanho e modelos de suporte inteiro não são apropriados para florestas de espécies mistas de idade irregular, que requerem uma descrição mais detalhada para apoiar o processo de tomada de decisão do manejo florestal. Por essa razão, os modelos de crescimento e rendimento individual-árvore têm recebido maior atenção ao longo das últimas décadas devido à sua capacidade de fazer previsões para estandes florestais com uma variedade de composições de espécies, estruturas e estratégias de manejo9,10,11.
A regressão de quadrados mínimos comuns (OLS) é o método mais utilizado para o desenvolvimento de modelos de crescimento de árvores individuais12,13,14,15. Os conjuntos de dados para modelos de crescimento de árvores individuais coletados repetidamente ao longo de um período fixo de tempo na mesma unidade amostral (ou seja, parcela de amostra ou árvore) possuem uma estrutura estocástica hierárquica, com falta de independência e alta correlação espacial e temporal entre as observações10,16. A estrutura estocástica hierárquica viola os pressupostos fundamentais da regressão da OLS: ou seja, resíduos independentes e dados normalmente distribuídos com variâncias iguais. Portanto, o uso da regressão OLS inevitavelmente produz estimativas tendenciosas do erro padrão das estimativas de parâmetros para esses dados13,14.
Modelos de efeitos mistos fornecem uma ferramenta poderosa para analisar dados com estruturas complexas, como dados de medidas repetidas, dados longitudinais e dados multinóduos. Os modelos de efeitos mistos consistem em ambos os componentes fixos, comuns à população completa, e componentes aleatórios, que são específicos para cada nível de amostragem. Além disso, os modelos de efeitos mistos levam em conta a heteroscedasticidade e a correção automática no espaço e no tempo, definindo as matrizes da estrutura de variância não diagonal17,18,19. Por essa razão, os modelos de efeitos mistos têm sido amplamente utilizados na silvicultura, como nos modelos de altura de diâmetro20,21, modelos de coroa22,23, modelos de auto-afinamento24,25e modelos de crescimento26,27.
Aqui, o objetivo principal foi desenvolver um modelo de incremento de área basal de árvore individual utilizando uma abordagem linear de efeitos mistos. Esperamos que a abordagem dos efeitos mistos possa ser amplamente aplicada.
Access restricted. Please log in or start a trial to view this content.
Protocolo
1. Preparação de dados
- Prepare os dados de modelagem, que incluem informações individuais de árvores (espécies e diâmetro na altura da mama a 1,3 m) e informações de enredo (inclinação, aspecto e elevação). Neste estudo, os dados foram obtidos a partir do inventário florestal nacional chinês 8 (2009) e 9º (2014) na província de Xinjiang, noroeste da China, que inclui 21.898 observações de 779 parcelas amostrais. Estes gráficos de amostra são quadrados com um tamanho de 1 Mu (unidade chinesa de área equivalente a 0,067 ha) e são sistematicamente dispostos sobre uma grade de 4 km x 8 km.
NOTA: O incremento dos dados para modelagem (área basal) requer pelo menos um período de crescimento (ou seja, duas observações). - Divida aleatoriamente os dados em dois conjuntos de dados, com 80% dos dados das parcelas amostrais utilizadas para a montagem do modelo (conjunto de dados de desenvolvimento de modelos), que consiste em 17.145 observações de 623 parcelas amostrais e 20% para validação de modelo (conjunto de dados de validação de modelo) que consiste em 4.753 observações de 156 parcelas amostrais. As estatísticas descritivas das principais variáveis utilizadas estão previstas na Tabela 1.
NOTA: Esta etapa do procedimento de modelagem pode ser omitida, e todos os dados são usados para o desenvolvimento do modelo.
| Variáveis | Dados de montagem | Dados de validação | |||||||
| Min | Max | Média | S.d. | Min | Max | Média | S.d. | ||
| DBH1 (cm) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD (cm) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| ID (cm) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (m3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (árvores/ha) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (m2/ha) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| EL (m) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
Mesa 1. Estatísticas resumidas para montagem e validação de dados. DBH1: diâmetro inicial na altura da mama a 1,3 m (DBH), DBH2: DBH medido após 5 anos de crescimento, QMD: diâmetro médio quadrático, ID: incremento de diâmetro por 5 anos (DBH2 – DBH1), BAL: a área basal das árvores maior que a árvore objeto (a árvore de assunto: a árvore que foi calculada os índices de concorrência), NT: o número de árvores por hectare, BA: área basal por hectare, EL: elevação, S.D.: desvio padrão.
2. Desenvolvimento de modelos básicos
- Consulte referências para identificar variáveis que afetam os incrementos da área basal de árvores individuais.
- Selecione e calcule variáveis com base nos dados. Geralmente, o incremento da área basal de árvore individual é afetado por três grupos de variáveis: tamanho da árvore, competição e condição do local27,28,29,30.
- Considere efeitos em tamanho de árvore, como DBH1, quadrado de DBH1 (
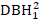 ), a transformação inversa de DBH1 (1/DBH1), e o logaritmo comum de DBH1 (logDBH1) ou combinações deles.
), a transformação inversa de DBH1 (1/DBH1), e o logaritmo comum de DBH1 (logDBH1) ou combinações deles. - Considere efeitos competitivos, como índices de competição de um e dois lados, para quantificar de forma mais abrangente o nível de competição vivenciado por uma árvore, bem como sua posição social dentro do estande. A concorrência unilateral inclui BAL e o índice de densidade relativa (RD=DBH1/QMD); competição de dois lados incluem NT, e BA.
NOTA: Os índices de concorrência dependentes da distância devem ser considerados se os dados estão disponíveis. - Considere os efeitos do local, como aspecto (ASP), inclinação (SL) e EL. SL e ASP devem ser incluídos usando a transformação do Stage31.
- Considere efeitos em tamanho de árvore, como DBH1, quadrado de DBH1 (
- Selecione o log(
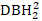 +
+ 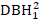 1)
1) 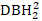 (denota o quadrado de DBH2) como a variável dependente.
(denota o quadrado de DBH2) como a variável dependente. - Desenvolva o modelo básico utilizando o método de regressão stepwise. Certifique-se de que o modelo é biologicamente razoável e apresenta diferenças significativas entre variáveis independentes. Utilize o fator de inflação de variância (VIF) para verificar a multicollinearidade.
- Deixe as variáveis independentes com p < 0,05 e VIF < 5 no modelo básico.
- Produzir os resultados básicos do modelo e a parcela residual. O modelo básico produzido aqui serve como base para o desenvolvimento de um modelo de efeitos mistos.
3. Desenvolvimento de modelo de efeitos mistos lineares com o pacote "nlme" no software R
- Leia o conjunto de dados de desenvolvimento do modelo e carregue o pacote "nlme".
>model.development.dataset=read.csv("E:/DATA/JoVE/modelagem.csv",
cabeçalho=TRUE)
>biblioteca(nlme) - Selecione gráficos de amostra como efeitos aleatórios para desenvolver o modelo de efeitos mistos.
- Encaixe todas as combinações possíveis de efeitos aleatórios com o método de máxima probabilidade (ML) e produza os resultados.
>Model<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset,
método="ML", aleatório =~1| ENREDO)
>resumo(Modelo)- Conjunto aleatório =~1 é a interceptação para parâmetros aleatórios. Altere as instruções aleatórias até que todas as combinações sejam encaixadas. Por exemplo, para definir 1/DBH1 e BAL como parâmetros aleatórios, o código é o seguinte: aleatório =~1/DBH1+BAL-1. Além disso, no processo de montagem, os códigos podem relatar erros devido à nãoconvergência do modelo montado.
- Selecione o melhor modelo pelo critério de informação de Akaike (AIC), o critério de informação bayesiana (BIC), a probabilidade de logaritmo (Loglik) e o teste de razão de probabilidade (LRT).
>anova (Modelo.1, Modelo.6)
>anova (Modelo.6, Modelo.23)
>anova (Modelo.23, Modelo.30) - Determine a estrutura de Ri. Dirija-se à heteroscedasticidade e à correção automática de Ri32. O Ri está escrito da seguinte forma:
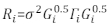 (1)
(1)
onde σ2 é um fator de dimensionamento desconhecido que é igual à variância residual do modelo, Gi é uma matriz diagonal descrevendo heteroscedasticidade, e Γi é uma matriz descrevendo a autocorrelação.- Observe se os resíduos têm heteroscedasticidade do lote residual. Se houver heteroscedasticidade (os resíduos têm um padrão ou tendência claros), introduza três funções de variância frequentemente utilizadas — a constante função de potência, a função de potência e a função exponencial — para modelar a estrutura de variância de erros.
>Modelo.30.1<-lme(Y~1/DBH1+BAL+NT+EL, data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| Enredo
pesos=varConstPower (form=~ montado(.))
>resumo (Modelo.30.1)
>Modelo.30.2<-lme(Y~1/DBH1+BAL+NT+EL, data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| Enredo
pesos=varPower (form=~ montado(.))
>resumo (Modelo.30.2)
>Modelo.30.3<-lme(Y~1/DBH1+BAL+NT+EL, data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| Enredo
pesos=varExp(form=~ montado(.))
>resumo (Modelo.30.3) - Determine a melhor função de variância para o modelo de acordo com o AIC, BIC, Loglik e LRT.
>anova (Modelo.30, Modelo.30.1)
>anova (Modelo.30, Modelo.30.2)
>anova (Modelo.30, Modelo.30.3) - Introduzir três estruturas de autocorrelação comumente usadas — a estrutura de simetria composta (CS), a estrutura autoregressiva de primeira ordem [AR(1)], e uma combinação de estruturas médias autoregressivas e móveis de primeira ordem [ARMA(1,1))– para explicar a correção automática.
>Model.30.3.1<-lme(Y~1/DBH1+BAL+NT+EL, data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| PLOT, pesos=varExp(form=~fitted(.)), corr= corCompSymm())
>resumo (Modelo.30.3.1)
>Model.30.3.2<-lme(Y~1/DBH1+BAL+NT+EL, data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| PLOT,pesos=varExp(form=~ montado(.)), corr=corAR1())
>resumo (Modelo.30.3.2)
>Model.30.3.3<-lme(Y~1/DBH1+BAL+NT+EL, data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| PLOT,pesos=varExp(form=~ montado(.)), corr=corARMA(q=1,p=1))
>resumo (Modelo.30.3.3) - Determine a melhor estrutura de autocorrelação de acordo com o AIC, BIC, Loglik e LRT.
>anova (Modelo.30.3, Modelo.30.3.2)
NOTA: O Gi e Γi não podem ser definidos se não houver heteroscedasticidade e autocorrelação. - Produzir os resultados finais do modelo de efeitos mistos utilizando o método de probabilidade máxima restrita (REML).
>Mixed.model<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="REML",random=~1/DBH1+BAL+NT| Enredo
pesos=varExp(form=~ montado(.)), corr=corAR1())
>resumo (Mixed.model)
- Observe se os resíduos têm heteroscedasticidade do lote residual. Se houver heteroscedasticidade (os resíduos têm um padrão ou tendência claros), introduza três funções de variância frequentemente utilizadas — a constante função de potência, a função de potência e a função exponencial — para modelar a estrutura de variância de erros.
4. Correção de viés
- Transforme os valores previstos de incremento da área basal usando o modelo final em uma escala logarítmica para a escala original. No entanto, essa transformação linear de valor previsto a partir de um modelo transformado em log produz um viés associado de transformação de log. Para lidar com o viés de log, um fator de correção foi derivado e integrado na equação de predição, que estima o incremento real da área basal prevista para uma determinada árvore [Equação (2)]:
 (2)
(2)
onde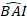 é previsto o valor logarítmico do incremento da área basal do modelo, enquanto é o valor
é previsto o valor logarítmico do incremento da área basal do modelo, enquanto é o valor 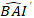 retrocedido previsto de incremento da área basal por 5 anos após a correção para viés de transformação de tronco
retrocedido previsto de incremento da área basal por 5 anos após a correção para viés de transformação de tronco 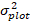 σ s.
σ s. - Converta o incremento da área basal
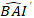 () para o incremento de diâmetro.
() para o incremento de diâmetro.
5. Previsão e avaliação do modelo
- Prepare o conjunto de dados de validação do modelo produzido na seção 1.2 para previsão.
- Use o modelo de efeitos mistos lineares para prever o incremento da área basal de árvore individual. Os componentes aleatórios foram calculados utilizando-se o seguinte melhor preditor linear imparcial:
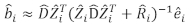 (3)
(3)
onde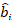 se trata de vetor para os componentes aleatórios; é a matriz de
se trata de vetor para os componentes aleatórios; é a matriz de 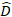 variância variância entre as parcelas; é a matriz de
variância variância entre as parcelas; é a matriz de 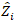 design para os componentes aleatórios que atuam nas observações complementares; é o
design para os componentes aleatórios que atuam nas observações complementares; é o 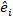 vetor residual cujos componentes são dados pela diferença entre os incrementos da área basal e os incrementos previstos utilizando o modelo de efeitos fixos.
vetor residual cujos componentes são dados pela diferença entre os incrementos da área basal e os incrementos previstos utilizando o modelo de efeitos fixos. - Avalie e compare a capacidade preditiva do modelo básico e do modelo linear de efeitos mistos utilizando os três indicadores estatísticos seguintes23,33.
 (4)
(4)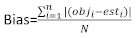 (5)
(5)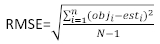 (6)
(6)
onde obji é o incremento da área basal, esti é o incremento de área basal previsto,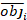 é a média de observações, e N é o número de observações.
é a média de observações, e N é o número de observações.
Access restricted. Please log in or start a trial to view this content.
Resultados
O modelo básico de incremento de área basal para P. asperata foi expresso como Equação (7). As estimativas do parâmetro, seus erros padrão correspondentes e as estatísticas de falta de ajuste são mostradas na Tabela 2. O enredo residual é mostrado na Figura 1. Observou-se heterocedasticidade pronunciada dos resíduos.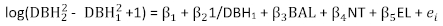 (7)
(7)
Access restricted. Please log in or start a trial to view this content.
Discussão
Uma questão crucial para o desenvolvimento de modelos de efeitos mistos é determinar quais parâmetros podem ser tratados como efeitos aleatórios e quais devem ser considerados efeitos fixos34,35. Dois métodos foram propostos. A abordagem mais comum é tratar todos os parâmetros como efeitos aleatórios e, em seguida, ter o melhor modelo selecionado por AIC, BIC, Loglik e LRT. Este foi o método empregado pelo nosso estudo35. Uma alte...
Access restricted. Please log in or start a trial to view this content.
Divulgações
Os autores não têm nada a revelar.
Agradecimentos
Esta pesquisa foi financiada pelos Fundos de Pesquisa Fundamental para as Universidades Centrais, número de bolsas 2019GJZL04. Agradecemos ao professor Weisheng Zeng da Academia de Inventário e Planejamento Florestal, Administração Nacional florestal e de pastagens da China por fornecer acesso aos dados.
Access restricted. Please log in or start a trial to view this content.
Materiais
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
Referências
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. Modeling Forest Trees and Stands. , Springer. Netherlands. (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , Springer. Boston, MA. (2007).
- Calama, R., Montero, G. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257(2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Access restricted. Please log in or start a trial to view this content.
Reimpressões e Permissões
Solicitar permissão para reutilizar o texto ou figuras deste artigo JoVE
Solicitar PermissãoThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados