Для просмотра этого контента требуется подписка на Jove Войдите в систему или начните бесплатную пробную версию.
Method Article
Разработка индивидуально-дерево Базальной модели прироста области с использованием линейного подхода смешанных эффектов
В этой статье
Резюме
Модели смешанных эффектов являются гибкими и полезными инструментами для анализа данных с иерархической стохастической структурой в лесном хозяйстве, а также могут быть использованы для существенного повышения эффективности моделей роста лесов. Здесь представлен протокол, который синтезирует информацию, относящуюся к линейным моделям смешанных эффектов.
Аннотация
Здесь мы разработали индивидуальную модель 5-летнего базального прироста площади на основе набора данных, включая 21898 деревьев Picea asperata из 779 выборочных участков, расположенных в провинции Синьцзян на северо-западе Китая. Чтобы предотвратить высокую корреляцию между наблюдениями из одного и того же блока выборки, мы разработали модель, используя линейный подход смешанных эффектов со случайным эффектом сюжета для учета стохастической изменчивости. Различные переменные уровня деревьев и стендов, такие как индексы размера деревьев, конкуренции и состояния участка, были включены в качестве фиксированных эффектов для объяснения остаточной изменчивости. Кроме того, гетероскрастичность и автокорреляция были описаны путем введения функций дисперсии и структур автокорреляции. Оптимальная модель линейных смешанных эффектов определялась несколькими подходящими статистическими данными: информационным критерием Акаике, байесовским информационным критерием, вероятностью логаритма и тестом коэффициента вероятности. Результаты показали, что значительными переменными прироста базальной площади отдельных деревьев являются обратная трансформация диаметра на высоте груди, базальная площадь деревьев, больше, чем дерево субъекта, количество деревьев на гектар и высота. Кроме того, ошибки в структуре дисперсии были наиболее успешно смоделированы экспоненциальной функцией, а автокорреляция была значительно исправлена авто регрессивной структурой первого порядка (AR(1)). Производительность линейной модели смешанных эффектов была значительно улучшена по сравнению с моделью с использованием обычной регрессии с наименьшими квадратами.
Введение
По сравнению с ровным возрастом монокультуры, неравномерного возраста смешанного вида лесопользования с несколькимицелями получил повышенное внимание в последнее время 1,2,3. Прогнозирование различных альтернатив управления необходимо для разработки надежных стратегий лесопользования, особенно для сложных неровных возрастов смешанных видов леса4. Модели роста и урожайности лесов широко используются для прогнозирования развития деревьев или стендов по различнымсхемам управления 5,6,7. Модели роста и урожайности лесов классифицируются на модели индивидуального дерева, модели размерного класса и моделироста 6,7,8. К сожалению, модели класса размеров и модели стендов не подходят для лесов смешанного вида неравномерного возраста, которые требуют более подробного описания для поддержки процесса принятия решений в области лесопользования. По этой причине, индивидуального роста деревьев и урожайности модели получили повышенное внимание в течение последних нескольких десятилетий из-за их способности делать прогнозы для лесных стендов с различными видами композиций, структур истратегий управления 9,10,11.
Обычная регрессия наименее квадратов (OLS) является наиболее часто используемым методом для разработкимоделей роста отдельных деревьев 12,13,14,15. Наборы данных для моделей роста отдельных деревьев, собранные неоднократно в течение фиксированного периода времени на одной и той же единице выборки (т.е. образец участка или дерева) имеют иерархическую стохастичную структуру, с отсутствием независимости и высокой пространственной и временнойкорреляцией между наблюдениями 10,16. Иерархическая стохастическая структура нарушает фундаментальные предположения регрессии OLS: а именно независимые остатки и обычно распределенные данные с равными отклонениями. Таким образом, использование регрессии OLS неизбежно приводит к необъективным оценкам стандартной погрешности оценок параметровдля этих данных 13,14.
Модели смешанных эффектов обеспечивают мощный инструмент для анализа данных со сложными структурами, такими как данные повторных мер, продольные данные и многоуровневые данные. Модели смешанных эффектов состоят как из фиксированных компонентов, общих для полной популяции, так и из случайных компонентов, характерных для каждого уровня выборки. Кроме того, модели смешанных эффектов учитывают гетероседактичность и автокорреляцию в пространстве и времени, определяя не диагональную дисперсию-ковариациюструктуры матриц 17,18,19. По этой причине, смешанные эффекты модели широко используются в лесном хозяйстве, таких как в диаметревысоты модели 20,21,коронные модели 22,23, самоубавки модели24,25, и рост модели26,27.
В этой связи основная цель заключалась в разработке модели прироста базальных областей отдельных деревьев с использованием линейного подхода к смешанным эффектам. Мы надеемся, что подход, связанный со смешанными последствиями, может быть широко применен.
протокол
1. Подготовка данных
- Подготовь данные моделирования, которые включают информацию об индивидуальном дереве (виды и диаметр на высоте груди 1,3 м) и информацию о участке (склон, аспект и высота). В этом исследовании данные были получены с 8-го (2009) и 9-го (2014) Китайского национального лесного кадастра в провинции Синьцзян на северо-западе Китая, который включает 21 898 наблюдений 779 выборочных участков. Эти участки квадратной формы размером 1 Му (китайская единица площади, эквивалентная 0,067 га) и систематически расположены по сетке 4 км х 8 км.
ПРИМЕЧАНИЕ: Данные для моделирования (базальной области) приращения требуют по крайней мере одного периода роста (т.е. двух наблюдений). - Случайным образом разделить данные на два набора данных, при этом 80% данных из выборочных участков, используемых для установки модели (набор данных разработки модели), который состоит из 17 145 наблюдений из 623 выборочных участков и 20% для проверки модели (набор данных проверки модели), который состоит из 4753 наблюдений из 156 выборочных участков. Описательная статистика по ключевым используемым переменным представлена в таблице 1.
ПРИМЕЧАНИЕ: Этот этап процедуры моделирования может быть опущен, и все данные используются для разработки модели.
| Переменные | Установка данных | Данные проверки | |||||||
| Мин | Макс | Означает | Памяти. | Мин | Макс | Означает | Памяти. | ||
| DBH1 (см) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| ЗМД (см) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| Идентификатор (см) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| БАЛ(м 3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (деревья/га) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (м2/га) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| ЭЛЬ (м) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
Таблица 1. Краткая статистика для данных установки и проверки. DBH1: начальный диаметр на высоте груди 1,3 м (DBH), DBH2: DBH измеряется после 5 лет роста, ЗМД: квадратный средний диаметр, ID: диаметр приращения в течение 5 лет (DBH2 - DBH1), BAL: базальная площадь деревьев больше, чем предмет дерева (субъект дерево: дерево, которое было рассчитано индексы конкуренции), NT: количество деревьев на гектар, BA: базальная площадь на гектар, EL: высота, S.D.: стандартное отклонение.
2. Развитие базовой модели
- Проконсультируйтесь со ссылками для определения переменных, влияющих на прирост базальной области отдельных деревьев.
- Выберите и вычислите переменные на основе данных. Как правило, на прирост базальной области индивидуального дерева влияют три группы переменных: размер дерева, конкуренция исостояние участка 27,28,29,30.
- Рассмотрим эффекты размером сдерево, такие какDBH 1 , квадрат DBH1
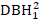 (), обратная трансформация DBH1 (1/DBH1), и общий logarithm DBH1 (logDBH1) или их комбинации.
(), обратная трансформация DBH1 (1/DBH1), и общий logarithm DBH1 (logDBH1) или их комбинации. - Рассмотрите такие конкурентные эффекты, как односторонние и двусторонние индексы конкуренции, с тем чтобы более всесторонне количественно оценить уровень конкуренции, с которыми сталкиваются дерево, а также его социальное положение в рамках стенда. Односторонняя конкуренция включает в себя BAL и индекс относительной плотности (РДЗДХ1/ ЗМД); двусторонний конкурс включают NT, и BA.
ПРИМЕЧАНИЕ: При наличии данных следует учитывать зависящие от расстояния индексы конкуренции. - Рассмотрим сайт эффекты, такие как аспект (ASP), наклон (SL), и EL. SL и ASP должны быть включены с помощью преобразования этап31.
- Рассмотрим эффекты размером сдерево, такие какDBH 1 , квадрат DBH1
- Выберите журнал
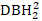 (-
(- 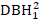 No1)
No1) 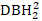 (обозначает квадрат DBH2) в качестве зависимой переменной.
(обозначает квадрат DBH2) в качестве зависимой переменной. - Разработайте базовую модель с помощью метода регрессии пошаговой стрелки. Убедитесь, что модель является биологически разумной и имеет значительные различия между независимыми переменными. Используйте коэффициент инфляции дисперсии (VIF) для проверки на многовечность.
- Оставьте независимые переменные с p lt; 0.05 и VIF lt; 5 в базовой модели.
- Выход основных результатов модели и остаточного участка. Базовая модель, произведенная здесь, служит основой для дальнейшего развития модели смешанных эффектов.
3. Линейное развитие модели смешанных эффектов с пакетом "nlme" в программном обеспечении R
- Прочитайте набор данных разработки модели и загрузите пакет "nlme".
(gt;model.development.dataset)read.csv ("E:/DATA/JoVE/modelingdata.csv",
заголовок -TRUE)
Библиотека (nlme) - Выберите выборочные участки в качестве случайных эффектов для разработки модели смешанных эффектов.
- Подгонка все возможные комбинации случайных эффектов с максимальной вероятностью (ML) метод и вывод результатов.
«Gt;Model»lt;-lme(Y-1/DBH1»BAL»NT-EL,data-model.development.dataset,
метод "ML", случайный No1| УЧАСТОК)
(Модель)- Установить случайный No 1 является перехват случайных параметров. Измените случайные операторы до тех пор, пока не будут установлены все комбинации. Например, чтобы установить 1/DBH1 и BAL в качестве случайных параметров, код таков: случайный No1/DBH1NO BAL-1. Кроме того, в процессе установки коды могут сообщать об ошибках из-за неуверенности установленной модели.
- Выберите лучшую модель по информационному критерию Акаике (AIC), байесовскому информационному критерию (BIC), вероятности логаритма (Loglik) и тесту коэффициента вероятности (LRT).
Ганова (Модель.1, Модель.6)
йgt;anova (Модель.6, Модель.23)
Ганова (Модель.23, Модель.30) - Определите структуру Ri. Адрес гетеросестичность и автокорреляция Ri32. Ri написан следующим образом:
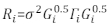 (1)
(1)
где σ2 является неизвестным фактором масштабирования, который равен модели остаточной дисперсии, G i является диагональной матрицей, описывающей гетероседактичность, и Γя матрица, описывающая автокорреляцию.- Обратите время на то, имеют ли остатки гетеросестичность остаточного участка. Если есть гетеросестичность (остатки имеют четкую закономерность или тренд), ввемите три часто используемые функции дисперсии - постоянную плюс функцию питания, функцию питания и экспоненциальную функцию - для моделирования структуры дисперсии ошибок.
В то же время,Модель.30.1'lt;-lme(Y-1/DBH1(БАЛЗНТЗЕЛА), data-model.development.dataset, метод""ML", случайный No1/DBH1(БАЛЗНТ| Печати
весы»varConstPower (форма) установлена (.)))
В то же время,резюме (Модель.30.1)
В то же время,Модель.30.2'lt;-lme(Y-1/DBH1(БАЛЗНТЗЕЛА), data-model.development.dataset, метод,"ML", случайный No1/DBH1(БАЛЗНТ| Печати
весы»varPower (форма) установлена (.)))
В то же время,резюме (Модель.30.2)
В то же время,Модель.30.3'lt;-lme(Y-1/DBH1(БАЛЗНТЗЕЛА), data-model.development.dataset, метод""ML", случайный No1/DBH1(БАЛЗНТ| Печати
весы »varExp (форма) установлена (.)))
Резюме(Модель.30.3) - Определите лучшую функцию дисперсии для модели в соответствии с AIC, BIC, Loglik и LRT.
В то же время,anova (Модель.30, Модель.30.1)
В то же время,anova (Модель.30, Модель.30.2)
Анова(Модель.30, Модель.30.3) - Ввести три широко используемые структуры автокорреляции – структуру комбинированной симметрии (CS), ауторегрессивную структуру первого порядка «AR(1)» и сочетание ауторегрессивных и движущихся средних структур первого порядка (ARMA(1,1)».
«Gt;Model.30.3.1»lt;-lme(Y-1/DBH1»BAL»NT-EL,data-model.development.dataset, method»ML»,
случайный No 1/DBH1(БАЛЗНТ| PLOT, вес-varExp (форма)установлена (.)), корре corCompSymm ())
Резюме (Модель.30.3.1)
«Gt;Model.30.3.2»lt;-lme(Y-1/DBH1»BAL»NT-EL,data-model.development.dataset, method»ML»,
случайный No 1/DBH1(БАЛЗНТ| PLOT,весы-varExp (форма) установлена (.)), corr'corAR1 ())
Резюме (Модель.30.3.2)
«Gt;Model.30.3'lt;-lme(Y-1/DBH1»BAL»NT-EL,data-model.development.dataset, method»ML»,
случайный No 1/DBH1(БАЛЗНТ| PLOT,весы -varExp (форма) установлена (.)), корр-корАРМА (кв.1, стр.1))
Резюме (Модель.30.3.3) - Определите лучшую структуру автокорреляции в соответствии с AIC, BIC, Loglik и LRT.
Анова(Модель.30.3, Модель.30.3.2)
ПРИМЕЧАНИЕ: Gi и qi не могут быть определены, если нет гетеросестичность и автокорреляция. - Вывод окончательных результатов модели смешанных эффектов с использованием метода ограниченной максимальной вероятности (REML).
«Gt;Mixed.model»lt;-lme(Y-1/DBH1»BAL»NT-EL,data-model.development.dataset, method»»REML», случайный »1/DBH1»BAL»NT| Печати
весы (форма) установлена (.)), corr'corAR1 ())
Резюме (Mixed.model)
- Обратите время на то, имеют ли остатки гетеросестичность остаточного участка. Если есть гетеросестичность (остатки имеют четкую закономерность или тренд), ввемите три часто используемые функции дисперсии - постоянную плюс функцию питания, функцию питания и экспоненциальную функцию - для моделирования структуры дисперсии ошибок.
4. Коррекция предвзятости
- Преобразование прогнозируемых значений прироста базальной области с помощью окончательной модели в логаритмической шкале в исходный масштаб. Однако такая линейная задняя трансформация прогнозируемого значения из преобразованной в журнал модели создает связанный с этим уклон преобразования журнала. Для борьбы с бревенчатым уклоном был получен и интегрирован в уравнение прогнозирования, которое оценивает фактически прогнозируемый прирост базальной области для данного дерева «Equation (2)»:
 (2)
(2)
где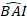 прогнозируется логаритмическое значение шагом базальной области от модели, в то время как прогнозируемое обратно преобразованное значение базального прироста области в течение 5 лет после коррекции для смещения преобразования журнала
прогнозируется логаритмическое значение шагом базальной области от модели, в то время как прогнозируемое обратно преобразованное значение базального прироста области в течение 5 лет после коррекции для смещения преобразования журнала 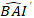
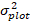 σ.
σ. - Преобразование базального прироста области
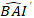 () к приросту диаметра.
() к приросту диаметра.
5. Прогнозирование и оценка моделей
- Подготовь набор данных проверки модели, подготовленный в разделе 1.2 для прогнозирования.
- Используйте линейную модель смешанных эффектов для прогнозирования прироста базальной площади отдельных деревьев. Случайные компоненты были рассчитаны с использованием следующего лучшего линейного беспристрастного предиктора:
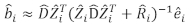 (3)
(3)
где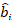 вектор для случайных компонентов;
вектор для случайных компонентов; 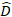 это матрица дисперсии-коварианса для изменчивости между участками; является матрицей проектирования для случайных компонентов, действующих при дополнительных наблюдениях; это остаточный вектор, компоненты которого
это матрица дисперсии-коварианса для изменчивости между участками; является матрицей проектирования для случайных компонентов, действующих при дополнительных наблюдениях; это остаточный вектор, компоненты которого 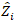
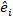 даются разницей между шагом базальной области и прогнозируемыми приращениями с использованием модели фиксированных эффектов.
даются разницей между шагом базальной области и прогнозируемыми приращениями с использованием модели фиксированных эффектов. - Оцените и сравните прогностический потенциал базовой модели и линейной модели смешанных эффектов, используя следующие тристатистических индикатора 23,33.
 (4)
(4)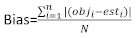 (5)
(5)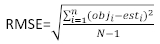 (6)
(6)
где objя базальной области шагом, estя предсказал базальных приращений области,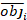 является средним наблюдений, и N является число наблюдений.
является средним наблюдений, и N является число наблюдений.
Результаты
Базовая модель прироста базальной области для P. asperata была выражена как Equation (7). Оценки параметров, соответствующие стандартные ошибки и статистика отсутствия соответствия показаны в таблице 2. Остаточный участок показан на рисунке 1. Наблюдалась выраженная гетер...
Обсуждение
Важнейшим вопросом для разработки моделей смешанных эффектов является определение параметров, которые можно рассматривать как случайные эффекты, а какие следует рассматривать какфиксированные эффекты 34,35. Были предложены два метода. Наиболее распрост...
Раскрытие информации
Авторов нечего раскрывать.
Благодарности
Это исследование финансировалось Фондами фундаментальных исследований для центральных университетов, грант no 2019GJ'L04. Мы благодарим профессора Вайшенга Цзэна из Академии лесных запасов и планирования, Национального управления лесного хозяйства и лугов, Китай, за предоставление доступа к данным.
Материалы
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
Ссылки
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. . Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. . Modeling Forest Trees and Stands. , (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. . Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , (2007).
- Calama, R., Montero, G. . Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257 (2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Перепечатки и разрешения
Запросить разрешение на использование текста или рисунков этого JoVE статьи
Запросить разрешениеThis article has been published
Video Coming Soon
Авторские права © 2025 MyJoVE Corporation. Все права защищены