Se requiere una suscripción a JoVE para ver este contenido. Inicie sesión o comience su prueba gratuita.
Method Article
Desarrollo de un modelo de incremento de área basal de árbol individual mediante un enfoque lineal de efectos mixtos
En este artículo
Resumen
Los modelos de efectos mixtos son herramientas flexibles y útiles para analizar datos con una estructura estocástica jerárquica en la silvicultura y también podrían utilizarse para mejorar significativamente el rendimiento de los modelos de crecimiento forestal. Aquí se presenta un protocolo que sintetiza información relacionada con modelos lineales de efectos mixtos.
Resumen
Aquí, desarrollamos un modelo de árbol individual de incrementos de área basal de 5 años basados en un conjunto de datos que incluye 21898 árboles picea asperata de 779 parcelas de muestra ubicadas en la provincia de Xinjiang, en el noroeste de China. Para evitar altas correlaciones entre las observaciones de la misma unidad de muestreo, desarrollamos el modelo utilizando un enfoque lineal de efectos mixtos con efecto de trazado aleatorio para tener en cuenta la variabilidad estocástica. Se incluyeron varias variables a nivel de árbol y stand, como índices para el tamaño de los árboles, la competencia y la condición del sitio, como efectos fijos para explicar la variabilidad residual. Además, se describió la heteroscedasticidad y la autocorrelación mediante la introducción de funciones de varianza y estructuras de autocorrelación. El modelo óptimo de efectos mixtos lineales fue determinado por varias estadísticas de ajuste: el criterio de información de Akaike, el criterio de información bayesiano, la probabilidad de logaritmo y una prueba de relación de probabilidad. Los resultados indicaron que variables significativas del incremento del área basal de los árboles individuales fueron la transformación inversa del diámetro a la altura de las mamas, el área basal de los árboles más grande que el árbol sujeto, el número de árboles por hectárea y la elevación. Además, los errores en la estructura de varianza fueron modelados con mayor éxito por la función exponencial, y la autocorrelación fue corregida significativamente por la estructura autoregresiva de primer orden (AR(1)). El rendimiento del modelo lineal de efectos mixtos se mejoró significativamente en relación con el modelo utilizando la regresión ordinaria de mínimos cuadrados.
Introducción
En comparación con el monocultivo envejecida uniforme, la gestión forestal de especies mixtas de edad desigual con múltiples objetivos ha recibido una mayor atención recientemente1,2,3. La predicción de diferentes alternativas de gestión es necesaria para formular estrategias sólidas de gestión forestal, especialmente para los complejos bosques de especies mixtas de edad desigual4. Los modelos de crecimiento y rendimiento de los bosques se han utilizado ampliamente para pronosticar el desarrollo y la cosecha de árboles o soportes en virtud de diversos esquemas de gestión5,6,7. Los modelos de crecimiento y rendimiento de los bosques se clasifican en modelos de árboles individuales, modelos de tamaño y modelos de crecimiento integral6,7,8. Desafortunadamente, los modelos de clase de tamaño y los modelos integrales no son apropiados para los bosques de especies mixtas de edad desigual, que requieren una descripción más detallada para apoyar el proceso de toma de decisiones de gestión forestal. Por esta razón, los modelos de crecimiento y rendimiento de árboles individuales han recibido una mayor atención a lo largo de las últimas décadas debido a su capacidad para hacer predicciones para los puestos forestales con una variedad de composiciones de especies, estructuras y estrategias de gestión9,10,11.
La regresión ordinaria de los mínimos cuadrados (OLS) es el método más utilizado para el desarrollo de modelos de crecimiento de árboles individuales12,13,14,15. Los conjuntos de datos para modelos de crecimiento de árboles individuales recopilados repetidamente durante un período de tiempo fijo en la misma unidad de muestreo (es decir, gráfica de muestra o árbol) tienen una estructura estocástica jerárquica, con una falta de independencia y una alta correlación espacial y temporal entre las observaciones10,16. La estructura estocástica jerárquica infringe los supuestos fundamentales de la regresión OLS: a saber, residuos independientes y datos normalmente distribuidos con desviaciones iguales. Por lo tanto, el uso de la regresión OLS produce inevitablemente estimaciones sesgadas del error estándar de las estimaciones de parámetros para estos datos13,14.
Los modelos de efectos mixtos proporcionan una potente herramienta para analizar datos con estructuras complejas, como datos de medidas repetidas, datos longitudinales y datos de varios niveles. Los modelos de efectos mixtos constan tanto de componentes fijos, comunes a la población completa, como de componentes aleatorios, que es específico de cada nivel de muestreo. Además, los modelos de efectos mixtos tienen en cuenta la heteroscedasticidad y la autocorrelación en el espacio y el tiempo mediante la definición de matrices de estructura de varianza-covarianza no diagonales17,18,19. Por esta razón, los modelos de efectos mixtos se han utilizado ampliamente en la silvicultura, como en los modelos de altura de diámetro20,21,modelos de corona22,23,modelos de auto-adelgazamiento24,25y modelos de crecimiento26,27.
Aquí, el objetivo principal era desarrollar un modelo de incremento de área basal de árbol individual utilizando un enfoque lineal de efectos mixtos. Esperamos que el enfoque de efectos mixtos pueda aplicarse ampliamente.
Access restricted. Please log in or start a trial to view this content.
Protocolo
1. Preparación de datos
- Preparar datos de modelado, que incluyen información de árboles individuales (especies y diámetro a la altura de la mama a 1,3 m) e información de la parcela (pendiente, aspecto y elevación). En este estudio, los datos se obtuvieron del 8º (2009) y el 9º (2014) Inventario Forestal Nacional Chino en la provincia de Xinjiang, en el noroeste de China, que incluye 21.898 observaciones de 779 parcelas de muestra. Estas parcelas de muestra tienen forma cuadrada con un tamaño de 1 Mu (unidad china de área equivalente a 0,067 ha) y están dispuestas sistemáticamente sobre una cuadrícula de 4 km x 8 km.
NOTA: Los datos para el incremento de modelado (área basal) requieren al menos un período de crecimiento (es decir, dos observaciones). - Divida aleatoriamente los datos en dos conjuntos de datos, con el 80% de los datos de las gráficas de muestra utilizadas para el ajuste del modelo (dataset de desarrollo de modelos), que consta de 17.145 observaciones de 623 gráficas de muestra y el 20% para la validación del modelo (dataset de validación del modelo), que consta de 4.753 observaciones de 156 gráficas de muestra. Las estadísticas descriptivas de las variables clave utilizadas se proporcionan en la Tabla 1.
NOTA: Este paso del procedimiento de modelado se puede omitir y todos los datos se utilizan para el desarrollo de modelos.
| Variables | Datos de adaptación | Datos de validación | |||||||
| Min | máximo | Decir | S.d. | Min | máximo | Decir | S.d. | ||
| DBH1 (cm) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD (cm) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| ID (cm) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (m3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (árboles/ha) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (m2/ha) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| EL (m) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
Tabla 1. Estadísticas de resumen para datos de adaptación y validación. DBH1: diámetro inicial a la altura de la mama a 1,3 m (DBH), DBH2: DBH medido después de 5 años de crecimiento, QMD: diámetro medio cuadrático, ID: incremento de diámetro durante 5 años (DBH2 – DBH1),BAL: el área basal de los árboles más grandes que el árbol sujeto (el árbol sujeto: el árbol que se calculó los índices de competencia), NT: el número de árboles por hectárea, BA: área basal por hectárea, EL: elevación, S.D.: desviación estándar.
2. Desarrollo básico del modelo
- Consulte referencias para identificar variables que afectan a incrementos de área basal de árbol individual.
- Seleccione y calcule variables en función de los datos. Generalmente, el incremento de área basal de árbol individual se ve afectado por tres grupos de variables: tamaño del árbol, competencia y condición del sitio27,28,29,30.
- Considere efectos de tamaño de árbol como DBH1, cuadrado de DBH1 (
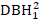 ), la transformación inversa de DBH1 (1/DBH1)y el logaritmo común de DBH1 (logDBH1) o combinaciones de ellos.
), la transformación inversa de DBH1 (1/DBH1)y el logaritmo común de DBH1 (logDBH1) o combinaciones de ellos. - Considere los efectos competitivos, como los índices de competencia unilaterales y de dos lados, para cuantificar más ampliamente el nivel de competencia experimentado por un árbol, así como su posición social dentro del stand. La competencia unilateral incluye BAL y el índice de densidad relativa (RD=DBH1/QMD); la competencia de dos lados incluye NT y BA.
NOTA: Los índices de competencia dependientes de la distancia deben tenerse en cuenta si hay datos disponibles. - Tenga en cuenta los efectos de sitio como aspecto (ASP), pendiente (SL) y EL. SL y ASP deben incluirse mediante la transformación31de Stage.
- Considere efectos de tamaño de árbol como DBH1, cuadrado de DBH1 (
- Seleccione log(
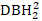 -
- 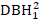 +1) (
+1) ( 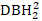 denota cuadrado de DBH2) como la variable dependiente.
denota cuadrado de DBH2) como la variable dependiente. - Desarrolle el modelo básico utilizando el método de regresión escalonada. Asegúrese de que el modelo sea biológicamente razonable y muestre diferencias significativas entre variables independientes. Utilice el factor de inflación de varianza (VIF) para comprobar la multicollinearidad.
- Deje las variables independientes con p < 0.05 y VIF < 5 en el modelo básico.
- Genere los resultados básicos del modelo y la gráfica residual. El modelo básico producido aquí sirve como base para el desarrollo posterior de un modelo de efectos mixtos.
3. Desarrollo lineal de modelos de efectos mixtos con el paquete "nlme" en el software R
- Lea el conjunto de datos de desarrollo del modelo y cargue el paquete "nlme".
>model.development.dataset=read.csv("E:/DATA/JoVE/modelingdata.csv",
header=TRUE)
>biblioteca(nlme) - Seleccione trazados de muestra como efectos aleatorios para desarrollar el modelo de efectos mixtos.
- Ajuste todas las combinaciones posibles de efectos aleatorios con el método de máxima probabilidad (ML) y genere los resultados.
>Modelo<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset,
method="ML", aleatorio =~1| PARCELA)
>summary(Modelo)- Establecer random =~1 es la intercepción a parámetros aleatorios. Cambie las instrucciones aleatorias hasta que se instalen todas las combinaciones. Por ejemplo, para establecer 1/DBH1 y BAL como parámetros aleatorios, el código es el siguiente: random =~1/DBH1+BAL-1. Además, en el proceso de adaptación, los códigos pueden notificar errores debido a la no convergencia del modelo ajustado.
- Seleccione el mejor modelo por criterio de información de Akaike (AIC), el criterio de información bayesiano (BIC), la probabilidad de logaritmo (Loglik) y la prueba de relación de probabilidad (LRT).
>anova(Model.1, Model.6)
>anova(Model.6, Model.23)
>anova(Model.23, Model.30) - Determinar la estructura de Ri. Abordar la heteroscedasticidad y autocorrelación de Ri32. El Ri está escrito de la siguiente manera:
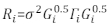 (1)
(1)
donde σ2 es un factor de escala desconocido que es igual a la varianza residual del modelo, Gi es una matriz diagonal que describe la heteroscedasticidad, y Γi es una matriz que describe la autocorrelación.- Observe si los residuos tienen heteroscedasticidad de la parcela residual. Si hay heteroscedasticidad (los residuos tienen un patrón o tendencia claros), introduzca tres funciones de varianza utilizadas con frecuencia (la función de potencia más constante, la función de potencia y la función exponencial) para modelar la estructura de varianza de errores.
>Model.30.1<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| conspirar
pesos=varConstPower(form=~ fitted(.)))
>resumen(Model.30.1)
>Model.30.2<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| conspirar
pesos=varPower(form=~ ajustado(.)))
>resumen(Model.30.2)
>Model.30.3<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| conspirar
pesos=varExp(form=~ fitted(.)))
>resumen(Model.30.3) - Determine la mejor función de varianza para el modelo según AIC, BIC, Loglik y LRT.
>anova(Model.30, Model.30.1)
>anova(Model.30, Model.30.2)
>anova(Model.30, Model.30.3) - Introduzca tres estructuras de autocorrelación de uso común (la estructura de simetría compuesta (CS), la estructura autoregresiva de primer orden [AR(1)] y una combinación de estructuras autoregresivas y de media móvil de primer orden [ARMA(1,1)], para tener en cuenta la autocorrelación.
>Model.30.3.1<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| PLOT, weights=varExp(form=~fitted(.)), corr= corCompSymm())
>resumen(Model.30.3.1)
>Model.30.3.2<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| PLOT,weights=varExp(form=~ fitted(.)), corr=corAR1())
>resumen(Model.30.3.2)
>Model.30.3.3<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| PLOT,weights=varExp(form=~ fitted(.)), corr=corARMA(q=1,p=1))
>resumen(Model.30.3.3) - Determine la mejor estructura de autocorrelación según la AIC, BIC, Loglik y LRT.
>anova(Model.30.3, Model.30.3.2)
NOTA: El Gi y el Ḥi no se pueden definir si no hay heteroscedasticidad y autocorrelación. - Genere los resultados finales del modelo de efectos mixtos utilizando el método de máxima probabilidad restringida (REML).
>Mixed.model<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="REML",random=~1/DBH1+BAL+NT| conspirar
pesos=varExp(form=~ ajustado(.)), corr=corAR1())
>resumen(Mixed.model)
- Observe si los residuos tienen heteroscedasticidad de la parcela residual. Si hay heteroscedasticidad (los residuos tienen un patrón o tendencia claros), introduzca tres funciones de varianza utilizadas con frecuencia (la función de potencia más constante, la función de potencia y la función exponencial) para modelar la estructura de varianza de errores.
4. Corrección de sesgo
- Transforme los valores predichos de incremento de área basal utilizando el modelo final en una escala logarítmica a la escala original. Sin embargo, una transformación posterior lineal del valor predicho a partir de un modelo transformado en registro produce un sesgo de transformación de registro asociado. Para hacer frente al sesgo de registro, se derivó e integró un factor de corrección en la ecuación de predicción, que estima el incremento real de área basal predicha para un árbol dado [Ecuación (2)]:
 (2)
(2)
donde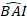 se predice el valor logarítmico del incremento de área basal del modelo, mientras que el valor transformado de fondo
se predice el valor logarítmico del incremento de área basal del modelo, mientras que el valor transformado de fondo 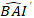 predicho de incremento de área basal durante 5 años después de corregir el sesgo de transformación de registro.
predicho de incremento de área basal durante 5 años después de corregir el sesgo de transformación de registro. 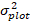 es la varianza de los efectos aleatorios en la gráfica y σ2 es la varianza residual.
es la varianza de los efectos aleatorios en la gráfica y σ2 es la varianza residual. - Convierta el incremento de área basal (
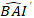 ) al incremento de diámetro.
) al incremento de diámetro.
5. Predicción y evaluación del modelo
- Prepare el dataset de validación del modelo generado en la sección 1.2 para la predicción.
- Utilice el modelo lineal de efectos mixtos para predecir el incremento de área basal de árbol individual. Los componentes aleatorios se calcularon utilizando el siguiente mejor predictor lineal imparcial:
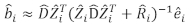 (3)
(3)
dónde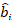 está un vector para los componentes
está un vector para los componentes 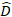 aleatorios; es la matriz de varianza-covarianza para la variabilidad entre trazados;
aleatorios; es la matriz de varianza-covarianza para la variabilidad entre trazados; 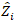 es la matriz de diseño para los componentes aleatorios que actúan en las observaciones complementarias;
es la matriz de diseño para los componentes aleatorios que actúan en las observaciones complementarias; 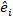 es el vector residual cuyos componentes se dan por la diferencia entre los incrementos de área basal y los incrementos predichos utilizando el modelo de efectos fijos.
es el vector residual cuyos componentes se dan por la diferencia entre los incrementos de área basal y los incrementos predichos utilizando el modelo de efectos fijos. - Evaluar y comparar la capacidad predictiva del modelo básico y el modelo lineal de efectos mixtos utilizando los tres indicadores estadísticos siguientes23,33.
 (4)
(4)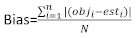 (5)
(5)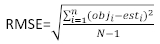 (6)
(6)
donde obji es el área basal incrementos, esti es el área basal predicha incrementos,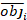 es la media de observaciones, y N es el número de observaciones.
es la media de observaciones, y N es el número de observaciones.
Access restricted. Please log in or start a trial to view this content.
Resultados
El modelo básico de incremento de área basal para P. asperata se expresó como Ecuación (7). Las estimaciones de parámetros, sus errores estándar correspondientes y las estadísticas de falta de ajuste se muestran en la Tabla 2. La gráfica residual se muestra en la Figura 1. Se observó heteroscedasticidad pronunciada de los residuos.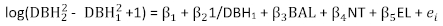 (7)
(7)
Access restricted. Please log in or start a trial to view this content.
Discusión
Un problema crucial para el desarrollo de modelos de efectos mixtos es determinar qué parámetros pueden tratarse como efectos aleatorios y cuáles deben considerarse efectos fijos34,35. Se han propuesto dos métodos. El enfoque más común es tratar todos los parámetros como efectos aleatorios y luego tener el mejor modelo seleccionado por AIC, BIC, Loglik y LRT. Este fue el método empleado por nuestro estudio35. Una alternativa es ada...
Access restricted. Please log in or start a trial to view this content.
Divulgaciones
Los autores no tienen nada que revelar.
Agradecimientos
Esta investigación fue financiada por los Fondos Fundamentales de Investigación para las Universidades Centrales, beca número 2019GJZL04. Agradecemos al Profesor Weisheng Zeng de la Academia de Inventario y Planificación Forestal, Administración Nacional Forestal y de Pastizales, China por proporcionar acceso a los datos.
Access restricted. Please log in or start a trial to view this content.
Materiales
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
Referencias
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. Modeling Forest Trees and Stands. , Springer. Netherlands. (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , Springer. Boston, MA. (2007).
- Calama, R., Montero, G. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257(2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Access restricted. Please log in or start a trial to view this content.
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados