Bu içeriği görüntülemek için JoVE aboneliği gereklidir. Oturum açın veya ücretsiz deneme sürümünü başlatın.
Method Article
Doğrusal Karma EfektLer Yaklaşımı Kullanılarak Tek Tek Ağaç Bazal Alan Artış Modelinin Geliştirilmesi
Bu Makalede
Özet
Karma efekt modelleri, ormancılıkta hiyerarşik stokastik bir yapıya sahip verileri analiz etmek için esnek ve kullanışlı araçlardır ve orman büyüme modellerinin performansını önemli ölçüde artırmak için de kullanılabilir. Burada, doğrusal karma efekt modelleri ile ilgili bilgileri sentezleyen bir protokol sunulmuştur.
Özet
Burada, Çin'in kuzeybatısındaki Sincan Eyaleti'nde bulunan 779 örnek arsadan 21898 Picea asperata ağacı içeren bir veri kümesine dayanarak 5 yıllık bazal alan artışlarından oluşan bir bireysel ağaç modeli geliştirdik. Aynı örnekleme ünitesinden gözlemler arasında yüksek korelasyonları önlemek için, stochastic değişkenliği hesaba katmak için rastgele çizim etkisine sahip doğrusal bir karma efekt yaklaşımı kullanarak modeli geliştirdik. Ağaç boyutu, rekabet ve site durumu endeksleri gibi çeşitli ağaç ve stand düzeyi değişkenleri, artık değişkenliği açıklamak için sabit efektler olarak dahil edildi. Ayrıca varyans fonksiyonları ve otokorrelasyon yapıları getirilerek heterosklastisite ve otokorrelasyon tanımlanmıştır. Optimal lineer karma efekt modeli birkaç uygun istatistikle belirlendi: Akaike'nin bilgi kriteri, Bayes bilgi kriteri, logaritma olasılığı ve olasılık oranı testi. Sonuçlar, bireysel ağaç bazal alan artışındaki önemli değişkenlerin, meme yüksekliğinde çapın ters dönüşümü, konu ağaçtan daha büyük ağaçların bazal alanı, hektar başına ağaç sayısı ve yükseklik olduğunu gösterdi. Ayrıca, varyans yapısındaki hatalar en başarılı şekilde üstel işlev tarafından modellenmiş ve otomatik ilişki birinci dereceden otoregressif yapı (AR(1)) ile önemli ölçüde düzeltilmiştir. Doğrusal karışık efektler modelinin performansı, sıradan en az kare gerilemesi kullanılarak modele göre önemli ölçüde geliştirilmiştir.
Giriş
Çift yaşlı monokültür ile karşılaştırıldığında, birden fazla hedefe sahip düzensiz yaşlı karma tür orman yönetimi son zamanlarda artan ilgi gördü1,2,3. Farklı yönetim alternatiflerinin öngörüsü, özellikle karmaşık düzensiz yaşlanmış karma türler ormanı4için sağlam orman yönetim stratejileri oluşturmak için gereklidir. Orman büyüme ve verim modelleri, çeşitli yönetim şemaları5,6,7altında ağaç veya stand geliştirme ve hasat tahmin etmek için yaygın olarak kullanılmıştır. Orman büyüme ve verim modelleri bireysel ağaç modelleri, boyut sınıfı modeller ve tüm stand büyüme modelleri6, 7,8olarak sınıflandırılır. Ne yazık ki, boyut sınıfı modeller ve tüm stand modelleri, orman yönetimi karar verme sürecini desteklemek için daha ayrıntılı bir açıklama gerektiren düzensiz yaşlı karma tür ormanları için uygun değildir. Bu nedenle, bireysel ağaç büyüme ve verim modelleri, çeşitli tür kompozisyonları, yapıları ve yönetim stratejileri 9 , 10,11ile orman standları için tahminlerde bulunma yetenekleri nedeniyle son birkaç on yıl boyunca artan ilgi gördü.
Sıradan en az kareler (OLS) gerilemesi, bireysel ağaç büyüme modellerinin geliştirilmesi için en yaygın kullanılan yöntemdir12,13,14,15. Aynı örnekleme ünitesinde (örn. örnek arsa veya ağaç) sabit bir süre boyunca tekrar tekrar toplanan bireysel ağaç büyüme modelleri için veri kümeleri, bağımsızlık eksikliği ve gözlemler arasında yüksek mekansal ve zamansal korelasyon ile hiyerarşik bir stokastik yapıya sahiptir10,16. Hiyerarşik stokastik yapı OLS gerilemesinin temel varsayımlarını ihlal eder: yani bağımsız artıklar ve normalde eşit farklılıklara sahip dağıtılmış veriler. Bu nedenle, OLS regresyonunun kullanımı kaçınılmaz olarak bu veriler için parametre tahminlerinin standart hatasının önyargılı tahminlerini üretir13,14.
Karma efekt modelleri, yinelenen ölçü verileri, boyuna veriler ve çok düzeyli veriler gibi karmaşık yapılarla verileri analiz etmek için güçlü bir araç sağlar. Karışık efekt modelleri, hem tam popülasyonda ortak olan sabit bileşenlerden hem de her örnekleme düzeyine özgü rastgele bileşenlerden oluşur. Buna ek olarak, karışık efektli modeller, diyagonal olmayan varyans-kovaryans yapısı matrisleri17 , 18,19tanımlayarak uzay ve zamanda heterosklastisiteyi ve otomatik tutarlılığı dikkate alır. Bu nedenle, karma efekt modelleri, çap yüksekliği modelleri20 , 21, taç modelleri 22,23,kendiliğinden inceltme modelleri24,25ve büyüme modelleri26,27gibi ormancılıkta yaygın olarak kullanılmaktadır.
Burada temel amaç, doğrusal bir karma efekt yaklaşımı kullanarak bireysel ağaç bazal alan artış modeli geliştirmekti. Karma efekt yaklaşımının geniş çapta uygulanabileceğini umuyoruz.
Access restricted. Please log in or start a trial to view this content.
Protokol
1. Veri hazırlama
- Bireysel ağaç bilgilerini (1,3 m'de meme yüksekliğinde tür ve çap) ve çizim bilgilerini (eğim, yön ve yükseklik) içeren modelleme verilerini hazırlayın. Bu çalışmada, Çin'in kuzeybatısındaki Sincan Eyaleti'ndeki 8'inci (2009) ve 9'uncu (2014) Çin Ulusal Orman Envanteri'nden elde edilen veriler, 779 örneklem arsasının 21.898 gözlemini içermektedir. Bu örnek parseller 1 Mu (0.067 ha'ya eşdeğer Çince alan birimi) boyutuyla kare şeklindedir ve sistematik olarak 4 km x 8 km'lik bir ızgara üzerinde düzenlenmiştir.
NOT: Modelleme (bazal alan) artışı için veriler en az bir büyüme dönemi (yani iki gözlem) gerektirir. - Verileri, 623 örnek çizimden 17.145 gözlemden oluşan model sığdırma (model geliştirme veri kümesi) için kullanılan örnek çizimlerden elde edilen verilerin %80'i ve 156 örnek çizimden 4.753 gözlemden oluşan model doğrulama (model doğrulama veri kümesi) için %20'si olmak üzere iki veri kümesine rastgele bölün. Kullanılan anahtar değişkenler için açıklayıcı istatistikler Tablo 1'de verilmiştir.
NOT: Modelleme yordamının bu adımı atlanabilir ve tüm veriler model geliştirme için kullanılır.
| Değişken | Verileri sığdırma | Doğrulama verileri | |||||||
| Dk | Max | Demek | S.d. | Dk | Max | Demek | S.d. | ||
| DBH1 (cm) | 5 | 124.8 | 19.9 | 13.2 | 5 | 101.5 | 19.5 | 13.4 | |
| QMD (cm) | 6.7 | 82.3 | 22.5 | 8.5 | 9.2 | 73.3 | 21.8 | 9.2 | |
| Kimlik (cm) | 0.1 | 14.4 | 1.1 | 1 | 0.1 | 16.9 | 1 | 1.1 | |
| BAL (m3) | 0 | 5.2 | 1.7 | 0.9 | 0 | 5.4 | 1.7 | 1 | |
| NT (ağaçlar/ha) | 14.9 | 3642 | 1072 | 673.7 | 14.9 | 3418 | 1205 | 829.3 | |
| BA (m2/ha) | 0.1 | 77.5 | 34.2 | 13.9 | 0.1 | 80.6 | 34.5 | 15.3 | |
| EL (m) | 2 | 3302 | 2189 | 340.3 | 1441 | 3380 | 2256 | 308.3 | |
Tablo 1. Verileri sığdırma ve doğrulama için özet istatistikler. DBH1: meme yüksekliğinde başlangıç çapı 1.3 m (DBH), DBH2: DBH 5 yıllık büyümeden sonra ölçüldü, QMD: ikinci dereceden ortalama çap, kimlik: 5 yıl boyunca çap artışı (DBH2 –DBH 1),BAL: konu ağacından daha büyük ağaçların bazal alanı (konu ağacı: rekabet endeksleri hesaplanan ağaç), NT: hektar başına ağaç sayısı, BA: hektar başına bazal alan, EL: yükseklik, S.D.: standart sapma.
2. Temel model geliştirme
- Tek tek ağaç bazal alan artışlarını etkileyen değişkenleri tanımlamak için başvurulara başvurun.
- Verileri temel alan değişkenleri seçin ve hesaplayın. Genellikle, tek tek ağaç bazal alan artışı üç değişken grubundan etkilenir: ağaç boyutu, rekabet ve site durumu27,28,29,30.
- DBH 1 ,DBH 1karesi ( ),DBH 1'in
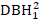 ters dönüşümü (1/DBH1) veDBH 1'inortak logaritması (logDBH1) veyabunlarınkombinasyonları gibi ağaç boyutu etkilerini göz önünde bulundurun.
ters dönüşümü (1/DBH1) veDBH 1'inortak logaritması (logDBH1) veyabunlarınkombinasyonları gibi ağaç boyutu etkilerini göz önünde bulundurun. - Bir ağacın yaşadığı rekabet seviyesini ve stand içindeki sosyal konumunu daha kapsamlı bir şekilde ölçmek için rekabetin hem tek hem de iki taraflı endeksleri gibi rekabetçi etkileri göz önünde bulundurun. Tek taraflı rekabet BAL ve göreli yoğunluk indeksini içerir (RD=DBH1/QMD); iki taraflı rekabet NT ve BA'yı içerir.
NOT: Veriler mevcutsa mesafeye bağlı rekabet endeksleri dikkate alınmalıdır. - Sahne Alanı'nın dönüşümü31kullanılarak aspect (ASP), eğim (SL) ve EL. SL ve ASP gibi site efektlerinin dahil edilmesi gerektiğini göz önünde bulundurun.
- DBH 1 ,DBH 1karesi ( ),DBH 1'in
- Bağımlı değişken olarak log(
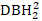 -
- 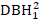 +1)
+1) 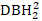 (DBH2'ninkaresini gösterir) seçeneğini belirleyin.
(DBH2'ninkaresini gösterir) seçeneğini belirleyin. - Adım adım regresyon yöntemini kullanarak temel modeli geliştirin. Modelin biyolojik olarak makul olduğundan ve bağımsız değişkenler arasında önemli farklılıklar sergilediğini sağlayın. Çok renkli olup olmadığını kontrol etmek için varyans enflasyon faktörünü (VIF) kullanın.
- Bağımsız değişkenleri temel modelde p < 0.05 ve VIF < 5 ile bırakın.
- Temel model sonuçlarını ve artık çizimi çıktısını elde edin. Burada üretilen temel model, karma efektli bir modelin daha da geliştirilmesi için bir temel görevi görür.
3. R yazılımında "nlme" paketi ile doğrusal karışık efekt modeli geliştirme
- Model geliştirme veri kümesini okuyun ve "nlme" paketini yükleyin.
>model.development.dataset=read.csv("E:/DATA/JoVE/modelingdata.csv",
üstbilgi=DOĞRU)
>kitaplık(nlme) - Karışık efekt modelini geliştirmek için örnek çizimleri rastgele efektler olarak seçin.
- Rastgele efektlerin olası tüm kombinasyonlarını maksimum olasılık (ML) yöntemiyle sığdırın ve sonuçları çıktısını çıkarın.
>Model<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset,
method="ML", rastgele =~1| ARSA)
>özet(Model)- Random =~1'i ayarlamak, rastgele parametrelere kesişme noktasıdır. Tüm birleşimler takılana kadar rasgele deyimleri değiştirin. Örneğin, 1/DBH1 ve BAL'ı rasgele parametreler olarak ayarlamak için kod aşağıdaki gibidir: random =~1/DBH1+BAL-1. Ek olarak, montaj sürecinde, kodlar takılan modelin nonconvergence nedeniyle hataları bildirebilir.
- Akaike'nin bilgi kriteri (AIC), Bayes bilgi kriteri (BIC), logaritma olasılığı (Loglik) ve olasılık oranı testi (LRT) ile en iyi modeli seçin.
>anova(Model.1, Model.6)
>anova(Model.6, Model.23)
>anova(Model.23, Model.30) - Ri'ninyapısını belirleyin. Ri32'ninheterosklastisitesini ve otomatik düzeltilmesini ele alın. Ri aşağıdaki gibi yazılmıştır:
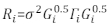 (1)
(1)
burada σ2, model kalıntısı varyansına eşit bilinmeyen bir ölçekleme faktörüdür, Gi heteroskedastisiteyi tanımlayan çapraz bir matristir ve Γi otomatik ilişkiyi tanımlayan bir matristir.- Artıkların artık arsadan heteroskedasiteye sahip olup olmadığını gözlemleyin. Heterosklastisite varsa (artıkların açık bir deseni veya eğilimi vardır), hataların varyans yapısını modellemek için sık kullanılan üç varyans işlevini (sabit artı güç işlevi, güç işlevi ve üstel işlev) tanıtın.
>Model.30.1<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| Arsa
weights=varConstPower(form=~ takılmış(.)))
>özet(Model.30.1)
>Model.30.2<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| Arsa
weights=varPower(form=~ takılmış(.)))
>özet(Model.30.2)
>Model.30.3<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",random=~1/DBH1+BAL+NT| Arsa
weights=varExp(form=~ takılmış(.)))
>özet(Model.30.3) - AIC, BIC, Loglik ve LRT'ye göre model için en iyi varyans işlevini belirleyin.
>anova(Model.30, Model.30.1)
>anova(Model.30, Model.30.2)
>anova(Model.30, Model.30.3) - Otomatik ilişkiyi hesaba katmak için yaygın olarak kullanılan üç otomatik ilişki yapısını (bileşik simetri yapısı (CS), birinci dereceden otomatik gerileyen yapı [AR(1)] ve birinci dereceden otomatik gerileyen ve hareketli ortalama yapıların [ARMA(1,1)] birleşimini tanıtın.
>Model.30.3.1<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| ARSA, weights=varExp(form=~fitted(.)), corr= corCompSymm())
>özet(Model.30.3.1)
>Model.30.3.2<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| ARSA,weights=varExp(form=~ takılmış(.)), corr=corAR1())
>özet(Model.30.3.2)
>Model.30.3.3<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="ML",
random=~1/DBH1+BAL+NT| ARSA,weights=varExp(form=~ fitted(.)), corr=corARMA(q=1,p=1))
>özet(Model.30.3.3) - AIC, BIC, Loglik ve LRT'ye göre en iyi otomatik ilişki yapısını belirleyin.
>anova(Model.30.3, Model.30.3.2)
NOT: Heteroskedasticity ve autocorrelation yoksa Gi ve Φi tanımlanamaz. - Sınırlı maksimum olasılık (REML) yöntemini kullanarak karma efekt modelinin nihai sonuçlarını çıktısını elde edin.
>Mixed.model<-lme(Y~1/DBH1+BAL+NT+EL,data=model.development.dataset, method="REML",random=~1/DBH1+BAL+NT| Arsa
weights=varExp(form=~ takılmış(.)), corr=corAR1())
>özet(Mixed.model)
- Artıkların artık arsadan heteroskedasiteye sahip olup olmadığını gözlemleyin. Heterosklastisite varsa (artıkların açık bir deseni veya eğilimi vardır), hataların varyans yapısını modellemek için sık kullanılan üç varyans işlevini (sabit artı güç işlevi, güç işlevi ve üstel işlev) tanıtın.
4. Önyargı düzeltmesi
- Logaritmik ölçekteki son modeli kullanarak bazal alan artışı için öngörülen değerleri özgün ölçeğe dönüştürün. Ancak, günlük dönüştürülmüş bir modelden tahmin edilen değerin böyle doğrusal bir geri dönüşümü ilişkili bir günlük dönüştürme yanlılığı üretir. Günlük yanlılığıyla başa çıkmak için, belirli bir ağaç için gerçek tahmin edilen bazal alan artışlarını tahmin eden bir düzeltme faktörü türetilmiş ve tahmin denklemine entegre edilmiştir [Denklem (2)]:
 (2)
(2)
burada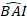 modelden bazal alan artışı logaritmik değeri tahmin edilirken,
modelden bazal alan artışı logaritmik değeri tahmin edilirken, 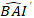 log-dönüşüm yanlılığı için düzeltildikten sonra 5 yıl boyunca bazal alan artışlarının tahmin edilen geri dönüştürülmüş değeri
log-dönüşüm yanlılığı için düzeltildikten sonra 5 yıl boyunca bazal alan artışlarının tahmin edilen geri dönüştürülmüş değeri 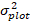 σ dir.
σ dir. - Bazal alan artış (
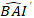 ) çap artışına dönüştürün.
) çap artışına dönüştürün.
5. Model tahmini ve değerlendirmesi
- Bölüm 1.2'de üretilen model doğrulama veri kümesini tahmin için hazırlayın.
- Tek tek ağaç bazal alan artışını tahmin etmek için doğrusal karışık efektler modelini kullanın. Rastgele bileşenler aşağıdaki en iyi doğrusal tarafsız tahmin edici kullanılarak hesaplanmıştır:
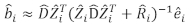 (3)
(3)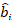 rastgele bileşenler için bir vektör
rastgele bileşenler için bir vektör 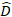 nerededir; çizimler arasındaki değişkenlik için varyans-kovaryans
nerededir; çizimler arasındaki değişkenlik için varyans-kovaryans 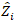 matrisidir; tamamlayıcı gözlemlerde hareket eden rastgele bileşenler için tasarım matrisidir; bileşenleri
matrisidir; tamamlayıcı gözlemlerde hareket eden rastgele bileşenler için tasarım matrisidir; bileşenleri 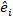 bazal alan artışları ile sabit efektler modeli kullanılarak öngörülen artışlar arasındaki farkla verilen artık vektördür.
bazal alan artışları ile sabit efektler modeli kullanılarak öngörülen artışlar arasındaki farkla verilen artık vektördür. - Aşağıdaki üç istatistiksel göstergeyi kullanarak temel modelin ve doğrusal karma efektler modelinin tahmin yeteneğini değerlendirin ve karşılaştırın23,33.
 (4)
(4)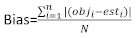 (5)
(5)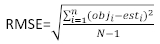 (6)
(6)
burada obji bazal alan artışlarıdır, esti tahmin edilen bazal alan artışlarıdır,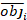 gözlemlerin ortalamasıdır ve N gözlem sayısıdır.
gözlemlerin ortalamasıdır ve N gözlem sayısıdır.
Access restricted. Please log in or start a trial to view this content.
Sonuçlar
P. asperata için temel bazal alan artış modeli Denklem (7) olarak ifade edildi. Parametre tahminleri, karşılık gelen standart hataları ve uygun olmayan istatistikler Tablo 2'de gösterilmiştir. Kalan arsa Şekil 1'de gösterilmiştir. Kalıntılarda belirgin heterosklastisite gözlendi.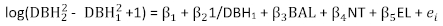 (7)
(7)
| Tahmin |
Access restricted. Please log in or start a trial to view this content.
Tartışmalar
Karma efektli modellerin geliştirilmesi için önemli bir konu, hangi parametrelerin rastgele efektler olarak değerlendirilebileceğini ve hangilerinin sabit efekt olarak kabul edilmesi gerektiğini belirlemektir34,35. İki yöntem önerildi. En yaygın yaklaşım, tüm parametreleri rasgele efektler olarak ele almak ve ardından AIC, BIC, Loglik ve LRT tarafından seçilen en iyi modele sahip olmaktır. Çalışmamızın kullandığı yöntem buydu
Access restricted. Please log in or start a trial to view this content.
Açıklamalar
Yazarların açıklayacak bir şeyi yok.
Teşekkürler
Bu araştırma, 2019GJZL04 hibe numarası olan Merkez Üniversiteler için Temel Araştırma Fonları tarafından finanse edildi. Orman Envanteri ve Planlaması Akademisi, Ulusal Ormancılık ve Çayır İdaresi, Çin'deki Profesör Weisheng Zeng'e verilere erişim sağladığı için teşekkür ederiz.
Access restricted. Please log in or start a trial to view this content.
Malzemeler
| Name | Company | Catalog Number | Comments |
| Computer | acer | ||
| Microsoft Office 2013 | |||
| R x64 3.5.1 |
Referanslar
- Meng, J., Lu, Y., Ji, Z. Transformation of a Degraded Pinus massoniana Plantation into a Mixed-Species Irregular Forest: Impacts on Stand Structure and Growth in Southern China. Forests. 5 (12), 3199-3221 (2014).
- Sharma, A., Bohn, K., Jose, S., Cropper, W. P. Converting even-aged plantations to uneven-aged stand conditions: A simulation analysis of silvicultural regimes with slash pine (Pinus elliottii Engelm). Forest Science. 60 (5), 893-906 (2014).
- Zhu, J., et al. Feasibility of implementing thinning in even-aged Larix olgensis plantations to develop uneven-aged larch–broadleaved mixed forests. Journal of Forest Research. 15 (1), 71-80 (2010).
- Leites, L. P., Robinson, A. P., Crookston, N. L. Accuracy and equivalence testing of crown ratio models and assessment of their impact on diameter growth and basal area increment predictions of two variants of the Forest Vegetation Simulator. Canadian Journal of Forest Research. 39 (3), 655-665 (2009).
- Pretzsch, H. Forest Dynamics, Growth and Yield. , (2009).
- Weiskittel, A. R., et al. Forest growth and yield modeling. Forest Growth & Yield Modeling. 7 (2), 223-233 (2002).
- Burkhart, H. E., Tomé, M. Modeling Forest Trees and Stands. , Springer. Netherlands. (2012).
- Zhang, X. Chinese Academy Of Forestry. A linkage among whole-stand model, individual-tree model and diameter-distribution model. Journal of Forest Science. 56 (56), 600-608 (2010).
- Peng, C. Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology & Management. 132 (2), 259-279 (2000).
- Lhotka, J. M., Loewenstein, E. F. An individual-tree diameter growth model for managed uneven-aged oak-shortleaf pine stands in the Ozark Highlands of Missouri, USA. Forest Ecology & Management. 261 (3), 770-778 (2011).
- Porté, A., Bartelink, H. H. Modelling mixed forest growth: a review of models for forest management. Ecological Modelling. 150 (1), 141-188 (2002).
- Moses, L. E., Gale, L. C., Altmann, J. Methods for analysis of unbalanced, longitudinal, growth data. American Journal of Primatology. 28 (1), 49-59 (2010).
- Biging, G. S. Improved Estimates of Site Index Curves Using a Varying-Parameter Model. Forest Science. 31 (31), 248-259 (1985).
- Kowalchuk, R. K., Keselman, H. J. Mixed-model pairwise multiple comparisons of repeated measures means. Psychological Methods. 6 (3), 282-296 (2001).
- Hayes, A. F., Cai, L. Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior Research Methods. 39 (4), 709-722 (2007).
- Gutzwiller, K. J., Riffell, S. K. Using Statistical Models to Study Temporal Dynamics of Animal-Landscape Relations. , Springer. Boston, MA. (2007).
- Calama, R., Montero, G. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. 39, (2005).
- Vonesh, E. F., Chinchilli, V. M. Linear and nonlinear models for the analysis of repeated measurements. Journal of Biopharmaceutical Statistics. 18 (4), 595-610 (1996).
- Zobel, J. M., Ek, A. R., Burk, T. E. Comparison of Forest Inventory and Analysis surveys, basal area models, and fitting methods for the aspen forest type in Minnesota. Forest Ecology & Management. 262 (2), 188-194 (2011).
- Sharma, M., Parton, J. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach. Forest Ecology & Management. 249 (3), 187-198 (2007).
- Crecente-Campo, F., Tomé, M., Soares, P., Diéguez-Aranda, U. A generalized nonlinear mixed-effects height–diameter model for Eucalyptus globulus L. in northwestern Spain. Forest Ecology & Management. 259 (5), 943-952 (2010).
- Fu, L., Sharma, R. P., Hao, K., Tang, S. A generalized interregional nonlinear mixed-effects crown width model for Prince Rupprecht larch in northern China. Forest Ecology & Management. 389 (2017), 364-373 (2017).
- Hao, X., Yujun, S., Xinjie, W., Jin, W., Yao, F. Linear mixed-effects models to describe individual tree crown width for China-fir in Fujian Province, southeast China. Plos One. 10 (4), 0122257(2015).
- Vanderschaaf, C. L., Burkhart, H. E. Comparing methods to estimate Reineke's Maximum Size-Density Relationship species boundary line slope. Forest Science. 53 (3), 435-442 (2007).
- Zhang, L., Bi, H., Gove, J. H., Heath, L. S. A comparison of alternative methods for estimating the self-thinning boundary line. Canadian Journal of Forest Research. 35 (6), 1507-1514 (2005).
- Hart, D. R., Chute, A. S. Estimating von Bertalanffy growth parameters from growth increment data using a linear mixed-effects model, with an application to the sea scallop Placopecten magellanicus. Ices Journal of Marine Science. 66 (9), 2165-2175 (2009).
- Uzoh, F. C. C., Oliver, W. W. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology & Management. 256 (3), 438-445 (2008).
- Condés, S., Sterba, H. Comparing an individual tree growth model for Pinus halepensis Mill. in the Spanish region of Murcia with yield tables gained from the same area. European Journal of Forest Research. 127 (3), 253-261 (2008).
- Pokharel, B., Dech, J. P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry. 85 (2), 255-270 (2012).
- Wykoff, W. R. A basal area increment model for individual conifers in the northern Rocky Mountains. Forest Science. 36 (4), 1077-1104 (1990).
- Stage, A. R. Notes: An Expression for the Effect of Aspect, Slope, and Habitat Type on Tree Growth. Forest Science. 22 (4), 457-460 (1976).
- Gregorie, T. G. Generalized Error Structure for Forestry Yield Models. Forest Science. 33 (2), 423-444 (1987).
- Zhao, L., Li, C., Tang, S. Individual-tree diameter growth model for fir plantations based on multi-level linear mixed effects models across southeast China. Journal of Forest Research. 18 (4), 305-315 (2013).
- Hall, D. B., Bailey, R. L. Modeling and Prediction of Forest Growth Variables Based on Multilevel Nonlinear Mixed Models. Forest Science. 47 (3), 311-321 (2001).
- Yang, Y., Huang, S., Meng, S. X., Trincado, G., Vanderschaaf, C. L. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands : Journal canadien de la recherche forestière. Revue Canadienne De Recherche Forestière. 39 (39), 2203-2214 (2009).
- Pinheiro, J. C., Bates, D. M. Mixed-effects models in S and S-Plus. Publications of the American Statistical Association. 96 (455), 1135-1136 (2000).
Access restricted. Please log in or start a trial to view this content.
Yeniden Basımlar ve İzinler
Bu JoVE makalesinin metnini veya resimlerini yeniden kullanma izni talebi
Izin talebiThis article has been published
Video Coming Soon
JoVE Hakkında
Telif Hakkı © 2020 MyJove Corporation. Tüm hakları saklıdır