通过开源数字图像相关 测量 肌腱中的局部组织应变

摘要

本文介绍了一种用于测量肌腱外植体内局部二维组织菌株的开源数字图像相关算法。该技术的准确性已使用多种技术进行了验证，并且可供公众使用。

摘要

了解肌腱细胞原 位 经历的菌株以及这些菌株如何影响组织重塑具有相当大的科学兴趣。基于这种兴趣，已经开发了几种分析技术来测量加载过程中肌腱外植体内的局部组织菌株。然而，在一些情况下，这些技术的准确性和灵敏度尚未被报道，并且没有一种算法是公开可用的。这使得更广泛地测量肌腱外植体中的局部组织菌株变得困难。因此，本文的目的是创建一个经过验证的分析工具，用于测量肌腱外植体中的局部组织菌株，该工具易于获得且易于使用。具体而言，一种公开可用的增强拉格朗日数字图像相关（ALDIC）算法通过跟踪单轴张力下小鼠跟腱内细胞核的位移来测量2D菌株。此外，通过分析数字转换的图像，以及将应变与独立技术确定的值（即光漂白线）进行比较，验证了计算菌株的准确性。最后，将一种技术纳入算法中，利用计算出的位移场重建参考图像，可用于在没有已知应变值或二次测量技术的情况下评估算法的精度。该算法能够测量高达 0.1 的应变，精度为 0.00015。将重建的参考图像与实际参考图像进行比较的技术成功地识别了具有错误数据的样本，并表明在具有良好数据的样本中，大约85%的位移场是准确的。最后，在小鼠跟腱中测量的菌株与先前的文献一致。因此，该算法是准确测量肌腱局部组织应变的非常有用且适应性强的工具。

引言

肌腱是机械敏感组织，响应^{机械负荷而}适应和退化1，²，^3，4。由于机械刺激在肌腱细胞生物学中的作用，人们对了解肌腱细胞在加载过程中在天然组织环境中经历的菌株非常感兴趣。已经开发了几种实验和分析技术来测量肌腱中的局部组织菌株。其中包括使用斑点图案或光漂白线（PBL^）对表面应变进行2D/3D数字图像相关（DIC）分析5，⁶，^7，8，^{测量组织内}单个细胞核的质心到质心距离的变化9，^10，以及最近的全场3D DIC方法^，该方法考虑了面外运动和3D变形¹¹.然而，这些技术的准确性和灵敏度仅在少数情况下被报道，并且这些技术都没有公开，这使得这些技术的广泛采用和利用变得困难。

这项工作的目的是创建一个经过验证的分析工具，用于测量肌腱外植体中的局部组织菌株，该工具易于获得且易于使用。所选择的方法基于由Yang和Bhattacharya¹²开发的用MATLAB编写的公开可用的增强拉格朗日数字图像相关（ALDIC）算法。该算法适用于分析肌腱样品，并通过将其应用于数字转换图像并将实际肌腱样品中测量的应变与从光漂白线获得的结果进行比较来验证。此外，算法中还实现了附加功能，即使在没有已知应变值或二次测量技术的情况下，也能确认计算出的位移场的准确性。因此，该算法是准确测量肌腱局部二维组织应变的非常有用且适应性强的工具。

研究方案

这项研究得到了宾夕法尼亚州立大学机构动物护理和使用委员会的批准。

1. 组织准备

1. 对于该协议，从2-4个月大的雄性C57BL / 6小鼠中收获跟腱。
   注意：也可以使用来自小鼠或其他小动物的不同肌腱或韧带。
   1. 在跟腱表面的皮肤上切开一个切口，露出足底肌腱和周围的结缔组织。然后，使用手术刀片将其取出。
   2. 将暴露的比目鱼肌和腓肠肌与后肢分开，并用手术刀片小心地将它们从跟腱上刮下来
   3. 用旋转工具上的切割轮附件将跟骨与脚的其余部分分开。
2. 在室温下，在旋转混合器上将组织染色在 1.5 mL 的 5-（4，6-二氯三嗪基）氨基荧光素 （DTAF） 和 0.1 M 碳酸氢钠缓冲液中的 5 μg/mL 溶液中 20 分钟。该溶液对组织中的蛋白质（例如细胞外基质）进行染色。
   注意：在这 20 分钟内，应完成步骤 1.3。
3. 在磷酸盐缓冲盐水 （PBS） 中制备 1：1，000 的 DRAQ5 溶液以染色细胞核。使用涡旋混合器使溶液均质化。
4. 在步骤1.2中的20分钟孵育期后，将组织从DTAF溶液转移到DRAQ5溶液中，并在室温下在黑暗空间中孵育10分钟。

2. 肌腱负荷和图像采集

注意：此协议需要一个可以安装在共聚焦显微镜顶部的拉伸装置。在这项研究中，使用了Peterson和Szczesny¹³ 描述的微拉伸装置。

1. 将肌腱放入拉伸加载装置的夹具中。在将夹具安装到装载装置中之前，请使用数字卡尺测量跟骨附件与另一侧夹具之间的距离。这个距离是肌腱规格的长度。
   1. 或者，在插入肌腱之前将夹具安装到加载装置中，并推动接触以定义零排量电机位置。插入肌腱后电机的位移可以提供可能更准确的夹具到夹具规格长度。
2. 将夹具安装到装有PBS的装载装置中，以保持组织水合作用。将肌腱尽可能与显微镜图像的x轴或y轴对齐，以便算法的x应变和y应变输出与肌腱轴相对应。
   注意：在本研究中，肌腱与x轴对齐。如果无法将肌腱与图像轴完美对齐，则可以使用标准应变变换方程¹⁴ 变换算法的 x 应变和 y 应变输出以与肌腱的纵向/垂直轴对齐。
3. 用 1 g 的张力预加载肌腱，如果需要，应用循环加载以预处理样品。在该协议中，没有使用预处理，因为研究目的是验证测量的局部组织菌株而不是测量组织材料特性。如果有兴趣测量宏观尺度的材料属性（取决于加载历史），则建议进行预处理。预处理和恢复后，重新施加 1 g 预载荷。
4. 如果需要，在组织的中心区域光漂白一组间隔80μm的四条线（参见Peterson和Szczesny¹³ 以获取更多详细信息）。
   注意：光漂白线用于验证ALDIC算法的测量值，对于执行ALDIC本身不是必需的。可以调整线条的数量和间距，并且应选择线条的位置，以避免样本中出现任何会降低线条清晰度的伪影。
5. 在夹具附近的组织的左右两端重复光漂白程序。
6. 使用共聚焦显微镜，在 1 g 预载荷下获取 DTAF 和 DRAQ5 荧光的体积图像（x，y：1.25 μm/像素，z：2.5 μm/像素）。
7. 以 0.5%/s 至 2% 的应变进行应变斜坡。请注意，可以调整应变率和增量应变大小。
8. 让组织压力放松10分钟。
   注意：应力松弛的持续时间应选择，以使样品在图像采集过程中处于近似准静态载荷下。为了确定应力松弛持续时间是否可接受，请确定应力松弛最后一分钟期间力-时间曲线的斜率（补充图1），并将该斜率乘以总成像持续时间。在这项研究中，施加在最大应变增量下的力从未变化超过5%。
9. 在变形后拍摄组织的另一张体积图像。
10. 重复步骤2.7-2.9，直到达到所需的最终应变。本文选择的最终应变值为12%。

3. 图像处理

1. 使用 ImageJ 或斐济为 DRAQ5（核）通道的每个体积图像创建最大 z 投影。这将作为ALDIC的2D斑点图像。
2. 将最大强度 z 投影另存为.tiff文件，并根据以下命名约定对其进行命名。
   1. 使用数字作为映像名称的第一个字符。
   2. 使数字与应变分析期间考虑图像的顺序相对应。例如，第一个图像应以 1 开头，第二个图像应以 2 开头。可以选择不同的数字，但它们必须按顺序增加。命名约定示例如下：“0_Experiment1_MaxZProjection”。
3. 将所有重命名的最大强度 z 投影保存到一个文件夹中。

4、光漂白线分析代码安装与应用

注意：仅当需要使用光漂白线确认ALDIC算法的准确性时，才需要执行这些步骤。该代码将局部组织应变计算为光漂白线集中每条光漂白线之间距离的平均归一化变化。在这项研究中，然后将所有光漂白线组（即中心和左/右端）的平均局部值平均，以确定每个样品的单个平均局部组织应变值。然后使用该值来估计ALDIC算法的准确性。

1. 从 GitHub 下载 “PBL Code” 文件夹 （https://github.com/Szczesnytendon/TendonStrainCalc），并将所有内容移动到 MATLAB 中的工作目录。
2. 打开“Micro_Mech_Template.m”MATLAB 脚本。
   1. 按 “运行”键，然后选择一个包含体积图像的图像文件。体积图像可以是以下任何文件类型：.lsm、.tiff、.nd2。
   2. 该软件将自动加载文件夹中的所有图像，并显示参考体积图像的投影图像。出现提示时， 单击鼠标左键 以创建跟踪样本左端和右端的多点线。 右键单击 以终止行。处理完输入后，如果边缘正确，请按 Ok 接受结果。
   3. 出现提示时，在样品上绘制一条随机对角线作为参考线。
   4. 输入创建的光漂白线数，并使用多点线跟踪光漂白线。
   5. 如果结果可以接受，请接受它。如果结果错误，请进行调整并重新处理。
3. 对所有图像重复步骤 4.2，并将跟踪线的所有图像移动到单个文件夹中。
4. 打开脚本“Micro_Mech_Strain.m”。
   1. 按 “运行” 执行代码，然后选择一个跟踪光漂白线的已保存图像。
   2. 按 “确定”（Ok） 选择图像后，确认所选随附图像正确无误。

5. 创建数字转换图像

注意：仅当需要使用数字转换图像确认ALDIC算法的准确性时，才需要执行这些步骤。这些图像通过人工变换参考图像来模拟已知大小的均匀二维应变场。

1. 从 GitHub 下载代码“Digital_strain.m”（https://github.com/Szczesnytendon/TendonStrainCalc）。
2. 打开并运行代码。
3. 出现提示时，插入最大施加应变、应用应变增量和泊松比的所需值。按 确定。
   注：本实验最大施加应变为0.1（10%），施加应变增量为0.02（2%），泊松比为1，与肌腱拉伸试验^15，16的实验数据一致。该代码使用嵌入式 MATLAB 函数扭曲和输入值（例如，应变增量、泊松比）来创建经过数字转换的图像。
4. 出现提示时，选择未变形的参考图像。
5. 对于每个应变增量，将显示参考图像和转换后的图像的叠加。转换后的图像将保存到标题为“DigitallyTransformedX%Strain”的目录中，其中X是应变增量。

6. 应变计算与验证代码安装与应用

1. 从 GitHub 下载“应变计算和验证代码”文件夹 （https://github.com/Szczesnytendon/TendonStrainCalc），并将所有内容移动到 MATLAB 工作目录
2. 根据 Yang 和 Bhattacharya¹² 安装一个 mex C/C++ 编译器。这些步骤总结如下。
   1. 检查 MATLAB 以查看是否已安装 mex C/C++ 编译器，方法是在 MATLAB 命令窗口中键入“mex -setup”并按 Enter 键。
   2. 如果出现错误，指示编译器不受支持或不存在，请继续执行步骤 6.3 和步骤 6.4。
   3. 如果不存在错误，请继续执行步骤 6.5
3. 要下载 mex C/C++ 编译器，请转到“https：/tdm-gcc.tdragon.net/”，然后选择 TDM-gcc 编译器。
4. 将下载的编译器安装到已知位置。
5. 返回 MATLAB 命令窗口， 键入：“setenv（”MW_MINGW64_LOC“，”[在此处键入安装路径]“）”。 例如，这可以是“setenv（”MW_MINGW64_LOC“，”C：\TDM-GCC-64“）”。如果此命令成功执行，则 mex 编译器已正确安装。
6. 输入“main_aldic.m”函数脚本，并更改第 22 行以匹配在步骤 6.5 中执行的命令。
7. 打开脚本“Strain_calc_and_validate.m”。
8. 按 运行 开始影像分析。
9. 出现提示时，根据需要更改 ALDIC 参数的值。
   注意：窗口大小应为子集大小的 0.25 到 1 倍。有关参数选择的详细信息，请参阅在线用户手册：（https://www.researchgate.net/publication/344796296_Augmented_Lagrangian_Digital
   _Image_Correlation_AL-DIC_Code_Manual）。
   1. 本研究使用了以下值：
      子集大小（像素）：20
      窗口大小（像素）：10
      求解ALDIC的方法：有限差分（1）
      未使用并行计算 （1）
      初始猜测的计算方法：基于图像金字塔的多网格搜索 （0）
10. 出现提示时，选中“是”复选框，让算法自动保存所需变量集合（例如 X 应变、y 应变、剪切应变、坏区域等）的平均值、标准偏差和 2D 图。选择应保存的变量，然后按 Ok。
11. 出现提示时，根据需要更改参数。
    1. 本实验中使用以下值：
       计算应变的周围点（numP）：12
       坏区识别的相关系数（corr_threshold）：0.5
       坏区域分析的子区域大小（像素）（子大小）：32
12. 出现提示时，选择包含重命名的最大强度 z 投影的文件夹。请注意，软件会自动执行增量ALDIC以确定变形图像的应变场。也就是说，每个变形图像都充当下一个变形图像的新“参考”图像。与执行累积ALDIC相比，这提高了结果的准确性（补充图2），其中每个变形图像与原始（0%应变）参考图像进行比较。要执行累积分析，请加载图像，但仅选择原始参考图像和感兴趣的变形图像。
    注意：法向应变计算为 λ - 1，其中 λ 是组织拉伸。组织拉伸的计算依据为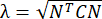 ，其中 N = [1 0]T 或 [0 1]T 分别表示 x 方向和 y 方向，C = F ^T F，其中 F 是使用 ALDIC 算法输出的每个数据点周围的“numP”点计算的变形梯度。剪切应变的计算公式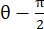为 ，其中 。
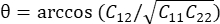13. 出现提示时，左键单击以创建一个四点面，以定义用于测量应变的感兴趣区域。从左上角的点开始，然后按顺时针方向分配后续点。
    注意：保存在 MATLAB 工作区中的变量“存储”包含平均 X 应变、X 应变标准偏差、平均 y 应变、y 应变标准偏差、平均剪切应变、剪切应变标准偏差和坏区域百分比的所有值。坏区域根据在步骤6.13中选择的感兴趣区域内的相关系数分析进行定义。文件夹“核跟踪结果”（可以通过调整行555和556重命名）存储步骤6.10中指定的所有图。此文件夹还包含一个名为“Results”的电子表格文件，该文件存储步骤 6.10 中指定的所有均值和标准差。

结果

在分析实际组织样品中的应变场之前，首先使用小鼠跟腱内细胞核的数字应变/转换图像验证ALDIC方案。具体来说，将图像转换为在 2%、4%、6%、8% 和 10% 应变的 x 方向上以数字方式产生均匀应变，模拟泊松比为 1^15，16。然后通过将计算出的平均应变值与已知的数字应变值进行比较来评估ALDIC算法的准确性。此外，还评估了应变值的标准偏差以确定应变场的...

讨论

本文的目的是提供一种开源的、经过验证的方法来测量拉伸载荷下肌腱中的二维应变场。该软件的基础是基于公开可用的ALDIC算法¹²。该算法被嵌入到更大的 MATLAB 代码中，并增加了增量（相对于累积）应变分析的功能。然后将这种适应的算法应用于肌腱的拉伸测试，并通过两种不同的技术（即，数字转换图像和使用光漂白线的应变测量）评估其准确性。此外，还增加了一种功能?...

材料

Name	Company	Catalog Number	Comments
5-DTAF (5-(4,6-Dichlorotriazinyl) Aminofluorescein), single isomer	ThermoFisher	D16
Calipers	Mitutoyo	500-196-30
Confocal Microscope	Nikon	A1R HD
Corning LSE Vortex Mixer	Coning	6775
DRAQ5 Fluorescent Probe Solution (5 mM)	ThermoFisher	62554
MATLAB	MathWorks	R2022b
Tensile Loading Device	N/A	N/A	Tensile loading device described in Peterson et al, 2020. (ref 13)
Tube Revolver Rotator	ThermoFisher	88881001